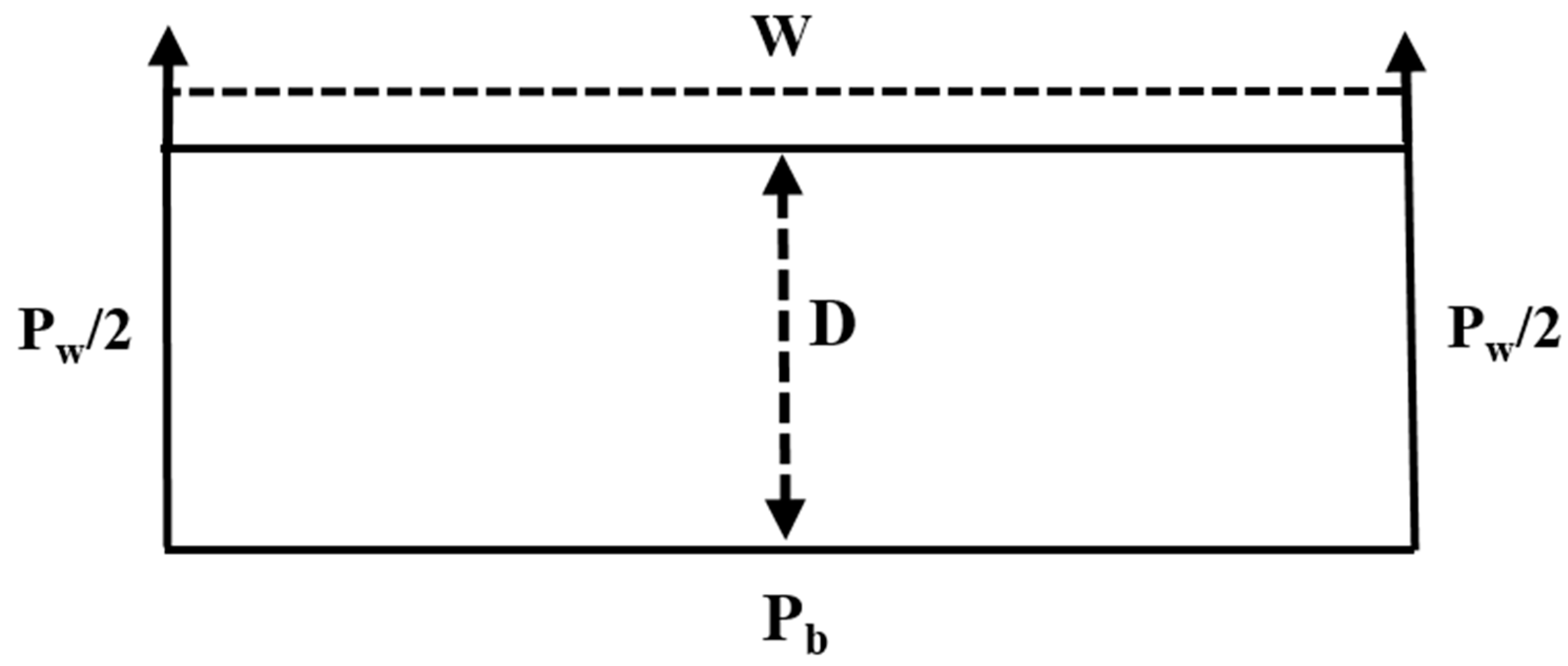
4.1. Equilibrium Hydraulic Geometry in the State of
Under the assumption that the sediment on a riverbed has reached a critical incipient motion state, i.e.,
, the critical hydraulic geometric expression can be derived by concurrently solving Formulas (13) and (26):
In relationships (27), the correlation coefficients
,
, and
are determined by the following relationships:
Building upon the framework established by Formula (28), we introduced specified parameters, setting variable
n at 0.03,
d at 0.3 mm,
at 2650 kg/m
3, and
at 1000 kg/m
3. Subsequently, we varied the coefficient
across values of 0.1, 0.5, 1, and 2 to represent the changing relative roughness of riverbanks to a riverbed. Analysis of the results presented in
Table 2 demonstrated that as
transitioned from lower to higher values, coefficients
a,
b, and
c exhibited distinct variations within a narrow range. In more precise terms, with
values of 0.1, 0.5, 1, and 2,
a assumed the respective values of 4.4642, 3.9633, 3.7919, and 3.6405, while
b took on values of 1.4266, 1.6015, 1.8960, and 2.2524. The coefficient
c registered values of 2.6736 × 10⁻⁵, 2.6267 × 10⁻⁵, 1.8698 × 10⁻⁵, and 1.3268 × 10⁻⁵. Notably, as
increased,
a gradually decreased, while
b steadily increased. This implies that in scenarios where a river operates under a lower threshold state, a smaller
value leads to adopting a narrower and deeper cross-sectional configuration for sediment transport.
4.2. Averaged Equilibrium Hydraulic Geometry at the State of
Formulas (23) and (24) reveal that the width–depth ratio variable, as dictated by Formula (20), can span any positive range of values. A series of mathematical transformations must be applied to derive the geometric relationship for average river hydraulic characteristics. Consequently, Equations (11)–(13), (22), and (23), and the condition
, were simultaneously solved to eliminate the variable energy gradient
. Through this process, the relationships among the optimal width–depth ratio, variable flow discharge, sediment discharge, sediment size, the relative roughness of riverbanks to a riverbed, and roughness were ascertained as the following:
Consequently, Equation (29) was combined with Equations (12), (13), (22), and (23) to express the equilibrium channel slope
, width
, and depth
as
Theoretically, the optimal width–depth ratio can encompass any positive integer greater than
, implying that the range of the optimal width–depth ratio extends from
to positive infinity. However, considering the practical constraints of river evolution, it is highly unlikely for a river’s width–depth ratio to exceed 1000. Therefore, for mathematical analysis, this study posits an upper limit of the optimal width–depth ratio at 1000.
Table 2 illustrates that the relative roughness of riverbanks to a riverbed (represented by
) significantly influences the critical optimal width–depth ratio (
). When
is set to 0.1, the range of possible values for
spans from
to 1000. Calculations revealed that the variation range of
extended from 1 to 195.7 within this context. Similarly, when
was set to 0.5, 1, and 2, with
varying within the same range, the corresponding variation range of
could be calculated. The results are presented in
Table 3.
The terms involving in Formulas (29)–(32) are notably intricate. Mathematical transformations become imperative to streamline the computational process. For instance, when the relative roughness of riverbanks to a riverbed equals 1, a variation range for the optimal width–depth ratio is established, ranging from 4 to 1000, with increments of 1.
An exponential fitting analysis of the terms dependent on
within Formulas (29)–(32) was performed using Excel. Consequently, the terms containing
in these formulas could be approximated by the following expressions:
Combining the terms of
contained in Equations (33)–(36) into Equations (29)–(32), could yield the following average hydraulic geometric relationship:
The same methodology was employed to derive the average hydraulic geometric relationships for
being the values of 0.5, 1, and 2, with the outcomes presented in
Table 4. A comparative analysis of the hydraulic geometric relationships for these varying relative roughness values indicated that roughness
, sediment size
, flow discharge
, and sediment discharge
all exerted a substantial influence on the final equilibrium river width, depth, and specific gradient. To assess the relative impact of
on these four variables, the exponential variation ranges of these variables in the four sets of average hydraulic geometric relationships were statistically compiled. The findings are the following:
In Equation (38), coefficients , , and are correlation coefficients, respectively.
Equation (38) revealed that as the relative roughness values of riverbanks to a riverbed changed, specifically at 0.1, 0.5, 1, and 2, the coefficients of the four main variables—sediment discharge, flow discharge, roughness, and sediment size—within the formula exhibited minimal fluctuations. Consequently, these variable coefficients in Equation (38) could be approximated as constants in analyzing specific river geometries. When the values of
were set to 0.1, 0.5, 1, and 2, the variation trends of the correlation coefficients
,
, and
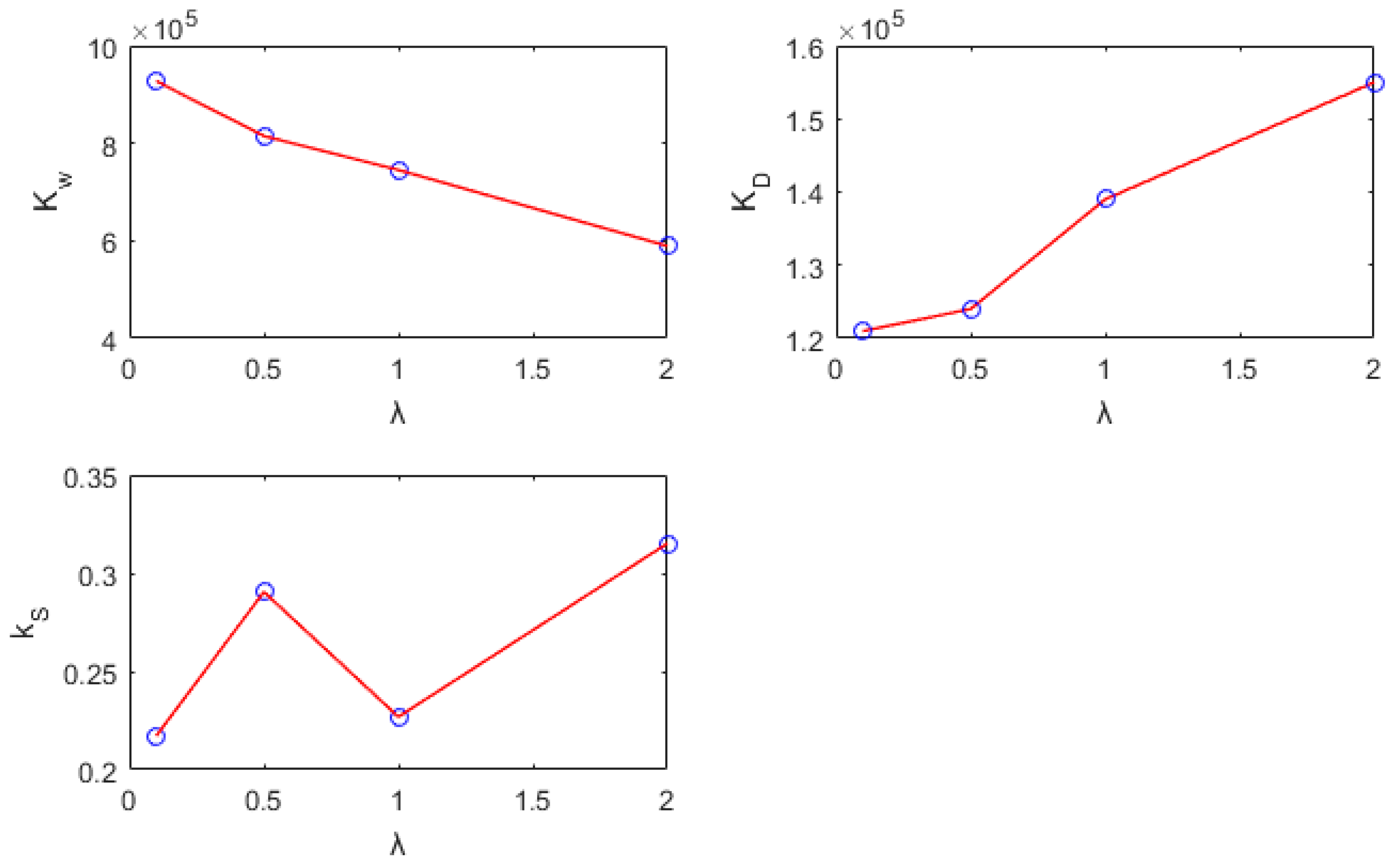
in Equation (38) are depicted in
Figure 3. It is evident that with an increase in the relative roughness of the riverbank to the riverbed,
experienced a gradual decrease, with values of 9.2753 × 10
5, 8.1486 × 10
5, 7.4526 × 10
5, and 5.8931 × 10
5 representing a decrease of up to 36.64%. Meanwhile,
gradually increased, with values of 0.0121 × 10
7, 0.0124 × 10
7, 0.0139 × 10
5, and 0.0155 × 10
7, respectively. However,
did not demonstrate a specific trend, with values ranging from 0.2172 to 0.2905, 0.2269, and 0.3152, respectively. This suggests that the coefficient
remains relatively stable or experiences minimal change and can thus be considered a constant. In summary, as the relative roughness of riverbanks to a riverbed increases, the river tends to adjust itself by adopting a wider and shallower cross-section for sediment transport and vice versa. However, the relative roughness of riverbanks to a riverbed has little influence on
, indicating a weak correlation between the two.
To facilitate a comparison with previous studies, we considered the energy gradient as an independent variable. By combining Formula (37) with Formula (1), we could derive hydraulic geometric relationships that related river width, river depth, flow velocity, roughness, flow, and energy gradient. These relationships are expressed as the following:
Similarly, the average hydraulic geometric relationships were derived for cases in which the relative roughness of riverbanks to a riverbed was set to 0.5, 1, and 2. These results are presented in
Table 5. Upon comparing and analyzing the hydraulic geometric relationships across these different values of relative roughness, as shown in
Table 4, it became evident that roughness, sediment size, flow discharge, and energy gradient all exerted a significant influence on the final equilibrium river width, depth, and velocity. To assess the degree of influence of
on these four variables, we statistically summarized the exponential variation ranges of these variables across the four sets of average hydraulic geometric relationships. The results are the following:
In Equation (40), , , and are correlation coefficients, respectively.
As indicated in Formula (40), when varying the values of the relative roughness of riverbanks to a riverbed at 0.1, 0.5, 1, and 2, the coefficients associated with the four key variables—namely, energy gradient, flow discharge, roughness, and sediment size in Formula (40)—exhibited only minimal fluctuations. Consequently, within the context of specific river geometry analysis, these coefficients within Formula (38) could be reasonably approximated as constants.
When we considered different values of
, specifically 0.1, 0.5, 1, and 2, and examined the trends of the correlation coefficients
,
, and
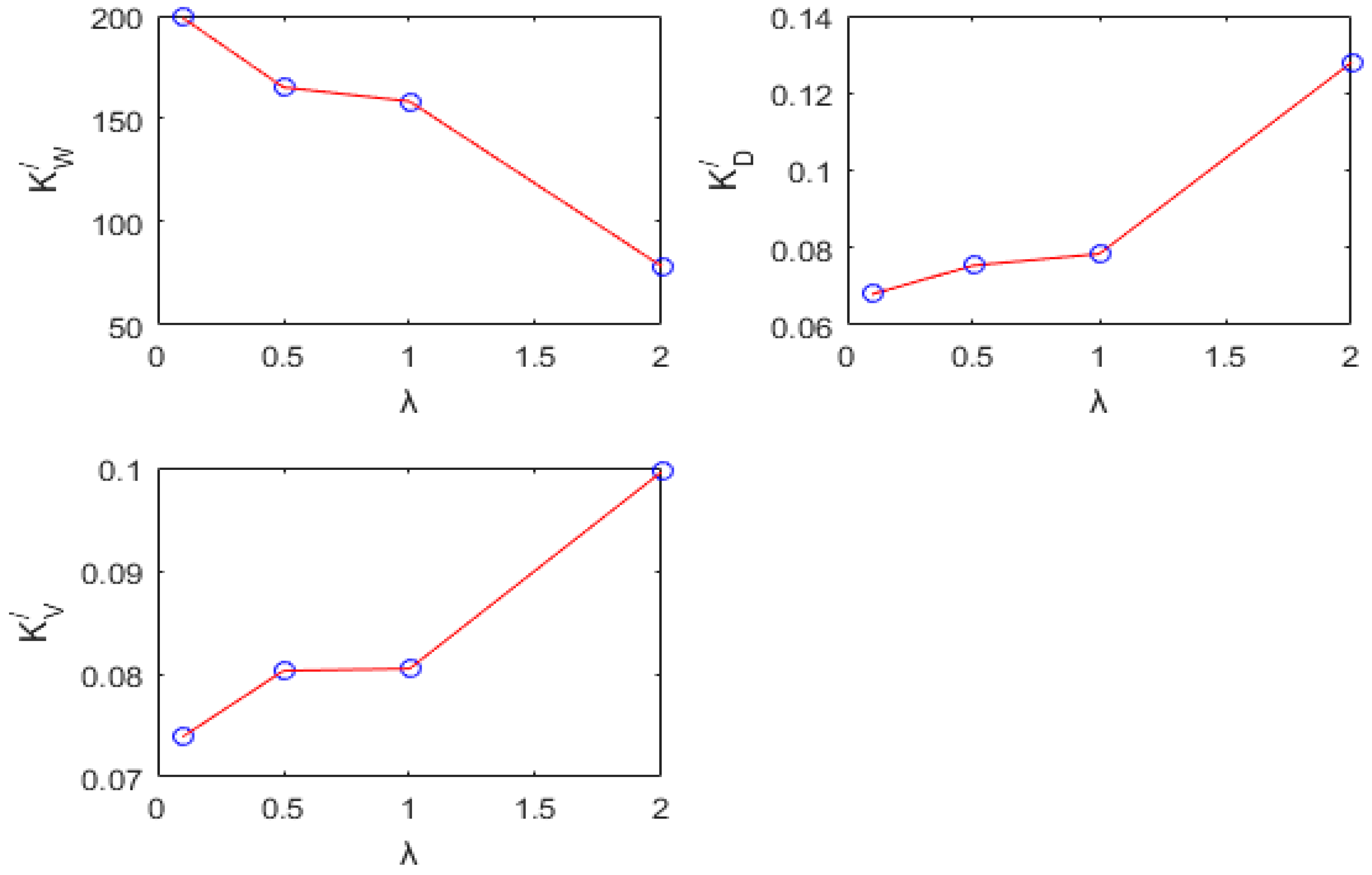
within Formula (40), a discernible pattern emerged (see
Figure 4). As the relative roughness of riverbanks to a riverbed increased, coefficient
exhibited a gradual decrease, with values of 199.0, 165.2629, 158.4510, and 78.4891, respectively. In contrast, coefficient
displayed a progressive increase, with values of 0.068, 0.0754, 0.0784, and 0.1279. Meanwhile, coefficient
initially showed a slow increase followed by a more rapid rise, with values of 0.0739, 0.0803, 0.0805, and 0.0996, respectively. In broad terms, as the relative roughness of riverbanks to a riverbed diminishes, the river tends to adopt a wider and shallower cross-section for sediment transport and vice versa.