Wastewater Treatment System Optimization for Sustainable Operation of the SHARON–Anammox Process under Varying Carbon/Nitrogen Loadings
Abstract
1. Introduction
2. Materials and Methods
2.1. Problem Statement
- The data include the influent flowrate and the flowrate of the components, such as nitrate, ammonia, and oxygen, as well as the sludge concentration, among others in form of model input data such as nitrite, C/N ratio, solids, particulate matter, etc. All of these are required for the model.
- The processes of a simple biological treatment are given in the WWTP model as one primary clarifier, five biological reactors, one secondary clarifier, one AD, one SHARON, and one Anammox reactor.
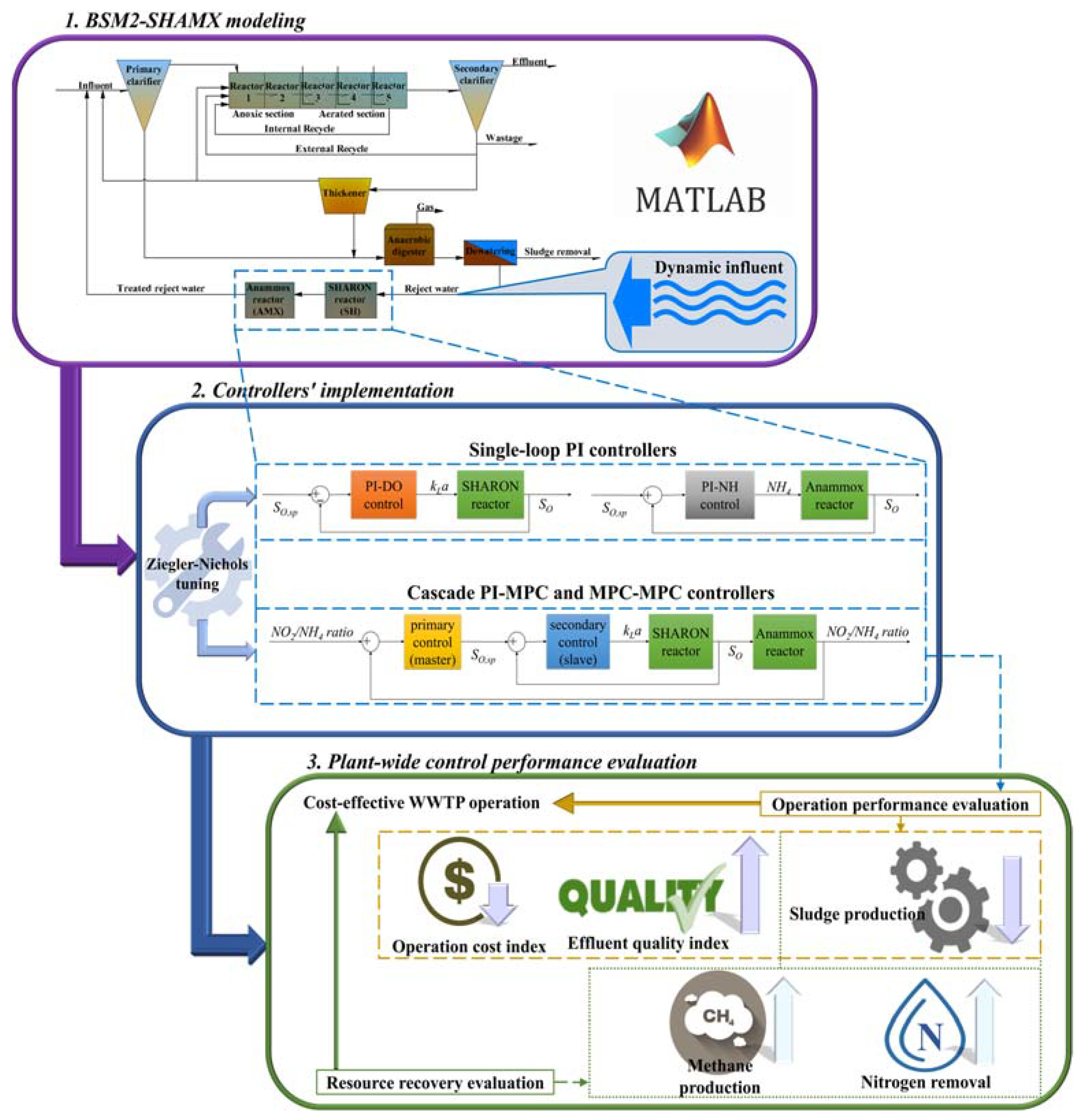
2.2. Proposed Method
2.3. BSM2-SHAMX Model
2.4. MPC State Space Model
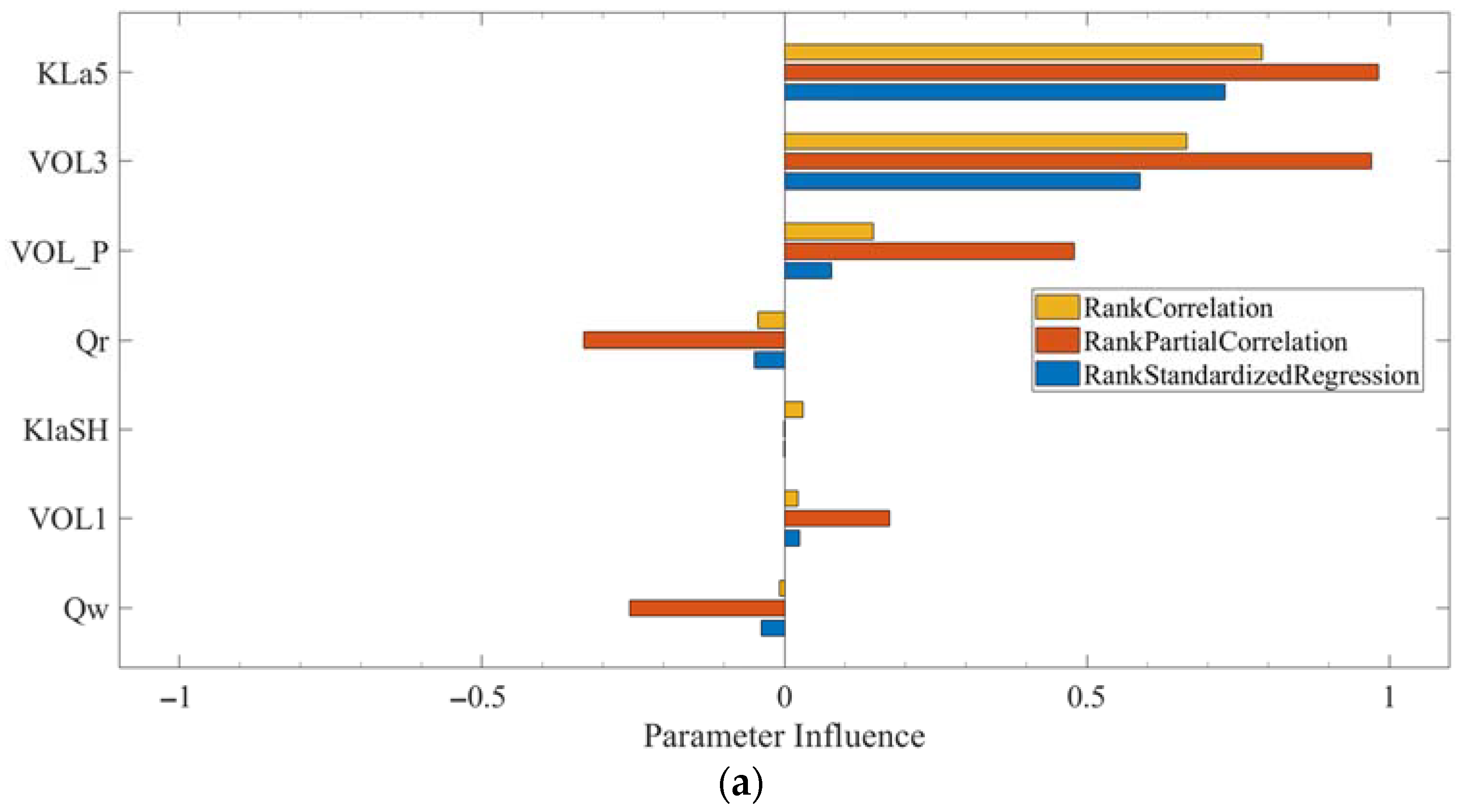
2.5. Sensitivity Analysis of BSM2-SHAMX
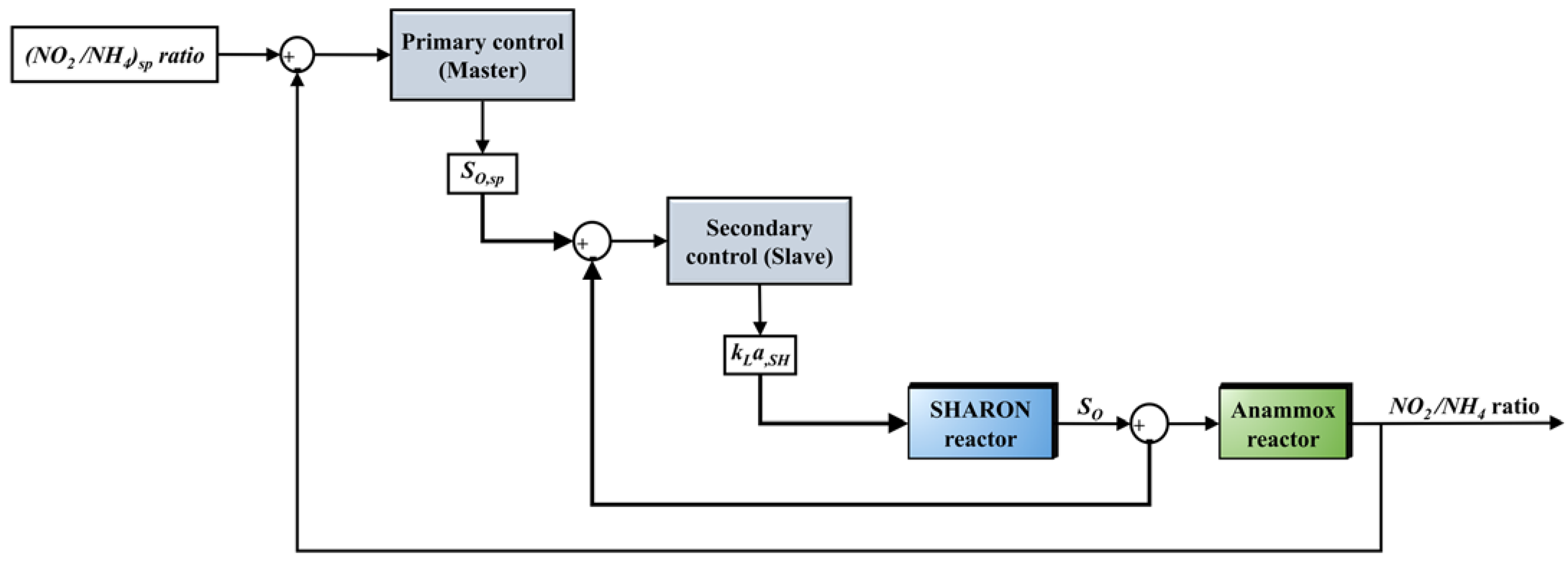
2.6. Control Strategy Modeling and Evaluation
2.6.1. Implementation of the Control Strategies
2.6.2. Control Performance Indices
2.6.3. Resource Recovery Evaluation
3. Results and Discussion
3.1. Sensitivity Analysis
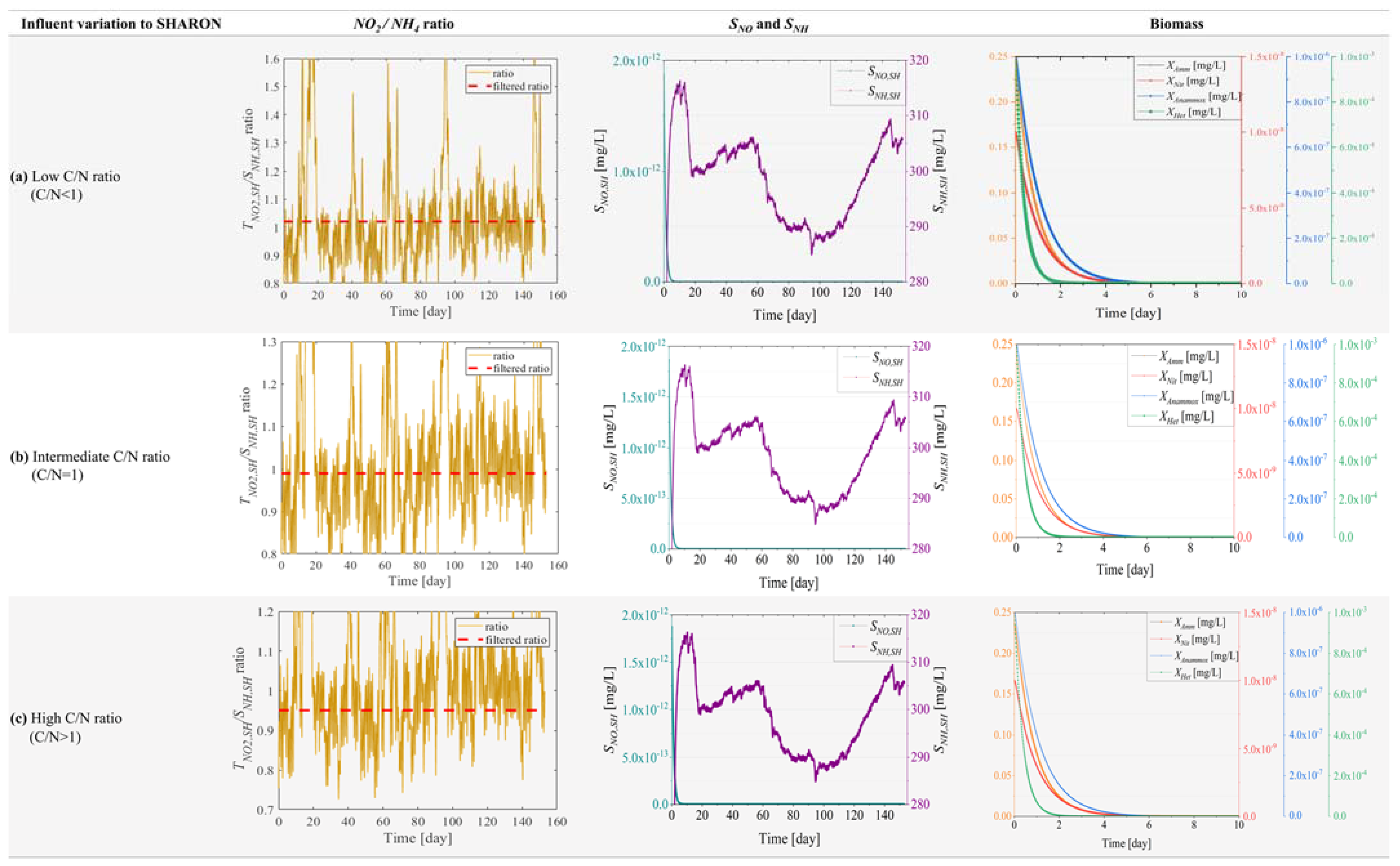
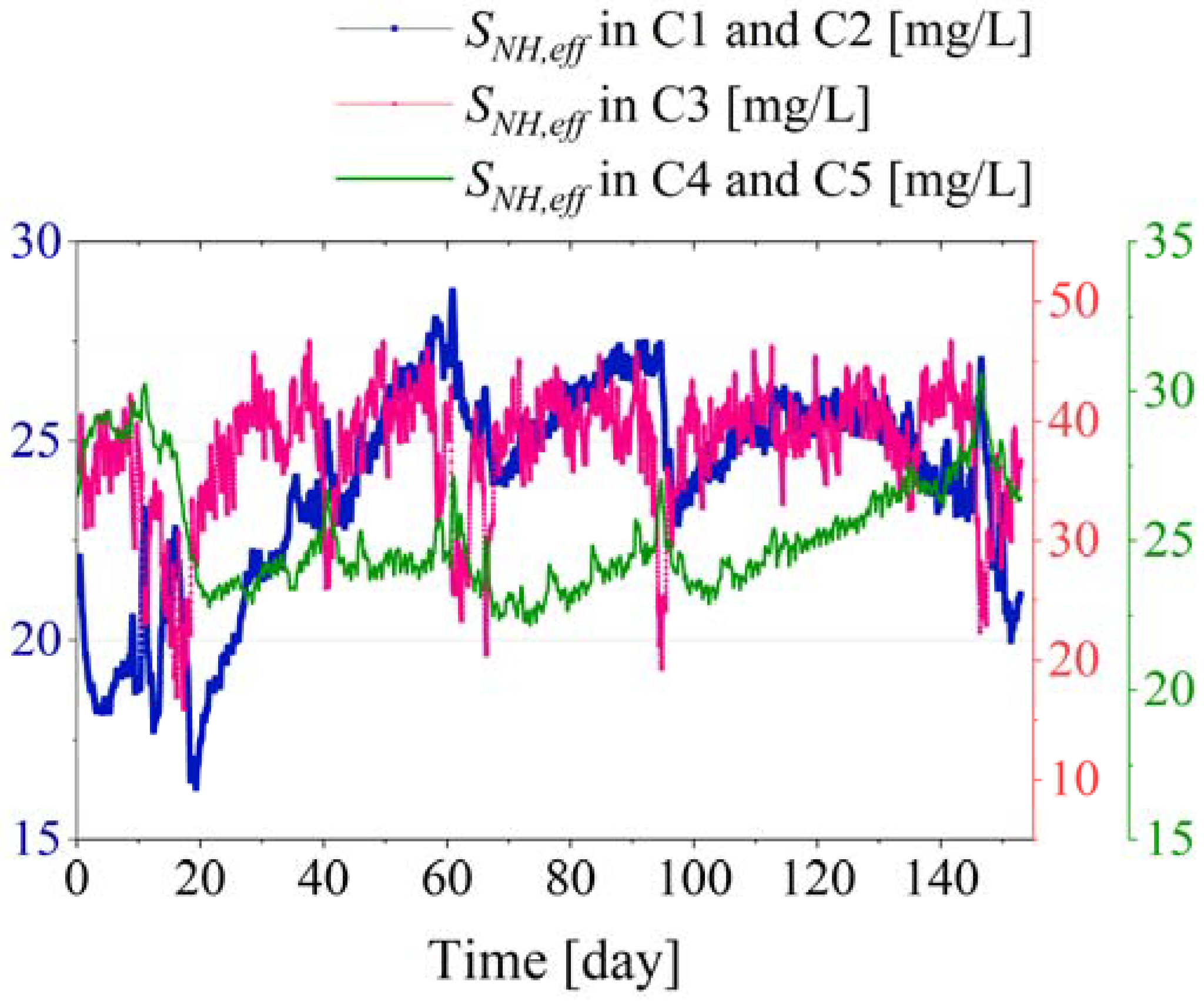
3.2. Control Performance
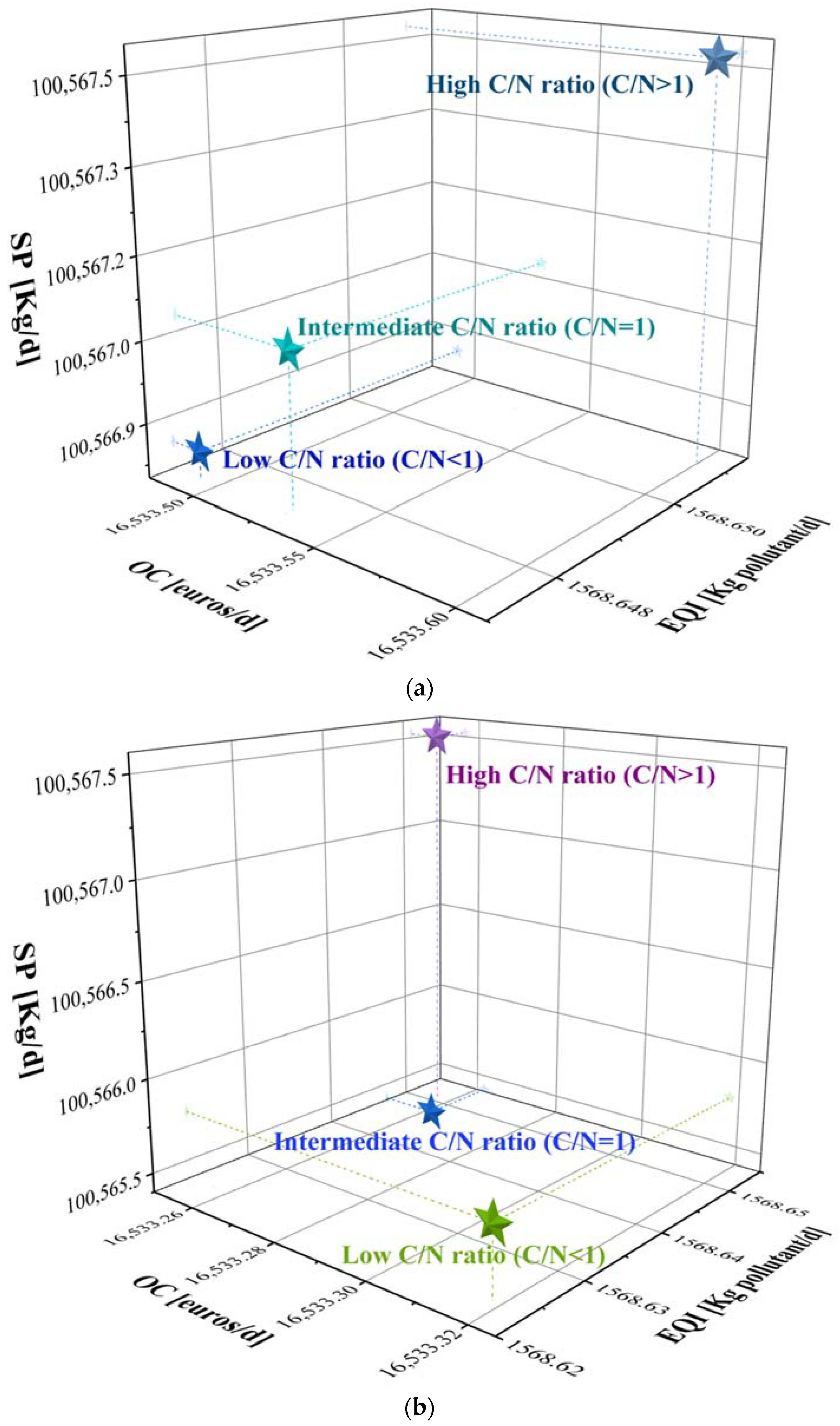
3.3. Resource Recovery Potential
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Langone, M. Simultaneous Partial Nitritation, Anammox and Denitrification (SNAD) Process for Treating Ammonium-Rich Wastewaters. Ph.D. Thesis, University of Trento, Trento, Italy, 2013. [Google Scholar]
- Safder, U.; Kim, J.; Pak, G.; Rhee, G.; You, K. Investigating Machine Learning Applications for Effective Real-Time Water Quality Parameter Monitoring in Full-Scale Wastewater Treatment Plants. Water 2022, 14, 3147. [Google Scholar] [CrossRef]
- Rahimi, S.; Modin, O.; Mijakovic, I. Technologies for Biological Removal and Recovery of Nitrogen from Wastewater. Biotechnol. Adv. 2020, 43, 107570. [Google Scholar] [CrossRef]
- Volcke, E.I.P. Modelling, Analysis and Control of Partial Nitritation in a SHARON Reactor. Ph.D. Thesis, Ghent University, Gent, Belgium, 2006. [Google Scholar]
- Leong, C.L.; How, S.W.; Rabuni, M.F.; Mohd Aris, A.; Khor, B.C.; Curtis, T.P.; Chua, A.S.M. Pilot Study of Oxic–Anoxic Process under Low Dissolved Oxygen for Nitrogen Removal from Low COD/N Tropical Wastewater. Water 2023, 15, 2070. [Google Scholar] [CrossRef]
- Wang, J.; Liu, S.; Zhang, Y.; Zhang, S.; Liu, J. Effect of Anammox Granular Sludge Type on the CANON Process with Immobilized Fillers Treating Domestic Wastewater. Water 2023, 15, 354. [Google Scholar] [CrossRef]
- Sri Shalini, S.; Joseph, K. Combined SHARON and ANAMMOX Processes for Ammoniacal Nitrogen Stabilisation in Landfill Bioreactors. Bioresour. Technol. 2018, 250, 723–732. [Google Scholar] [CrossRef]
- Sri Shalini, S.; Joseph, K. Nitrogen Management in Landfill Leachate: Application of SHARON, ANAMMOX and Combined SHARON–ANAMMOX Process. Waste Manag. 2012, 32, 2385–2400. [Google Scholar] [CrossRef]
- Peng, Y.; Zhu, G. Biological Nitrogen Removal with Nitrification and Denitrification via Nitrite Pathway. Appl. Microbiol. Biotechnol. 2006, 73, 15–26. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.; Okabe, S. Anammox-Based Technologies for Nitrogen Removal: Advances in Process Start-up and Remaining Issues. Chemosphere 2015, 141, 144–153. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, S.; Nawaz, T.; Beaudry, J. Nitrogen and Phosphorus Recovery from Wastewater. Curr. Pollut. Rep. 2015, 1, 155–166. [Google Scholar] [CrossRef]
- Gut, L.; Płaza, E.; Hultman, B. Assessment of a Two-Step Partial Nitritation/Anammox System with Implementation of Multivariate Data Analysis. Chemom. Intell. Lab. Syst. 2007, 86, 26–34. [Google Scholar] [CrossRef]
- Saxena, N.; Nawaz, A.; Lee, M. Comprehensive Review of Control and Operational Strategies for Partial Nitration/ANAMMOX System. Ind. Eng. Chem. Res. 2019, 58, 10635–10651. [Google Scholar] [CrossRef]
- Valverde-Pérez, B.; Mauricio-Iglesias, M.; Sin, G. Systematic Design of an Optimal Control System for the SHARON-Anammox Process. J. Process Control 2016, 39, 1–10. [Google Scholar] [CrossRef]
- Barbu, M.; Vilanova, R.; Meneses, M.; Santin, I. On the Evaluation of the Global Impact of Control Strategies Applied to Wastewater Treatment Plants. J. Clean. Prod. 2017, 149, 396–405. [Google Scholar] [CrossRef]
- Regmi, P.; Bunce, R.; Miller, M.W.; Park, H.; Chandran, K.; Wett, B.; Murthy, S.; Bott, C.B. Ammonia-Based Intermittent Aeration Control Optimized for Efficient Nitrogen Removal. Biotechnol. Bioeng. 2015, 112, 2060–2067. [Google Scholar] [CrossRef]
- Shannon, J.M. Partial Nitritation-Anammox Using PH-Controlled Aeration in Submerged Attached Growth Bioreactors; University of Iowa: Iowa City, IA, USA, 2014; Volume 1560696. [Google Scholar]
- Valverde-Pérez, B.; Mauricio-Iglesias, M.; Sin, G. Modelling and Control Design for SHARON/Anammox Reactor Sequence. In Proceedings of the 17th Nordic Process Control Workshop, Kgs Lyngby, Denmark, 25–27 January 2012. [Google Scholar]
- Durán, U.; Val Del Río, A.; Campos, J.L.; Mosquera-Corral, A.; Méndez, R. Enhanced Ammonia Removal at Room Temperature by PH Controlled Partial Nitrification and Subsequent Anaerobic Ammonium Oxidation. Environ. Technol. 2014, 35, 383–390. [Google Scholar] [CrossRef] [PubMed]
- Pang, J.; Yang, S.; He, L.; Chen, Y.; Ren, N. Intelligent Control/Operational Strategies in WWTPs through an Integrated Q-Learning Algorithm with ASM2d-Guided Reward. Water 2019, 11, 927. [Google Scholar] [CrossRef]
- Nikita, S.; Lee, M. Control of a Wastewater Treatment Plant Using Relay Auto-Tuning. Korean J. Chem. Eng. 2019, 36, 505–512. [Google Scholar] [CrossRef]
- Stare, A.; Hvala, N.; Vrečko, D. Modeling, Identification, and Validation of Models for Predictive Ammonia Control in a Wastewater Treatment Plant—A Case Study. ISA Trans. 2006, 45, 159–174. [Google Scholar] [CrossRef]
- Mauricio-Iglesias, M.; Katrine, A.; Gernaey, K.V.; Smets, B.F.; Sin, G. A Novel Control Strategy for Single-Stage Autotrophic Nitrogen Removal in SBR. Chem. Eng. J. 2015, 260, 64–73. [Google Scholar] [CrossRef]
- Fux, C.; Boehler, M.; Huber, P.; Brunner, I.; Siegrist, H. Biological Treatment of Ammonium-Rich Wastewater by Partial Nitritation and Subsequent Anaerobic Ammonium Oxidation (Anammox) in a Pilot Plant. J. Biotechnol. 2002, 99, 295–306. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, C.; Wang, X.; Xu, S.; Zhuang, X. Application of Internal Carbon Source from Sewage Sludge: A Vital Measure to Improve Nitrogen Removal Efficiency of Low c/n Wastewater. Water 2021, 13, 2338. [Google Scholar] [CrossRef]
- Chen, M.; Tang, Q.; Zou, J.; Lv, X.; Deng, Y.; Ma, X.; Ma, S. Sugarcane Bagasse as Carbon Source and Filler to Enhance the Treatment of Low C/N Wastewater by Aerobic Denitrification Flora. Water 2022, 14, 3355. [Google Scholar] [CrossRef]
- Jamilis, M.; Garelli, F.; De Battista, H.; Volcke, E.I.P. Stability and Control of a Partial Nitritation Reactor with Biomass Retention. Chem. Eng. Res. Des. 2016, 144, 318–333. [Google Scholar] [CrossRef]
- Alex, J.; Benedetti, L.; Copp, J.; Gernaey, K.V.; Jeppsson, U.; Nopens, I.; Pons, M.; Rieger, L.; Rosen, C.; Steyer, J.P.; et al. Benchmark Simulation Model No. 2 (BSM2) Report; IWA Task Group on Benchmarking of Control Strategies for WWTPs: London, UK, 2008. [Google Scholar]
- Henze, M.; Grady, C.; Gujer, W.; Marais, G.; Matsuo, T. Activated Sludge Model No. 1. IAWPRC Sci. Tech. Reports, 1. Water Sci. Technol. 1987, 29. [Google Scholar]
- Tang, X.; Sun, Y.; Zhou, G.; Miao, F. Coordinated Control of Multi-Type Energy Storage for Wind Power Fluctuation Suppression. Energies 2017, 10, 1212. [Google Scholar] [CrossRef]
- Weijers, S.R.; Preisig, H.A. Robustness Analysis of Model Predictive Control of Activated Sludge Plants. IFAC Proc. Vol. 2000, 33, 545–550. [Google Scholar] [CrossRef]
- Lund, N.S.V.; Falk, A.K.V.; Borup, M.; Madsen, H.; Steen Mikkelsen, P. Model Predictive Control of Urban Drainage Systems: A Review and Perspective towards Smart Real-Time Water Management. Crit. Rev. Environ. Sci. Technol. 2018, 48, 279–339. [Google Scholar] [CrossRef]
- Neumann, M.B. Comparison of Sensitivity Analysis Methods for Pollutant Degradation Modelling: A Case Study from Drinking Water Treatment. Sci. Total Environ. 2012, 433, 530–537. [Google Scholar] [CrossRef]
- Ruano, M.V.; Ribes, J.; De Pauw, D.J.W.; Sin, G. Parameter Subset Selection for the Dynamic Calibration of Activated Sludge Models (ASMs): Experience versus Systems Analysis. Water Sci. Technol. 2007, 56, 107–115. [Google Scholar] [CrossRef][Green Version]
- Vilela, P.; Liu, H.; Lee, S.; Hwangbo, S.; Nam, K.; Yoo, C. A Systematic Approach of Removal Mechanisms, Control and Optimization of Silver Nanoparticle in Wastewater Treatment Plants. Sci. Total Environ. 2018, 633, 989–998. [Google Scholar] [CrossRef]
- Jamilis, M.; Garelli, F.; De Battista, H.; Volcke, E.I.P. Combination of Cascade and Feed-Forward Constrained Control for Stable Partial Nitritation with Biomass Retention. J. Process Control 2020, 95, 55–66. [Google Scholar] [CrossRef]
- Vilela, P.; Safder, U.; Heo, S.K.; Nguyen, H.T.; Lim, J.Y.; Nam, K.J.; Oh, T.S.; Yoo, C.K. Dynamic Calibration of Process-Wide Partial-Nitritation Modeling with Airlift Granular for Nitrogen Removal in a Full-Scale Wastewater Treatment Plant. Chemosphere 2022, 305, 135411. [Google Scholar] [CrossRef] [PubMed]
- Sung, S.W.; Lee, J.; Lee, I.-B. Process Identification and PID Control; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Guerrero, J.; Guisasola, A.; Vilanova, R.; Baeza, J.A. Improving the Performance of a WWTP Control System by Model-Based Setpoint Optimisation. Environ. Model. Softw. 2011, 26, 492–497. [Google Scholar] [CrossRef]
- Ostace, G.S.; Baeza, J.A.; Guerrero, J.; Guisasola, A.; Cristea, V.M.; Agachi, P.Ş.; Lafuente, J. Development and Economic Assessment of Different WWTP Control Strategies for Optimal Simultaneous Removal of Carbon, Nitrogen and Phosphorus. Comput. Chem. Eng. 2013, 53, 164–177. [Google Scholar] [CrossRef]
- Ferreira Matafome, B. Techno-Economic Analysis and Benchmarking of Resource Recovery Technologies for Wastewater Treatment Plants; Instituto Superior Técnico: Lisbon, Portugal, 2016; pp. 1–11. [Google Scholar]
- Kehrein, P.; Van Loosdrecht, M.; Osseweijer, P.; Garfí, M.; Dewulf, J.; Posada, J. A Critical Review of Resource Recovery from Municipal Wastewater Treatment Plants-Market Supply Potentials, Technologies and Bottlenecks. Environ. Sci. Water Res. Technol. 2020, 6, 877–910. [Google Scholar] [CrossRef]
- Alex, J.; Beteau, J.F.; Copp, J.B.; Hellinga, C.; Jeppsson, U.; Marsili-Libelli, S.; Pons, M.N.; Spanjers, H.; Vanhooren, H. Benchmark for Evaluating Control Strategies in Wastewater Treatment Plants. In Proceedings of the 1999 European Control Conference (ECC), Karlsruhe, Germany, 31 August–3 September 1999; pp. 3746–3751. [Google Scholar]
- Alex, J.; Benedetti, L.; Copp, J.; Gernaey, K.V.; Jeppsson, U.; Nopens, I.; Pons, M.; Rieger, L.; Rosen, C.; Steyer, J.P.; et al. Benchmark simulation model No. 2 (BSM2) report: General protocol and exploratory case studies. Water Sci. Technol. 2007, 56, 67–78. [Google Scholar]
- Jeppsson, U.; Pons, M.N. The COST Benchmark Simulation Model-Current State and Future Perspective. Control Eng. Pract. 2004, 12, 299–304. [Google Scholar] [CrossRef]
- Iacopozzi, I.; Innocenti, V.; Marsili-Libelli, S.; Giusti, E. A Modified Activated Sludge Model No. 3 (ASM3) with Two-Step Nitrification-Denitrification. Environ. Model. Softw. 2007, 22, 847–861. [Google Scholar] [CrossRef]
- Henze, M.; Gujer, W.; Mino, T.; van Loosdrecht, M. Activated Sludge Models ASM1, ASM2, ASM2D, ASM3; IWA publishing: London, UK, 2000. [Google Scholar]
- Bozkurt, H.; Quaglia, A.; Gernaey, K.V.; Sin, G. Environmental Modelling & Software A Mathematical Programming Framework for Early Stage Design of Wastewater Treatment Plants. Environ. Model. Softw. 2015, 64, 164–176. [Google Scholar] [CrossRef]
- Ostace, G.S.; Cristea, V.M.; Agachi, P.Ş. Cost Reduction of the Wastewater Treatment Plant Operation by MPC Based on Modified ASM1 with Two-Step Nitrification/Denitrification Model. Comput. Chem. Eng. 2011, 35, 2469–2479. [Google Scholar] [CrossRef]
- Giusti, E.; Marsili-libelli, S.; Spagni, A. Environmental Modelling & Software Modelling Microbial Population Dynamics in Nitritation Processes. Environ. Model. Softw. 2011, 26, 938–949. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Runger, G.C.; Hubele, N.F. Engineering Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- COST European Cooperation of Scientific and Technical Research. The COST Simulation Benchmark: Description and Simulator Manual; COST: Brussels, Belgium, 1998. [Google Scholar]
- Kim, M.; Rao, A.S.; Yoo, C. Dual Optimization Strategy for N and P Removal in a Biological Wastewater Treatment Plant. Ind. Eng. Chem. Res. 2009, 48, 6363–6371. [Google Scholar] [CrossRef]
- Frey, H.C.; Patil, S.R. Identification and Review of Sensitivity Analysis Methods. Risk Anal. 2002, 22, 553–578. [Google Scholar] [CrossRef] [PubMed]
- Hamby, D.M. A Review of Techniques for Parameter Sensitivity. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef]
- Benesty, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Sin, G.; Gernaey, K.V.; Neumann, M.B.; van Loosdrecht, M.C.M.; Gujer, W. Global Sensitivity Analysis in Wastewater Treatment Plant Model Applications: Prioritizing Sources of Uncertainty. Water Res. 2011, 45, 639–651. [Google Scholar] [CrossRef] [PubMed]

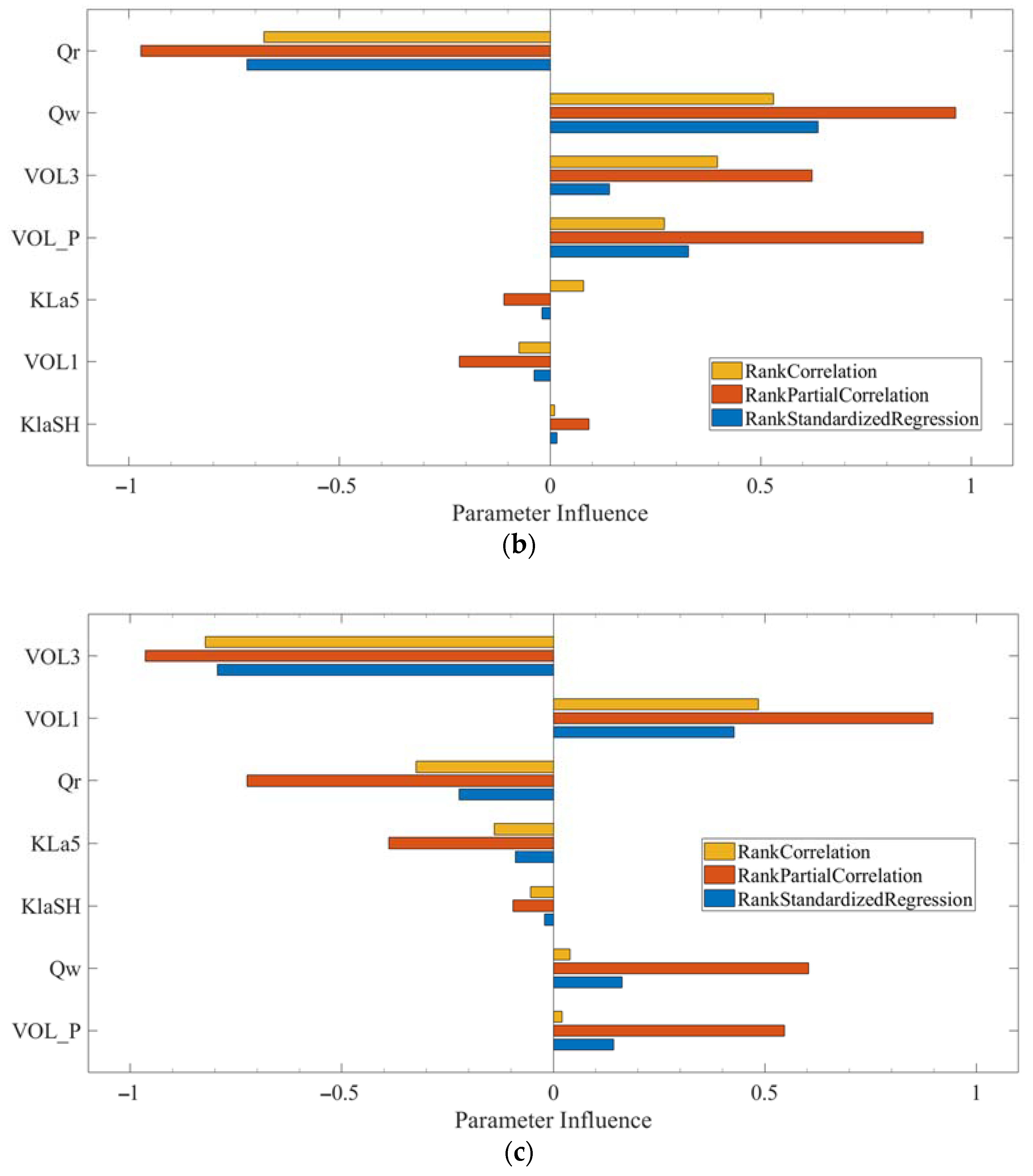
| Control Strategy | Base Case C0 | C1 | C2 | C3 | C4 | C5 |
|---|---|---|---|---|---|---|
| Controlled variable | - | SO from SHARON reactor (SO,SH) | SNH from Anammox reactor (SNH,AMX) | SNH from Anammox reactor (SNH,AMX) | SNH from Anammox reactor (SNH,AMX) | SNH from Anammox reactor (SNH,AMX) |
| Set point | - | SO,SH = 0.0354 * mg/L | SNH,AMX = 12 * mg/L | SNH,AMX = 12 * mg/L | SNH,AMX = 12 * mg/L | SNH,AMX = 12 * mg/L |
| Manipulated variable | - | KLa in SHARON reactor (KLa,SH) | KLa,SH; SO,SH | KLa,SH; SO,SH | KLa,SH; SO,SH | KLa,SH; SO,SH |
| Measured variable | - | SO,SH | SNH,AMX | SNH,AMX | SNH,AMX | SNH,AMX |
| Control algorithm | - | 1 feedback PI control | 1 feedback PI control | 1 cascade PI-PI control | 1 cascade PI-MPC control | 1 cascade MPC-MPC control |
| Proportional gain (Kp) | - | 689.23 | 79.88 | 0.181 | 79.88 | - |
| Integral gain (Ti) | - | 1.98 | 3.17 | 3.33 | 3.17 | - |
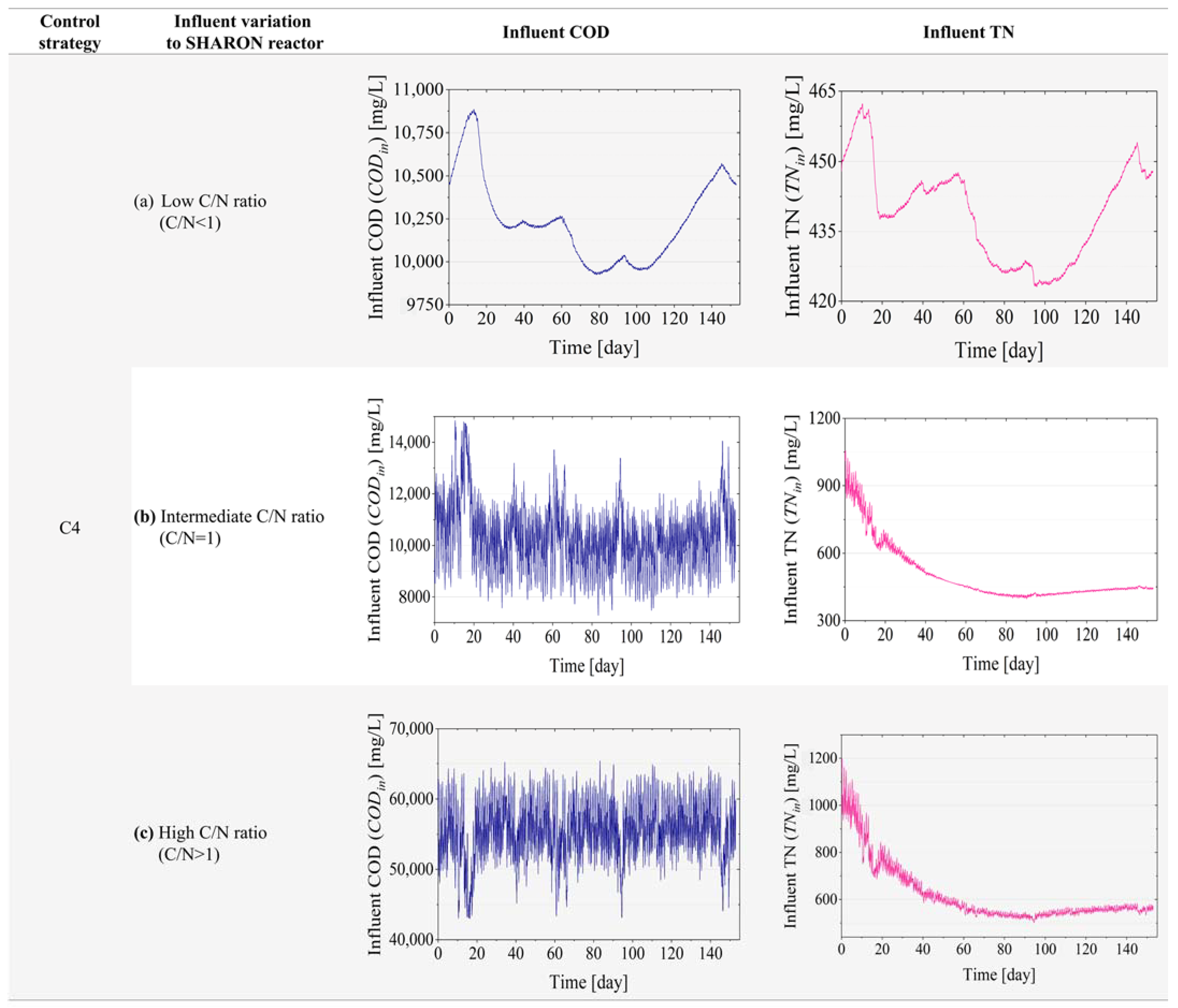
| Influent Variation to SHARON | Control Strategy | Base Case C0 | C1 | C2 | C3 | Improvement (%) | C4 | Improvement (%) | C5 | Improvement (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| Low C/N ratio (C/N < 1) | EQI (kg of pollutants/d) | 916.53 | 916.49 | 916.50 | 944.08 | −3.01% | 1568.65 | −71.15% | 1568.65 | −71.15% |
| OC (EUR/d) | 26,129.97 | 26,129.98 | 26,130.02 | 26,130.02 | 0.00% | 26,130.02 | 0.00% | 16,533.26 | 36.73% | |
| SP (kg/d) | 160,544.83 | 160,544.92 | 160,545.13 | 160,545.13 | 0.00% | 160,545.13 | 0.00% | 100,565.38 | 37.36% | |
| Intermediate C/N ratio (C/N = 1) | EQI (kg of pollutants/d) | 916.53 | 916.49 | 916.50 | 944.08 | −3.01% | 1568.65 | −71.15% | 1568.62 | −71.15% |
| OC (EUR/d) | 26,129.97 | 26,129.98 | 26,130.02 | 26,488.35 | −1.37% | 16,533.53 | 36.73% | 16,533.32 | 36.73% | |
| SP (kg/d) | 160,544.83 | 160,544.92 | 160,545.13 | 162,784.71 | −1.40% | 100,567.08 | 37.36% | 100,565.76 | 37.36% | |
| High C/N ratio (C/N > 1) | EQI (kg of pollutants/d) | 916.53 | 916.49 | 916.50 | 944.08 | −3.01% | 1568.65 | −71.15% | 1568.65 | −71.15% |
| OC (EUR/d) | 26,129.97 | 26,129.98 | 26,130.02 | 26,130.02 | 0.00% | 26,130.02 | 0.00% | 16,533.26 | 36.73% | |
| SP (kg/d) | 160,544.83 | 160,544.92 | 160,545.13 | 160,545.13 | 0.00% | 160,545.13 | 0.00% | 100,565.41 | 37.36% |
| Influent Variation to SHARON | Evaluation Criteria | Control Strategies | |||||
|---|---|---|---|---|---|---|---|
| Base Case C0 | C1 | C2 | C3 | C4 | C5 | ||
| Low C/N ratio (C/N < 1) | Effluent nitrogen concentration (mg/L) | 0.00 | 0.00 | ||||
| Sludge production (kg/d) | 160,544.83 | 160,544.92 | 160,545.1 | 162,784.71 | 100,567.52 | 100,565.38 | |
| Methane production (kg CH4/d) | 980.17 | 980.48 | 980.47 | 994.22 | 0.00 | 0.00 | |
| Intermediate C/N ratio (C/N = 1) | Effluent nitrogen concentration (mg/L) | 0.00 | 0.00 | ||||
| Sludge production (kg/d) | 160,544.83 | 160,544.92 | 160,545.1 | 162,784.71 | 100,567.08 | 100,565.76 | |
| Methane production (kg CH4/d) | 980.17 | 980.48 | 980.47 | 994.22 | 0.00 | 0.00 | |
| High C/N ratio (C/N > 1) | Effluent nitrogen concentration (mg/L) | 0.00 | 0.00 | ||||
| Sludge production (kg/d) | 160,544.83 | 160,544.92 | 160,545.1 | 162,784.71 | 100,566.85 | 100,565.41 | |
| Methane production (kg CH4/d) | 980.17 | 980.48 | 980.47 | 994.22 | 0.00 | 0.00 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vilela, P.; Nam, K.; Yoo, C. Wastewater Treatment System Optimization for Sustainable Operation of the SHARON–Anammox Process under Varying Carbon/Nitrogen Loadings. Water 2023, 15, 4015. https://doi.org/10.3390/w15224015
Vilela P, Nam K, Yoo C. Wastewater Treatment System Optimization for Sustainable Operation of the SHARON–Anammox Process under Varying Carbon/Nitrogen Loadings. Water. 2023; 15(22):4015. https://doi.org/10.3390/w15224015
Chicago/Turabian StyleVilela, Paulina, Kijeon Nam, and Changkyoo Yoo. 2023. "Wastewater Treatment System Optimization for Sustainable Operation of the SHARON–Anammox Process under Varying Carbon/Nitrogen Loadings" Water 15, no. 22: 4015. https://doi.org/10.3390/w15224015
APA StyleVilela, P., Nam, K., & Yoo, C. (2023). Wastewater Treatment System Optimization for Sustainable Operation of the SHARON–Anammox Process under Varying Carbon/Nitrogen Loadings. Water, 15(22), 4015. https://doi.org/10.3390/w15224015








