Assessment of Tidal Current Energy Resources in the Pearl River Estuary Using a Numerical Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Setup
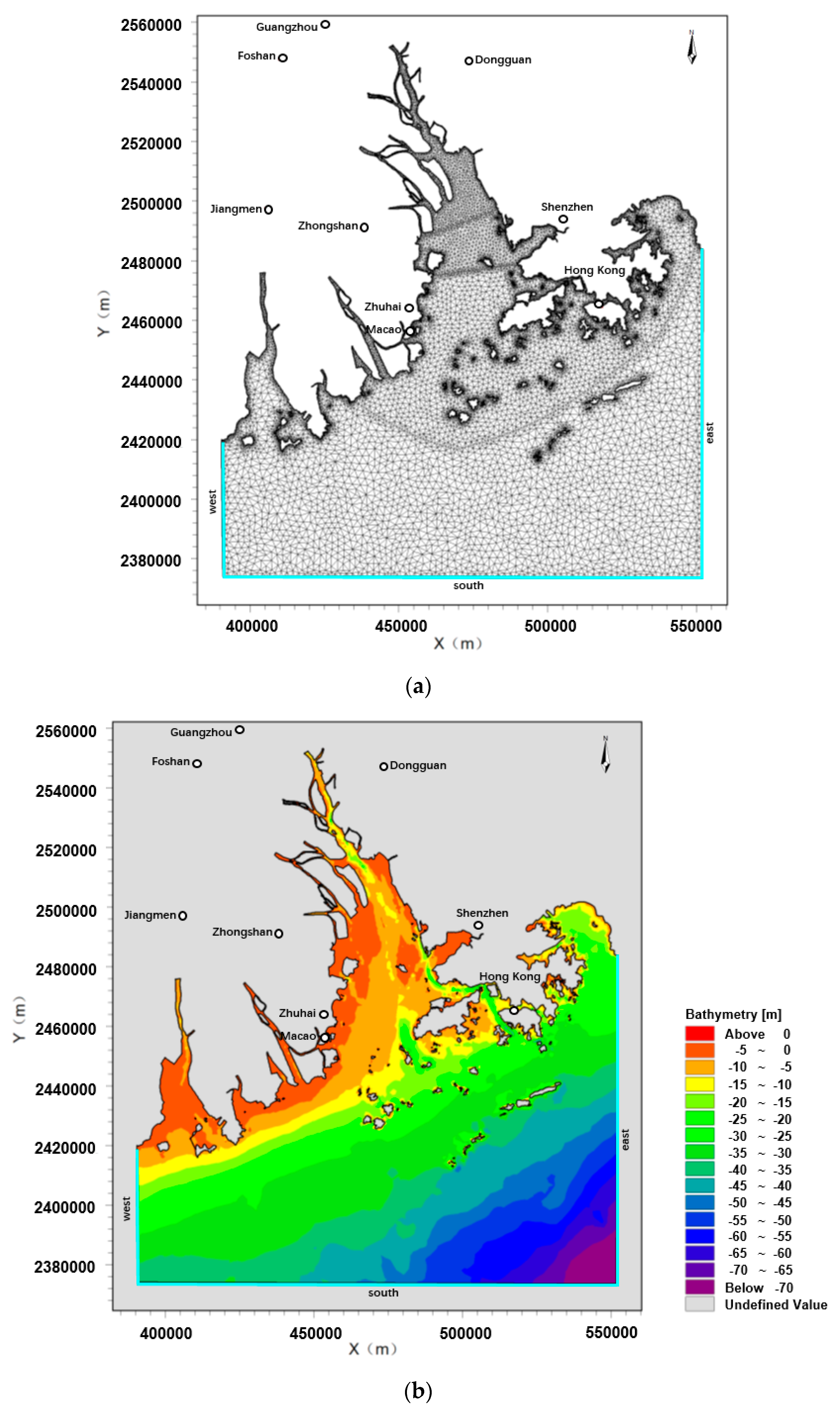
2.2. Computation Domain and Bathymetry
2.3. Model Validation
3. Tidal Characteristics
3.1. The Current Speed Fields of the Rapid Flood and Ebb Tides
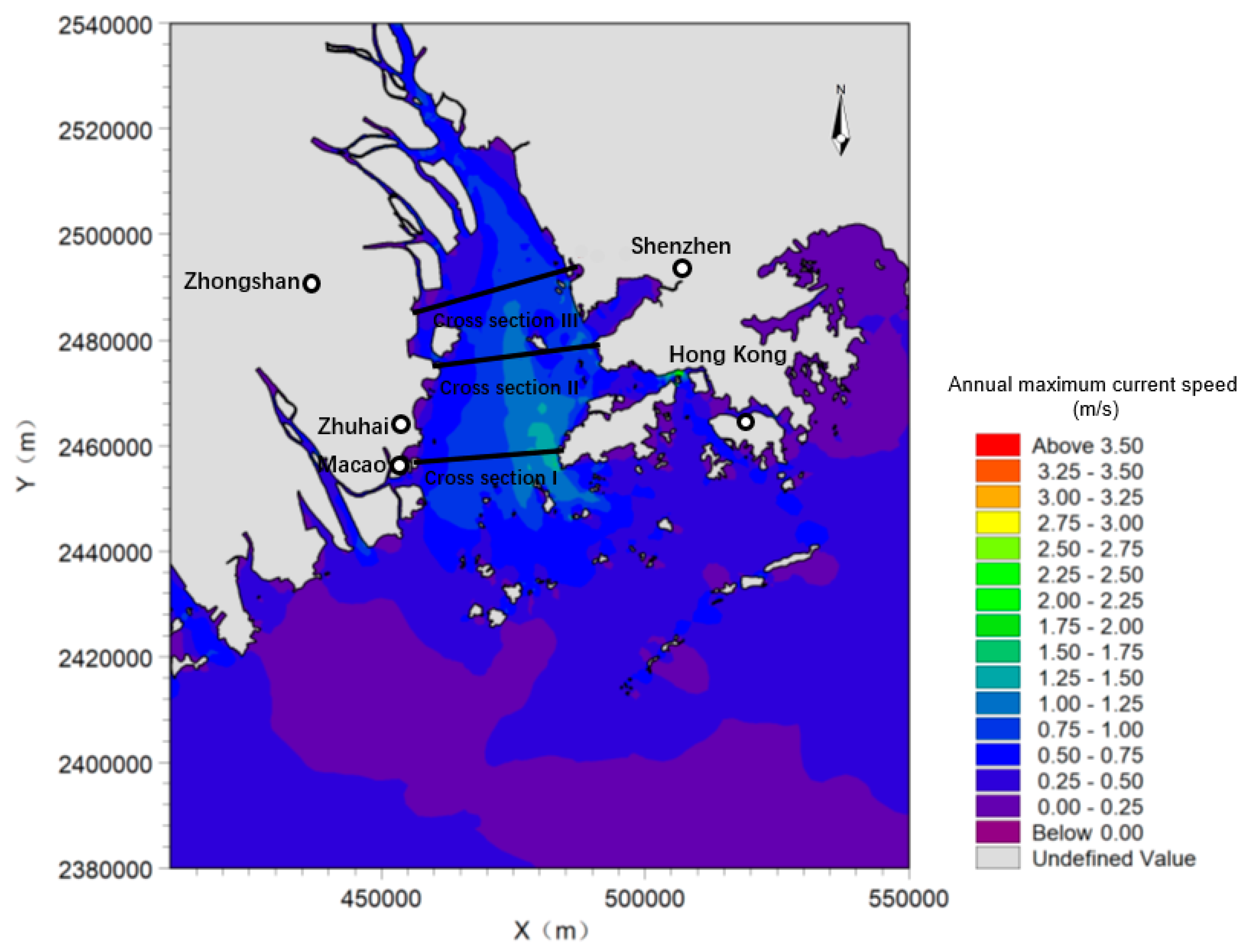
3.2. The Annual Current Speed
4. Tidal Current Energy Estimation
4.1. Average Tidal Current Energy Power Density
4.2. Potential Resources
5. Conclusions
- The distribution of annual average tidal current power density in the Pearl River Estuary is generally consistent with the distribution of the tidal current fields. The average power densities of tidal currents in summer and autumn are larger, followed by winter, and it is the smallest in spring.
- The annual average power density of tidal energy is generally smaller than 0.10 kW/m2. The theoretical resource potential increases with the increase in water depth. The theoretical potential of tidal energy resources in the Pearl River Estuary was finally assessed to be about 11,000 kW.
- The tidal range in the Pearl River Estuary is small, resulting in a relatively weak tidal power and low average power density of tidal energy. Therefore, the tidal energy resources in the estuary are limited.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Greenhouse Gas Bulletin: Another Year Another Record. Available online: https://public.wmo.int/en/media/press-release/greenhouse-gas-bulletin-another-year-another-record (accessed on 25 October 2021).
- Lamy, J.V.; Azevedo, I.L. Do tidal stream energy projects offer more value than offshore wind farms? A case study in the United Kingdom. Energy Policy 2018, 113, 28–40. [Google Scholar] [CrossRef]
- Fraenkel, P. Marine Current Turbines: Feedback on Experience so Far. Seatech Week, Brest, CDROM Proc. 20–21 October 2004. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=5e76e6ea7194538170cb3603fc2d802b&site=xueshu_se (accessed on 25 October 2021).
- Gonz’alez-Gorbenña, E.; Rosman, P.C.; Qassim, R.Y. Assessment of the tidal current energy resource in S͠ao Marcos Bay, Brazil. J. Ocean Eng. Mar. Ener. 2015, 1, 421–433. [Google Scholar] [CrossRef]
- Coles, D.; Blunden, L.; Bahaj, A. Assessment of the energy extraction potential at tidal sites around the Channel Islands. Energy 2017, 124, 171–186. [Google Scholar] [CrossRef]
- Bonar, P.A.J.; Schnabl, A.M.; Lee, W.K.; Adcock, T.A.A. Assessment of the Malaysian tidal stream energy resource using an upper bound approach. J. Ocean Eng. Mar. Ener. 2018, 4, 99–109. [Google Scholar] [CrossRef]
- Park, J.S.; Lee, C.Y.; Park, J.S.; Choi, H.W.; Ko, D.H.; Lee, J.K. Assessment of tidal stream energy resources using a numerical model in southwestern sea of Korea. Ocean Sci. J. 2019, 54, 529–541. [Google Scholar] [CrossRef]
- Karsten, R.H.; McMillan, J.M.; Lickley, M.J.; Haynes, R.D. Assessment of tidal current energy in the Minas Passage, Bay of Fundy. J. Power Energy 2008, 222, 493–507. [Google Scholar] [CrossRef]
- Wang, T.; Yang, Z. A tidal hydrodynamic model for cook inlet, Alaska, to support tidal energy resource characterization. J. Mar. Sci. Eng. 2020, 8, 254. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Wang, T.P.; Xiao, Z.Y.; Kilcher, L.; Haas, K.; Xue, H.J.; Feng, X. Modeling assessment of tidal energy extraction in the western passage. J. Mar. Sci. Eng. 2020, 8, 411. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, W.C.; Hsu, M.H. Modeling assessment of tidal current energy at Kinmen Island, Taiwan. Renew. Energy 2013, 50, 1073–1082. [Google Scholar] [CrossRef]
- Burić, M.; Grgurić, S.; Mikulčić, H.; Wang, X. A numerical investigation of tidal current energy resource potential in a sea strait. Energy 2021, 234, 121241. [Google Scholar] [CrossRef]
- Pearl River Delta: Opportunities and Challenges. Available online: http://www.geopolitika.hu/en/2018/07/23/pearl-river-delta-opportunities-and-challenges (accessed on 23 July 2018).
- DHI. MIKE 21 & MIKE 3 Flow Model FM, Hydrodynamic and Transport Module, Scientific Documentation; DHI Water & Environment: Hørsholm, Denmark, 2017; pp. 3–45. [Google Scholar]
- Symonds, A.M.; Vijverberg, T.; Post, S.; Van Der Sperk, B.; Henrtotte, J.; Sokolewicz, M. Comparison between Mike 21 FM, Delft3D and Delft3D FM flow models of western port bay, Australia. Coast. Eng. 2016, 2, 1–12. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean Tech. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- He, J.; Xin, W. Analysis and numerical simulation of abnormal siltation in foundation trench of immersed tube tunnel of Hongkong-Zhuhai-Macao Bridge. Adv. Water Sci. 2019, 30, 823–833. (In Chinese) [Google Scholar]
- Lu, X.; Qiao, F. Advances in study on tidal current energy resource assessment methods. Adv. Mar. Sci. 2008, 26, 98. (In Chinese) [Google Scholar]
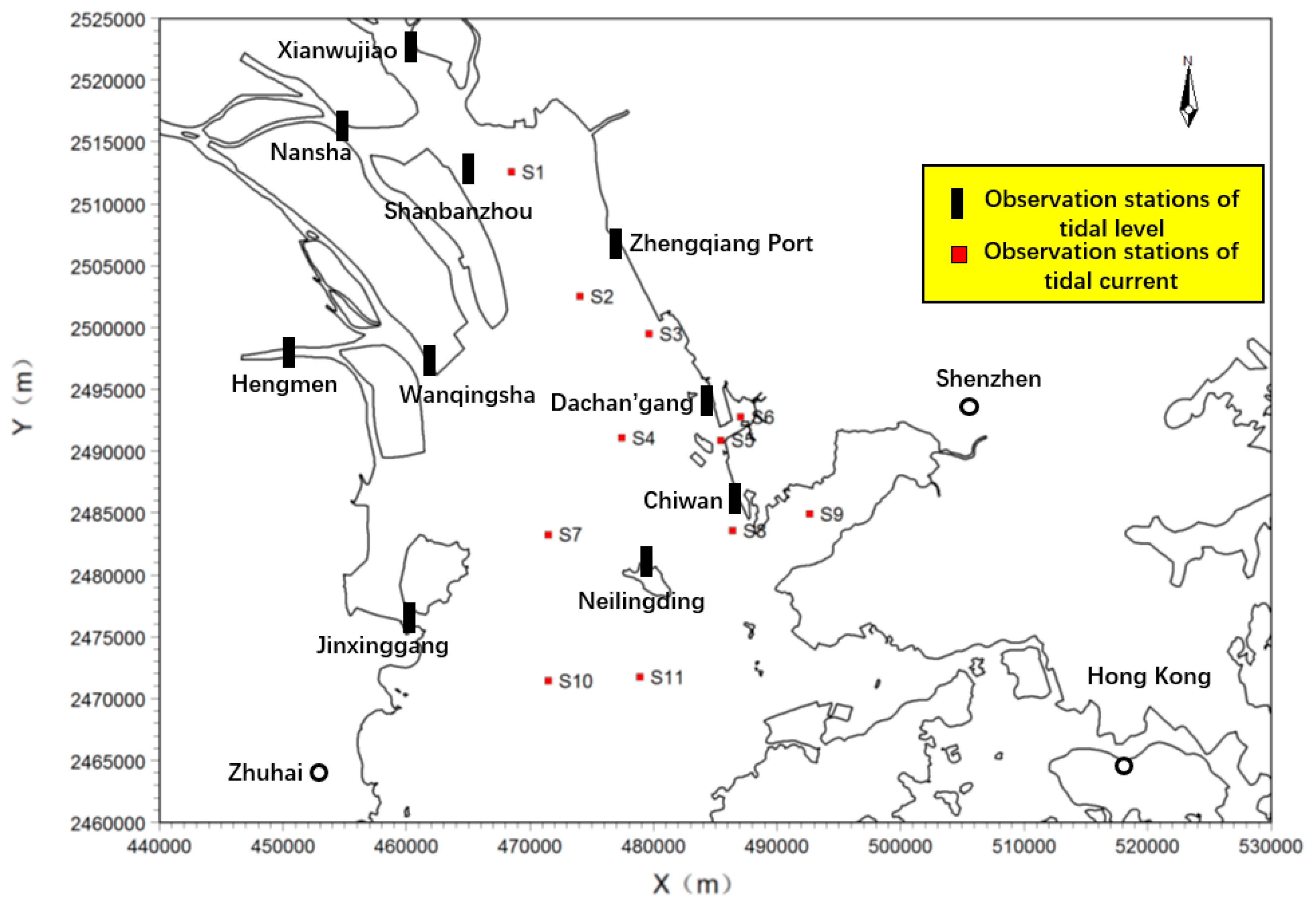
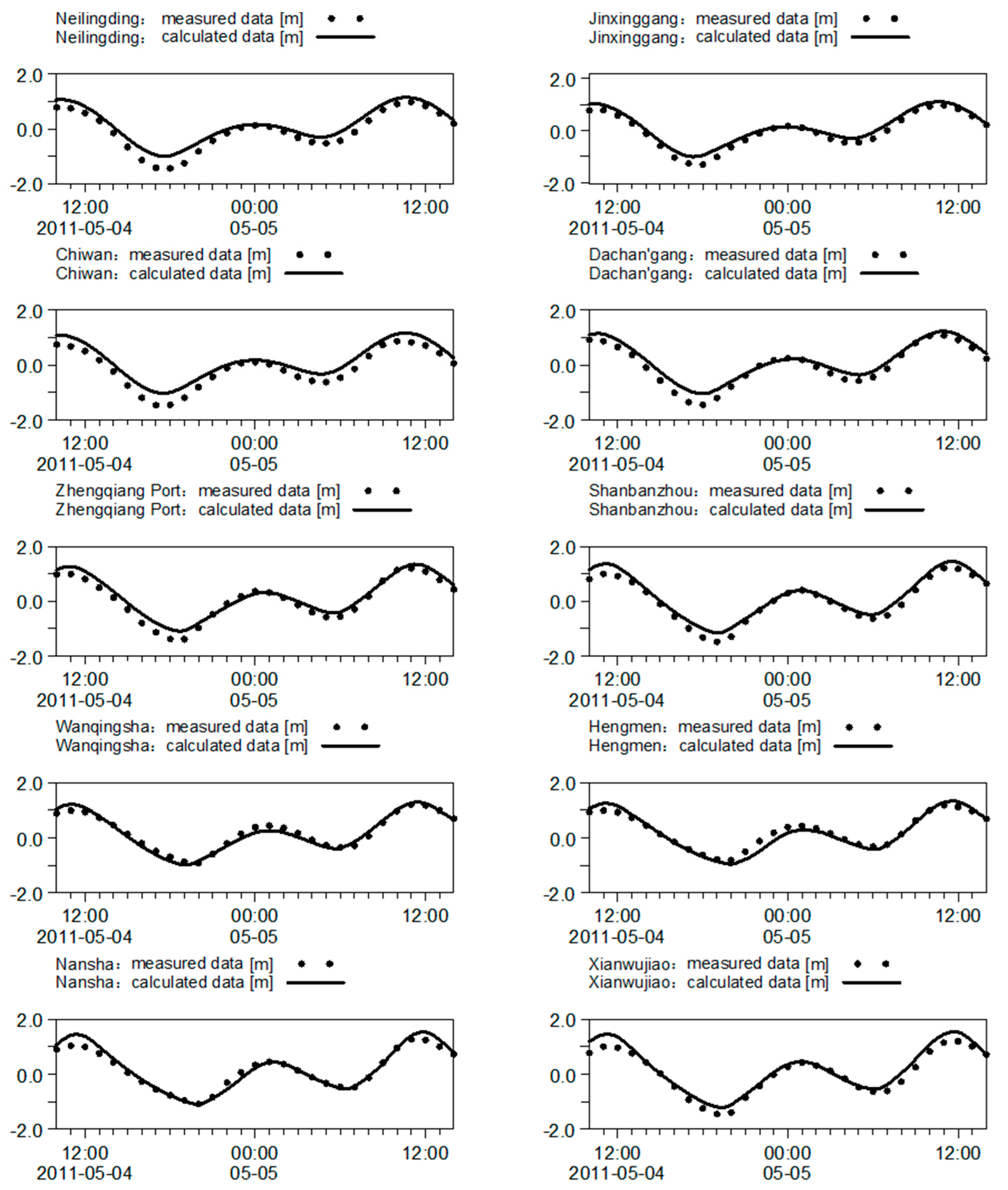
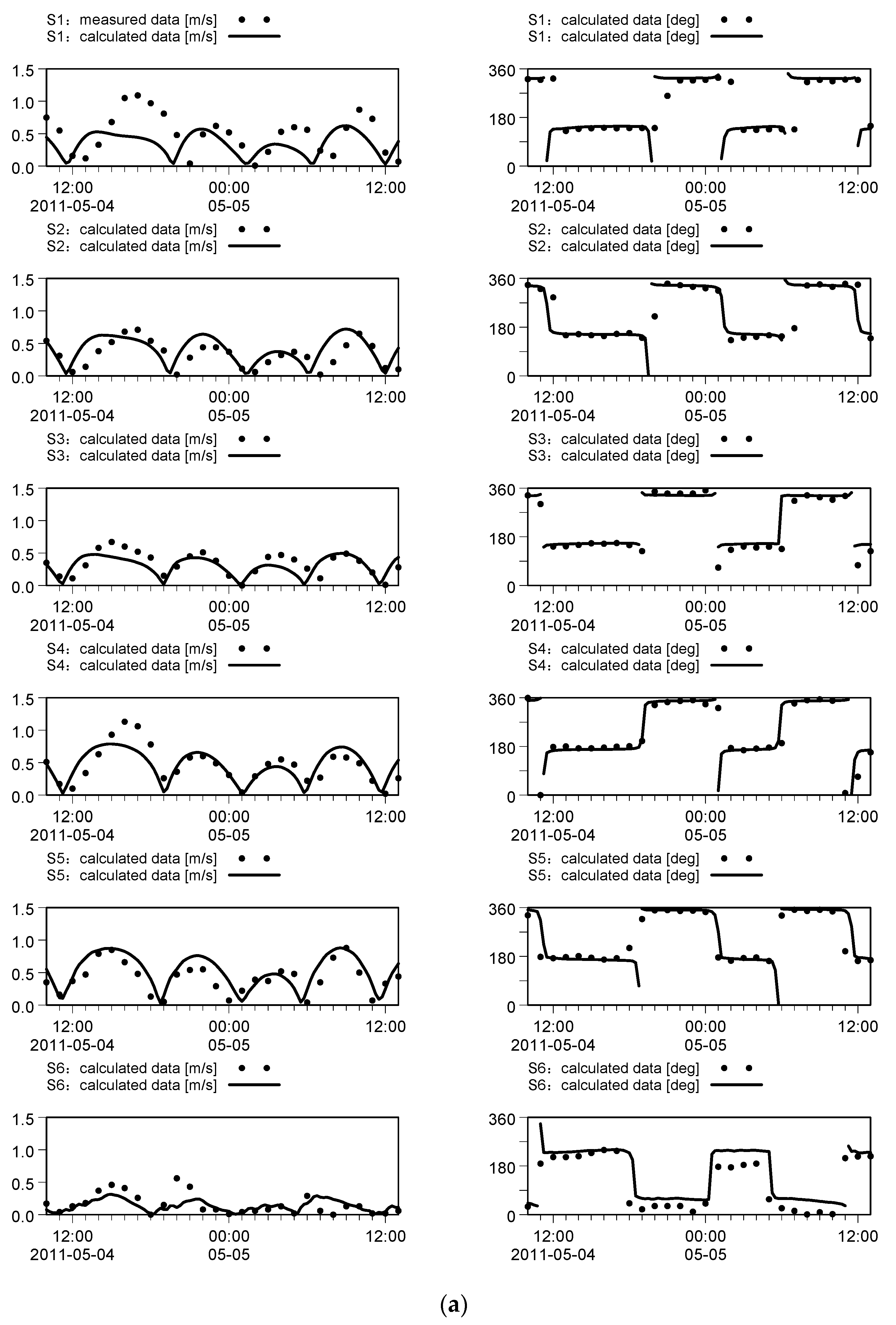






| Station Full Name | Longitude (°, E) | Latitude (°, N) |
|---|---|---|
| Neilingding | 113.8017 | 22.4265 |
| Jinxinggang | 113.6151 | 22.3816 |
| Chiwan | 113.8698 | 22.4710 |
| Dachan’gang | 113.8484 | 22.5452 |
| Zhengqiang Port | 113.7765 | 22.6570 |
| Shanbanzhou | 113.6605 | 22.7125 |
| Wanqingsha | 113.6287 | 22.5689 |
| Hengmen | 113.5199 | 22.5762 |
| Nansha | 113.5615 | 22.7435 |
| Xianwujiao | 113.6157 | 22.7997 |
| Station | Longitude (°, E) | Latitude (°, N) |
|---|---|---|
| S1 | 113.6934 | 22.7107 |
| S2 | 113.7474 | 22.6201 |
| S3 | 113.8019 | 22.5926 |
| S4 | 113.7804 | 22.5168 |
| S5 | 113.8586 | 22.5150 |
| S6 | 113.8739 | 22.5333 |
| S7 | 113.7227 | 22.4460 |
| S8 | 113.8678 | 22.4491 |
| S9 | 113.9282 | 22.4612 |
| S10 | 113.7231 | 22.3392 |
| S11 | 113.7952 | 22.3421 |
| Station | Observation (m/s) | Model (m/s) | ARE (%) |
|---|---|---|---|
| S1 | 0.49 | 0.35 | −29 |
| S2 | 0.33 | 0.41 | 24 |
| S3 | 0.33 | 0.30 | −9 |
| S4 | 0.45 | 0.45 | 0 |
| S5 | 0.41 | 0.52 | 27 |
| S6 | 0.16 | 0.13 | −18 |
| S7 | 0.42 | 0.39 | −9 |
| S8 | 0.38 | 0.45 | 18 |
| S9 | 0.21 | 0.20 | −4 |
| S10 | 0.45 | 0.39 | −12 |
| S11 | 0.45 | 0.42 | −7 |
| Cross Section | Width (m) | Average Water Depth (m) | Cross-Sectional Area (m2) | Annual Average Power Density (kW/m2) | Theoretical Potential Resource (10,000 kW) |
|---|---|---|---|---|---|
| I | 26,466 | 8.4 | 223,110.7 | 0.05 | 1.1 |
| II | 28,455 | 6.4 | 183,252.5 | 0.05 | 0.9 |
| III | 29,187 | 4.5 | 129,883.7 | 0.04 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Hu, Z.; Li, M.; Zhang, H. Assessment of Tidal Current Energy Resources in the Pearl River Estuary Using a Numerical Method. Water 2023, 15, 3990. https://doi.org/10.3390/w15223990
Wang W, Hu Z, Li M, Zhang H. Assessment of Tidal Current Energy Resources in the Pearl River Estuary Using a Numerical Method. Water. 2023; 15(22):3990. https://doi.org/10.3390/w15223990
Chicago/Turabian StyleWang, Weiyuan, Zijun Hu, Mengyu Li, and Hongxing Zhang. 2023. "Assessment of Tidal Current Energy Resources in the Pearl River Estuary Using a Numerical Method" Water 15, no. 22: 3990. https://doi.org/10.3390/w15223990
APA StyleWang, W., Hu, Z., Li, M., & Zhang, H. (2023). Assessment of Tidal Current Energy Resources in the Pearl River Estuary Using a Numerical Method. Water, 15(22), 3990. https://doi.org/10.3390/w15223990





