Study on the Cavitation Characteristics of Shroud Clearance in Prototype and Model of a Kaplan Turbine
Abstract
:1. Introduction
2. Research Object and Methodology
2.1. Numerical Techniques
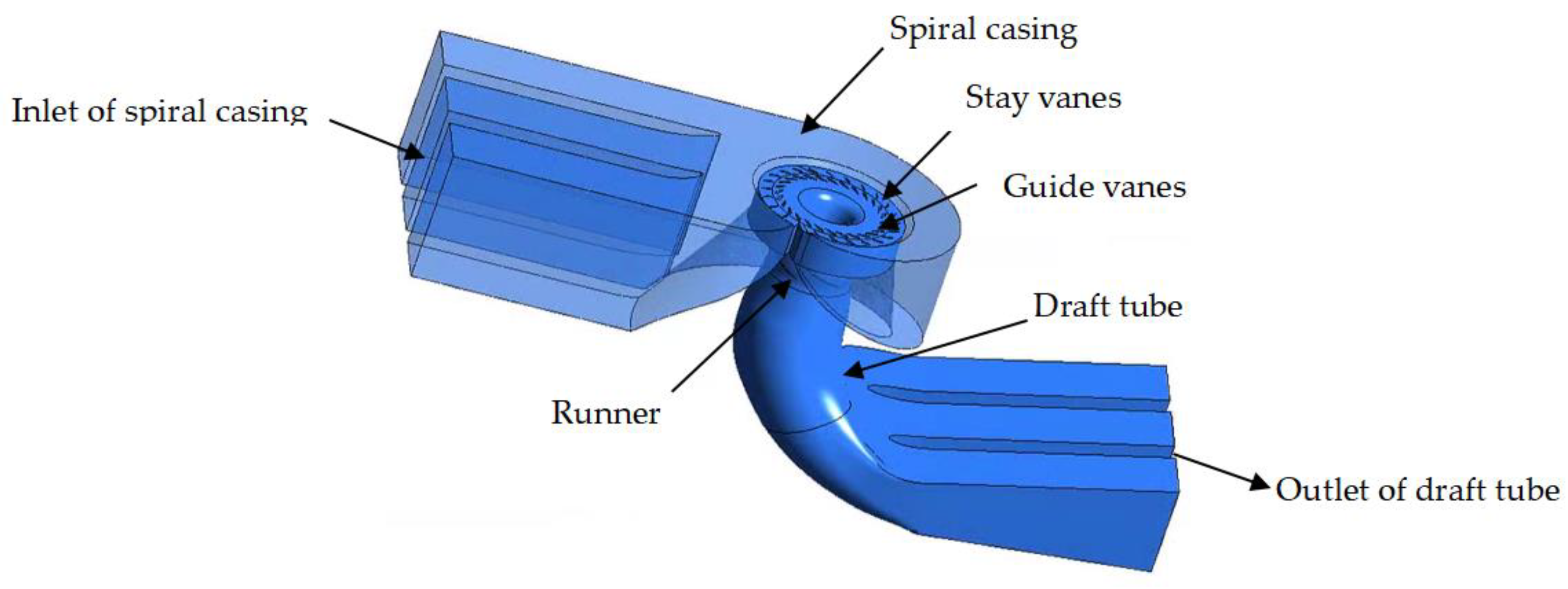
2.2. Object of Study
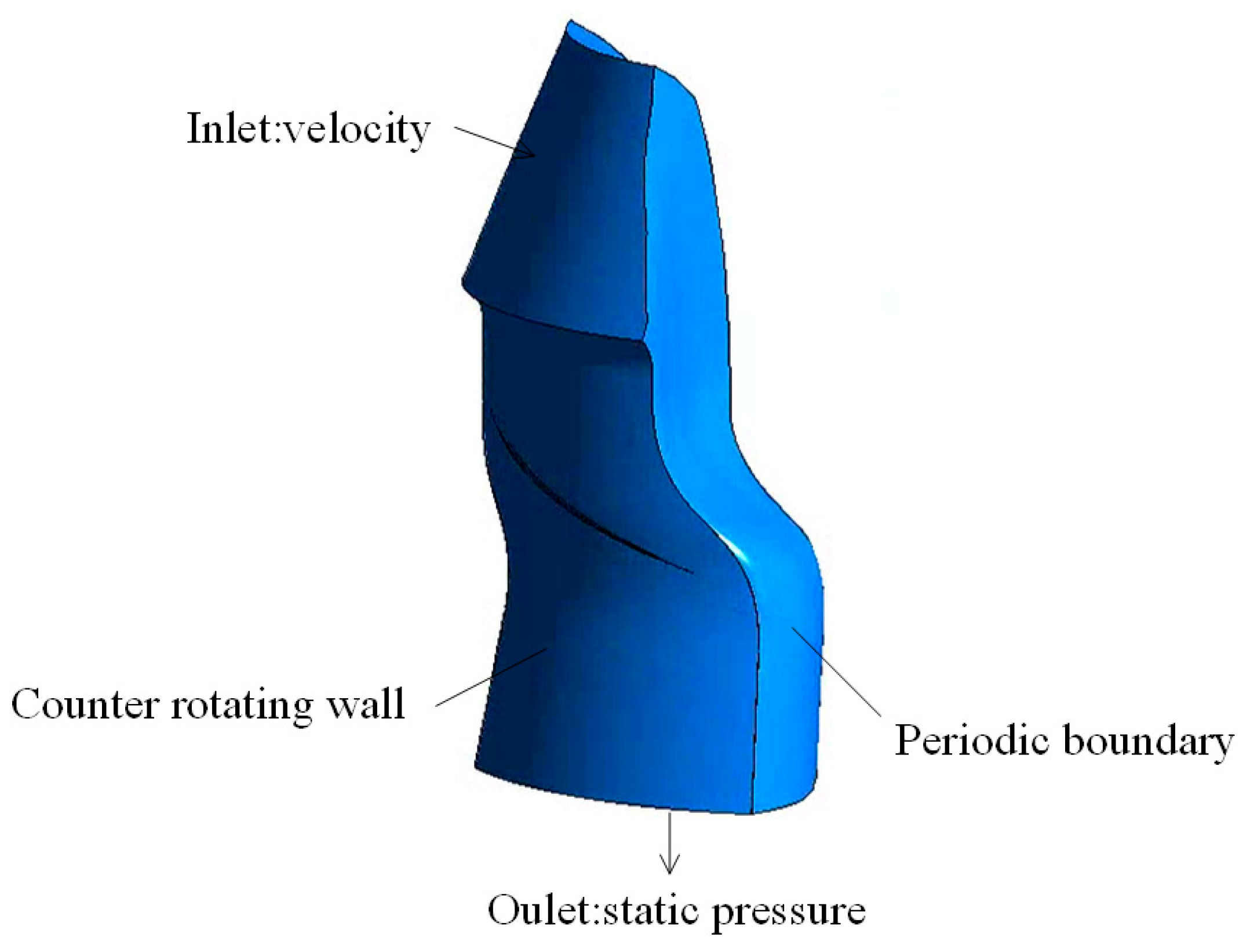
2.3. Computation Domain
2.4. Operating Conditions and Boundary Conditions
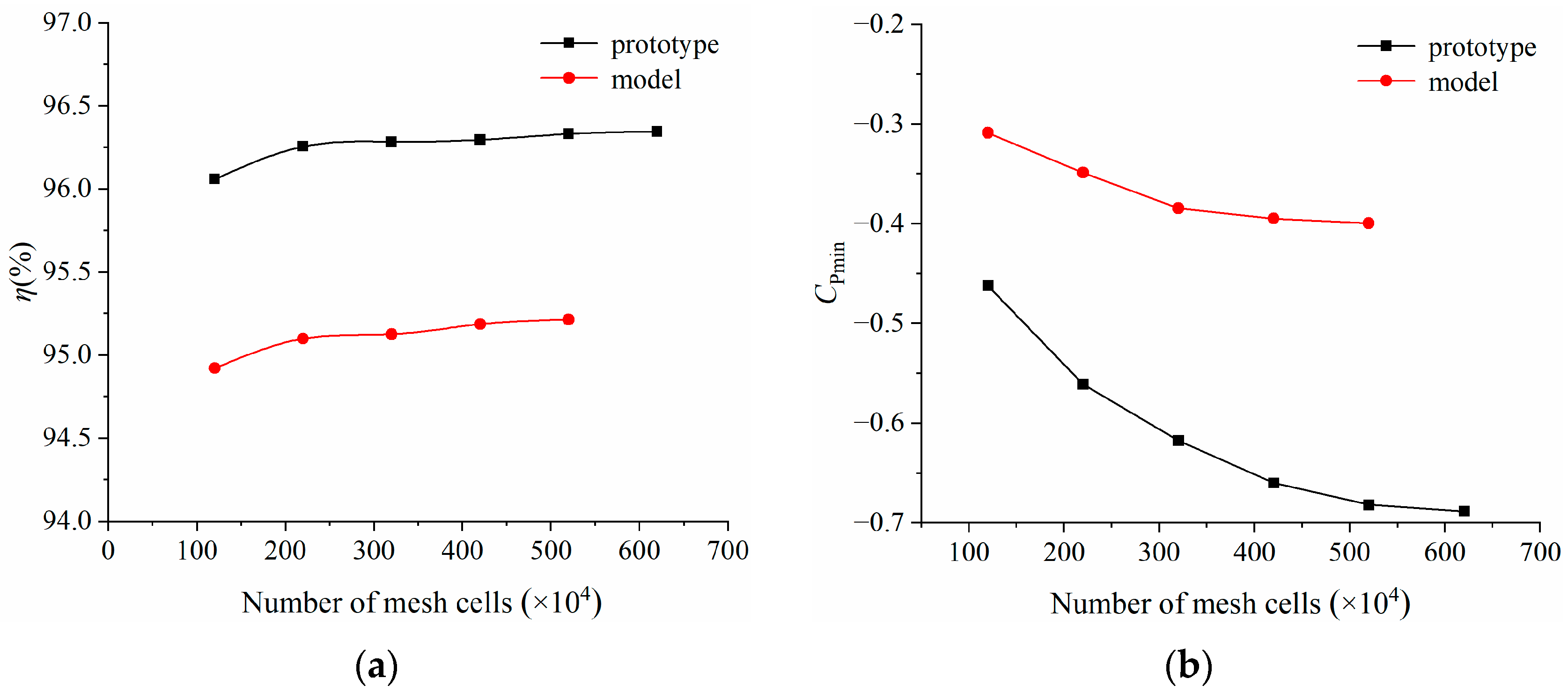
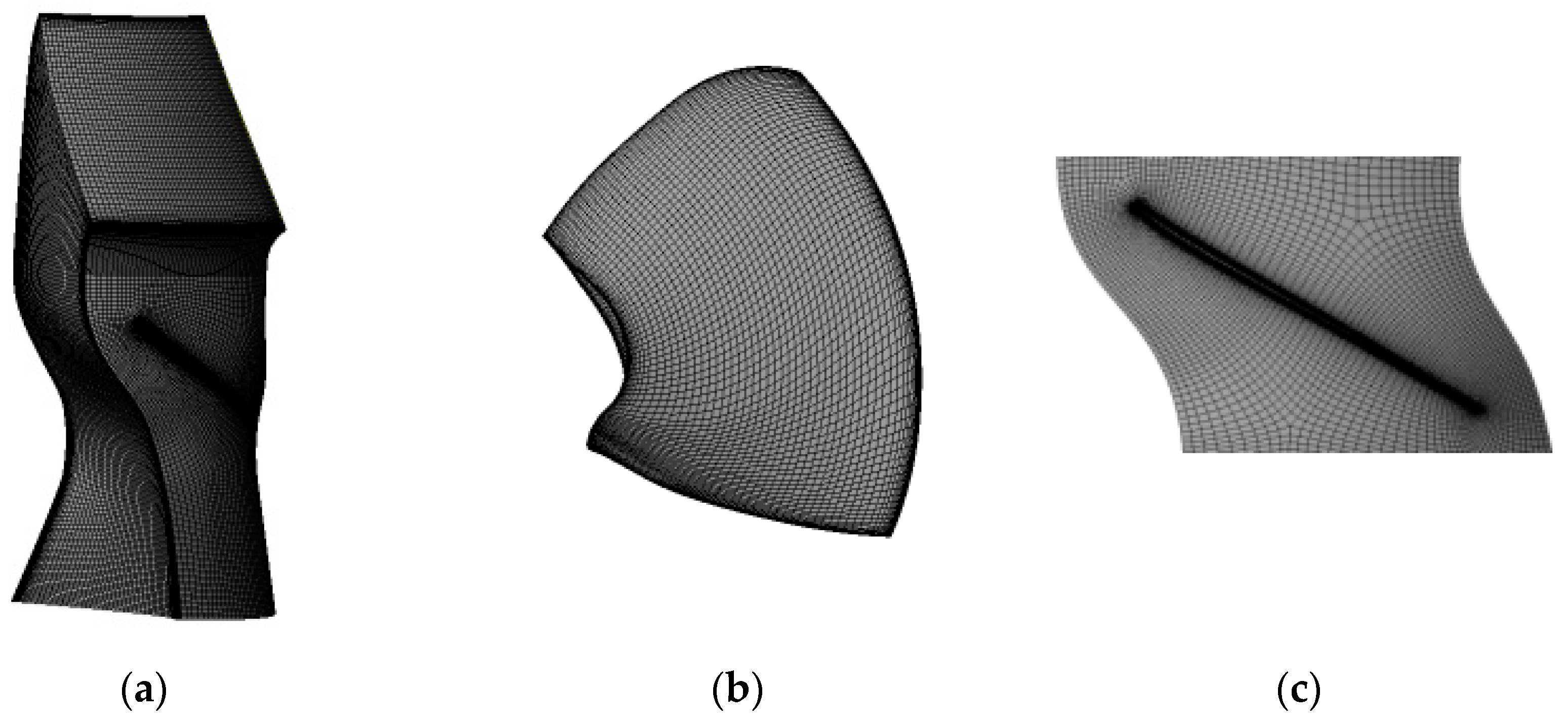
2.5. Mesh Independence Verification
3. Calculation Results
3.1. Analysis of Calculation Results
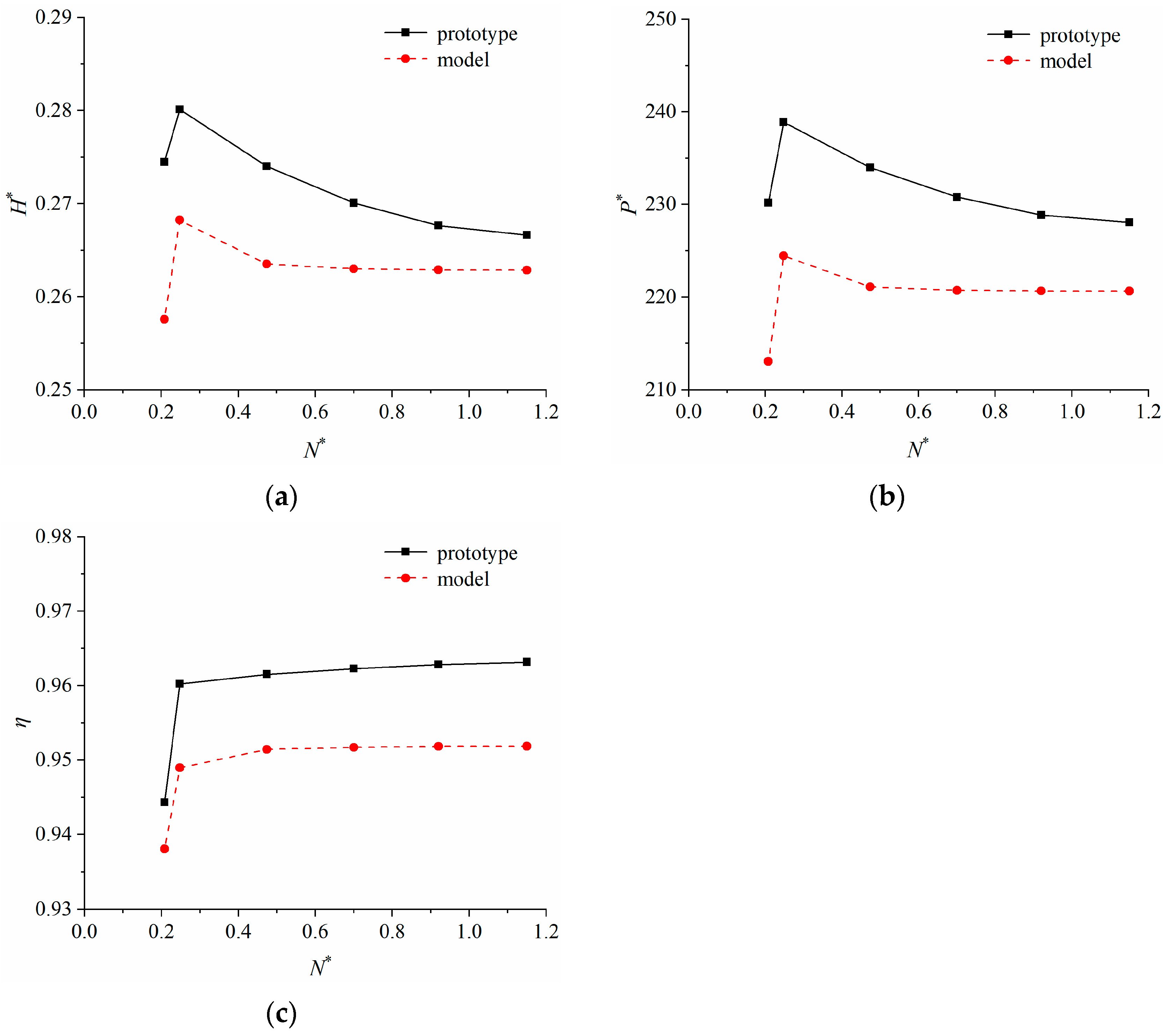
3.1.1. Energy Characteristics
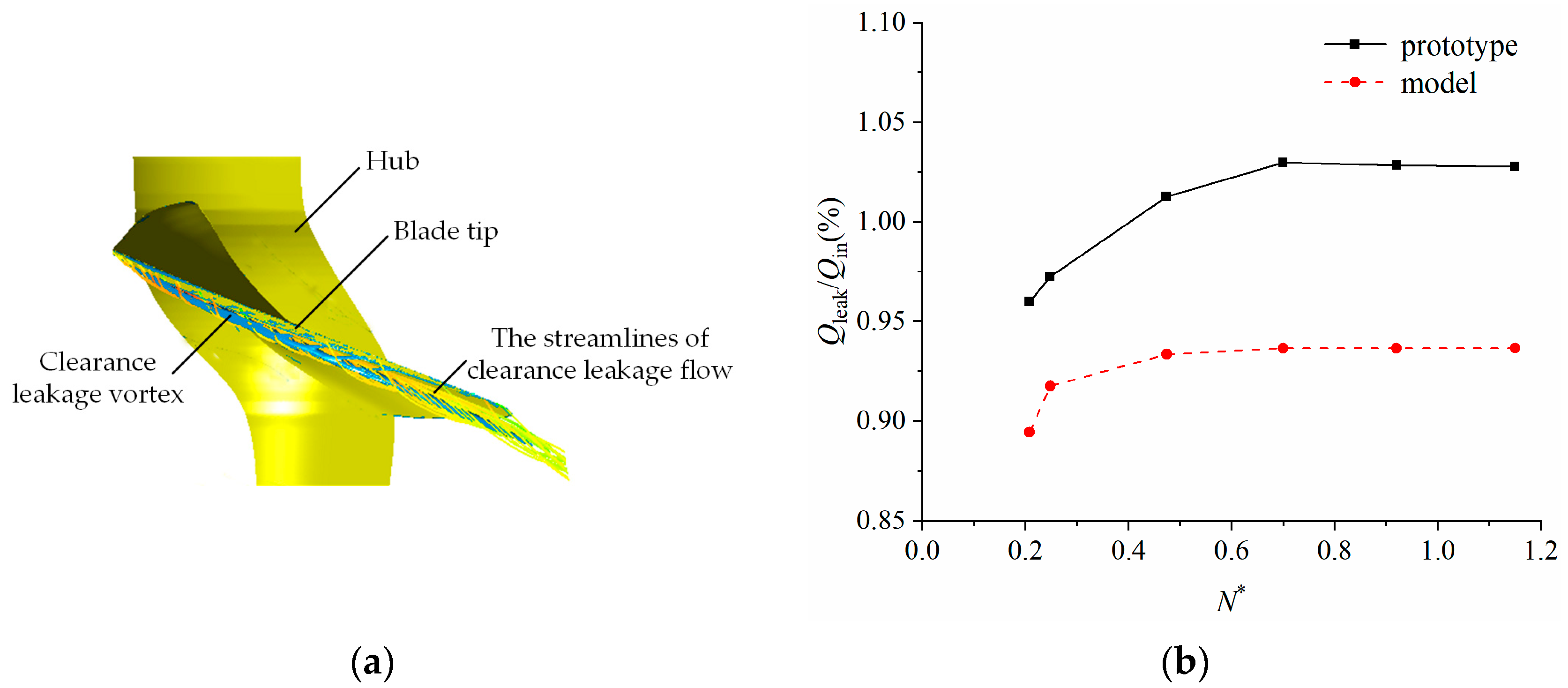
3.1.2. Clearance Leakage Characteristics
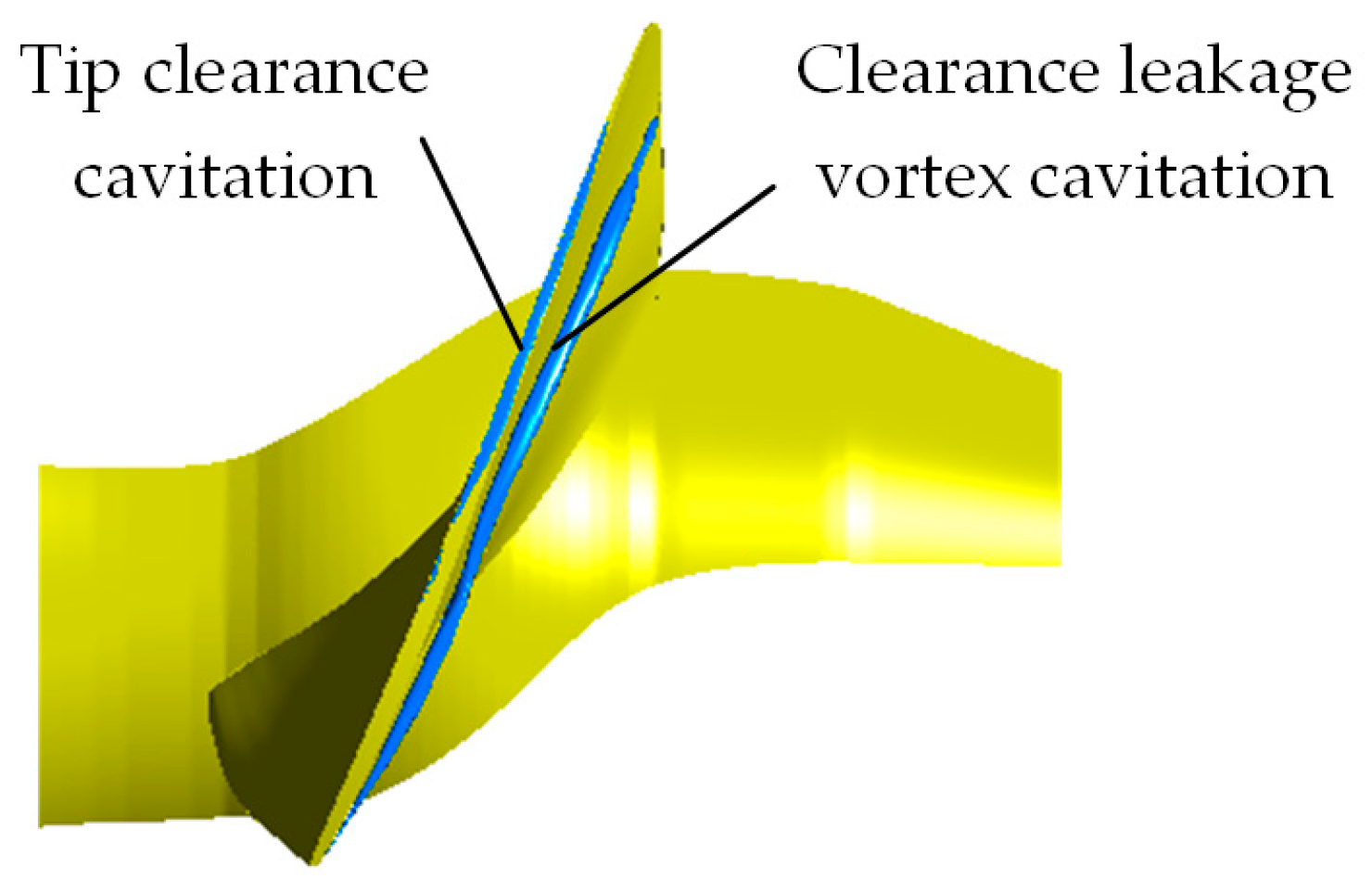
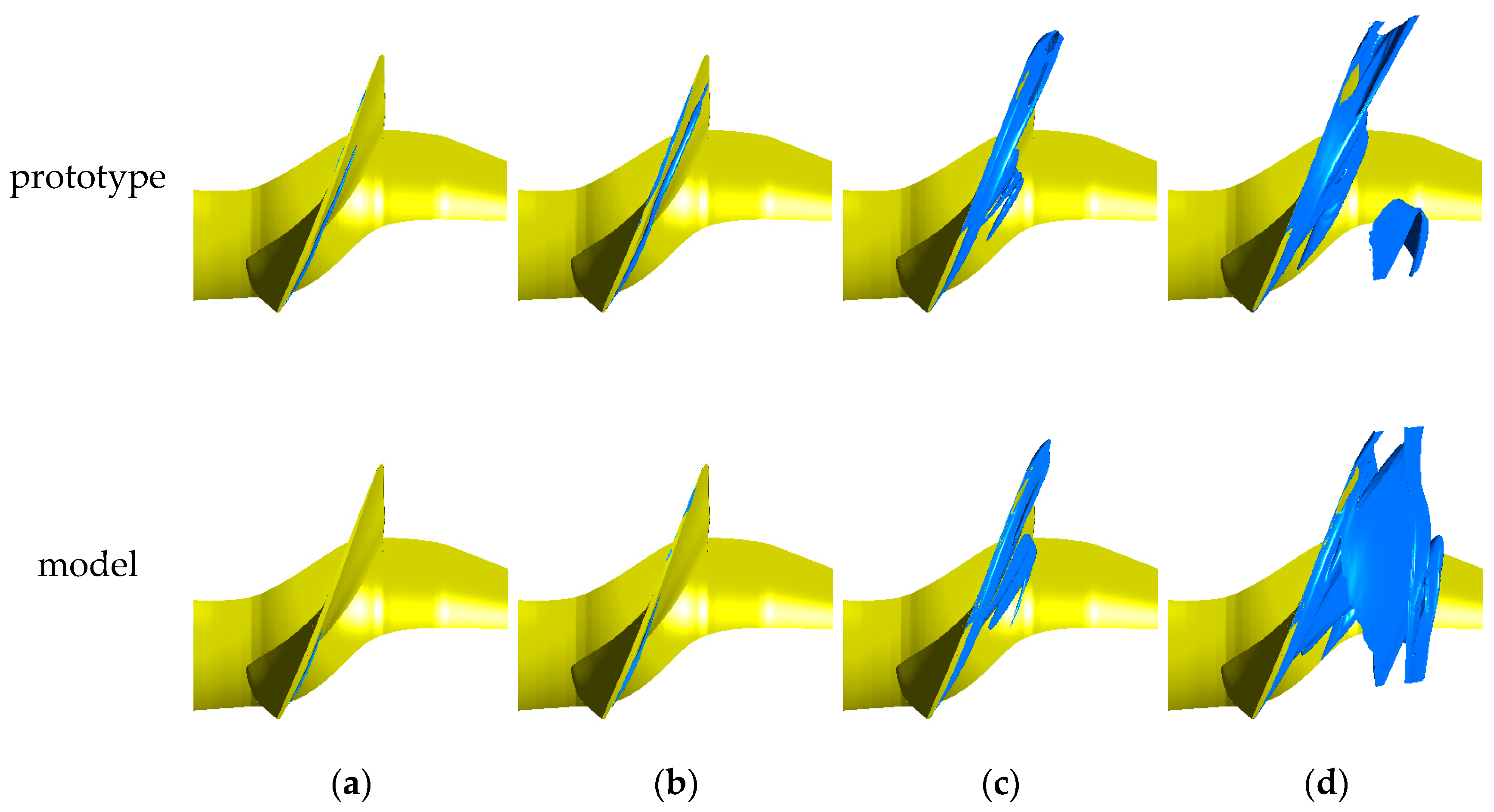
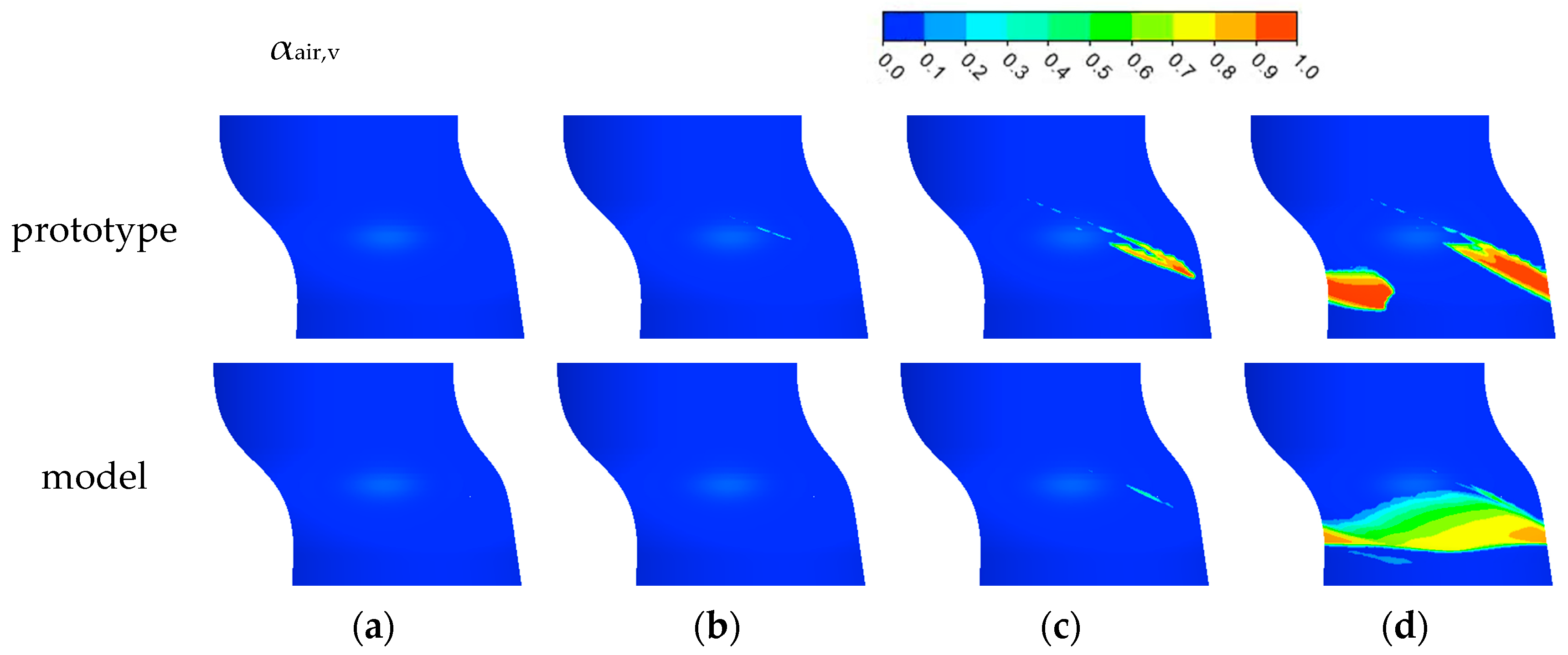
3.1.3. Cavitation Distribution near the Blade Tip
3.1.4. Volume Change of the Runner Cavitation
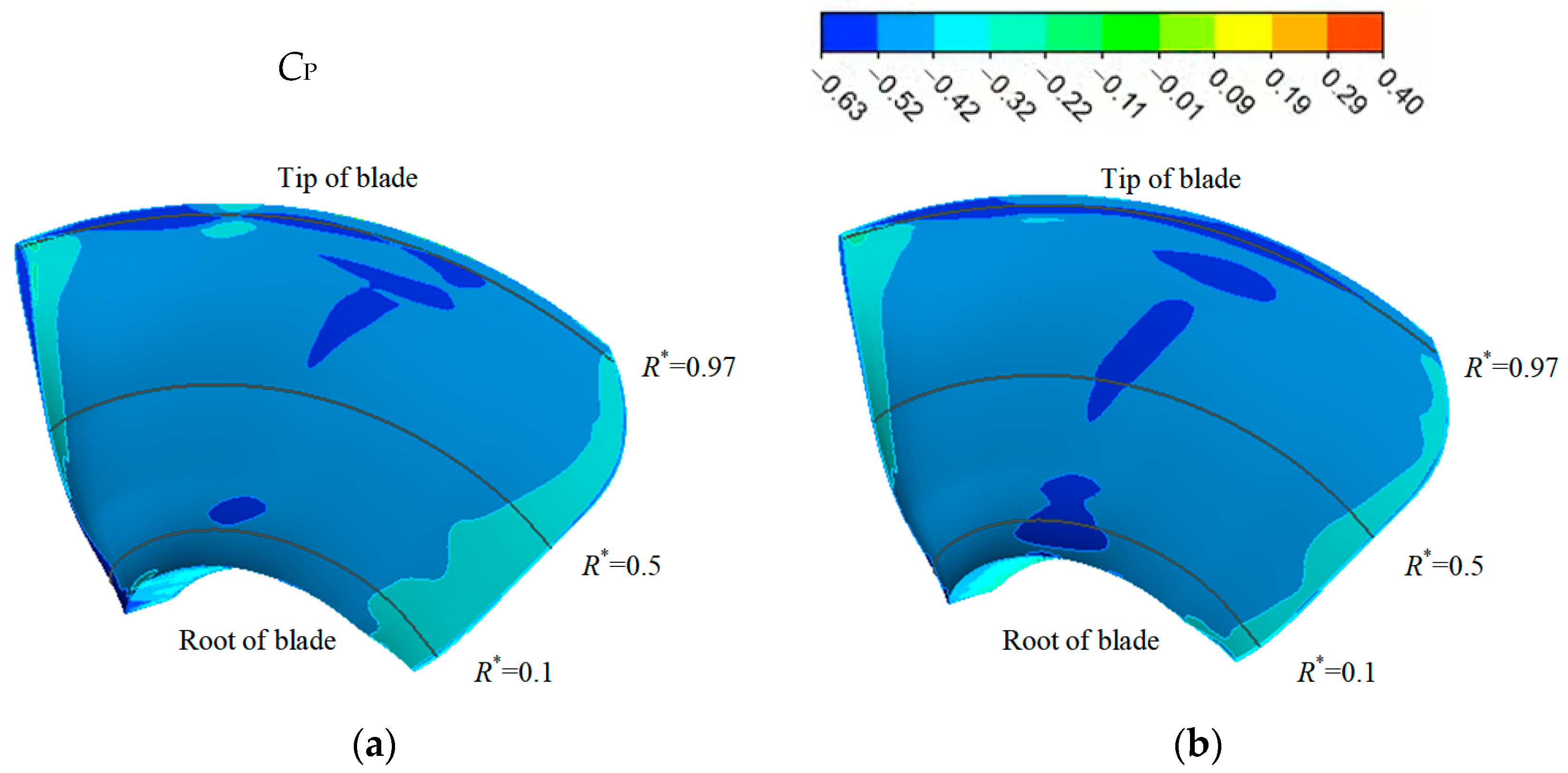
3.1.5. Distribution of Pressure Coefficients on the Blade Surfaces
3.1.6. Cavitation Characteristics of the Runner Chamber
4. Conclusions
- Under the cavitation conditions, the energy characteristics (head coefficient, power coefficient, and efficiency) of the prototype are higher than those of the model. The operating conditions where the energy characteristics drop rapidly are the same. In addition, the critical cavitation coefficient of the prototype is close to that of the model. To some extent, the critical cavitation coefficient calculated by the model has reference significance for the prototype.
- When the cavitation coefficient is larger than the critical cavitation coefficient, the cavitation characteristics of the blade and the runner chamber in the prototype are more serious than those in the model. When the cavitation coefficient is less than the critical cavitation coefficient, the degree of cavitation in the runner domain of the model is intensified. The cavitation characteristic of the runner chamber of the model is more serious than that of the prototype.
- With the decrease in the cavitation coefficient, the cavitation of the runner chamber in the prototype occurs earlier than that in the model. The runner chamber in the prototype experiences cavitation at the device cavitation coefficient, while the runner chamber in the model does not. When the cavitation coefficient is reduced to close to the critical cavitation coefficient, the energy characteristics of the runner do not change much, but the cavitation significantly intensifies in the prototype and model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, A.M.; Huang, W.C.; Li, D.F. Problems in the operation of Kaplan turbine. China Urban Econ. 2011, 30, 260. [Google Scholar]
- Liao, W.L.; Liu, S.Z.; Zhang, L.F. Experimental investigation of the tip clearance cavitations on blades flange of Kaplan turbine. J. Hydroelectr. Eng. 2005, 4, 67–72. [Google Scholar]
- Chen, Q.F.; Luo, Y.Y.; Li, X.G.; Ahn, S.H.; Zhang, J.; Wang, Z.W.; Xiao, Y.X. Influence of runner clearance on efficiency and cavitation in Kaplan turbine. IOP Conf. Ser. Earth Environ. Sci. 2018, 163, 012068. [Google Scholar] [CrossRef]
- You, D.; Wang, M.; Moin, P.; Mittal, R. Vortex dynamics and low-pressure fluctuations in the vortex dynamics and tip-clearance flow. J. Fluids Eng. 2007, 129, 1002–1014. [Google Scholar] [CrossRef]
- Tan, D.Q.; Han, X.L.; Liu, B.; Liu, W.J.; Wei, X.Z. Research on differences between clearance cavitation and airfoil cavitation in axial flow turbine. Large Electr. Mach. Hydraul. Turbine 2012, 2, 34–37. [Google Scholar]
- Xiao, X.W.; McCarter, A.A.; Lakshminarayana, B. Tip clearance effects in a turbine rotor: Part I—Pressure field and loss. J. Turbomach. 2001, 123, 296–304. [Google Scholar] [CrossRef]
- Amiri, K.; Mulu, B.; Cervantes, M.J. Experimental investigation of the interblade flow in a Kaplan runner at several operating points using Laser Doppler Anemometry. J. Fluids Eng. 2016, 138, 021106. [Google Scholar] [CrossRef]
- Ma, Y.; Qian, B.; Feng, Z.G.; Wang, X.; Shi, G.T.; Liu, Z.K.; Liu, X.B. Flow behaviors in a Kaplan turbine runner with different tip clearances. Adv. Mech. Eng. 2021, 13, 1069494471. [Google Scholar] [CrossRef]
- Wu, Y.Z.; Wang, X.H.; Yang, X.L.; Ding, J.F.; Zhu, D.; Tao, R.; Wang, H.M.; Xiao, R.F. Prediction of the influence of runner tip clearance on the performance of tubular turbine. J. Mar. Sci. Eng. 2022, 10, 136. [Google Scholar] [CrossRef]
- Liu, J.-S.; Bozzola, R. Three-dimensional Navier-Stokes analysis of tip clearance flow in linear turbine cascades. AIAA J. 1993, 31, 2068–2074. [Google Scholar] [CrossRef]
- Nikiforova, K.; Semenov, G.; Kuznetsov, I.; Spiridonov, E. Numerical investigation of tip clearance cavitation in Kaplan runners. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 092008. [Google Scholar] [CrossRef]
- Kim, H.-H.; Rakibuzzaman, M.; Kim, K.; Suh, S.-H. Flow and fast fourier transform analyses for tip clearance effect in an operating Kaplan turbine. Energies 2019, 12, 264. [Google Scholar] [CrossRef]
- Wang, L.K.; Lu, J.L.; Liao, W.L.; Zhao, Y.P.; Wang, W. Numerical simulation of the tip leakage vortex characteristics in a semi-open centrifugal pump. Appl. Sci. 2019, 9, 5244. [Google Scholar] [CrossRef]
- Zhou, J.L. Selection problems for pump station equipment. Drain. Irrig. Mach. 2001, 19, 3–12. [Google Scholar]
- Osterwalder, J. Efficiency scale-up for hydraulic turbo-machines with due consideration of surface roughness. J. Hydraul. Res. 2010, 16, 55–76. [Google Scholar] [CrossRef]
- Zheng, Y.C.; He, Z.R.; Chen, J.; Liu, D.X. Discussion on conversion method of performance parameters of the large pump unit. J. Hydraul. Eng. 1995, 10, 47–52. [Google Scholar]
- Hutton, S.P. Component losses in Kaplan turbines and the prediction of efficiency from model tests. Proc. Inst. Mech. Eng. 1954, 168, 743–762. [Google Scholar] [CrossRef]
- Ida, T. Analysis of scale effects on performance characteristics of hydraulic turbines—Part I. J. Hydraul. Res. 1989, 27, 809–831. [Google Scholar] [CrossRef]
- Ida, T. Analysis of scale effects on performance characteristics of hydraulic turbines—Part II. J. Hydraul. Res. 1990, 28, 93–104. [Google Scholar] [CrossRef]
- Ida, T. New formulae for scaling-up hydraulic efficiency of hydraulic turbines. J. Hydraul. Res. 1995, 33, 147–162. [Google Scholar] [CrossRef]
- Chen, S.S.; Ma, X.Z.; Chen, J.Q.; Zhou, Z.F.; He, Z.N. The conversion method of characteristic parameters of pump and pump set between prototype and model. J. Yangzhou Univ. (Nat. Sci. Ed.) 2015, 18, 45–48. [Google Scholar]
- McCormick, B.W. On cavitation produced by a vortex trailing from a lifting surface. J. Basic Eng. 1962, 84, 369–378. [Google Scholar] [CrossRef]
- Ren, J.; Chang, J.S. The scale effect of cavitation in the large hydraulic unit. Water Resour. Hydropower Eng. 1998, 29, 22–25. [Google Scholar]
- Ni, H.G. Correction of incipient cavitation coefficient for scale effect. J. Hydraul. Eng. 1999, 30, 28–32. [Google Scholar]
- Angulo, M.; Luciano, C.; Botero, F.; Rivetti, A.; Liscia, S. Dynamic measurements on a Kaplan turbine: Model—Prototype comparison. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 022006. [Google Scholar] [CrossRef]
- Angulo, M.; Rivetti, A.; Díaz, L.; Liscia, S. Air injection test on a Kaplan turbine: Prototype—Model comparison. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 022006. [Google Scholar] [CrossRef]
- Zeng, C.J.; Xiao, Y.X.; Zhang, J.; Gui, Z.H.; Wang, S.H.; Luo, Y.Y.; Fan, H.G.; Wang, Z.W. Numerical prediction of hydraulic performance in model and homologous prototype Pelton turbine. IOP Conf. Ser. Earth Environ. Sci. 2018, 163, 012016. [Google Scholar] [CrossRef]
- Li, Z.J.; Wang, Z.W.; Bi, H.L. Numerical study of similarity in prototype and model pumped turbines. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 032049. [Google Scholar] [CrossRef]
- Guo, Q. Study on the Characteristics of the Blade Tip Leakage Vortex Flow and the Cavitating Flow Field. Ph.D. Thesis, Agricultural University, Beijing, China, 2017. [Google Scholar]
- Zhang, Y.L.; Wu, Y.B.; Wei, J.W.; Wang, Z.W.; Zhou, L.J. Clearance flow field characteristics of Kaplan turbine under different flange clearance. IOP Conf. Ser. Earth Environ. Sci. 2022, 1037, 012023. [Google Scholar] [CrossRef]


| Geometry | Prototype | Model |
|---|---|---|
| Runner diameter D1 | 29.71 Dm | Dm |
| Stay vanes Zs | 25 | 25 |
| Guide vanes Zg | 28 | 28 |
| Runner blades Z | 6 | 6 |
| shroud clearance width ω | 4% Dm~4.57% Dm | 1.34‰ Dm~1.54‰ Dm |
| Computational Domain | Q* | H* | P* | η | CP |
|---|---|---|---|---|---|
| Whole passage | 0.545 | 0.266 | 1349 | 95.13% | −0.929 |
| Single-blade | 0.541 | 0.263 | 1324 | 95.19% | −1.074 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Luo, W.; Chen, T.; Zhou, L.; Wang, Z. Study on the Cavitation Characteristics of Shroud Clearance in Prototype and Model of a Kaplan Turbine. Water 2023, 15, 3960. https://doi.org/10.3390/w15223960
Zhang Y, Luo W, Chen T, Zhou L, Wang Z. Study on the Cavitation Characteristics of Shroud Clearance in Prototype and Model of a Kaplan Turbine. Water. 2023; 15(22):3960. https://doi.org/10.3390/w15223960
Chicago/Turabian StyleZhang, Yali, Wendong Luo, Tao Chen, Lingjiu Zhou, and Zhengwei Wang. 2023. "Study on the Cavitation Characteristics of Shroud Clearance in Prototype and Model of a Kaplan Turbine" Water 15, no. 22: 3960. https://doi.org/10.3390/w15223960





