Abstract
Speed governing control is significant in ensuring the stable operation of pumped storage units. In this study, a state-space equation mathematical model of the pumped storage governing system considering the complex hydraulic pipeline structure of the pumped storage plant is proposed to describe the system’s dynamic behaviors under small disturbance conditions. Considering the frequent operating condition transitions and the complicated nonlinear dynamic characteristics of the pumped storage units, the fractional-order PID (FOPID) scheme that possesses a higher degree of control freedom than the traditional PID scheme is discussed in detail. To optimize the control parameters of the unit governor, an improved gravitational search algorithm (IGSA) that combines the basic searching mechanisms of the gravitational search algorithm and chaotic search, elastic sphere boundary treatment, and elite guidance strategy is developed. Comparative studies have been carried out under frequency and load disturbance conditions. Simulation results indicate that the control performance of FOPID is better than that of PID under diverse operating conditions and the proposed IGSA has satisfactory parameter optimization capability.
1. Introduction
With the gradual increase in the proportion of new energy sources such as wind power and solar energy in the electrical network [1,2], pumped storage is becoming more and more important as an effective regulation power source [3]. As the core control system of pumped storage units, the pumped storage governing system (PSGS) undertakes the important tasks of manipulating the start-up and shutdown of the unit, the working condition conversions, and the peak regulation and frequency regulation [4]. PSGS is a nonlinear complex system, which may present complicated dynamic behavior during operation. Therefore, the establishment of an accurate and effective simulation model [5] as well as the optimization of governor control parameters [6] can achieve a better control effect on the unit and ensure the stable operation of the unit.
With the development of pumped storage power plants, extensive studies have been reported on the modeling and control of PSGS. A typical PSGS consists of a hydraulic system, pump-turbine, generator, governor and electro-hydraulic servomechanism [7]. In system modeling, the PSGS is similar to the conventional hydraulic turbine governing system (HTGS) in turbine mode. Usually, time-domain models are utilized to simulate the evolution of state variables during the transition process. The state-of-the-art methods include the method of characteristics (MOC) [8,9], the finite difference method [8,10], and the differential equation model [10], etc. Under small disturbance conditions, the system model ignores the system nonlinearities and selects a rigid water hammer model for the pipes and six-parameter model for the pump-turbine [11]; hence, the PSGS model can be described by linearized state space equations [12]. For the speed governor, PID controller is the most commonly used for PSGS due to its structural simplicity and applicability. With the in-depth study of PID control laws, PID-like control laws such as nonlinear PID [13] and FOPID [14] are increasingly used. FOPID is widely used in various engineering fields [15], e.g., the chemical industry [16], nuclear power [17], and aerospace [18]. Compared with traditional PID control, FOPID control possesses two more adjustable parameters, i.e., the differential order and the integral order. It allows the FOPID controller to have better robustness and control performance than the PID controller, but at the same time increases the difficulty of parameter optimization [19].
In pumped storage regulation systems, the governor is a very important component. The system’s control performances are mainly decided by the tunable control parameters, and the optimization of these parameters can prominently enhance the system stability level. For the controller parameter optimization problem, the traditional rectification methods include the orthogonal test approach [20] and the simplex approach [21]. Although these methods are simple to operate, they are not accurate enough to obtain the optimal parameters under complex operating circumstances. The meta-heuristic algorithms [22] (MA) have achieved better results in optimizing the controller parameters of hydropower units. MA include the Genetic Algorithm [23] (GA) based on Darwinian evolutionary theory, the Particle Swarm Optimization algorithm [24] (PSO) based on bird predation, the Differential Evolution Algorithm [25] (DEA) that uses the differences between random vectors to generate new vectors, the Gradient Descent Algorithm [26] (GDA) that uses the gradient search algorithm to keep approaching the optimal result, the Pattern Search Algorithm [27] (PSA) with axial exploration in the direction of feasible descent, and the Simulated Annealing Algorithm [28] (SA) based on the annealing process of solids. The Sine Cosine Algorithm (SCA) achieves close to the optimal result by the exact solution of the sine–cosine function [29], and the Gravity Search Algorithm [30] (GSA) based on gravity, etc. Unlike GA and PSO, which are based on biological phenomena, GSA is an optimization method based on the laws of gravity and mass interaction in physics. GSA has been verified to be more efficient than other optimization methods in optimizing the controller parameters [31], but still suffers from localized and premature convergence problems. However, almost all of the above research works have used the conventional PID controller which ultimately leads to a sub-optimal response. The superiority of the FOPID controllers are demonstrated in the results of the research work in this paper.
The accuracy and efficiency of optimization algorithms are crucial in solving engineering problems. In recent years, scholars have performed various research works in related fields and proposed many effective improvement ideas, including boundary processing, strategy improvement, algorithm fusion and parameter improvement. To improve the capability of GSA, Li et al. [32] proposed an improved gravitational search algorithm combining PSO and GSA. Sarafrazi et al. [33] proposed fusing GSA with a physics-inspired Kepler algorithm to speed up the algorithm’s search and improve accuracy. Zhang et al. [34] designed and proposed a hybrid strategy based on Cauchy and Gaussian mutation to improve the exploration of GSA. Yin et al. [35] incorporate a cross-search in the GSA to improve the algorithm’s development capability. He et al. [36] introduced the concept of repulsive force and proposed an improved gravitational search algorithm under the joint effect of repulsive and gravitational forces. Tian et al. [37] combined the Water Cycle Algorithm (WCA) with the GSA and use the concepts of watersheds and evapotranspiration to enhance the search capability. Based on previous research, this paper proposes an improved GSA (IGSA) in which the following four improvement strategies are incorporated into the GSA. Firstly, the chaotic operator is added to increase the diversity of the population and the randomness of the search; secondly, the adaptive gravitational decay factor is introduced to improve the change rule of the gravitational constant; subsequently, the elastic sphere strategy is carried out in the searching boundary treatment process; finally, the population of elite particles are applied to accelerate the convergence rate of the algorithm.
When using MA to optimize controller parameters, defining a proper objective function is crucial for the optimization of results. Usually, the input of the objective function is the parameter to be optimized, and the output value is the fitness value. In this paper, we select an objective function that comprehensively takes account of the rotational speed error and the water pressure fluctuation during the transition process.
Most of the traditional models do not take into account the hydraulic structures of the pumped storage power plant, such as the surge tanks, and cannot reflect the transient processes of the crucial components. In order to improve the dynamic description ability of the model, this paper establishes an accurate state-space model of the PSGS which fully considers the hydraulic characteristics of the pipes, surge tanks and pump-turbine. In order to obtain better control performance, the FOPID controller with higher control degrees of freedom is chosen and compared to the conventional PID controller. In addition, the standard GSA algorithm was improved in this study to better optimize the control parameters.
The rest of this paper is organized as follows: In Section 2, the mathematical equations of the PSGS derived from the state-space equations are established. In Section 3, the fractional order calculus and the structure of the FOPID controller are introduced. Subsequently, Section 4 introduces the GSA algorithm and the proposed improvements. Then, the simulation results are analyzed in Section 5. Finally, the conclusions of this study are condensed in Section 6.
2. Mathematical Model
The hydroelectric power plant is an important component in the modern power system that converts water energy into electricity. Pumped storage power plant is a special kind of hydroelectric power plant, which uses water as an energy storage medium to store and manage electrical energy through the mutual conversion of electrical energy and potential energy.
The PSGS is composed of upstream and downstream reservoirs, penstock, surge tanks, pump-turbine, generator and speed governor. Water flows from the upstream reservoir through the diversion pipeline, upstream surge tank and penstock to the pump-turbine inlet, the kinetic energy of the running water drives the runner of the pump-turbine to rotate and generates mechanical energy, the shaft of the pump-turbine is connected to the generator and drives the generator rotor to rotate synchronously. The speed governor guarantees the system’s frequency stability by regulating the guide vane opening.
This paper divides the PSGS into five parts: hydraulic system, pump-turbine, generator and load, speed governor, and hydraulic servomechanism, with combined modeling of the PSGS based on mathematical models of each component.
2.1. Hydraulic Systems’ Modeling
A typical layout of a pumped storage plant with two surge tanks is shown in Figure 1. In order to study the control strategy for the speed governor, this work divides the PSGS into five parts: the hydraulic system, pump-turbine, generator and load, speed governor, and hydraulic servomechanism.
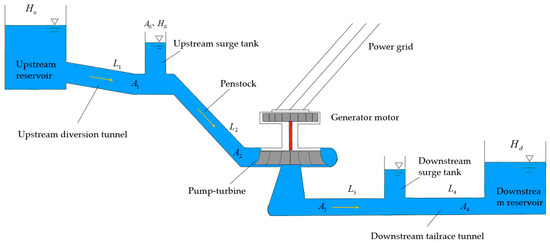
Figure 1.
Typical layout of a pumped storage plant with two surge tanks.
As shown in Figure 1, the water level of the upstream reservoir in the pumped storage power plant is (in meters), the cross-sectional areas of the diversion tunnel, penstock and downstream tailrace tunnel are ,,, (in square meters), the lengths are ,,, (in meters), the cross-sectional areas of the upstream and downstream surge tanks are ,, and the water levels are ,. Finally, a downstream reservoir with a water level of can be seen on the far right of the Figure 1, where the reservoir levels and are considered as constants.
2.1.1. Overall Pipeline Modeling
In applied hydraulic transients [38], if the pipe length is less than 600–800 m, or the governing system operates in small fluctuations conditions, the error of the rigid water hammer model can meet the engineering requirements.
If head loss is considered, the rigid water strike transfer function can be obtained as follows:
where is water inertia time constant; is the head loss of the tunnel.
As depicted in Figure 1, the overall pipeline is divided into three parts: the upstream diversion tunnel, the penstock and the downstream tailwater tunnel. Using the rigid water strike transfer function, the mathematical model of the dynamic relationship between these three sections of the tunnel is given below.
- Upstream diversion tunnel:
As displayed in Figure 1, the upstream diversion tunnel connects the upstream reservoir and the upstream surge tank. Since the upstream reservoir is constant, the water pressure deviation remains constant. The end of the diversion tunnel is connected to the upstream surge tank, so the pressure deviation of the surge tank can be considered the same as the pressure deviation of the diversion tunnel. The mathematical model of the upstream diversion tunnel is derived from the rigid water strike Equation (1):
where:
—water inertia time constant of the diversion tunnel;
—relative head loss of the diversion tunnel;
,—relative water pressure deviation of the diversion tunnel and the upstream surge tank;
—the relative flow deviation of the diversion tunnel.
- 2.
- Penstock:
As presented in Figure 1, the penstock connects the upstream surge tank and pump-turbine inlet, and the tailrace tunnel connects the pump-turbine outlet and downstream surge tank. The inertia of water flow is also considered in the penstock, and the mathematical model of the penstock is deduced as follows:
where:
,—water inertia time constant of the penstock and the tailrace tunnel;
,—relative head loss of the penstock and the tailrace tunnel;
,,—relative water pressure deviation of the upstream surge tank, the penstock and the tailrace tunnel;
—relative flow deviation of the pump-turbine.
- 3.
- Downstream tailwater tunnel
As displayed in Figure 1, the tailrace tunnel connects the downstream surge tank and the downstream reservoir, the downstream reservoir is constant and the water pressure deviation is kept constant, the mathematical model of the downstream tailrace tunnel is deduced as follows:
where
—water inertia time constant of the downstream tailrace tunnel;
—relative head loss of the downstream tailrace tunnel;
—relative water pressure deviation of the downstream tailrace tunnel;
—relative flow deviation of the downstream tailrace tunnel.
2.1.2. Surge Tank Modeling
As shown in Figure 1, the upstream and downstream surge tanks are straight cylinder surge tanks. The surge tank plays the role of reflecting water hammer waves and reducing water hammer pressure. In omitting the surge tank inlet damping, the straight cylinder surge tank can be described as:
where:
—water level in the surge tank changes, and water level rises as positive;
—flow in and out of the surge tank, inflow is positive;
—cross-sectional area of the surge tank.
Taking the relative value of Equation (5):
where:
—time constant of the surge tank;
—relative water pressure deviation;
—relative flow deviation.
Considering the flow continuity, the relationship between the flows in the upstream and downstream surge tanks can be deduced as follows [38]:
where ,,,, respectively, are the relative flow deviations of the penstock, the tailrace tunnel, the upstream surge tank, and the downstream surge tank.
2.2. Pump-Turbine Modeling
For the study of the mathematical model of the pump-turbine, a six-parameter linear model can be used to describe the dynamic characteristics of the hydraulic turbine for small fluctuation problems, and the parameters of the pump-turbine are shown in Appendix A, and near a stable operating point, the linear model of the hydraulic turbine can be expressed as [11]:
where:
—relative value of hydraulic turbine torque deviation;
—relative value of hydraulic turbine head deviation;
—relative value of rotation speed deviation;
—relative value of guide vane opening deviation;
The six transfer functions are , , , , , .
2.3. Generator Modeling
In the modeling of the governing system of a pumped storage power plant, the most frequently used model for the synchronous generator is the first-order model. That is, considering only the dynamic response process of rotor motion, and treating the generating motor as a rotating rigid shaft, which is coaxial with the pump-turbine and connected by a coupling, and the parameters of the generator are shown in Appendix B. The dynamic model considering the load is expressed as [11]:
where:
—load torque;
—load self-regulation factor;
—time constant of mechanical inertia of the generator, expressed as:
where is the flywheel torque of the rotating part of the unit; is the rated speed of the unit; is the rated output of the unit.
The transition process of the pumped storage power plant governing system, the change in is usually regarded as a load disturbance to the PSGS.
2.4. Modeling of Electro-Hydraulic Servomechanism
The electro–hydraulic servomechanism is the actuator of the governor. It receives output signals from the controller and performs electro–hydraulic conversion and hydraulic amplification of the electrical control signals. Eventually, the electrical signal is converted into the displacement signal of the receiver. The electro–hydraulic servo mechanism is usually simplified to a first-order inertia link, as stated in Equation (10) [39],
where:
—control signal output by the controller;
—stroke of the servo motor;
—servomotor response time.
2.5. PSGS Model
Based on the separate mathematical models of each link of the governing system of the pumped storage power plant established earlier, a block diagram of the transfer function of the pumped storage power plant governing system can be obtained, as presented in Figure 2:
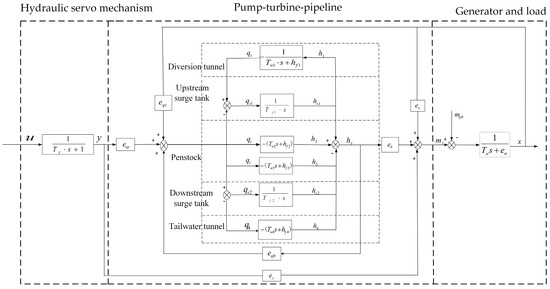
Figure 2.
Block diagram of the transfer function of the pumped storage power plant governing system.
As shown in Figure 2, the physical state variables , , , , , , , that can be measured, are chosen to describe the overall PSGS model in the form of the state space equations, as displayed in Equation (11),
Based on the mathematical model of the penstock, the equation is discretized, and the flow values obtained using adjacent discrete sampling times are used to calculate , then, , can be expressed as:
3. Fractional PID Algorithm of the Speed Governor
3.1. Definition of Fractional Calculus
Fractional calculus [40] is a mathematical theory that studies the properties of calculus and integral operators of arbitrary order, and it extends the order of calculus to the field of fractions and even plurals. Fractional calculus is a generalization of differentiation and integration of non-integer order, and its operation basic operation operator is (, is the upper and lower bounds of the operation operator, is the order of the calculus).
The calculus operation operator unifies the differentiation and integration, and a variety of definitions of fractional calculus emerge from the theory of fractional calculus, such as the definition, the () definition, the () and the definition etc.
In this paper, using the definition, the calculus of order for a certain continuously derivable function is:
where . is the largest integer smaller than the real number , and is the calculation step.
3.2. FOPID Controller Structure
Compared with the traditional integer-order PID, FOPID controller introduces differential order and integral order , which has two more degrees of freedom and can achieve better control effects. The PID and FOPID structure diagrams are given in Figure 3. The transfer function of the FOPID controller can be expressed as:
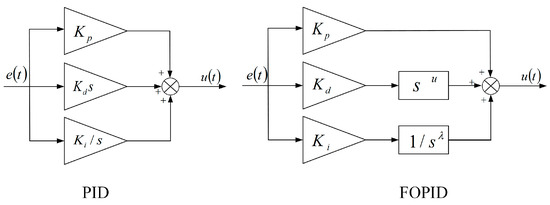
Figure 3.
Comparison of the PID and FOPID structure diagram.
Its time domain expression is:
where is the error signal, is the controller output signal, ,, are the controller gain parameters, , are the fractional calculus orders, and , . When , the FOPID controller is transformed into the integer-order PID controller.
4. Improved Chaotic Gravitational Search Algorithm
4.1. Standard Gravitational Search Algorithm
Inspired by the law of universal gravity, Rashedi et al. proposed a new swarm intelligence optimization algorithm—the gravitational search algorithm (GSA) in 2009 [30]. The law of gravity is a law that explains the relationship between objects interacting with each other. In the gravitational search algorithm, gravity is equivalent to an information transfer tool that enables information sharing among individuals and optimal search by the group under the effect of gravity.
Assuming that there are N particles, the position and velocity of the ith individual in the D-dimensional space are denoted as and , where and , respectively, denote the position and velocity components of individual in the d-dimensions, and the position denotes the solution of the problem. The position and velocity are first initialized in the solution space and velocity space, the objective function values of each individual are calculated and evaluated, the mass, gravitational force and acceleration of each individual are calculated, and finally the velocity and position of the individual are updated [41].
According to Newton’s gravitation theory, in the dimensions, the gravitational force of individual j on is expressed as:
where , , respectively, are the universal gravitational constants at the tth iteration and the Euclidean distances of individuals and j, with the following expressions:
where , and are constants, is the current number of iterations and is the maximum number of iterations, , and .
In the dimensions, the combined force on individual is:
where is a random variable obeying a uniform distribution between , and is the collection of the top individuals with the optimal fitness value and maximum quality.
The updated velocity and position can be obtained as:
4.2. Improved Gravitational Search Algorithm (IGSA)
In order to improve the global search capability of GSA and avoid falling into a local optimum, the following four improvement strategies are incorporated in this paper:
Chaos operator.
Chaos [42] is a seemingly random movement that cannot be repeated precisely that occurs in nature. Chaotic motion is a complex state of motion unique to deterministic nonlinear dynamical systems, it has characteristics such as class randomness, initial value sensitivity, and ergodicity.
Chaos mapping is a mapping (evolutionary function) that exhibits some chaotic behavior, some common chaos mappings include Logistic map, Sinusoidal map, Tent map, Sine map and Bernoulli map.
In this paper, we introduce the chaos operator to improve the GSA by choosing the ergodic logistic mapping, namely:
where control parameters , and , is the number of chaos generated in the tth iteration.
In the position update phase, chaos sequences are introduced to improve the convergence of the algorithm, while chaos perturbations can help individuals escape from their current position when they fall into a local optimum. The steps are as follows:
(1) A d-dimensional random vector is generated, and the control parameter , that is a fully chaos state is reached by Equation (20): , , generating a chaos vector with denoting the number of individuals;
(2) The generated chaos vector is added to the search space, at which point the speed update equation in the improved algorithm is:
where is the factor that controls the range of chaos;
(3) Using the improved velocity update equation to calculate the position at the next moment:
Adaptive universal gravitational constant decay factor.
From the gravitational force calculation Equation (16), we can see that the universal gravitational constant is positively related to the gravitational force value, and its value plays an important role in the calculation of the gravitational force. When takes a larger value, the search range of the algorithm is wider to avoid falling into the local optimum, while when takes a smaller value, the algorithm can better converge to the global optimum. From Equation (17), it can be seen that the universal gravitational constant decay factor in the standard GSA is taken as a constant, which limits the performance of the algorithm. Therefore, an adaptive universal gravitational constant decay factor is proposed:
where is the initial value of the gravitational decay factor, and are scaling factors, , , is the shift factor, which is taken in this paper as , , 0, .
As the number of iterations increases, the universal gravitational constant shows a nonlinear decrease, then the improved algorithm has a large gravitational constant at the beginning to enhance the search ability, and the algorithm reduces the gravitational constant at the later stage to accelerate the convergence of the algorithm.
Elastic ball boundary treatment.
Boundary constraints are added when initializing individuals, but as the iteration proceeds, there may be individuals that cross the boundary after the position update, and for the individuals that cross the boundary, the elastic ball boundary is handled by:
It can be seen from Equation (24) that the elastic ball boundary treatment increases the individual positions, enhances the search capability of the algorithm, and reduces the risk of the algorithm falling into a local optimum.
Elite Guidance.
The velocity update formula of GSA only considers the effect of acceleration, while the velocity update in the particle swarm seeking algorithm takes into account the individual memory and group information exchange, it is more convergent for particle seeking. Therefore, the velocity update of IGSA combined with the chaos arithmetic and PSO velocity update mechanism is obtained:
where , are the adaptive learning factors that vary with the number of iterations, and denote the individual optimal position and the global optimal position in the d-dimensions, respectively.
Because the addition of the optimal position in the velocity update equation will reduce the search capability of the algorithm, the adaptive learning factor is added to balance the global search capability and local optimization capability of the algorithm. , update equations [43] are:
Based on the above improvement strategies, a new improved gravitational search algorithm (IGSA) is proposed in this paper with the following steps:
Step 1: Random initialization of the population and setting parameters. The setup parameters include the population size N, the maximum number of iterations T, the boundary of the position , the initial value of the universal gravitational force and the initial value of the gravitational decay factor . The population individual positions are randomly initialized.
Step 2: It is determined whether the updated individual position is out of bounds. The transgression uses the elastic ball boundary strategy of Equation (24) to assign a new position.
Step 3: Calculate the fitness value of all individuals in the population, and determine whether the fitness value is NaN (Not A Number) or not, if it is, then randomly initialize the position of the individual and calculate the fitness value again, and repeat this step until the fitness value is an output table value.
Step 4: Update global optimal position and individual optimal position , if < , then = , = .
Step 5: Calculating the individual mass , the gravitational parameter is calculated according to Equations (17) and (23), the gravitational force is calculated according to Equations (16) and (18), finally calculating the acceleration .
Step 6: The adaptive learning factor is calculated according to Equations (26), and the speed and position are updated according to Equations (25) and (19).
Step 7: The number of iterations , if , go to step 2, otherwise end the loop and obtain the optimal objective function value and the optimal position vector .
The algorithm flow chart of IGSA is indicated in Figure 4:
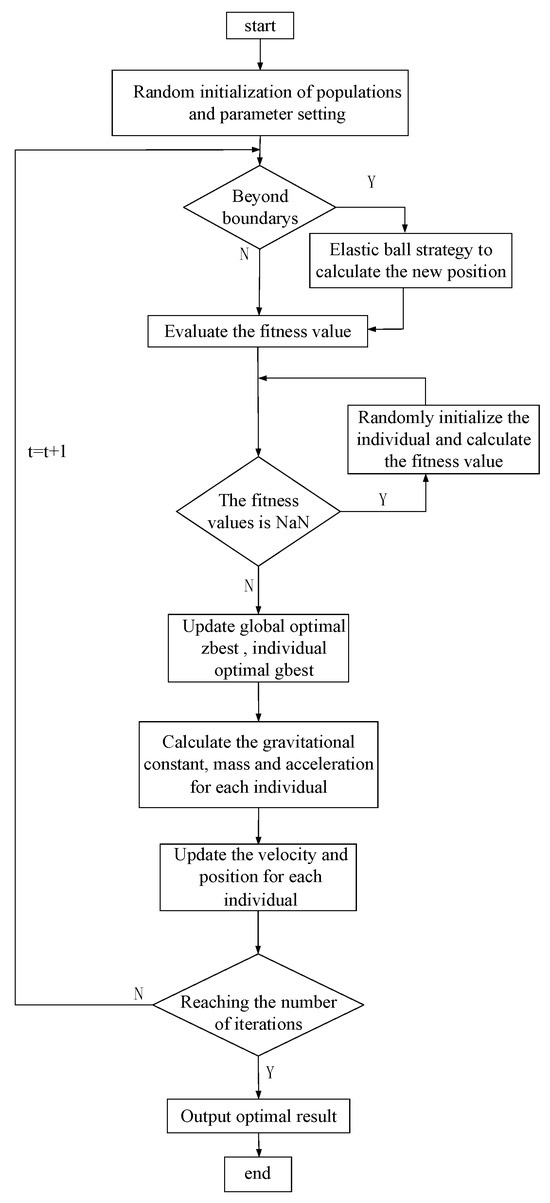
Figure 4.
Algorithm flow chart of IGSA.
4.3. Objective Function
Time multiplied by the integral of the absolute value of the error (ITAE) is often used as an evaluation index for the performance of the speed regulation system of hydropower units. The objective function proposed in this paper takes into account the rotational speed error value and the water pressure deviation. The calculated ratio of ITAE to the number of samples is taken as the first output, and the second output is the absolute value of water pressure deviation minimum value during the transition process. By adjusting the weights of both during the parameter optimization process to ensure that the two output values are approximately equal. The objective function can be presented as:
Its discrete expression is given by:
where , are weighting factors, is the number of samples, indicates the time sequence and indicates the minimum value of water pressure deviation.
5. Simulation Results Analysis
5.1. Simulation Parameter Setting
In this section, the HTGS model proposed in Section 2.5 is simulated in the MATLAB R2020b software environment, the simulation environment is under a 2.4 GHz inteli7 CPU and 16G RAM. Table 1 and Table 2 show the simulation parameters of HTGS and the transfer coefficients of the pump-turbine, respectively. The values of the boundary on the FOPID and PID tuning parameters are given in Table 3.

Table 1.
HTGS simulation parameters [44].

Table 2.
Transfer coefficients of water pump-turbine.

Table 3.
The values of the boundary on the FOPID and PID tuning parameters.
Based on the above unit parameters, the frequency disturbance and load disturbance simulation tests are performed in this study.
5.2. Load Disturbance Scenario
According to the model established in this paper, under a 10% load disturbance, the optimization performances of four parameter optimization algorithms (i.e., SA, GA, PSO and IGSA) and the control effects of the PID and FOPID are compared, respectively.
5.2.1. Comparison of SA, GA, PSO and IGSA
The parameters of SA are set as follows: initial temperature , termination temperature , temperature decay factor , maximum number of iterations , maximum number of iterations at temperature Lk = 30.
The parameters of GA are set as follows: population size , maximum number of iterations , crossover probability , variance probability .
The parameters of PSO are set as follows: population size , maximum number of iterations , learning factor , velocity weight .
The parameters of IGSA are set as follows: population size , maximum number of iterations , , the gravitational constant decay factor parameter is set the same as revealed in Section 4.2.
When the weight factor , , after 100 iterations, the convergence curves of the fitness functions of SA, GA, PSO and IGSA are shown in Figure 5:
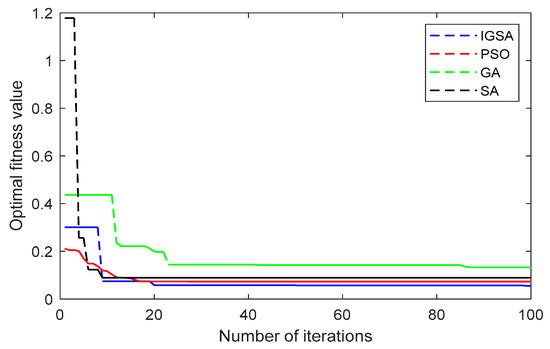
Figure 5.
Convergence curves of the fitness functions under load disturbance.
According to the fitness convergence trend displayed in Figure 5, it can be seen that among the four algorithms, the final fitness value of GA is the largest and that of IGSA is the smallest. From the convergence curve, SA starts with the largest fitness value and decreases the fastest, PSO decreases the fitness more slowly during the descent process, and GA converges the slowest. Comparing the final fitness values, it can be seen that SA, GA and PSO easily fall into the local optimum and have difficulty in jumping out of it, while the final fitness value of IGSA is smaller. This shows that as the number of iterations increases, the fitness value of IGSA has been decreasing. The chaos perturbations added in the position update phase enables IGSA to jump out of the local optimum continuously, which indicates that IGSA has better global exploration ability.
Table 4 shows the dynamic indicators for SA, GA, PSO and IGSA with optimal control parameters:

Table 4.
Dynamic indicators of SA, GA, PSO and IGSA optimal control parameters under load disturbance.
Figure 6 compares the relative values of rotation speed deviation , guide vane opening deviation and hydraulic turbine head deviation variation curves under the optimal control parameters of SA, GA, PSO and IGSA during load disturbance:

Figure 6.
Variation curves of of four algorithms under load disturbance.
Combining Table 4 and Figure 6, the dynamic indexes under the optimal control parameters of IGSA are significantly better than the other three algorithms. In Table 4, IGSA has the smallest objective function, stabilization time and absolute value of the minimum value of water pressure deviation. It can also be seen in Figure 6 that the unit speed deviation transition process optimized by the IGSA algorithm is significantly improved compared to the other three algorithms. The speed increase process is smoother, the stabilization time is shorter, and the absolute value of the minimum value of the water pressure deviation is also the smallest, which achieves better control parameter optimization. Overall, the transition process of , , under the optimal control parameters of IGSA is obviously improved.
5.2.2. Comparison of PID and FOPID
In order to prove that FOPID control has a better control effect than PID control in the parameter optimization of pumped storage speed regulation systems, tests select the optimal control parameters for both controls. Figure 7 compares , and variation curves of the model under the load disturbance of the two controllers:

Figure 7.
Variation curves of of two controllers under load disturbance.
Table 5 shows the dynamic indicators for PID and FOPID with optimal control parameters:

Table 5.
Dynamic indicators of PID and FOPID optimal control parameters under load disturbance.
In Figure 7, it is obvious that the dynamic performance of the FOPID controller is significantly better than that of the PID controller during load disturbance. From the data presented in Table 5, it can be concluded that the values of the objective function, stabilization time and absolute value of the minimum value of water pressure deviation under the FOPID control are reduced by 0.0053, 19 and 0.0042, respectively, which verifies the superiority of the FOPID control.
5.3. Frequency Disturbance Scenario
Under a 5% frequency disturbance, this section compares four different parameter optimization algorithms of SA, GA, PSO and IGSA and the control effects of the two controllers PID and FOPID.
5.3.1. Comparison of SA, GA, PSO and IGSA
The SA, GA, PSO and IGSA parameters are set the same as in Section 5.2.1. When the weight factor , , after 100 iterations, the convergence curves of the fitness functions of SA, GA, PSO and IGSA are displayed in Figure 8:
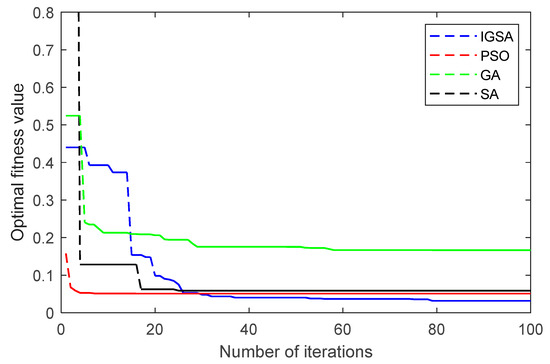
Figure 8.
Convergence curves of the fitness functions under frequency disturbance.
According to the fitness convergence trend displayed in Figure 8, in the 5% frequency disturbance, SA starts with the largest fitness value and the fitness value falls into the local optimum after two decreases, PSO falls into the local optimum after about seven iterations, and GA has the largest fitness value after the continuous optimization search. Comparing the final fitness values of the four algorithms, it is observed that SA, GA and PSO easily fall into the local optimum and have difficulty jumping out of it. The proposed IGSA has a wider search range and better search capability, and the optimal fitness value decreases continuously during the iterative process. It proves that the IGSA has better applicability and explorability.
Table 6 shows the dynamic indicators for SA, GA, PSO and IGSA with optimal control parameters:

Table 6.
Dynamic indicators of SA, GA, PSO and IGSA optimal control parameters under frequency disturbance.
Figure 9 compares , and variation curves under the optimal control parameters of SA, GA, PSO and IGSA during frequency disturbance:

Figure 9.
Variation curves of of four algorithms under frequency disturbance.
Combining Table 6 and Figure 9, the dynamic indexes under the optimal control parameters of IGSA are significantly better than the other three algorithms. In Table 6, the values of the objective function, overshoot, stabilization time and absolute value of the minimum value of water pressure deviation of IGSA are lower than the other three algorithms. From Figure 9, the speed deviation transition process of the unit optimized by the IGSA algorithm is significantly improved compared to the other three algorithms. The speed increase process is smoother and reaches stability faster, the speed overshoot is almost nothing, and the absolute value of the minimum value of the hydraulic pressure deviation is also the smallest, which achieves a better optimization of the control parameters. In conclusion, the transition process of , , under the optimal control parameters of IGSA is obviously improved.
5.3.2. Comparison of PID and FOPID
Figure 10 compares , and variation curves of the model under the frequency disturbance of the two controllers:

Figure 10.
Variation curves of of two controllers under frequency disturbance.
Table 7 shows the dynamic indicators for PID and FOPID with optimal control parameters:

Table 7.
Dynamic indicators of PID and FOPID optimal control parameters under frequency disturbance.
It is evident from Figure 10 that the FOPID controller achieves better results in PSGS control at frequency disturbance. By analyzing the results of each parameter in Table 6, it is found that the values of the objective function, overshoot, stabilization time and absolute value of the minimum value of water pressure deviation are reduced by 0.0198, 43.7%, 13.7 and 0.0255, respectively. Combined with Table 7 and Figure 10, it is found that under frequency disturbance, the adjustment quality improvement under FOPID control is more obvious.
5.4. Results Analysis
Through the frequency disturbance and load disturbance tests on the model, comparing the four algorithms of SA, GA, PSO and IGSA, it is proved that the optimization results of IGSA are better than those of SA, GA and PSO, and IGSA has better search ability, while the FOPID parameters optimized by IGSA can make the pumped storage regulation system have better dynamic performance; comparing the control effects of both FOPID and PID controllers, it can be seen that the dynamic performance obtained through the action of the FOPID controller is better than that of the PID controller.
6. Conclusions
This paper establishes a simulation model of a pumped storage speed regulation system with double surge tanks and compares the control effects of two controllers PID and FOPID. The IGSA is proposed to optimize the governor parameters. By comparing the convergence curves of the fitness function under load disturbance and frequency disturbance, it is verified that the IGSA proposed in this paper has better search capability than SA, GA and PSO, and it can address the algorithm precociousness and the local optimum trapping problem. In addition, under load disturbance and frequency disturbance, comparing the control effects under two different controllers PID and FOPID, it is found that FOPID has better comprehensive control performances.
In summary, the main contribution of this paper lies in the following two aspects:
(1). A new PSGS state-space equation model which fully considers the hydraulic characteristics of the pipes, surge tanks and pump-turbine and the eletromechanical behaviors of the generator and hydraulic servomechanism is proposed.
(2). An improved GSA optimizer combining the basic searching mechanisms of the gravitational search algorithm and chaotic search, elastic sphere boundary treatment, and elite guidance strategy is developed for the control parameter optimization of the FOPID scheme. Through comparative case studies under load disturbance and frequency disturbance, it is proved that the proposed IGSA shows superiority over parameter optimizers on governor parameter optimization.
Future work will also focus on comparing simulation results with experimental results.
Author Contributions
Conceptualization, Y.Z. (Yang Zheng) and X.Z.; writing—original draft preparation, X.Z.; methodology, B.X.; writing—review and editing, W.L. and Y.Z. (Yidong Zou); visualization, J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Hubei Provincial Nature Science Foundation of China [Grant No. 2022CFD165] and the Fundamental Research Funds for the Central Universities (Grant No. 2042022kf1022).
Data Availability Statement
For the sake of information security, the original data used in this paper will not be disclosed.
Conflicts of Interest
B.X. was employed by the company Technology and Research Center, China Yangtze Power Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclature
| PSGS: | |
| water inertia time constant | |
| head loss of the tunnel | |
| water inertia time constant of diversion tunnel, penstock, tailrace tunnel and downstream tailrace tunnel | |
| relative water pressure deviation | |
| relative water pressure deviation of upstream surge tank and downstream tailrace tunnel | |
| relative water pressure deviation of the diversion tunnel, penstock, tailrace tunnel | |
| relative head loss of diversion tunnel, penstock, tailrace tunnel and downstream tailrace tunnel | |
| relative flow deviation | |
| relative flow deviation of diversion tunnel, penstock, tailrace tunnel, downstream tailrace tunnel, upstream surge tank and downstream surge tank | |
| water level in the surge tank changes | |
| flow in and out of surge tank | |
| cross-sectional area of surge tank | |
| time constant of surge tank | |
| time constant of upstream surge tank and downstream surge tank | |
| relative value of hydraulic turbine torque deviation | |
| relative value of hydraulic turbine head deviation | |
| relative flow deviation of the pump-turbine at moments and | |
| relative value of rotate speed deviation and guide vane opening deviation | |
| stroke of the servo motor | |
| partial derivatives of the torque with respect to head, guide vane and turbine speed | |
| partial derivatives of the flow with respect to head, guide vane and turbine speed | |
| time constant of mechanical inertia of the generator | |
| load torque | |
| load self-regulation factor | |
| synthetic self-regulation coefficient | |
| flywheel torque of rotating part of the unit | |
| rated speed of the unit | |
| rated output of the unit | |
| control signal output by the controller | |
| servomotor response time | |
| FOPID: | |
| operation basic operation operator of fractional calculus | |
| upper and lower bounds of the operation operator | |
| order of the calculus | |
| calculation step | |
| the largest integer smaller than the real number | |
| proportional adjustment coefficient | |
| integral adjustment coefficient | |
| differential adjustment coefficient | |
| error signal | |
| controller output signal | |
| integral order and differential order | |
| s | the Laplace operator |
| IGSA: | |
| the position and velocity components of individual in the d-dimensions | |
| gravitational force of individual j on | |
| the universal gravitational constants at the tth iteration and the Euclidean distances of individuals and j | |
| gravitational constant | |
| , | current number of iterations and the maximum number of iterations |
| a random variable obeying a uniform distribution between | |
| the collection of the top individuals with the optimal fitness value and maximum quality | |
| the acceleration of individual in the d-dimensions | |
| the number of chaos generated in the tth iteration | |
| chaos control parameters | |
| a d-dimensional random vector | |
| factor that controls the range of chaos | |
| initial value of the gravitational decay factor | |
| , | scaling factors |
| shift factor | |
| , | the upper and lower boundaries of the positions of the individuals in d-dimension |
| , | adaptive learning factors |
| , | individual optimal position and the global optimal position in the d-dimensions |
| fitness value | |
| , | weighting factors |
| , | the number of samples and time sequence |
| the minimum value of water pressure deviation |
Appendix A

Table A1.
The parameters of the pump-turbine.
Table A1.
The parameters of the pump-turbine.
| Parameters | Values |
|---|---|
| Rated rotation speed | 500 r/min |
| Power frequency | 50 Hz |
| Maximum head | 565 m |
| Rated head | 540 m |
| Minimum head | 526 m |
| Rated discharge | 62.09 m3/s |
| 100% GVO | 20.47° |
| Rated Power output | 300 MW |
Appendix B

Table A2.
The parameters of the generator.
Table A2.
The parameters of the generator.
| Parameters | Values |
|---|---|
| Rated capacity (generator) | 334 MVA |
| Rated power (generator) | 300 MW |
| Rated capacity (electric motor) | 338 MVA |
| Rated power (electric motor) | 325 MW |
| Rated voltage | 15.75 kV |
| Power factor (generator) | 0.9 |
| Power factor (electric motor) | 0.975 |
| Rated rotation speed | 500 rpm |
| Number of rotor magnetic poles | 12 (Pole logarithm 6) |
| Rated frequency | 50 Hz |
References
- Liang, Y.Y.; Yu, B.Y.; Wang, L. Costs and benefits of renewable energy development in China’s power industry. Renew. Energy 2019, 131, 700–712. [Google Scholar] [CrossRef]
- Zhu, L.; Xu, Y.; Pan, Y.J. Enabled comparative advantage strategy in China’s solar PV development. Energy Policy 2019, 133, 9. [Google Scholar] [CrossRef]
- Barbour, E.; Wilson, I.A.G.; Radcliffe, J.; Ding, Y.L.; Li, Y.L. A review of pumped hydro energy storage development in significant international electricity markets. Renew. Sust. Energ. Rev. 2016, 61, 421–432. [Google Scholar] [CrossRef]
- Kong, Y.G.; Kong, Z.G.; Liu, Z.Q.; Wei, C.M.; Zhang, J.F.; An, G.C. Pumped storage power stations in China: The past, the present, and the future. Renew. Sust. Energ. Rev. 2017, 71, 720–731. [Google Scholar] [CrossRef]
- Jiang, X.P.; Chen, X.F.; Wang, Z.W.; IOP. Research on Modeling and Control Strategy of Hydraulic Turbine Governing System Based on Improved Genetic Algorithm. In Proceedings of the 30th IAHR Symposium on Hydraulic Machinery and Systems (IAHR), Electr Network, Lausanne, Switzerland, 21–26 March 2021. [Google Scholar]
- Jiang, C.W.; Ma, Y.C.; Wang, C.M. PID controller parameters optimization of hydro-turbine governing systems using deterministic-chaotic-mutation evolutionary programming (DCMEP). Energy Convers. Manag. 2006, 47, 1222–1230. [Google Scholar] [CrossRef]
- Yu, X.D.; Yang, X.W.; Zhang, J. Stability analysis of hydro-turbine governing system including surge tanks under interconnected operation during small load disturbance. Renew. Energy 2019, 133, 1426–1435. [Google Scholar] [CrossRef]
- Chaudhry, H.M. Applied Hydraulic Transients; Springer: London, UK, 2014. [Google Scholar]
- Ramos, H.M.; Coronado-Hernandez, O.E.; Morgado, P.A.; Simao, M. Mathematic Modelling of a Reversible Hydropower System: Dynamic Effects in Turbine Mode. Water 2023, 15, 2034. [Google Scholar] [CrossRef]
- Yang, J.D.; Wang, M.J.; Wang, C.; Guo, W.C. Linear Modeling and Regulation Quality Analysis for Hydro-Turbine Governing System with an Open Tailrace Channel. Energies 2015, 8, 11702–11717. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, D.Y.; Xu, B.B.; Wang, F.F. Nonlinear modeling and dynamic analysis of hydro-turbine governing system in the process of load rejection transient. Energy Convers. Manag. 2015, 90, 128–137. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, Q.J.; Yan, D.L.; Liu, W.Y. A two-stage numerical simulation framework for pumped-storage energy system. Energy Convers. Manag. 2020, 210, 18. [Google Scholar] [CrossRef]
- Ibrahim, A.A.S.; IEEE. Nonlinear PID controller design using fuzzy logic. In Proceedings of the 11th IEEE Mediterranean Electrotechnical Conference (IEEE MELECON 2002), Cairo, Egypt, 7–9 May 2002; pp. 595–599. [Google Scholar]
- Li, J.Y.; Chen, Q.J. Fractional Order Controller Designing with Firefly Algorithm and Parameter Optimization for Hydroturbine Governing System. Math. Probl. Eng. 2015, 2015, 11. [Google Scholar] [CrossRef]
- Padula, F.; Visioli, A. Tuning rules for optimal PID and fractional-order PID controllers. J. Process. Control. 2011, 21, 69–81. [Google Scholar] [CrossRef]
- Singh, A.; Sharma, V.; IEEE. Concentration Control of CSTR Through Fractional Order PID Controller by Using Soft Techniques. In Proceedings of the 4th International Conference on Computing, Communications and Networking Technologies (ICCCNT), Tiruchengode, India, 4–6 July 2013. [Google Scholar]
- Das, S.; Pan, I.; Das, S. Fractional order fuzzy control of nuclear reactor power with thermal-hydraulic effects in the presence of random network induced delay and sensor noise having long range dependence. Energy Convers. Manag. 2013, 68, 200–218. [Google Scholar] [CrossRef]
- Saraji, A.M.; Ghanbari, M. Fractional order PID controller for improvement of PMSM speed control in Aerospace Applications. In Proceedings of the 10th International Conference on Mathematical Problems in Engineering, Aerospace and Sciences (ICNPAA), Narvik Univ Coll, Narvik, Norway, 15–18 July 2014; pp. 959–967. [Google Scholar]
- Chen, Z.H.; Yuan, X.H.; Ji, B.; Wang, P.T.; Tian, H. Design of a fractional order PID controller for hydraulic turbine regulating system using chaotic non-dominated sorting genetic algorithm II. Energy Convers. Manag. 2014, 84, 390–404. [Google Scholar] [CrossRef]
- Li, Z.H.; Malik, O.P. An orthogonal test approach based control parameter optimization and its application to a hydro-turbine governor. IEEE Trans. Energy Convers. 1997, 12, 388–393. [Google Scholar] [CrossRef]
- Hedlund, P.; Gustavsson, A. Design and evaluation of an improved simplex method. Anal. Chim. Acta 1998, 371, 9–21. [Google Scholar] [CrossRef]
- Yang, X.S. Nature-inspired optimization algorithms: Challenges and open problems. J. Comput. Sci. 2020, 46, 8. [Google Scholar] [CrossRef]
- Rasheed, K.; Hirsh, H. Learning to be selective in genetic-algorithm-based design optimization. AI EDAM-Artif. Intell. Eng. Des. Anal. Manuf. 1999, 13, 157–169. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks—Conference Proceedings, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Ramezani, F.; Lotfi, S. The Modified Differential Evolution Algorithm (MDEA). In Proceedings of the 4th International Scientific Asian Conference on Intelligent Information and Database Systems (ACIIDS), Kaohsiung, Taiwan, 19–21 March 2012; pp. 109–118. [Google Scholar]
- Ahmadianfar, I.; Bozorg-Haddad, O.; Chu, X.F. Gradient-based optimizer: A new metaheuristic optimization algorithm. Inf. Sci. 2020, 540, 131–159. [Google Scholar] [CrossRef]
- Chun, J.; Wu, Y.L.; Dai, Y.F.; Li, S.Y. Fiber optic active alignment method based on a pattern search algorithm. Opt. Eng. 2006, 45, 045005. [Google Scholar] [CrossRef]
- Lv, P.; Yuan, L.; Zhang, J.F. Cloud theory-based simulated annealing algorithm and application. Eng. Appl. Artif. Intell. 2009, 22, 742–749. [Google Scholar] [CrossRef]
- Bhookya, J.; Jatoth, R.K. Optimal FOPID/PID controller parameters tuning for the AVR system based on sine-cosine-algorithm. Evol. Intell. 2019, 12, 725–733. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Norlina, M.S.; Mazidah, P.; Sin, N.D.M.; Rusop, M.; IEEE. Application of Metaheuristic Algorithms in Nano-process Parameter Optimization. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; pp. 2625–2630. [Google Scholar]
- Li, C.S.; Zhou, J.Z. Parameters identification of hydraulic turbine governing system using improved gravitational search algorithm. Energy Convers. Manag. 2011, 52, 374–381. [Google Scholar] [CrossRef]
- Sarafrazi, S.; Nezamabadi-Pour, H.; Seydnejad, S.R. A novel hybrid algorithm of GSA with Kepler algorithm for numerical optimization. J. King Saud. Univ.—Comput. Inform. Sci. 2015, 27, 288–296. [Google Scholar] [CrossRef]
- Zhang, N.; Li, C.S.; Li, R.H.; Lai, X.J.; Zhang, Y.C. A mixed-strategy based gravitational search algorithm for parameter identification of hydraulic turbine governing system. Knowl.-Based Syst. 2016, 109, 218–237. [Google Scholar] [CrossRef]
- Yin, B.Y.; Guo, Z.L.; Liang, Z.P.; Yue, X.Z. Improved gravitational search algorithm with crossover. Comput. Electr. Eng. 2018, 66, 505–516. [Google Scholar] [CrossRef]
- He, S.S.; Zhu, L.; Wang, L.; Yu, L.; Yao, C.H. A Modified Gravitational Search Algorithm for Function Optimization. IEEE Access 2019, 7, 5984–5993. [Google Scholar] [CrossRef]
- Tian, M.N.; Liu, J.H.; Yue, W.; Zhou, J. A Novel Integrated Heuristic Optimizer Using a Water Cycle Algorithm and Gravitational Search Algorithm for Optimization Problems. Mathematics 2023, 11, 1880. [Google Scholar] [CrossRef]
- Fang, H.Q.; Chen, L.; Dlakavu, N.; Shen, Z.Y. Basic Modeling and simulation tool for analysis of hydraulic transients in hydroelectric power plants. IEEE Trans. Energy Convers. 2008, 23, 834–841. [Google Scholar] [CrossRef]
- Zeng, Y.; Guo, Y.K.; Zhang, L.X.; Xu, T.M.; Dong, H.K. Nonlinear hydro turbine model having a surge tank. Math. Comput. Model. Dyn. Syst. 2013, 19, 12–28. [Google Scholar] [CrossRef]
- Shah, P.; Agashe, S. Review of fractional PID controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
- Jiang, S.H.; Wang, Y.; Ji, Z.C. Convergence analysis and performance of an improved gravitational search algorithm. Appl. Soft. Comput. 2014, 24, 363–384. [Google Scholar] [CrossRef]
- Lanza, M.L. Nonlinear dynamics: Chaos and catastrophe theory. J. Nurs. Care Qual. 2000, 15, 55–65. [Google Scholar] [CrossRef] [PubMed]
- Li, M.A.; Li-tao, L.I.U. Analysis and Improvement of Gravitational Search Algorithm. Microelectron. Comput. 2015, 32, 76–80. [Google Scholar] [CrossRef]
- Wei, S.P. Simulation of Hydraulic Turbine Regulation System; Huazhong University of Science and Technology Press: Wuhan, China, 2011; p. 457. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).