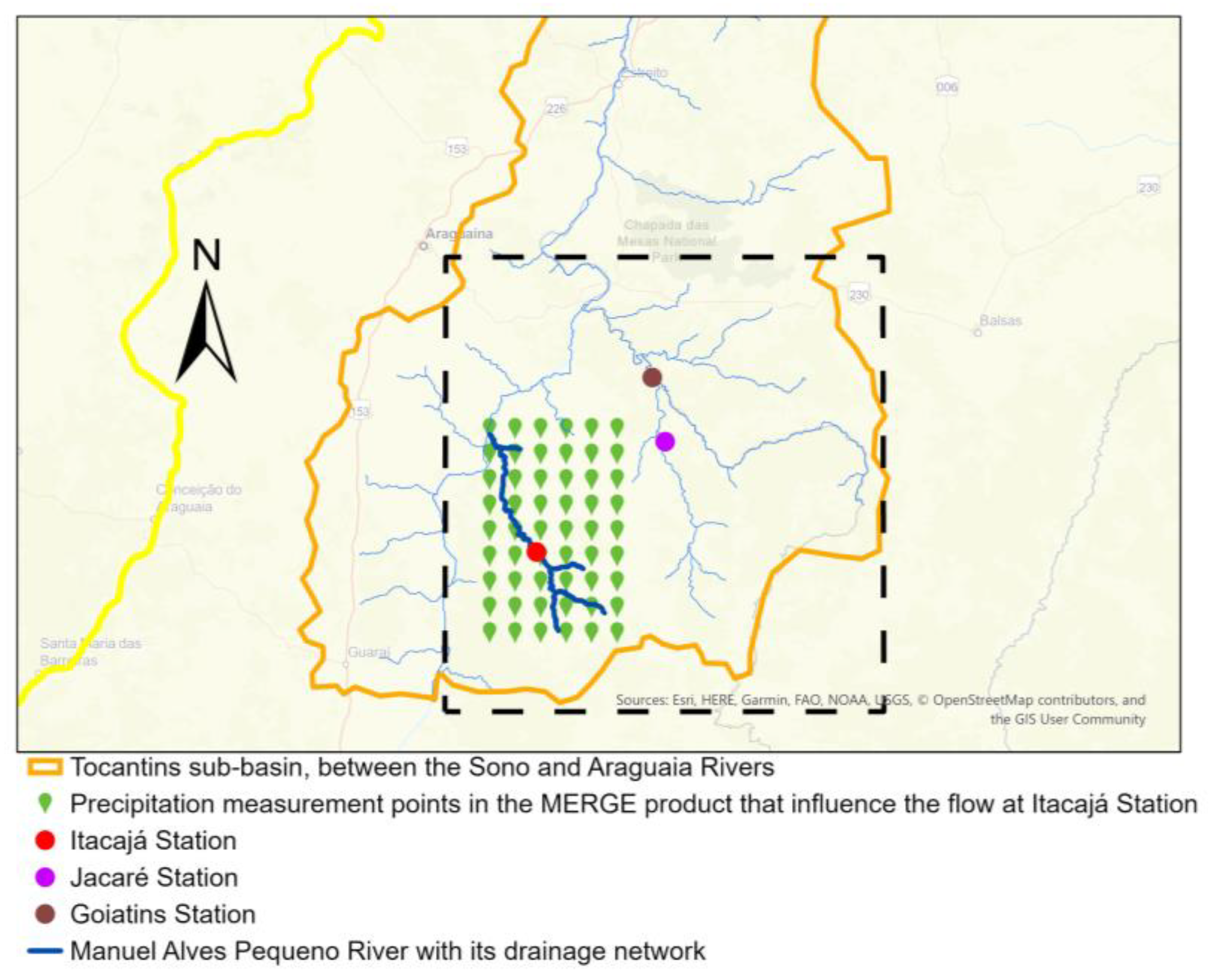
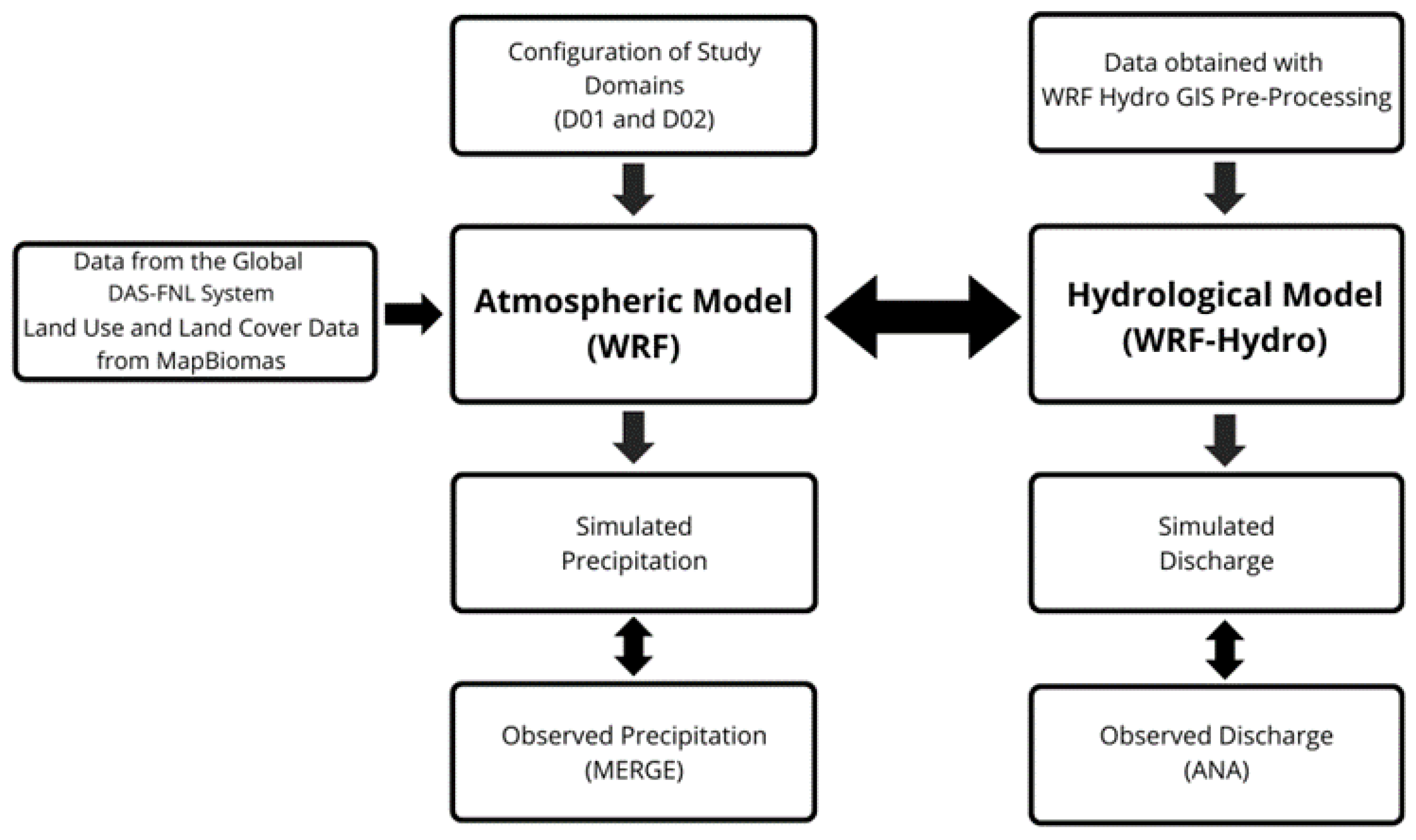
3.1. Sensitivity Tests of Hydrological Parameters in Itajacá
The calibration procedure for hydrological parameters was based on several studies in the literature [
16,
17,
19,
20,
49]. Sensitivity tests were initially conducted for the Manuel Alves Pequeno River using discharge data from the Itacajá station, focusing first on the REFKDT parameter that controls the hydrograph volume. Its default value is 3, with a feasible range from 0.1 to 10 [
20]. This parameter can significantly affect the simulated discharge values, depending on climatic conditions and runoff generation mechanisms in different watersheds. Even in a physics-based model like WRF-Hydro, adjusting REFKDT and the other three empirical parameters is inevitable, a result of our inability to model all processes [
48]. Based on the reviewed literature in this study, the values chosen for testing were 0.1, 0.3, 0.4, 0.5, 0.6, 1, 2, 3, and 4.
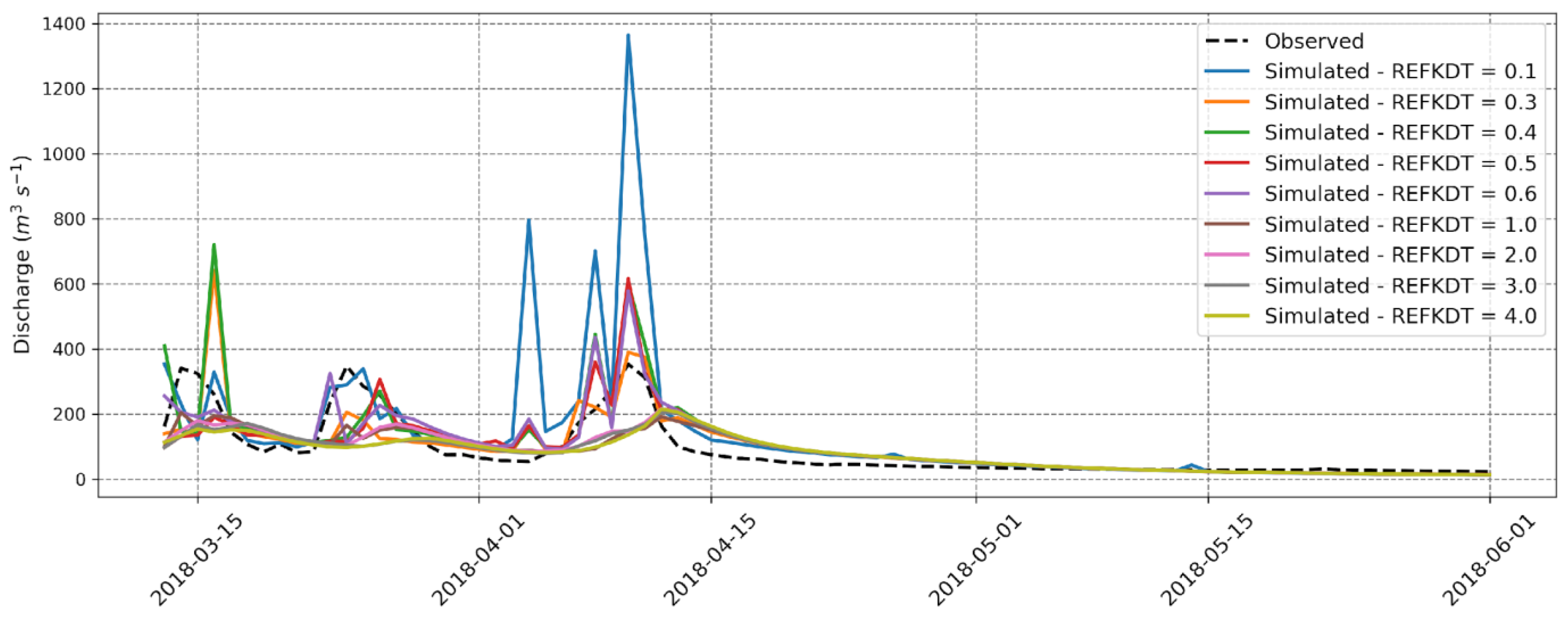
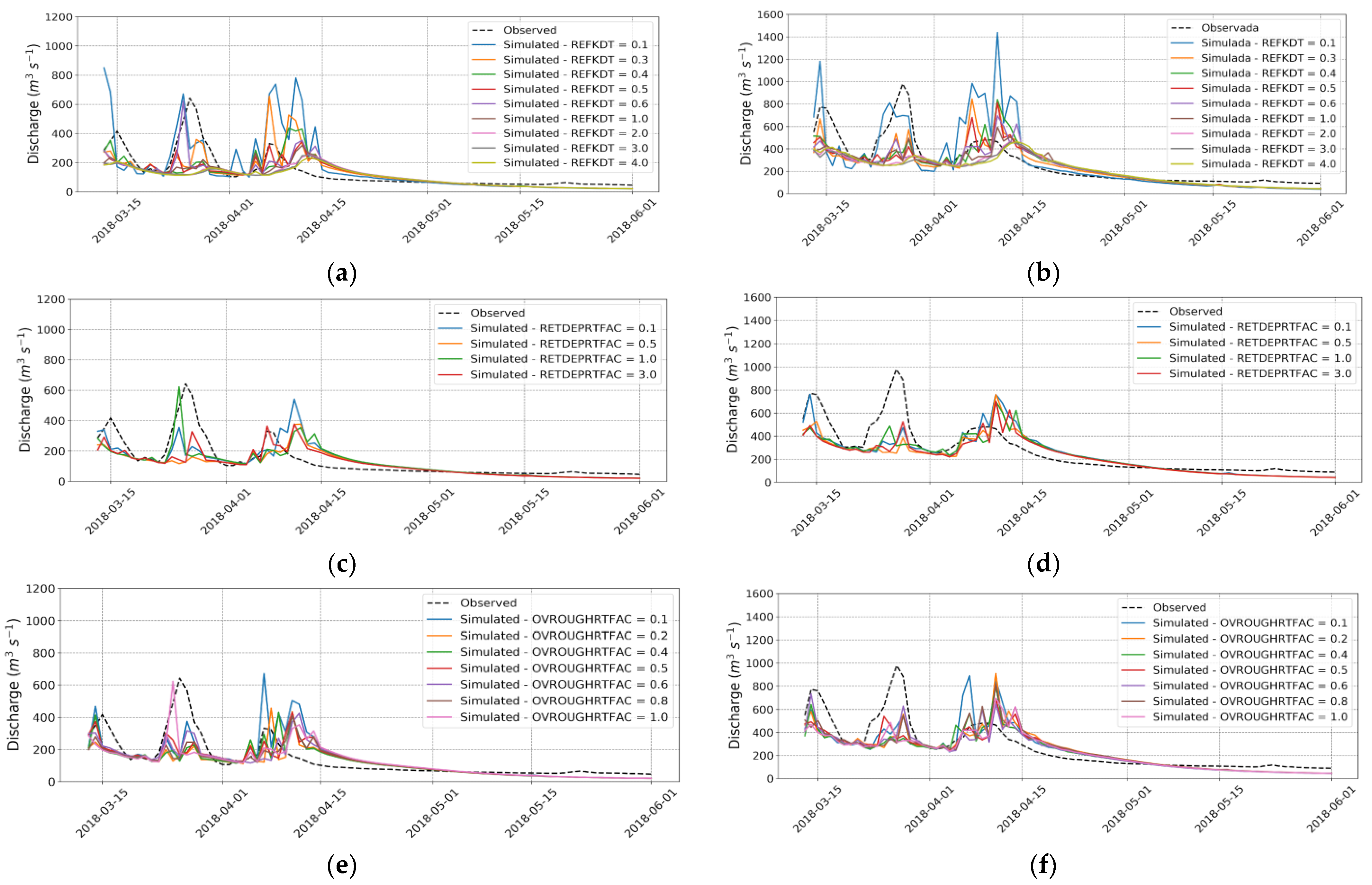
Figure 4 illustrates the observed and WRF-Hydro-simulated discharges at the Itacajá station location for the specified REFKDT values from 13 March to 1 June 2018.
A significant impact of the infiltration factor (REFKDT) on model discharge results is observed, highlighting the sensitivity of this parameter, as demonstrated in [
19] for the case in the Ouémé River, in [
20] for the Upper Tana River Basin, both in West Africa, and by [
47] on the Korean Peninsula. [
49] conducted a calibration process similar to that of WRF-Hydro simulations. They used various values for REFKDT, REFDK, and OVROUGHRTFAC to identify the most effective parameter values for their basin, located in western Turkey. Their findings highlighted that REFKDT is the parameter with the highest sensitivity when it comes to regulating runoff reactions during rainfall events. They also observed that higher REFKDT values lead to a reduction in discharge. In the WRF-Hydro model, the water entering the channel, affecting the discharge, is primarily derived from the amount of precipitation exceeding the infiltration capacity at each grid cell [
17]. As illustrated in studies in the Mediterranean region [
16] and in the Daqinghe Basin in northern China [
17], it is generally observed that an increase in REFKDT results in a decrease in surface runoff and, consequently, a reduction in simulated discharge. This trend is visible in the graph for the period from 1 April to 15 April 2018, where REFKDT = 0.1 shows a peak discharge close to 1400 m
3 s
−1, REFKDT = 0.5, around 600 m
3 s
−1, and for REFKDT values of 2, 3, and 4, the peak is around 200 m
3 s
−1.
Table 2 presents the statistical coefficients
NSE,
RSR,
R, and
PBIAS when comparing simulated and observed discharge for each REFKDT value.
This finding aligns with [
54], who emphasizes the WRF-Hydro model’s capability to adeptly manage and simulate conditions of peak flows. Incorporating these advanced features of the WRF-Hydro model, our work strategically portrays a detailed and enriched understanding of flood peaks and their dynamic behaviors. Such precise modeling, supported by robust empirical evidence, amplifies the reliability of our hydrological forecasts and analyses, making them especially pertinent in navigating and managing scenarios characterized by extreme hydrological events.
The PBIAS index generally indicates a decrease in average discharge with the increase in REFKDT, representing maximum overestimation (PBIAS = 50.43) for REFKDT = 0.1 and the highest magnitude of underestimation (PBIAS = −12.56) when REFKDT = 4. The REFKDT values of 0.5, 0.6, 1, and 2 yielded similar statistical indices. REFKDT = 0.6 was selected as it exhibited the best correlation (R = 0.78), one of the highest NSE values, and the lowest error (RSR = 0.73). The results of the statistical metrics are also interesting for REFKDT = 0.3, as it showed a lower PBIAS and reasonable values for other metrics. However, we did not use this value because, during the second peak flow, around 22 March 2018, the simulated discharge showed a significant underestimation.
With the selection of REFKDT = 0.6, values of 0.1, 0.5, 1, and 3 were analyzed for the parameter RETDEPRTFAC. Its default value is 1, and it has a function similar to REFKDT, potentially influencing the calculation of surface runoff. This is because RETDEPRTFAC serves as a factor of maximum retention depth; before that, the flow is routed as overland flow [
13].
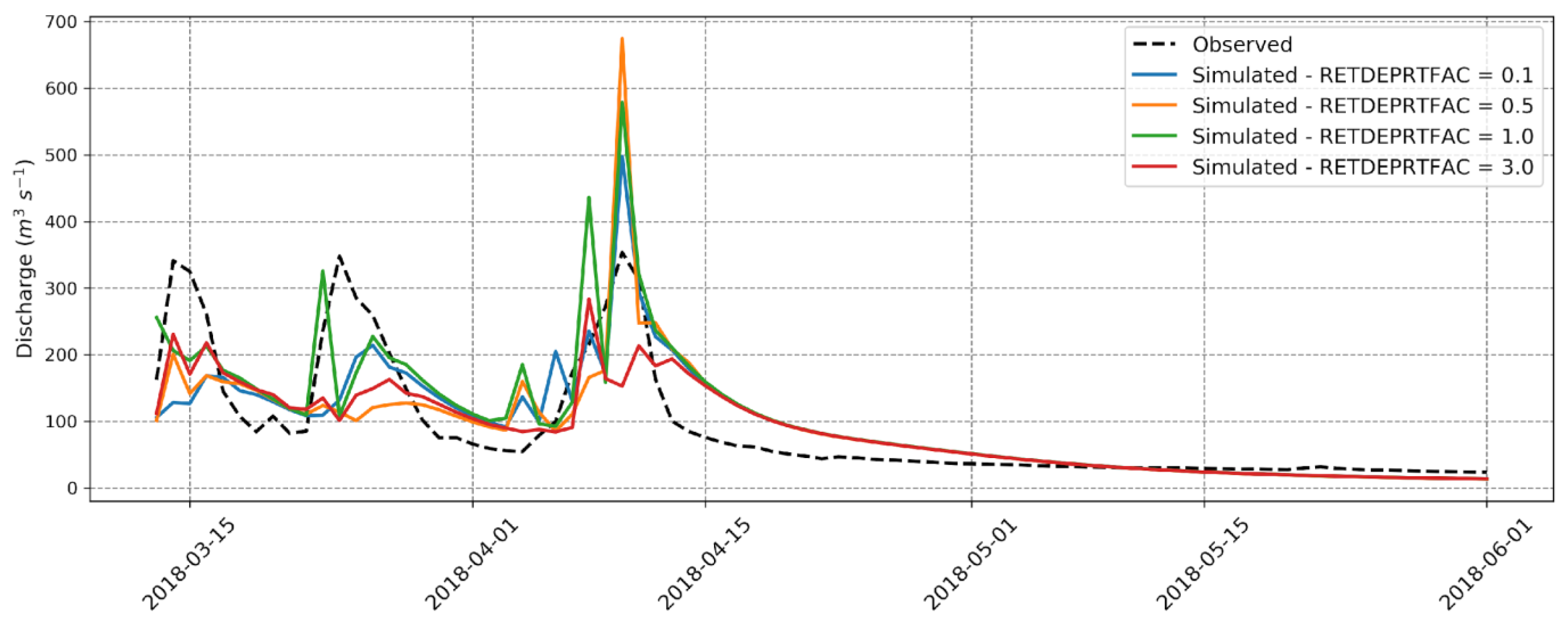
Figure 5 presents the observed discharge values at the hydrological station and the simulated values for the mentioned RETDEPRTFAC parameters.
The values of RETDEPRTFAC 0.1, 0.5, and 1 evaluated in [
17] showed virtually no influence on their discharge results. In this study, there is a slight variation in the simulated discharge at these values, specifically at peak points around 10 April 2018, suggesting that the influence of the RETDEPRTFAC parameter on channel discharge is not evident.
Table 3 presents the statistical coefficients derived from the data represented in the plot.
In the WRF-Hydro modeling system, it is generally expected that surface runoff, and consequently, discharge should decrease with an increase in RETDEPRTFAC. This trend was not consistently observed except for the highest value, RETDEPRTFAC = 3, which displayed the lowest PBIAS index (−2.60), indicating the only underestimation of the simulated data relative to the observed data.
As observed in [
17], or in cases in the Kaidu River Basin in China [
55], in the Eastern Black Sea and Mediterranean regions [
18], where discharge results showed nearly no response to RETDEPRTFAC, the statistical indices demonstrate lower variability compared to the other parameters, suggesting that RETDEPRTFAC has weaker sensitivity in simulating discharge among the parameters tested in this study. This may be due to significant variations in altitude and terrain in the study area, as suggested in [
17], where little accumulation occurs on steep surfaces. Despite its limited influence, the default value, RETDEPRTFAC = 1, yielded the best correlation (
R) and an
NSE closest to 1.
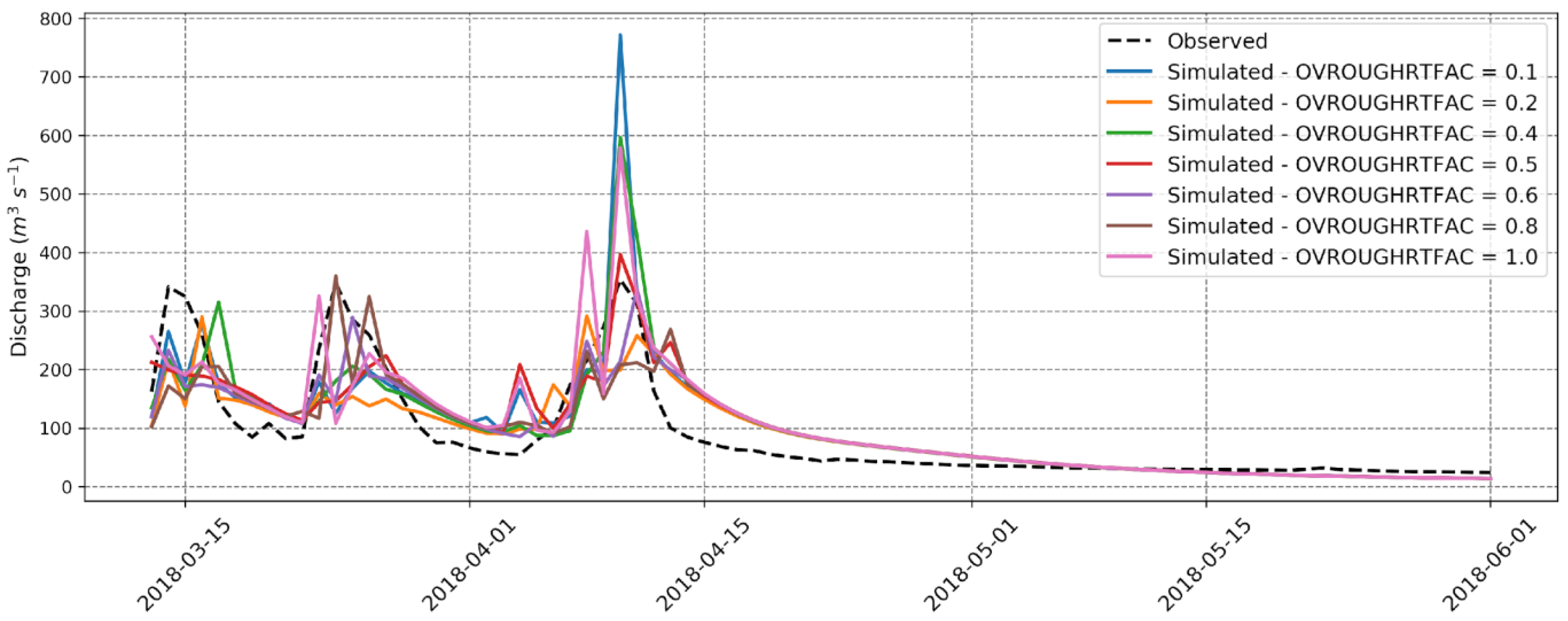
Figure 6 presents the discharge rates observed at the Itacajá station and those simulated by WRF-Hydro with sensitivity tests for OVROUGHRTFAC.
Just as in the study conducted in the Upper Trinity River Basin, located in North-Central Texas, USA [
48], infiltration processes were more sensitive to REFKDT and OVROUGHRTFAC. Consequently, significantly altering the discharge data at certain OVROUGHRTFAC values changes the shape of the hydrographs in these cases, showing peak discharges at separate times and values. At the maximum point of the observed simulations, for example, around 10 April 2018, the discharge is greater when OVROUGHRTFAC is 0.1 than when this parameter is 0.5, which in turn is greater when OVROUGHRTFAC = 0.8.
Table 4 shows the statistical coefficients for all parameters.
It is observed, as in [
17], that this parameter had a quite significant impact on improving the statistical indices when varying OVROUGHRTFAC relative to its default value, except when OVROUGHRTFAC = 0.1. In these cases of improvement, the
NSE, which is the statistical index used in all WRF-Hydro flow studies, improved by a scale of 21% to 47%. The other statistical indices also improved considerably, making it, along with REFKDT, the parameter that most influenced the flow simulation in this study.
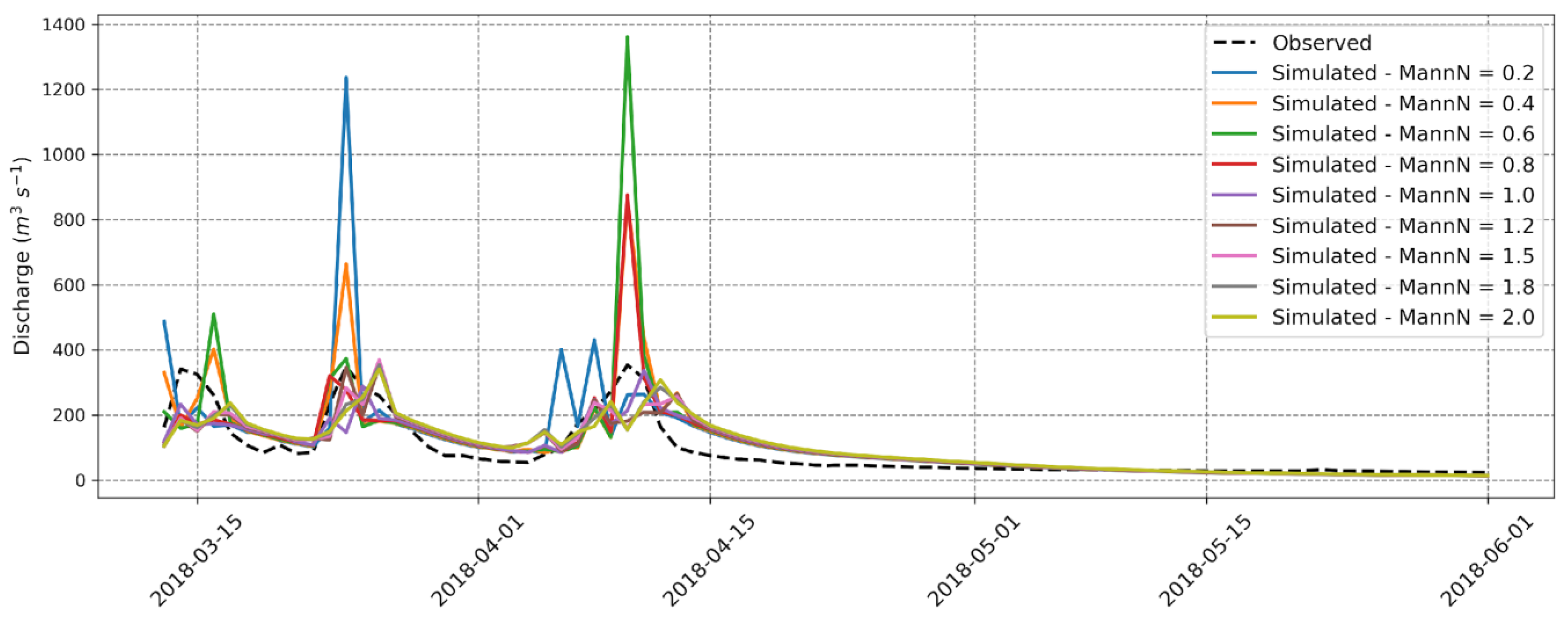
Lastly, after analyzing the transmission of surface runoff to the river network, the transport of water along the channels was assessed through the sensitivity test of the channel roughness parameter (MannN). This transport can also affect the shape of the hydrograph. The channel geometric properties were set to their default values because there are no available channel cross-section data for the region concerning stream orders. In WRF-Hydro, channel properties such as average channel base width (Bw), initial water depth (HLINK), channel slope (Ch SSlp), and Manning’s coefficient (MannN) are introduced based on each stream order. The default values of the channel parameters are provided in
Table 5.
The adjustment of the Manning coefficient is carried out by multiplying each initial MannN value by a scaling factor, thereby preserving the spatial patterns of the parameters during calibration. This scaling factor becomes the calibration parameter, generating MannN values for all the river channels. In this study, the values were established to cover a range between 0.2 and 2, including increments of 0.2 [
19].
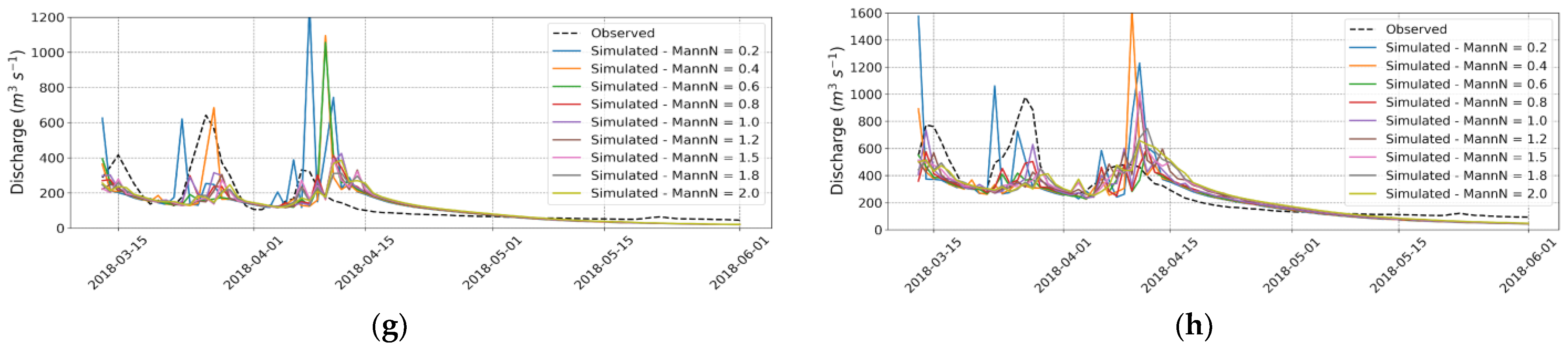
Figure 7 displays the simulated flow rates with their respective MannN parameters and the flow rate measured at the hydrological station.
When the MannN coefficients ranged from 0.2 to 0.8, the simulated flow rate peaks were significantly higher than the values obtained when MannN equals or exceeds 1. Flow rates exceeding 400 m
3 s
−1 were not observed within this range, indicating a stabilization of the flow rate peaks.
Table 6 displays the statistical indices for each observed MannN value.
The more pronounced overestimation displayed graphically when MannN is less than 1 is corroborated by the PBIAS index, which shows higher results in these cases, reaching over 5 times the smallest value obtained when MannN is 1 (PBIAS = 4.99). All other statistical indices were better at the default value of the channel roughness parameter when MannN = 1.
Therefore, the best performance in flow rate simulation with WRF-Hydro in this study was achieved when REFKDT = 0.6, RETDEPRTFAC = 1.0, OVROUGHRTFAC = 0.6, and MannN = 1.0. The statistical indices
NSE = 0.69,
RSR = 0.56,
R = 0.83, and
PBIAS = 4.99 indicate superior results. According to [
51], the range of
NSE > 0.65 and
RSR ≤ 0.60 is considered good for the evaluation of hydrological models, and the
PBIAS index ≤ ±10% is considered exceptionally good. In their best flow rate simulation with WRF-Hydro in coupled mode, [
19] obtained a correlation index
R = 0.84, [
44] achieved
R = 0.83 and
NSE = 0.7, and [
20] reported
NSE = 0.71 and
RSR = 0.51.
3.2. Results at the Other Two Hydrological Stations
In the Jacaré and Goiatins stations, which measure the flow of the Vermelho and Manuel Alves Grande rivers, the same rain event from the Itacajá station was analyzed, covering the period from 13 March to 1 June 2018. Since it is the same simulation, the standard choice of hydrological model parameter values was maintained.
Table 7 shows the statistical parameters for the results of these simulations.
Similarly, in the analysis conducted at the Itacajá station, the same values assigned to REFKDT, RETDEPRTFAC, OVROUGHRTFAC, and MannN converged to the best statistical indices in most cases of the simulations that were analyzed with the Jacaré and Goiatins stations. Furthermore, the improvement in results was more pronounced when changing the parameters REFKDT and OVROUGHRTFAC.
The statistical coefficient
PBIAS is often lower as the hydrological model parameters are larger, especially for the REFKDT parameter, indicating a decrease in surface runoff and a consequent reduction in simulated flow.
Figure 8 shows the simulations compared with the Jacaré and Goiatins stations.
Indeed, it is noticeable that lower REFKDT values exhibit higher peak points compared to higher values, which show flow results close to each other. It can be observed in the first two peaks of the observed flow. The simulations, in the majority of cases, have their values underestimated. However, at the last peak, the simulated flows are overestimated.
Despite the three stations belonging to the same watershed and the same simulation tests being carried out, it is evident that the statistical indices of the simulations compared to the Jacaré and Goiatins stations are lower than those of the simulation conducted with the Itacajá station. This could be related to an increased disparity in the distribution of rainfall in both spatial and temporal dimensions, which worsens the WRF-Hydro simulations. This could result from errors in the directional data, in this case, the GDAS-FNL data used in the WRF, which indirectly affects the WRF-Hydro’s performance in flow simulation [
17].
3.3. Error in Simulated Precipitation
The values of simulated precipitation, when compared to the values of measured precipitation using the MERGE product in the drainage network region of the Rio Manuel Alves Pequeno (where the Itacajá station is located), exhibit a more uniform distribution of rainfall over time than in the drainage network regions of the Rio Manuel Alves Grande and Vermelho (where the Goiatins and Jacaré stations are located, respectively). This directly affects the difference between the peaks of simulated and observed flows and the timing at which they occur.
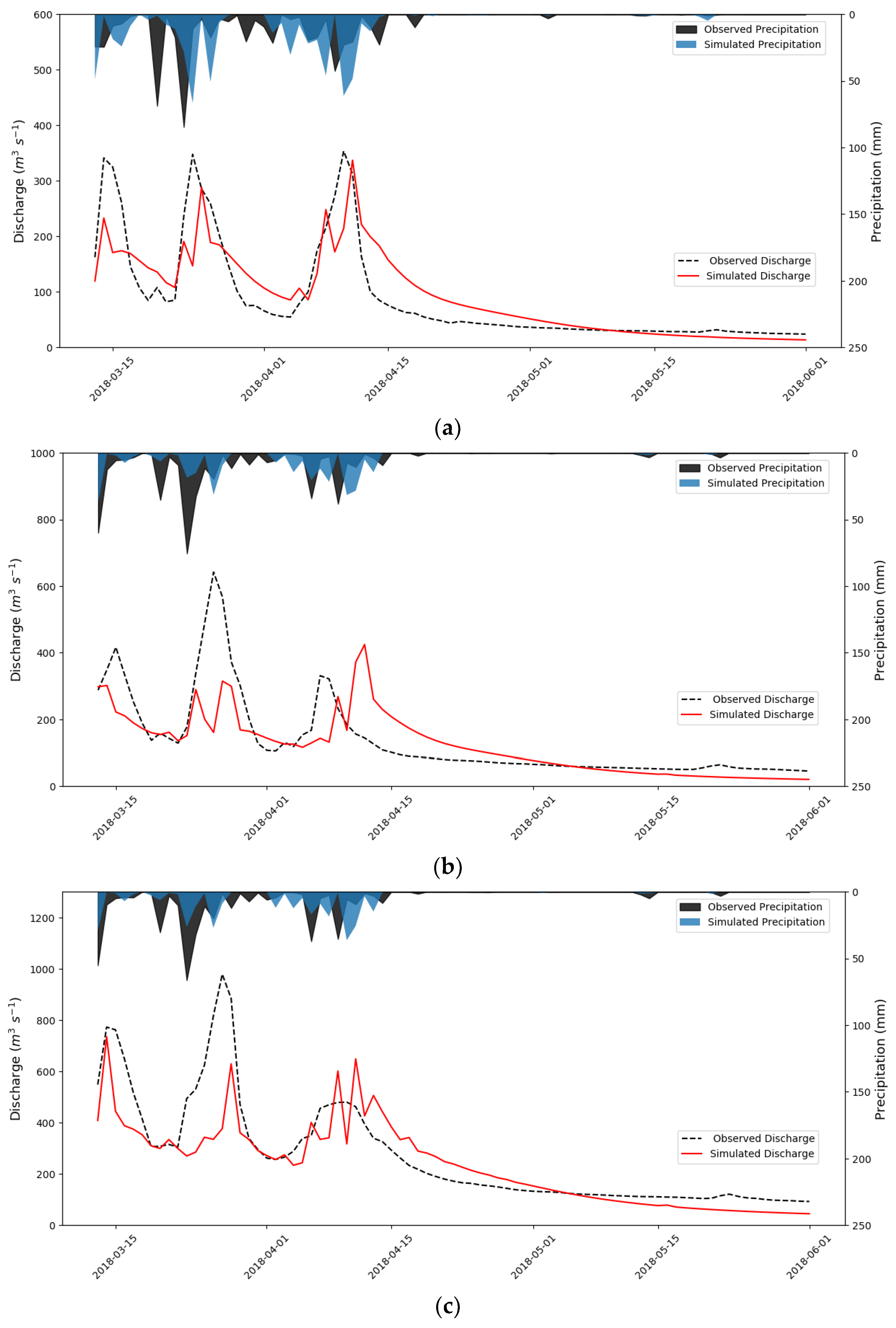
Figure 9 displays the daily averages of precipitation obtained from the MERGE product within the drainage network area of each river, as well as those simulated by the WRF within the same area. It also shows the observed flows at river gauge stations and simulated flows in the WRF-Hydro model under the best-performing conditions, characterized by REFKDT = 0.6, RETDEPRTFAC = 1.0, OVROUGHRTFAC = 0.6, and MannN = 1.0.
It can be observed that the simulated precipitation in the observed data presented in
Figure 9b,c is underestimated, while
Figure 9a exhibits a seemingly smaller overestimation. It is also noteworthy that the inherent uncertainty in climate predictions resulting from the WRF simulation, conducted with GDAS-FNL input data, has impacted the results of the WRF-Hydro simulation.
Table 8 displays the relative errors of accumulated simulated and observed rainfall events within the drainage networks of the three analyzed rivers.
Indeed, the drainage network area of the Rio Manuel Alves Pequeno demonstrates the best results in precipitation simulation among the other two areas, with the smallest absolute value of ER = 10.66%. Conversely, the WRF model exhibits the poorest performance in simulating rainfall accumulation for the Rio Vermelho, with the highest relative error. This discrepancy could potentially impact the results of flow simulation in WRF-Hydro. Therefore, it is essential to emphasize that the calibration of WRF-Hydro parameters in this study cannot eliminate the errors in rainfall simulation originating from input data, directly influencing flow results. However, even with errors stemming from precipitation and considering the possibility of improving data through further study of WRF-Hydro in Brazilian regions, the strong correlation observed between simulated and observed flows when modifying hydrological parameters can serve as a starting point for using this hydrometeorological model in future research related to water resources management in Brazil.
3.4. Implications for Water Resources Management
Our study contributes valuable insights into the hydrological dynamics of the Manuel Alves Pequeno, Vermelho, and Manuel Alves Grande rivers, providing a foundation for improved water resources management practices in the MATOPIBA region. The accurate representation of hydrological parameters, such as soil infiltration, surface retention depth, and land surface roughness, is critical for making informed decisions regarding water allocation, especially in areas experiencing climate change and rapid urban and agricultural expansions.
Water resource management is a crucial aspect of ensuring sustainable water allocation, addressing the challenges posed by climate change, and expanding urban and agricultural areas. Accurate representation of hydrological parameters by numerical models such as WRF-Hydro is essential for making informed decisions regarding water resources [
13]. By accurately simulating streamflow, the research serves as a benchmark for future hydrological modeling efforts in the MATOPIBA region, guiding water resource management strategies to meet the demands of a changing climate and evolving land use patterns. The efficient simulation of streamflow is a prerequisite for any effective water management plan. For example, [
56] assessed a water security threat index for the western region of Bahia, an area within the MATOPIBA region and one of Brazil’s primary areas for agricultural exploitation. The authors estimated that 66% of agricultural enterprises effectively manage the water resources in the region. However, their results suggest that threats to water availability in the region will significantly increase by 2040.
Environmental exploitation, stemming from Brazil’s international significance as a food exporter, climate change, land use/land cover (LULC) changes, and desertification processes are key factors exacerbating this issue. LULC and climate change can significantly affect surface runoff, which is a key component of water resource management. Models that investigate the changes in hydrological pathways caused by climate and human activities can provide valuable frameworks for understanding and managing surface runoff [
57,
58]. Analyzing the impact of climate change on net irrigation water demand can help assess the future water resources in areas equipped for irrigation [
59]. Therefore, considering the use of modern hydrometeorological models like WRF-Hydro can assist decision-makers, whether in the public or private sectors, in better managing the available water resources.
Climate change significantly impacts water resources and agriculture, highlighting the crucial need to understand how climate shifts interact with human activities in assessing water availability and food production [
60]. In the bigger picture, global climate change poses threats to farming by messing with natural resources, especially rainfall patterns. Extreme downpours linked to climate change boost rainfall erosivity, causing more soil erosion. On the other hand, less rain creates water shortages for farming. Realizing how vital it is to model climate conditions under global change, particularly where rainfall data are on the rise, a study focusing on the MATOPIBA region becomes a big deal.
Ref. [
61] projected rainfall erosivity in the Tocantins-Araguaia River basin for the 21st century under IPCC AR5 scenarios (RCP4.5 and RCP8.5). Using downscaling from four CMIP5 global climate models via the Eta regional climate model, the study showed a drop in erosivity for both scenarios due to less rainfall. But, even with this drop, the erosivity values are still significant, shouting out the need for robust soil conservation practices. Plus, the lower rainfall hints at less water for long-cycle crops and more uneven and less intense rainfall. In this complicated mix of climate challenges, our results with WRF-Hydro rainfall and streamflow simulation in the MATOPIBA region stand out, giving vital insights for managing water resources and planning agriculture to mitigate future scarcity.
Coupled hydrologic models, such as WRF-Hydro, are valuable tools for estimating water balance, analyzing groundwater levels and surface water discharges, and extrapolating to different scenarios and large basins [
62,
63]. In hydrological studies, the availability of data is vital. Data on rainfall, runoff, and other hydrological parameters are essential for accurate modeling and understanding of the dynamics of river basins [
64]. These models can provide detailed information for water resource management and help analyze the impacts of meteorological and LULC changes.
Additionally, our research serves as a benchmark for future hydrological modeling efforts in the MATOPIBA region, guiding water resources management strategies to meet the demands of a changing climate and evolving land use patterns. While the manuscript may not explicitly delve into the policy and management aspects, the accurate simulation of streamflow is a prerequisite for any effective water management plan.