High-Order Boussinesq Equations for Water Wave Propagation in Porous Media
Abstract
:1. Introduction
2. Derivation of High Order of Boussinesq-Type Equations
2.1. Governing Equations and Boundary Conditions
2.2. Dimensionless Equations
2.3. Power Series Solution to the Laplace Equations
2.4. Boussinesq Equations in Terms of Velocity at the Free Surface
2.5. Boussinesq Equations in Terms of Depth-Averaged Velocity
2.6. Boussinesq Equations in Terms of Velocity at an Arbitrary Water Column
2.7. Boussinesq Models Extended to Deeper Water Depth
2.7.1. The Improvement of Equations in Terms of Depth-Averaged Velocity
- (1)
- Keeping at order
- (2)
- Keeping at order
2.7.2. The Improvement of Equations in Terms of
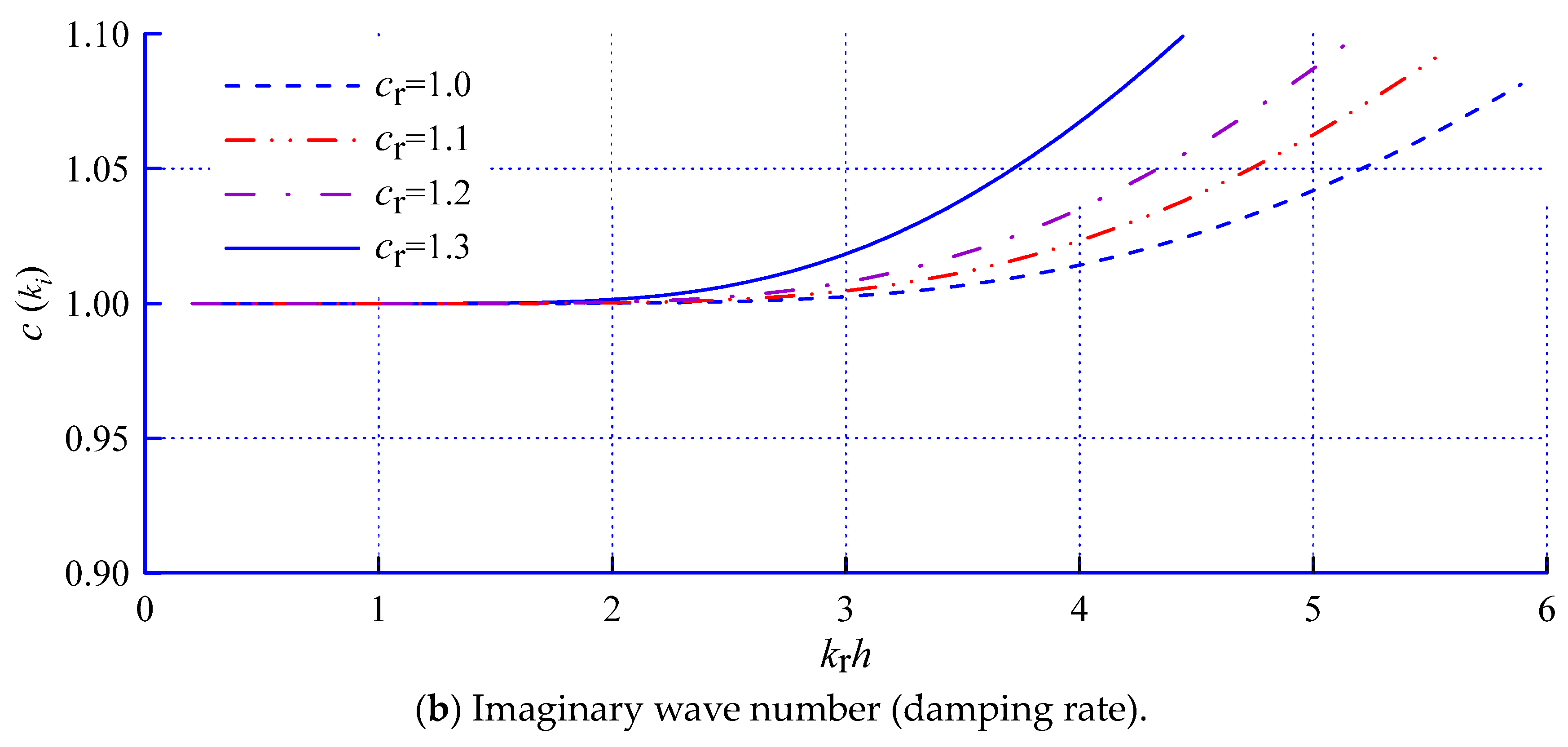
3. Dispersive Analysis on a Horizontal Bottom
4. Numerical Implementation and Validation
4.1. Numerical Implementation
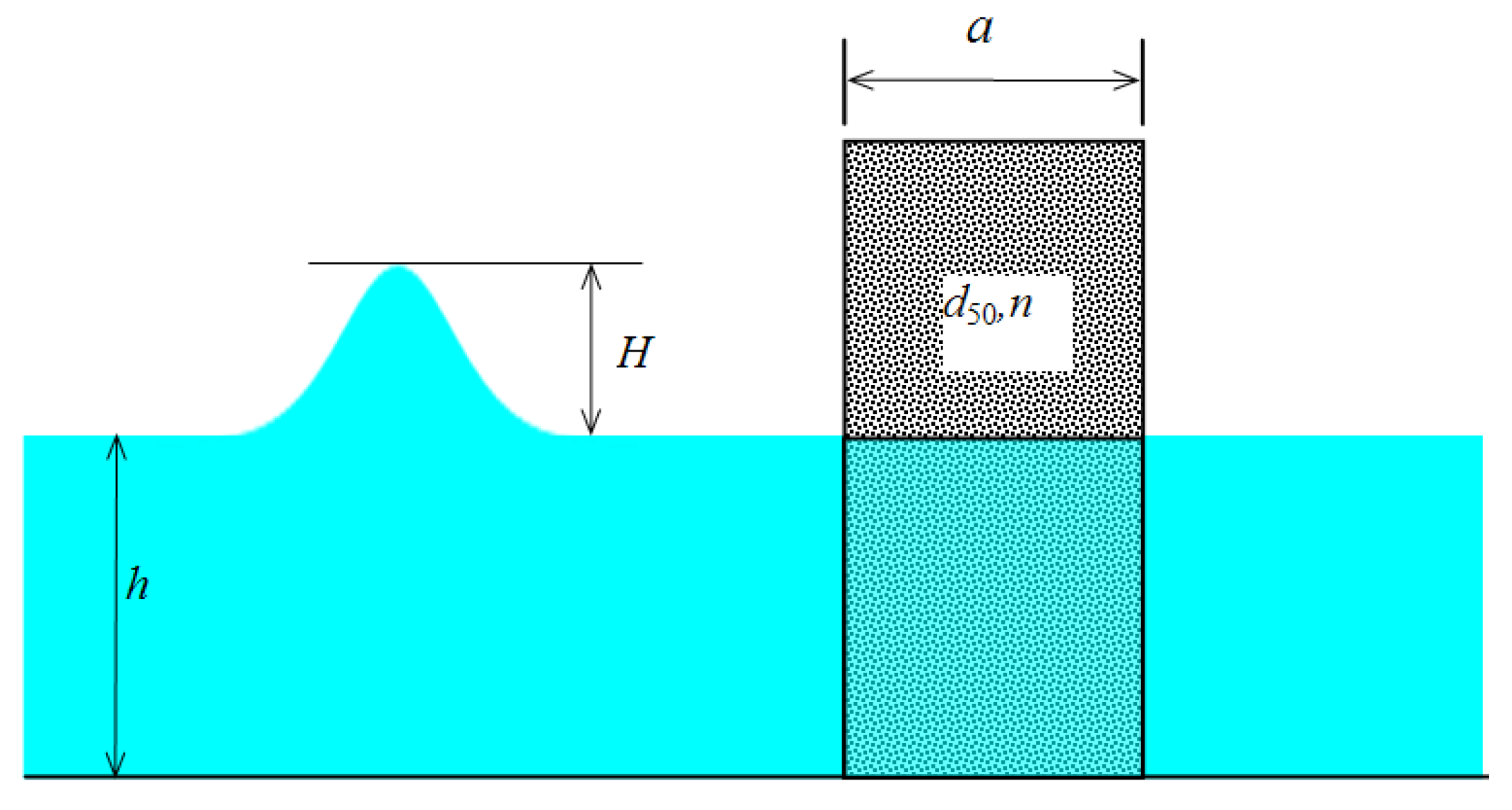
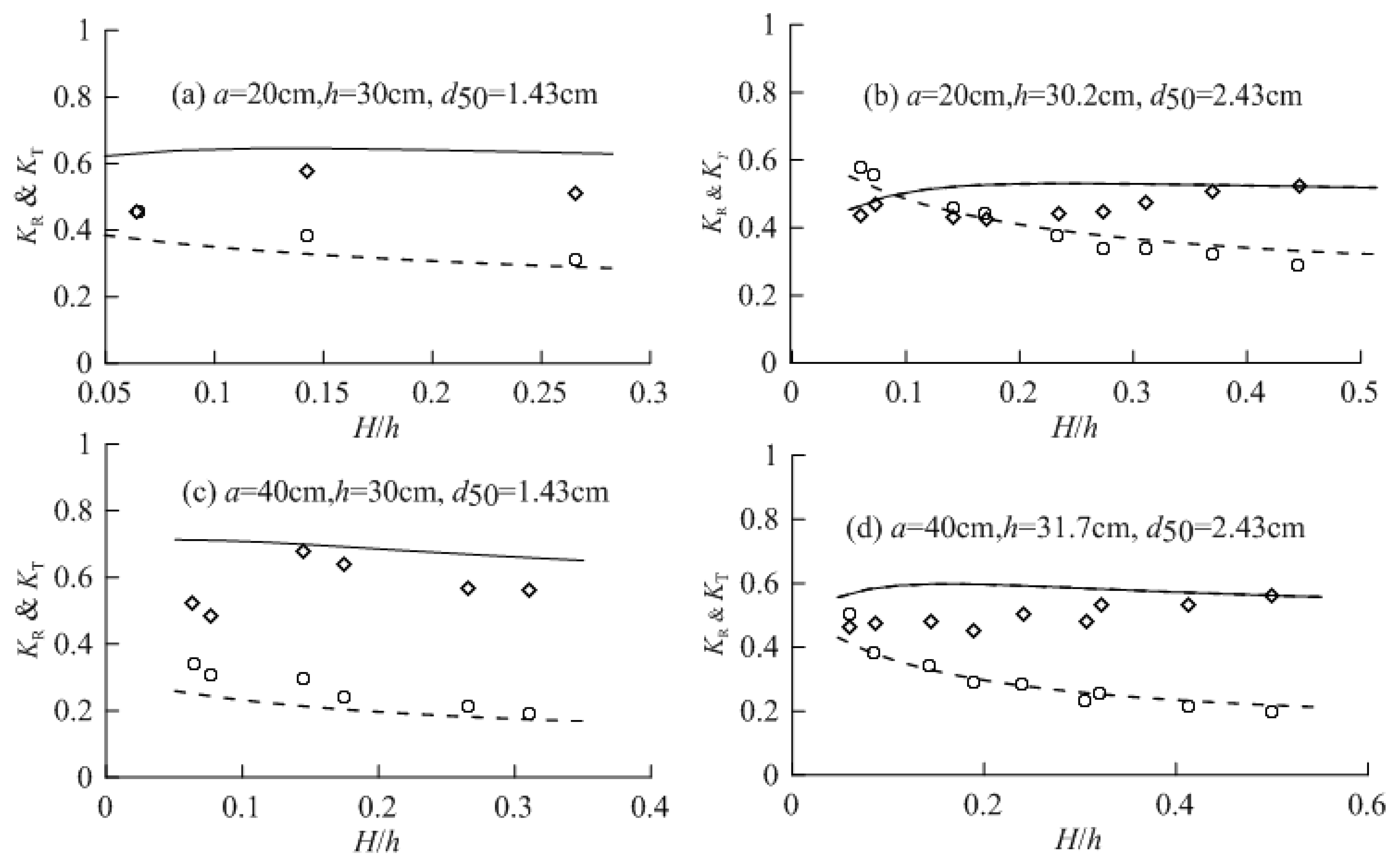
4.2. Model Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Losada, I.J.; Patterson, M.D.; Losada, M.A. Harmonic generation past a submerged porous step. Coast. Eng. 1997, 31, 281–304. [Google Scholar] [CrossRef]
- Gu, Z.; Wang, H. Gravity waves over porous bottoms. Coast. Eng. 1991, 15, 497–524. [Google Scholar] [CrossRef]
- Lara, J.L.; Losada, I.J.; Liu, P.L.F. Breaking waves over a mild gravel slope: Experimental and numerical analysis. J. Geophys. Res. 2006, 111, C11019. [Google Scholar] [CrossRef]
- Lynett, P.J.; Liu, P.L.F.; Losada, I.J. Solitary wave interaction with porous breakwaters. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 314–322. [Google Scholar] [CrossRef]
- Losada, I.J.; Lara, J.L.; Guanche, R.; Gonzalez-Ondina, J.M. Numerical analysis of wave overtopping of rubble mound breakwaters. Coast. Eng. 2008, 55, 47–62. [Google Scholar] [CrossRef]
- Cheng, Y.Z.; Jiang, C.B.; Wang, Y.Y. A coupled numerical model of wave interaction with porous medium. Ocean Eng. 2009, 36, 952–959. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Three-dimensional interaction of waves and porous coastal structures using OpenFOAM®. Part I: Formulation and validation. Coast. Eng. 2014, 83, 243–258. [Google Scholar] [CrossRef]
- Sasikumar, A.; Kamath, A.; Bihs, H. Modeling porous coastal structures using a level set method based VRANS-solver on staggered grids. Coast. Eng. J. 2020, 62, 198–216. [Google Scholar] [CrossRef]
- Mohamed, K. A finite volume method for numerical simulation of shallow water models with porosity. Comput. Fluids 2014, 104, 9–19. [Google Scholar] [CrossRef]
- Ren, B.; Wen, H.; Dong, P.; Wang, Y. Improved SPH simulation of wave motions and turbulent flows through porous media. Coast. Eng. 2016, 107, 14–27. [Google Scholar] [CrossRef]
- Gao, J.L.; Zhou, X.J.; Zhou, L.; Zang, J.; Chen, H.Z. Numerical investigation on effects of fringing reefs on low-frequency oscillations within a harbor. Ocean Eng. 2019, 172, 86–95. [Google Scholar] [CrossRef]
- Gao, J.L.; Ma, X.Z.; Zang, J.; Dong, G.H.; Ma, X.J.; Zhu, Y.Z.; Zhou, L. Numerical investigation of harbor oscillations induced by focused transient wave groups. Coast. Eng. 2020, 158, 103670. [Google Scholar] [CrossRef]
- Gao, J.L.; Ma, X.Z.; Chen, H.Z.; Zang, J.; Dong, G.H. On hydrodynamic characteristics of transient harbor resonance excited by double solitary waves. Ocean Eng. 2021, 219, 108345. [Google Scholar] [CrossRef]
- Buccino, M.; Tuozzo, S.; Ciccaglione, M.C.; Calabrese, M. Predicting Crenulate Bay Profiles from Wave Fronts: Numerical Experiments and Empirical Formulae. Geosciences 2021, 11, 208. [Google Scholar] [CrossRef]
- Kirby, J.T. Boussinesq models and applications to nearshore wave propagation, surf zone processes and wave induced-current. In Advances in Coastal Modelling; Lakhan, V.C., Ed.; Elsevier Science: Amsterdam, The Netherlands, 2003; pp. 1–41. [Google Scholar]
- Madsen, P.A.; Fuhrman, D.R. High-order Boussinesq-type modeling of nonlinear wave phenomena in deep and shallow water. In Advances in Numerical Simulation of Nonlinear Water Waves; Ma, Q.W., Ed.; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2010; pp. 245–285. [Google Scholar]
- Brocchini, M.A. reasoned overview on Boussinesq-type models: The interplay between physics, mathematics and numerics. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2013, 469, 20130496. [Google Scholar] [CrossRef]
- Kirby, J.T. Boussinesq models and their application to coastal processes across a wide range of scales. J. Waterw. Port Coast. Ocean Eng. 2016, 142, 03116005. [Google Scholar] [CrossRef]
- Sun, J.W.; Fang, K.Z.; Liu, Z.B.; Fan, H.X.; Sun, Z.C.; Wang, P. A review on the theory and application of Boussinesq-type equations for water waves. Haiyang Xuebao 2020, 42, 1–11. (In Chinese) [Google Scholar]
- Gao, J.L.; Shi, H.B.; Zang, J.; Liu, Y.Y. Mechanism analysis on the mitigation of harbor resonance by periodic undulating topography. Ocean Eng. 2023, 281, 114923. [Google Scholar] [CrossRef]
- Gao, J.L.; Ma, X.Z.; Dong, G.H.; Chen, H.Z.; Liu, Q.; Zang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Madsen, P.A.; Murray, R.; Sørensen, O.R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Coast. Eng. 1991, 15, 371–388. [Google Scholar] [CrossRef]
- Madsen, P.A.; Sørensen, O.R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Part 2. A slowly-varying bathymetry. Coast. Eng. 1992, 18, 183–204. [Google Scholar] [CrossRef]
- Nwogu, O. Alternative form of Boussinesq equations for nearshore wave propagation. J. Waterw. Port Coast. Ocean Eng. 1993, 119, 618–638. [Google Scholar] [CrossRef]
- Schäffer, H.A.; Madsen, P.A. Further enhancements of Boussinesq-type equations. Coast. Eng. 1995, 26, 1–14. [Google Scholar] [CrossRef]
- Zou, Z.L. Higher-order Boussinesq equations for rapidly varying topography. Haiyang Xuebao 2001, 23, 109–119. (In Chinese) [Google Scholar]
- Liu, Z.B.; Sun, Z.C. Two sets of higher-order Boussinesq-type equations for water waves. Ocean Eng. 2005, 32, 1296–1310. [Google Scholar] [CrossRef]
- Wei, G.; Kirby, J.T.; Grilli, S.T.; Subramanya, R. A fully nonlinear Boussinesq model for surface waves. Part I. Highly nonlinear unsteady waves. J. Fluid Mech. 1995, 294, 71–92. [Google Scholar] [CrossRef]
- Gobbi, M.F.; Kirby, J.T.; Wei, G. A fully nonlinear Boussinesq model for surface waves. Part 2. Extension to O(kh)4. J. Fluid Mech. 2000, 405, 181–210. [Google Scholar] [CrossRef]
- Lynett, P.J.; Liu, P.L.F. Linear analysis of the multi-layer model. Coast. Eng. 2004, 51, 439–454. [Google Scholar] [CrossRef]
- Zou, Z.L.; Fang, K.Z. Alternative forms of the higher-order Boussinesq equations: Derivations and validations. Coast. Eng. 2008, 55, 506–521. [Google Scholar] [CrossRef]
- Liu, Z.B.; Fang, K.Z. Two-layer Boussinesq models for coastal water waves. Wave Motion 2015, 57, 88–111. [Google Scholar] [CrossRef]
- Madsen, P.A.; Bingham, H.B.; Liu, H. A new method for fully nonlinear waves from shallow water to deep water. J. Fluid Mech. 2002, 462, 1–30. [Google Scholar] [CrossRef]
- Chazel, F.; Benoit, M.; Ern, A.; Piperno, S. A double-layer Boussinesq-type model for highly nonlinear and dispersive waves. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2009, 465, 2319–2346. [Google Scholar] [CrossRef]
- Liu, Z.B.; Fang, K.Z. A new two-layer Boussinesq model for coastal waves from deep to shallow water: Derivation and analysis. Wave Motion 2016, 67, 1–14. [Google Scholar] [CrossRef]
- Liu, Z.B.; Fang, K.Z.; Cheng, Y.Z. A new multi-layer irrotational Boussinesq-type model for highly nonlinear and dispersive surface waves over a mildly sloping seabed. J. Fluid Mech. 2018, 842, 323–853. [Google Scholar] [CrossRef]
- Liu, Z.B.; Han, P.X.; Fang, K.Z.; Liu, Y. A high-order nonlinear Boussinesq-type model for internal waves over a mildly-sloping topography in a two-fluid system. Ocean Eng. 2023, 285, 115283. [Google Scholar] [CrossRef]
- Cruz, E.C.; Isobe, M.; Watanabe, A. Boussinesq equations for wave transformation on porous beds. Coast. Eng. 1997, 30, 125–156. [Google Scholar] [CrossRef]
- Hsiao, S.; Liu, P.L.F.; Chen, Y. Nonlinear water waves propagating over a permeable bed. Philos. Trans. R. Soc. Lond. Ser. A 2002, 458, 1291–1322. [Google Scholar] [CrossRef]
- Chen, Q. Fully nonlinear Boussinesq-type equations for waves and currents over porous beds. J. Eng. Mech. 2006, 132, 220–230. [Google Scholar] [CrossRef]
- Liu, Z.B.; Sun, Z.C. Wave propagating model over a porous seabed. China Sci. Pap. 2011, 6, 374–379. (In Chinese) [Google Scholar]
- Klonaris, G.T.; Memos, C.D. Compound Boussinesq-type modelling over porous beds. Appl. Ocean Res. 2020, 105, 102422. [Google Scholar] [CrossRef]
- Hsiao, S.; Hu, K.; Hwung, H. Extended Boussinesq Equations for Water-Wave Propagation in Porous Media. J. Eng. Mech. 2010, 136, 625–640. [Google Scholar] [CrossRef]
- Fang, K.Z.; Huang, M.H.; Chen, G.L.; Wu, J.; Wu, H.; Jiang, T. Boussinesq Simulation of Coastal Wave Interaction with Bottom-Mounted Porous Structures. J. Mar. Sci. Eng. 2022, 10, 1367. [Google Scholar] [CrossRef]
- Madsen, P.A.; Schäffer, H.A. Higher-order Boussinesq-type equations for surface gravity waves: Derivation and analysis. Philos. Trans. R. Soc. Lond. Ser. A 1998, 356, 3123–3184. [Google Scholar] [CrossRef]
- Zou, Z.L.; Liu, Z.B.; Fang, K.Z. Further improvements to the higher-order Boussinesq equations: Bragg reflection. Coast. Eng. 2009, 56, 672–687. [Google Scholar] [CrossRef]
- Peregrine, D.H. Long waves on a beach. J. Fluid Mech. 1967, 27, 815–827. [Google Scholar] [CrossRef]
- Liu, Z.B.; Fang, K.Z.; Zou, Z.L. Boussinesq wave equations with full nonlinear characteristics at order O(µ2). J. Harbin Eng. Univ. 2012, 33, 556–561. (In Chinese) [Google Scholar]
- Kirby, J.T.; Wei, G.; Chen, Q.; Kennedy, A.B.; Dalrymple, R.A. FUNWAVE 1.0 Fully Nonlinear BOUSSINESQ Wave Model Documentation and User’s Manual; Report, Center for Applied Coastal Research; University of Delawar: Newwark, NJ, USA, 1998. [Google Scholar]
- Vidal, C.; Losada, M.A.; Medina, R.; Rubio, J. Solitary wave transmission through porous breakwaters. In Proceedings of the 24th International Conference on Coastal Engineering, Costa del Sol-Malaga, Spain, 20–25 June 1988; pp. 1073–1083. [Google Scholar]
- Lin, P.; Karunarathna, S.A. Numerical study of Solitary wave interaction with porous breakwater. J. Waterw. Port Coast. Ocean Eng. 2007, 133, 352–363. [Google Scholar] [CrossRef]
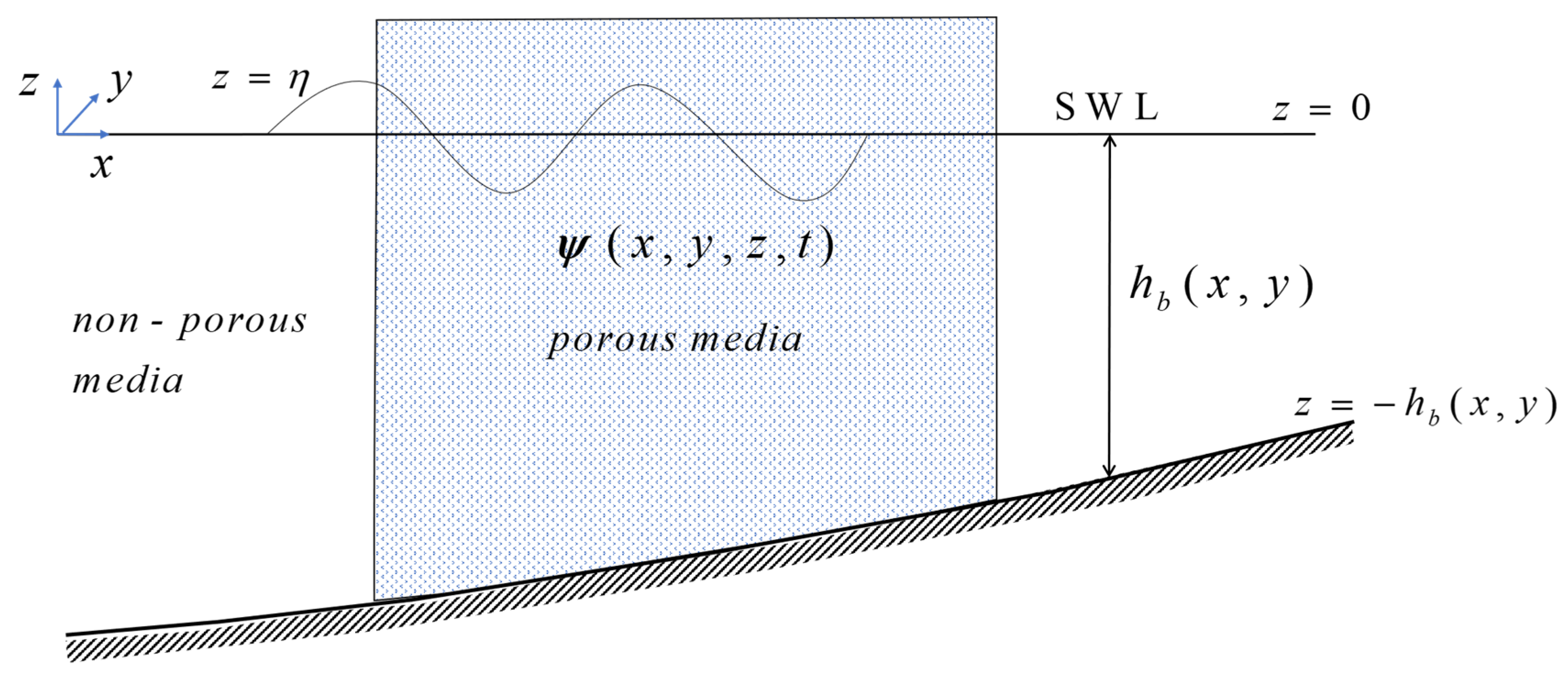
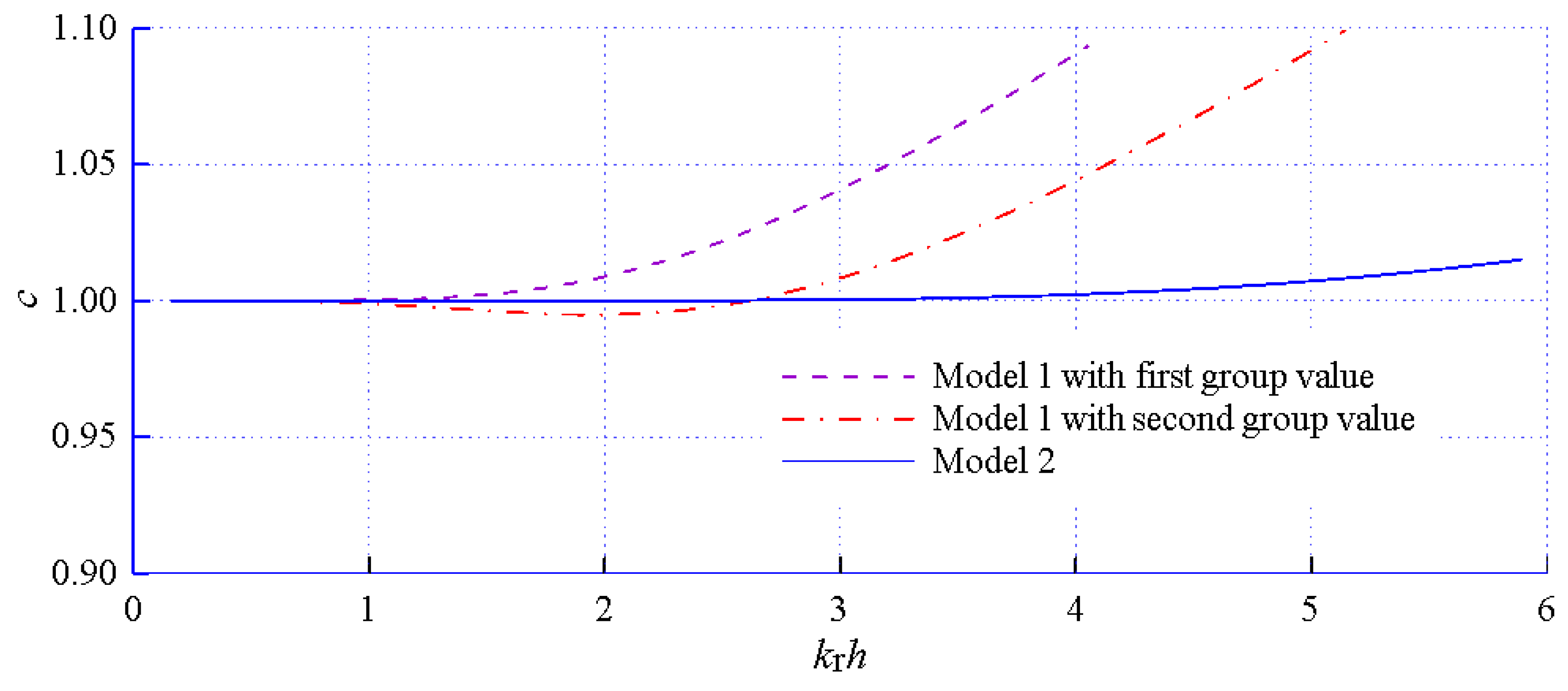
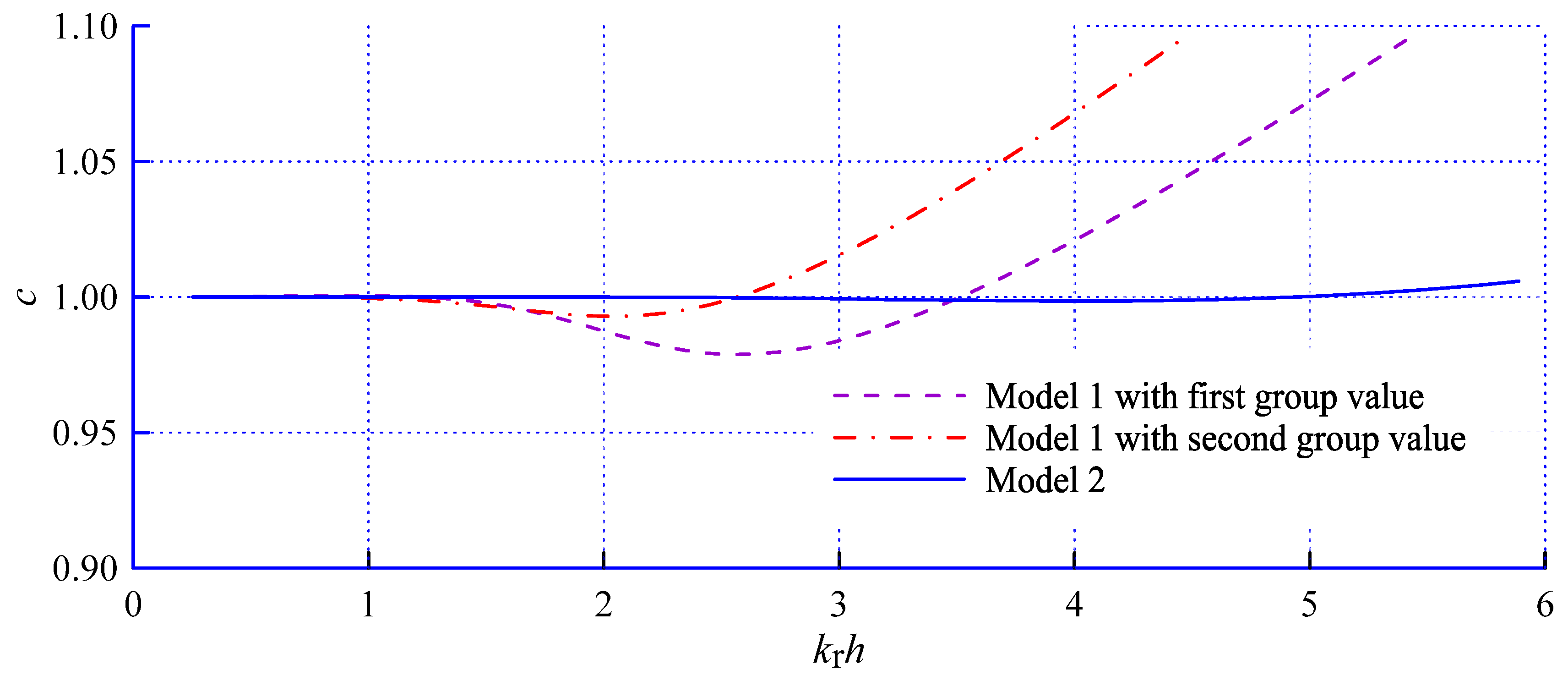
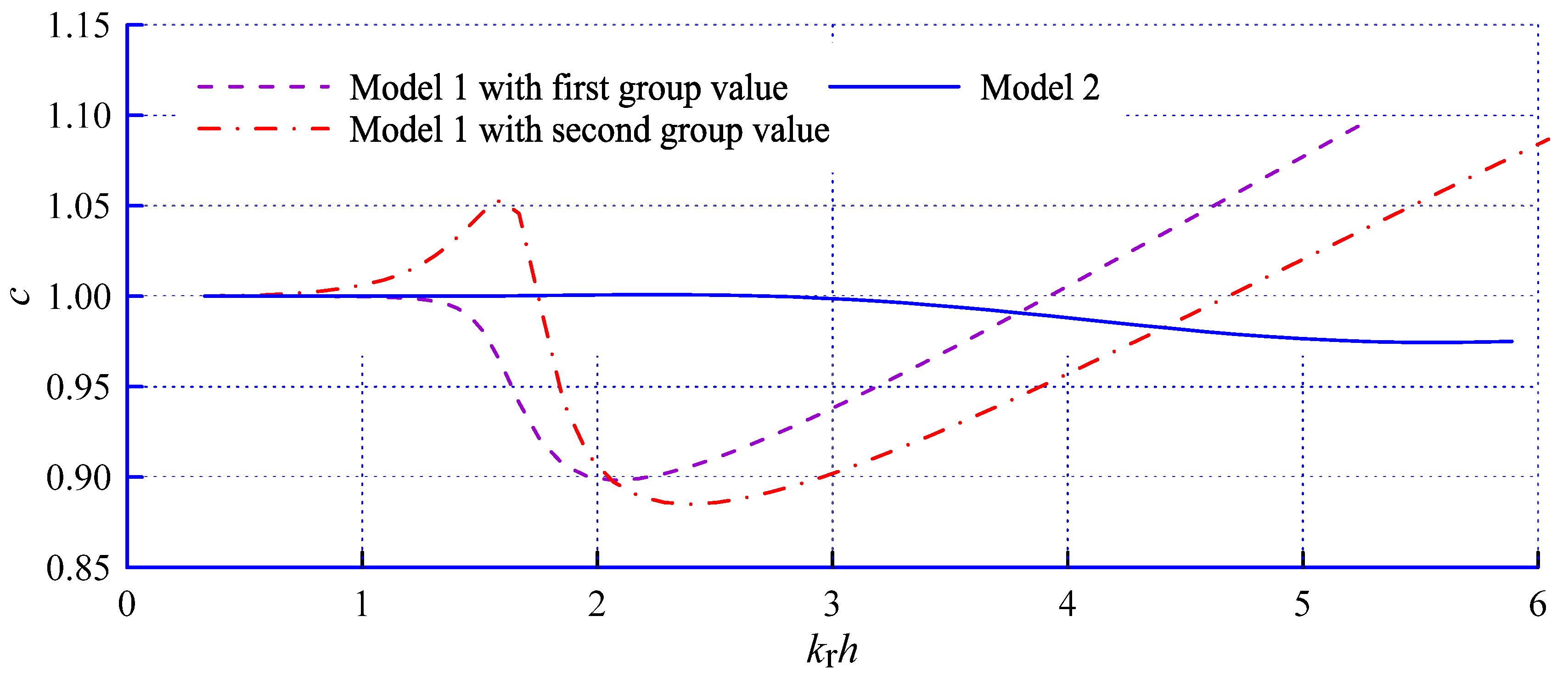
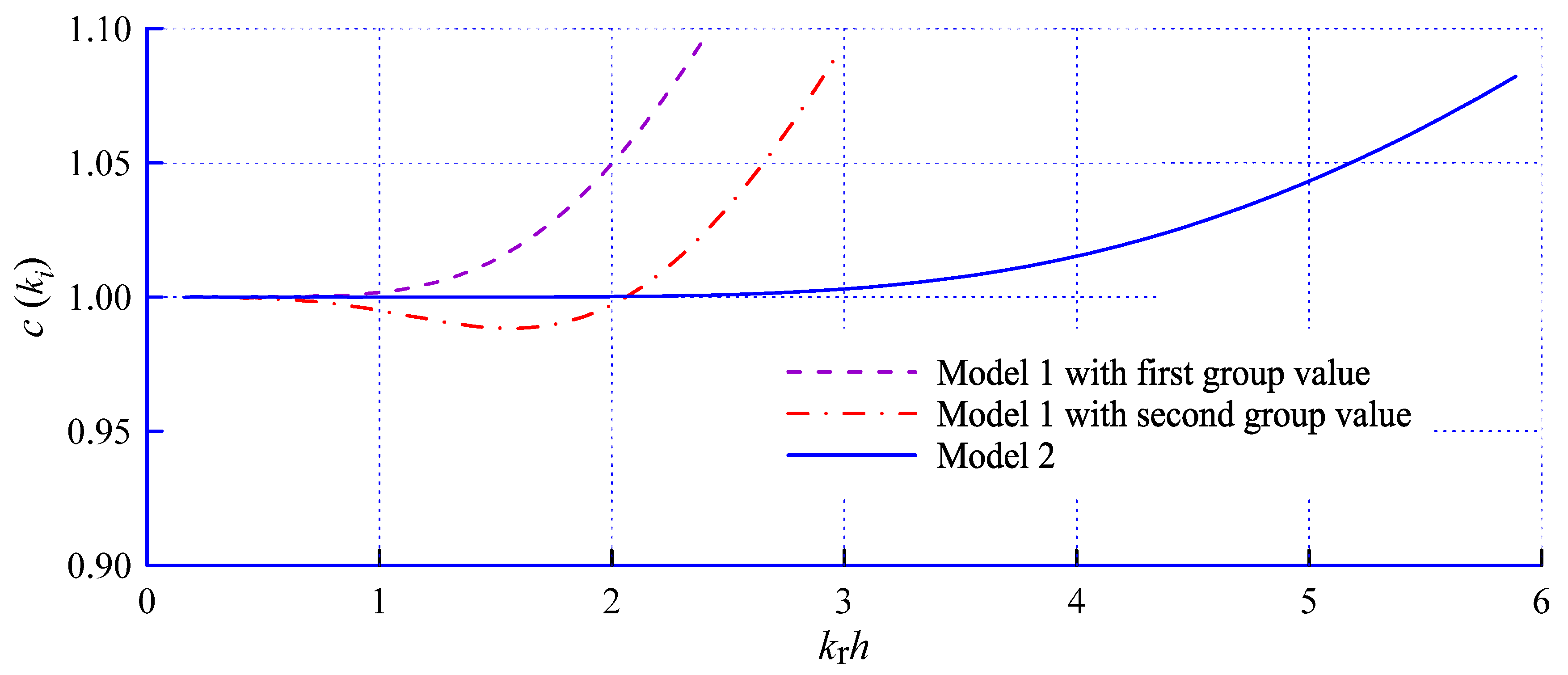
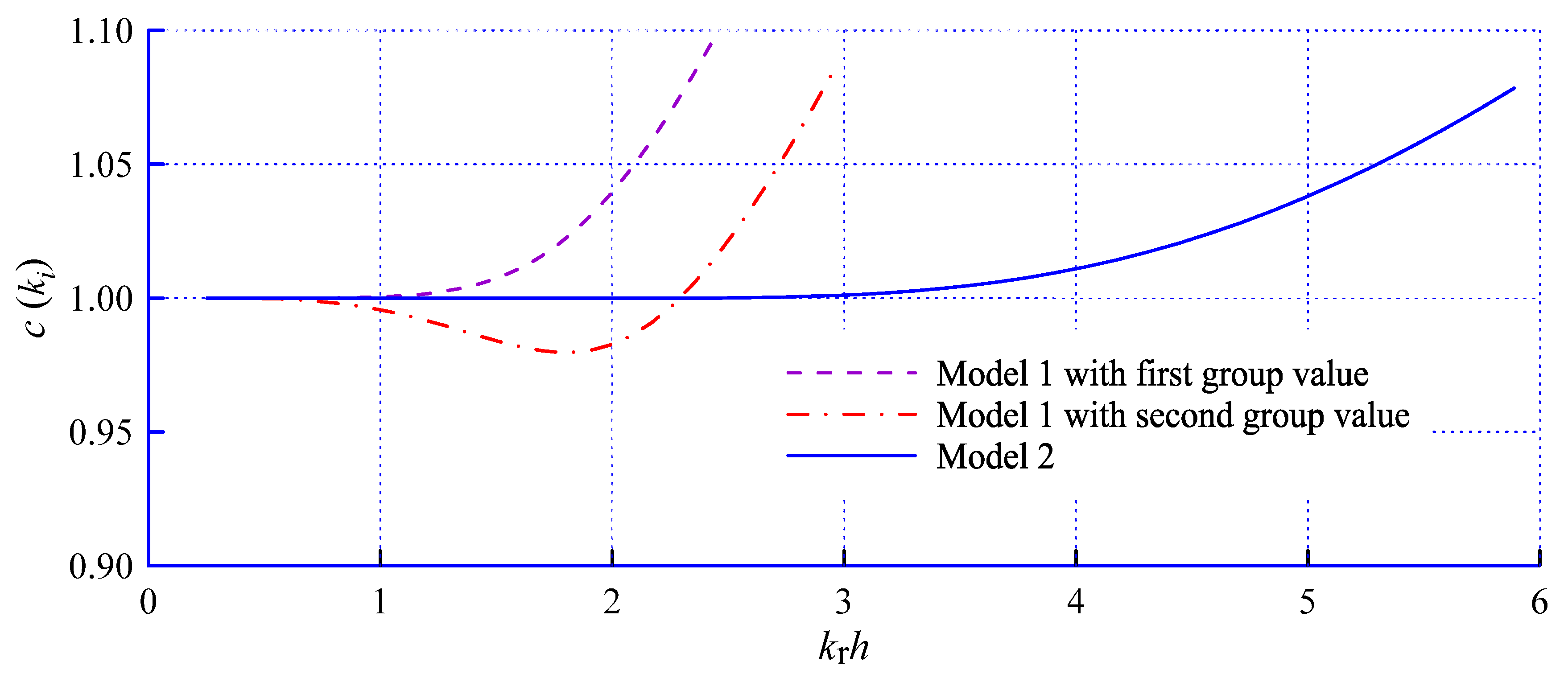
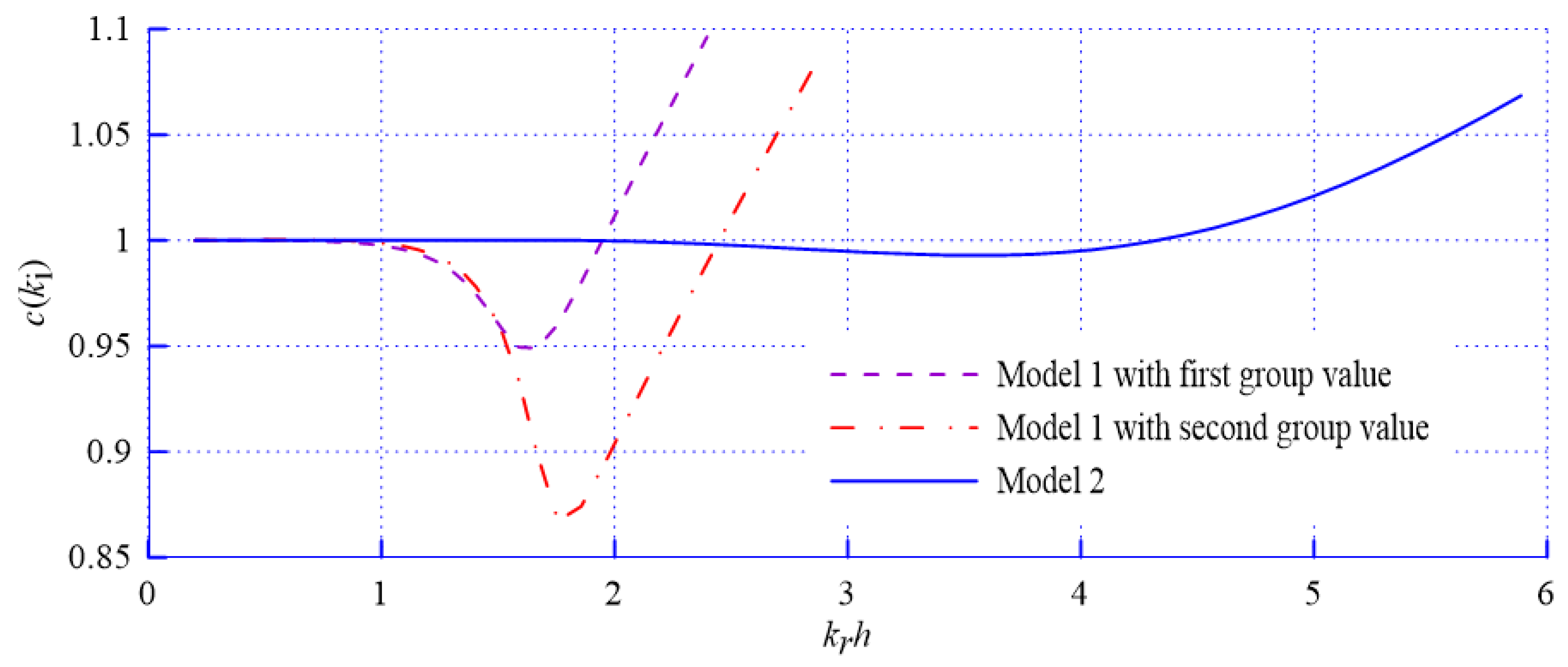
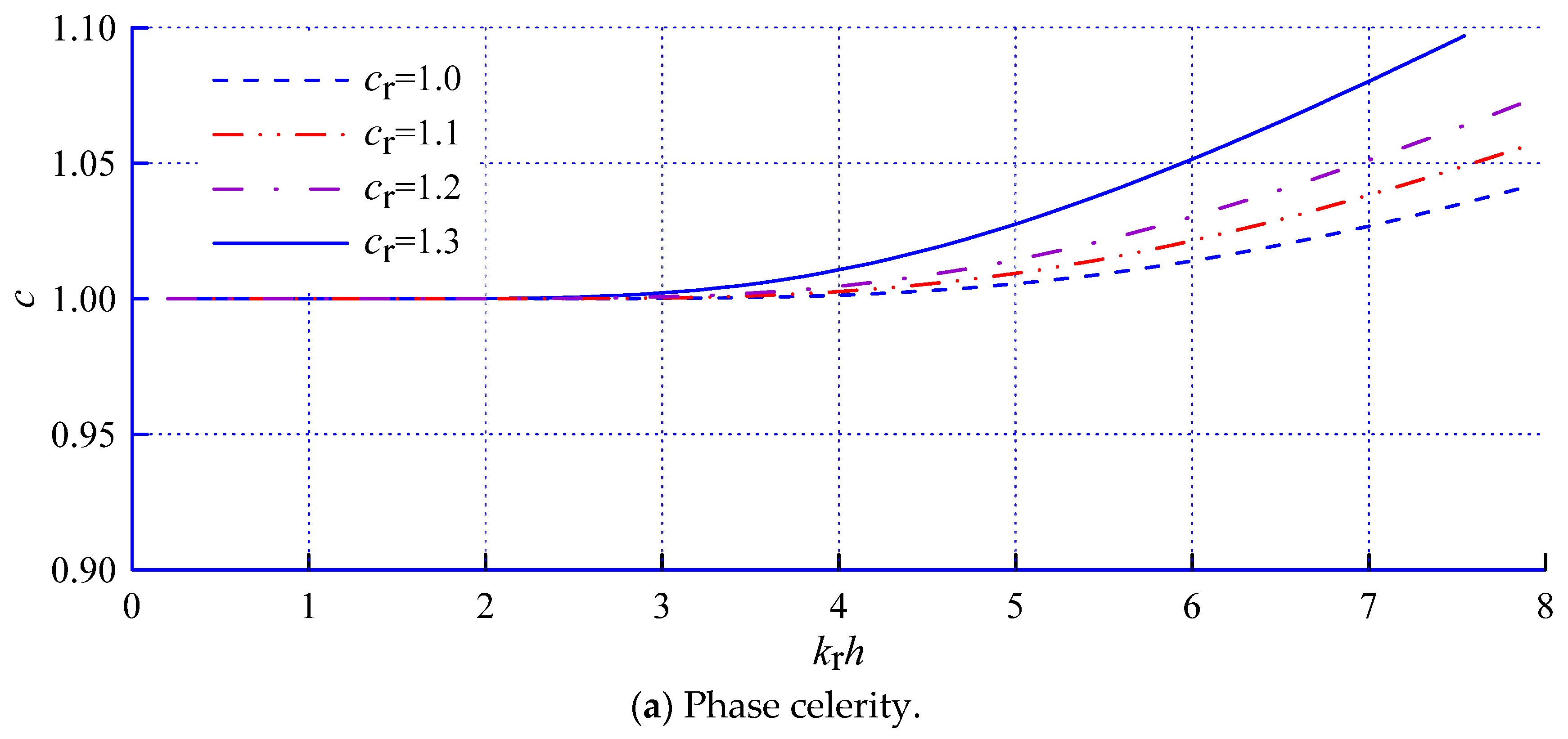

| Model Sets | Parameter Values |
|---|---|
| 1 | β1 = −0.0013, β2 = −0.0654 (I) or β1 = 0.0073, β2 = −0.064 (II) |
| 2 | γ1 = 1/9, γ2 = 0.146488, γ3 = 1/945, γ4 = 0.00798359 |
| 3 | B = −0.4 or B = −0.395 |
| 4 | δ1= 0.101, δ3 = 0.039, B = −0.305, δ3 = 0.082 *, δ4 = 0.162 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Liu, Z.; Fang, K.; Sun, J.; Gou, D. High-Order Boussinesq Equations for Water Wave Propagation in Porous Media. Water 2023, 15, 3900. https://doi.org/10.3390/w15223900
Wang P, Liu Z, Fang K, Sun J, Gou D. High-Order Boussinesq Equations for Water Wave Propagation in Porous Media. Water. 2023; 15(22):3900. https://doi.org/10.3390/w15223900
Chicago/Turabian StyleWang, Ping, Zhongbo Liu, Kezhao Fang, Jiawen Sun, and Daxun Gou. 2023. "High-Order Boussinesq Equations for Water Wave Propagation in Porous Media" Water 15, no. 22: 3900. https://doi.org/10.3390/w15223900





