Modeling and Analysis of Cutoff Wall Performance Beneath Water Structures by Feed-Forward Neural Network (FFNN)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Governing Equations
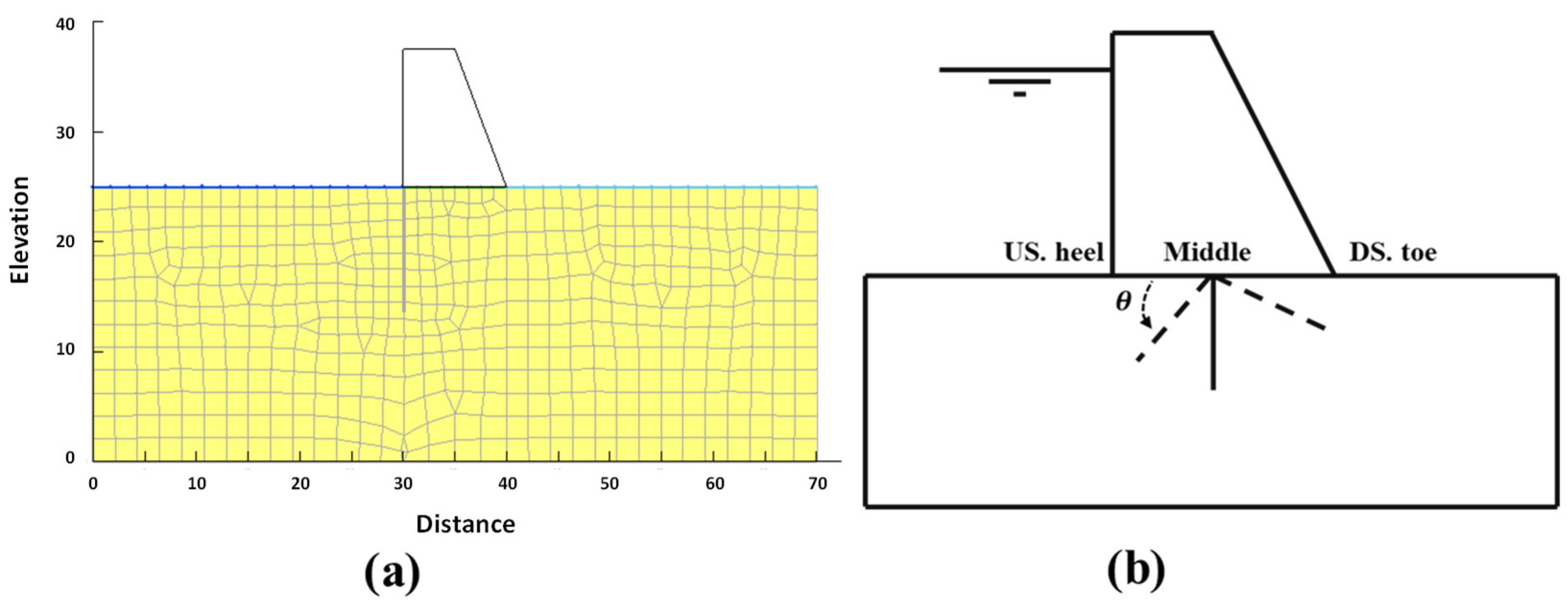
2.2. Numerical Simulation
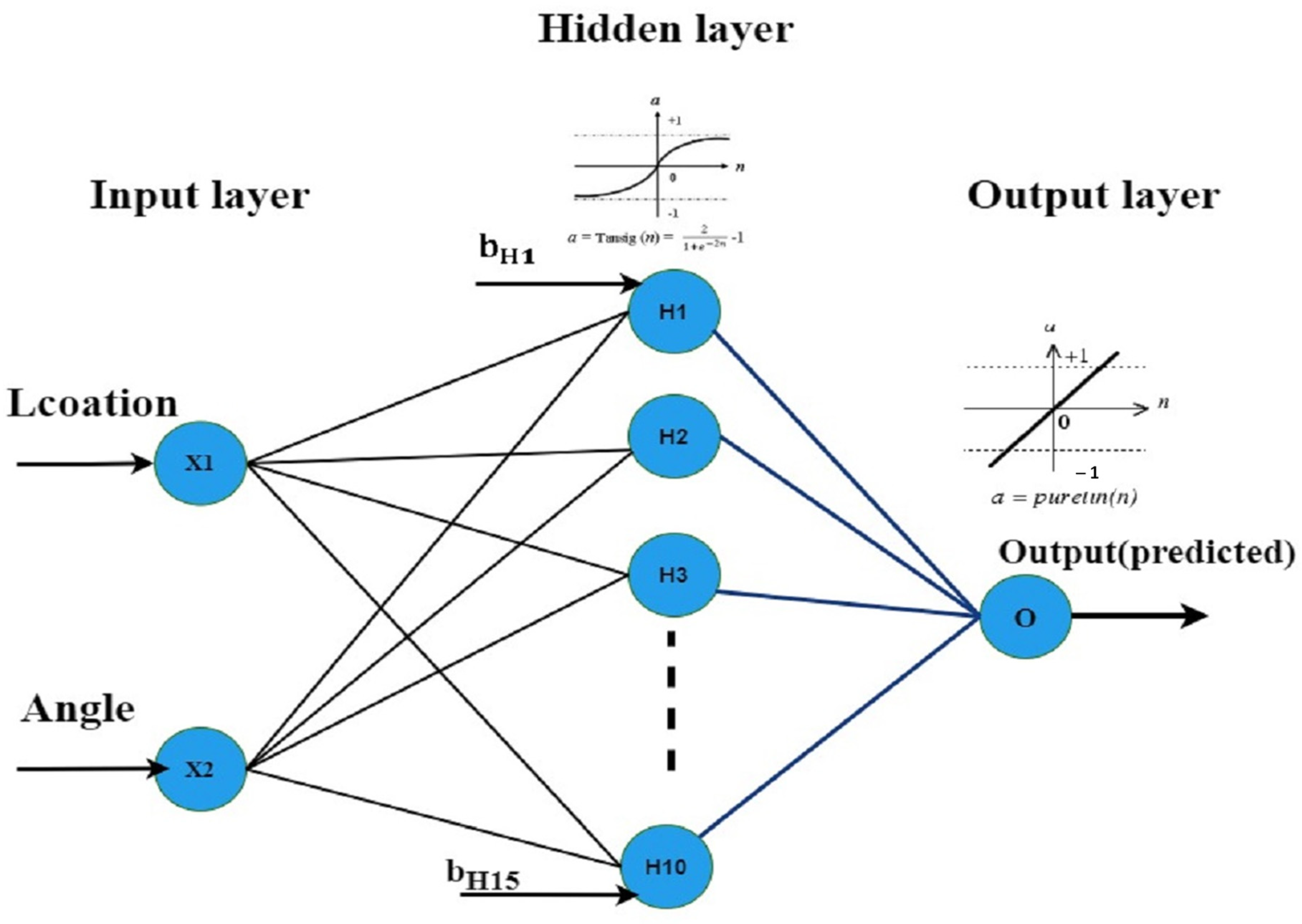
2.3. Artificial Neural Networks
3. Results and Discussion
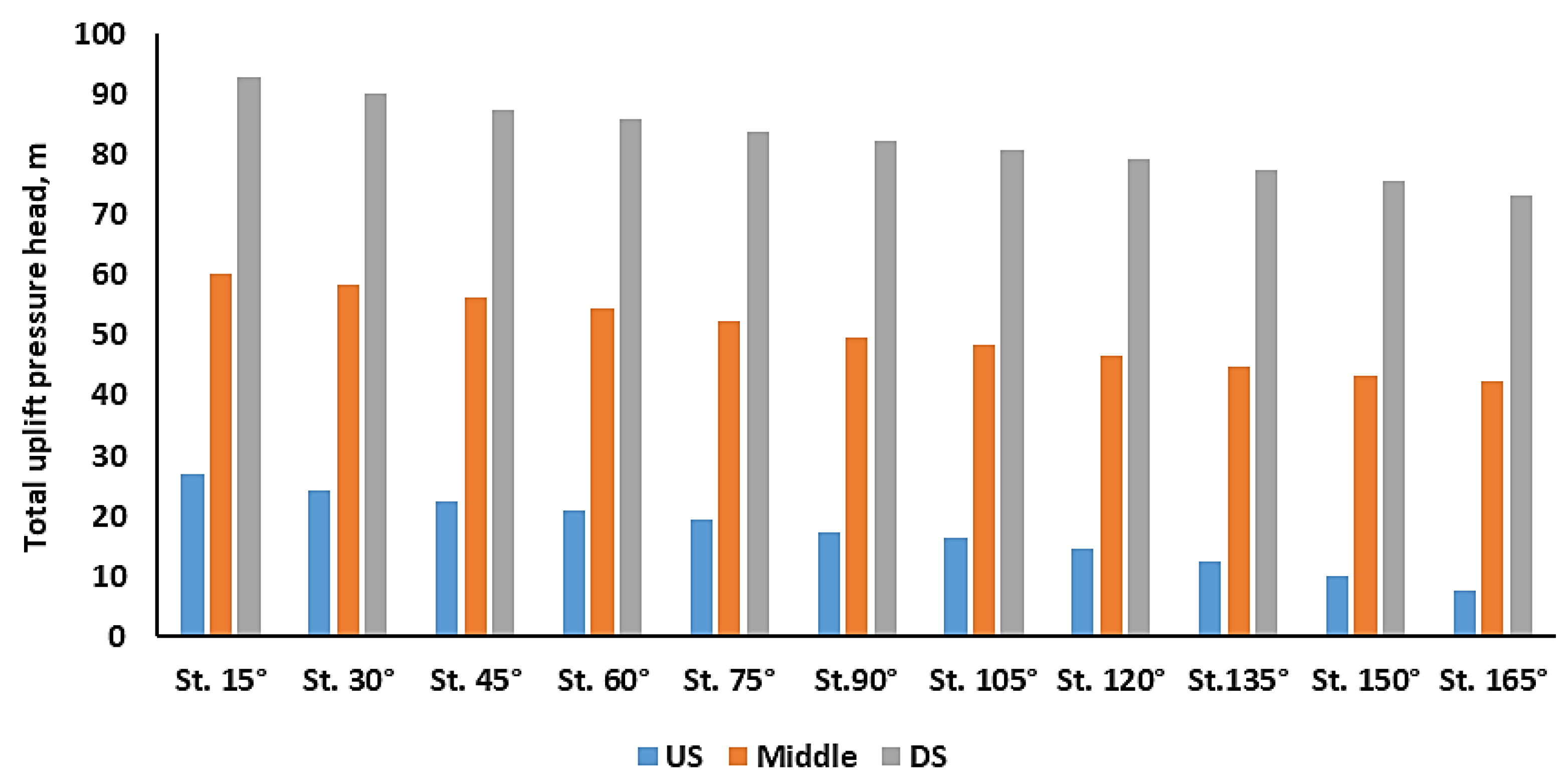
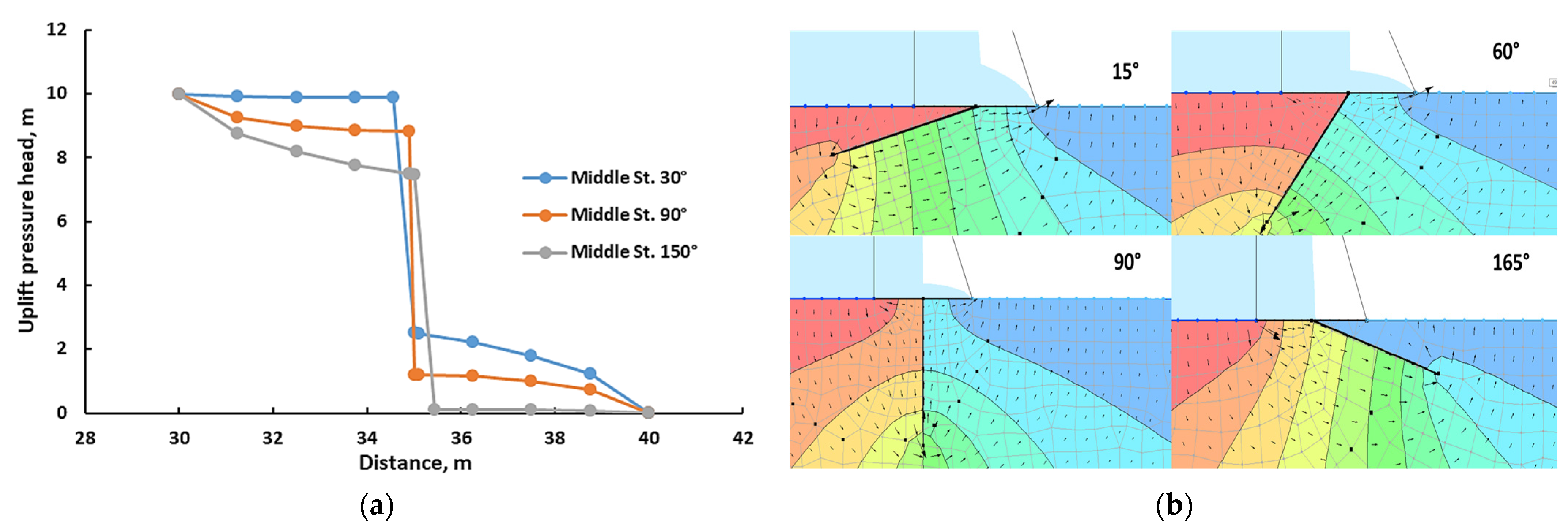
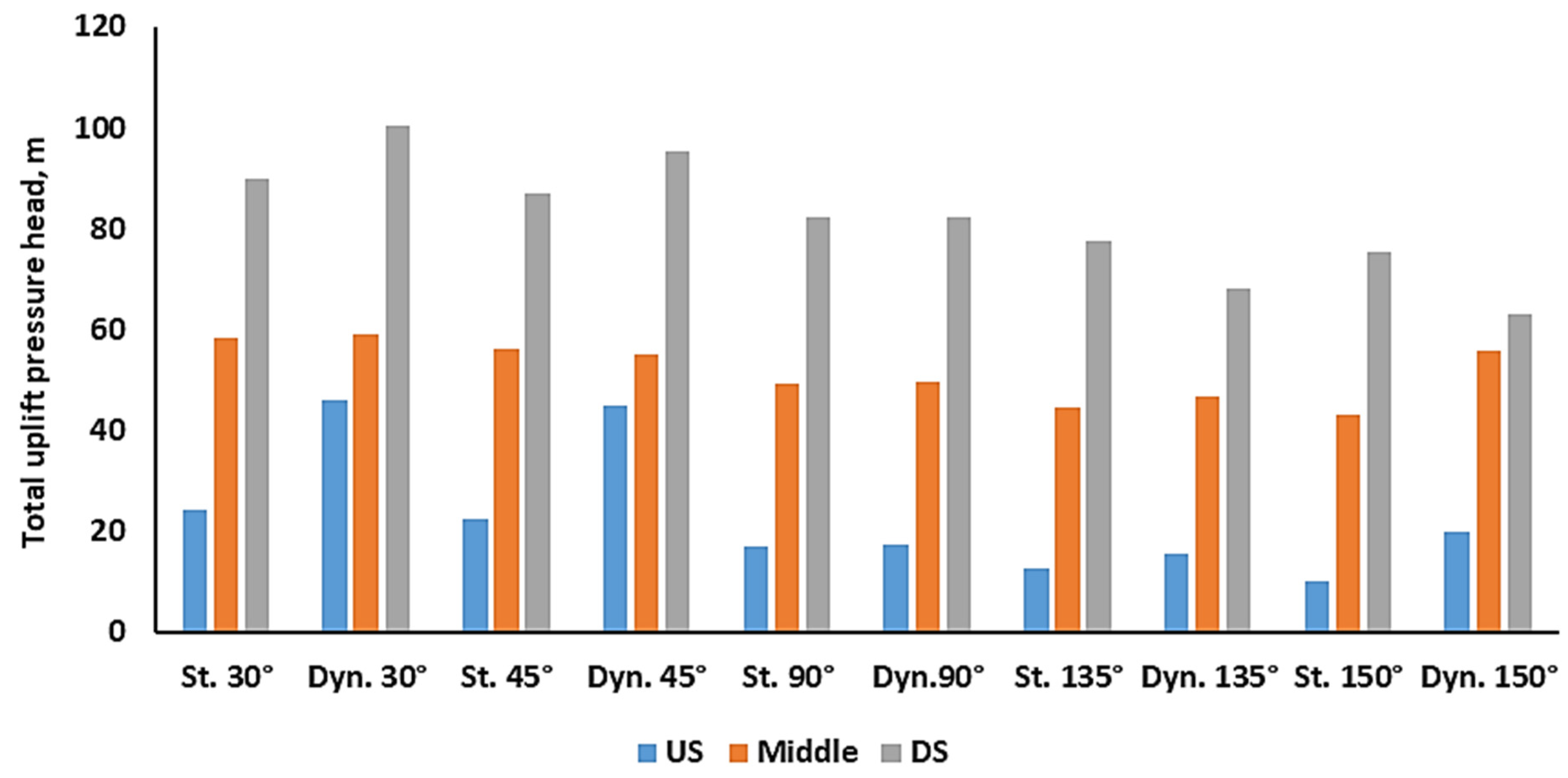
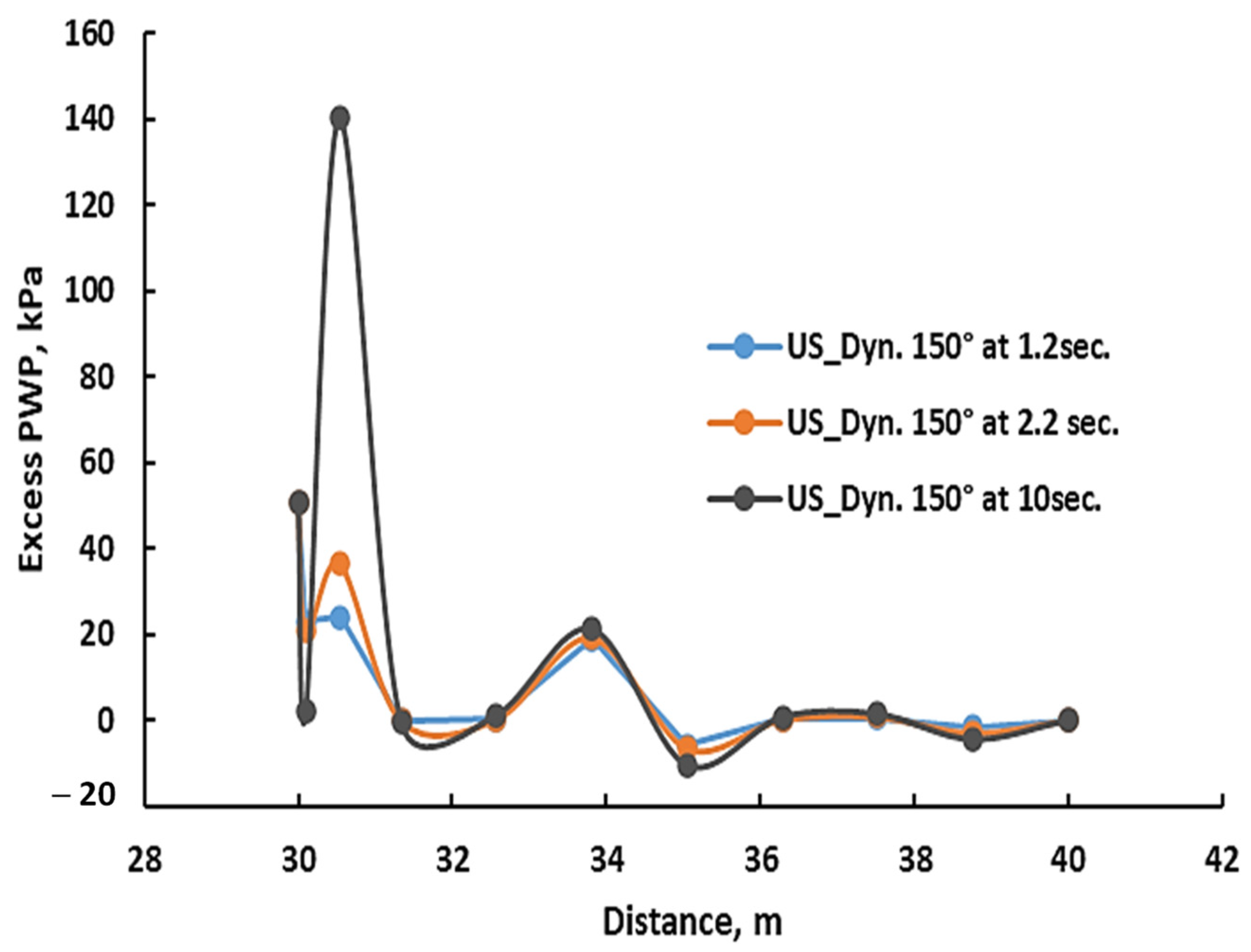
3.1. Uplift Pressure
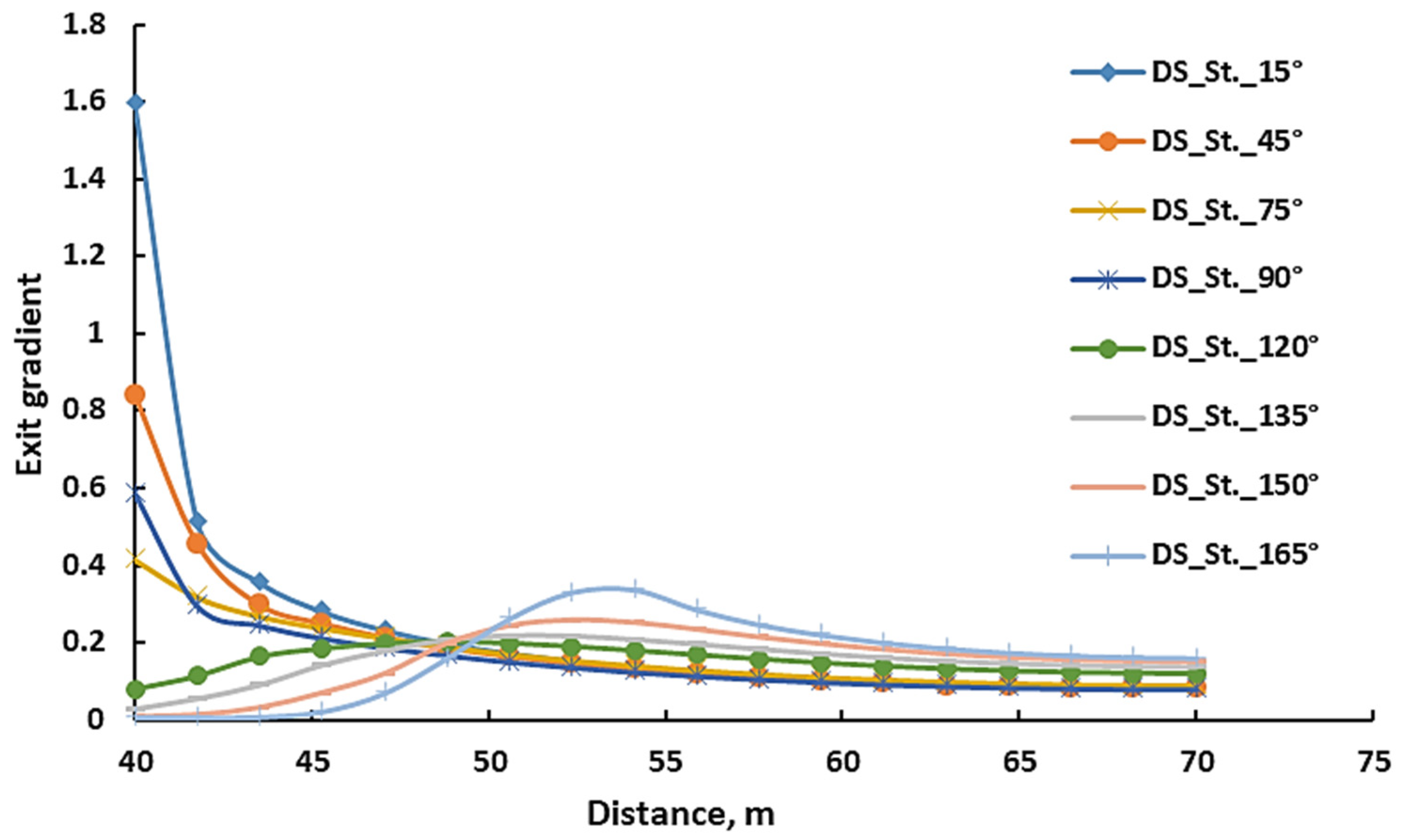
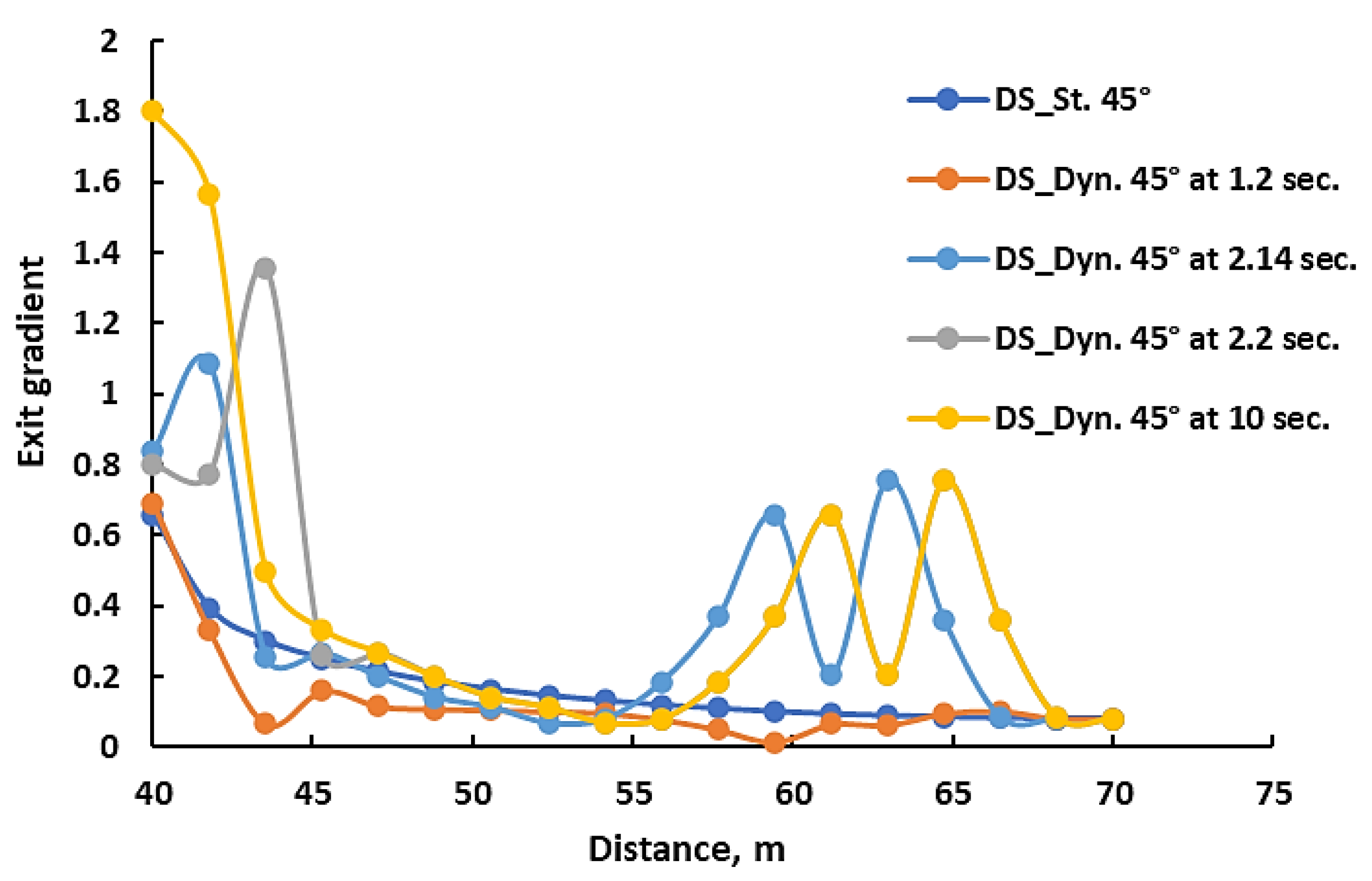
3.2. Exit Hydraulic Gradient
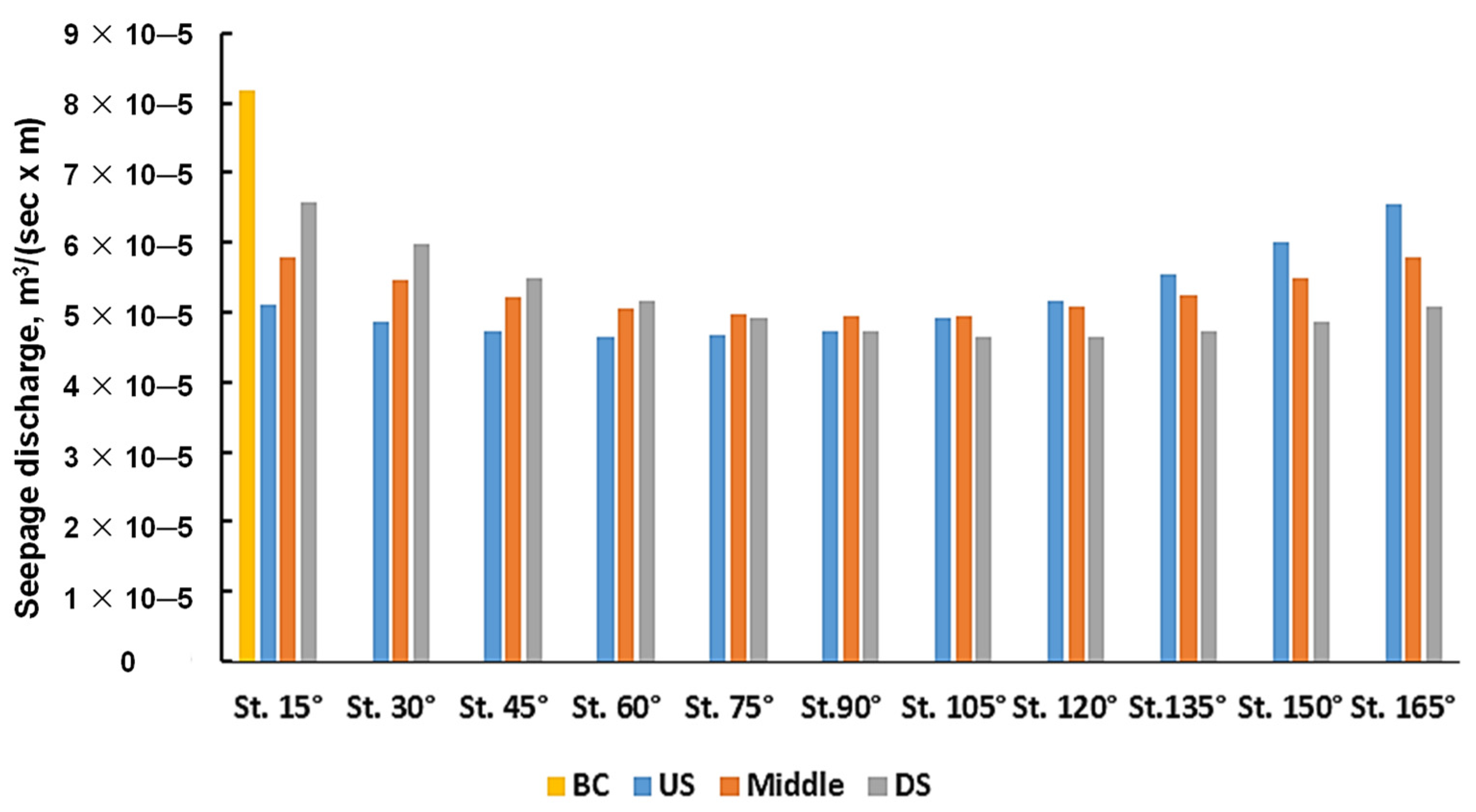
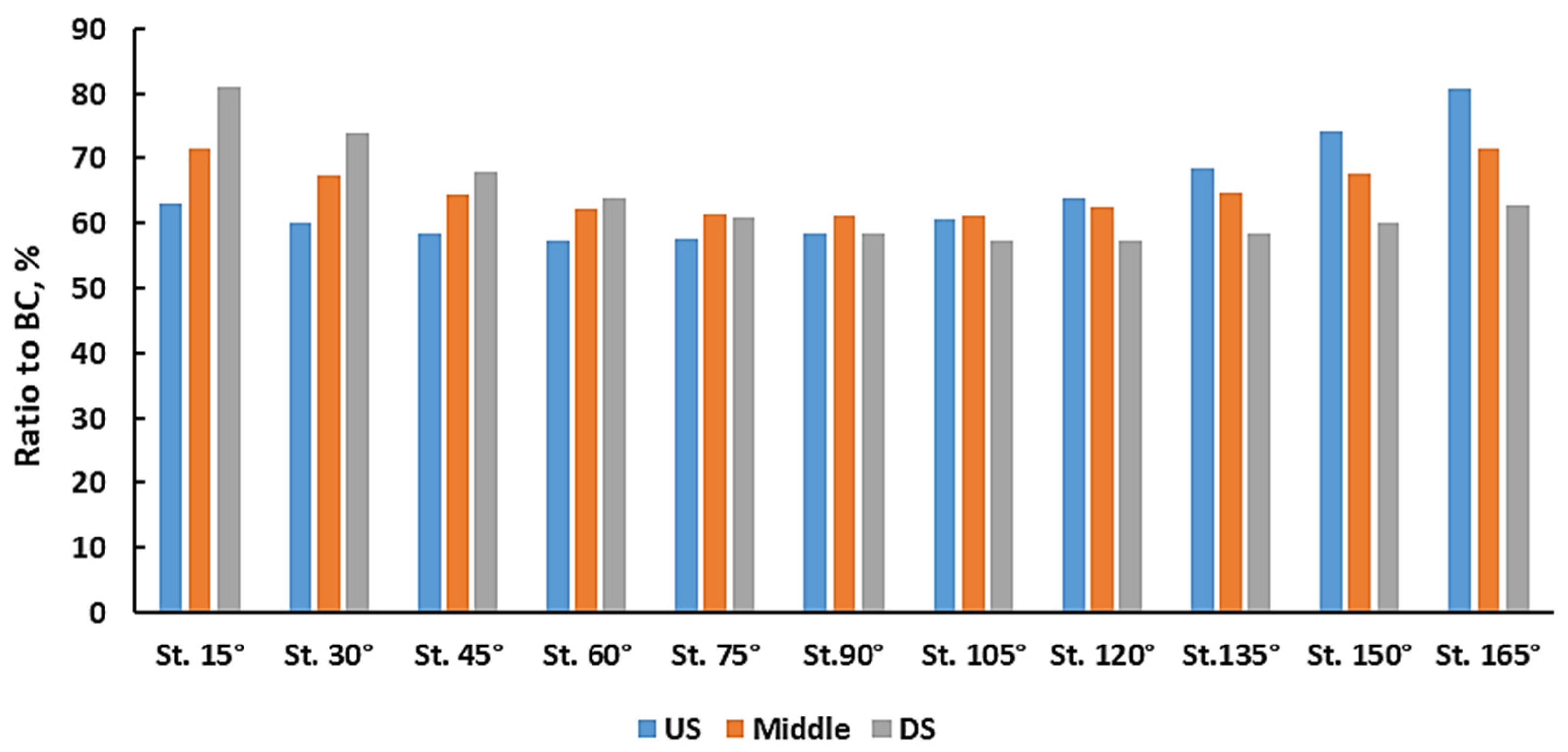
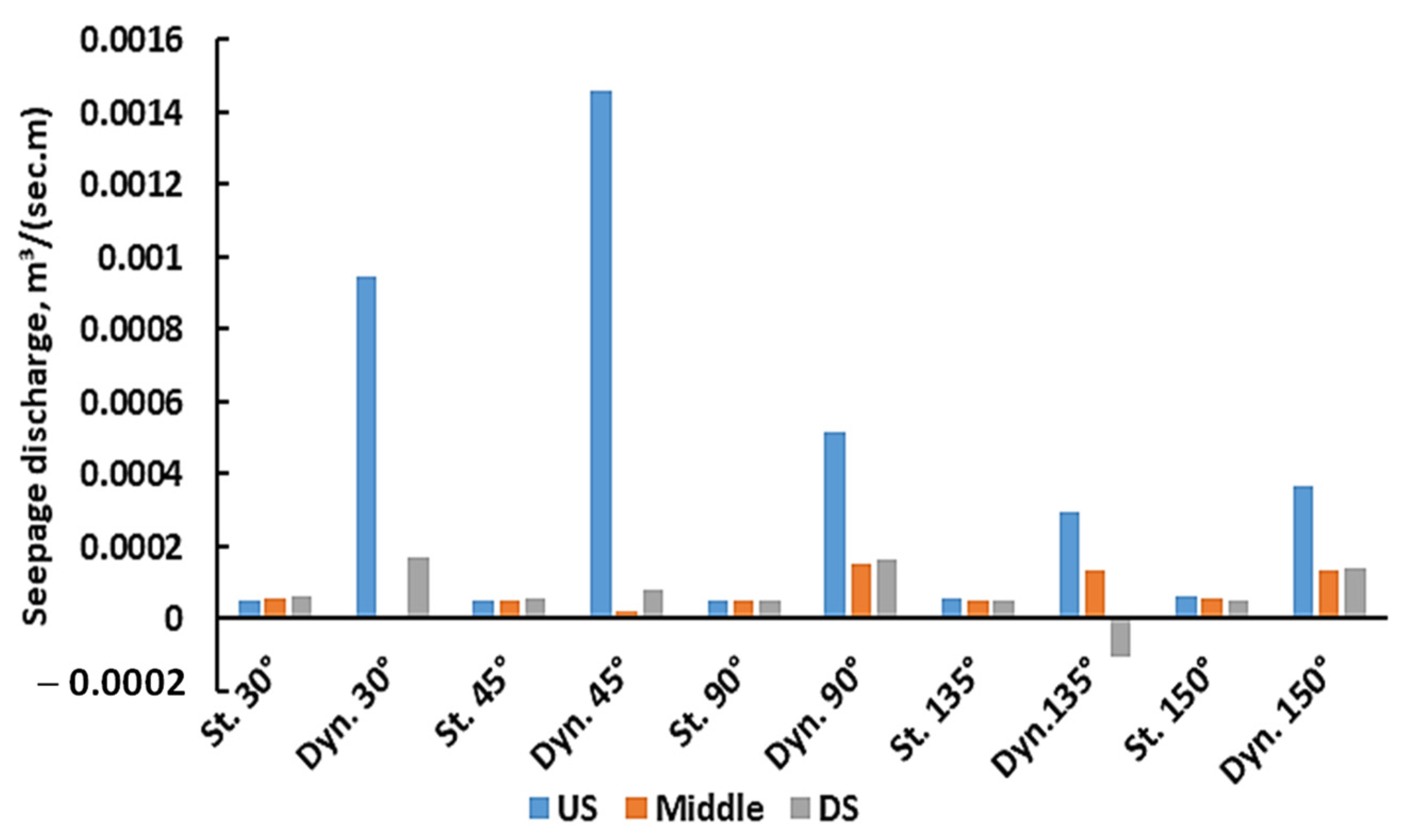
3.3. Seepage Discharge
3.4. Neural Network Modeling
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mansuri, B.; Salmasi, F.; Oghati, B. Effect of Location and Angle of Cutoff Wall on Uplift Pressure in Diversion Dam. Geotech. Geol. Eng. 2014, 32, 1165–1173. [Google Scholar] [CrossRef]
- Nourani, B.; Salmasi, F.; Abbaspour, A.; Oghati Bakhshayesh, B. Numerical Investigation of the Optimum Location for Vertical Drains in Gravity Dams. Geotech. Geol. Eng. 2017, 35, 799–808. [Google Scholar] [CrossRef]
- Norouzi, R.; Salmasi, F.; Arvanaghi, H. Uplift pressure and hydraulic gradient in Sabalan Dam. Appl. Water Sci. 2020, 10, 111. [Google Scholar] [CrossRef]
- Salmasi, F.; Khatibi, R.; Nourani, B. Investigating reduction of uplift forces by longitudinal drains with underlined canals. ISH J. Hydraul. Eng. 2018, 24, 81–91. [Google Scholar] [CrossRef]
- Tokaldany, E.A.; Shayan, H.K. Uplift force, seepage, and exit gradient under diversion dams. Proc. Inst. Civ. Eng. Water Manag. 2013, 166, 452–462. [Google Scholar] [CrossRef]
- Okeke, A.C.-U.; Wang, F. Critical hydraulic gradients for seepage-induced failure of landslide dams. Geoenviron. Disasters 2016, 3, 9. [Google Scholar] [CrossRef]
- Sivakumar, S.; Begum, N.A.; Premalatha, P.V. Deformation analysis of suspended type cut off wall of diversion structures. Heliyon 2019, 5, e02213. [Google Scholar] [CrossRef]
- Moharrami, A.; Moradi, G.; Bonab, M.H.; Katebi, J.; Moharrami, G. Performance of Cutoff Walls Under Hydraulic Structures Against Uplift Pressure and Piping Phenomenon. Geotech. Geol. Eng. 2015, 33, 95–103. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, C.; Zheng, H. A numerical solution to seepage problems with complex drainage systems. Comput. Geotech. 2008, 35, 383–393. [Google Scholar] [CrossRef]
- Bligh, W. Dams, barrages and weirs on porous foundations. Eng. News 1910, 64, 708–710. [Google Scholar]
- Lane, E.W. Security from under-seepage-masonry dams on earth foundations. Trans. Am. Soc. Civ. Eng. 1935, 100, 1235–1272. [Google Scholar] [CrossRef]
- Khosla, R.B.A.; Bose, N.K.; Taylor, E.M. Design of Weirs on Permeable Foundations; Central Board of Irrigation and Power: New Delhi, India, 1936. [Google Scholar]
- Harr, M. Groundwater and Seepage; McGraw-Hill Book Co. Inc.: New York, NY, USA, 1962; p. 249. [Google Scholar]
- Elkamhawy, E.; Wang, H.; Zhou, B.; Yang, Z. Failure mechanism of a slope with a thin soft band triggered by intensive rainfall. Environ. Earth Sci. 2018, 77, 340. [Google Scholar] [CrossRef]
- Elkamhawy, E.; Zelenakova, M.; Abd-Elaty, I. Numerical canal seepage loss evaluation for different lining and crack techniques in arid and semi-arid regions: A case study of the river Nile, Egypt. Water 2021, 13, 3135. [Google Scholar] [CrossRef]
- Hassan, W.H. Application of a genetic algorithm for the optimization of a cutoff wall under hydraulic structures. J. Appl. Water Eng. Res. 2017, 5, 22–30. [Google Scholar] [CrossRef]
- Hassan, W.H. Application of a Genetic Algorithm for the Optimization of a Location and Inclination Angle of a Cut-Off Wall for Anisotropic Foundations Under Hydraulic Structures. Geotech. Geol. Eng. 2019, 37, 883–895. [Google Scholar] [CrossRef]
- Javanmard, M.; Mottaghi, R.; Hosseini, S.M.M. Investigating the influence of penetration length of cut-off wall on its dynamic interaction with core and foundation of earth dam. Civ. Eng. J. 2018, 4, 3019–3026. [Google Scholar] [CrossRef]
- Armanuos, A.M.; Negm, A.M.; Javadi, A.A.; Abraham, J.; Gado, T.A. Impact of inclined double-cutoff walls under hydraulic structures on uplift forces, seepage discharge and exit hydraulic gradient. Ain Shams Eng. J. 2022, 13, 101531. [Google Scholar] [CrossRef]
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Neural network toolbox. In User’s Guide MathWorks; The MathWorks, Inc.: Natick, MA, USA, 2010; Volume 2, pp. 77–81. [Google Scholar]
- Alrowais, R.; Abdel daiem, M.M.; Li, R.; Maklad, M.A.; Helmi, A.M.; Nasef, B.M.; Said, N. Groundwater Quality Assessment for Drinking and Irrigation Purposes at Al-Jouf Area in KSA Using Artificial Neural Network, GIS, and Multivariate Statistical Techniques. Water 2023, 15, 2982. [Google Scholar] [CrossRef]
- Abdel Daiem, M.M.; Hatata, A.; El-Gohary, E.H.; Abd-Elhamid, H.F.; Said, N. Application of an artificial neural network for the improvement of agricultural drainage water quality using a submerged biofilter. Environ. Sci. Pollut. Res. 2021, 28, 5854–5866. [Google Scholar] [CrossRef]
- Abdel Daiem, M.M.; Hatata, A.; Galal, O.H.; Said, N.; Ahmed, D. Prediction of biogas production from anaerobic co-digestion of waste activated sludge and wheat straw using two-dimensional mathematical models and an artificial neural network. Renew. Energy 2021, 178, 226–240. [Google Scholar] [CrossRef]
- Abdel Daiem, M.M.; Hatata, A.; Said, N. Modeling and optimization of semi-continuous anaerobic co-digestion of activated sludge and wheat straw using Nonlinear Autoregressive Exogenous neural network and seagull algorithm. Energy 2022, 241, 122939. [Google Scholar] [CrossRef]
- Adib, A.; Poorveis, D.; Mehraban, F. Comparison between results of solution of Burgers’ equation and Laplace’s equation by Galerkin and least-square finite element methods. Appl. Water Sci. 2018, 8, 42. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Sadeghfam, S.; Adami, R.; Abbaszadeh, H. Numerical Analysis of Seepage in Steady and Transient Flow State by the Radial Basis Function Method. Numer. Methods Civ. Eng. 2023, 8, 58–68. [Google Scholar]
- Krahn, J. Seepage Modeling with SEEP/W: An Engineering Methodology; GEO-SLOPE International Ltd.: Calgary, AL, Canada, 2004. [Google Scholar]
- Krahn, J. Stress and Deformation Modeling with SIGMA/W: An Engineering Methodology; GEO-SLOPE International Ltd.: Calgary, AL, Canada, 2004. [Google Scholar]
- Krahn, J. Dynamic Modeling with QUAKE/W: An Engineering Methodology; GEO-SLOPE International Ltd.: Calgary, AL, Canada, 2004. [Google Scholar]
- Allen, T.I.; Wald, D.J.; Hotovec, A.J.; Lin, K.; Earle, P.S.; Marano, K.D. An Atlas of ShakeMaps for Selected Global Earthquakes; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2008.













| Model | Error | Number of Neurons | |||
|---|---|---|---|---|---|
| 2 | 5 | 10 | 15 | ||
| Uplift (m) | RMSE | 0.4134 | 0.1840 | 0.0830 | 0.0697 |
| 0.9998 | 1.00 | 1.00 | 1.00 | ||
| Seepage (m3/(s.m)) | RMSE | 0.0163 | 0.0024 | 0.0021 | 0.0032 |
| 0.9567 | 0.9992 | 0.9994 | 0.9985 | ||
| Exit gradient (dimensionless) | RMSE | 0.0471 | 0.0328 | 0.0059 | 0.0102 |
| 0.9802 | 0.9905 | 0.9997 | 0.9991 | ||
| Model | Activation Function of the Hidden Layer’s | Error | Training Algorithm | ||
|---|---|---|---|---|---|
| Trainlm | Trainscg | Trainbr | |||
| Uplift pressure (m) | tansig | RMSE | 0.0406 | 0.3505 | 0.1862 |
| 1.00 | 0.9998 | 1.0000 | |||
| radbas | RMSE | 0.3571 | 1.2833 | 0.1849 | |
| 0.9998 | 0.9978 | 1.00 | |||
| tribas | RMSE | 0.2070 | 0.3181 | 0.4286 | |
| 0.9999 | 0.9999 | 0.9998 | |||
| Seepage (m3/(s.m)) | tansig | RMSE | 0.0021 | 0.0042 | 0.0014 |
| 0.9994 | 0.9971 | 0.9997 | |||
| radbas | RMSE | 0.0024 | 0.0031 | 0.0014 | |
| 0.9991 | 0.9985 | 0.9997 | |||
| tribas | RMSE | 0.0028 | 0.0047 | 0.0781 | |
| 0.9987 | 0.9964 | 0.7722 | |||
| Exit gradient (dimensionless) | tansig | RMSE | 0.0059 | 0.0457 | 0.0419 |
| 0.9997 | 0.9813 | 0.9844 | |||
| radbas | RMSE | 0.0367 | 0.0507 | 0.0668 | |
| 0.9888 | 0.9771 | 0.9605 | |||
| tribas | RMSE | 0.0691 | 0.0286 | 0.1088 | |
| 0.9590 | 0.9928 | 0.8996 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alrowais, R.; Alwushayh, B.; Bashir, M.T.; Nasef, B.M.; Ghazy, A.; Elkamhawy, E. Modeling and Analysis of Cutoff Wall Performance Beneath Water Structures by Feed-Forward Neural Network (FFNN). Water 2023, 15, 3870. https://doi.org/10.3390/w15213870
Alrowais R, Alwushayh B, Bashir MT, Nasef BM, Ghazy A, Elkamhawy E. Modeling and Analysis of Cutoff Wall Performance Beneath Water Structures by Feed-Forward Neural Network (FFNN). Water. 2023; 15(21):3870. https://doi.org/10.3390/w15213870
Chicago/Turabian StyleAlrowais, Raid, Bandar Alwushayh, Muhammad Tariq Bashir, Basheer M. Nasef, Ahmed Ghazy, and Elsayed Elkamhawy. 2023. "Modeling and Analysis of Cutoff Wall Performance Beneath Water Structures by Feed-Forward Neural Network (FFNN)" Water 15, no. 21: 3870. https://doi.org/10.3390/w15213870







