1. Introduction
The soil surface temperature is the temperature of the top layer of soil. It is influenced by a number of factors, including the air temperature, the amount of sunlight, and the wind speed [
1]. Soil surface temperature can be measured through in situ ground investigations, as well as via satellite data [
2,
3]. Many scholars point to the fact that soil temperature at any depth beneath the earth’s surface remains constant throughout the year [
4,
5]. However, some studies indicate that soil temperatures at shallow depths present notable fluctuations on a daily and annual basis [
6,
7].
The amount of moisture in the soil, the temperature of the soil, and the temperature at the surface are important factors in hydrology that determine different land surface activities [
8]. Soil moisture, land surface temperature, and their relationship can be influenced by multiple factors such as soil emissivity, evapotranspiration, and thermal inertia [
9]. These parameters change over space and time, and variations in surface temperature can help to identify target properties [
10]. Additionally, as soil temperature increases, the rate of evaporation also increases. This can lead to a decrease in soil moisture, especially in the surface layers of the soil. The soil temperature is inversely proportional to the soil moisture [
11]. The removal of canopy cover and loss of organic matter can result in a reduction in soil moisture and an increase in soil temperature at the soil’s surface [
12].
The groundwater level plays a significant role in fulfilling the water requirements of crops, especially in arid and semi-arid zones [
13,
14]. The level of groundwater in an aquifer can be affected by a number of factors, including irrigation, which can add water to the ground and raise the water table; filtration, which can remove water from the ground and lower the water table; soil surface temperature, which can affect the rate of evaporation and thus the amount of water that is available to recharge the aquifer; and leakage of water into the drains, which can remove water from the ground and lower the water table [
15]. The use of mathematical modeling can help us to obtain more precise results about the effects of climate change on water table depth and salinity changes in different regions [
16,
17]. Drying climate, intensive pumping for irrigation purposes, and changes in land use can impact the water table [
18,
19,
20]. Climate change has caused longer and more intense heat waves, which reduce groundwater levels [
21]. The relationship between the soil surface temperature and groundwater level is complex. In general, as the soil surface temperature increases, water evaporates more quickly from the soil. This can lead to a decrease in groundwater level [
22,
23].
Several variables can influence the relationship between soil surface temperature and groundwater level. These include the following: the soil type—sandy soils have a reduced ability to retain water compared with clay soils, making them more prone to evaporation; the amount of vegetation cover—vegetation helps to shade the soil and reduce evaporation; the amount of water in the soil—the more water that is in the soil, the less water will evaporate; the wind speed—wind can increase evaporation by blowing away water vapor; the amount of sunlight—sunlight provides the energy for evaporation; and the air temperature—the higher the air temperature, the more water will evaporate [
24].
The impacts of the relationship between soil surface temperature and groundwater level can be significant and can have a number of negative ramifications for ecosystems and human society [
25]. These impacts include the following:
Reduced water availability—as soil surface temperature increases, water evaporates more quickly from the soil [
26,
27]. This can lead to a decrease in groundwater level. This can reduce the amount of water available for drinking, irrigation, and other uses;
Increased risk of waterborne diseases—as water levels decrease, water becomes more stagnant and can become contaminated with bacteria and other microorganisms [
28]. This can increase the risk of waterborne diseases such as cholera, typhoid fever, and diarrhea.
In this study, we investigated solar radiation as a factor contributing to the potential lifting of soil surface temperatures. This involved an assessment of the relationship between solar radiation and the soil surface temperature. Solar radiation is the energy that comes from the sun and reaches the earth’s surface. It is the primary source of heat for the earth’s surface and atmosphere. When solar radiation hits the earth’s surface, it is absorbed by the soil, rocks, and other objects. This absorption of solar radiation causes the earth’s surface to heat up [
29].
The relationship between solar radiation and soil surface temperature is a strong positive one. This means that as solar radiation increases, so does the soil surface temperature [
30]. This relationship is influenced by a number of factors, including the time of the day, the season, the latitude, the presence of clouds, the air temperature, and the soil moisture. Our study focuses on the relationship between soil surface temperature and groundwater measurements because solar radiation does not directly impact to the changes on groundwater levels.
The current research aims to examine the relationship between soil surface temperature and groundwater level through analyzing data collected throughout the growing season, spanning from April to September, between the years 1991 and 2020. The specific objectives of this research are (1) to comprehend the changes in groundwater level and soil surface temperature over time; and (2) to establish a statistical correlation between soil surface temperature and groundwater level using data collected from the Hydrometeorological Service Agency.
The main hypothesis of this research is that soil surface temperature has a significant impact on changes in groundwater level in the study area.
3. Results and Discussion
The study’s findings for average annual air temperature indicate that the minimum mean annual air temperature was 14.6 °C, the maximum was 17.1 °C, and the mean was 16.1 °C during 1991–2020. The data for air temperature were collected from the Bukhara Meteorological Station. The standard deviation was 0.563 °C (
Table 2).
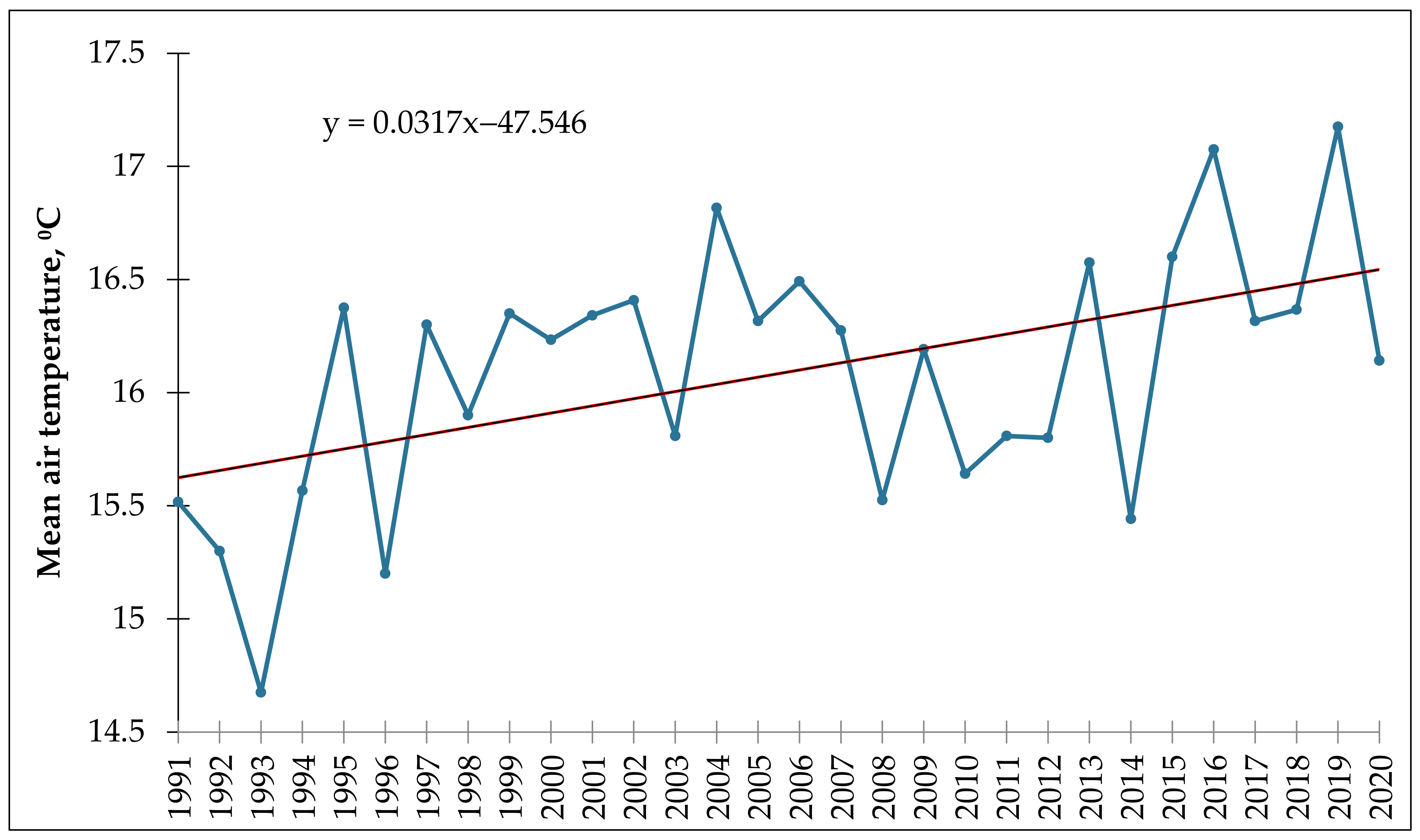
Figure 2 shows the change in annual average air temperature in the Bukhara region from 1991 to 2020. The average air temperature in Bukhara has been increasing over the past 20 years, with a particularly sharp increase in the last decade. In 1991, the average air temperature in Bukhara was 15.3 °C. By 2020, the average air temperature had increased to 17.2 °C. This represents an increase of over 1.9 °C in just 30 years.
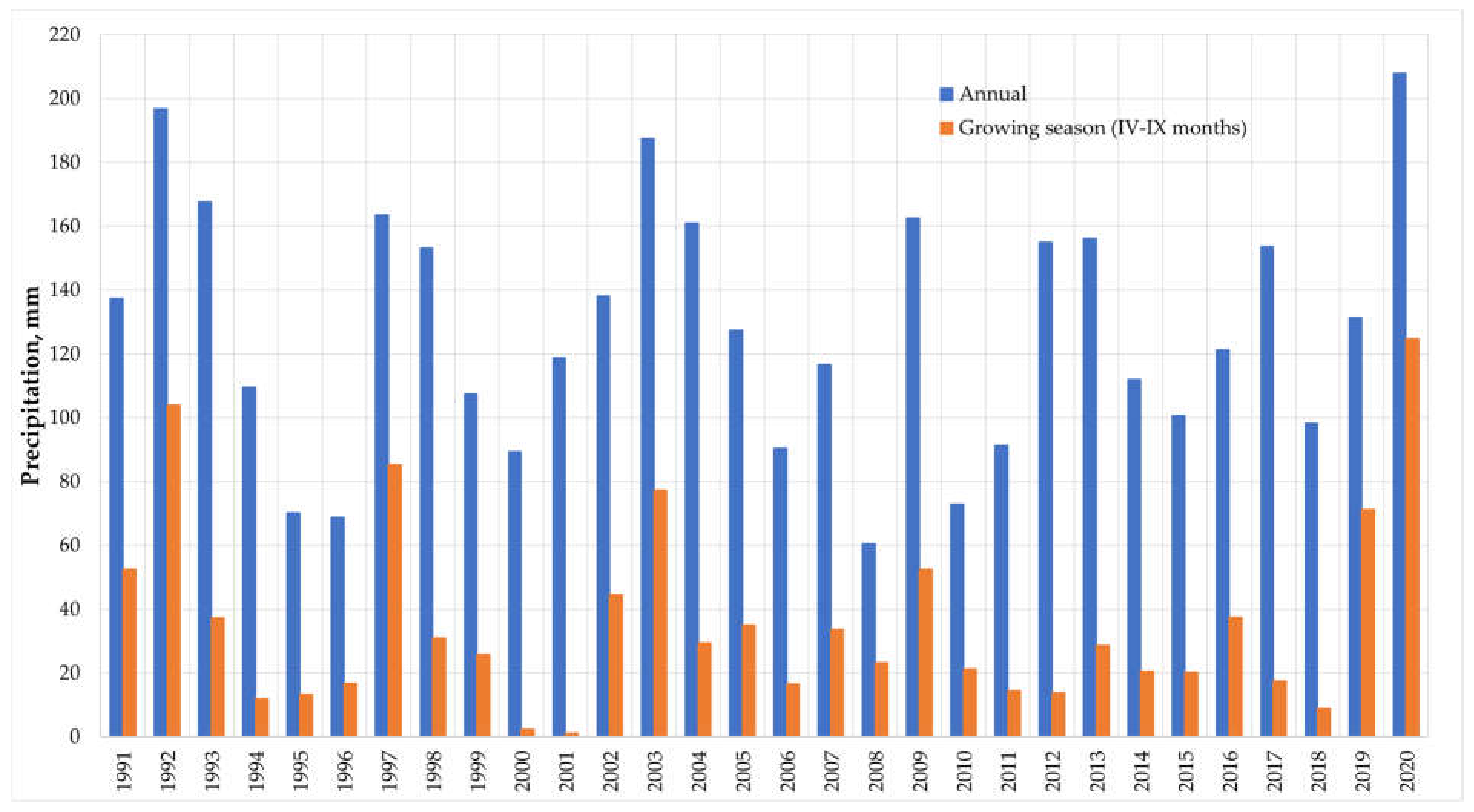
Furthermore, the annual and growing season rainfall values were analyzed for the period of 1991–2020. The annual precipitation is the total amount of precipitation that falls in a year, while the growing season precipitation is the amount of precipitation that falls during the vegetation season, which is typically defined as the period from April to September (
Figure 3). The figure shows that the annual precipitation in Bukhara has varied significantly over the past 30 years, from a minimum of 60.5 mm in 2008 to a maximum of 207.9 mm in 2020. The growing season precipitation has also varied significantly, from a minimum of 1.0 mm in 2001 to a maximum of 124.9 mm in 2020. The mean annual precipitation in the region over the past 30 years was 127.58 mm, and the mean growing season precipitation was 35.74 mm. The standard deviation of the annual precipitation was 39.12 mm, and the standard deviation of the growing season precipitation was 29.85 mm. This figure provides a useful overview of the annual and growing season precipitation in Bukhara region over the past 30 years. It can be used to assess the variability of precipitation in the region and to identify trends over time. This information can be used to inform decisions about water management and agricultural practices.
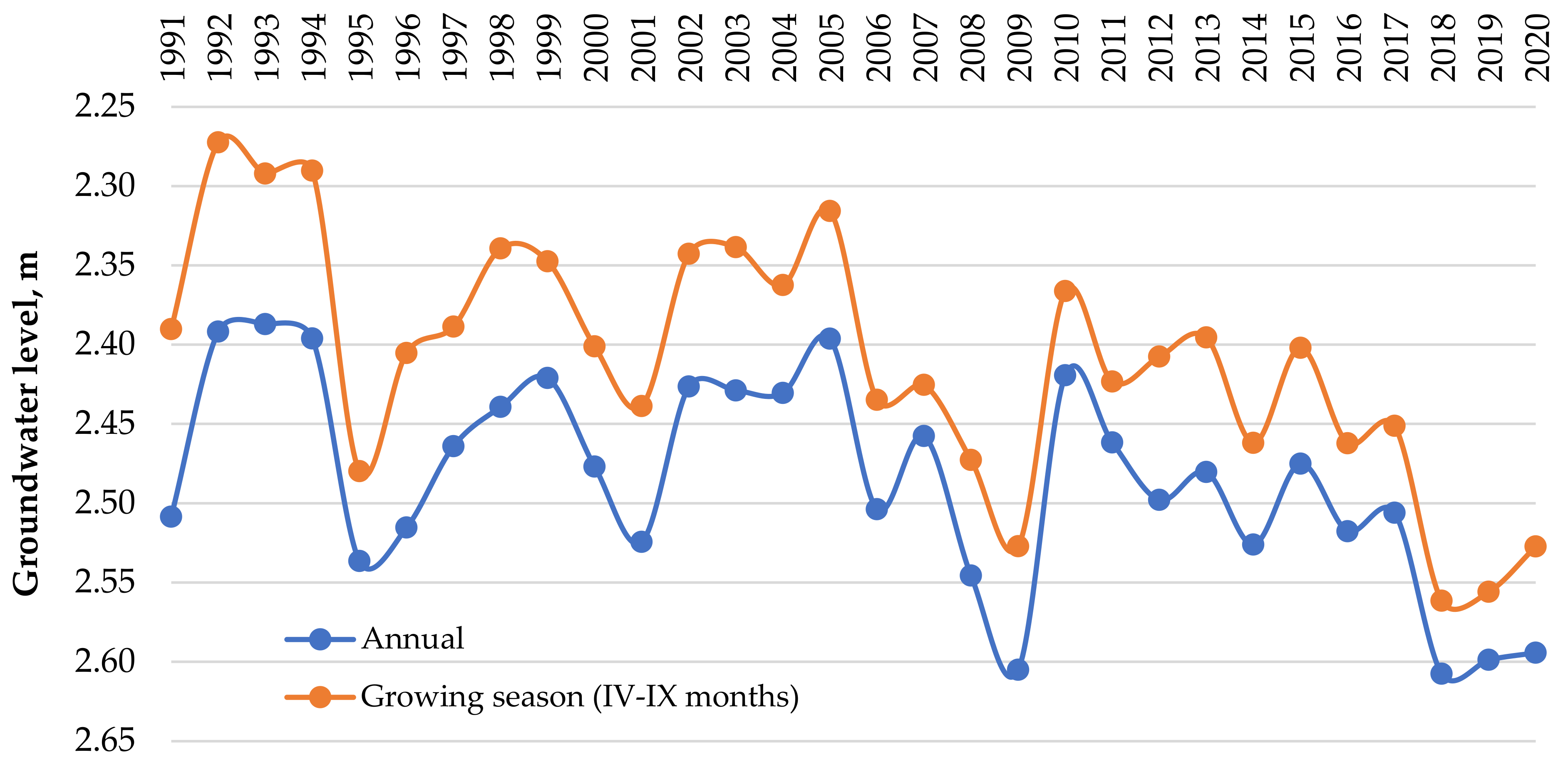
In addition, changes in the level of groundwater during the annual and vegetation period from 1991 to 2020 were studied. The annual groundwater level is the average depth of the water table over the entire year, while the growing season groundwater level is the average depth of the water table during the six months of the growing season (
Figure 4).
Figure 4 shows that the annual groundwater level in the region has decreased over the past three decades. In 1991, the annual groundwater level was around 2.5 m below the surface. By 2020, it had decreased to around 2.6 m below the surface. The growing season groundwater level has also decreased over time. In 1991, the growing season groundwater level was around 2.4 m below the surface. By 2020, it had decreased to around 2.55 m below the surface. Additionally, the decline in groundwater level has been more pronounced during growing seasons than during the rest of the year. This is likely due to the increased demand for water for irrigation during the growing season. Overall, the decline in groundwater level in Bukhara is a serious concern, as it could have a negative impact on agricultural production and water supply for human consumption. A decrease in the groundwater level can be associated with the intensive use of advanced water-saving irrigation technologies (drip and sprinkler irrigation) and increased risks of water scarcity and climate change.
Furthermore, given that solar radiation does not have a direct impact on groundwater, we conducted a study concerning soil surface temperature.
Table 3 shows a correlation matrix that illustrates the correlation coefficients between two variables: solar radiation and soil surface temperature.
The correlation coefficient is a measure of the strength of the relationship between two variables. A correlation coefficient of 1 indicates a perfect positive correlation, meaning that the two variables always move in the same direction. In
Table 3, the correlation coefficient between solar radiation and soil surface temperature is 0.840. This indicates a strong positive correlation between the two variables. In other words, solar radiation and soil surface temperature tend to move in the same direction. When solar radiation increases, soil surface temperature also tends to increase. And when solar radiation decreases, soil surface temperature also tends to decrease. This is because solar radiation is the main source of energy for heating the earth’s surface. When more solar radiation reaches the earth’s surface, the ground absorbs more heat and warms up. When less solar radiation reaches the earth’s surface, the ground absorbs less heat and cools down.
However, it is important to note that correlation does not equal causation. Just because two variables are correlated does not mean that one causes the other. There could be other factors that are causing the changes in both variables. For example, changes in weather patterns could be causing changes in both solar radiation and soil surface temperature.
To determine whether there is a causal relationship between solar radiation and soil surface temperature, further research would be needed. This research could involve conducting experiments to isolate the effects of solar radiation on soil surface temperature.
Table 4 displays the results of a regression analysis of the variable “soil surface temperature”.
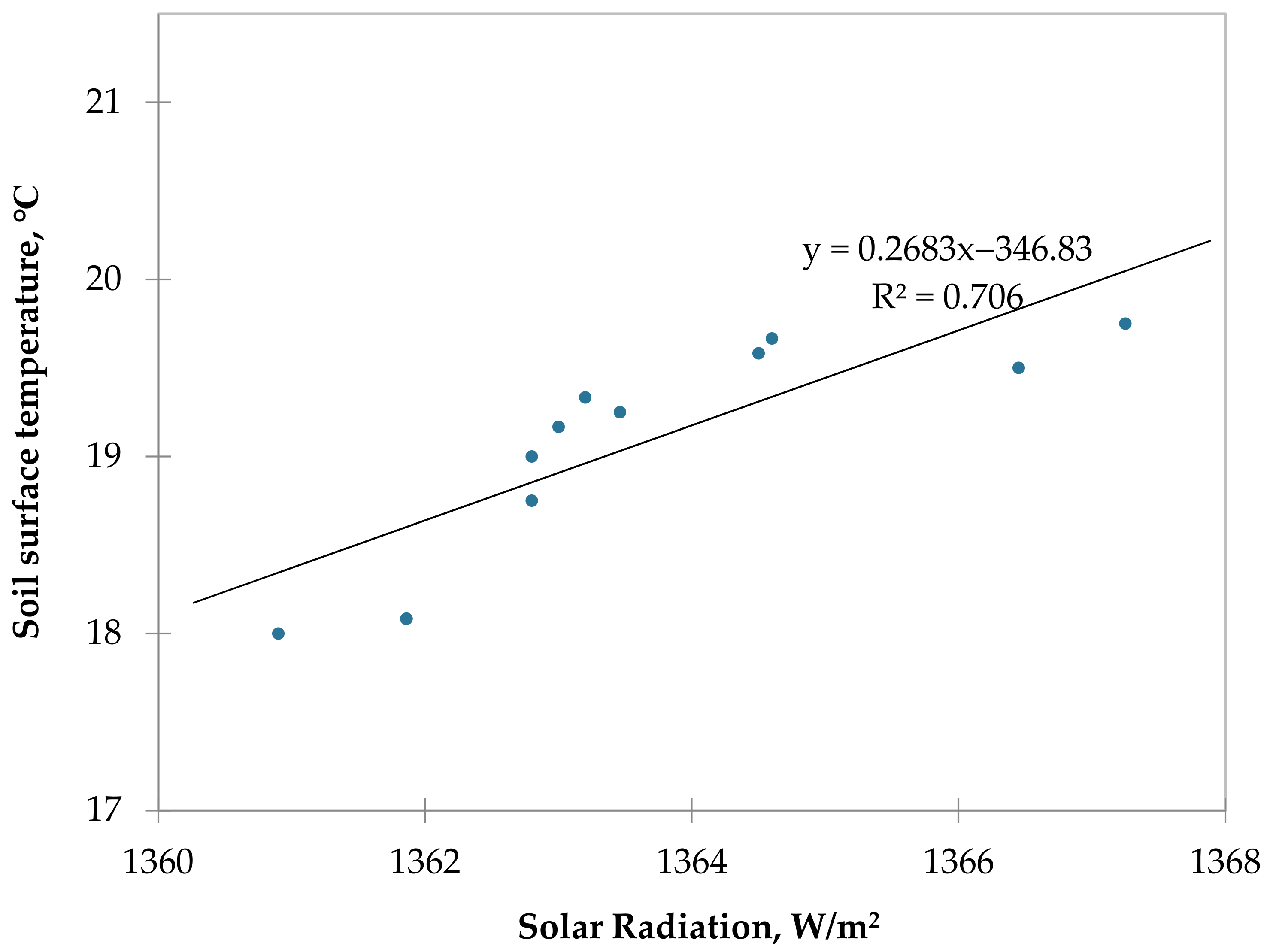
The regression of the variable soil surface temperature has a good fit, with an R² value of 0.706 (
Figure 5). This means that 70.6% of the variation in soil surface temperature can be explained by the regression model. The adjusted R² value is 0.674, which means that 67.4% of the variation in soil surface temperature can be explained by the model after taking into account the number of independent variables in the model.
The mean squared error (MSE) is 0.117, which means that the average squared difference between the predicted and actual soil surface temperatures is 0.117. The root mean squared error (RMSE), a measure of the standard deviation of the residuals, is 0.343. The mean absolute percentage error (MAPE) is 1.528, which means that on average, the predicted soil surface temperatures are 15.28% different from the actual values.
The Durbin–Watson statistic (DW) is 1.482, which is close to 2.0, indicating that there is no autocorrelation between the residuals. The Akaike information criterion (AIC), a measure of how well the model fits the data, is −21.777. A lower AIC value indicates a better fit. The Schwarz Bayesian criterion (SBC), another measure of how well the model fits the data, is −20.981. A lower SBC value indicates a better fit.
The PRESS statistic, a measure of how well the model predicts new data, is 1.765. A lower PRESS value indicates a better prediction. The Q² statistic, a measure of how well the model explains the variance in the dependent variable, is 0.509. A higher Q² value indicates a better explanation.
Overall, the regression of the variable soil surface temperature has a good fit and is able to explain a significant amount of the variation in soil surface temperature. The model can be used to predict soil surface temperatures with a reasonable degree of accuracy.
Table 5 shows the standardized coefficients for the relationship between solar radiation and soil surface temperature.
The standardized coefficient is a measure of the strength of the relationship between two variables, after taking into account the standard deviations of both variables.
In
Table 5, the standardized coefficient for solar radiation is 0.840. This means that for every 1 standard deviation increase in solar radiation, there is a 0.840 standard deviation increase in soil surface temperature.
The standard error of the coefficient is 0.181. This means that we can be 95% confident that the true standardized coefficient is within 0.181 of 0.840.
The t-statistic is 4.651. This is greater than the critical t-value of 2.776, so we can reject the null hypothesis that the true standardized coefficient is equal to 0. In other words, there is a statistically significant relationship between solar radiation and soil surface temperature.
The p-value is 0.001, which is less than 0.05. This means that the probability of obtaining the observed standardized coefficient by chance is less than 0.05. Therefore, we can conclude that the relationship between solar radiation and soil surface temperature is statistically significant.
The lower bound of the 95% confidence interval is 0.432 and the upper bound is 1.249. This means that we can be 95% confident that the true standardized coefficient is between 0.432 and 1.249.
In conclusion,
Table 4 shows that there is a statistically significant positive relationship between solar radiation and soil surface temperature. This means that an increase in solar radiation is associated with an increase in soil surface temperature.
Below, we will consider the relationship between the mean soil surface temperature and the level of groundwater in the months of April–September in Bukhara in 1991–2020. We derived 117 observations for each variable. The minimum groundwater level was 1.720 m, and the maximum was 2.29 m. The mean groundwater level was 2.051 m, and the standard deviation was 0.132 m. The minimum soil surface temperature was 18.0 °C, and the maximum was 39.0 °C. The mean soil surface temperature was 30.444 °C, and the standard deviation was 4.996 °C (
Table 6).
The data in
Table 6 suggest that the groundwater level and soil surface temperature varied significantly over the time period studied. The groundwater level was highest in the middle of the growing season (July) and lowest at the beginning and end of the growing season (April and September). The soil surface temperature was highest in the middle of the day (noon) and lowest at night.
The data in
Table 6 can be used to track changes in groundwater level and soil surface temperature over time. This information can be used to understand the effects of climate change on these important environmental variables.
ANOVA Test
Table 7 provided below is an ANOVA table. ANOVA is a statistical test that is used to compare the means of two or more groups. It has been used for global sensitivity analyses for various models [
43]. It can be used to measure the statistical significance of the difference between two different methods or more [
44]. In this case, the ANOVA is being used to compare the groundwater levels of different locations.
Source—This column identifies the source of variation in the data. In this case, the source of variation is the location of the groundwater level measurements;
DF—This column stands for degrees of freedom. Degrees of freedom are a measure of the variability in the data. In this case, there are 1.0 degrees of freedom for the model and 115.0 degrees of freedom for the error;
Sum of squares—This column shows the amount of variation in the data that is explained by the model. In this case, the model explains 1.077 of the variation in the data;
Mean squares—This column is calculated by dividing the sum of squares by the degrees of freedom. In this case, the mean square for the model is 1.077;
F—This column is the F statistic. The F statistic is a measure of the significance of the model. In this case, the F statistic is 132.506;
Pr > F—This column is the p-value. The p-value is a measure of the probability of obtaining the observed results if the null hypothesis is true. In this case, the p-value is <0.0001;
Signification codes—This column shows the significance of the results. A significance code of * indicates that the results are significant at the 0.05 level. A significance code of ** indicates that the results are significant at the 0.01 level, and a significance code of *** indicates that the results are significant at the 0.001 level.
In this case, the p-value is <0.0001, which is less than 0.05. This means that the results are significant at the 0.05 level. Therefore, we can conclude that the model is significant and that the location of the groundwater level measurements does have an impact on the groundwater level.
In other words, the groundwater level is not the same everywhere. It varies depending on the location. The ANOVA table shows that the location of the groundwater level measurements explains 1.077 m of the variation in the data. This is a significant amount of variation, and it means that the location of the measurements is a factor that can affect the groundwater level.
Table 8 below is a table of model parameters for groundwater level.
Table 8 has six columns:
Source—This column identifies the source of the parameter. In this case, the source of the parameters is the model;
Value—This column shows the value of the parameter. In this case, the value of the intercept is 1.464 and the value of soil surface temperature (SST), °C is 0.019;
Standard error—This column shows the standard error of the parameter. In this case, the standard error of the intercept is 0.052 and the standard error of SST, °C is 0.002;
t—This column is the t-statistic for the parameter. The t-statistic is a measure of the significance of the parameter. In this case, the t-statistic for the intercept is 28.324 and the t-statistic for SST, °C is 11.511;
Pr > |t|—This column is the p-value for the parameter. The p-value is a measure of the probability of obtaining the observed results if the null hypothesis is true. In this case, the p-value for the intercept is <0.0001 and the p-value for SST, °C is <0.0001;
Signification codes—This column shows the significance of the results. A significance code of * indicates that the results are significant at the 0.05 level. A significance code of ** indicates that the results are significant at the 0.01 level, and a significance code of *** indicates that the results are significant at the 0.001 level.
In this case, the p-values for both the intercept and SST, °C are less than 0.05. This means that the results are significant at the 0.05 level. Therefore, we can conclude that both the intercept and SST, °C are significant factors that can affect the groundwater level.
Table 8.
Model parameters (groundwater level, m).
Table 8.
Model parameters (groundwater level, m).
| Source | Value | Standard Error | t | Pr > |t| | Lower Bound (95%) | Upper Bound (95%) | p-Values Signification Codes |
|---|
| Intercept | 1.464 | 0.052 | 28.324 | <0.0001 | 1.362 | 1.566 | *** |
| Soil surface temperature (SST), °C | 0.019 | 0.002 | 11.511 | <0.0001 | 0.016 | 0.023 | *** |
In other words, the groundwater level is not the same everywhere. It varies depending on the location and the temperature.
Table 8 shows that the intercept is 1.464, which means that the groundwater level is expected to be 1.464 m above sea level if the temperature is 0 °C.
Table 8 also shows that SST, °C is 0.019, which means that the groundwater level is expected to increase by 0.019 m for every 1 degree Celsius increase in temperature.
It is important to note that these are just the estimated values of the parameters. The actual values of the parameters may be different.
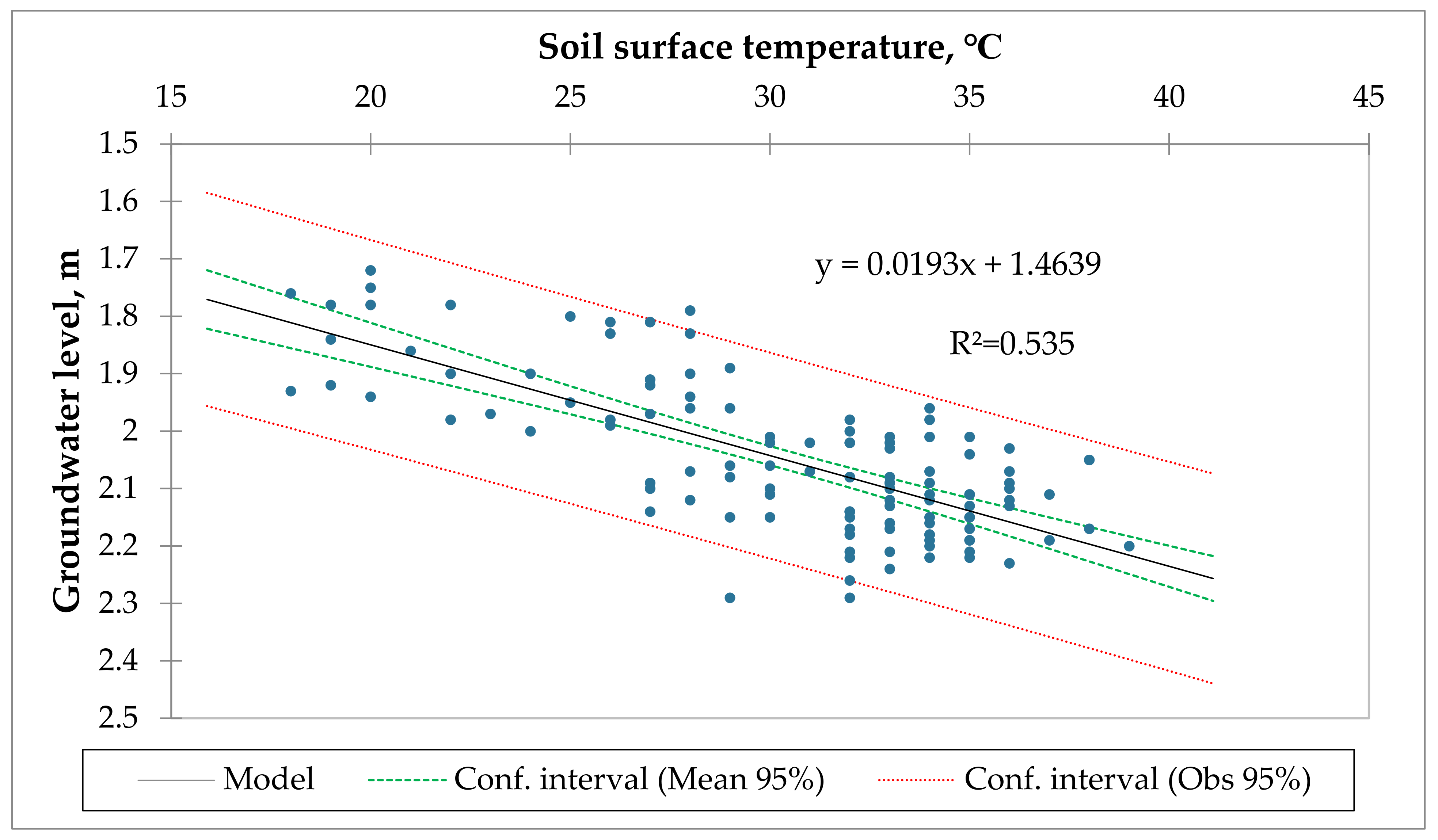
Table 9 shows the results of a regression analysis of the variable groundwater level. The analysis was conducted on 117 observations, with a sum of weights of 117. The degrees of freedom (DF) are 115. The R² value is 0.535, which indicates that 53.5% of the variation in the groundwater level variable is explained by the regression model (
Figure 3). The adjusted R² value is 0.531, which is a more accurate measure of the model’s fit, as it takes into account the number of variables in the model. The mean squared error (MSE) is 0.008, which indicates that the average error between the predicted and actual values of the groundwater level variable is 0.008. The root mean squared error (RMSE) is 0.090, which is a more interpretable measure of the error, as it is in the same units as the groundwater level variable. The mean absolute percentage error (MAPE) is 3.581, which indicates that the average absolute percentage error between the predicted and actual values of the groundwater level variable is 3.581%. The Durbin–Watson (DW) statistic is 1.529, which indicates that there is no evidence of autocorrelation in the residuals. The Cp statistic is 2.000, which indicates that the model is not overfit. The Akaike information criterion (AIC) is −561.094, which indicates that the model has a good fit to the data. The Schwarz Bayesian criterion (SBC) is −555.570, which indicates that the model has a good fit to the data. The partial correlation coefficient (PC) is 0.481, which indicates that the groundwater level variable is moderately correlated with the other variables in the model.
In summary, the regression analysis of the variable groundwater level indicates that the model is a good fit to the data and that the groundwater level variable is moderately correlated with the other variables in the model.
As can be seen from this
Figure 6, as the temperature of the soil surface increases, the groundwater level decreases.
The article discusses the relationship between soil surface temperature and groundwater level, and its impacts on ecosystems and human society. The results show that soil surface temperature and groundwater levels varied significantly over time and were influenced by various factors such as the type of soil, amount of vegetation, water in the soil, wind speed, amount of sunlight, and air temperature. Analysis elsewhere has also indicated that soil surface temperature can be a good proxy for assessing the groundwater level, especially in tropical peatlands [
45].
Statistical analysis using a linear regression model and ANOVA tests showed that both soil surface temperature and the location of groundwater level measurements were significant factors that affect the groundwater level. The correlation between the soil surface temperature and groundwater level was found to have an R
2 value of 0.428 in other research [
24]. Moreover, the correlation between the soil temperature and groundwater level was R
2 = 0.49 when the soil temperature was measured at 5 cm, and R
2 = 0.59 when the soil temperature was measured at 10 cm [
46].
The analysis also showed that 53.5% of the variation in the groundwater level variable is explained by the regression model, indicating a moderately correlated relationship between the groundwater level and soil surface temperature in the model. Additionally, the ANOVA regression results from Indian Punjab suggest that groundwater level may also vary significantly with respect to agro-climatic regions, crop diversity, and farmer education [
47].
The impacts of the relationship between the soil surface temperature and groundwater level include reduced water availability, increased risk of waterborne diseases, reduced habitat for groundwater-dependent plants and animals, and increased erosion of shorelines and stream banks. The findings of this study are important in developing an understanding of the effects of climate change on these important environmental variables and can be used to develop sustainable water management strategies. Climate change has also caused the average temperature of the earth’s atmosphere to increase, and it has changed the way that precipitation falls around the world. These changes can directly affect the levels of groundwater [
48]. Machine learning models can also provide valuable insights into the prediction of groundwater levels, especially in water-deficient areas [
49], like in Uzbekistan. Finally, the findings of this research are in line with the hypothesis set in the beginning of this manuscript: soil surface temperature has a significant impact on changes in groundwater level.