A Novel Algorithm for the Retrieval of Chlorophyll a in Marine Environments Using Deep Learning
Abstract
:1. Introduction
2. Data and Preprocessing
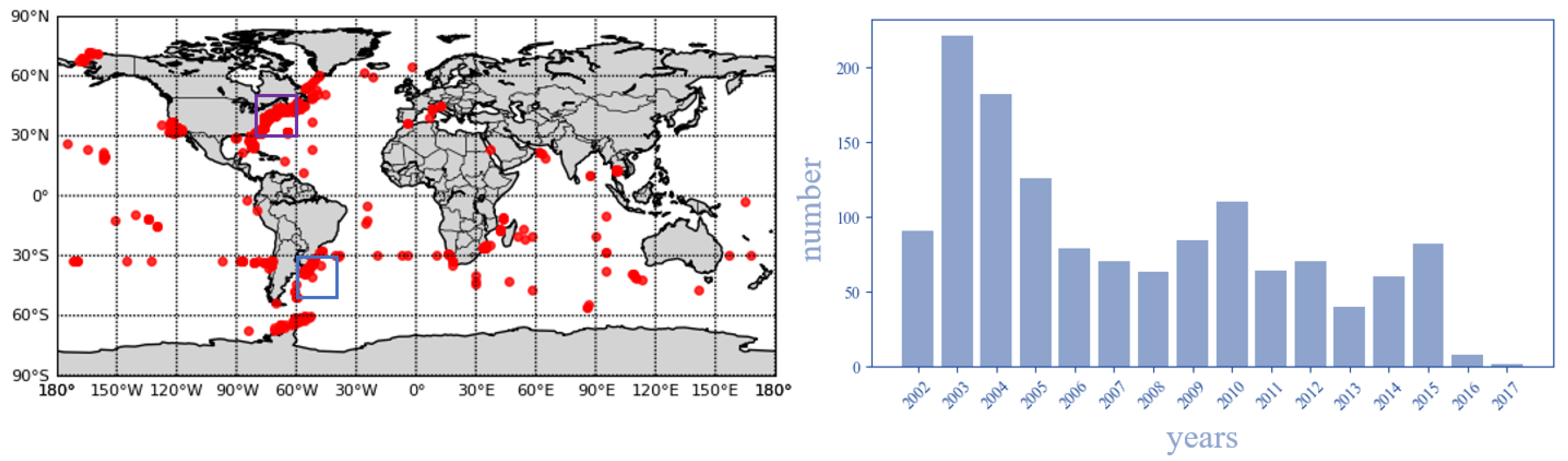
2.1. Data Source
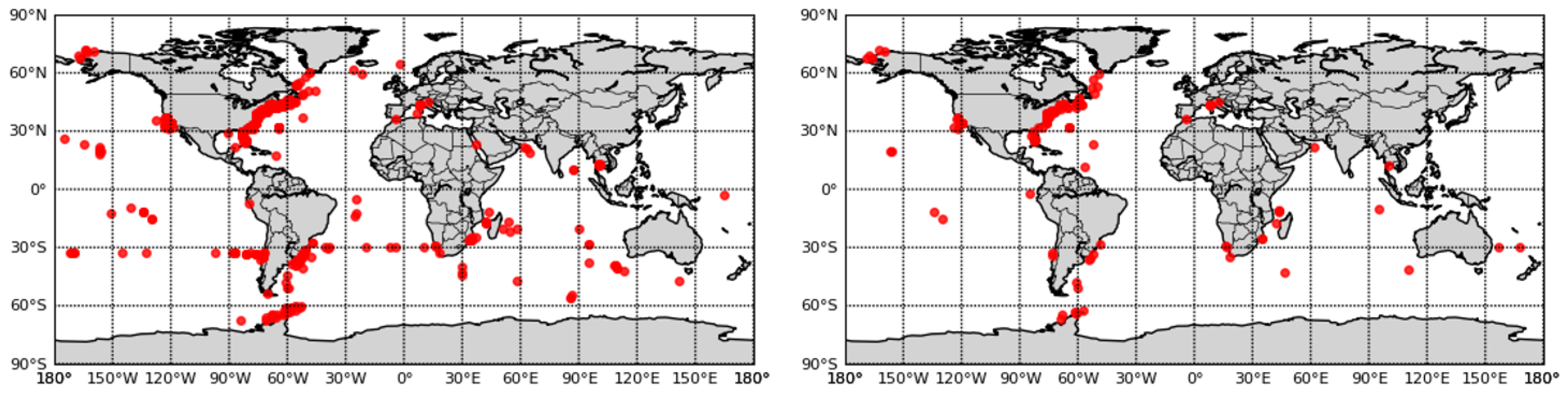
2.2. Data Preprocessing
3. Model Development
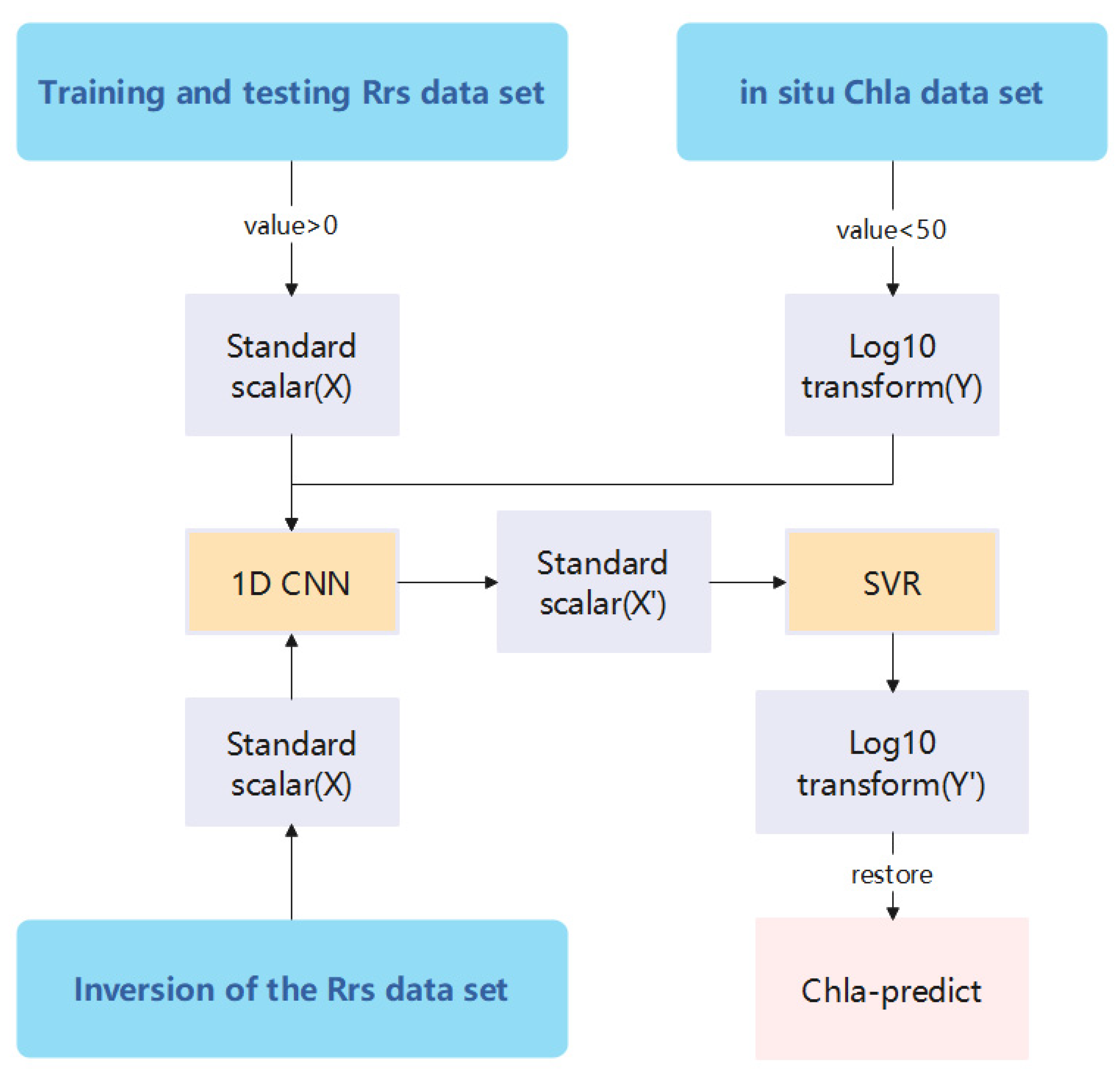
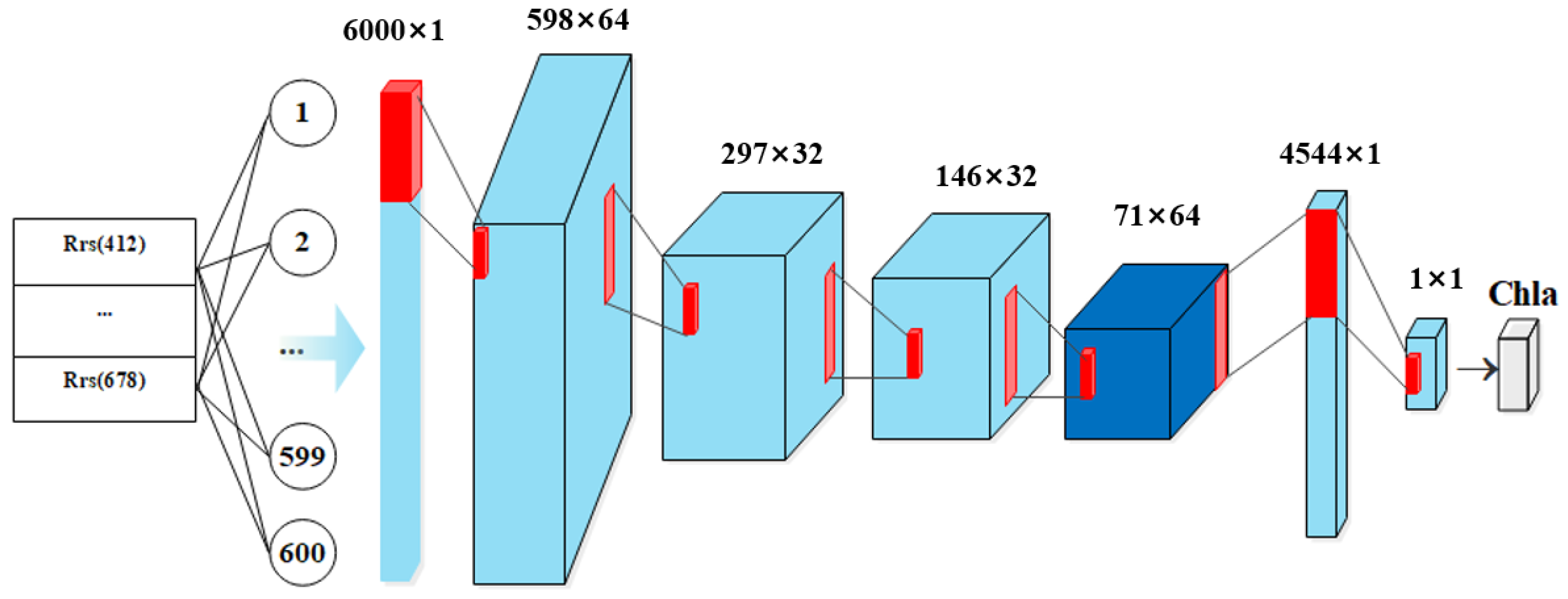
3.1. 1D CNN/SVR Model Design
3.2. Inversion Model Evaluation Metrics
4. Experiments and Results
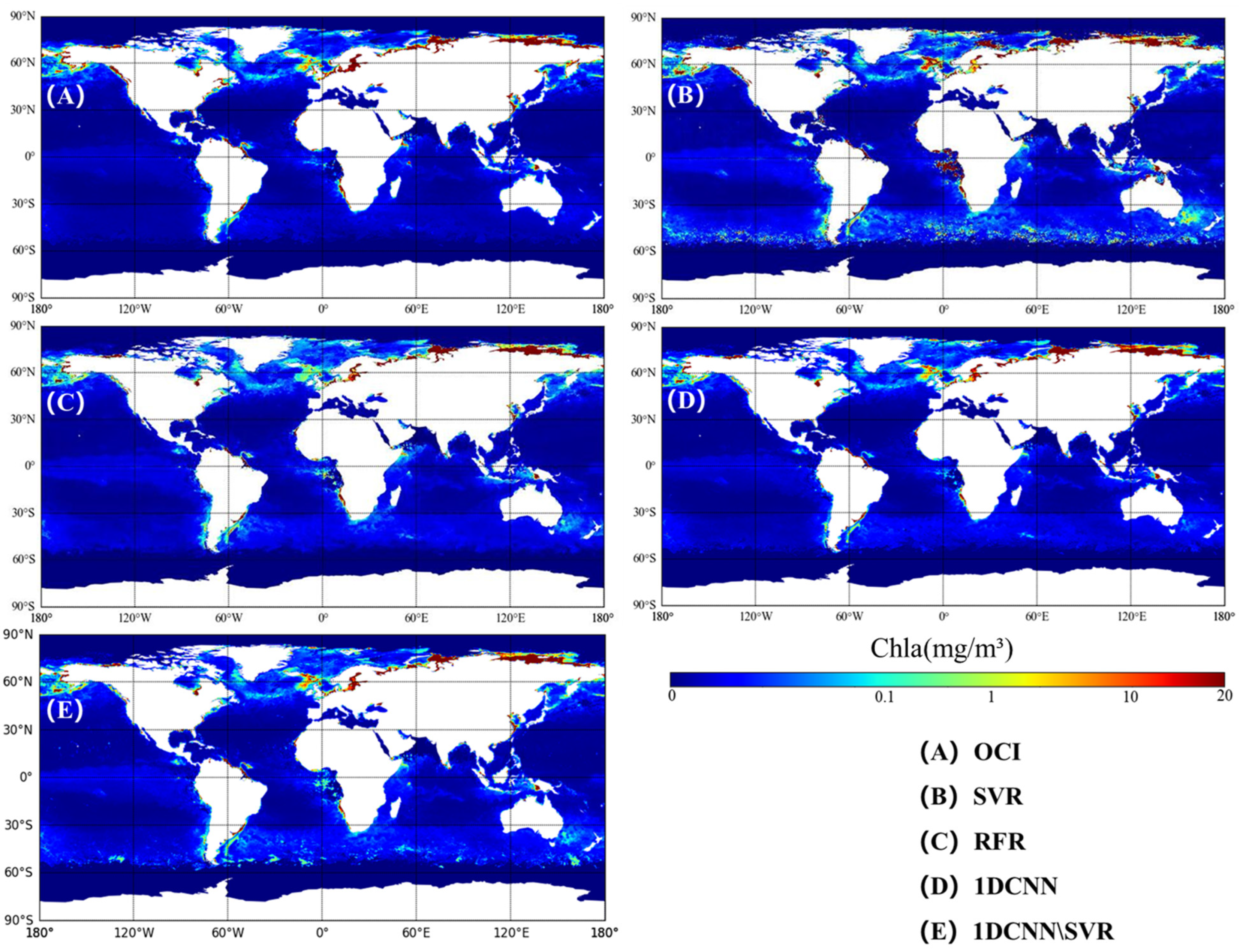
4.1. Model Performance Evaluation
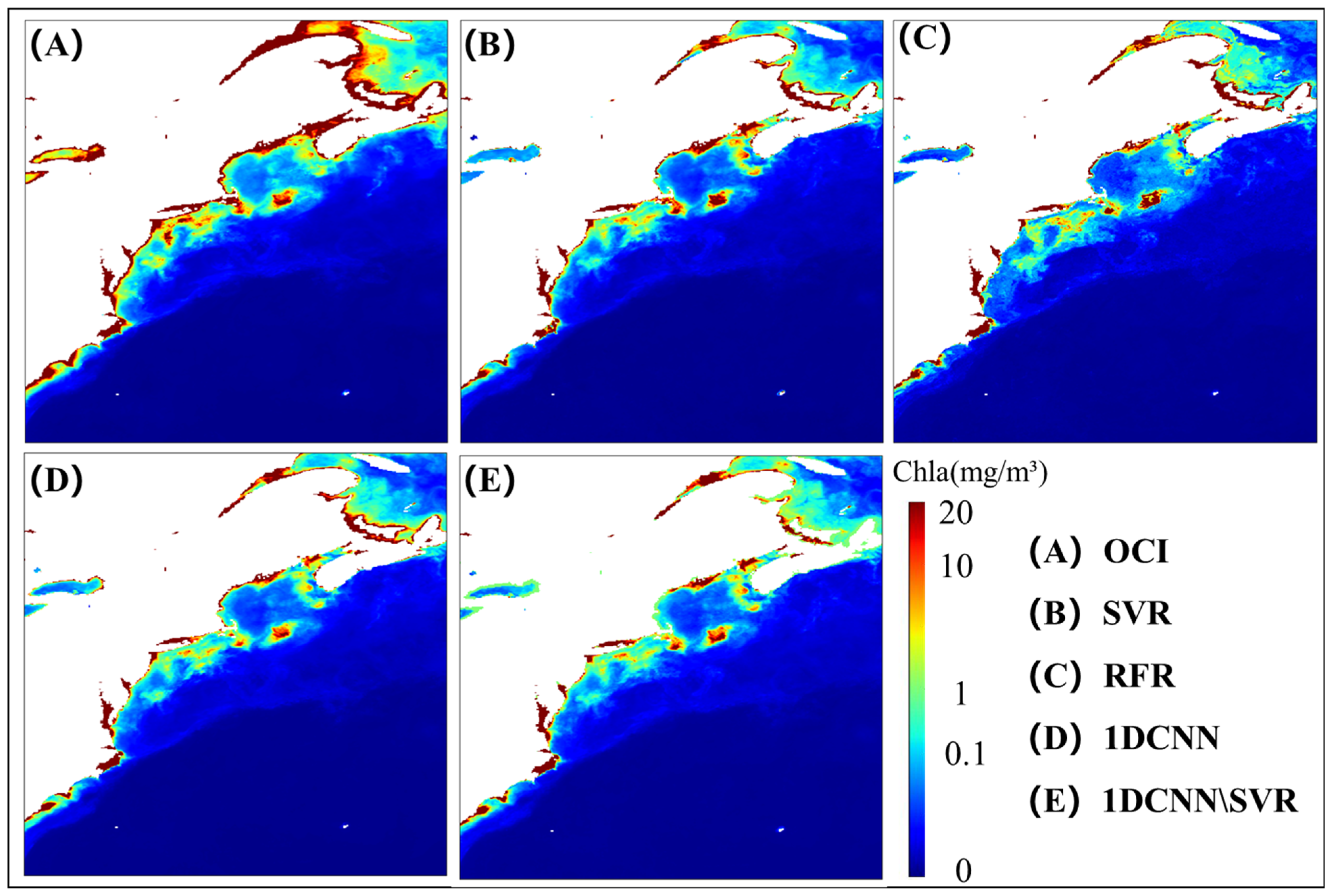
4.2. Evaluation of the Inversion Capability of the Model at Different Trophic Levels
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kasprzak, P.; Padisák, J.; Koschel, R.; Krienitz, L.; Gervais, F. Chlorophyll a concentration across a trophic gradient of lakes: An estimator of phytoplankton biomass? Limnologica 2008, 38, 327–338. [Google Scholar] [CrossRef]
- Amin, S.A.; Hmelo, L.R.; Van Tol, H.M.; Durham, B.P.; Carlson, L.T.; Heal, K.R.; Morales, R.L.; Berthiaume, C.T.; Parker, M.S.; Djunaedi, B.; et al. Interaction and signalling between a cosmopolitan phytoplankton and associated bacteria. Nature 2015, 522, 98–101. [Google Scholar] [CrossRef]
- Ma, J.; Qin, B.; Wu, P.; Zhou, J.; Niu, C.; Deng, J.; Niu, H. Controlling cyanobacterial blooms by managing nutrient ratio and limitation in a large hyper-eutrophic lake: Lake Taihu, China. J. Environ. Sci. 2015, 27, 80–86. [Google Scholar] [CrossRef] [PubMed]
- Brooks, B.W.; Lazorchak, J.M.; Howard, M.D.; Johnson, M.V.V.; Morton, S.L.; Perkins, D.A.; Reavie, E.D.; Scott, G.I.; Smith, S.A.; Steevens, J.A. Are harmful algal blooms becoming the greatest inland water quality threat to public health and aquatic ecosystems? Environ. Toxicol. Chem. 2016, 35, 6–13. [Google Scholar] [CrossRef] [PubMed]
- Lopez, C.B.; Jewett, E.B.; Dortch QT, W.B.; Walton, B.T.; Hudnell, H.K. Scientific Assessment of Freshwater Harmful Algal Blooms; Interagency Working Group on Harmful Algal Blooms, Hypoxia, and Human Health of the Joint Subcommittee on Ocean Science and Technology: Washington, DC, USA, 2008.
- Madrid, Y.; Zayas, Z.P. Water sampling: Traditional methods and new approaches in water sampling strategy. TrAC Trends Anal. Chem. 2007, 26, 293–299. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Werdell, P.J. Chlorophyll algorithms for ocean color sensors—OC4, OC5 & OC6. Remote Sens. Environ. 2019, 229, 32–47. [Google Scholar] [PubMed]
- Hu, C. A novel ocean color index to detect floating algae in the global oceans. Remote Sens. Environ. 2009, 113, 2118–2129. [Google Scholar] [CrossRef]
- Li, Y.; Guo, J.; Guo, X.; Hu, Z.; Tian, Y. PlanktonmDetection with Adversarial Learning and a Densely Connected Deep Learning Model for Class Imbalanced Distribution. J. Mar. Sci. Eng. 2021, 9, 636. [Google Scholar] [CrossRef]
- Bayindir, C. Predicting the Ocean Currents using Deep Learning. arXiv 2019, arXiv:1906.08066. [Google Scholar]
- Blondeau-Patissier, D.; Gower, J.F.; Dekker, A.G.; Phinn, S.R.; Brando, V.E. A review of ocean color remote sensing methods and statistical techniques for the detection, mapping and analysis of phytoplankton blooms in coastal and open oceans. Prog. Oceanogr. 2014, 123, 123–144. [Google Scholar] [CrossRef]
- Tilstone, G.H.; Pardo, S.; Dall’Olmo, G.; Brewin, R.J.; Nencioli, F.; Dessailly, D.; Kwiatkowska, E.; Casal, T.; Donlon, C. Performance of Ocean Colour Chlorophyll a algorithms for Sentinel-3 OLCI, MODIS-Aqua and Suomi-VIIRS in open-ocean waters of the Atlantic. Remote Sens. Environ. 2021, 260, 112444. [Google Scholar] [CrossRef]
- Hu, C.; And, Z.L.; Franz, B. Chlorophyll algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. Ocean. 2012, 117, C1. [Google Scholar] [CrossRef]
- Gurlin, D.; Gitelson, A.A.; Moses, W.J. Remote estimation of chl-a concentration in turbid productive waters—Return to a simple two-band NIR-red model? Remote Sens. Environ. 2011, 115, 3479–3490. [Google Scholar] [CrossRef]
- Dall Olmo, G.; Gitelson, A.A. Effect of bio-optical parameter variability on the remote estimation of chlorophyll-a concentration in turbid productive waters: Experimental results. Appl. Opt. 2005, 44, 412–422. [Google Scholar] [CrossRef]
- Li, L.; Yin, Q.; Xu, H.; Gong, C.; Chen, Z. Estimating chlorophyll a concentration in lake water using space-borne hyperspectral data. In Proceedings of the 2010 IEEE International Geoscience & Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010. [Google Scholar]
- Liu, F.F.; Chen, C.Q.; Tang, S.L.; Liu, D.Z. Retrieval of chlorophyll a concentration from a fluorescence enveloped area using hyperspectral data. Int. J. Remote Sens. 2011, 32, 3611–3623. [Google Scholar] [CrossRef]
- Gower, J. On the use of satellite-measured chlorophyll fluorescence for monitoring coastal waters. Int. J. Remote Sens. 2015, 37, 2077–2086. [Google Scholar] [CrossRef]
- Neil, C.; Spyrakos, E.; Hunter, P.D.; Tyler, A.N. A global approach for chlorophyll-a retrieval across optically complex inland waters based on optical water types. Remote Sens. Environ. 2019, 229, 159–178. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Cao, Z.; Ma, R.; Alikas, K.; Kangro, K.; Gurlin, D.; Hà, N.; et al. Seamless retrievals of chlorophyll-a from Sentinel-2 (MSI) and Sentinel-3 (OLCI) in inland and coastal waters: A machine-learning approach. Remote Sens. Environ. 2020, 240, 111604. [Google Scholar] [CrossRef]
- Hafeez, S.; Wong, M.S.; Ho, H.C.; Nazeer, M.; Nichol, J.; Abbas, S.; Tang, D.; Lee, K.H.; Pun, L. Comparison of Machine Learning Algorithms for Retrieval of Water Quality Indicators in Case-II Waters: A Case Study of Hong Kong. Remote Sens. 2019, 11, 617. [Google Scholar] [CrossRef]
- Le, C.; Hu, C.; Cannizzaro, J.; English, D.; Muller-Karger, F.; Lee, Z. Evaluation of chlorophyll-a remote sensing algorithms for an optically complex estuary. Remote Sens. Environ. 2013, 129, 75–89. [Google Scholar] [CrossRef]
- Sadaiappan, B.; Balakrishnan, P.; Vishal, C.R.; Vijayan, N.T.; Subramanian, M.; Gauns, M.U. Applications of Machine Learning in Chemical and Biological Oceanography. ACS Omega 2023, 8, 15831–15853. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.; Xu, L.; Peng, J.; Hu, Z.; Wong, A. Global chlorophyll-a concentration estimation from moderate resolution imaging spectroradiometer using convolutional neural networks. J. Appl. Remote Sens. 2020, 14, 034520. [Google Scholar] [CrossRef]
- Wang, W.; Shi, K.; Zhang, Y.; Li, N.; Sun, X.; Zhang, D.; Zhang, Y.; Qin, B.; Zhu, G. A ground-based remote sensing system for high-frequency and real-time monitoring of phytoplankton blooms. J. Hazard. Mater. 2022, 439, 129623. [Google Scholar] [CrossRef] [PubMed]
- Lei, F.; Yu, Y.; Zhang, D.; Feng, L.; Guo, J.; Zhang, Y.; Fang, F. Water remote sensing eutrophication inversion algorithm based on multilayer convolutional neural network. J. Intell. Fuzzy Syst. 2020, 39, 5319–5327. [Google Scholar] [CrossRef]
- Zhao, X.; Xu, H.; Ding, Z.; Wang, D.; Deng, Z.; Wang, Y.; Wu, T.; Li, W.; Lu, Z.; Wang, G. Comparing deep learning with several typical methods in prediction of assessing chlorophyll-a by remote sensing: A case study in Taihu Lake, China. Water Supply 2021, 21, 3710–3724. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6999–7019. [Google Scholar] [CrossRef]
- Tang, W.; Long, G.; Liu, L.; Zhou, T.; Jiang, J.; Blumenstein, M. Rethinking 1D-CNN for Time Series Classification: A Stronger Baseline. arXiv 2020, arXiv:2002.10061. [Google Scholar]
- Seegers, B.N.; Stumpf, R.P.; Schaeffer, B.A.; Loftin, K.A.; Werdell, P.J. Performance metrics for the assessment of satellite data products: An ocean color case study. Opt. Express 2018, 26, 7404–7422. [Google Scholar] [CrossRef]
| Data Type | Before Preprocessing | After Preprocessing | ||||
|---|---|---|---|---|---|---|
| Min | Max | Mean | Min | Max | Mean | |
| Rrs_412 (sr−1) | −0.00354 | 0.01914 | 0.00336 | 0.00001 | 0.01914 | 0.00355 |
| Rrs_443 (sr−1) | −0.00201 | 0.02393 | 0.00327 | 0.00009 | 0.02393 | 0.00344 |
| Rrs_469 (sr−1) | −0.00129 | 0.02973 | 0.00373 | 0.00055 | 0.02973 | 0.00388 |
| Rrs_488 (sr−1) | −0.00073 | 0.03174 | 0.00378 | 0.00049 | 0.03174 | 0.00392 |
| Rrs_531 (sr−1) | 0.000883 | 0.02765 | 0.00415 | 0.00088 | 0.02765 | 0.00425 |
| Rrs_547 (sr−1) | 0.000846 | 0.02539 | 0.00418 | 0.00102 | 0.02539 | 0.00427 |
| Rrs_555 (sr−1) | 0.000795 | 0.02306 | 0.00403 | 0.00102 | 0.02306 | 0.00410 |
| Rrs_645 (sr−1) | −0.00047 | 0.01438 | 0.00156 | 0.00001 | 0.01438 | 0.00159 |
| Rrs_667 (sr−1) | −0.00041 | 0.01277 | 0.00127 | 0.00001 | 0.01277 | 0.00130 |
| Rrs_678 (sr−1) | −0.00032 | 0.01226 | 0.00130 | 0.00002 | 0.01226 | 0.00133 |
| Chla (mg/m3) | 0.019 | 58.099 | 4.945 | 0.019 | 46.350 | 4.708 |
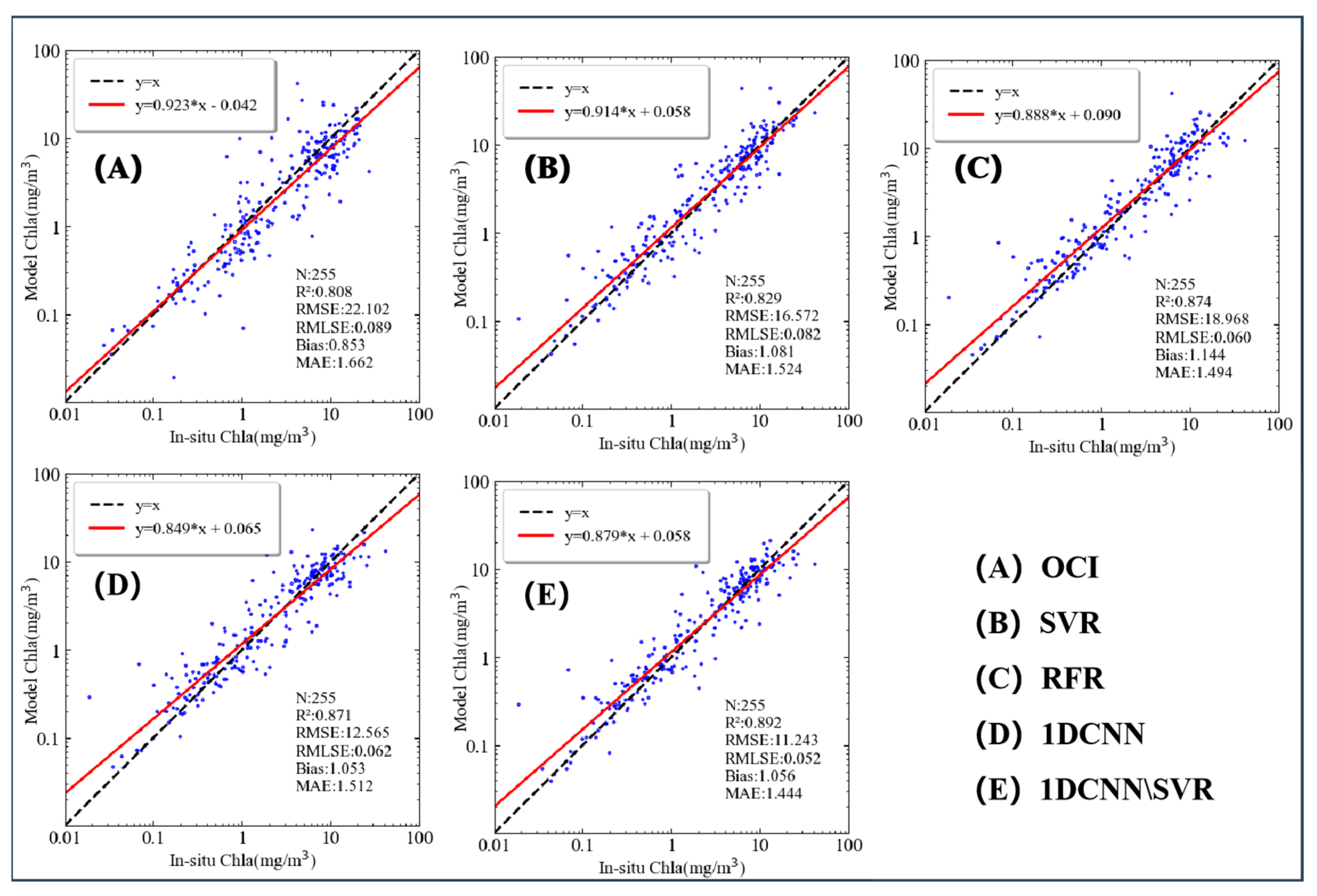
| Algorithm | R2 | Slope | RMSE (mg/m3) | RMLSE | Bias | MAE |
|---|---|---|---|---|---|---|
| OCI | 0.808 | 0.923 | 22.102 | 0.089 | 0.853 | 1.662 |
| SVR | 0.829 | 0.914 | 16.572 | 0.082 | 1.081 | 1.524 |
| RFR | 0.871 | 0.849 | 12.565 | 0.062 | 1.053 | 1.512 |
| 1DCNN | 0.874 | 0.888 | 18.968 | 0.060 | 1.144 | 1.494 |
| 1DCNN/SVR | 0.892 | 0.879 | 11.243 | 0.052 | 1.056 | 1.444 |
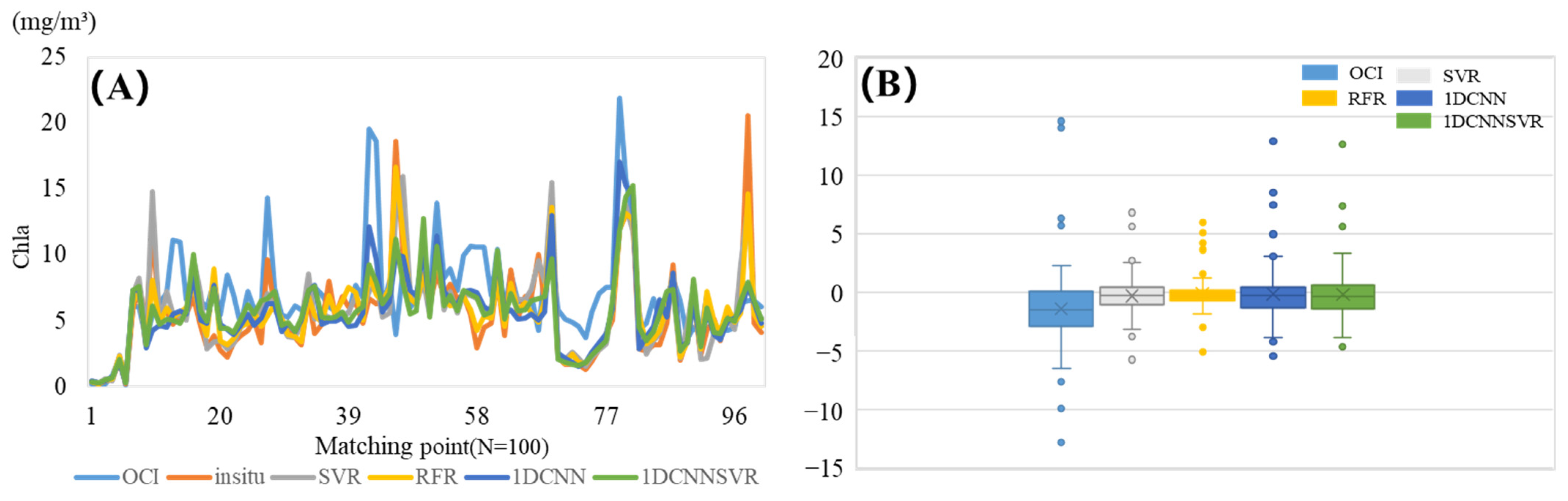
| OCI | SVR | RFR | 1DCNN | 1DCNN\SVR | |
|---|---|---|---|---|---|
| Min | −12.804 | −5.747 | −5.092 | −5.429 | −4.651 |
| Max | 14.619 | 6.810 | 5.968 | 12.940 | 12.669 |
| Average | −1.416 | −0.296 | −0.130 | −0.154 | −0.190 |
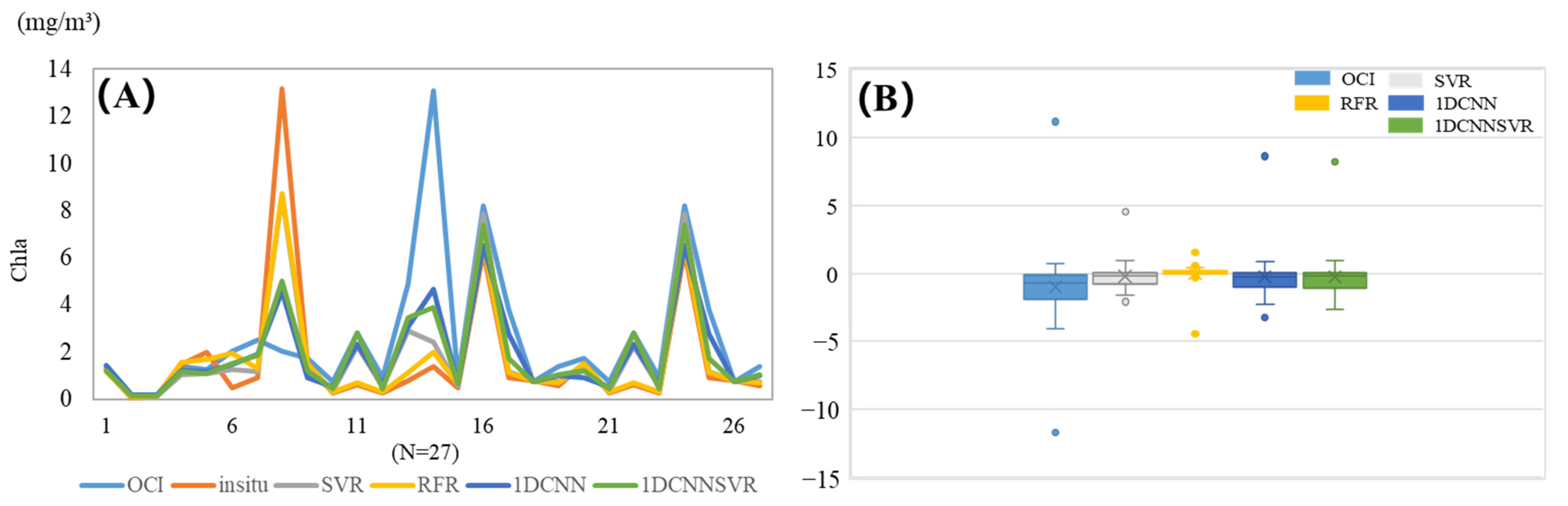
| OCI | SVR | RFR | 1DCNN | 1DCNN\SVR | |
|---|---|---|---|---|---|
| Min | −11.695 | −2.096 | −4.446 | −3.254 | −2.667 |
| Max | 11.156 | 4.553 | 1.5071 | 8.611 | 8.173 |
| Average | −1.007 | −0.219 | −0.009 | −0.254 | −0.268 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Y.; Liang, T.; Fan, D.; He, H. A Novel Algorithm for the Retrieval of Chlorophyll a in Marine Environments Using Deep Learning. Water 2023, 15, 3864. https://doi.org/10.3390/w15213864
Zeng Y, Liang T, Fan D, He H. A Novel Algorithm for the Retrieval of Chlorophyll a in Marine Environments Using Deep Learning. Water. 2023; 15(21):3864. https://doi.org/10.3390/w15213864
Chicago/Turabian StyleZeng, You, Tianlong Liang, Donglin Fan, and Hongchang He. 2023. "A Novel Algorithm for the Retrieval of Chlorophyll a in Marine Environments Using Deep Learning" Water 15, no. 21: 3864. https://doi.org/10.3390/w15213864
APA StyleZeng, Y., Liang, T., Fan, D., & He, H. (2023). A Novel Algorithm for the Retrieval of Chlorophyll a in Marine Environments Using Deep Learning. Water, 15(21), 3864. https://doi.org/10.3390/w15213864






