Dynamic Evolution and Copula-Based Multivariable Frequency Analysis of Meteorological Drought Considering the Spatiotemporal Variability in Northwestern China
Abstract
:1. Introduction
2. Materials and Methods
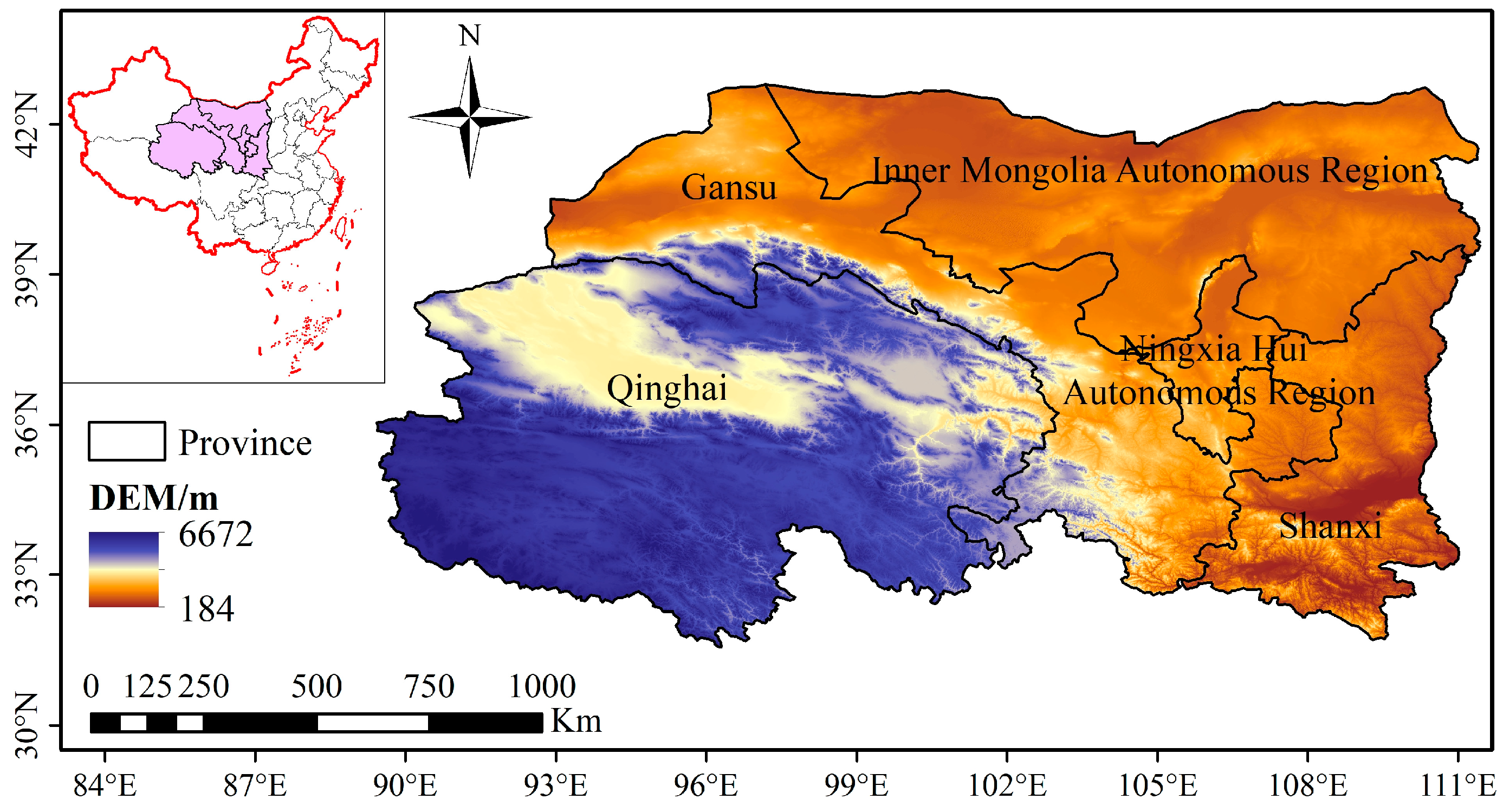
2.1. Study Area
2.2. Dataset
2.3. Methods
2.3.1. Standardized Precipitation Evapotranspiration Index
2.3.2. Modified Mann-Kendall Test (MMK)
2.3.3. R/S Analysis
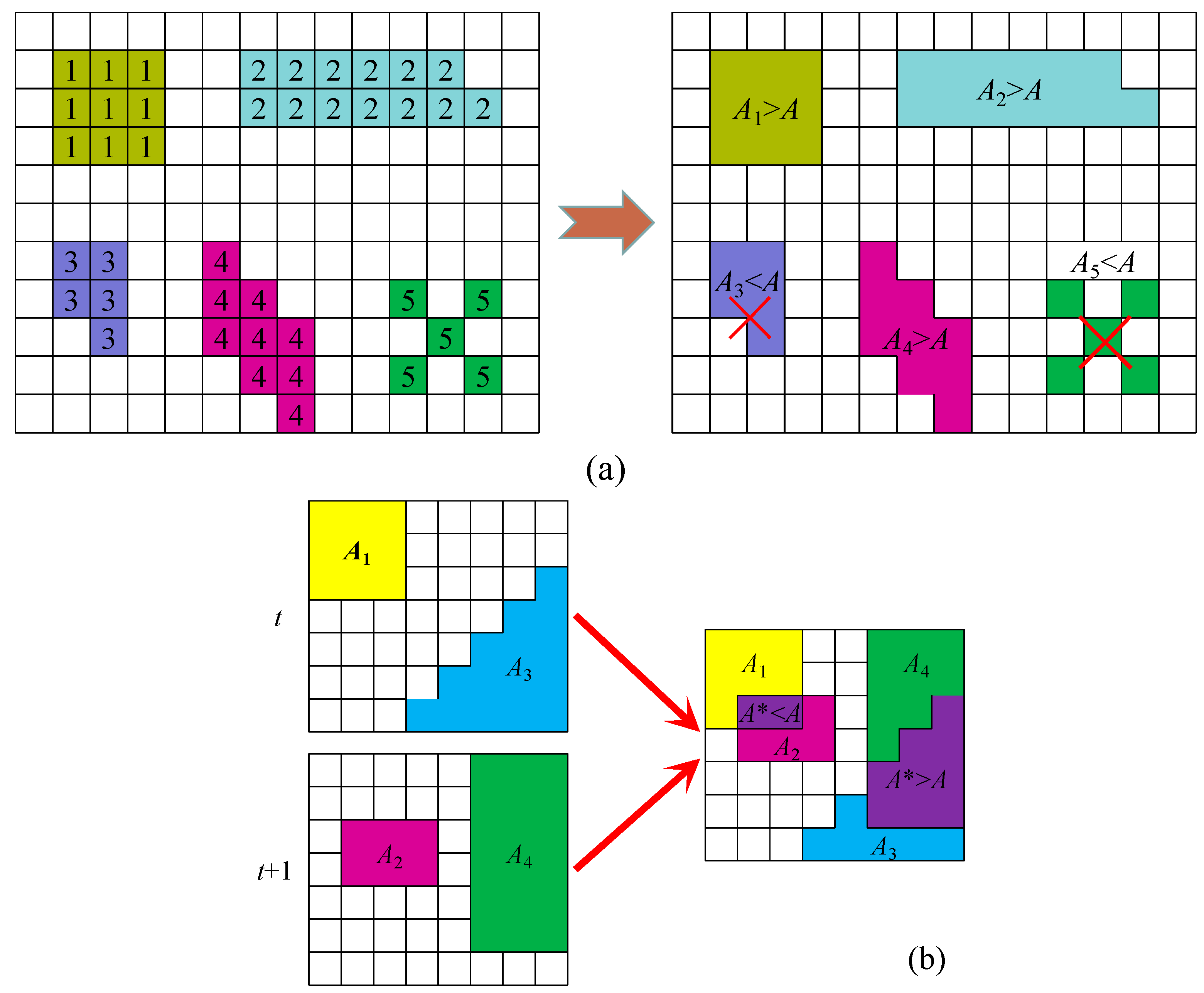
2.3.4. Identification of Drought Events by a 3D Clustering Method
2.3.5. Copula-Based Multivariable Frequency Analysis of Drought Events
Marginal Distribution of Drought Variables
Determination of the Optimal Copula Function
Copula-Based Multivariable Probability Calculation
3. Results
3.1. Spatial-Temporal Variation of Drought at Multiple Time Scales
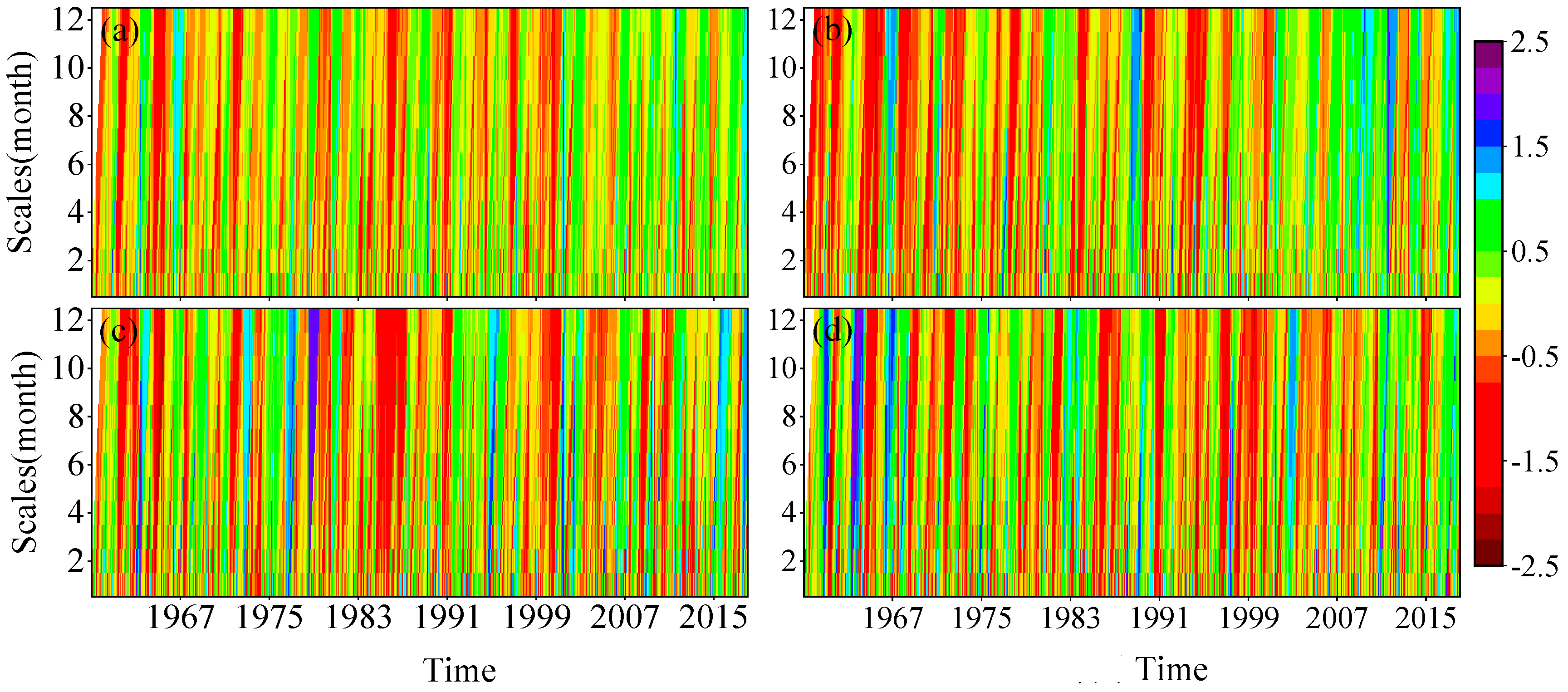
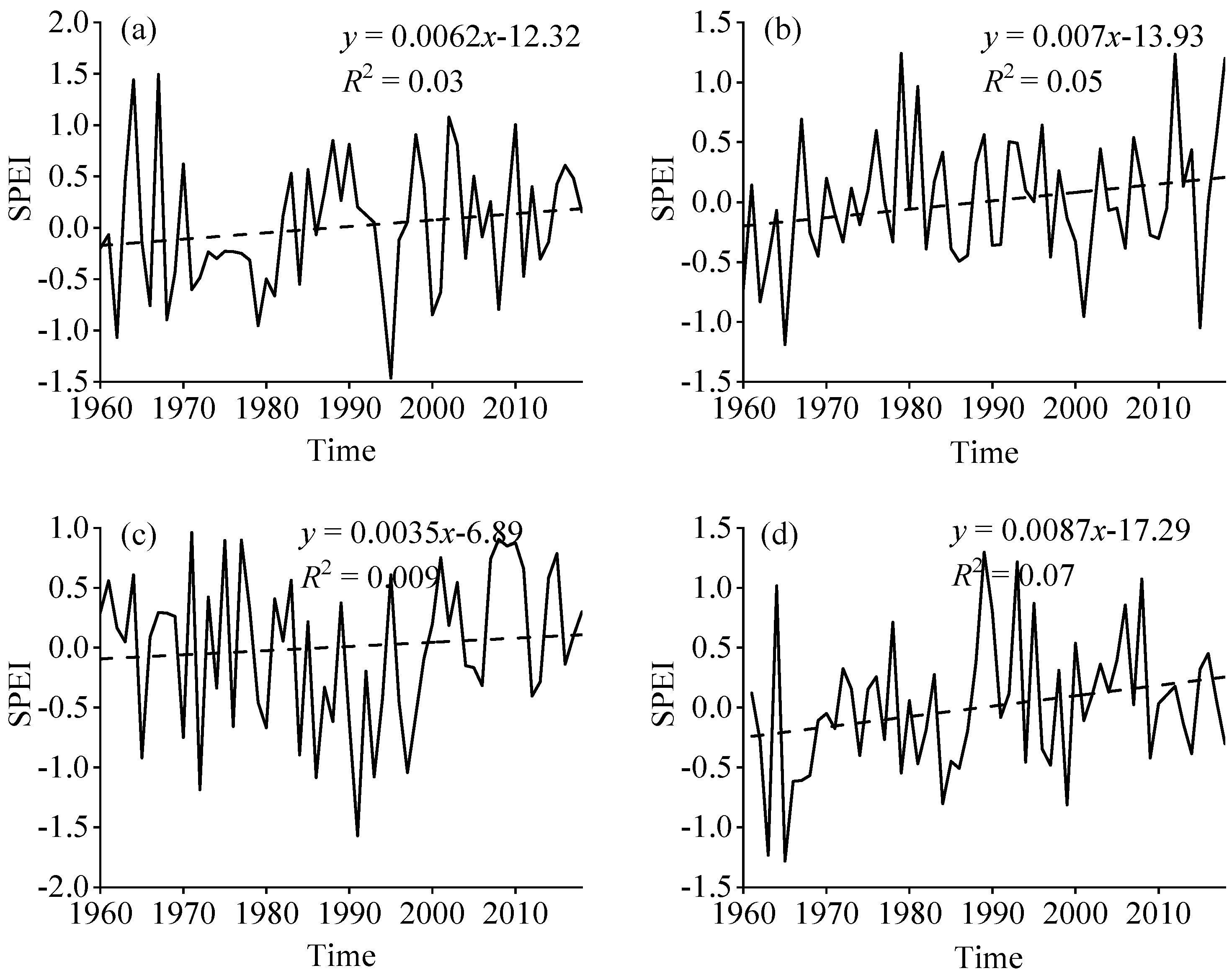
3.1.1. Temporal Evolution Characteristics of Drought at Different Time Scales
3.1.2. Spatial-Temporal Characteristics of Seasonal and Annual Drought Variation Trends
Temporal Characteristics of Drought Variation Trend
Temporal Characteristics of Drought Variation Trend
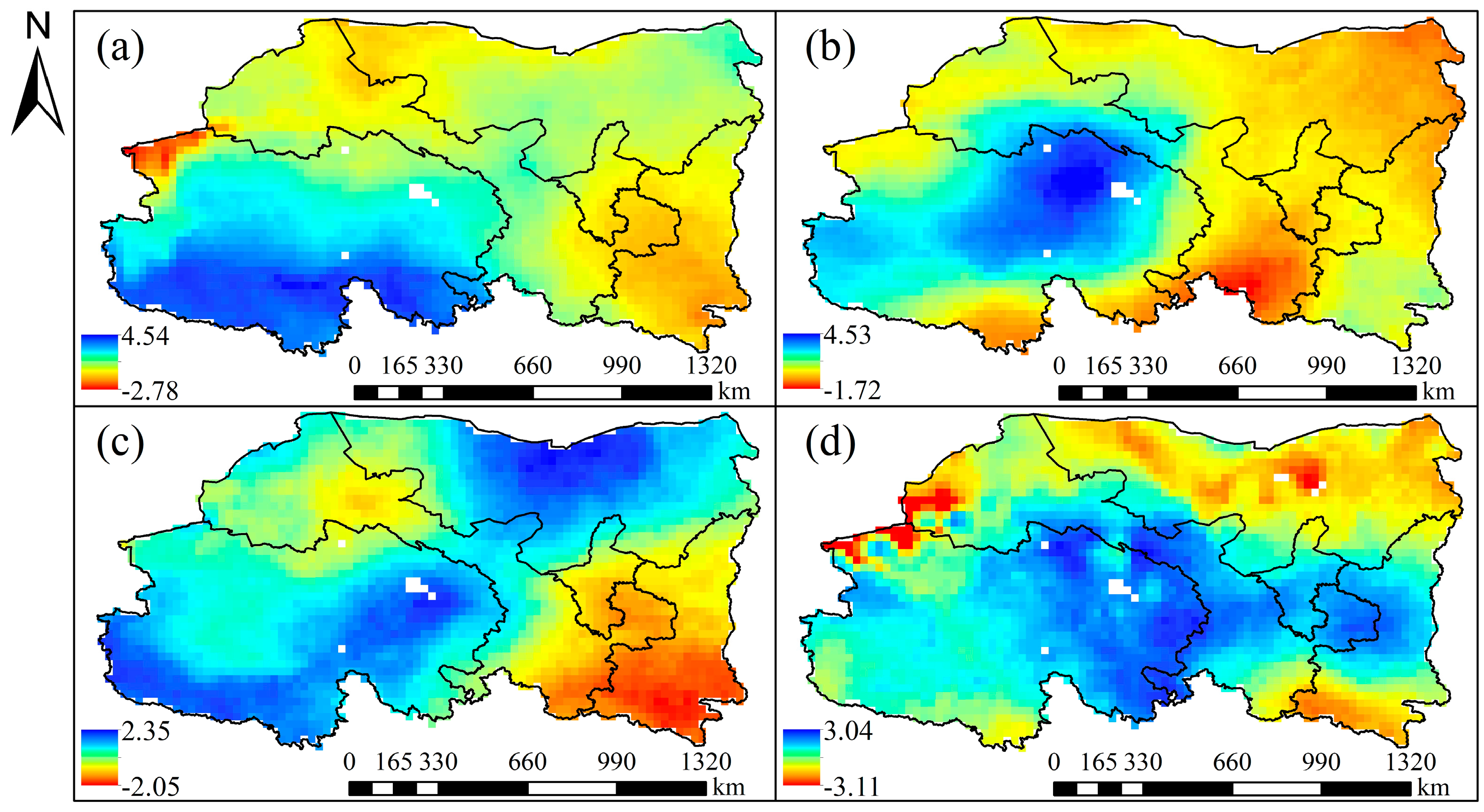
Spatial Characteristics of Drought Variation Trend
3.1.3. Spatial Variation Characteristics of Drought Intensity and Frequency
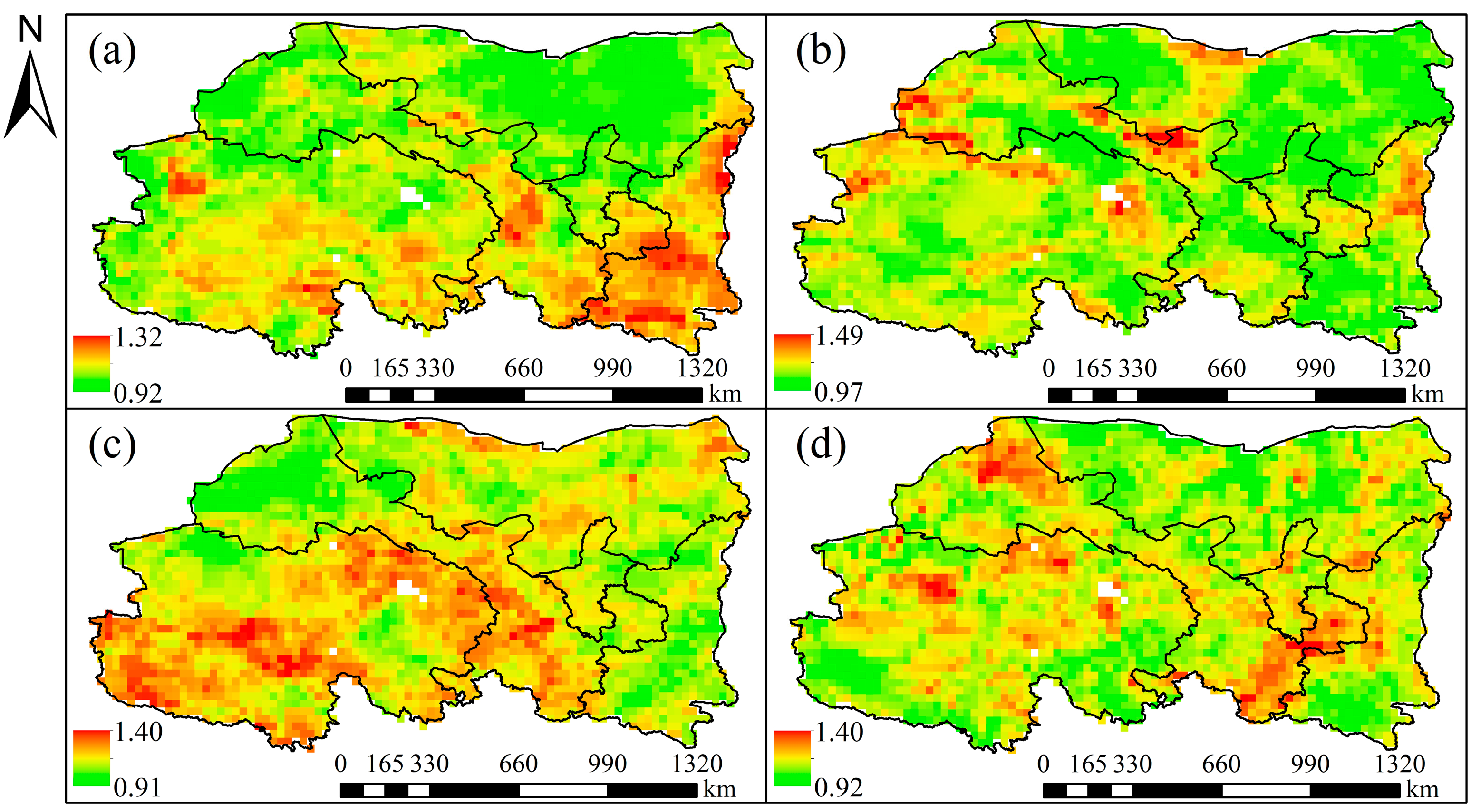
Spatial Characteristics of Drought Intensity
Spatial Characteristics of Drought Frequency
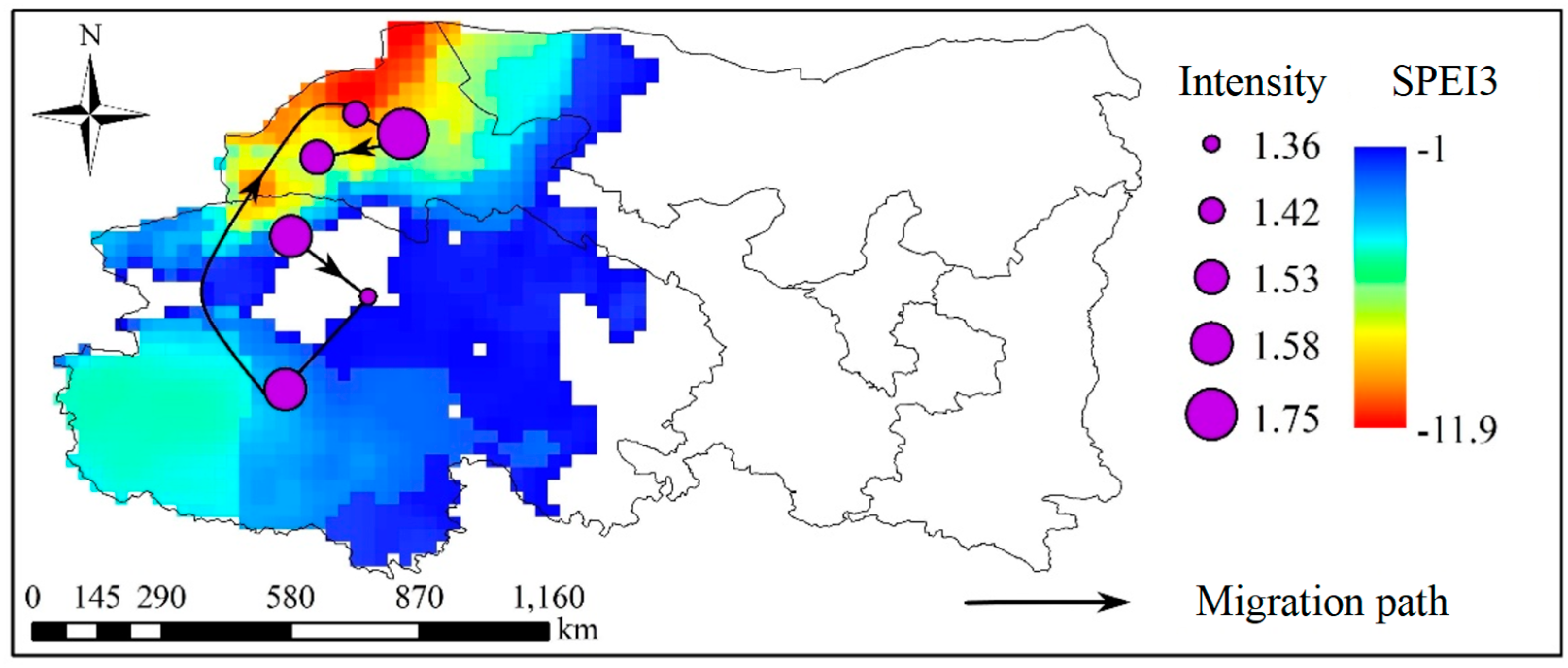
3.2. Dynamic Evolution of Typical Drought Event
Temporal Evolution Characteristics of Drought at Different Time Scales
3.3. Multivariable Frequency Analysis of Drought
3.3.1. Correlation Analysis of Drought Variables
3.3.2. Selection of Marginal Distributions for Drought Variables
3.3.3. Selection of Optimal Copula Functions
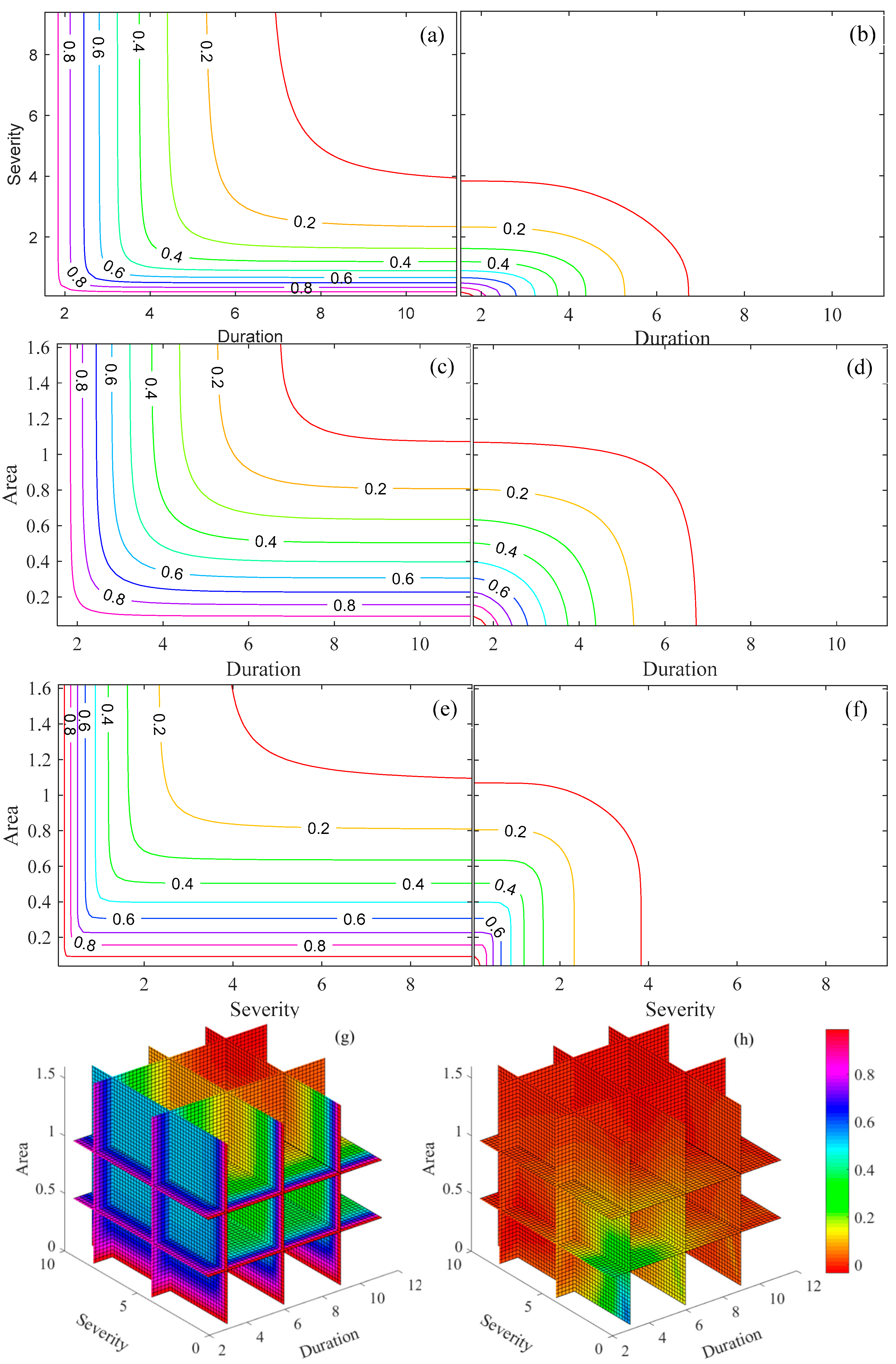
3.3.4. Joint Occurrence Probability of Drought
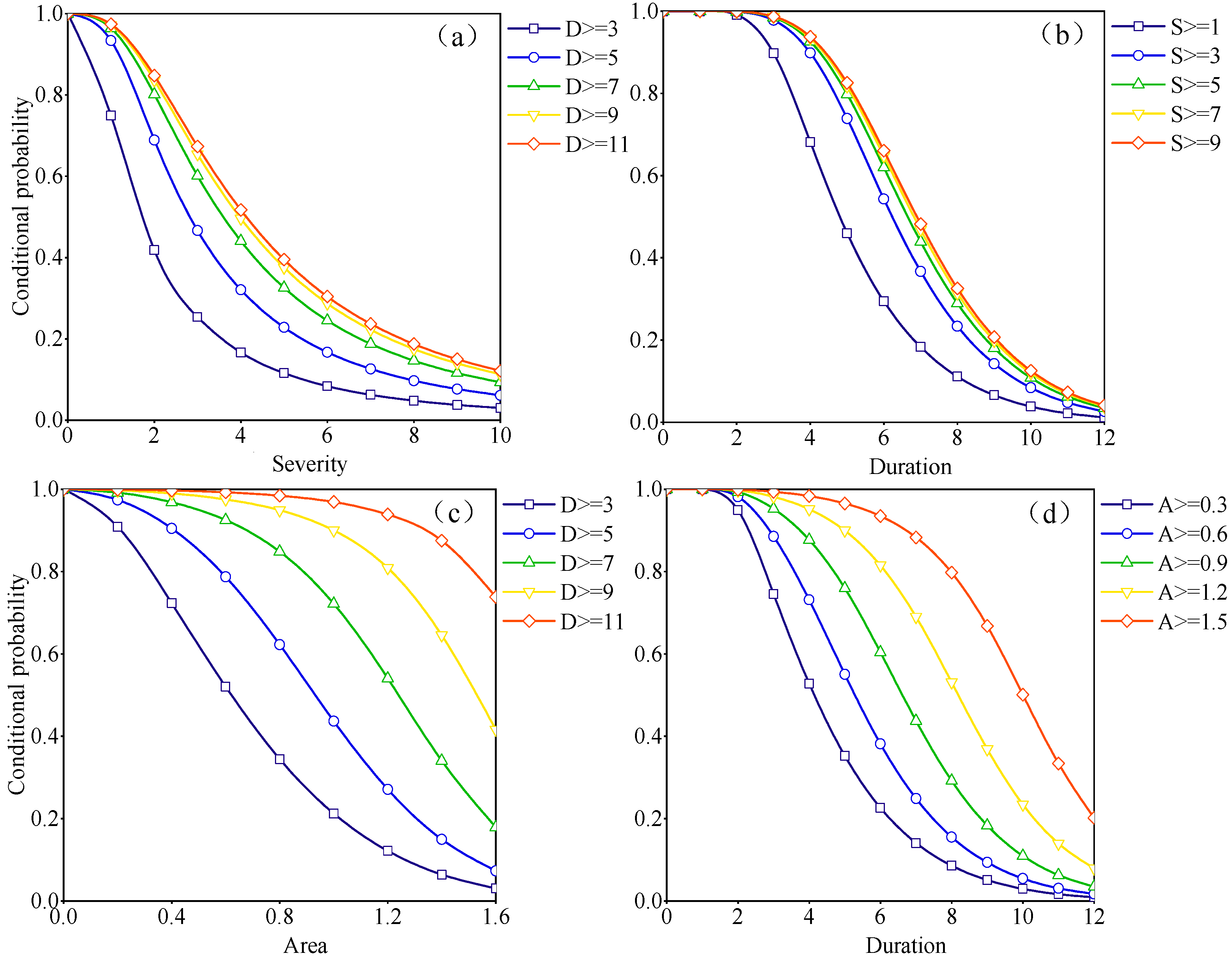
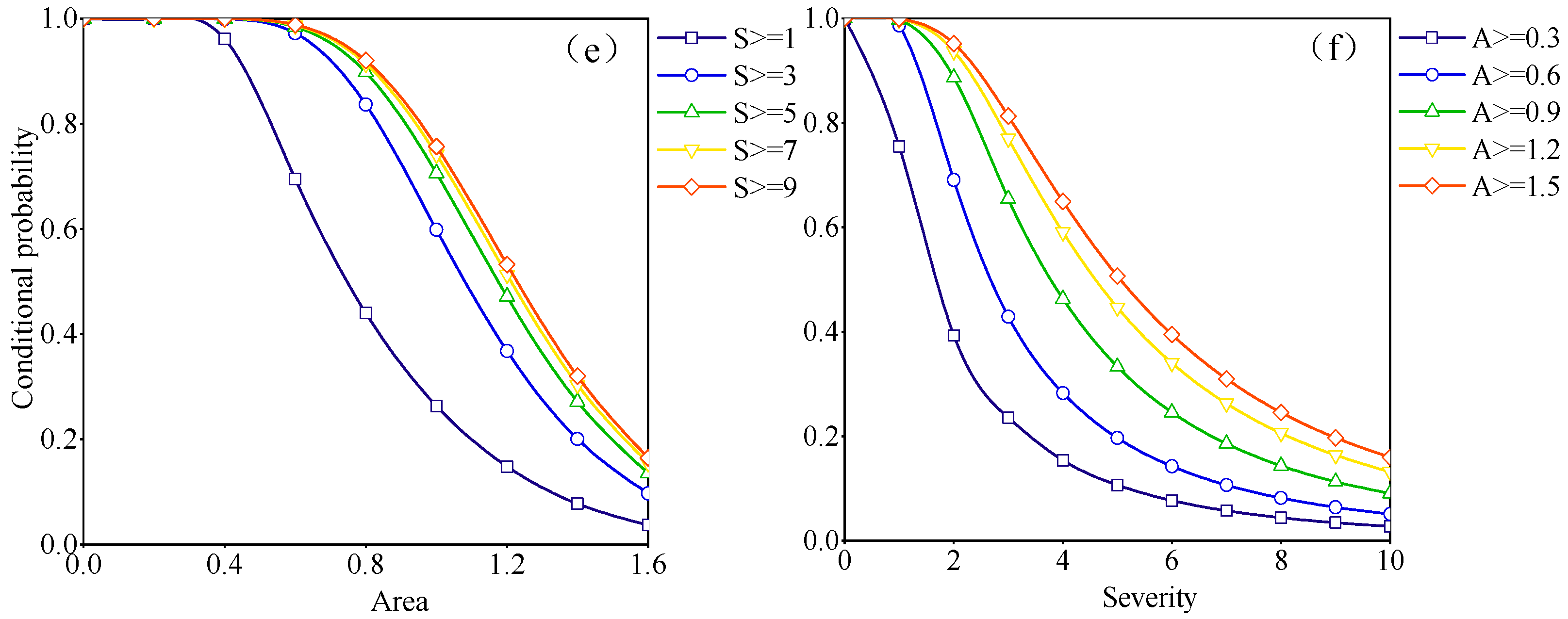
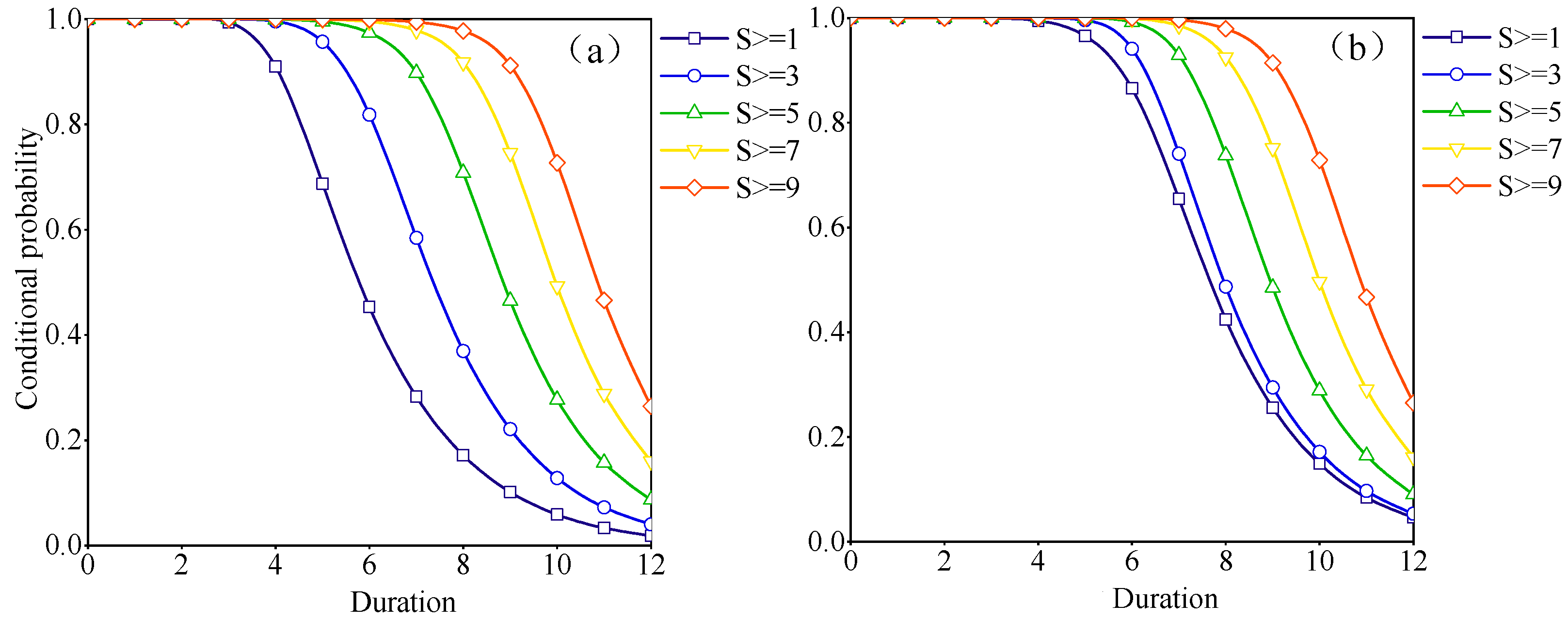
3.3.5. Conditional Probability of Drought
4. Discussion
5. Conclusions
- (1)
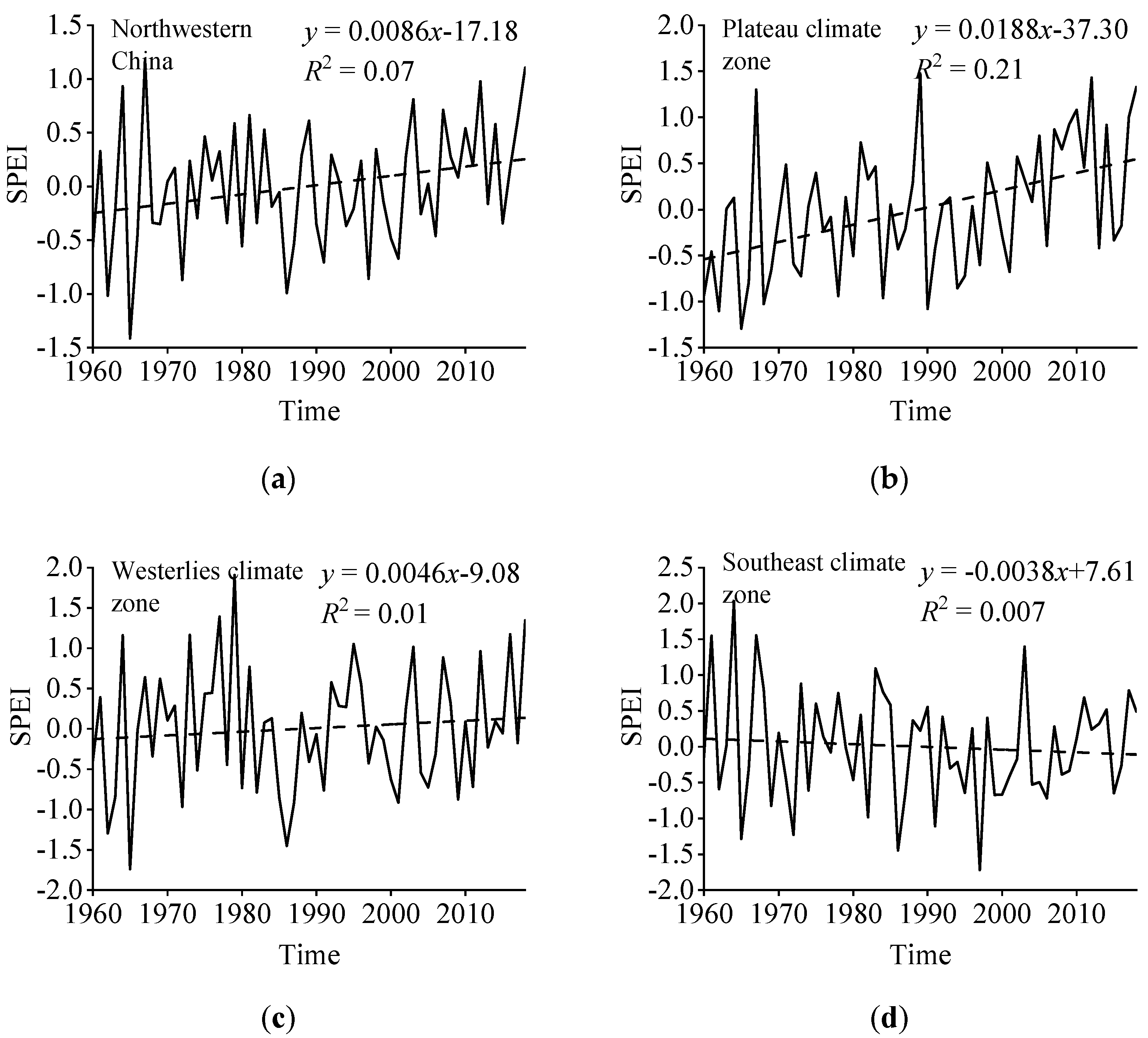
- Overall, the SPEI showed an upward trend in the plateau climate zone and the westerly climate zone, with rates of 0.188/10a and 0.046/10a, indicating a mitigation of drought. Conversely, the SPEI demonstrated a descending trend (−0.038/10a) in the southeast climate zone, suggesting an intensified drought situation.
- (2)
- The variation trend of drought in different seasons was mainly downward in the west part and upward in the east part of Northwestern China. From spring to winter, the humidification trend expanded towards the east, and the areas with a significant humidification trend gradually shifted towards the east.
- (3)
- The spatial distribution of drought intensity and frequency in different seasons exhibited opposite characteristics. For example, the southeastern part of the study area experienced a high drought intensity but a low drought frequency in spring. This indicated that the likelihood of high-intensity meteorological drought events occurring in the same area was relatively low, whereas low-intensity drought events were frequent.
- (4)
- The most severe drought event occurred from January 1961 to October 1962 and experienced five processes: occurrence, aggravation, mitigation, re-aggravation, and termination. The migration path was characterized by north-south oscillation.
- (5)
- The joint occurrence probabilities were consistently higher in the “or” situation than in the “and” situation for the same combination of drought variables. Furthermore, the conditional probability of drought variables, given specific conditional factors, declined as the values of these factors increased. Notably, as the conditional factors increased, there was a noticeable reduction in the drought occurrence probability for drought variables with lower values.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vicente-Serrano, S.; Beguería, S.; López-Moreno, J.I. A Multi-scalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Tong, S.; Lai, Q.; Zhang, J.; Bao, Y.; Lusi, A.; Ma, Q.; Li, X.; Zhang, F. Spatiotemporal drought variability on the Mongolian Plateau from 1980–2014 based on the SPEI-PM, intensity analysis and Hurst exponent. Sci. Total Environ. 2018, 615, 1557–1565. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Li, Q.; Li, J.; Wang, G.; Zhou, S.; Chai, R.; Hua, W.; Deng, P.; Wang, J.; Lou, W. Revisiting the evolution of the 2009–2011 meteorological drought over Southwest China. J. Hydrol. 2019, 568, 385–402. [Google Scholar] [CrossRef]
- Yoo, J.; Kim, J.; Kwon, H.; Kim, T. A new drought monitoring approach using three-dimensional drought properties based on a dynamic drought detection technique algorithm. J. Hydrol. Reg. Stud. 2022, 44, 101270. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Spatiotemporal characteristics of drought in Serbia. J. Hydrol. 2014, 510, 110–123. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, G. Analysis of drought hazards in North China: Distribution and interpretation. Nat. Hazards 2013, 65, 279–294. [Google Scholar] [CrossRef]
- He, B.; Chang, J.; Wang, Y.; Wang, Y.; Zhou, S.; Chen, C. Spatio-temporal evolution and non-stationary characteristics of meteorological drought in inland arid areas. Ecol. Indic. 2021, 126, 107644. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, Y.; Liu, Y. An Approach to Tracking Meteorological Drought Migration. Water Resour. Res. 2019, 55, 3266–3284. [Google Scholar] [CrossRef]
- Wen, X.; Tu, Y.; Tan, Q.; Li, W.; Fang, G.; Ding, Z.; Wang, Z. Construction of 3D drought structures of meteorological drought events and their spatio-temporal evolution characteristics. J. Hydrol. 2020, 590, 125539. [Google Scholar] [CrossRef]
- Lloyd-Hughes, B.A. spatio-temporal structure-based approach to drought characterisation. Int. J. Climatol. 2012, 32, 406–418. [Google Scholar] [CrossRef]
- Tosunoglu, F.; Can, I. Application of copulas for regional bivariate frequency analysis of meteorological droughts in Turkey. Nat. Hazards 2016, 82, 1457–1477. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Multivariate real-time assessment of droughts via copula-based multi-site Hazard Trajectories and Fans. J. Hydrol. 2015, 526, 101–115. [Google Scholar] [CrossRef]
- Lee, T.; Modarres, R.; Ouarda, T.B.M.J. Data-based analysis of bivariate copula tail dependence for drought duration and severity. Hydrol. Process. 2013, 27, 1454–1463. [Google Scholar] [CrossRef]
- Huang, S.; Hou, B.; Chang, J.; Huang, Q.; Chen, Y. Copulas-based probabilistic characterization of the combination of dry and wet conditions in the Guanzhong Plain, China. J. Hydrol. 2014, 519, 3204–3213. [Google Scholar] [CrossRef]
- Ma, M.; Song, S.; Ren, L.; Jiang, S.; Song, J. Multivariate drought characteristics using trivariate Gaussian and Student t copulas. Hydrol. Process. 2013, 27, 1175–1190. [Google Scholar] [CrossRef]
- Ma, M.; Zang, H.; Wang, W.; Cui, H.; Sun, Y.; Cheng, Y. Copula-Based Severity-Duration-Frequency (SDF) Analysis of Streamflow Drought in the Source Area of the Yellow River, China. Water 2023, 15, 2741. [Google Scholar] [CrossRef]
- Xu, K.; Yang, D.; Xu, X.; Lei, H. Copula based drought frequency analysis considering the spatio-temporal variability in Southwest China. J. Hydrol. 2015, 527, 630–640. [Google Scholar] [CrossRef]
- Hua, L.; Zhong, L.; Ma, Z. Decadal transition of moisture sources and transport in northwestern China during summer from 1982 to 2010. J. Geophys. Res. Atmos. 2017, 122, 12522–12540. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, J.; Wang, W.; Ma, P.; Lu, G.; Liu, X.; Yu, H.; Fang, F. Climatic warming and humidification in the arid region of Northwest China: Multi-scale characteristics and impacts on ecological vegetation. J. Meteorol. Res. 2021, 35, 113–127. [Google Scholar] [CrossRef]
- Liu, C.; Huang, W.; Feng, S.; Chen, J.; Zhou, A. Spatiotemporal variations of aridity in China during 1961–2015: Decomposition and attribution. Sci. Bull. 2018, 63, 1187–1199. [Google Scholar] [CrossRef]
- Park, C.E.; Jeong, S.J.; Ho, C.H.; Park, H.; Piao, S.; Kim, J.; Feng, S. Dominance of climate warming effects on recent drying trends over wet monsoon regions. Atmos. Chem. Phys. 2017, 17, 10467–10476. [Google Scholar] [CrossRef]
- Zhong, L.; Hua, L.; Yao, Y.; Feng, J. Interdecadal aridity variations in Central Asia during 1950–2016 regulated by oceanic conditions under the background of global warming. Clim. Dyn. 2021, 56, 3665–3686. [Google Scholar] [CrossRef]
- Jiang, T.; Su, X.; Singh, V.P.; Zhang, G. Spatio-temporal pattern of ecological droughts and their impacts on health of vegetation in Northwestern China. J. Environ. Manag. 2022, 305, 114356. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.; Zhang, B.; Yang, L.; He, C. Assessment of the impact of future climate change on maize yield and water use efficiency in agro-pastoral ecotone of Northwestern China. J. Agron. Crop Sci. 2021, 207, 317–331. [Google Scholar] [CrossRef]
- Cao, S.; He, Y.; Zhang, L.; Chen, Y.; Yang, W.; Yao, S.; Sun, Q. Spatiotemporal characteristics of drought and its impact on vegetation in the vegetation region of Northwest China. Ecol. Indic. 2021, 133, 108420. [Google Scholar] [CrossRef]
- Zhang, G.; Su, X.; Ayantobo, O.O.; Feng, K.; Guo, J. Remote-sensing precipitation and temperature evaluation using soil and water assessment tool with multi-objective calibration in the Shiyang River Basin, Northwest China. J. Hydrol. 2020, 590, 125416. [Google Scholar] [CrossRef]
- Feng, K.; Li, Y.; Wang, F.; Su, X.; Wu, H. Analysis of drought events in Northwest China based on an improved three-dimensional identification method. Water Resour. Prot. 2023, 39, 63–72. [Google Scholar]
- Yang, M.; Yan, D.; Yu, Y.; Yang, Z.; Gonzalez, J.E. SPEI-Based Spatiotemporal Analysis of Drought in Haihe River Basin from 1961 to 2010. Adv. Meteorol. 2016, 2016, 7658015. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Zhang, Z.; Shen, D.; Zhang, L. The best-fitting distribution of water balance and the spatiotemporal characteristics of drought in Guizhou Province, China. Theor. Appl. Climatol. 2021, 143, 1097–1112. [Google Scholar] [CrossRef]
- Mathbout, S.; Lopez-Bustins, J.A.; Martin-Vide, J.; Bech, J.; Rodrigo, F.S. Spatial and temporal analysis of drought variability at several time scales in Syria during 1961–2012. Atmos. Res. 2018, 200, 153–168. [Google Scholar] [CrossRef]
- Wable, P.; Jha, M.; Shekhar, A. Comparison of Drought Indices in a Semi-Arid River Basin of India. Water Resour. Manag. 2019, 33, 75–102. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Z.; Yang, H.; Di, D.; Zhao, Y.; Liang, Q. Utilizing GRACE-based groundwater drought index for drought characterization and teleconnection factors analysis in the North China Plain. J. Hydrol. 2020, 585, 124849. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, S.; Huang, Q.; Wang, H.; Fang, W.; Yang, Y.; Wang, L. Assessing socioeconomic drought based on an improved Multivariate Standardized Reliability and Resilience Index. J. Hydrol. 2019, 568, 904–918. [Google Scholar] [CrossRef]
- Wang, F.; Yang, H.; Wang, Z.; Zhang, Z.; Li, Z. Drought Evaluation with CMORPH Satellite Precipitation Data in the Yellow River Basin by Using Gridded Standardized Precipitation Evapotranspiration Index. Remote Sens. 2019, 11, 485. [Google Scholar] [CrossRef]
- Araujo, M.V.O.; Celeste, A.B. Rescaled range analysis of streamflow records in the São Francisco River Basin, Brazil. Theor. Appl. Climatol. 2019, 135, 249–260. [Google Scholar] [CrossRef]
- Zhang, D.; Ge, W.; Zhang, Y. Evaluating the vegetation restoration sustainability of ecological projects: A case study of Wuqi County in China. J. Clean. Prod. 2020, 264, 121751. [Google Scholar] [CrossRef]
- Li, J.; Wu, C.; Xia, C.; Yeh, P.J.-F.; Chen, B.; Lv, W.; Hu, B.X. A voxel-based three-dimensional framework for flash drought identification in space and time. J. Hydrol. 2022, 608, 127568. [Google Scholar] [CrossRef]
- Diaz, V.; Corzo Perez, G.A.; Van Lanen, H.A.J.; Solomatine, D.; Varouchakis, E.A. An approach to characterizing spatio-temporal drought dynamics. Adv. Water Resour. 2020, 137, 103512. [Google Scholar] [CrossRef]
- Ayantobo, O.O.; Wei, J.; Wang, G. Modeling Joint Relationship and Design Scenarios Between Precipitation, Surface Temperature, and Atmospheric Precipitable Water Over Mainland China. Earth Space Sci. 2021, 8, e1513E–e2020E. [Google Scholar] [CrossRef]
- Xiao, M.; Yu, Z.; Zhu, Y. Copula-based frequency analysis of drought with identified characteristics in space and time: A case study in Huai River basin, China. Theor. Appl. Climatol. 2019, 137, 2865–2875. [Google Scholar] [CrossRef]
- Pontes Filho, J.; Souza Filho, F.; Martins, E.; de Carvalho Studart, T. Copula-Based Multivariate Frequency Analysis of the 2012–2018 Drought in Northeast Brazil. Water 2020, 12, 834. [Google Scholar] [CrossRef]
- Azam, M.; Maeng, S.; Kim, H.; Murtazaev, A. Copula-based stochastic simulation for regional Drought risk assessment in South Korea. Water 2018, 10, 359. [Google Scholar] [CrossRef]
- Kim, J.E.; Yoo, J.; Chung, G.H.; Kim, T.-W. Hydrologic Risk Assessment of Future Extreme Drought in South Korea Using Bivariate Frequency Analysis. Water 2019, 11, 2052. [Google Scholar] [CrossRef]
- Zhao, L.; Li, J.; Shi, Q. The temporal and spatial characteristics of drought in northwest China are analyzed based on Z index. Agric. Henan 2016, 5, 43–60. (In Chinese) [Google Scholar]
- Yusof, F.; Hui-Mean, F.; Suhaila, J.; Yusof, Z. Characterisation of Drought Properties with Bivariate Copula Analysis. Water Resour. Manag. 2013, 27, 4183–4207. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, J.; Duan, X.; Ma, P.; Lu, G.; Zhu, B.; Yue, P.; Wang, Y.; Liu, W. The eastward expansion of the climate humidification trend in northwest China and the synergistic influences on the circulation mechanism. Clim. Dynam. 2022, 59, 2481–2497. [Google Scholar] [CrossRef]
- Shi, Y.; Shen, Y.; Kang, E.; Li, D.; Ding, Y.; Zhang, G.; Hu, R. Recent and future climate change in northwest China. Clim. Chang. 2007, 80, 379–393. [Google Scholar] [CrossRef]
- Wu, P.; Liu, Y.; Ding, Y.; Li, X.; Wang, J. Modulation of sea surface temperature over the North Atlantic and Indian-Pacific warm pool on interdecadal change of summer precipitation over northwest China. Int. J. Clim. 2022, 42, 8526–8538. [Google Scholar] [CrossRef]
- Feng, K.P.; Tian, J.C.; Shen, H. Temperature variation characteristics of Northwest China based on K-means clustering partition in the past half century. Arid Land Geogr. 2019, 42, 1239–1252. (In Chinese) [Google Scholar]
- Zhang, Q.; Lin, J.; Liu, W.; Han, L. Precipitation seesaw phenomenon and its formation mechanism in the eastern and western parts of Northwest China during the flood season. Sci. China Earth Sci. 2019, 62, 2083–2098. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Lai, C.; Zeng, Z.; Zhong, R.; Chen, X.; Zhou, X.; Wang, M. Does drought in China show a significant decreasing trend from 1961 to 2009? Sci. Total Environ. 2017, 579, 314–324. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Hou, E.; Deng, J. Spatio-Temporal Differentiation Characteristic and Evolution Process of Meteorological Drought in Northwest China from 1960 to 2018. Front. Earth Sci. 2022, 10, 857953. [Google Scholar] [CrossRef]
- Wei, K.; Wang, L. Reexamination of the Aridity Conditions in Arid Northwestern China for the Last Decade. J. Clim. 2013, 26, 9594–9602. [Google Scholar] [CrossRef]
- Wen, X.; Wu, X.; Gao, M. Spatiotemporal variability of temperature and precipitation in Gansu Province (Northwest China) during 1951–2015. Atmos. Res. 2017, 197, 132–149. [Google Scholar] [CrossRef]
- Shiau, J. Fitting Drought Duration and Severity with Two-Dimensional Copulas. Water Resour. Manag. 2006, 20, 795–815. [Google Scholar] [CrossRef]







| Drought Level | SPEI | Drought Severity |
|---|---|---|
| I | −0.5 < SPEI | No drought |
| II | −1.0 < SPEI ≤ −0.5 | Mild drought |
| III | −1.5 < SPEI ≤ −1.0 | Moderate drought |
| IV | −2.0 < SPEI ≤ −1.5 | Severe drought |
| V | SPEI ≤ −2 | Extreme drought |
| Distribution Types | Cumulative Probability Distribution | Parameters |
|---|---|---|
| Gam | α: shape parameter β: scale parameter | |
| LogL | α: shape parameter (α > 0) β: scale parameter (β > 0) | |
| LogN | μ: location parameter σ: scale parameter | |
| Wb | α: shape parameter β: scale parameter | |
| P-III | α: shape parameter β: scale parameter μ: location parameter | |
| GEV | k: shape parameter σ: scale parameter (σ>0) μ: location parameter | |
| GP | k: shape parameter σ: scale parameter (σ > 0) μ: location parameter |
| Copula | Function Expression | Parameters |
|---|---|---|
| Frank | ||
| Clayton | ||
| Gumbel | ||
| Joe | ||
| Normal | ||
| Student t |
| SPEI Series | Trend Statistics | Hurst Index | Past Trend | Persistence and Future Trend | |
|---|---|---|---|---|---|
| Northwestern regions | Spring | 1.73 | 0.54 | Significant increase | Persistence: increase |
| Summer | 1.75 | 0.52 | Significant increase | Persistence: increase | |
| Autumn | 0.90 | 0.62 | Increase | Persistence: increase | |
| Winter | 2.09 | 0.59 | Significant increase | Persistence: increase | |
| Plateau climate zone | Spring | 2.99 | 0.63 | Significant increase | Persistence: increase |
| Summer | 3.06 | 0.57 | Significant increase | Persistence: increase | |
| Autumn | 1.49 | 0.60 | Increase | Persistence: increase | |
| Winter | 2.19 | 0.64 | Significant increase | Persistence: increase | |
| Westerlies climate zone | Spring | 0.18 | 0.48 | Increase | Unsustainability: decrease |
| Summer | 0.56 | 0.53 | Increase | Persistence: increase | |
| Autumn | 0.90 | 0.56 | Increase | Persistence: increase | |
| Winter | 0.34 | 0.49 | Increase | Unsustainability: decrease | |
| Southeast climate zone | Spring | 0.10 | 0.47 | Increase | Unsustainability: decrease |
| Summer | 0.12 | 0.55 | Increase | Persistence: increase | |
| Autumn | −0.86 | 0.65 | Decrease | Persistence: decrease | |
| Winter | 1.77 | 0.53 | Significant increase | Persistence: increase | |
| Drought Variables | Pearson | Kendall | Spearman |
|---|---|---|---|
| Duration-Severity | 0.83 ** | 0.67 ** | 0.82 ** |
| Duration-Area | 0.77 ** | 0.57 ** | 0.72 ** |
| Severity-Area | 0.93 ** | 0.84 ** | 0.97 ** |
| Drought Variables | K-S Test | A-D Statistics | Optimal Distribution | Parameters | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gam | LogL | LogN | Wb | P-III | GEV | GP | Gam | LogL | LogN | Wb | P-III | GEV | GP | |||
| Duration | √ | √ | √ | × | √ | √ | √ | 2.63 | 2.13 | 1.82 | 5.69 | 0.42 | 1.25 | 0.35 | GP | k = −0.077 σ = 2.438 μ = 1.581 |
| Severity | √ | √ | √ | × | √ | × | √ | 2.39 | 1.08 | 0.67 | 2.92 | 5.24 | 2.19 | 1.10 | LogN | σ = 1.134 μ = −0.114 |
| Area | √ | √ | √ | √ | √ | √ | √ | 0.64 | 1.50 | 1.12 | 0.81 | 0.31 | 1.13 | 0.16 | GP | k = −0.199 σ = 0.561 μ = 0.034 |
| Copula Function | Gumbel | Clayton | Frank | Joe | Normal | t | Optimal Copula | Parameters | |
|---|---|---|---|---|---|---|---|---|---|
| D-S | AIC | −1195.90 | −1094.77 | −1235.56 | −1149.28 | −1181.84 | −1139.16 | Frank | 8.01 |
| BIC | −1192.82 | −1091.70 | −1232.49 | −1146.20 | −1178.76 | −1136.09 | |||
| RMSE | 0.023 | 0.032 | 0.021 | 0.027 | 0.025 | 0.028 | |||
| D-A | AIC | −1226.21 | −1050.26 | −1205.33 | −1215.57 | −1174.88 | −1150.98 | Gumbel | 2.04 |
| BIC | −1223.14 | −1047.19 | −1202.26 | −1212.49 | −1171.81 | −1147.90 | |||
| RMSE | 0.021 | 0.037 | 0.023 | 0.022 | 0.025 | 0.027 | |||
| S-A | AIC | −1231.89 | −1300.85 | −1270.51 | −1061.98 | −1266.06 | −1259.59 | Clayton | 10.63 |
| BIC | −1228.82 | −1297.77 | −1267.43 | −1058.90 | −1262.99 | −1256.51 | |||
| RMSE | 0.021 | 0.017 | 0.019 | 0.036 | 0.019 | 0.02 | |||
| D-S-A | AIC | −1204.64 | −1056.04 | −1202.06 | −983.64 | −1147.71 | −1140.11 | Gumbel | 3.62 |
| BIC | −1201.57 | −1052.97 | −1198.99 | −980.56 | −1144.63 | −1137.04 | |||
| RMSE | 0.022 | 0.037 | 0.023 | 0.046 | 0.028 | 0.029 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Feng, K.; Wang, F.; Wang, W.; Zhang, Z.; Wang, Y.; Huang, S. Dynamic Evolution and Copula-Based Multivariable Frequency Analysis of Meteorological Drought Considering the Spatiotemporal Variability in Northwestern China. Water 2023, 15, 3861. https://doi.org/10.3390/w15213861
Zhang W, Feng K, Wang F, Wang W, Zhang Z, Wang Y, Huang S. Dynamic Evolution and Copula-Based Multivariable Frequency Analysis of Meteorological Drought Considering the Spatiotemporal Variability in Northwestern China. Water. 2023; 15(21):3861. https://doi.org/10.3390/w15213861
Chicago/Turabian StyleZhang, Weijie, Kai Feng, Fei Wang, Wenjun Wang, Zezhong Zhang, Yingying Wang, and Shengzhi Huang. 2023. "Dynamic Evolution and Copula-Based Multivariable Frequency Analysis of Meteorological Drought Considering the Spatiotemporal Variability in Northwestern China" Water 15, no. 21: 3861. https://doi.org/10.3390/w15213861





