Drought Characterization in Croatia Using E-OBS Gridded Data
Abstract
:1. Introduction
2. Materials and Methods
- (i)
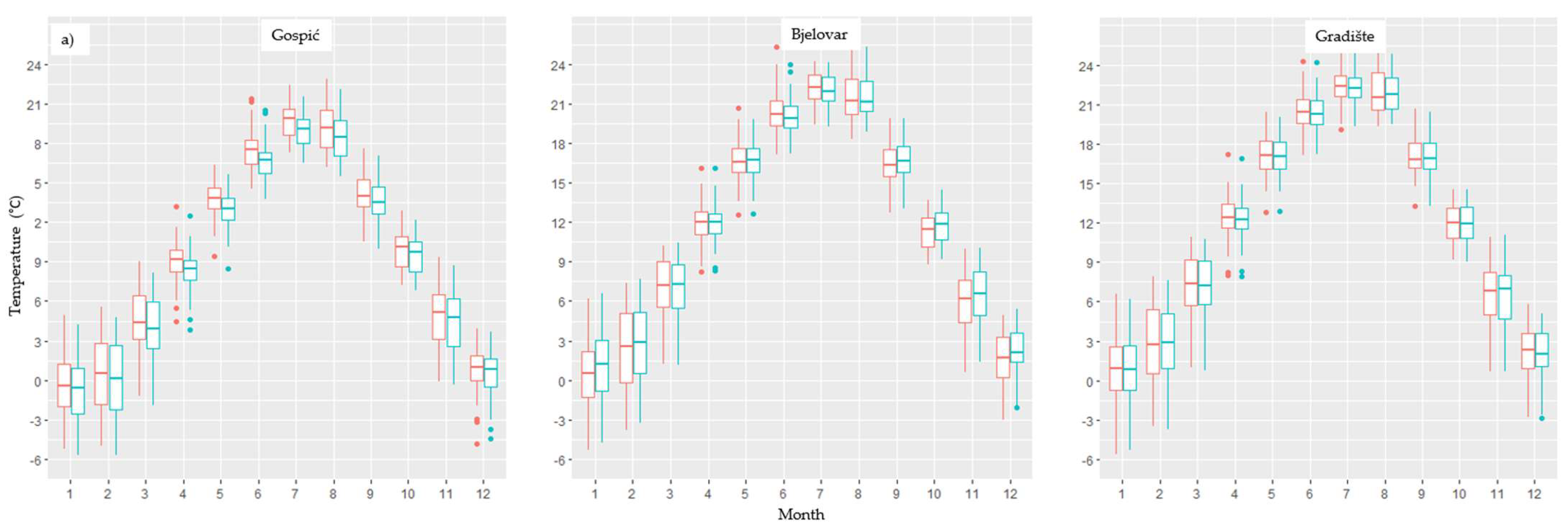
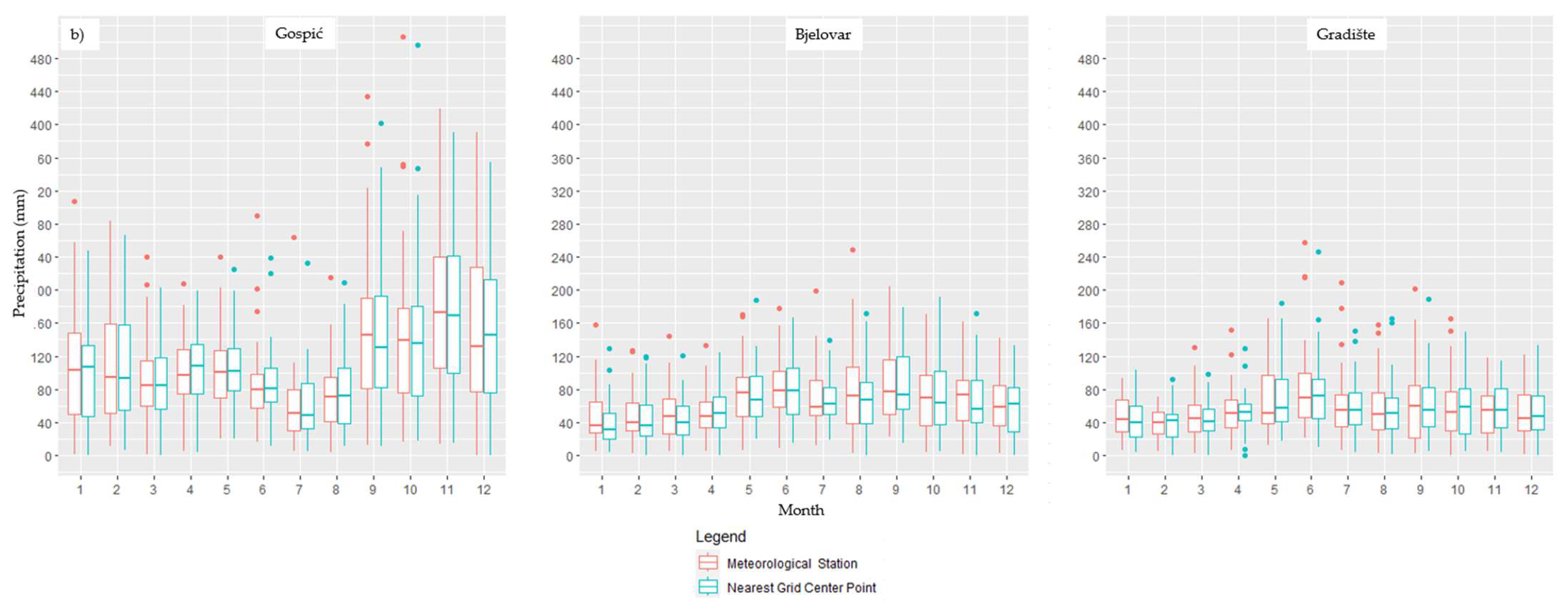
- Data validation: E-OBS precipitation and temperature datasets are first validated with records from meteorological stations at different locations in Croatia.
- (ii)
- Drought index calculation: SPEIs with a 6- and 12-month time-scale (SPEI6 and SPEI12) are calculated to ascertain the sub-annual and annual temporal variability of droughts.
- (iii)
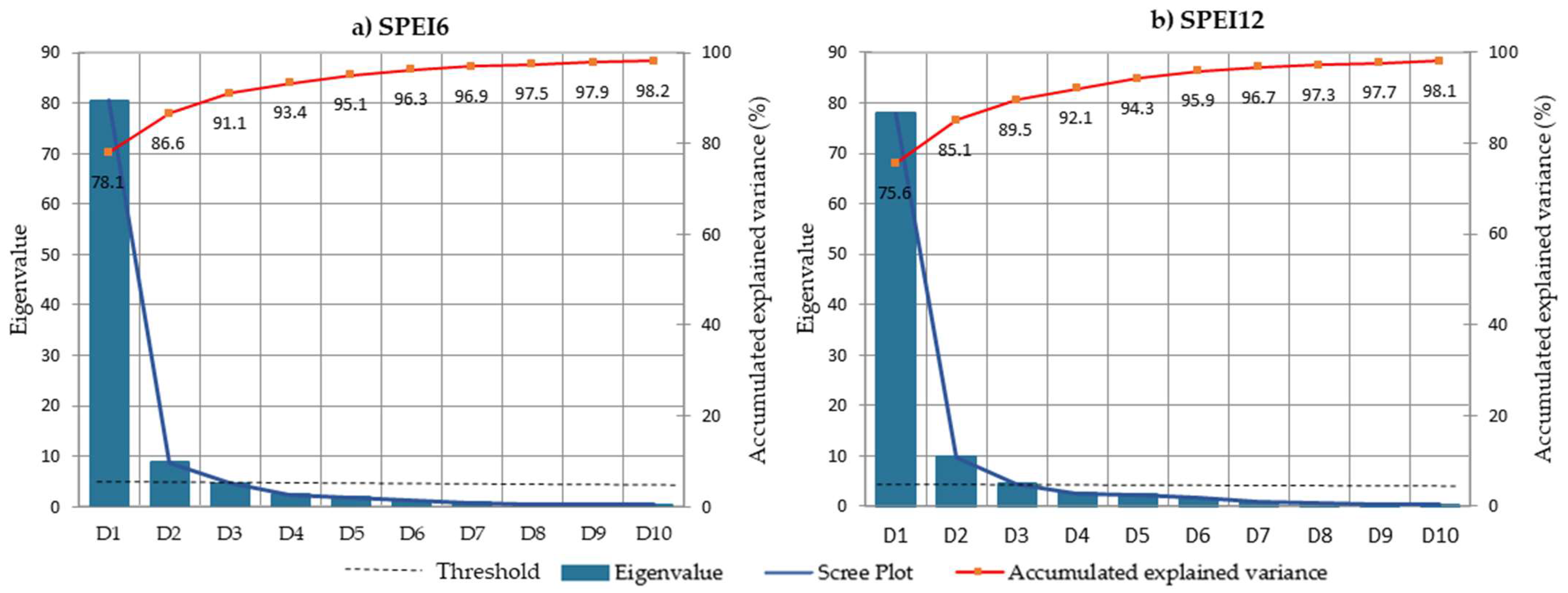
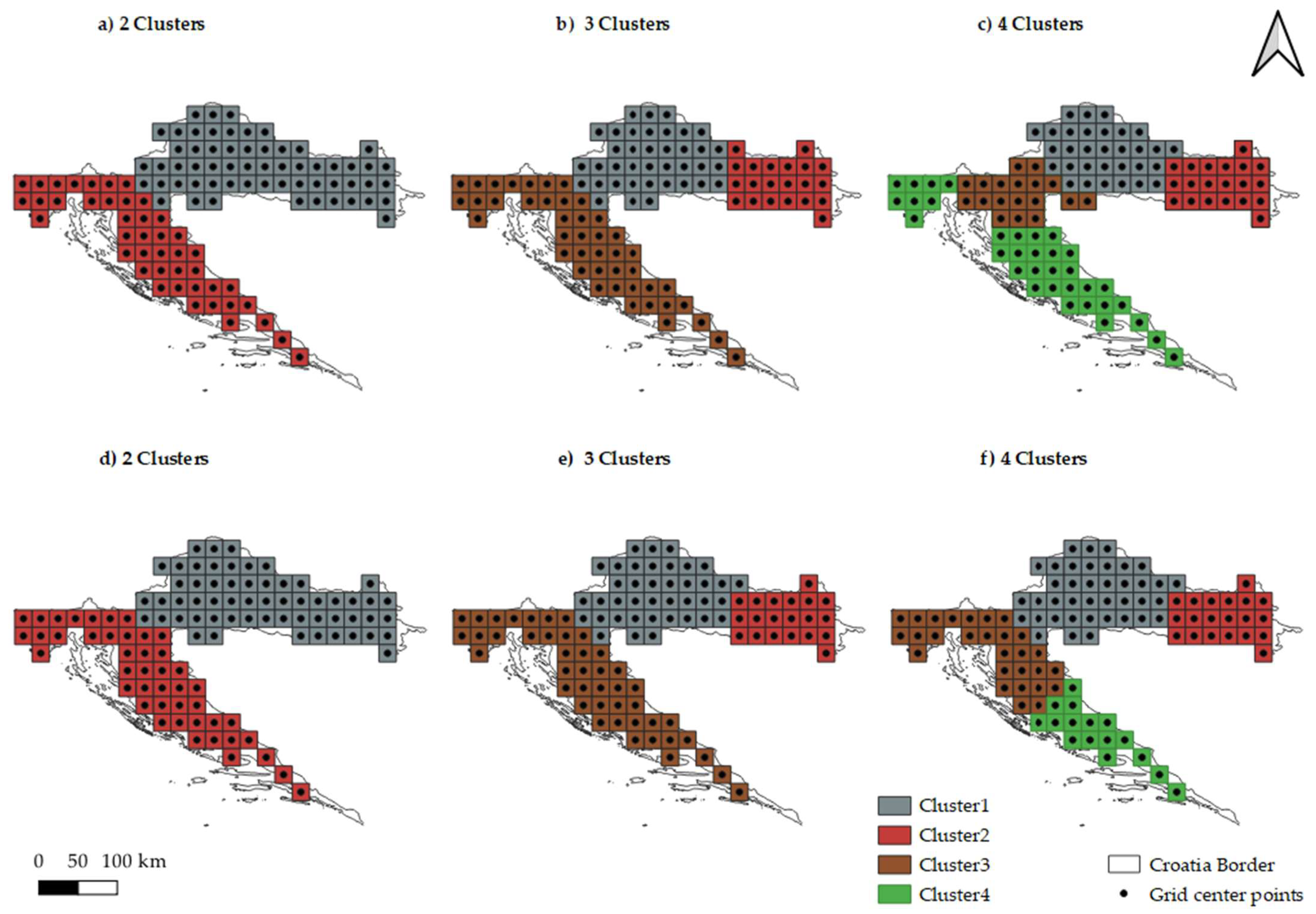
- Drought regional patterns: Principal Component Analysis (PCA) was applied to the previous SPEI time series, aiming to identify homogeneous regions. The K-means clustering method (K-means) was used to validate the regions identified from the PCA.
- (iv)
- Temporal evolution of drought areas: Drought areal evolution of the SPEI6 and SPEI12 fields in each of the identified regions is achieved by assigning an area of influence to each grid cell.
- (v)
- Yearly frequency analysis of drought occurrences: A kernel occurrence rate estimator (KORE) is used to analyse the yearly frequency of the periods under drought conditions for different drought categories according to the regionalized SPEI time series given by the factor scores previously obtained by the PCA.
- (vi)
- Trend analysis: The Modified Mann–Kendall (MMK) trend test, coupled with the Sen’s Slope estimator test, is used to detect the temporal variability of drought intensities within the SPEI6 and SPEI12 fields in each of the regions.
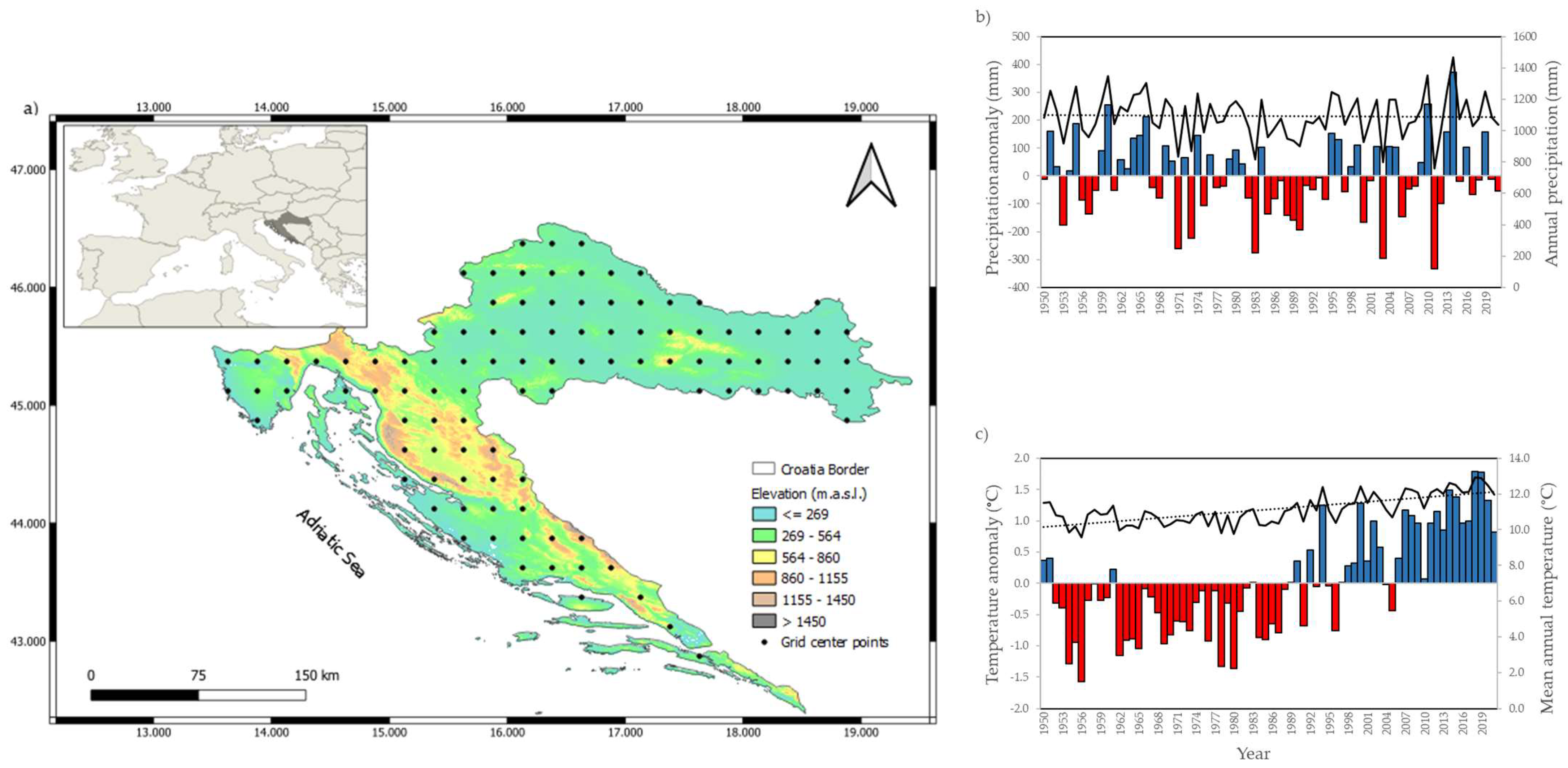
2.1. Study Area
2.2. E-OBS Data
2.3. Drought Index
2.4. Drought Regional Patterns
2.5. Drought Yearly Occurrence Rate and Trend Analysis
3. Results
3.1. Spatial Drought Patterns
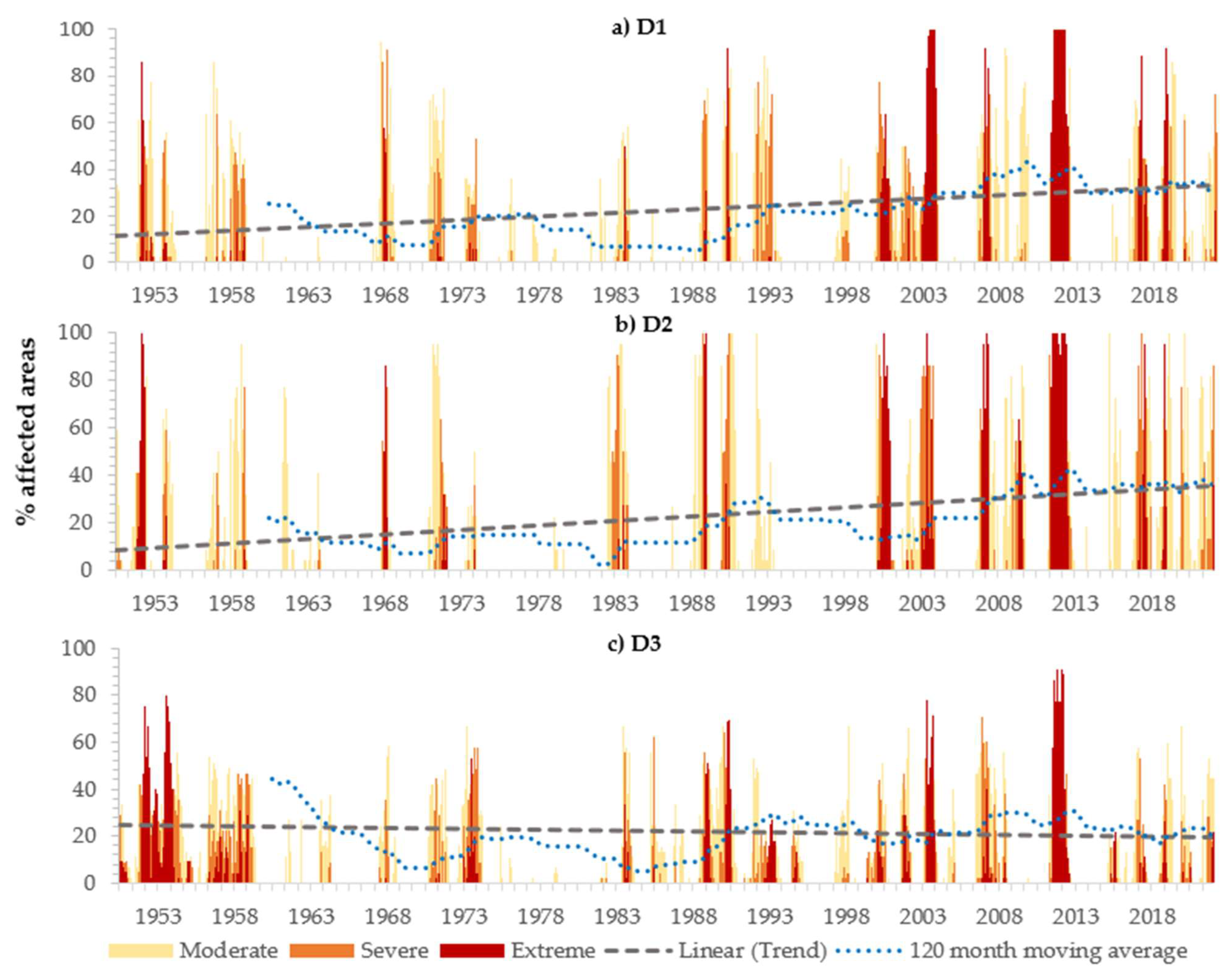
3.2. Temporal Evolution of Drought Areas
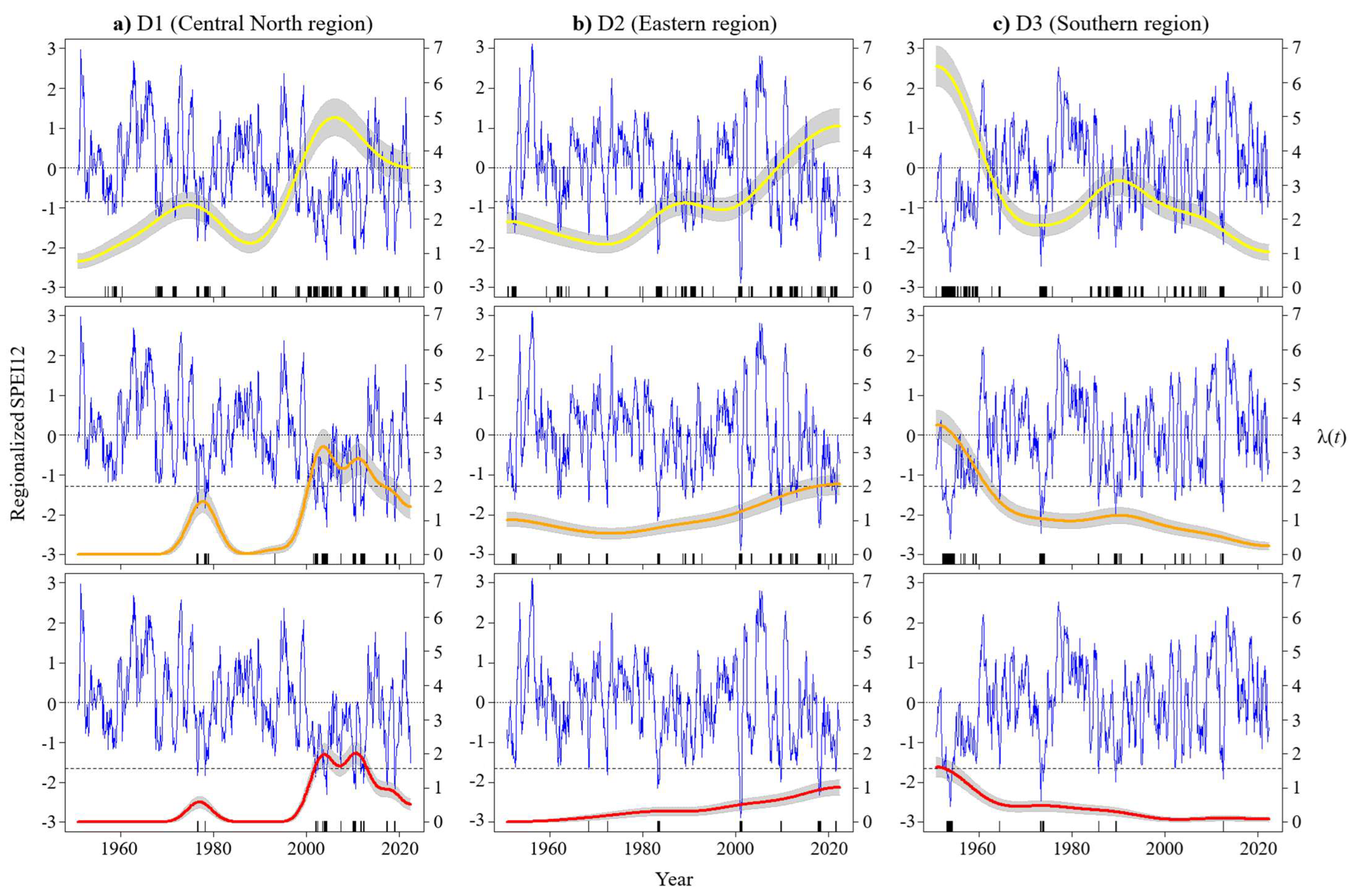
3.3. Changes in Yearly Drought Occurrence Rate
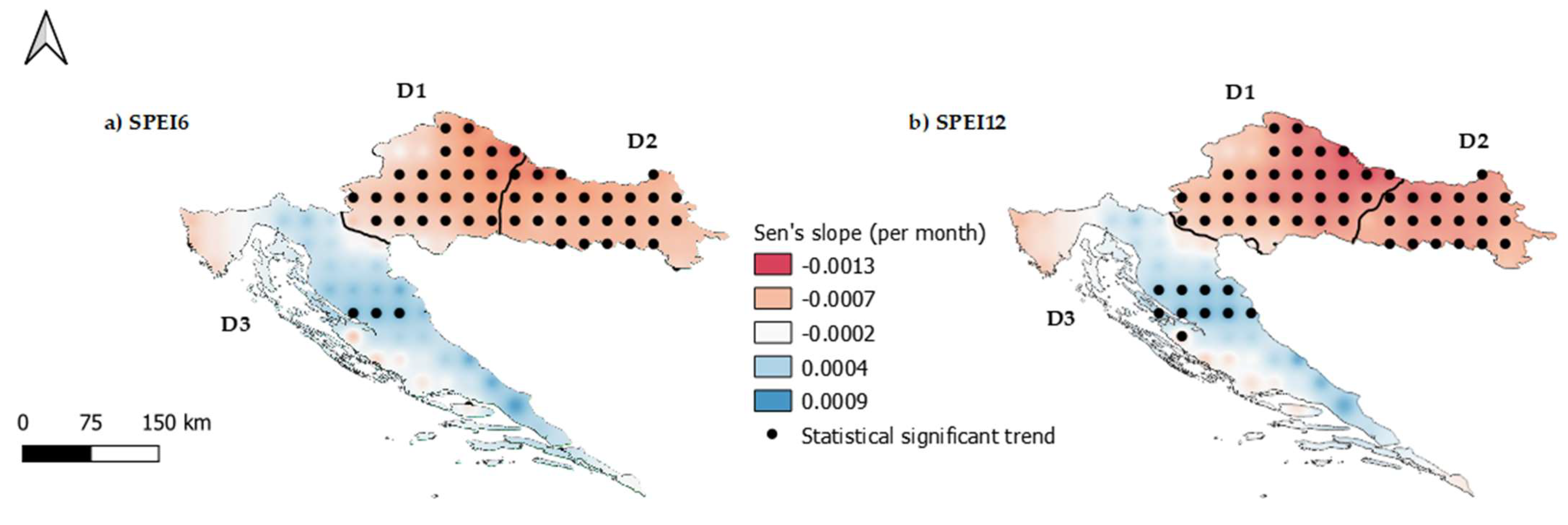
3.4. Temporal Trend Analysis
4. Discussion
5. Conclusions
- (1)
- Based on PCA and K-means validation, Croatia was divided into three homogeneous regions: the central north region (D1), eastern region (D2) and southern region (D3).
- (2)
- The central north region (D1) and eastern region (D2) showed an upward trend in the percentage of areas affected by drought in the whole study period for both SPEI6 and SPEI12, but in the southern region (D3), a negligible trend was obtained for SPEI6 and a downward trend was seen, meaning that progressively fewer areas affected by drought were obtained for SPEI12. Both the D1 and D2 areas have large amounts of non-irrigated agricultural land and grassland, resulting in high ecological vulnerability.
- (3)
- Region D1 (the central north region) experienced an increase in the drought occurrence rate from 1950 until around 2010, and some decreases occurred in the last 10 years, which were especially pronounced in SPEI12. The eastern region (D2) experienced a generalized continuous increase in the drought occurrence rate from 1950 to 2022 in all drought categories and at SPEI time-scales. In the southern region (D3), a decrease in the drought occurrence rate was obtained with one interruption peak. According to the nature of the SPEI calculation procedure, an increase in the number of drought occurrences over the years means that there are progressively longer periods of time with negative water balances, which necessarily lead to to bigger challenges in water management practices.
- (4)
- A generalized change towards increased susceptibility to drought conditions in most areas of D1 and D2 was obtained using the MMK test, with strong statistical significance in both SPEI6 and SPEI12. Given the Sen’s slope values obtained from the trend analysis applied to the SPEI series, more intense drought events are expected in those areas. In the southern region (D3), the trend of less susceptibility to drought conditions spatially follows the mountainous areas of the Dinarides, with less statistical significance. The region of Istria and some coastal parts of Zadar and Sibenik-Knin are the exceptions to the general pattern found in D3, since some localized areas will become a bit more susceptible to drought, which is seen in both SPEI time-scales.
- (5)
- In general terms, the west (Mediterranean climate) is becoming less susceptible to drought, while the east (continental climate) is becoming more prone to an intensification of drought events, showing a greater increase in the areas affected by drought over the years and an increasing rate of occurrence for annual droughts. Although the Mediterranean region is usually at the center of drought research, it is in the mainly agricultural mainland of Croatia that drought conditions seem to have worsened.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dadson, S.; Penning-Rowsell, E.; Garrick, D.; Hope, R.; Hall, J.; Hughes, J. Water Science, Policy, and Management: A Global Challenge; Wiley Blackwell: Hoboken, NJ, USA; Chichester, UK, 2020; ISBN 978-1-119-52060-3. [Google Scholar]
- United Nations Convention to Combat Desertification (UNCCD). Drought in Numbers 2022-Restoration for Readiness and Resilience; United Nations: Abidjan, Côte d’Ivoire, 2022.
- World Meteorological Organization (WMO). Drought and Water Scarcity (WMO-No. 1284); World Climate Programme (WCP): Geneve, Switzerland, 2022. [Google Scholar]
- Van Loon, A.F.; Van Lanen, H.A.J. Making the Distinction between Water Scarcity and Drought Using an Observation-Modeling Framework: Distinguishing between Water Scarcity and Drought. Water Resour. Res. 2013, 49, 1483–1502. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; 17, pp. 179–183. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M. Spatial and Temporal Analysis of Droughts in the Iberian Peninsula (1910–2000). Hydrol. Sci. J. 2006, 51, 83–97. [Google Scholar] [CrossRef]
- Santos, J.F.; Pulido-Calvo, I.; Portela, M.M. Spatial and Temporal Variability of Droughts in Portugal. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Raziei, T.; Martins, D.S.; Bordi, I.; Santos, J.F.; Portela, M.M.; Pereira, L.S.; Sutera, A. SPI Modes of Drought Spatial and Temporal Variability in Portugal: Comparing Observations, PT02 and GPCC Gridded Datasets. Water Resour. Manag. 2015, 29, 487–504. [Google Scholar] [CrossRef]
- Espinosa, L.A.; Portela, M.M. Grid-Point Rainfall Trends, Teleconnection Patterns, and Regionalised Droughts in Portugal (1919–2019). Water 2022, 14, 1863. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F. Spatio-Temporal Analysis of Drought in Southern Italy: A Combined Clustering-Forecasting Approach Based on SPEI Index and Artificial Intelligence Algorithms. Stoch. Environ. Res. Risk Assess. 2023, 37, 2349–2375. [Google Scholar] [CrossRef]
- Xie, P.; Lei, X.; Zhang, Y.; Wang, M.; Han, I.; Chen, Q. Cluster Analysis of Drought Variation and Its Mutation Characteristics in Xinjiang Province, during 1961–2015. Hydrol. Res. 2018, 49, 1016–1027. [Google Scholar] [CrossRef]
- Araneda-Cabrera, R.J.; Bermudez, M.; Puertas, J. Revealing the Spatio-Temporal Characteristics of Drought in Mozambique and Their Relationship with Large-Scale Climate Variability. J. Hydrol. Reg. Stud. 2021, 38, 100938. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Vogt, J.; Barbosa, P. European Drought Climatologies and Trends Based on a Multi-Indicator Approach. Glob. Planet. Change 2015, 127, 50–57. [Google Scholar] [CrossRef]
- Blauhut, V.; Stoelzle, M.; Ahopelto, L.; Brunner, M.I.; Teutschbein, C.; Wendt, D.E.; Akstinas, V.; Bakke, S.J.; Barker, L.J.; Bartošová, L.; et al. Lessons from the 2018–2019 European droughts: A collective need for unifying drought risk management. Nat. Hazards Earth Syst. Sci. 2022, 22, 2201–2217. [Google Scholar] [CrossRef]
- Barron, E.; van Manen, H. The World Climate and Security Report 2022: Climate Security Snapshot-The Balkans; Product of the Expert Group of the International Military Council on Climate and Security; An institute of the Council on Strategic Risks; Center for Climate and Security: The Hague, The Netherlands, 2022. [Google Scholar]
- Knez, S.; Štrbac, S.; Podbregar, I. Climate Change in the Western Balkans and EU Green Deal: Status, Mitigation and Challenges. Energy Sustain. Soc. 2022, 12, 1. [Google Scholar] [CrossRef]
- Juraj, J.; Tadić, L.; Brleković, T.; Potočki, K.; Leko-Kos, M. Application of Principal Component Analysis to Drought Indicators of Three Representative Croatian Regions. Elektron. Časopis Građev. Fak. Osijek 2021, 12, 41–55. [Google Scholar] [CrossRef]
- Brleković, T.; Tadić, L. Hydrological Drought Assessment in a Small Lowland Catchment in Croatia. Hydrology 2022, 9, 79. [Google Scholar] [CrossRef]
- Pandžić, K.; Likso, T.; Curić, O.; Mesić, M.; Pejić, I.; Pasarić, Z. Drought Indices for the Zagreb-Grič Observatory with an Overview of Drought Damage in Agriculture in Croatia. Theor. Appl. Climatol. 2020, 142, 555–567. [Google Scholar] [CrossRef]
- Revelle, W. An Introduction to Psychometric Theory with Applications in R, 2023rd ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Hamed, K.H.; Ramachandra Rao, A. A Modified Mann-Kendall Trend Test for Autocorrelated Data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Perčec Tadić, M.; Pasarić, Z.; Guijarro, J.A. Croatian High-Resolution Monthly Gridded Dataset of Homogenised Surface Air Temperature. Theor. Appl. Climatol. 2023, 151, 227–251. [Google Scholar] [CrossRef]
- Gajić-Čapka, M.; Cindrić, K.; Pasarić, Z. Trends in Precipitation Indices in Croatia, 1961–2010. Theor. Appl. Climatol. 2015, 121, 167–177. [Google Scholar] [CrossRef]
- Perčec Tadić, M.; Gajić-Čapka, M.; Zaninović, K.; Cindric, K. Drought Vulnerability in Croatia. Agric. Conspec. Sci. 2014, 79, 31–38. [Google Scholar]
- Cindric Kalin, K.; Patalen, L.; Marinovic, I.; Pasaric, Z. Trends in Temperature and Precipitation Indices in Croatia, 1961–2020. In Proceedings of the Copernicus Meetings, EMS Annual Meeting 2022, Bonn, Germany, 5–9 September 2022. [Google Scholar]
- Cornes, R.C.; Van Der Schrier, G.; Van Den Besselaar, E.J.M.; Jones, P.D. An Ensemble Version of the E-OBS Temperature and Precipitation Data Sets. J. Geophys. Res. Atmos. 2018, 123, 9391–9409. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55. [Google Scholar] [CrossRef]
- Alam, N.M.; Sharma, G.C.; Moreira, E.; Jana, C.; Mishra, P.K.; Sharma, N.K.; Mandal, D. Evaluation of Drought Using SPEI Drought Class Transitions and Log-Linear Models for Different Agro-Ecological Regions of India. Phys. Chem. Earth Parts ABC 2017, 100, 31–43. [Google Scholar] [CrossRef]
- Dikshit, A.; Pradhan, B.; Huete, A. An Improved SPEI Drought Forecasting Approach Using the Long Short-Term Memory Neural Network. J. Environ. Manag. 2021, 283, 111979. [Google Scholar] [CrossRef] [PubMed]
- Svoboda, M.D.; Fuchs, B.A. Handbook of Drought Indicators and Indices; World Meteorological Organization: Geneva, Switzerland, 2016; ISBN 978-92-63-11173-9. [Google Scholar]
- Liu, C.; Yang, C.; Yang, Q.; Wang, J. Spatiotemporal Drought Analysis by the Standardized Precipitation Index (SPI) and Standardized Precipitation Evapotranspiration Index (SPEI) in Sichuan Province, China. Sci. Rep. 2021, 11, 1280. [Google Scholar] [CrossRef]
- Agnew, C. Using the SPI to Identify Drought. Drought Network News, May 2000; 12p. [Google Scholar]
- López-Moreno, J.I.; Vicente-Serrano, S.M.; Zabalza, J.; Beguería, S.; Lorenzo-Lacruz, J.; Azorin-Molina, C.; Morán-Tejeda, E. Hydrological Response to Climate Variability at Different Time Scales: A Study in the Ebro Basin. J. Hydrol. 2013, 477, 175–188. [Google Scholar] [CrossRef]
- Bonaccorso, B.; Bordi, I.; Cancelliere, A.; Rossi, G.; Sutera, A. Spatial Variability of Drought: An Analysis of the SPI in Sicily. Water Resour. Manag. 2003, 17, 273–296. [Google Scholar] [CrossRef]
- Smith, L.I. A Tutorial on Principal Components Analysis; Cornell University: Ithaca, NY, USA, 2002. [Google Scholar]
- Hair, J.F. Multivariate Data Analysis, 6th ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2006; ISBN 978-0-13-032929-5. [Google Scholar]
- Woods, C.M.; Edwards, M.C. Essential Statistical Methods for Medical Statistics; Rao, C.R., Miller, J.P., Rao, D.C.R., Eds.; Elsevier: Amsterdam, The Netherlands, 2011; ISBN 978-0-444-53737-9. [Google Scholar]
- Vicente-Serrano, S.; González-Hidalgo, J.; De Luis, M.; Raventós, J. Drought Patterns in the Mediterranean Area: The Valencia Region (Eastern Spain). Clim. Res. 2004, 26, 5–15. [Google Scholar] [CrossRef]
- Kahya, E.; Kalaycı, S.; Piechota, T.C. Streamflow Regionalization: Case Study of Turkey. J. Hydrol. Eng. 2008, 13, 205–214. [Google Scholar] [CrossRef]
- Shukla, S.; Mostaghimi, S.; Petrauskas, B.; Al-Smadi, M. Multivariate Technique for Baseflow Separation Using Water Quality Data. J. Hydrol. Eng. 2000, 5, 172–179. [Google Scholar] [CrossRef]
- Mudelsee, M.; Börngen, M.; Tetzlaff, G.; Grünewald, U. No Upward Trends in the Occurrence of Extreme Floods in Central Europe. Nature 2003, 425, 166–169. [Google Scholar] [CrossRef]
- Silva, A.T.; Portela, M.M.; Naghettini, M. Nonstationarities in the Occurrence Rates of Flood Events in Portuguese Watersheds. Hydrol. Earth Syst. Sci. 2012, 16, 241–254. [Google Scholar] [CrossRef]
- Portela, M.M.; Dos Santos, J.F.; Silva, A.T.; Benitez, J.B.; Frank, C.; Reichert, J.M. Drought Analysis in Southern Paraguay, Brazil and Northern Argentina: Regionalization, Occurrence Rate and Rainfall Thresholds. Hydrol. Res. 2015, 46, 792–810. [Google Scholar] [CrossRef]
- Portela, M.M.; Santos, J.F.; Purcz, P.; Silva, A.T.; Hlavatá, H. A Comprehensive Drought Analysis in Slovakia Using SPI. Eur. Water 2015, 51, 15–31. [Google Scholar]
- Diggle, P. A Kernel Method for Smoothing Point Process Data. Appl. Stat. 1985, 34, 138. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Almazroui, M.; Salam, M.A.; Mondol, M.A.H.; Rahman, M.M.; Deb, L.; Kundu, P.K.; Zaman, M.A.U.; Islam, A.R.M.T. Spatiotemporal Drought Analysis in Bangladesh Using the Standardized Precipitation Index (SPI) and Standardized Precipitation Evapotranspiration Index (SPEI). Sci. Rep. 2022, 12, 20694. [Google Scholar] [CrossRef]
- Cindrić, K.; Telišman Prtenjak, M.; Herceg-Bulić, I.; Mihajlović, D.; Pasarić, Z. Analysis of the Extraordinary 2011/2012 Drought in Croatia. Theor. Appl. Climatol. 2016, 123, 503–522. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis, 1st ed.; Routledge: London, UK, 2018; ISBN 978-1-315-14091-9. [Google Scholar]
- Climate change adaptation strategy in the Republic of Croatia for the period up to 2040 with a view to 2070. Official Gazette of the Republic of Croatia 46/2020. Available online: https://faolex.fao.org/docs/pdf/cro207819.pdf (accessed on 11 June 2023).
- Seventh National Communication of the Republic of Croatia under the United Nation Framework Convention on the Climate Change (UNFCCC). 2018. Available online: https://unfccc.int/sites/default/files/resource/IDR7_HRV_complete.pdf (accessed on 20 May 2023).
- Cindrić Kalin, K.; Pasarić, Z. Regional Patterns of Dry Spell Durations in Croatia. Int. J. Climatol. 2022, 42, 5503–5519. [Google Scholar] [CrossRef]
- Agricultural Regions of Croatia. The Soils of Croatia; World Soils Book Series; Springer: Dordrecht, The Netherlands, 2013; pp. 23–36. ISBN 978-94-007-5814-8. [Google Scholar]
- Vrsalović, A.; Andrić, I.; Bonacci, O.; Kovčić, O. Climate Variability and Trends in Imotski, Croatia: An Analysis of Temperature and Precipitation. Atmosphere 2023, 14, 861. [Google Scholar] [CrossRef]
- Roushangar, K.; Ghasempour, R. Multi-Temporal Analysis for Drought Classifying Based on SPEI Gridded Data and Hybrid Maximal Overlap Discrete Wavelet Transform. Int. J. Environ. Sci. Technol. 2022, 19, 3219–3232. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Food and Agriculture Organization of the United Nations, Ed.; FAO Irrigation and Drainage Paper; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; ISBN 978-92-5-104219-9. [Google Scholar]



| Nonexceedance Probability | SPEI | Drought Category |
|---|---|---|
| 0.05 | >1.65 | Extremely wet |
| 0.1 | >1.28 | Severely wet |
| 0.2 | >0.84 | Moderately wet |
| 0.6 | >−0.84 and <0.84 | Normal |
| 0.2 | <−0.84 | Moderate drought |
| 0.1 | <−1.28 | Severe drought |
| 0.05 | <−1.65 | Extreme drought |
| SPEI6 | Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | SPEI12 | Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 |
|---|---|---|---|---|---|---|---|---|---|
| Two Classification Groups | Two Classification Groups | ||||||||
| Cluster 1 | 0.000 | Cluster 1 | 0.000 | ||||||
| Cluster 2 | 0.546 | 0.000 | Cluster 2 | 0.584 | 0.000 | ||||
| Three Classification Groups | Three Classification Groups | ||||||||
| Cluster 1 | 0.000 | Cluster 1 | 0.000 | ||||||
| Cluster 2 | 0.526 | 0.000 | Cluster 2 | 0.532 | 0.000 | ||||
| Cluster 3 | 0.719 | 0.525 | 0.000 | Cluster 3 | 0.570 | 0.753 | 0.000 | ||
| Four Classification Groups | Four Classification Groups | ||||||||
| Cluster 1 | 0.000 | Cluster 1 | 0.000 | ||||||
| Cluster 2 | 0.740 | 0.000 | Cluster 2 | 0.532 | 0.000 | ||||
| Cluster 3 | 0.391 | 0.669 | 0.000 | Cluster 3 | 0.578 | 0.783 | 0.000 | ||
| Cluster 4 | 0.597 | 0.528 | 0.417 | 0 | Cluster 4 | 0.674 | 0.795 | 0.479 | 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, J.F.; Tadic, L.; Portela, M.M.; Espinosa, L.A.; Brleković, T. Drought Characterization in Croatia Using E-OBS Gridded Data. Water 2023, 15, 3806. https://doi.org/10.3390/w15213806
Santos JF, Tadic L, Portela MM, Espinosa LA, Brleković T. Drought Characterization in Croatia Using E-OBS Gridded Data. Water. 2023; 15(21):3806. https://doi.org/10.3390/w15213806
Chicago/Turabian StyleSantos, João F., Lidija Tadic, Maria Manuela Portela, Luis Angel Espinosa, and Tamara Brleković. 2023. "Drought Characterization in Croatia Using E-OBS Gridded Data" Water 15, no. 21: 3806. https://doi.org/10.3390/w15213806
APA StyleSantos, J. F., Tadic, L., Portela, M. M., Espinosa, L. A., & Brleković, T. (2023). Drought Characterization in Croatia Using E-OBS Gridded Data. Water, 15(21), 3806. https://doi.org/10.3390/w15213806










