A Concept of Fuzzy Dual Permeability of Fractured Porous Media
Abstract
:1. Introduction
2. Summary of Field Ponded Infiltration Tests
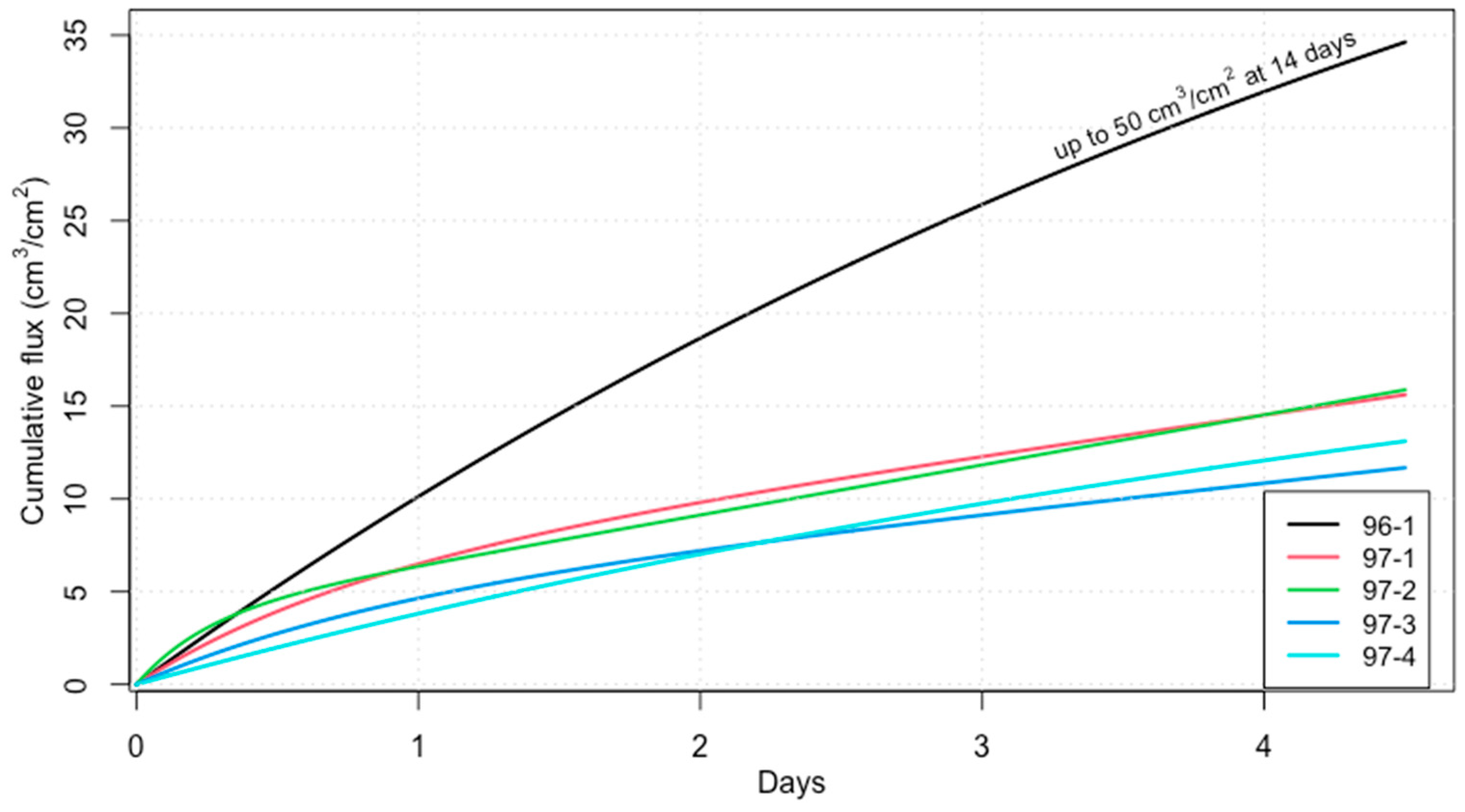
2.1. HHA Infiltration Tests
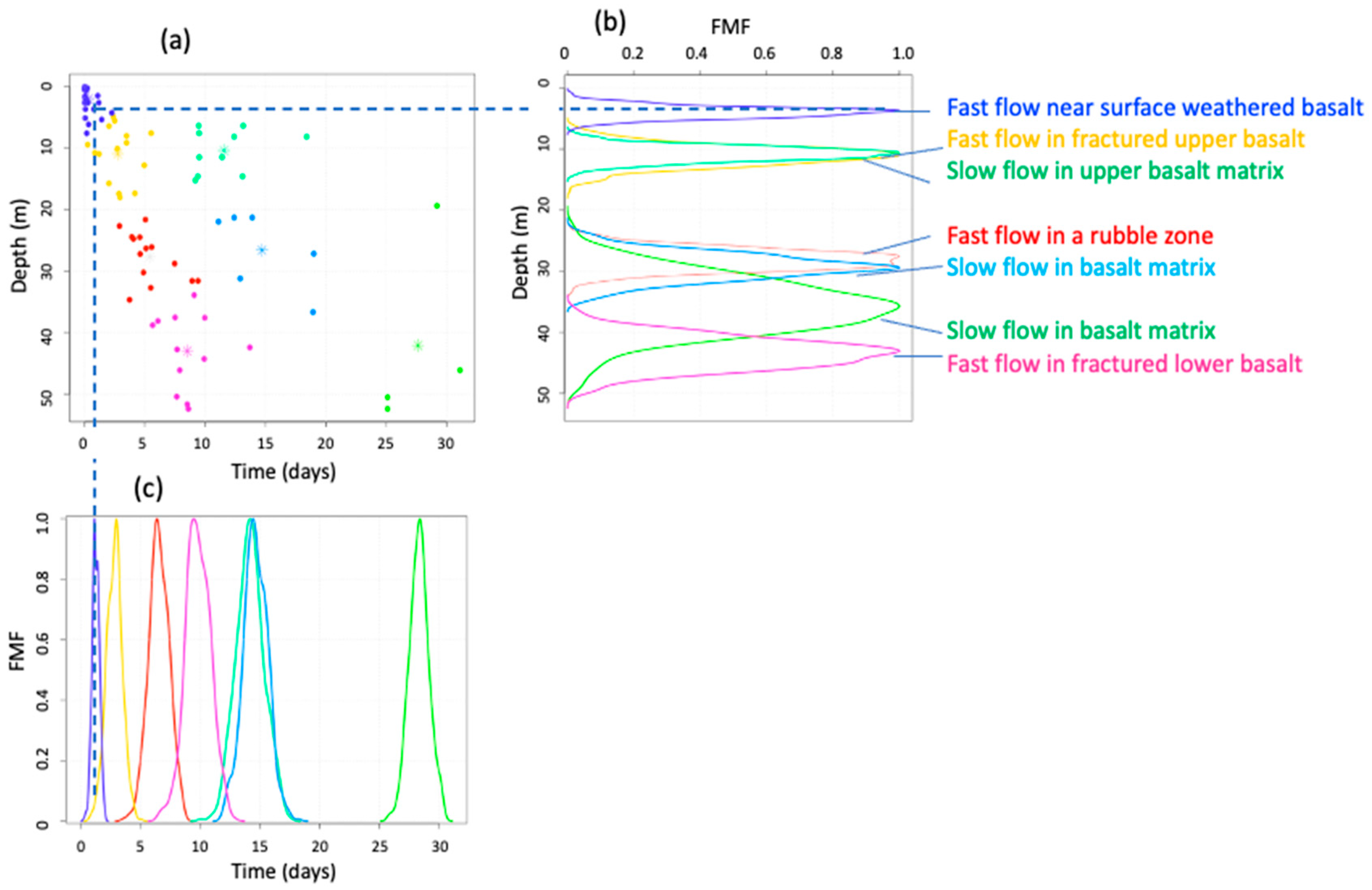
2.2. Box Canyon Infiltration Tests
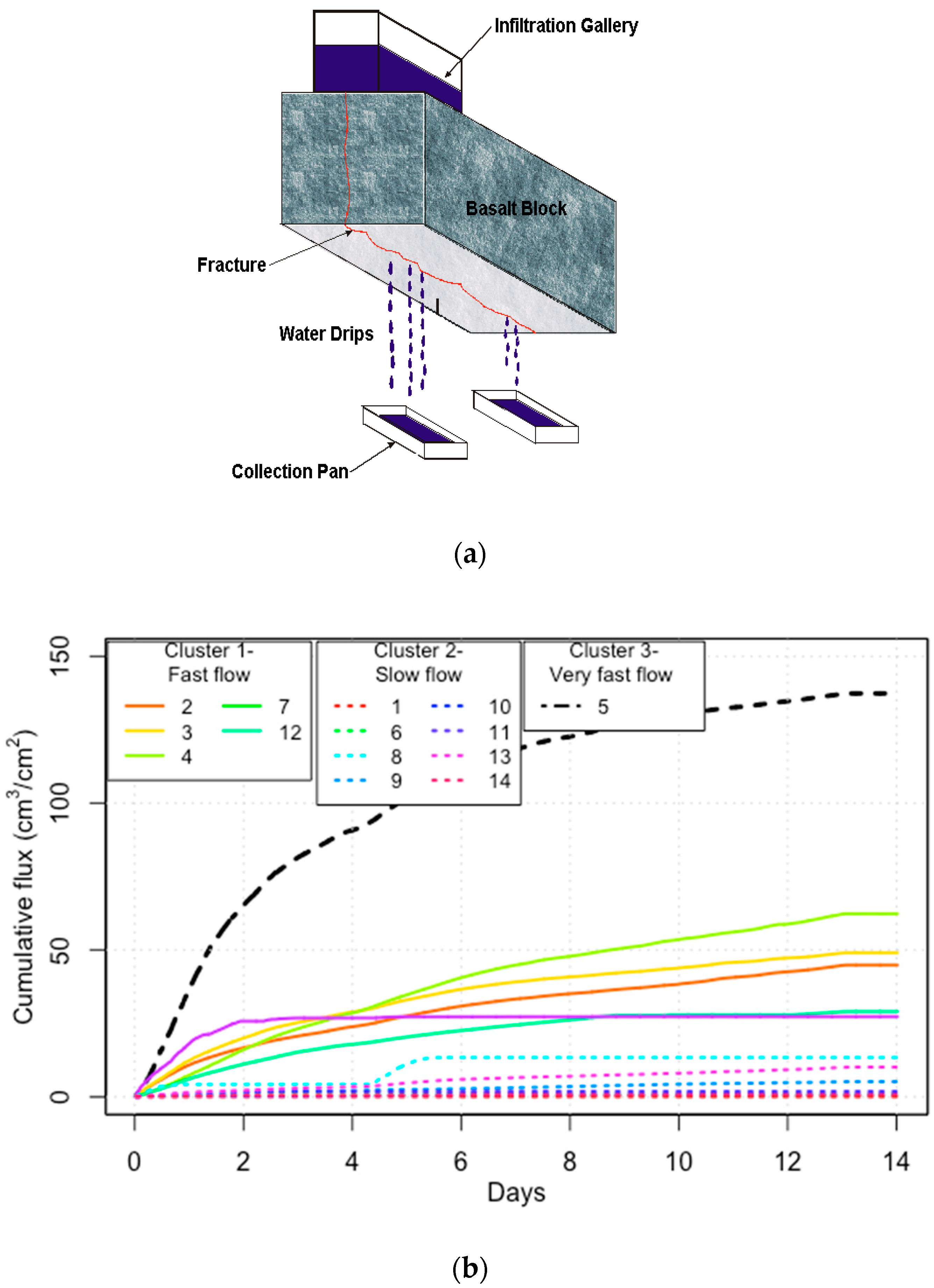
2.3. Large-Scale Infiltration Test at the Radioactive Waste Management Complex at INL
3. Methods of Fuzzy Data Analysis
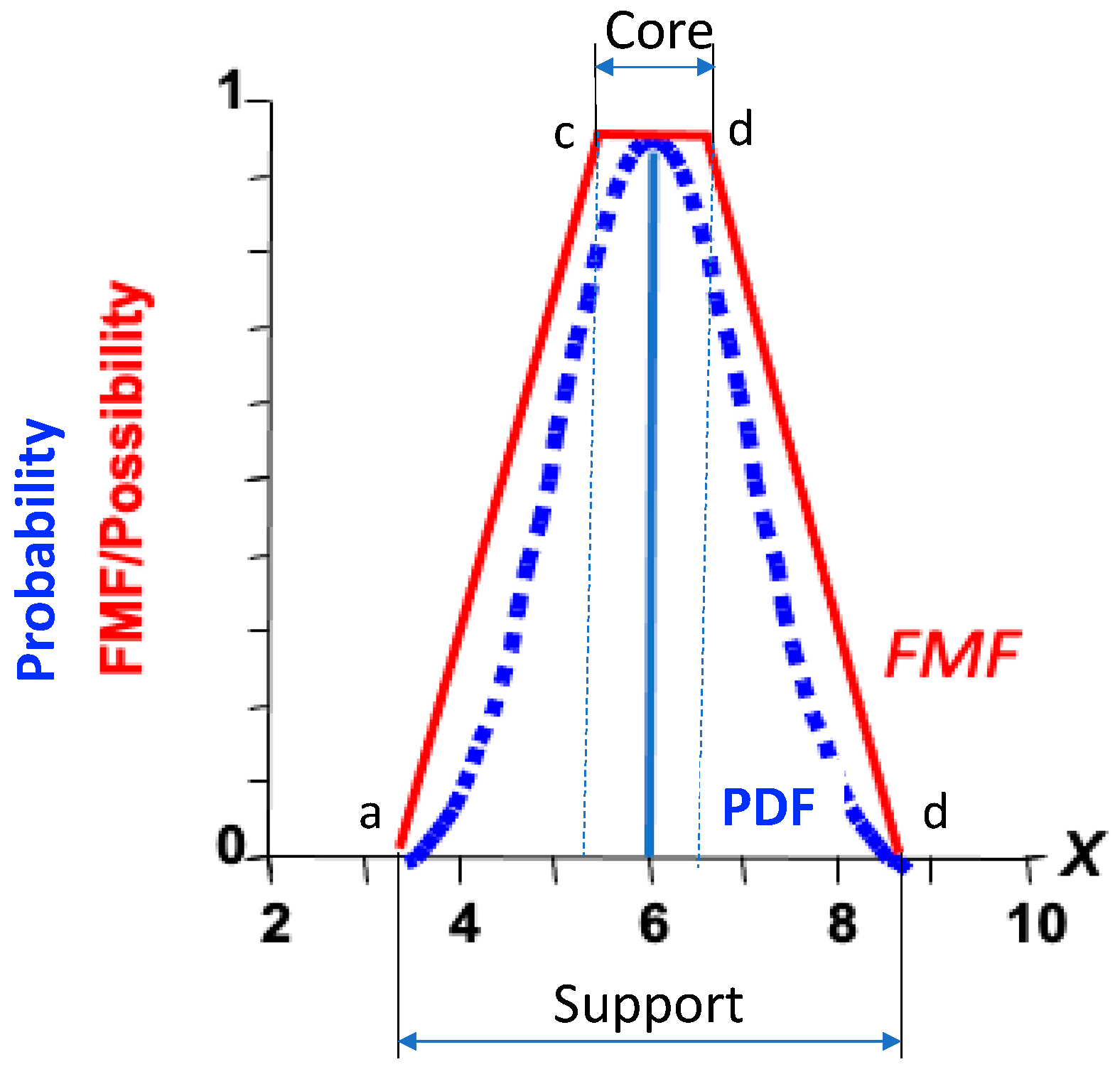
3.1. General Idea of Fuzzy Data Analysis and a Fuzzy Membership Function
3.2. Fuzzy Clustering and Fuzzy Regression
4. Results of Fuzzy Data Analysis
4.1. Fuzzy Clustering and Fuzzy Regression of the Time-Depth Waterfront Penetration
4.2. Fuzzy Analysis of the Infiltration Rate and Parameters of Horton’s Infiltration Model
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ramirez, J.A.; Lichter, M.; Coulthard, T.J.; Skinner, C. Hyper-resolution mapping of regional storm surge and tide flooding: Comparison of static and dynamic models. Nat. Hazards 2016, 82, 571–590. [Google Scholar] [CrossRef]
- Ahmed, A.; Hewa, G.; Alrajhi, A. Flood susceptibility mapping using a geomorphometric approach in South Australian basins. Nat. Hazards 2021, 106, 629–653. [Google Scholar] [CrossRef]
- Argyrokastritis, I.; Psychogiou, M.; Londra, P.A. Infiltration under Ponded Conditions. Water 2021, 13, 3492. [Google Scholar] [CrossRef]
- Manna, F.; Cherry, J.A.; McWhorter, D.B.; Parker, B.L. Groundwater recharge assessment in an upland sandstone aquifer of southern California. J. Hydrol. 2016, 541, 787–799. [Google Scholar] [CrossRef]
- Medici, G.; Langman, J.B. Pathways and Estimate of Aquifer Recharge in a Flood Basalt Terrain; A Review from the South Fork Palouse River Basin (Columbia River Plateau, USA). Sustainability 2022, 14, 11349. [Google Scholar] [CrossRef]
- Pyrak-Nolte, L.J.; Nolte, D.D.; Cook, N.G.W. Hierarchical cascades and the single fracture: Percolation and seismic detection. In Fractals in Petroleum Geology and Earth Processes; Barton, C.C., La Pointe, P.R., Eds.; Plenum Press: New York, NY, USA, 1995; pp. 143–178. [Google Scholar]
- Newman, M.E.; Dunnivant, F.M. Results from the Large-Scale Aquifer Pumping and Infiltration Test: Transport of Tracers through Fractured Media; Rep. INEL-95/146 ER-WAG7-77; Idaho National Engineering and Environmental Laboratory: Idaho Falls, ID, USA, 1995. [Google Scholar]
- Barenblatt, G.I.; Zheltov, I.P.; Kochina, I.N. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks [strata]. J. Appl. Math. Mech. 1960, 24, 1286–1303. [Google Scholar] [CrossRef]
- Beven, K.; Germann, P. Macropores and water flow in soils revisited. Water Resour. Res. 2013, 49, 3071–3092. [Google Scholar] [CrossRef]
- Gerke, H.H.; Dusek, J.; Vogel, T.; Khne, J.M. Two-dimensional dual-permeability analyses of a bromide tracer experiment on a tile-drained field. Vadose Zone J. 2007, 6, 651–667. [Google Scholar] [CrossRef]
- Šimůnek, J.; Jarvis, N.J.; Van Genuchten, M.T.; Gärdenäs, A. Review and comparison of models for describing non-equilibrium and preferential flow and transport in the vadose zone. J. Hydrol. 2003, 272, 14–35. [Google Scholar] [CrossRef]
- Pruess, K.; Faybishenko, B.; Bodvarsson, G.S. Alternative concepts and approaches for modeling flow and transport in thick unsaturated zones of fractured rocks. J. Contam. Hydrol. Spec. Issue 1999, 38, 281–322. [Google Scholar] [CrossRef]
- Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- Faybishenko, B.; Doughty, C.; Steiger, M.; Long, J.; Wood, T.; Jacobsen, J.; Lore, J.; Zawislanski, P. Conceptual model of the geometry and physics of water flow in a fractured basalt vadose zone. Water Resour. Res. 2000, 37, 3499–3522. [Google Scholar] [CrossRef]
- Podgorney, R.; Wood, T.; Faybishenko, B.; Stoops, T. Spatial and Temporal Instabilities in Water Flow through Variably Saturated Fractured Basalt on a One-Meter Scale; Geophysical Monograph No. 122; “Dynamics of Fluids in Fractured Rock” American Geophysical Union: Washington, DC, USA, 2000; pp. 129–146. [Google Scholar]
- Gourley, J.J.; Vieux, B.E. A method for identifying sources of model uncertainty in rainfall-runoff simulations. J. Hydrol. 2006, 327, 68–80. [Google Scholar] [CrossRef]
- Dohnal, M.; Jelinkova, V.; Snehota, M.; Dusek, J.; Brezina, J. Tree-Dimensional Numerical Analysis of Water Flow Affected by Entrapped Air: Application on of Noninvasive Imaging Techniques. Vadose Zone J. 2013, 12, 1–12. [Google Scholar] [CrossRef]
- Bárdossy, A.; Disse, M. Fuzzy rule-based models for infiltration. Water Resour. Res. 1993, 29, 373–382. [Google Scholar] [CrossRef]
- Bárdossy, A.; Duckstein, L. Fuzzy Rule Based Modeling with Application to Geophysical, Biological and Engineering Systems; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar] [CrossRef]
- Shu, C.; Ouarda, T.B.M.J. Regional flood frequency analysis at ungauged sites using the adaptive neuro-fuzzy inference system. J. Hydrol. 2008, 349, 31–43. [Google Scholar] [CrossRef]
- Nayak, P.C. Explaining Internal Behavior in a Fuzzy If-Then Rule-Based Flood-Forecasting Model. J. Hydrol. Eng. 2010, 15, 20–28. [Google Scholar] [CrossRef]
- Londoño, O.M.Q.; Romanell, A.; Lima, M.L.; Massone, H.E.; Martínez, D.E. Fuzzy logic-based assessment for mapping potential infiltration areas in low-gradient watersheds. J. Environ. Manag. 2016, 176, 101–111. [Google Scholar] [CrossRef]
- Kambalimath, S.; Deka, P.C. A basic review of fuzzy logic applications in hydrology and water resources. Appl. Water Sci. 2020, 10, 8. [Google Scholar] [CrossRef]
- Zhang, D.; Shu, L.; Li, S. Fuzzy structural element method for solving fuzzy dual medium seepage model in reservoir. Soft Comput. 2020, 24, 16097–16110. [Google Scholar] [CrossRef]
- Wood, T.R.; Norrell, G.T. Integrated Large-Scale Aquifer Pumping and Infiltration Tests: Groundwater Pathways OU 7-06; Summary Report, Rep. INEL-96/0256; Idaho National Engineering and Environmental Laboratory: Idaho Falls, ID, USA, 1996. [Google Scholar]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall: Hoboken, NJ, USA, 1979. [Google Scholar]
- Faybishenko, B. Hydraulic behavior of quasi-saturated soils in the presence of entrapped air: Laboratory experiments. Water Resour. Res. 1995, 31, 2421–2435. [Google Scholar] [CrossRef]
- Neuman, S.P. Wetting front pressure head in the infiltration model of Green and Ampt. Water Resour. Res. 1976, 12, 564–566. [Google Scholar] [CrossRef]
- Faybishenko, B.; Finsterle, S. On tensiometry in fractured rocks. In Theory, Modeling, and Field Investigation in Hydrogeology; A Special Volume in Honor of Shlomo P. Neuman’s 60th Birthday; Zhang, D., Winter, L., Eds.; Geological Society of America: Boulder, Colorado, USA, 2000. [Google Scholar]
- Horton, R.E. An approach towards physical interpretation of infiltration capacity. Proc. Soil Sci. Soc. Am. 1940, 5, 399–417. [Google Scholar] [CrossRef]
- Beven, K.; Robert, E. Horton’s perceptual model of infiltration processes. Hydrol. Process 2004, 18, 3447–3460. [Google Scholar]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis, Monographs on Statistics and Applied Probability; Chapman and Hall: London, UK, 1986. [Google Scholar]
- Chen, W.-C.; Tareen, A.; Kinney, J.B. Density estimation on small datasets. Phys. Rev. Lett. 2018, 121, 160605. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Plenum Press: New York, NY, USA, 1981. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013; ISBN 3-900051-07-0. Available online: http://www.R-project.org/ (accessed on 1 October 2023).
- Gagolewski, M.; Caha, J. FuzzyNumbers Package: Tools to Deal with Fuzzy Numbers in R. 2021. Available online: https://github.com/gagolews/FuzzyNumbers/ (accessed on 1 October 2023).
- Ferraro, M.; Giordani, P.; Serafini, A. Fclust: An R Package for Fuzzy Clustering. R J. 2019, 11. Available online: https://journal.r-project.org/archive/2019/RJ-2019-017/RJ-2019-017.pdf (accessed on 1 October 2023). [CrossRef]
- Škrabánek, P.; Martínková, N. Algorithm 1017: Fuzzyreg: An R Package for Fuzzy Linear Regression Models. ACM Trans. Math. Softw. 2021, 47, 29. [Google Scholar] [CrossRef]
- Zeileis, A.; Grothendieck, G. zoo: S3 Infrastructure for Regular and Irregular Time Series. J. Stat. Softw. 2005, 14, 1–27. [Google Scholar] [CrossRef]

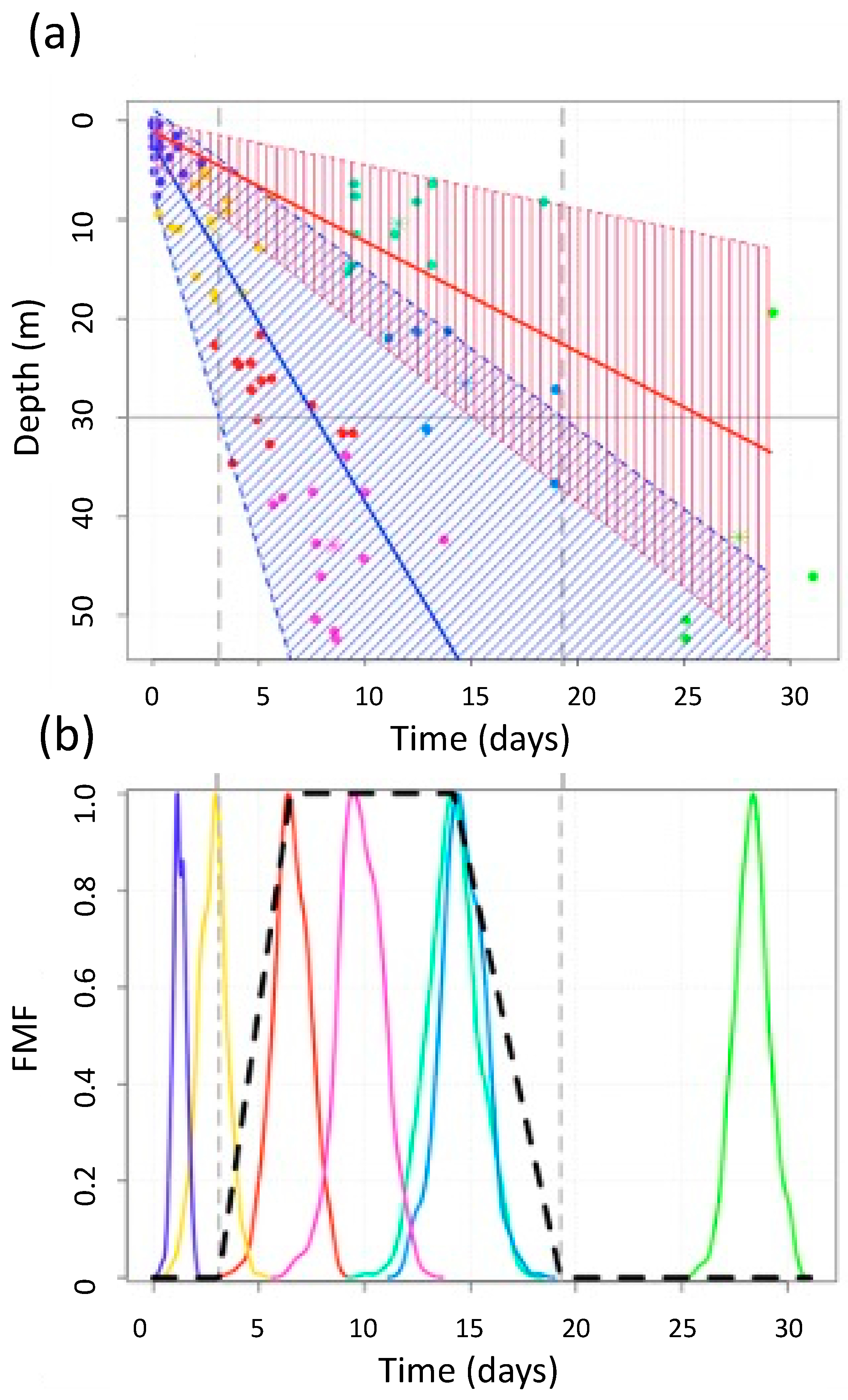
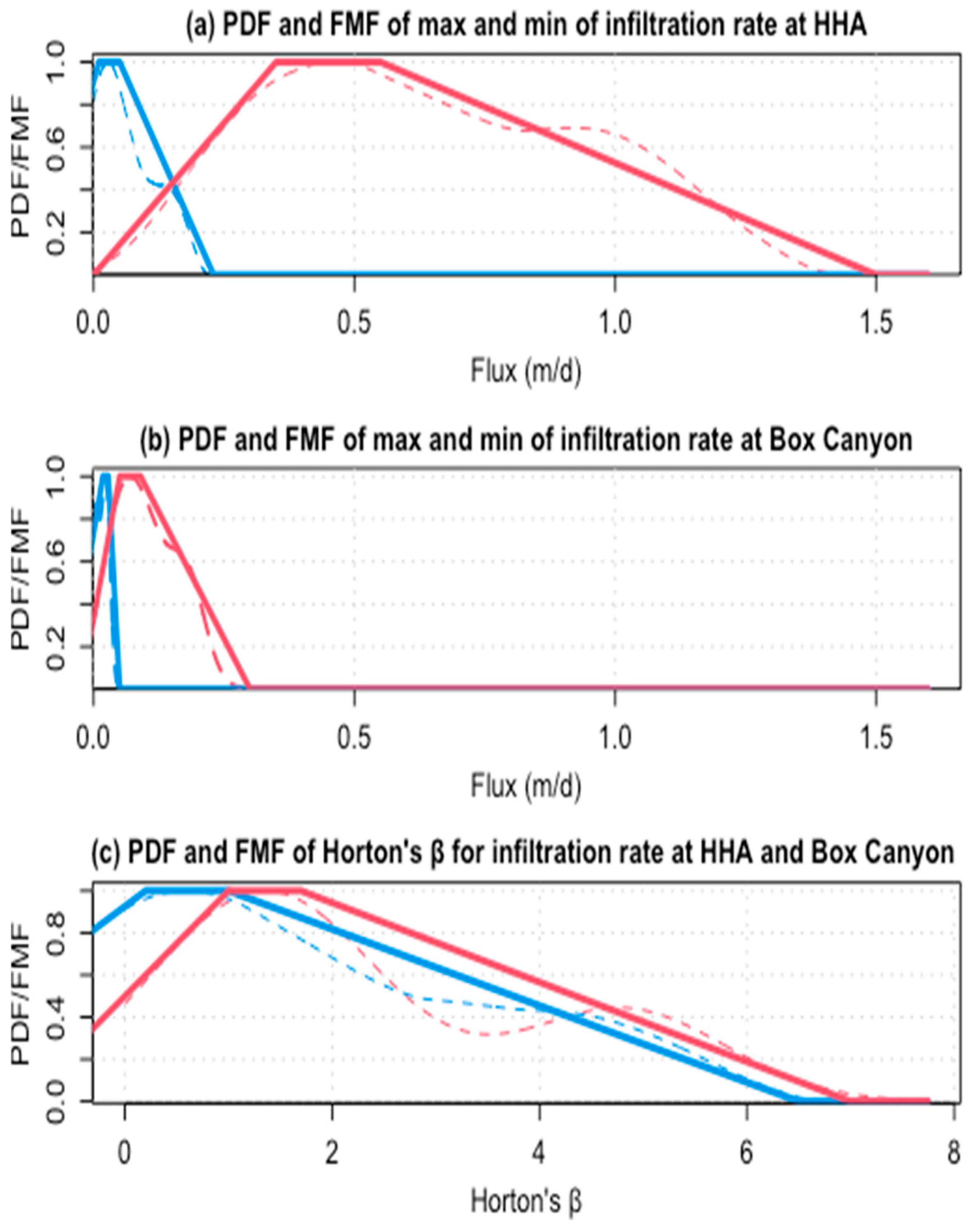
| Test | io | if | b |
|---|---|---|---|
| 96-1 | 11.01 | 0 | 0.17 |
| 97-1 | 9.96 | 2.16 | 1.32 |
| 97-2 | 17.7 | 2.7 | 4.02 |
| 97-3 | 6.74 | 1.63 | 1.17 |
| 97-4 | 4.16 | 0.63 | 0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faybishenko, B. A Concept of Fuzzy Dual Permeability of Fractured Porous Media. Water 2023, 15, 3752. https://doi.org/10.3390/w15213752
Faybishenko B. A Concept of Fuzzy Dual Permeability of Fractured Porous Media. Water. 2023; 15(21):3752. https://doi.org/10.3390/w15213752
Chicago/Turabian StyleFaybishenko, Boris. 2023. "A Concept of Fuzzy Dual Permeability of Fractured Porous Media" Water 15, no. 21: 3752. https://doi.org/10.3390/w15213752
APA StyleFaybishenko, B. (2023). A Concept of Fuzzy Dual Permeability of Fractured Porous Media. Water, 15(21), 3752. https://doi.org/10.3390/w15213752






