The Impact of the Elemental Interactions on Soil Fertility and Toxicity in the Presence of Wastewater and Biosolids: A Quantitative Evaluation
Abstract
:1. Introduction
2. Materials and Methods
- Treated Municipal Wastewater (TMWW).
- Biosolid (BSD).
- Treated Municipal Wastewater and Biosolid (TMWW + BSD).
- Fresh irrigation water (CONTROL).
2.1. Seedbed Preparation
- The surface of the soil was cleaned so as to be firm and free of residues and weeds.
- The soil was plowed carefully, disced, and worked to fine tilth so as to come in close contact with the small fescue seeds as much as possible.
- The laying out of the experimental design on the soil surface was followed, and in turn, soil sampling was followed, taking one sample from each experimental plot, collecting in total 12 samples from a soil depth of 0–30cm.
- The seed was sown by uniform hand spreading on the surface of each plot, and then covering the seeds with a layer of soil 1–1.5 cm, followed by compacting it by means of a small roller so as to secure as much as possible better contact of the seeds with the soil, to facilitate effective seed germination.
2.2. Wastewater and Biosolids
| No | Elements | Concentration |
|---|---|---|
| 1 | pH | 7.70 |
| 2 | EC (μS/cm) (*) | 429.70 |
| 3 | COD (mg/L) (*) | 49.60 |
| 4 | TC (mg/L) (*) | 57.50 |
| 5 | TN (mg/L) (*) | 12.70 |
| 6 | NH4-N (mg/L) | 12.60 |
| 7 | NO3-N (mg/L) | 0.70 |
| 8 | PO4-P (mg/L) | 3.94 |
| 9 | Ca (mg/L) | 2.84 |
| 10 | Mg (mg/L) | 26.77 |
| 11 | Fe (mg/L) | 32.50 |
| 12 | Mn (mg/L) | BDL (*) |
| 13 | Zn (mg/L) | 35.00 |
| 14 | Cu (mg/L) | 18.20 |
| 15 | Cd (mg/L) | BDL (*) |
| 16 | Co (mg/L) | 0.20 |
| 17 | Cr (mg/L) | BDL (*) |
| No | Elements | Concentration |
|---|---|---|
| 1 | NO3 (mg/kg) | 166.30 |
| 2 | Fe (mg/kg) | 72.00 |
| 3 | Zn (mg/kg) | 141.0 |
| 4 | Mn (mg/kg) | 21.60 |
| 5 | Cu (mg/kg) | 20.00 |
| 6 | Cd (mg/kg) | BDL (*) |
| 7 | Co (mg/kg) | BDL (*) |
| 8 | Cr (mg/kg) | BDL (*) |
| 9 | Ca CO3(%) | 5.55 |
2.3. Irrigation of Plants
2.4. Soil Analysis
2.5. Statistical Analysis
3. Results and Discussion
3.1. The Role of Interactions in the Ecosystem’s Function between Minerals, Nutrients, and Soil Properties
3.2. Evaluation of the Interactions Contribution to Metals and Nutrients
3.3. Contribution of Interactions in Macro and Micronutrients
3.4. Interactive Regression Equations between Heavy Metals and Nutrients in the Experimental Soil of Festuca arundinacea Schreb
- (i)
- Regression equations of Nitrogen contribution (N)
(R2 = 0.40 sig = 0.029 N = 12)
- (ii)
- Regression equations of phosphorus contribution (P)
(R2 = 0.66 sig = 0.008 N = 12)
(R2 = 0.70 sig = 0.001 N = 12)
(R2 = 0.53 sig = 0.0034 N = 12)
(R2 = 0.75 sig = 0.002 N = 12)
(R2 = 0.53 sig = 0.033 N = 12)
- (iii)
- Regression equations of potassium, contribution (K)
(R2 = 0.54 sig = 0.029 N = 12)
(R2 = 0.60 sig = 0.01 N = 12)
(R2 = 0.96 sig < 0.001 N = 12)
(R2 = 0.59 sig = 0.019 N = 12)
(R2 = 0.64 sig = 0.032 N = 12)
(R2 = 0.85 sig < 0.001 N = 12)
(R2 = 0.57 sig = 0.004 N = 12)
(R2 = 0.41 sig = 0.045 N = 12)
- (iv)
- Regression equations of Ca contribution (Ca)
(R2 = 0.50 sig = 0.047 N = 12)
(R2 = 0.57 sig = 0.01 N = 12)
(R2 = 0.63 sig = 0.010 N = 12)
(R2 = 0.54 sig = 0.035 N = 12)
(R2 = 0.54 sig = 0.031 N = 12)
- (v)
- Regression equations of Magnesium contribution (Mg)
(R2 = 0.55 sig = 0.029 N = 12)
(R2 = 0.60 sig = 0.016 N = 12)
(R2 = 0.70 sig = 0.004 N = 12)
(R2 = 0.64 sig = 0.010 N = 12)
(R2 = 0.52 sig = 0.036 N = 12)
(R2 = 0.57 sig = 0.005 N = 12)
(R2 = 0.50 sig = 0.003 N = 12)
- (vi)
- Regression equations of Sodium contribution (Na)
(R2 = 0.92 sig < 0.001 N = 12)
(R2 = 0.63 sig = 0.011 N = 12)
(R2 = 0.65 sig = 0.010 N = 12)
(R2 = 0.63 sig = 0.015 N = 12)
(R2 = 0.61 sig = 0.015 N = 12)
- (vii)
- Regression equations of iron contribution (Fe)
(R2 = 0.55 sig = 0.006 N = 12)
(R2 = 0.64 sig = 0.010 N = 12)
(R2 = 0.67 sig = 0.006 N = 12)
(R2 = 0.84 sig = 0.001 N = 12)
(R2 = 0.78 sig = 0.001 N = 12)
(R2 = 0.92 sig < 0.001 N = 12)
(R2 = 0.81 sig < 0.001 N = 12)
- (viii)
- Regression equations of Zinc contribution (Zn)
(R2 = 0.72 sig = 0.0013 N = 12)
- (ix)
- Copper contribution equations (Cu)
(R2 = 0.41 sig = 0.025 N = 12)
(R2 = 0.37 sig = 0.036 N = 12)
(R2 = 0.66 sig = 0.008 N = 12)
(R2 = 0.81 sig < 0.001 N = 12)
(R2 = 0.64 sig = 0.012 N = 12)
(R2 = 0.85 sig < 0.001 N = 12)
(R2 = 0.77 sig = 0.001 N = 12)
- (x)
- Regression equations of Manganese contribution (Mn)
(R2 = 0.45 sig = 0.0017 N = 12)
(R2 = 0.68 sig = 0.001 N = 12)
- (xi)
- Regression equations of Boron contribution (B)
(R2 = 0.48 sig = 0.0013 N = 12)
(R2 = 0.62 sig = 0.001 N = 12)
- The study of the above regression equations from Equations (4)–(53) shows that each group of equations includes the same dependent variable, which within the same group is a function of various metals, nutrients, or physical and chemical properties of the soil as shown in each respective regression equation. Each equation within the same group contributes a corresponding amount of the dependent variable according to its interactive orientation (synergistic or antagonistic) and consequently affects the dependent variable and, hence, the soil conditions.
3.5. Contribution of Interactions in Macro and Micronutrients in the Experimental Soil of Lactuca sativa var. Longifolia (1st Soil Sampling)
| # | Macro and Micronutrients Interacting in Soil | Average Interactive Contribution to Macro and Micronutrients (mg/kg) | Average Value in Soil Macro and Micronutrients (mg/kg) | Contribution in Interactive Macro and Micronutrients (mg/kg) | Percent Interactive Contribution (%) |
|---|---|---|---|---|---|
| 1 | N (%) | 0.132 | 0.132 | 0.00 | 0.00 |
| 2 | P(mg/kg) | 100.22 | 101.71 | 2.49 | −1.49 |
| 3 | K(mg/kg) | 124.79 | 128.36 | −2.86 | −2.29 |
| 4 | Ca(mg/kg) | 207.84 | 206.02 | 0.12 | +0.88 |
| 5 | Mg(mg/kg) | 31.54 | 30.18 | 1.36 | +4.31 |
| 6 | Zn(mg/kg) | 2.29 | 2.24 | 0.05 | +2.18 |
| 7 | Fe(mg/kg) | 20.63 | 22.77 | −2.14 | −10.37 |
| 8 | Mn(mg/kg) | 33.59 | 33.50 | 0.09 | +0.27 |
| 9 | Cu(mg/kg) | 2.50 | 2.10 | 0.40 | +16.00 |
| Experimental Soil | Elements Contributed | mg/kg Soil | Contributed Fertilizer | kg/ha |
|---|---|---|---|---|
| Fescue experiment | K | 0.80 | Potassium sulfate (50% K2O) | 7.80 |
| Mn | 0.09 | Manganese sulfate (35% Mn) | 1.00 | |
| B | 0.54 | Borax (11.5% B) | 19.60 | |
| Lettuce experiment | P | 2.49 | 0-46-0 (N-P2O5-K2O) | 57.60 |
| Ca | 0.12 | CaCO3 | 1.40 | |
| Mg | 1.36 | MgSO2 (25% Mg) | 31.3 | |
| Zn | 0.05 | ZnSO4.7H2O (25% Zn) | 0.50 | |
| Mn | 0.02 | MnSO4 (35% Mn) | 0.29 | |
| Cu | 0.40 | CuSO4 (25% Cu) | 1.86 |
3.6. Regression Equations and the Contribution of Their Interactions in Macro and Micronutrients to the Soil of Lettuce (Lactuca sativa var. Longifolia) (1st Soil Sampling)
- (i)
- Regression equations of Nitrogen contribution (N)
(R2 = 0.21 sig < 0.001 N = 48)
(R2 = 0.17 sig < 0.013 N = 48)
- (ii)
- Regression equations of phosphorus contribution (P)
(R2 = 0.48 sig < 0.001 N = 48)
(R2 = 0.29 sig < 0.001 N = 48)
(R2 = 0.59 sig < 0.001 N = 48)
(R2 = 0.77 sig < 0.001 N = 48)
(R2 = 0.68 sig < 0.001 N = 48)
(R2 = 0.81 sig < 0.001 N = 48)
(R2 = 0.40 sig < 0.001 N = 48)
(R2 = 0.75 sig < 0.001 N = 48)
- (iii)
- Regression equations of potassium contribution (K)
(R2 = 0.16 sig = 0.021 N = 48)
(R2 = 0.47 sig < 0.001 N = 48)
(R2 = 0.45 sig < 0.001 N = 48)
(R2 = 0.33 sig < 0.001 N = 48)
(R2 = 0.45 sig < 0.001 N = 48)
(R2 = 0.27 sig < 0.001 N = 48)
(R2 = 0.48 sig < 0.001 N = 48)
- (iv)
- Regression equations of calcium contribution (Ca)
(R2 = 0.10 sig < 0.001 N = 48)
(R2 = 0.13 sig = 0.048 N = 48)
(R2 = 0.53 sig < 0.001 N = 48)
(R2 = 0.50 sig < 0.001 N = 48)
(R2 = 0.43 sig < 0.001 N = 48)
(R2 = 0.50 sig < 0.001 N = 48)
(R2 = 0.29 sig < 0.001 N = 48)
(R2 = 0.62 sig < 0.001 N = 48)
- (v)
- Regression equations of Magnesium contribution (Mg)
(R2 = 0.12 sig = 0.003 N = 48)
(R2 = 0.84 sig = 0.037 N = 48)
(R2 = 0.21 sig = 0.006 N = 48)
(R2 = 0.22 sig < 0.001 N = 48)
(R2 = 0.15 sig = 0.0030 N = 48)
(R2 = 0.50 sig = 0.020 N = 48)
- (vi)
- Regression equations of Iron contribution (Fe)
(R2 = 0.32 sig < 0.001 N = 48)
(R2 = 0.33 sig < 0.001 N = 48)
(R2 = 0.69 sig < 0.001 N = 48)
(R2 = 0.65 sig < 0.001 N = 48)
(R2 = 0.50 sig < 0.001 N = 48)
(R2 = 0.57 sig = 0.001 N = 48)
(R2 = 0.67 sig = 0.001 N = 48)
(R2 = 0.34 sig < 0.001 N = 48)
- (vii)
- Regression equations of Zinc contribution (Zn)
(R2 = 0.43 sig < 0.001 N = 48)
(R2 = 0.13 sig = 0.041 N = 48)
(R2 = 0.22 sig = 0.003 N = 48)
(R2 = 0.14 sig = 0.010 N = 48)
(R2 = 0.23 sig = 0.003 N = 48)
(R2 = 0.10 sig = 0.030 N = 48)
(R2 = 0.23 sig = 0.003 N = 48)
- (viii)
- Regression equations of Manganese contribution (Mn)
(R2 = 0.23 sig = 0.003 N = 48)
(R2 = 0.46 sig < 0.001 N = 48)
(R2 = 0.48 sig < 0.001 N = 48)
(R2 = 0.45 sig < 0.001 N = 48)
(R2 = 0.55 sig < 0.001 N = 48)
(R2 = 0.52 sig < 0.001 N = 48)
(R2 = 0.48 sig < 0.001 N = 48)
(R2 = 0.14 sig < 0.031 N = 48)
(R2 = 0.26 sig < 0.001 N = 48)
(R2 = 0.15 sig < 0.030 N = 48)
(R2 = 0.20 sig < 0.007 N = 48)
(R2 = 0.31 sig < 0.001 N = 48)
- (ix)
- Regression equations of copper contribution (Cu)
(R2 = 0.32 sig < 0.001 N = 48)
(R2 = 0.18 sig = 0.013 N = 48)
(R2 = 0.16 sig = 0.019 N = 48)
(R2 = 0.11 sig = 0.048 N = 48)
(R2 = 0.28 sig < 0.001 N = 48)
(R2 = 0.25 sig = 0.003 N = 48)
(R2 = 0.61 sig < 0.001 N = 48)
(R2 = 0.41 sig = 0.019 N = 48)
(R2 = 0.67 sig < 0.001 N = 48)
- Similarly, the study of the above regression equations from Equations (54)–(120) shows that each group of equations includes the same dependent variable, which is a function of various metals, nutrients, or physical and chemical properties of the soil. Each regression equation within the same group contributes a corresponding amount of the dependent variable according to its interactive orientation (synergistic or antagonistic) and consequently affects the contribution of the dependent variable and, hence, the conditions of soil related to fertility or toxicity.
3.7. Elemental Interactions and Their Contribution in Heavy Metals to the Experimental Soil of Fescue (Festuca arundinacea Schreb)
3.7.1. Interactive Regression Equations between Heavy metals and Nutrients in the Fescue (Festuca arundinacea Schreb) Experimental Soil
- (i)
- Regression equations of zinc contribution (Zn)
(R2 = 0.72 sig = 0.0013 N = 12)
- (ii)
- Regression equations of manganese contribution (Mn)
(R2 = 0.45 sig = 0.0017 N = 12)
(R2 = 0.68 sig = 0.001 N = 12)
- (iii)
- Regression equations of copper (Cu)
(R2 = 0.41 sig = 0.025 N = 12)
(R2 = 0.37 sig = 0.036 N = 12)
(R2 = 0.66 sig = 0.008 N = 12)
(R2 = 0.82 sig < 0.001 N = 12)
(R2 = 0.64 sig = 0.012 N = 12)
- (iv)
- Regression equations of cadmium contribution (Cd)
(R2 = 0.45 sig = 0.018 N = 12)
(R2 = 0.54 sig = 0.032 N = 12)
(R2 = 0.57 sig = 0.004 N = 12)
(R2 = 0.57 sig = 0.005 N = 12)
(R2 = 0.67 sig = 0.006 N = 12)
(R2 = 0.61 sig = 0.013 N = 12)
(R2 = 0.46 sig = 0.039 N = 12)
(R2 = 0.86 sig = 0.009 N = 12)
(R2 = 0.83 sig < 0.001 N = 12)
(R2 = 0.60 sig = 0.003 N = 12)
(R2 = 0.92 sig < 0.001 N = 12)
(R2 = 0.77 sig < 0.001 N = 12)
- (v)
- Regression equations of cobalt contribution (Co)
(R2 = 0.77 sig = 0.004 N = 12)
(R2 = 0.51 sig = 0.039 N = 12)
- (vi)
- Regression equations of Nickel contribution (Ni)
(R2 = 0.45 sig = 0.016 N = 12)
(R2 = 0.55 sig = 0.027 N = 12)
(R2 = 0.63 sig = 0.011 N = 12)
(R2 = 0.89 sig < 0.001 N = 12)
(R2 = 0.69 sig < 0.001 N = 12)
(R2 = 0.92 sig < 0.001 N = 12)
(R2 = 0.98 sig < 0.001 N = 12)
- (vii)
- Regression equations of Lead contribution (Pb)
(R2 = 0.83 sig < 0.001 N = 12)
(R2 = 0.77 sig < 0.001 N = 12)
(R2 = 0.69 sig = 0.005 N = 12)
(R2 = 0.84 sig < 0.001 N = 12)
| # | Micronutrients and Heavy Metals that Interact | Contribution of Heavy Metal Interactions after the Application of Interventions (mg/kg) | Average Value of Content Soil in Metals (mg/kg) under Control | Difference Contribution of Interactions in Metals (mg/kg) | Percentage Contribution of Interactions (%) |
|---|---|---|---|---|---|
| 1 | Ζn | 1.048 | 0.495 | 0.553 | 52.76 |
| 2 | Cu | 3.289 | 2.934 | 0.355 | 10.79 |
| 3 | Mn | 7.800 | 6.35 | 1.45 | 18.59 |
| 4 | Cd | 0.026 | 0.026 | 0.00 | 0.00 |
| 5 | Co | 0.028 | 0.024 | 0.004 | 14.29 |
| 7 | Ni | 0.904 | 0.599 | 0.305 | 33.74 |
| 8 | Pb | 5.22 | 4.15 | 1.07 | 20.50 |
| Pollution indices | Mean value of pollution indices due to the contribution of Interactions | Value of soil pollution indices under Control | Difference in indices due to the contribution to interactions | Percentage contribution to indices (%) | |
| HML | 1.58 | 1.40 | 0.18 | 11.39 | |
| EPI | 0.81 | 0.31 | 0.52 | 64.20 |
| # | Interacting Heavy Metals | Contribution in Metals by the Heavy Metal Interactions (mg/kg) | Mean Level of Soil Heavy Metals (mg/kg) | The Actual Contribution by the Heavy Metal Interactions (mg/kg) | Percent (%) Contribution in Heavy Metals (mg/kg) |
|---|---|---|---|---|---|
| 1 | Zn | 2.29 | 2.24 | 0.05 | 2.18 |
| 2 | Cu | 2.50 | 2.12 | 0.38 | 15.20 |
| 3 | Mn | 33.09 | 33.50 | −0.41 | −1.24 |
| 4 | Cr | 0.054 | 0.050 | 0.004 | 7.41 |
| 5 | Co | 0.096 | 0.050 | 0.046 | 47.20 |
| 6 | Ni | 0.361 | 0.132 | 0.229 | 63.43 |
| 7 | Pb | 4.19 | 3.27 | 0.92 | 21.96 |
| Pollution Index | Mean contribution to the indices due to interactions | Value of indices under Control | Differences due to interactions contribution | Percent contribution to indices (%) | |
| HML | 1.71 | 1.70 | 0.01 | 0.58 | |
| EPI | 1.06 | 0.74 | 0.32 | 30.19 |
3.7.2. Regression Equations between Heavy Metals and Plant Nutrients and Their Contribution in Heavy Metals to the Experimental Soil of Lettuce (Lactuca sativa var. Longifolia) (1st Soil Sampling)
3.7.3. Regression Equations Contributing Exclusively Interactive Heavy Metals in the Soil of the Lactuca sativa Lettuce Experiment
- (i)
- Regression equations of Zinc contribution (Zn)
(R2 = 0.43 sig < 0.001 N = 48)
(R2 = 0.13 sig = 0.041 N = 48)
(R2 = 0.22 sig = 0.003 N = 48)
(R2 = 0.14 sig = 0.010 N = 48)
(R2 = 0.23 sig = 0.003 N = 48)
(R2 = 0.10 sig = 0.030 N = 48)
(R2 = 0.23 sig = 0.003 N = 48)
- (ii)
- Regression equations of Manganese contribution (Mn)
(R2 = 0.23 sig = 0.003 N = 48)
(R2 = 0.46 sig < 0.001 N = 48)
(R2 = 0.47 sig < 0.001 N = 48)
(R2 = 0.45 sig < 0.001 N = 48)
(R2 = 0.56 sig < 0.001 N = 48)
(R2 = 0.52 sig < 0.001 N = 48)
(R2 = 0.48 sig < 0.001 N = 48)
(R2 = 0.14 sig = 0.031 N = 48)
(R2 = 0.26 sig = 0.001 N = 48)
(R2 = 0.14 sig = 0.030 N = 48)
(R2 = 0.20 sig = 0.007 N = 48)
(R2 = 0.31 sig < 0.001 N = 48)
- (iii)
- Regression equations of Copper contribution (Cu)
(R2 = 0.32 sig < 0.001 N = 48)
(R2 = 0.18 sig = 0.013 N = 48)
(R2 = 0.16 sig = 0.019 N = 48)
(R2 = 0.11 sig = 0.048 N = 48)
(R2 = 0.28 sig < 0.001 N = 48)
(R2 = 0.23 sig = 0.003 N = 48)
(R2 = 0.41 sig = 0.019 N = 48)
(R2 = 0.67 sig < 0.001 N = 48)
- (iv)
- Regression equations of Chromium contribution (Cr)
(R2 = 0.15 sig = 0.024 N = 48)
(R2 = 0.31 sig < 0.001 N = 48)
(R2 = 0.21 sig = 0.004 N = 48)
(R2 = 0.23 sig = 0.003 N = 48)
(R2 = 0.47 sig < 0.001 N = 48)
(R2 = 0.17 sig = 0.016 N = 48)
(R2 = 0.44 sig < 0.001 N = 48)
(R2 = 0.36 sig < 0.001 N = 48)
(R2 = 0.17 sig = 0.016 N = 48)
(R2 = 0.44 sig < 0.001 N = 48)
- (v)
- Regression equations of cobalt contribution (Co)
(R2 = 0.23 sig = 0.003 N = 48)
(R2 = 0.12 sig = 0.008 N = 48)
(R2 = 0.16 sig = 0.022 N = 48)
- (vi)
- Regression equations of Nickel contribution (Ni)
(R2 = 0.18 sig = 0.011 N = 48)
(R2 = 0.19 sig = 0.010 N = 48)
(R2 = 0.64 sig < 0.001 N = 48)
(R2 = 0.17 sig = 0.016 N = 48)
(R2 = 0.13 sig = 0.040 N = 48)
(R2 = 0.10 sig = 0.031 N = 48)
(R2 = 0.13 sig < 0.048 N = 48)
(R2 = 0.29 sig < 0.001 N = 48)
- (vii)
- Regression equations of lead contribution (Pb)
(R2 = 0.16 sig < 0.019 N = 48)
(R2 = 0.17 sig < 0.015 N = 48)
(R2 = 0.16 sig < 0.019 N = 48)
(R2 = 0.26 sig < 0.001 N = 48)
(R2 = 0.48 sig < 0.001 N = 48)
(R2 = 0.41 sig < 0.001 N = 48)
3.7.4. Interactions between Metals and Chemical and Physical Soil Properties and Their Contribution to the Characteristics of Festuca arundinacea Schreb Experimental Soil
- Increase of very fineS by +27.83%.
- Si by +0.12%,
- OM by +0.49%, and calcium carbonate by +0.41%.
| # | Soil Properties | Effect of Interactions on the Mean Soil Properties Values | Mean Value of Soil Properties | Contribution of Interactions to Soil Properties | Percent Change of Soil Properties |
|---|---|---|---|---|---|
| 1 | Sand (S) (%) | 46.30 | 18.47 | +27.83 | +60.11 |
| 2 | Silt (Si) (%) | 43.46 | 43.00 | +0.12 | +0.28 |
| 3 | Clay (C) (%) | 21.51 | −38.17 | −16.66 | −77.45 |
| 4 | OM (%) | 3.75 | 3.26 | +0.49 | +13.07 |
| 6 | CaCO3 (%) | 5.54 | 5.13 | +0.41 | +7.40 |
| 7 | pH(sat paste) | 7.83 | 7.94 | −0.11 | −1.41 |
3.7.5. Regression Equations between Metals and Chemical and Physical Soil Properties Related to the Festuca arundinacea Schreb Experimental Soil
- (i)
- Regression equations of fine sand contribution (S)
(R2 = 0.73 sig < 0.001 N = 12)
(R2 = 0.52 sig = 0.036 N = 12)
(R2 = 0.42 sig = 0.023 N = 12)
- (ii)
- Regression equations of sludge contribution (Si)
(R2 = 0.86 sig < 0.001 N = 12)
(R2 = 0.36 sig = 0.040 N = 12)
(R2 = 0.67 sig = 0.007 N = 12)
(R2 = 0.58 sig = 0.023 N = 12)
(R2 = 0.65 sig = 0.009 N = 12)
- (iii)
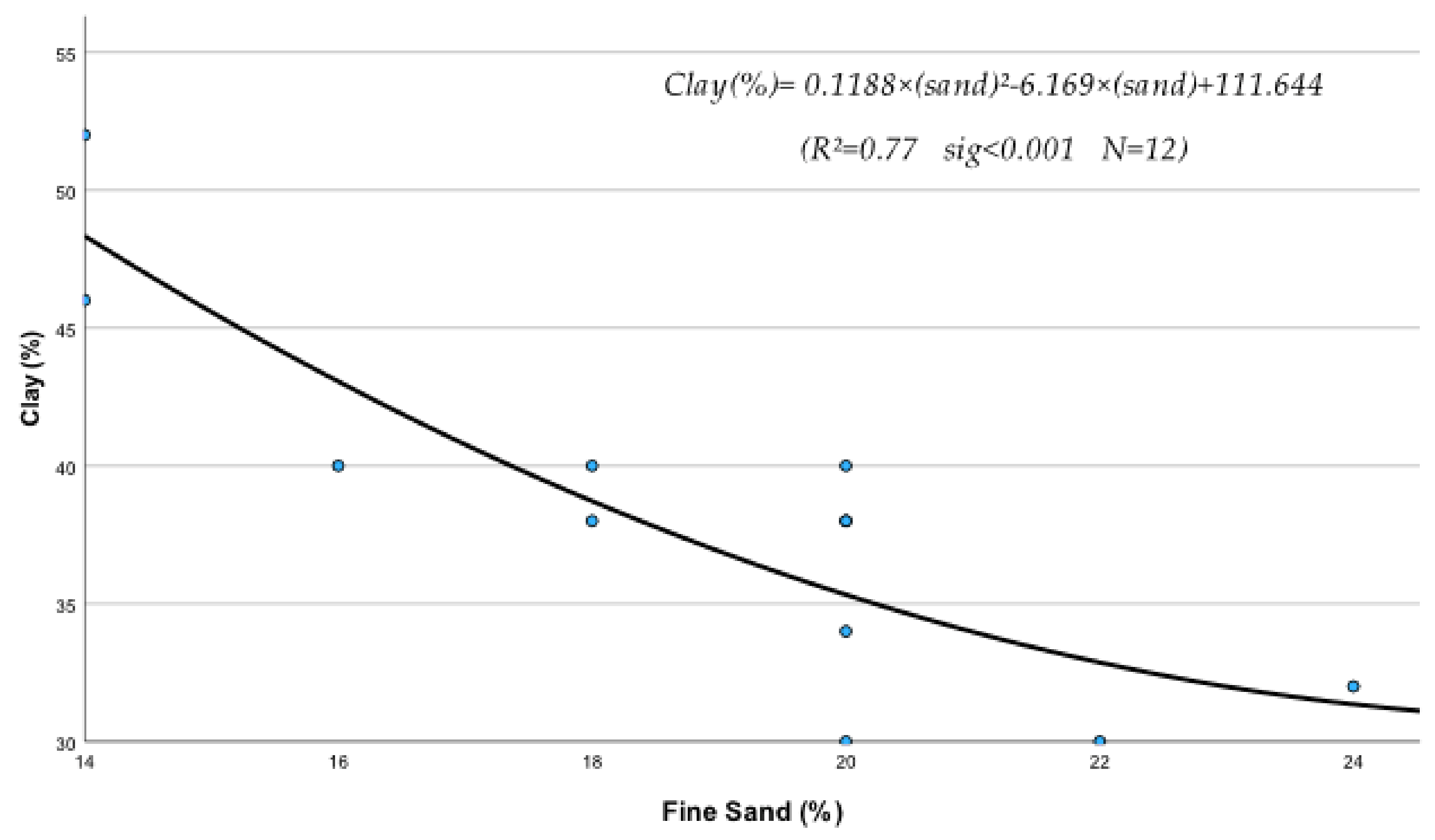
- Regression equations of clay contribution (C)
(R2 = 0.78 sig < 0.001 N = 12)
(R2 = 0.87 sig < 0.001 N = 12)
(R2 = 0.60 sig = 0.016 N = 12)
(R2 = 0.57 sig = 0.023 N = 12)
(R2 = 0.69 sig = 0.005 N = 12)
(R2 = 0.36 sig = 0.0382 N = 12)
- (iv)
- Equations of covariation of organic substance (OM)
(R2 = 0.38 sig = 0.033 N = 12)
(R2 = 0.57 sig = 0.022 N = 12)
(R2 = 0.37 sig = 0.035 N = 12)
- (v)
- Regression equations of pH contribution (pHsat paste)
(R2 = 0.66 sig = 0.008 N = 12)
(R2 = 0.86 sig < 0.001 N = 12)
(R2 = 0.69 sig = 0.005 N = 12)
(R2 = 0.53 sig = 0.075 N = 12)
(R2 = 0.59 sig = 0.019 N = 12)
- (vi)
- Regression equations of calcium carbonate contribution (CaCO3)
(R2 = 0.40 sig = 0.029 N = 12)
3.7.6. Interactions between Metals, and Physical and Chemical Properties of Soil, and Their Contribution to the Characteristics of the Lettuce (Lactuca sativa var. Longifolia) Experimental Soil
3.7.7. Regression Equations between Soil Properties with Metals, Nutrients and Soil Characteristics during 1st and 2nd Sampling of the Lettuce (Lactuca sativa var. Longifolia) Experimental Soil
Regression Equations of the 1st Soil Sampling
- (i)
- Regression equations of pH contribution (pH)
(R2 = 0.33 sig < 0.001 N = 48)
(R2 = 0.46 sig < 0.001 N = 48)
(R2 = 0.34 sig < 0.001 N = 48)
(R2 = 0.42 sig < 0.001 N = 48)
- (ii)
- Regression equations of Electrical conductivity contribution (EC)
(R2 = 0.70 sig < 0.001 N = 48)
- (iii)
- Regression equations of Organic matter contribution (OM)
(R2 = 0.25 sig = 0.002 N = 48)
(R2 = 0.17 sig = 0.014 N = 48)
(R2 = 0.57 sig < 0.001 N = 48)
(R2 = 0.39 sig = 0.001 N = 48)
(R2 = 0.30 sig < 0.001 N = 48)
(R2 = 0.32 sig < 0.001 N = 48)
- (i)
- Regression equations of pH contribution(pH)
(R2 = 0.99 sig < 0.001 N = 48)
(R2 = 0.99 sig < 0.001 N = 48)
(R2 = 0.99 sig < 0.001 N = 48)
(R2 = 0.86 sig < 0.001 N = 48)
(R2 = 0.99 sig < 0.001 N = 48)
- (ii)
- Regression equations of electrical conductivity contribution (EC)
(R2 = 0.60 sig < 0.001 N = 48)
(R2 = 0.60 sig = 0.001 N = 48)
(R2 = 0.62 sig < 0.001 N = 48)
(R2 = 0.54 sig < 0.001 N = 48)
(R2 = 0.60 sig < 0.001 N = 48)
(R2 = 0.60 sig < 0.001 N = 48)
- (iii)
- Regression equations of Organic matter contribution (OM)
(R2 = 0.12 sig = 0.016 N = 48)
(R2 = 0.12 sig = 0.017 N = 48)
(R2 = 0.13 sig = 0.043 N = 48)
(R2 = 0.17 sig = 0.016 N = 48)
(R2 = 0.21 sig = 0.001 N = 48)
(R2 = 0.59 sig < 0.001 N = 48)
(R2 = 0.12 sig = 0.017 N = 48)
(R2 = 0.30 sig < 0.001 N = 48)
(R2 = 0.32 sig = 0.001 N = 48)
4. Conclusions
- Hundreds of elemental interactions between metals, macro micronutrients, and the physical and chemical properties of soil occur in the soil environment, which contribute to heavy metals and nutrients affecting soil fertility and toxicity.
- Depending on their interactive synergistic or antagonistic orientation of the regression equations, they contribute quantitatively and affect positively or negatively their interacting dependent variable, hence influencing the function of soils.
- In the present work, the elemental interactions not only contributed to fescue and lettuce soil considerable quantities of plant nutrients. It was also possible to quantitatively evaluate them, expressed in the form of corresponding fertilizers accumulating in the soil, i.e., in the fescue experiment, 7.80 kg/ha of potassium sulfate (0-0-50) and 19.6 kg/ha of borax, while in the lettuce soil the fertilizers accumulated were: 57.6 kg/ha of supper phosphate (0-46-0); and 31.3 kg/ha magnesium sulfate (25% Mg). These fertilizer quantities could complementarily participate in soil fertility, and further improve plant growth and yields.
- However, the low interactive contribution to the soil in terms of heavy metals did cause a minimum increase in their metal concentration in both the fescue and lettuce soils, indicating low pollution indices, which suggested very low to limited soil toxicity.
- It was concluded that the elemental interactions could be a helpful method for the quantitative evaluation of metals and nutrients accumulating in soil under the reuse of wastewater and biosolids by the elemental interactions.
5. Highlights
- Elemental interactions can provide a useful tool for the evaluation of the interactive contribution to soil fertility in terms of heavy metals.
- The interactions may provide or remove nutrients and heavy metals from/to soil depending on their interactive orientation (synergistic or competitive).
- They contribute positive or negative changes to soil’s physical and chemical properties and affect its functions.
- They may also determine, to a significant extent, the fertility and toxicity of the soil by adding to soil or removing heavy metals from it, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kalavrouziotis, I.K.; Koukoulakis, P.H. Contribution of Elemental Interactions in Total Essential Nutrient and Heavy Metal Content in Cabbage under Treated Wastewater Irrigation. Plant Biosyst. Int. J. Deal. All Asp. Plant Biol. 2012, 146, 491–499. [Google Scholar] [CrossRef]
- Gola, D.; Malik, A.; Shaikh, Z.A.; Sreekrishnan, T.R. Impact of Heavy Metal Containing Wastewater on Agricultural Soil and Produce: Relevance of Biological Treatment. Environ. Process. 2016, 3, 1063–1080. [Google Scholar] [CrossRef]
- Giannakopoulos, E.; Kalavrouziotis, I.K.; Dimitrelos, H.; Koukoulakis, P.H.; Varnavas, S.P.; Papadopoulos, F. Evaluation of Interactions among Sewage Sludge Bioavailable Metals from WWTPs Using DTPA Agent. Desalinat. Water Treat. 2017, 71, 25–31. [Google Scholar] [CrossRef]
- Kalavrouziotis, I.K.; Koukoulakis, P.H. Plant Nutrition Aspects under Treated Wastewater Reuse Management. Water Air Soil Pollut. 2011, 218, 445–456. [Google Scholar] [CrossRef]
- Farman, M.; Nawaz, F.; Majeed, S.; Ahmad, K.S.; Rafeeq, R.; Shehzad, M.A.; Shabbir, R.N.; Usmani, M.M. Interplay between Selenium and Mineral Elements to Improve Plant Growth and Development. In Handbook of Bioremediation; Elsevier: Amsterdam, The Netherlands, 2021; pp. 221–236. ISBN 978-0-12-819382-2. [Google Scholar]
- Long, Y.; Peng, J. Interaction between Boron and Other Elements in Plants. Genes 2023, 14, 130. [Google Scholar] [CrossRef]
- Koukoulakis, P.; Chatzissavvidis, C.; Papadopoulos, A.; Pontikis, D. Interactions between Leaf Macronutrients, Micronutrients and Soil Properties in Pistachio (Pistacia vera L.) Orchards. Acta Bot. Croat. 2013, 72, 295–310. [Google Scholar] [CrossRef]
- Zhao, X.Q.; Shen, R.F. Aluminum–Nitrogen Interactions in the Soil–Plant System. Front. Plant Sci. 2018, 9, 807. [Google Scholar] [CrossRef]
- Seo, B.H.; Kim, H.S.; Kwon, S.I.; Owens, G.; Kim, K.R. Heavy Metal Accumulation and Mobility in a Soil Profile Depend on the Organic Waste Type Applied. J. Soils Sediments 2019, 19, 822–829. [Google Scholar] [CrossRef]
- Roivainen, P.; Makkonen, S.; Holopainen, T.; Juutilainen, J. Element Interactions and Soil Properties Affecting the Soil-to-Plant Transfer of Six Elements Relevant to Radioactive Waste in Boreal Forest. Radiat. Environ. Biophys. 2012, 51, 69–78. [Google Scholar] [CrossRef]
- Li, Y.; Liu, J.; Wang, Y.; Tang, X.; Xu, J.; Liu, X. Contribution of Components in Natural Soil to Cd and Pb Competitive Adsorption: Semi-Quantitative to Quantitative Analysis. J. Hazard. Mater. 2023, 441, 129883. [Google Scholar] [CrossRef]
- Kalavrouziotis, I.K.; Koukoulakis, P.H.; Ntzala, G.; Papadopoulos, A.H. Proposed Indices for Assessing Soil Pollution Under the Application of Sludge. Water Air Soil Pollut. 2012, 223, 5189–5196. [Google Scholar] [CrossRef]
- Papaioannou, D. Comparative Investigation of Soil Pollutant Load Indices through Artificial Heavy Metal Enrichment under the Influence of Treated Wastewater. Ph.D. Thesis, Hellenic Open University, Patras, Greece, 2017. (In Greek). [Google Scholar]
- Kalavrouziotis, I.K.; Koukoulakis, P.H. Elemental Antagonism in Vegetables under Treated Municipal Wastewater. J. Plant Interact. 2010, 5, 101–109. [Google Scholar] [CrossRef]
- Jacoby, R.; Peukert, M.; Succurro, A.; Koprivova, A.; Kopriva, S. The Role of Soil Microorganisms in Plant Mineral Nutrition—Current Knowledge and Future Directions. Front. Plant Sci. 2017, 8, 1617. [Google Scholar] [CrossRef] [PubMed]
- Kalavrouziotis, I.K.; Koukoulakis, P.H.; Sakellariou-Makrantonaki, M.; Papanikolaou, C. Effects of Treated Municipal Wastewater on the Essential Nutrient Interactions in the Plant of Brassica Oleracea Var. Italica. Desalination 2009, 242, 297–312. [Google Scholar] [CrossRef]
- Bolan, N.S.; Adriano, D.C.; Naidu, R.; De La Luz Mora, M.; Santiagio, M. Phosphorus-Trace Element Interactions in Soil-Plant Systems. In Agronomy Monographs; Sims, J.T., Sharpley, A.N., Eds.; American Society of Agronomy, Crop Science Society of America, and Soil Science Society of America: Madison, WI, USA, 2015; pp. 317–352. ISBN 978-0-89118-269-6. [Google Scholar]
- Maurya, A.; Barik, M.; Das, A.B. Interaction of Whey Protein Isolate and Natural Deep Eutectic Solvents: Effect on Conductivity, Surface Tension, Stability, and Flow Behaviour. J. Mol. Liq. 2022, 367, 120361. [Google Scholar] [CrossRef]
- Violante, A.; Cozzolino, V.; Perelomov, L.; Caporale, A.G.; Pigna, M. Mobility and bioavailability of heavy metals and metalloids in soil environments. J. Soil Sci. Plant Nutr. 2010, 10, 268–292. [Google Scholar] [CrossRef]
- Waliullah, R.M.; Rehan, A.I.; Awual, M.E.; Rasee, A.I.; Sheikh, C.; Salman, M.S.; Hossain, M.S.; Hasan, M.M.; Kubra, K.T.; Hasan, M.N.; et al. Optimization of Toxic Dye Removal from Contaminated Water Using Chitosan-Grafted Novel Nanocomposite Adsorbent. J. Mol. Liq. 2023, 388, 122763. [Google Scholar] [CrossRef]
- Awual, R. A Novel Facial Composite Adsorbent for Enhanced Copper(II) Detection and Removal from Wastewater. Chem. Eng. J. 2015, 266, 368–375. [Google Scholar] [CrossRef]
- Awual, R. New Type Mesoporous Conjugate Material for Selective Optical Copper(II) Ions Monitoring & Removal from Polluted Waters. Chem. Eng. J. 2017, 307, 85–94. [Google Scholar] [CrossRef]
- Awual, R. Novel Nanocomposite Materials for Efficient and Selective Mercury Ions Capturing from Wastewater. Chem. Eng. J. 2017, 307, 456–465. [Google Scholar] [CrossRef]
- Rasee, A.I.; Awual, E.; Rehan, A.I.; Hossain, M.S.; Waliullah, R.M.; Kubra, K.T.; Sheikh, M.C.; Salman, M.S.; Hasan, N.; Hasan, M.M.; et al. Efficient Separation, Adsorption, and Recovery of Samarium(III) Ions Using Novel Ligand-Based Composite Adsorbent. Surf. Interfaces 2023, 41, 103276. [Google Scholar] [CrossRef]
- Awual, R.; Khraisheh, M.; Alharthi, N.H.; Luqman, M.; Islam, A.; Karim, M.R.; Rahman, M.M.; Khaleque, A. Efficient Detection and Adsorption of Cadmium(II) Ions Using Innovative Nano-Composite Materials. Chem. Eng. J. 2018, 343, 118–127. [Google Scholar] [CrossRef]
- Sheikh, C.; Hasan, M.M.; Hasan, M.N.; Salman, M.S.; Kubra, K.T.; Awual, M.E.; Waliullah, R.M.; Rasee, A.I.; Rehan, A.I.; Hossain, M.S.; et al. Toxic Cadmium(II) Monitoring and Removal from Aqueous Solution Using Ligand-Based Facial Composite Adsorbent. J. Mol. Liq. 2023, 389, 122854. [Google Scholar] [CrossRef]
- Bouyoucos, G.J. A Recalibration of the Hydrometer Method for Making Mechanical Analysis of Soils. Agron. J. 1951, 43, 434–438. [Google Scholar] [CrossRef]
- Gee, G.W.; Bauder, J.W. Particle-Size Analysis. In Methods of Soil Analysis: Part 1 Physical and Mineralogical Methods; Klute, A., Ed.; SSSA Book Series; Soil Science Society of America, American Society of Agronomy: Madison, WI, USA, 2018; pp. 383–411. ISBN 978-0-89118-864-3. [Google Scholar]
- Miller, J.; Curtin, D. Electrical Conductivity and Soluble Ions. In Soil Sampling and Methods of Analysis, 2nd ed.; Carter, M., Gregorich, E., Eds.; CRC Press: Boca Raton, FL, USA, 2007; ISBN 978-0-8493-3586-0. [Google Scholar]
- Jackson, M.L. Soil Chemical Analysis; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 1958. [Google Scholar]
- Nelson, D.W.; Sommers, L.E. Total Carbon, Organic Carbon, and Organic Matter. In Methods of Soil Analysis: Part 3 Chemical Methods; Sparks, D.L., Page, A.L., Helmke, P.A., Loeppert, R.H., Soltanpour, P.N., Tabatabai, M.A., Johnston, C.T., Sumner, M.E., Eds.; SSSA Book Series; Soil Science Society of America, American Society of Agronomy: Madison, WI, USA, 2018; pp. 961–1010. ISBN 978-0-89118-866-7. [Google Scholar]
- Schumacher, B.A. Methods for the Determination of Total Organic Carbon (Toc) in Soils and Sediments; U.S. Environmental Protection Agency: Washington, DC, USA, 2002; EPA/600/R-02/069 (NTIS PB2003-100822); p. 25.
- Olsen, S.R. Estimation of Available Phosphorus in Soils by Extraction with Sodium Bicarbonate; U.S. Department of Agriculture: Washington, DC, USA, 1954.
- Lanyon, L.E.; Heald, W.R. Magnesium, Calcium, Strontium, and Barium. In Agronomy Monographs; Page, A.L., Ed.; American Society of Agronomy, Soil Science Society of America: Madison, WI, USA, 2015; pp. 247–262. ISBN 978-0-89118-977-0. [Google Scholar]
- Ntzala, G. Investigation on the pollution degree of soil with treated municipal wastewater reuse and sludge and their impact on soils and on Lettuce (Lactuca sativa, L. var Longifolia). Master’s Thesis, University of Ioannina, Ioannina, Greece, 2011. (In Greek). [Google Scholar]
- Olaniran, A.; Balgobind, A.; Pillay, B. Bioavailability of Heavy Metals in Soil: Impact on Microbial Biodegradation of Organic Compounds and Possible Improvement Strategies. Int. J. Mol. Sci. 2013, 14, 10197–10228. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Cai, G.; Gu, J.; Tan, Y.; Chen, C.; Yin, Z. Effect of Clay on Internal Erosion of Clay-Sand-Gravel Mixture. Adv. Civ. Eng. 2020, 2020, 8869289. [Google Scholar] [CrossRef]


| Treatments | Replications (kg/ha) | Mean (kg/ha) | ||
|---|---|---|---|---|
| Ι | ΙΙ | ΙΙΙ | ||
| CONTROL | 30.00 | 29.00 | 31.00 | 30.00 |
| TMWW | 37.00 | 38.00 | 38.00 | 37.70 |
| TMWW + BSD | 82.00 | 80.00 | 79.00 | 80.33 |
| BSD | 62.00 | 67.00 | 71.00 | 67.70 |
| Elements | TMWW | TMWW + BSD | BSD | CONTROL | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | StdDev | Mean | StdDev | Mean | StdDev | Mean | StdDev | |
| pH | 7.80 | 0.02 | 7.79 | 0.05 | 7.72 | 0.11 | 7.83 | 0.01 |
| EC (mS/cm) | 0.92 | 0.17 | 0.88 | 0.14 | 1.18 | 0.47 | 0.79 | 0.13 |
| OM (%) | 3.42 | 0.07 | 2.62 | 0.58 | 3.56 | 0.60 | 3.45 | 0.58 |
| CaCO3 (%) | 8.77 | 4.21 | 4.83 | 6.33 | 3.33 | 2.02 | 5.13 | 5.30 |
| NO3 (mg/kg) | 29.32 | 7.68 | 27.18 | 4.23 | 36.20 | 5.70 | 27.89 | 13.91 |
| NO3-N (mg/kg) | 6.62 | 1.73 | 6.14 | 0.96 | 8.17 | 1.29 | 6.30 | 3.14 |
| P (mg/kg) | 18.22 | 1.51 | 15.33 | 1.14 | 25.59 | 10.67 | 16.65 | 2.20 |
| K (mg/kg) | 753.22 | 46.28 | 657.28 | 37.42 | 615.13 | 224.63 | 716.73 | 97.30 |
| Mg (mg/kg) | 561.26 | 49.72 | 502.10 | 29.67 | 479.49 | 146.84 | 525.17 | 80.63 |
| Ca (mg/kg) | 8574.43 | 307.50 | 7794.23 | 982.89 | 8442.61 | 1867.97 | 8626.04 | 701.70 |
| Fe (mg/kg) | 32.84 | 2.00 | 25.59 | 9.24 | 30.44 | 15.67 | 25.09 | 9.92 |
| Zn (mg/kg) | 1.56 | 1.85 | 0.74 | 0.19 | 1.42 | 1.03 | 0.48 | 0.07 |
| Mn (mg/kg) | 6.96 | 0.55 | 6.98 | 0.82 | 7.35 | 0.82 | 6.37 | 0.47 |
| Cu (mg/kg) | 3.59 | 0.12 | 2.86 | 0.51 | 3.35 | 0.66 | 2.93 | 0.84 |
| B (mg/kg) | 1.41 | 0.52 | 1.32 | 0.33 | 1.48 | 0.65 | 1.22 | 0.39 |
| Na (mg/kg) | 226.26 | 51.55 | 164.12 | 19.01 | 176.22 | 75.16 | 189.22 | 89.64 |
| Cd (mg/kg) | 0.0303 | 0.0012 | 0.0217 | 0.0064 | 0.0270 | 0.0085 | 0.0250 | 0.0053 |
| Co (mg/kg) | 0.0230 | 0.0062 | 0.0193 | 0.0015 | 0.0203 | 0.0032 | 0.0177 | 0.0015 |
| Cr (mg/kg) | 0.0074 | 0.0005 | 0.0071 | 0.0000 | 0.0074 | 0.0005 | 0.0081 | 0.0017 |
| Ni (mg/kg) | 0.7217 | 0.0641 | 0.5517 | 0.1348 | 0.6733 | 0.2057 | 0.5990 | 0.1216 |
| Pb (mg/kg) | 1.8353 | 0.1903 | 1.4010 | 0.3312 | 1.5540 | 0.2998 | 1.4523 | 0.2812 |
| # | Macro and Micronutrients Interacting in Soil | Average Interactive Contribution in Macro and Micronutrients (mg/kg) (a) | Average Value in Soil Macro and Micronutrients (mg/kg) (b) | Contribution in Interactive Macro and Micronutrients (mg/kg) (c) | Percent Interactive Contribution (%) (d) |
|---|---|---|---|---|---|
| 1 | NO3 | 30.15 | 30.15 | 0.00 | 0.00 |
| 2 | P | 14.33 | 18.98 | −0.200 | −1.39 |
| 3 | K | 686.39 | 685.59 | 0.80 | +0.12 |
| 4 | Mg | 378.33 | 517.00 | −138.67 | −36.65 |
| 5 | Ca | 8359.22 | 8359.33 | −0.11 | −0.001 |
| 6 | Cu | 2.32 | 3.19 | −0.87 | −37.50 |
| 7 | Mn | 7.00 | 6.92 | 0.088 | +1.26 |
| 8 | Zn | 1.05 | 1.05 | 0.00 | 0.00 |
| 9 | B | 1.90 | 1.36 | 0.54 | +28.42 |
| Physical and Chemical Soil Properties | Effect of Interactions on the Mean Level of Soil Properties | Mean Soil Properties Level | Actual Contribution of Interaction to Soil Properties | Percent Changes of Soil Properties Level |
|---|---|---|---|---|
| 1st Soil sampling | ||||
| pH | 5.61 | 5.62 | −0.01 | −0.18 |
| EC (S/cm) | 4.08 | 0.91 | 3.17 | +77.70 |
| OM (%) | 1.66 | 1.65 | 0.01 | +0.60 |
| 2nd Soil sampling | ||||
| pH | 5.61 | 5.62 | −0.01 | −0.18 |
| EC (S/cm) | 3.00 | 0.80 | 2.20 | +73.33 |
| OM (%) | 1.66 | 1.65 | 0.01 | +0.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koukoulakis, P.H.; Kanatas, P.; Kyritsis, S.S.; Ntzala, G.; Kalavrouziotis, I.K. The Impact of the Elemental Interactions on Soil Fertility and Toxicity in the Presence of Wastewater and Biosolids: A Quantitative Evaluation. Water 2023, 15, 3743. https://doi.org/10.3390/w15213743
Koukoulakis PH, Kanatas P, Kyritsis SS, Ntzala G, Kalavrouziotis IK. The Impact of the Elemental Interactions on Soil Fertility and Toxicity in the Presence of Wastewater and Biosolids: A Quantitative Evaluation. Water. 2023; 15(21):3743. https://doi.org/10.3390/w15213743
Chicago/Turabian StyleKoukoulakis, Prodromos H., Panos Kanatas, Spyridon S. Kyritsis, Georgia Ntzala, and Ioannis K. Kalavrouziotis. 2023. "The Impact of the Elemental Interactions on Soil Fertility and Toxicity in the Presence of Wastewater and Biosolids: A Quantitative Evaluation" Water 15, no. 21: 3743. https://doi.org/10.3390/w15213743
APA StyleKoukoulakis, P. H., Kanatas, P., Kyritsis, S. S., Ntzala, G., & Kalavrouziotis, I. K. (2023). The Impact of the Elemental Interactions on Soil Fertility and Toxicity in the Presence of Wastewater and Biosolids: A Quantitative Evaluation. Water, 15(21), 3743. https://doi.org/10.3390/w15213743







