Abstract
Accurate runoff prediction plays a pivotal role in facilitating effective watershed management and the rational allocation of water resources. Given the inherent challenges posed by the nonlinear and nonstationary nature of runoff sequences, this study introduces a novel coupled model, combining complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN), variational mode decomposition (VMD), long short-term memory (LSTM), and Informer techniques for monthly runoff prediction at the Wulong hydrological station of the Yangtze River Basin from 1973 to 2022. In addition, by comparing the prediction results of the traditional statistical model, which is the seasonal exponential smoothing model, with those of the machine learning model, the prediction accuracy of the machine learning model was found to be much higher than that of the traditional statistical mode. And the coupled model of secondary decomposition and secondary prediction was compared with other types of coupled models, such as one decomposition and one prediction. The CEEMDAN-VMD-LSTM-Informer model exhibited superior performance, as evidenced by an NSE value of 0.997, MAE of 1.327 × 108 m3, MAPE of 2.57%, and RMSE of 2.266 × 108 m3. The combined model proposed in this paper has the highest prediction accuracy, rendering it suitable for long-time series prediction. Accurate runoff prediction plays a pivotal role in facilitating effective watershed management and the rational allocation of water resources.
1. Introduction
Runoff prediction holds a pivotal role within the context of water resource management, serving as the foundational data for formulating operational strategies for water resource systems [1]. Its applications extend widely, encompassing critical areas such as drought mitigation, flood control, reservoir management, and equitable water resource allocation [2]. Nevertheless, escalating challenges including environmental degradation, inefficient industrial and agricultural water usage, and water contamination are exacerbating, placing increasing strain on water resources that underpin sustainable socio-economic and ecological development [3]. Therefore, the need for runoff prediction has become imperative [4]. The Yangtze River Basin, which spans approximately 20% of the nation’s land area, ranks as the world’s most populous basin [5]. However, within the context of global climate shifts, human activities are increasingly influencing the hydrological cycle processes within the basin [6]. Consequently, river runoff within the basin is perpetually in a state of flux, beset by issues like intermittent streamflows, excessive groundwater exploitation, and deteriorating water quality [7]. These challenges pose substantial obstacles to both the ecological environment and the sustainable socio-economic development of the region [8,9]. Hence, a systematic examination of the runoff evolution patterns in the Yangtze River and the development of sound predictive models have become imperative. The research findings serve as a dependable foundation for the judicious management and efficient utilization of water resources within the Yangtze River Basin and the construction of water-related infrastructure projects. Furthermore, they offer valuable insights for informing socio-economic development endeavors in the upper reaches of the Yangtze River and environmental conservation initiatives [10].
In recent decades, the relentless advancement of computer information technology and hydrological prediction theory has led to a proliferation of novel runoff prediction models proposed by scholars, thereby continually enhancing the theoretical framework of runoff prediction [11]. These runoff prediction models can be broadly categorized into two main approaches: process-driven models and data-driven modeling methods [12]. Process-driven models aim to simulate the intricate process of runoff formation, offering a simplified representation of the complex natural water cycle [13]. Prominent examples of process-driven models include the Xin’anjiang model [14], the soil and water assessment tool (SWAT) model [15], the soil conservation service (SCS) model [16], and the Hydrologiska Byråns Vattenbalansavdelning (HBV) model [17]. However, process-driven modeling necessitates extensive data inputs, accounting for various factors and processes influencing runoff formation, often entailing complex regional climatic constraints [18]. The applicability of these models varies across different watersheds and poses challenges in parameter determination. In contrast, data-driven models do not delve into the physical hydrological mechanisms or the hydrological movement processes. Instead, they primarily use predictors as model input data and predict runoff elements as output results, employing optimal algorithms to simulate the relationships between independent and dependent variables [19]. Data-driven models find widespread application in medium- and long-term runoff prediction and can be classified into two main categories: statistical models and artificial intelligence models [20]. In early runoff prediction research, statistical models like autoregressive (AR), autoregressive moving average (ARMA), and autoregressive integrated moving average (ARIMA) were extensively employed [21]. However, these statistical models require the assumption of a linear relationship between input and output, rendering them less effective for modeling nonlinear runoff sequences. Consequently, as computer technology research advances, machine learning models such as artificial neural networks (ANNs), support vector machines (SVMs), LSTM, and Informer have gained significant traction in runoff prediction due to their capacity to handle nonsmooth, nonlinear sequences effectively [22,23].
Nonetheless, it is essential to acknowledge that each modeling method possesses distinct characteristics and applicable conditions, rendering a single model inadequate for accurately predicting nonstationary and complex runoff sequences. Consequently, the pursuit of combined modeling has emerged as a prominent direction in the evolution of runoff prediction methodologies [24]. The advent of wavelet transform and Hilbert–Huang theory has significantly propelled advancements in hydrological prediction research [25]. These developments have introduced a novel concept of integrating runoff decomposition techniques with prediction models, giving rise to the “decomposition-prediction-reconstruction” framework within combined prediction methods. This approach hinges on employing decomposition algorithms to break down the original sequence into multiple subsequences, mitigating their inherent nonlinearity and non-smoothness [26]. Subsequently, these subsequences are incorporated into subsequent models, with the overarching objective of enhancing prediction accuracy. It is worth noting that the combination models employing the “decomposition-prediction-reconstruction” paradigm have consistently yielded more satisfactory results compared to single-method approaches. However, it is important to address some limitations of this model. Notably, the high-frequency component resulting from the decomposition process is characterized by pronounced fluctuations and substantial absolute values [27]. As a consequence, the prediction accuracy of this high-frequency component remains somewhat inadequate, potentially exerting a substantial influence on the overall prediction performance for the entire runoff sequence [28].
To address the challenges, in this study, we integrated the CEEMDAN-VMD-LSTM-Informer model and selected the first 75% of the sample as the training set and the last 25% as the verification set to explore the prediction accuracy of the model. Firstly, the original monthly runoff sequence underwent preprocessing with CEEMDAN, resulting in a set of intrinsic mode functions along with a residual component. Secondly, VMD was employed to decompose the highest-frequency components; the components of the first decomposition were predicted by Informer, and the components of the second decomposition were predicted by LSTM. Thirdly, the final prediction was achieved by summing the prediction results of these components. Fourthly, we used the expert modeler in SPSS 26to determine the traditional statistical prediction model and calculate the prediction results of the seasonal exponential smoothing method. Finally, a comparative analysis of the model’s prediction accuracy was performed in comparison to EEMD-VMD-LSTM-Informer, CEEMDAN-LSTM-Informer, CEEMDAN-LSTM, EMD-LSTM models, and the seasonal exponential smoothing method. This rigorous evaluation aims to affirm the model’s reliability and effectiveness in predicting nonstationary and nonlinear runoff sequences.
2. Materials and Methods
2.1. Decomposition–Prediction Model
2.1.1. CEEMDAN
Empirical mode decomposition (EMD) is a valuable technique employed for decomposing signals into several intrinsic mode functions (IMFs) of varying frequencies, accompanied by a residual component. It exhibits notable strengths in handling nonstationary signals [29]. However, it also exhibits certain inherent limitations: 1. Endpoint Effects: EMD relies on cubic spline interpolation to establish upper and lower envelopes during the sifting process. Any errors occurring at the signal endpoints may accumulate as the sifting iterations progress, leading to inaccuracies in the decomposition. 2. Mode Mixing: Mode mixing arises when an IMF encompasses significantly distinct characteristic time scales or when similar time scales are distributed across different IMFs. This phenomenon can result in the overlap of waveforms between neighboring IMFs, causing interference and making interpretation challenging [30]. To address the limitations of EMD, Wu et al. introduced ensemble empirical mode decomposition (EEMD). EEMD involves the addition of Gaussian white noise to the signal prior to performing EMD decomposition. White noise, characterized by a uniform frequency distribution and zero mean, prompts the signal to adapt to scales that best match the characteristics of the added noise. Across multiple iterations, the white noise gradually dissipates as the decomposition advances, somewhat alleviating the mode mixing issue. However, it also introduces increased computational complexity [31]. Building upon the foundation of EEMD, Torres et al. proposed the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN). This method effectively addresses the limitations of EEMD while significantly reducing computational demands, thereby enhancing data integrity [32]. The implementation of CEEMDAN involves the following steps:
- (1)
- The signal , with the addition of adaptive white noise , is decomposed using the EMD algorithm to obtain the first IMF component:
- (2)
- The first residual component signal is calculated:
- (3)
- are the k IMF components generated by EMD decomposition, and is decomposed until the first IMF component is decomposed, then the second IMF component is calculated:
Then the second residual component is calculated:
- (4)
- Repeat step (3) to obtain the k-th and the residual component :
- (5)
- Continue to perform step (4) until the residual signal cannot be decomposed further; that is, there are no more than two extreme points of the residual signal. At the end of the algorithm, there are K inherent modes, and the final residual signal is:
By adjusting the noise amplitude , it is possible to select different signal-to-noise ratios (SNRs) at each stage and achieve an adaptive decomposition process. The flowchart of the CEEMDAN algorithm is shown in Figure 1.
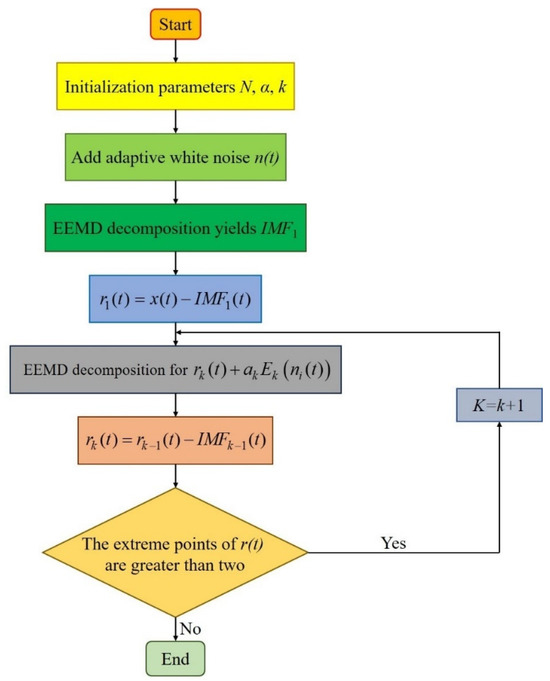
Figure 1.
Flowchart of the CEEMDAN algorithm.
2.1.2. VMD
VMD is an innovative technique for signal decomposition and estimation, particularly well-suited for the decomposition of runoff sequences into distinct variational modes (VMs). VMD operates on the premise that each VM possesses a finite bandwidth with distinct center frequencies. Moreover, it assumes that each VM has an exceedingly narrow bandwidth within the spectrum, thus minimizing the cumulative estimated bandwidth across all VMs [33]. The VMD method employs an alternating direction multiplier method to iteratively update each VM and its associated center frequency. This process gradually aligns each VM with its fundamental frequency band, ultimately extracting each VM and its corresponding center frequency. The specific algorithmic procedure unfolds as follows:
- (1)
- Using the central frequency observation method to determine the number of variational modes (VMs) extracted by VMD, let . Employ VMD for a secondary decomposition of IMF1. When , the center frequencies of the VMD-extracted modes are close to 0, then is the final selected number of modes.
- (2)
- For the highest frequency component within the IMF components, the Hilbert transform is applied to obtain the analytical signal of the original mode, which yields the one-sided spectrum.where is the unit pulse function; j represents an imaginary unit; is the r-th mode; and represents convolution.
- (3)
- Shift the spectrum of each mode to the baseband by adjusting the estimated center frequencies of the entire using the multiplication of by , bringing all the modes to the fundamental frequency band.
- (4)
- Utilize the constrained variational model to determine the bandwidth of each mode component.where is the angular frequency of each mode; is the highest frequency component to be decomposed twice; and means to take the partial derivative of t.
- (5)
- By introducing the quadratic penalty factor and the Lagrange multiplier operator , the optimal solution of the constrained variational model can be obtained, resulting in the optimal mode. The quadratic penalty factor ensures signal reconstruction accuracy, while the Lagrange multiplier operator reinforces the constraints.
2.1.3. LSTM
Recurrent neural networks (RNNs) are a type of neural network designed specifically for handling sequential data. This category includes simple RNNs as well as long short-term memory networks (LSTMs) [34]. RNNs are commonly used in training for time series prediction tasks but often encounter the issue of vanishing gradients. In the backpropagation process of RNNs, chain rule derivatives are used. As the sequence length grows, the number of derivative calculations also increases. If the derivative of the activation function is less than 1, a multiplication of many values smaller than 1 will cause the gradient to approach zero, resulting in the vanishing gradient problem. Conversely, if the derivative is greater than 1, the gradient increases exponentially, leading to the exploding gradient problem. This issue makes it challenging for RNNs to capture long-term dependencies in data, limiting their training and application. LSTM, a variant of RNNs, addresses these problems. LSTMs incorporate memory cells and unique gating structures, which greatly mitigate the issues of vanishing and exploding gradients commonly observed in RNNs [35]. Consequently, LSTMs have found widespread use in time series prediction tasks. LSTMs consist of a series of units arranged sequentially, with each unit containing an input gate, an output gate, a forget gate, and a memory cell. The specific structure is illustrated in Figure 2.
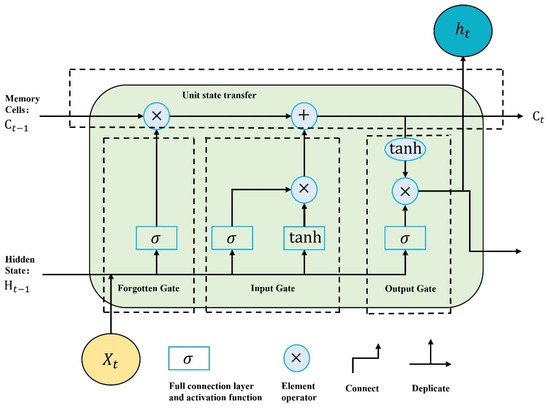
Figure 2.
LSTM model structure.
The exact calculation process is as follows:
where denotes the current input; and denote the output of the hidden layer at time and , respectively; and denote the cell state at time and ; , , and denote the output of the forgetting gate, input gate, and output gate at time , respectively; , , , and denote the weight vectors; , , , and denote the bias vectors; and and are the sigmoid function and the hyperbolic tangent function.
2.1.4. Informer
The Informer stands as an advanced deep neural network model expressly designed for the intricate task of long-time series prediction. It is meticulously engineered to construct a deep hierarchical network, replete with an attention mechanism meticulously crafted to capture dependencies inherent in lengthy time series data [36]. The model’s workflow commences with the preprocessing of input data into the requisite format, followed by a rigorous training regimen. The Informer model architecture can be dichotomized into two integral components: the encoder and the decoder. The encoder employs a sparse probability attention mechanism, known as ProbSparse self-attention, to engage in feature learning and mapping operations on the input data. In contrast, the decoder harnesses a masked multi-head attention mechanism, strategically employed to glean features from the masked input data. These self-attention mechanisms facilitate interplay between information assimilated by the initial two attention mechanisms. Subsequently, the model employs fully connected layers to generate the prediction target sequence in a singular step. During training, the model undertakes the crucial task of backpropagating the error between the predicted output values and the actual label values. This process serves to fine-tune the network’s parameters, progressively optimizing the model’s predictive efficacy. The comprehensive architecture encompasses multi-head sparse probability attention mechanisms, multi-head attention mechanisms, encoder layers, decoder layers, and various other components, all working in tandem to facilitate accurate long time series prediction [37]. The structural configuration is visually elucidated in Figure 3.
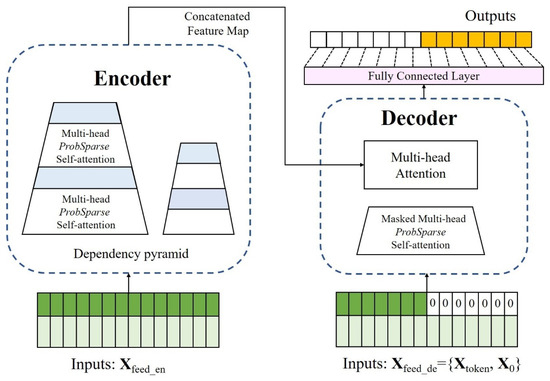
Figure 3.
The framework of Informer.
The traditional self-attention mechanism is mainly composed of a query, key, and value with the expression:
where , , , and d is the input dimension.
The definition of the i-th attention coefficient in a smoothed probability form is as follows:
Due to the sparsity of the self-attention matrix, the Kullback–Leibler scatter is used for defining the sparsity evaluation formula for the i-th query as:
By setting upper and lower bounds on , it can be approximated as:
This leads to the ProbSparse self-attention formula:
where and Q have the same size but contain only qi under sparse evaluation, i.e., the computational complexity is reduced from to .
In order to effectively save memory overhead and computation time, the distillation mechanism is introduced to halve the length of the sequence one at a time, and the expression for the distillation operation from the jth layer to the j + 1-th layer is:
where is the multi-head ProbSparse self-attention module, is a one-dimensional convolutional filter with time dimension, is the activation function, and is the maximum pooling function.
2.2. CEEMDAN-VMD-LSTM-Informer Coupled Model
This paper adopts a “Decompose-Secondary Decompose-Predict-Reconstruct” framework to build a combination prediction model based on secondary decomposition. Initially, the original runoff sequence is decomposed using CEEMDAN, resulting in a finite number of subsequences. Subsequently, the highest-frequency component, i.e., IMF1, from these subsequences is subjected to a secondary decomposition using the VMD model to obtain VM components. These VM components are then predicted using the LSTM model. The remaining components and the residual term obtained from CEEMDAN are predicted using Informer. Finally, the predictions from these components are reconstructed to obtain the ultimate prediction value. The specific calculation process is illustrated in Figure 4.
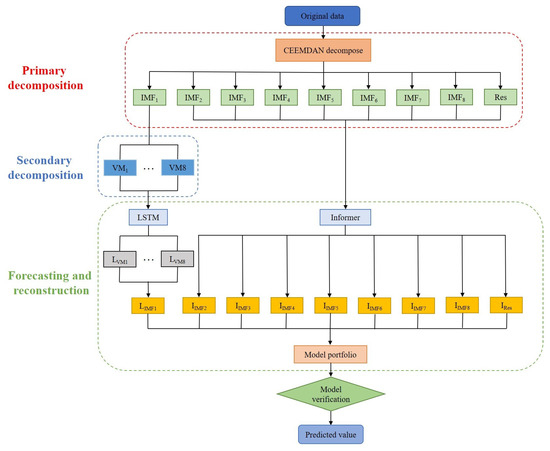
Figure 4.
Flowchart of CEEMDAN-VMD-LSTM-Informer coupling model.
2.3. Parameter Setting
Through continuous tuning, the parameters for the decomposition algorithm are determined as follows: For the CEEMDAN algorithm: Signal-to-noise ratio Nstd is set to 0.2. The number of noise additions NR is set to 100. The maximum iteration count MaxIter is set to 5000. The original runoff sequence is finally decomposed into 9 components, consisting of 8 IMF components and 1 residual component (Res). For the VMD algorithm: The number of modes K is set to 8. The penalty coefficient α is set to 1000. The convergence tolerance is set to 1 × 10−6. This paper utilizes the Bayesian optimization method to determine the hyperparameters for the LSTM and Informer models [38]. The Bayesian optimization algorithm selects a set of hyperparameters for training at each iteration within predefined parameter ranges. It adjusts the next set of parameters based on the training results. Through multiple iterations, the Bayesian optimization algorithm identifies the optimal hyperparameters to improve model performance and prediction accuracy. The hyperparameter settings for the prediction model are presented in Table 1. All the decomposition and prediction models were calculated using the MATLAB R2021a.

Table 1.
Hyperparameter configuration table for the prediction model.
2.4. Seasonal Exponential Smoothing Model
The seasonal exponential smoothing method is based on the historical data of the forecast object itself, which belongs to the category of traditional time series prediction techniques. The classical seasonal exponential smoothing model consists of the following three equations:
where , , and are smoothing coefficients; S is the level factor; B is the trend factor; C is the seasonal factor; x is the measured value; l is the length of the seasonal period; and t is the time t in the prediction period.
2.5. Evaluation Indicators
In this paper, Nash–Sutcliffe efficiency coefficient (NSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and root mean square error (RMSE) are used to evaluate the accuracy of the model, and the formulas are calculated as follows:
where and represent the predicted runoff series and its corresponding original runoff series, respectively, is the monthly average runoff volume of the original runoff series, and is the number of runoff series values.
3. Case Study
3.1. Study Area
The Yangtze River Basin encompasses three prominent geographical regions spanning Western, Central, and Eastern China, and it covers an expansive swath of approximately 20% of the nation’s total land area. The Yangtze River basin is located 24–35° N and 90–122° E (Figure 5). Originating from the Qinghai–Tibet Plateau, the Yangtze River courses eastward, ultimately emptying into the East China Sea. Along its journey, it traverses through 19 provinces, municipalities, and autonomous regions. Notably, the Yangtze River Basin intersects three distinct geographical terraces within China’s topography, yielding a region characterized by intricate terrain and diverse landscapes. This multifaceted landscape serves as a vital ecological security barrier for the nation [39]. Predominantly, the majority of the basin experiences a subtropical monsoon climate. The annual average temperature in the basin hovers around 13.0 °C. However, substantial temperature variations manifest across the basin, ranging from a milder average of 18.0 °C in the warmer downstream locales to a chillier average of −4.0 °C in the colder upstream regions. Annual average precipitation within the basin amounts to approximately 1067 mm, characterized by uneven temporal distribution throughout the year. A significant portion of this precipitation, exceeding 60%, is concentrated during the summer season. Furthermore, spatial disparities in precipitation levels are evident, with a gradual decline from east to west. Precipitation figures decrease markedly from roughly 2400 mm in the downstream areas to approximately 300 mm in the source region. This spatial and temporal irregularity in precipitation patterns serves as a primary driver for the recurrent occurrence of droughts and floods within the Yangtze River Basin.
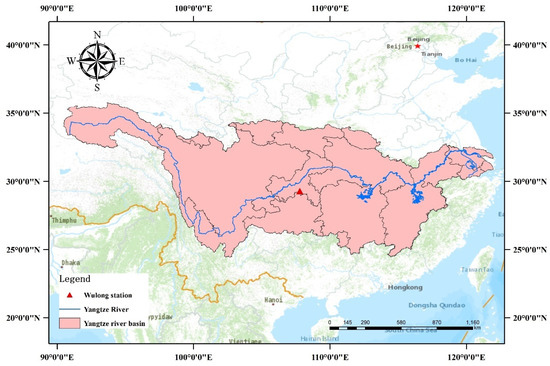
Figure 5.
Schematic diagram of the Yangtze River Basin.
3.2. Runoff Characteristics Analysis
3.2.1. Monthly Scale Analysis
The annual runoff distribution data at the Wulong hydrological station is presented in Figure 6, which offers a clear depiction of the marked unevenness in runoff throughout the year and highlights distinct seasonal variations. The period spanning from October to the following April corresponds to the non-flood season, characterized by relatively lower runoff levels. Conversely, the flood season, extending from June through October, showcases the highest runoff levels observed throughout the year, accounting for a substantial majority, exceeding 70%, of the annual total. Notably, the months of June and July stand out with the highest runoff, primarily attributed to significant precipitation [40]. Conversely, the months from December to February have the lowest runoff, during which runoff levels dip to less than 10% of the annual total. This pattern reflects the typical climatic dynamics of heightened precipitation during the summer and autumn months, contrasted with reduced precipitation during the winter and spring seasons.
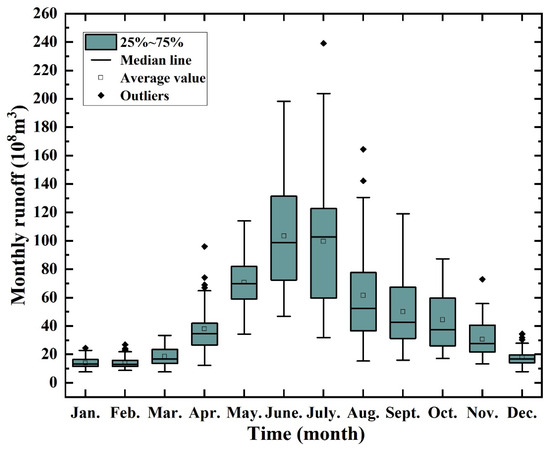
Figure 6.
Box plot of monthly runoff data.
3.2.2. Time Series Analysis
The monthly runoff data utilized in this research were meticulously sourced from the geographic remote sensing ecological network platform (www.gisrs.cn (accessed on 5 August 2023)) and were specifically procured from the Wulong hydrological station situated within the Yangtze River Basin. This dataset spans the temporal horizon from January 1973 to December 2022, encapsulating a comprehensive 600 months’ worth of monthly runoff data. In order to maintain the important time order and explore the prediction accuracy of the model, the dataset is divided into a training set and a validation set. The training set is the first 75% of the monthly scale data (1–450 values), and the last 25% of the monthly scale data is the validation set (451–600 values).
From Figure 7, it can be seen that the monthly runoff from the Wulong hydrological station from January 1973 to December 2022 showed an obvious fluctuation trend, and the time series was a nonstationary and nonrandom sequence. The sequence showed a long-term decreasing trend and a pattern with an annual cycle. In this paper, the total number of samples is 600, and we choose the maximum number of delays as 120 when calculating the autocorrelation and partial autocorrelation of the time series. And the dotted line is 450, which divides the training set from the validation set. From Figure 8, we can see that the autocorrelation diagram shows an obvious sinusoidal fluctuation rule, which is a typical feature of a nonstationary series with an annual cycle.
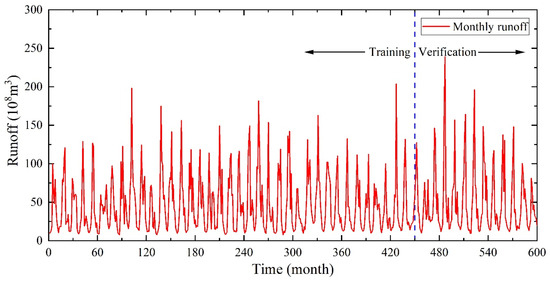
Figure 7.
Monthly runoff data of Wulong hydrological station from 1973 to 2022.
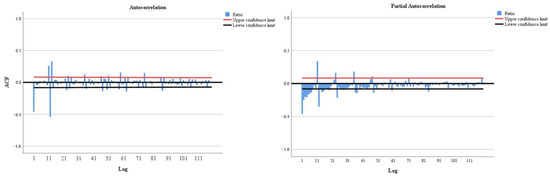
Figure 8.
Autocorrelation (left) and partial autocorrelation (right).
4. Results and Discussion
4.1. Results
4.1.1. Predicted Results of CEEMDAN-VMD-LSTM-Informer Coupled Model
CEEMDAN is an ideal nonstationary time series analysis method. Following the above steps of CEEMDAN, the monthly runoff data of the Wulong hydrological station was decomposed into eight IMFs and one Res, so as to stabilize the runoff series. The decomposition results are shown in Figure 9. IMF1 had the highest frequency, the shortest wavelength, and the largest amplitude. Compared with other components, IMF1 fluctuated more violently and was the closest to the original runoff series. The frequency of IMF2~IMF6 gradually decreased, and the wavelength gradually became longer, showing a certain period, and the fluctuation regularity was gradually prominent. The frequency of IMF7, IMF8, and Res was the least, and the fluctuation degree was the weakest.
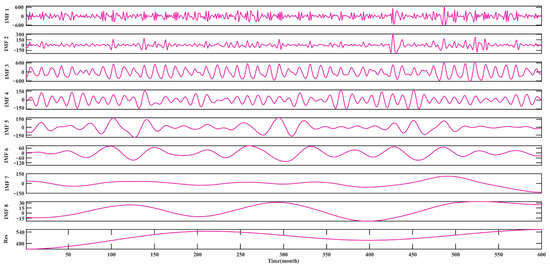
Figure 9.
CEEMDAN decomposition results for runoff data.
The VMD decomposition method was used to perform the secondary decomposition of the highest frequency component IMF1 obtained from CEEMDAN decomposition, and the decomposition results are shown in Figure 10. The results of the highest frequency component IMF1 through VMD decomposition are more regular and have obvious periodic characteristics, so as to achieve the sequence dimension reduction. Each VM component was subjected to a fast fourier transform (FFT) to further test the frequency extraction effect of VMD on IMF1. The results are shown in Figure 11. The variation characteristics of each VM component obtained by decomposition of IMF1 are similar, and all contain only one main frequency information, which is the main frequency information contained in IMF1, and the noise factor in the VM component is basically removed. In conclusion, the frequency information of the highest frequency component can be effectively extracted through the secondary decomposition of the highest frequency components IMF1 and M1 by VMD, and the purpose of noise reduction and simplification can be achieved.
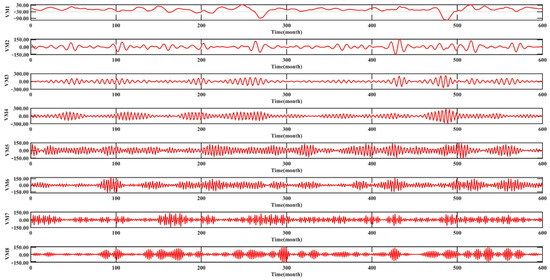
Figure 10.
IMF1 component VMD decomposition results.
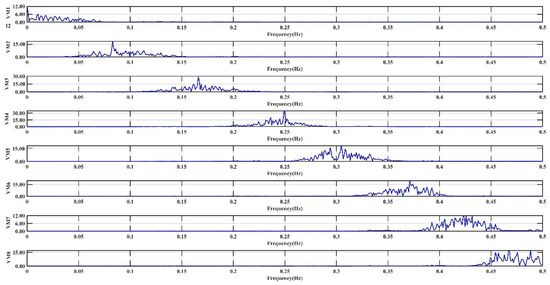
Figure 11.
FFT transform curves of VMD decomposition subsequences.
The prediction results of the monthly runoff of the Wulong hydrological station using the CEEMDAN-VMD-LSTM-Informer coupled model are shown in Figure 12. After calculation, NSE was 0.997, MAE was 1.327 × 108 m3, MAPE was 2.57%, and RMSE was 1.327 × 108 m3.
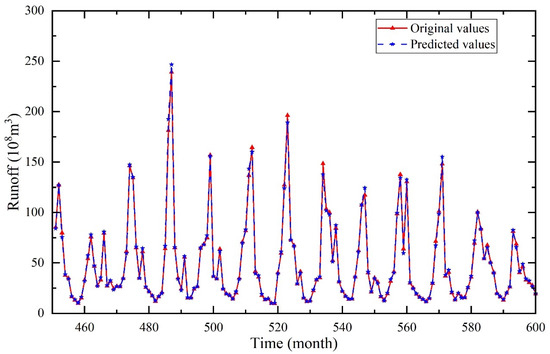
Figure 12.
Prediction results of CEEMDAN-VMD-LSTM-Informer coupled model.
4.1.2. Predicted Results of Seasonal Exponential Smoothing Model
In this paper, the first 75% of monthly scale runoff data was taken as the training set, and the last 25% was taken as the verification set. The expert modeler in SPSS 26 was used to select the optimal traditional model for time series prediction. The expert modeler chose the seasonal exponential smoothing model to predict the monthly scale runoff data; the stable R2 between the original value and the fitting value was 0.693, thus the model basically meets the requirements. It can be seen from the ACF and PACF of the residual sequence in Figure 13 that the residual basically fluctuated evenly around 0, and there was no autocorrelation when the order was 1–120, and all of them were within the confidence interval. Therefore, the residual sequence was classified as a white noise sequence, and the model fully extracted the information from the modeling sequence, and the model was effective. The prediction results of the seasonal exponential smoothing model are shown in Figure 14. By comparing the predicted value with the measured value, the NSE was calculated as 0.516, MAE as 8.629 × 108 m3, MAPE as 15.49%, and RMSE as 9.658 × 108 m3.
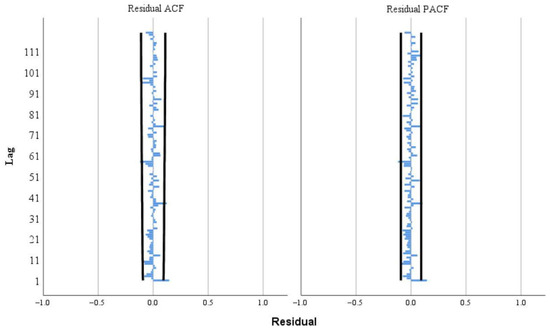
Figure 13.
The ACF and PACF of the residual sequence.
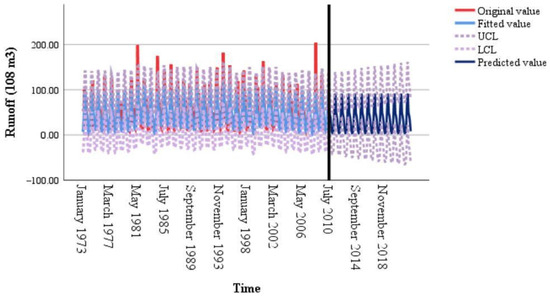
Figure 14.
Prediction results of seasonal exponential smoothing model.
4.2. Discussion
To assess the effectiveness of the combined CEEMDAN-VMD-LSTM-Informer model, we conducted a comparative analysis involving the prediction results from other models, including EEMD-VMD-LSTM-Informer, CEEMDAN-LSTM-Informer, CEEMDAN-LSTM, and EMD-LSTM. The accuracy of the prediction results for different model validation sets is visually depicted in Figure 15, while the corresponding evaluation index values are presented in Table 2. Upon scrutinizing and analyzing the predictive performance of the CEEMDAN-VMD-LSTM-Informer model in comparison to the other models, several noteworthy observations can be made: The CEEMDAN-VMD-LSTM-Informer model consistently exhibits the highest prediction accuracy among all the models, underscoring the efficacy of the proposed combined model in this study. Both Model 1 (CEEMDAN-VMD-LSTM-Informer) and Model 2 (EEMD-VMD-LSTM-Informer) outperform Model 3 (CEEMDAN-LSTM), Model 4 (CEEMDAN-LSTM), and Model 5 (EMD-LSTM), highlighting the advantages of employing quadratic decomposition in runoff prediction. Model 1 demonstrates superior accuracy compared to Model 2, while Model 4 outperforms Model 5. This performance discrepancy can be attributed to the introduction of adaptive white noise at each stage of CEEMDAN decomposition, effectively addressing issues like mode aliasing in EMD and residual noise in EEMD. Model 3 (CEEMDAN-LSTM-Informer) surpasses Model 4 (CEEMDAN-LSTM), attributed to the LSTM-Informer model’s ability to capture changes in peak and valley values. By applying different prediction methods to distinct components, the model’s overall accuracy is further enhanced, with specific improvements in predicting individual high peaks. In summary, the CEEMDAN-VMD-LSTM-Informer model emerges as the most accurate in predicting runoff, validating the effectiveness of the proposed combined model. The incorporation of quadratic decomposition techniques enhances predictive performance, and the introduction of adaptive white noise and LSTM-Informer models addresses specific challenges associated with runoff prediction, ultimately leading to superior results. The seasonal exponential smoothing model has the worst prediction result and a larger error.
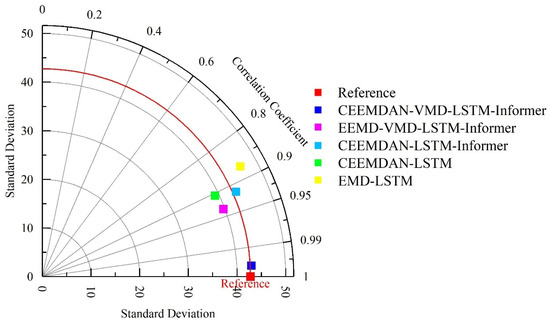
Figure 15.
Taylor diagram for comparison of prediction results of different machine learning models.

Table 2.
Precision comparison of different prediction models.
In conclusion, the seasonal exponential smoothing model belongs to the traditional mathematical statistical model; the prediction accuracy of the traditional statistical model is much lower than that of the machine model. Machine learning has stronger learning and fitting abilities, and it can reduce the impact of sequence randomness and volatility on prediction to a certain extent by capturing historical data changes and multi-dimensional data associations. However, when machine learning deals with nonstationary data, it is still difficult to learn enough sequence features, and there is a risk of data loss with periodic characteristics, which makes the prediction results inaccurate. Therefore, decomposition methods are combined with machine learning to obtain better predictive results. The decomposition method is to decompose the original data into components and use different prediction methods to predict the components so as to improve the prediction accuracy.
5. Conclusions
This paper used the CEEMDAN-VMD-LSTM-Informer coupled model and seasonal exponential smoothing model to predict monthly runoff at the Wulong hydrological station from 1973 to 2022. The prediction results of these models were compared with those from EEMD-VMD-LSTM-Informer, CEEMDAN-LSTM-Informer, CEEMDAN-LSTM, and EMD-LSTM. The key findings are summarized as follows:
- (1)
- Monthly scale runoff data at the Wulong hydrological station was a nonstationary and nonrandom sequence. The sequence showed a long-term decreasing trend and a pattern with an annual cycle. The predicted results of the seasonal exponential smoothing model showed that the prediction accuracy of the traditional statistical model is far inferior to that of machine learning models.
- (2)
- The application of the decomposition method provides a partial remedy for modal aliasing, resulting in more comprehensive and robust time series decomposition. This approach achieves a smoother monthly runoff series and reduces the interference of stochastic components with deterministic ones, ultimately enhancing the model’s predictive capabilities.
- (3)
- The combined model, which incorporates secondary decomposition, yields superior runoff prediction results. Specifically, the utilization of VMD for secondary decomposition of the highest-frequency component addresses the limitations of single-decomposition methods, resulting in a notable improvement in the accuracy of runoff predictions.
- (4)
- The CEEMDAN-VMD-LSTM-Informer model surpasses EEMD-VMD-LSTM-Informer, CEEMDAN-LSTM-Informer, CEEMDAN-LSTM, and EMD-LSTM in terms of prediction accuracy. The application of the CEEMDAN-VMD-LSTM-Informer model to monthly runoff time series prediction proves to be reliable and offers a novel approach to enhance research in monthly runoff prediction.
- (5)
- It is worth noting that this model solely considers runoff as a predictive factor. In future research endeavors, it would be advantageous to incorporate additional variables such as precipitation, evaporation, and temperature to further refine prediction accuracy.
In conclusion, this study presents a promising coupled prediction model that demonstrates superior performance in monthly runoff prediction. Its innovative approach and the incorporation of multiple decomposition techniques offer valuable insights for enhancing predictive accuracy in the field of hydrological prediction. However, this model still has some shortcomings. The universality of the model is low due to the model requiring large amounts of data for training. If the data for the study area are scarce or inconsistent, they may hinder the model’s generalization. In the future, data interpolation technology can be used to make up for the challenges caused by the lack of data in runoff prediction, such as the K-nearest neighbor (KNN) imputation technique.
Author Contributions
Conceptualization, Y.W.; methodology, Y.W.; software, Y.W.; validation, Y.W. and H.W.; formal analysis, Y.W.; investigation, H.W.; resources, H.W.; data curation, H.W.; writing—original draft preparation, Y.W.; writing—review and editing, J.L.; visualization, J.L.; supervision, J.L.; project administration, Y.C.; funding acquisition, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 51979107, No. 51909091, No. 52209018), the Science and Technology Projects of the Water Resources Department of Henan Province, China (GG202332 and GG202334), the China Scholarship Council (No. 202108410234), and the North China University of Water Resources and Electric Power Innovation Ability Improvement Project for Postgraduates (NCWUYC-2023027).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study can be accessed upon reasonable request from the corresponding author.
Acknowledgments
All authors thank the funding for their support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fang, S.; Xu, L.; Pei, H.; Liu, Y.; Liu, Z.; Zhu, Y.; Yan, J.; Zhang, H. An Integrated Approach to Snowmelt Flood Forecasting in Water Resource Management. IEEE Trans. Ind. Inform. 2013, 10, 548–558. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, X.; Xu, C.; Wu, P. Assessing Socioeconomic Drought Based on a Standardized Supply and Demand Water Index. Water Resour. Manag. 2022, 36, 1937–1953. [Google Scholar] [CrossRef]
- Meng, B.; Liu, J.-L.; Bao, K.; Sun, B. Water fluxes of Nenjiang River Basin with ecological network analysis: Conflict and coordination between agricultural development and wetland restoration. J. Clean. Prod. 2019, 213, 933–943. [Google Scholar] [CrossRef]
- Kurian, M. The water-energy-food nexus: Trade-offs, thresholds and transdisciplinary approaches to sustainable development. Environ. Sci. Policy 2017, 68, 97–106. [Google Scholar] [CrossRef]
- Wang, Z.; Shao, D.; Westerhoff, P. Wastewater discharge impact on drinking water sources along the Yangtze River (China). Sci. Total. Environ. 2017, 599–600, 1399–1407. [Google Scholar] [CrossRef] [PubMed]
- Dey, P.; Mishra, A. Separating the impacts of climate change and human activities on streamflow: A review of methodologies and critical assumptions. J. Hydrol. 2017, 548, 278–290. [Google Scholar] [CrossRef]
- Kotta, J.; Herkül, K.; Jaagus, J.; Kaasik, A.; Raudsepp, U.; Alari, V.; Arula, T.; Haberman, J.; Järvet, A.; Kangur, K.; et al. Linking atmospheric, terrestrial and aquatic environments: Regime shifts in the Estonian climate over the past 50 years. PLoS ONE 2018, 13, e0209568. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Guo, T.; Jiao, W. Destruction processes of mining on water environment in the mining area combining isotopic and hydrochemical tracer. Environ. Pollut. 2018, 237, 356–365. [Google Scholar] [CrossRef]
- Eisenmenger, N.; Pichler, M.; Krenmayr, N.; Noll, D.; Plank, B.; Schalmann, E.; Wandl, M.-T.; Gingrich, S. The Sustainable Development Goals prioritize economic growth over sustainable resource use: A critical reflection on the SDGs from a socio-ecological perspective. Sustain. Sci. 2020, 15, 1101–1110. [Google Scholar] [CrossRef]
- Hong, M.; Wang, D.; Wang, Y.; Zeng, X.; Ge, S.; Yan, H.; Singh, V.P. Mid- and long-term runoff predictions by an improved phase-space reconstruction model. Environ. Res. 2016, 148, 560–573. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, R.; Li, A.; Ji, C. Runoff forecast uncertainty considered load adjustment model of cascade hydropower stations and its application. Energy 2018, 158, 693–708. [Google Scholar] [CrossRef]
- Li, W.; Kiaghadi, A.; Dawson, C. High temporal resolution rainfall–runoff modeling using long-short-term-memory (LSTM) networks. Neural Comput. Appl. 2021, 33, 1261–1278. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Z.; Hu, Y.; Tao, S.; Dong, J. Runoff Forecasting using Convolutional Neural Networks and optimized Bi-directional Long Short-term Memory. Water Resour. Manag. 2023, 37, 937–953. [Google Scholar] [CrossRef]
- Bao, H.J.; Wang, L.L.; Li, Z.J.; Zhao, L.N.; Zhang, G.P. Hydrological daily rainfall-runoff simulation with BTOPMC model and comparison with Xin’anjiang model. Water Sci. Eng. 2010, 3, 121–131. [Google Scholar]
- Douglas-Mankin, K.R.; Srinivasan, R.; Arnold, J.G. Soil and Water Assessment Tool (SWAT) Model: Current Developments and Applications. Trans. ASABE 2010, 53, 1423–1431. [Google Scholar] [CrossRef]
- Mishra, S.K.; Singh, V.P. Long-term hydrological simulation based on the Soil Conservation Service curve number. Hydrol. Process. 2004, 18, 1291–1313. [Google Scholar] [CrossRef]
- Li, H.; Beldring, S.; Xu, C.-Y. Implementation and testing of routing algorithms in the distributed Hydrologiska Byråns Vattenbalansavdelning model for mountainous catchments. Hydrol. Res. 2013, 45, 322–333. [Google Scholar] [CrossRef][Green Version]
- Cerdan, O.; Souchère, V.; Lecomte, V.; Couturier, A.; Le Bissonnais, Y. Incorporating soil surface crusting processes in an expert-based runoff model: Sealing and Transfer by Runoff and Erosion related to Agricultural Management. Catena 2002, 46, 189–205. [Google Scholar] [CrossRef]
- Li, K.; Huang, G.; Wang, S.; Razavi, S. Development of a physics-informed data-driven model for gaining insights into hydrological processes in irrigated watersheds. J. Hydrol. 2022, 613, 128323. [Google Scholar] [CrossRef]
- Li, F.; Ma, G.; Chen, S.; Huang, W. An ensemble modeling approach to forecast daily reservoir inflow using bidirectional long-and short-term memory (Bi-LSTM), variational mode decomposition (VMD), and energy entropy method. Water Resour. Manag. 2021, 35, 2941–2963. [Google Scholar] [CrossRef]
- Liu, K.; Chen, Y.; Zhang, X. An Evaluation of ARFIMA (Autoregressive Fractional Integral Moving Average) Programs. Axioms 2017, 6, 16. [Google Scholar] [CrossRef]
- Chen, L.; Wu, T.; Wang, Z.; Lin, X.; Cai, Y. A novel hybrid BPNN model based on adaptive evolutionary Artificial Bee Colony Algorithm for water quality index prediction. Ecol. Indic. 2023, 146, 109882. [Google Scholar] [CrossRef]
- Gong, M.; Zhao, Y.; Sun, J.; Han, C.; Sun, G.; Yan, B. Load forecasting of district heating system based on Informer. Energy 2022, 253, 124179. [Google Scholar] [CrossRef]
- Meng, E.; Huang, S.; Huang, Q.; Fang, W.; Wu, L.; Wang, L. A robust method for non-stationary streamflow prediction based on improved EMD-SVM model. J. Hydrol. 2019, 568, 462–478. [Google Scholar] [CrossRef]
- Abda, Z.; Chettih, M. Forecasting daily flow rate-based intelligent hybrid models combining wavelet and Hilbert–Huang transforms in the mediterranean basin in northern Algeria. Acta Geophys. 2018, 66, 1131–1150. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, H.; Singh, V.P. Forward Prediction of Runoff Data in Data-Scarce Basins with an Improved Ensemble Empirical Mode Decomposition (EEMD) Model. Water 2018, 10, 388. [Google Scholar] [CrossRef]
- Bae, S.; Paris, S.; Durand, F. Two-scale tone management for photographic look. ACM Trans. Graph. (TOG) 2006, 25, 637–645. [Google Scholar] [CrossRef]
- He, C.; Chen, F.; Long, A.; Qian, Y.; Tang, H. Improving the precision of monthly runoff prediction using the combined non-stationary methods in an oasis irrigation area. Agric. Water Manag. 2023, 279, 108161. [Google Scholar] [CrossRef]
- Junsheng, C.; Dejie, Y.; Yu, Y. Research on the intrinsic mode function (IMF) criterion in EMD method. Mech. Syst. Signal Process. 2006, 20, 817–824. [Google Scholar] [CrossRef]
- Fan, X.; Zhang, Y.; Krehbiel, P.R.; Zhang, Y.; Zheng, D.; Yao, W.; Xu, L.; Liu, H.; Lyu, W. Application of Ensemble Empirical Mode Decomposition in Low-Frequency Lightning Electric Field Signal Analysis and Lightning Location. IEEE Trans. Geosci. Remote. Sens. 2020, 59, 86–100. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar] [CrossRef]
- Fu, W.; Shao, K.; Tan, J.; Wang, K. Fault Diagnosis for Rolling Bearings Based on Composite Multiscale Fine-Sorted Dispersion Entropy and SVM With Hybrid Mutation SCA-HHO Algorithm Optimization. IEEE Access 2020, 8, 13086–13104. [Google Scholar] [CrossRef]
- Shewalkar, A.; Nyavanandi, D.; Ludwig, S.A. Performance Evaluation of Deep Neural Networks Applied to Speech Recognition: RNN, LSTM and GRU. J. Artif. Intell. Soft Comput. Res. 2019, 9, 235–245. [Google Scholar] [CrossRef]
- Dong, M.; Grumbach, L. A Hybrid Distribution Feeder Long-Term Load Forecasting Method Based on Sequence Prediction. IEEE Trans. Smart Grid 2019, 11, 470–482. [Google Scholar] [CrossRef]
- Li, D.; Lin, K.; Li, X.; Liao, J.; Du, R.; Chen, D.; Madden, A. Improved sales time series predictions using deep neural networks with spatiotemporal dynamic pattern acquisition mechanism. Inf. Process. Manag. 2022, 59, 102987. [Google Scholar] [CrossRef]
- Chang, Y.; Li, F.; Chen, J.; Liu, Y.; Li, Z. Efficient temporal flow Transformer accompanied with multi-head probsparse self-attention mechanism for remaining useful life prognostics. Reliab. Eng. Syst. Saf. 2022, 226, 108701. [Google Scholar] [CrossRef]
- Habtemariam, E.T.; Kekeba, K.; Martínez-Ballesteros, M.; Martínez-Álvarez, F. A Bayesian Optimization-Based LSTM Model for Wind Power Forecasting in the Adama District, Ethiopia. Energies 2023, 16, 2317. [Google Scholar] [CrossRef]
- Xiaobing, Y.; Chenliang, L.; Tongzhao, H.; Zhonghui, J. Information diffusion theory-based approach for the risk assessment of meteorological disasters in the Yangtze River Basin. Nat. Hazards 2021, 107, 2337–2362. [Google Scholar] [CrossRef]
- Tamm, O.; Saaremäe, E.; Rahkema, K.; Jaagus, J.; Tamm, T. The intensification of short-duration rainfall extremes due to climate change–Need for a frequent update of intensity–duration–frequency curves. Clim. Serv. 2023, 30, 100349. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).