Surface Velocity to Depth-Averaged Velocity—A Review of Methods to Estimate Alpha and Remaining Challenges
Abstract
:1. Introduction
2. Methods to Estimate α
2.1. Alpha—Default Value
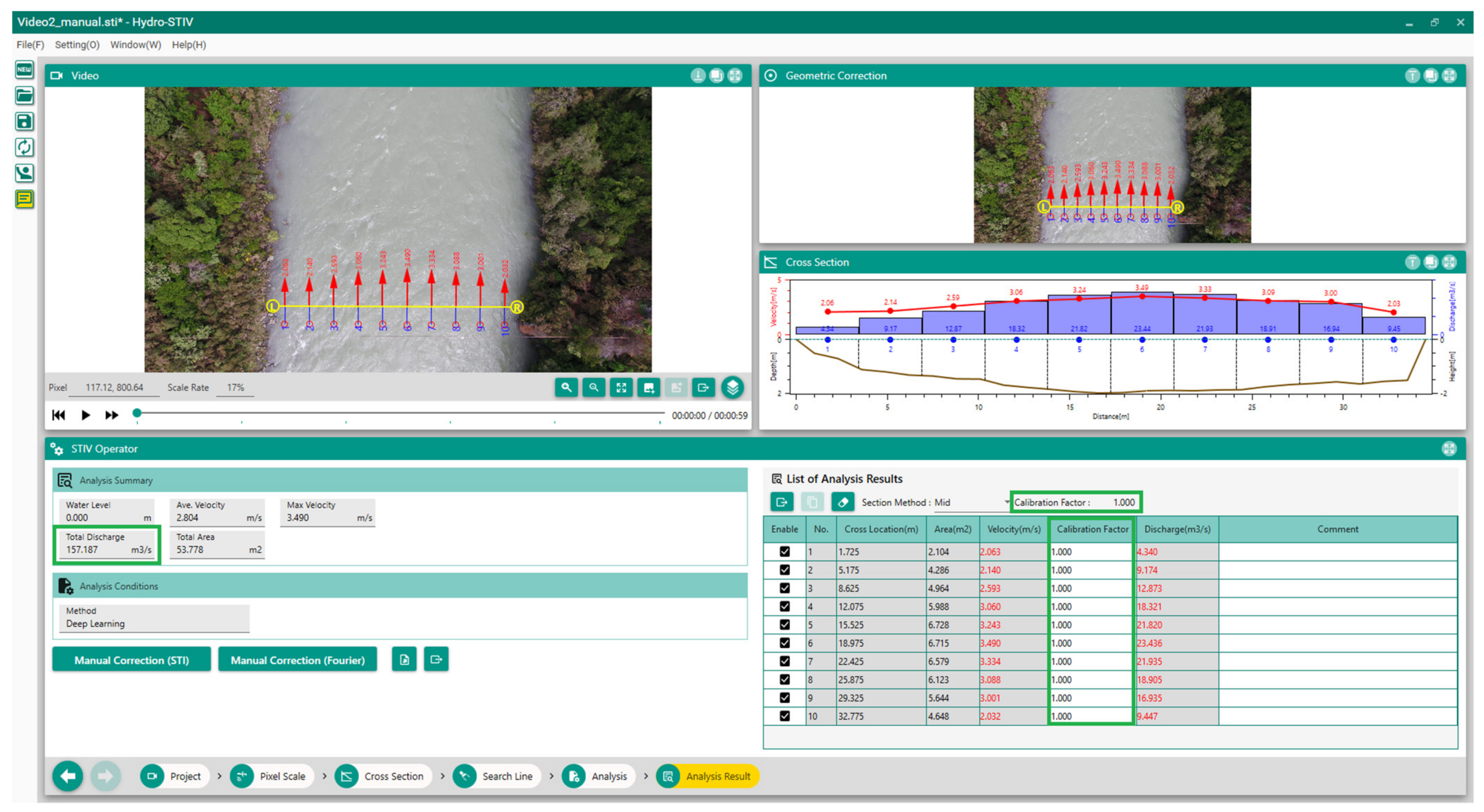
2.2. Site Alpha from Reference Discharge and Discharge from Surface Velocimetry with αi = 1
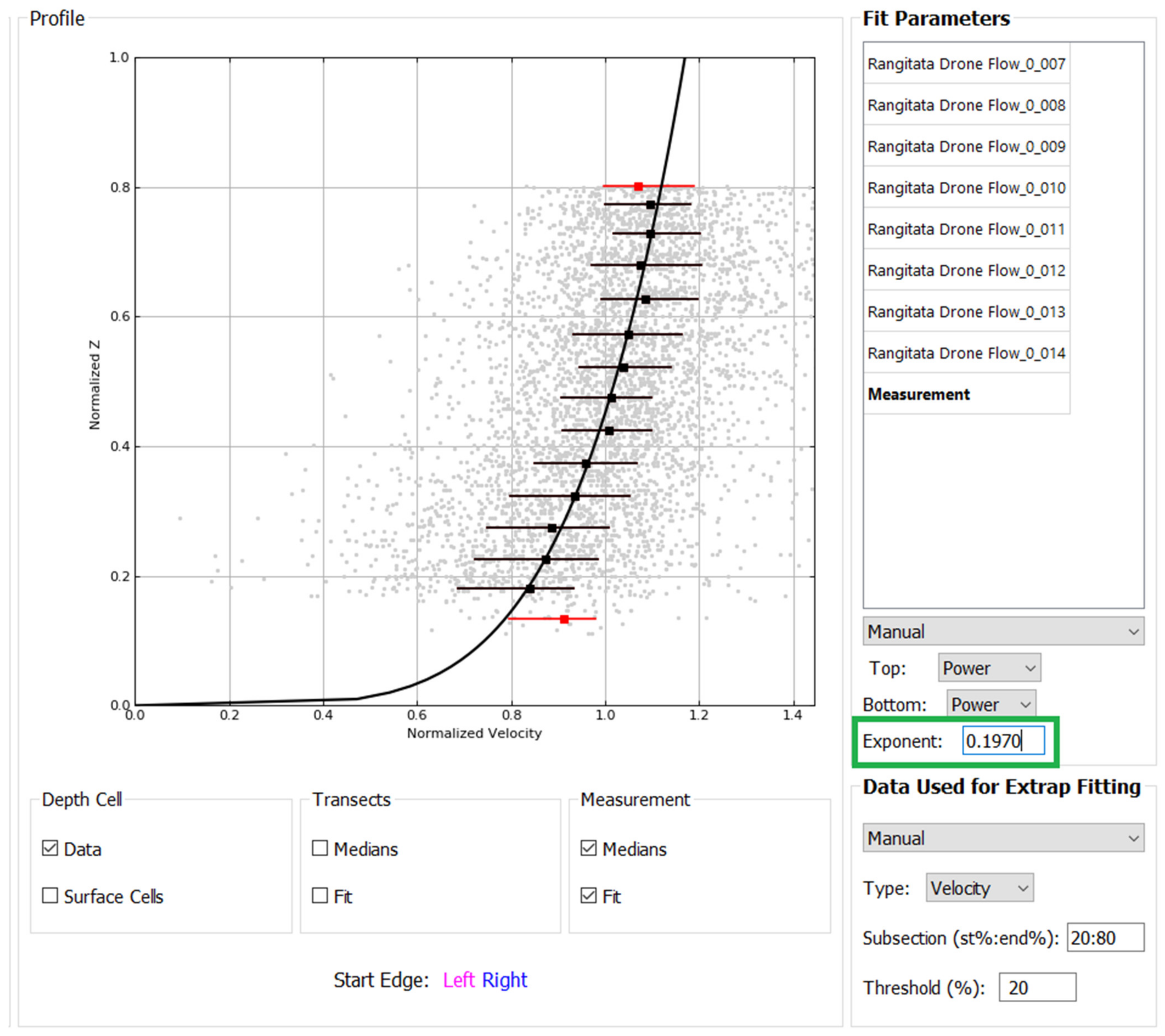
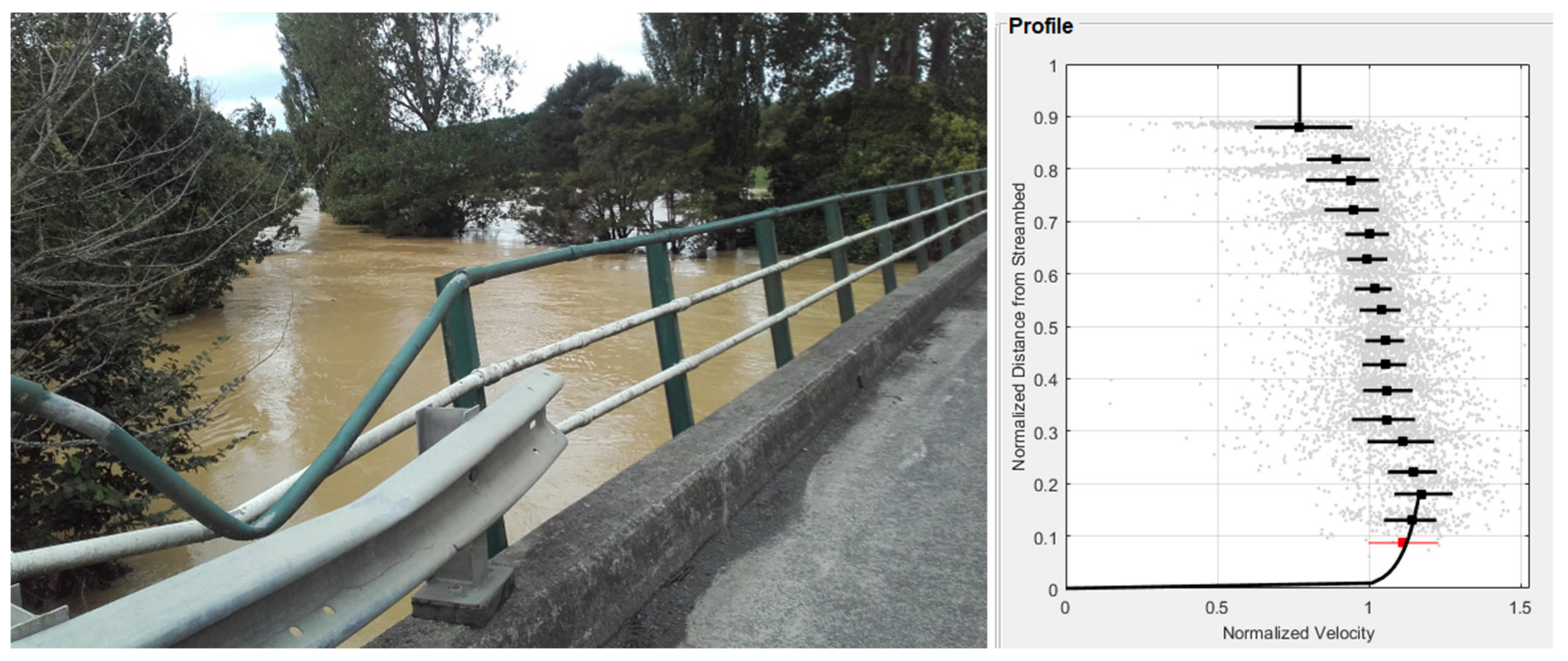
2.3. Site Alpha from Extrapolated Velocity Profiles
2.4. Alpha from Log Law Profiles—Extending from Bed to Surface
2.4.1. Alpha from Log Law Profiles—Theory and Derivations
2.4.2. Alpha from Log Law Profiles—Practical Implementation
2.4.3. Alpha from Log Law Profiles—Limitations
2.5. Alpha from Power Law Profiles—Extending from Bed to Surface
2.5.1. Alpha from Power Law Profiles—Theory and Derivations
2.5.2. Alpha from Power Law Profiles—Practical Implementation
2.5.3. Alpha from Power Law Profiles—Limitations
2.6. Alpha Estimation from Site Characteristics
- Natural rivers: ‘For water depth less than 2 m: consider using α = 0.8 with an uncertainty of about ±15% at 90% confidence level. For greater water depth, consider using α = 0.9 with an uncertainty of about ±15% at 90% confidence level.’
- Artificial concrete channels: ‘Consider using α = 0.9 with an uncertainty of about ±15% at 90% confidence level.’
2.7. Alpha—Additional Methods
2.7.1. Alpha from Shape Factor
2.7.2. Alpha from Surface Velocity Fluctuations
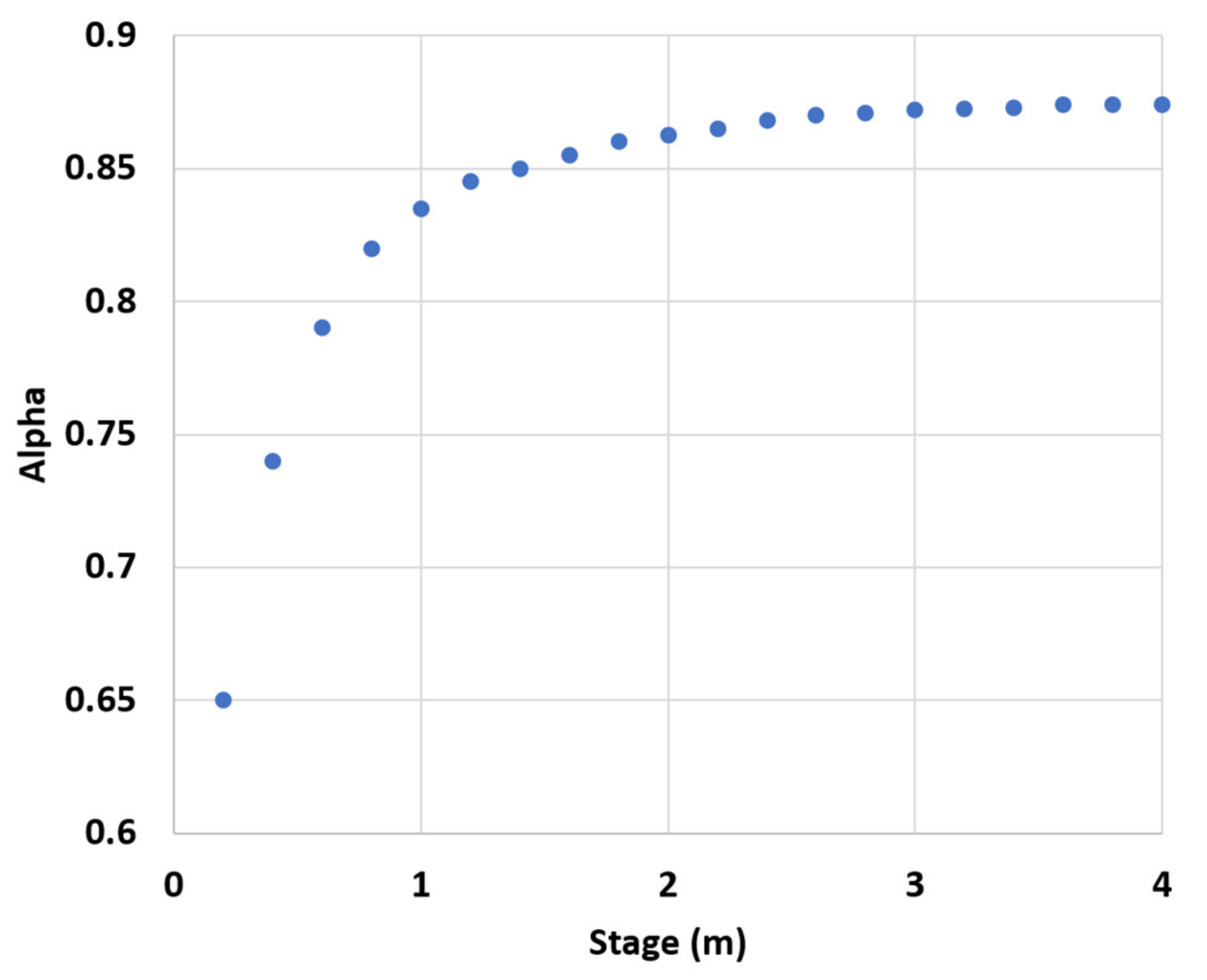
3. Stage to Alpha Rating Curves
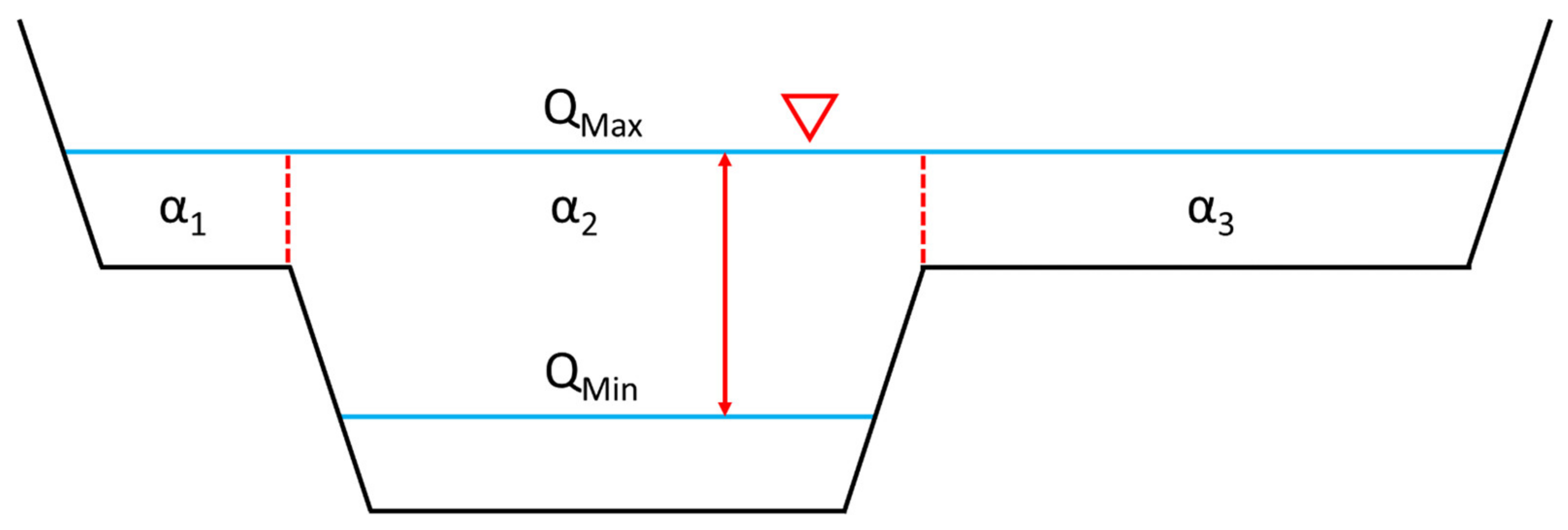
4. Site Alpha vs. Local Alpha
5. Divided Channel Method
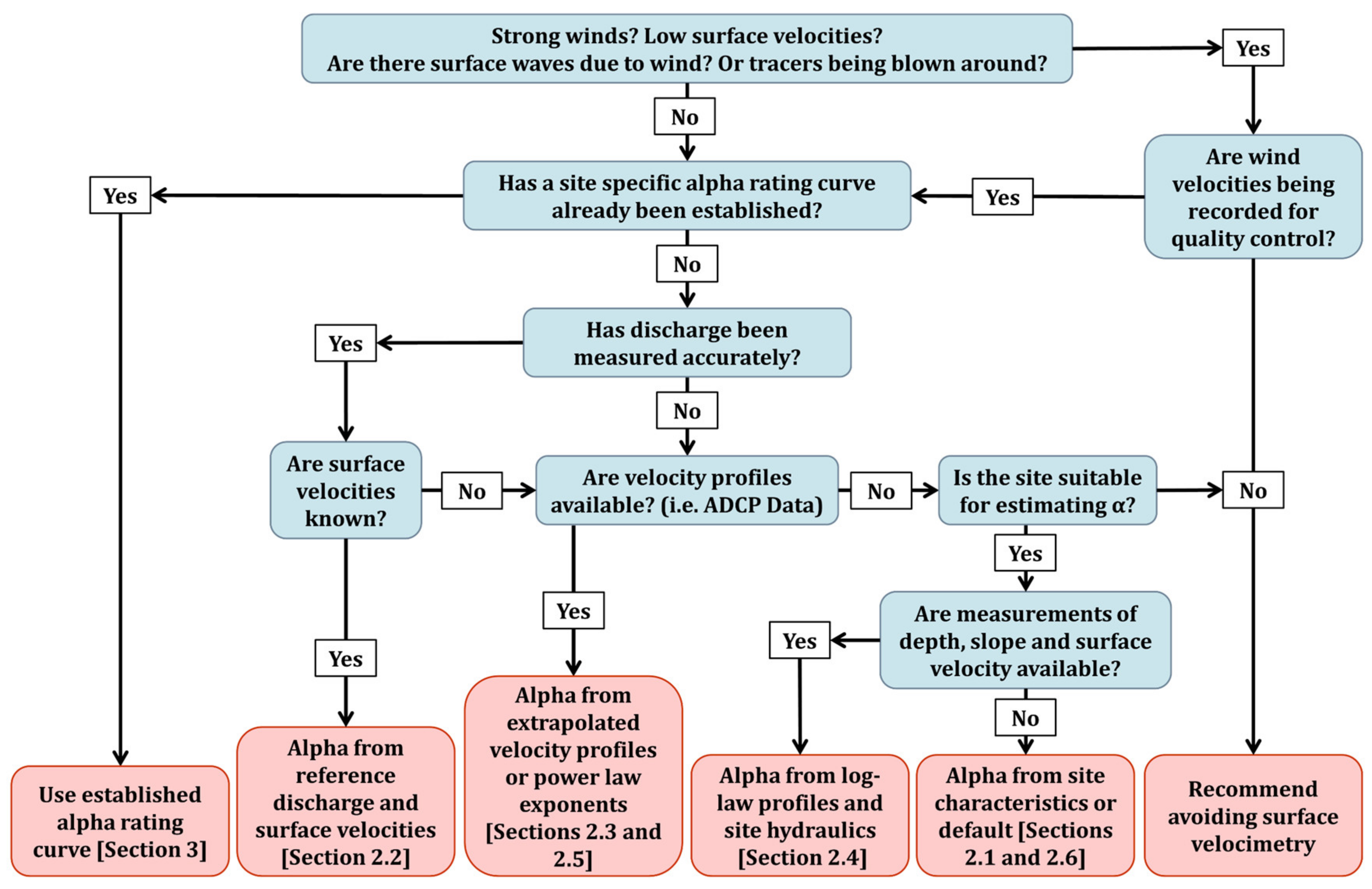
6. How to Select the Optimal Method for Estimating Alpha
7. Remaining Challenges and Future Directions
7.1. Surface Wind
7.2. Secondary Currents
7.3. Other Challenges
7.4. Future Directions
- Re-analysis of existing datasets (e.g., Welber et al. [4]; Hauet et al. [39]) with the inclusion of slope, which is a key driver of the shape of logarithmic velocity profiles (Section 2.4), and thus α.
- Conduct a systematic high-resolution laboratory investigation into the effect of surface wind on velocity profiles and α [62].
- Further investigate the turbulent outer region, secondary currents, compound velocity profiles, and how to practically estimate α using these compound profiles.
- Conduct a detailed field investigation into the spatial heterogeneity of α; the characteristics that make a measurement site suitable for the estimation of α; and the errors that may occur if these characteristics are not present.
- Develop methods to infer flow non-uniformity (e.g., acceleration/deceleration, convergence/divergence, secondary currents, etc.) from the surface velocity field.
8. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rantz, S. Measurement and computation of stream-flow: Measurement of stage and discharge. In U.S. Geological Survey Water Supply Paper 2175; United States Government Printing Office: Washington, DC, USA, 1982. [Google Scholar] [CrossRef]
- Buchanan, T.J.; Somers, W.P. Discharge Measurements at Gaging Stations. In United States Geological Survey 1969; US Government Printing Office: Washington, DC, USA, 1969. [Google Scholar]
- Costa, J.E.; Spicer, K.R.; Cheng, R.T.; Haeni, F.P.; Melcher, N.B.; Thurman, E.M.; Plant, W.J.; Keller, W.C. measuring stream discharge by non-contact methods: A Proof-of-Concept Experiment. Geophys. Res. Lett. 2000, 27, 553–556. [Google Scholar] [CrossRef]
- Welber, M.; Le Coz, J.; Laronne, J.B.; Zolezzi, G.; Zamler, D.; Dramais, G.; Hauet, A.; Salvaro, M. Field assessment of noncontact stream gauging using portable surface velocity radars (SVR). Water Resour. Res. 2016, 52, 1108–1126. [Google Scholar] [CrossRef]
- Fujita, I.; Muste, M.; Kruger, A. Large-scale particle image velocimetry for flow analysis in hydraulic engineering applications. J. Hydraul. Res. 1998, 36, 397–414. [Google Scholar] [CrossRef]
- Le Coz, J.; Hauet, A.; Pierrefeu, G.; Dramais, G.; Camenen, B. Performance of image-based velocimetry (LSPIV) applied to flash-flood discharge measurements in Mediterranean rivers. J. Hydrol. 2010, 394, 42–52. [Google Scholar] [CrossRef]
- Al-Mamari, M.M.; Kantoush, S.A.; Kobayashi, S.; Sumi, T.; Saber, M. Real-Time Measurement of Flash-Flood in a Wadi Area by LSPIV and STIV. Hydrology 2019, 6, 27. [Google Scholar] [CrossRef]
- Muste, M.; Ho, H.-C.; Kim, D. Considerations on direct stream flow measurements using video imagery: Outlook and research needs. J. Hydro-Environ. Res. 2011, 5, 289–300. [Google Scholar] [CrossRef]
- Detert, M.; Weitbrecht, V. Helicopter-based surface PIV experiments at Thur River. In Proceedings of the River Flow, Lausanne, Switzerland, 3–5 September 2014. [Google Scholar]
- Detert, M.; Johnson, E.D.; Weitbrecht, V. Proof-of-concept for low-cost and non-contact synoptic airborne river flow measurements. Int. J. Remote Sens. 2017, 38, 2780–2807. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Kinzel, P.J.; Laker, M.; Conaway, J.S. Moving Aircraft River Velocimetry (MARV): Framework and Proof-of-Concept on the Tanana River. Water Resour. Res. 2023, 59, e2022WR033822. [Google Scholar] [CrossRef]
- Hutley, N.R.; Beecroft, R.; Wagenaar, D.; Soutar, J.; Edwards, B.; Deering, N.; Grinham, A.; Albert, S. Adaptively monitoring streamflow using a stereo computer vision system. Hydrol. Earth Syst. Sci. 2023, 27, 2051–2073. [Google Scholar] [CrossRef]
- Puleo, J.A.; McKenna, T.E.; Holland, K.T.; Calantoni, J. Quantifying riverine surface currents from time sequences of thermal infrared imagery. Water Resour. Res. 2012, 48, 1–20. [Google Scholar] [CrossRef]
- Kinzel, P.J.; Legleiter, C.J. sUAS-Based Remote Sensing of River Discharge Using Thermal Particle Image Velocimetry and Bathymetric Lidar. Remote Sens. 2019, 11, 2317. [Google Scholar] [CrossRef]
- Schweitzer, S.A.; Cowen, E.A. Instantaneous River-Wide Water Surface Velocity Field Measurements at Centimeter Scales Using Infrared Quantitative Image Velocimetry. Water Resour. Res. 2021, 57, e2020WR029279. [Google Scholar] [CrossRef]
- Detert, M.; Cao, L.; Albayrak, I. Airborne Image Velocimetry Measurements at the Hydropower Plant Schiffmühle on Limmat River, Switzerland. In Proceedings of the 2nd International Symposium and Exhibition on Hydro-Environment Sensors and Software (HydroSenSoft), Madrid, Spain, 26 February–3 March 2019. [Google Scholar]
- Biggs, H.J.; Smith, B.; Detert, M.; Sutton, H. Surface image velocimetry: Aerial tracer particle distribution system and techniques for reducing environmental noise with coloured tracer particles. River Res. Appl. 2022, 38, 1192–1198. [Google Scholar] [CrossRef]
- Ljubičić, R.; Strelnikova, D.; Perks, M.T.; Eltner, A.; Peña-Haro, S.; Pizarro, A.; Sasso, S.F.D.; Scherling, U.; Vuono, P.; Manfreda, S. A comparison of tools and techniques for stabilising unmanned aerial system (UAS) imagery for surface flow observations. Hydrol. Earth Syst. Sci. 2021, 25, 5105–5132. [Google Scholar] [CrossRef]
- Le Coz, J.; Renard, B.; Vansuyt, V.; Jodeau, M.; Hauet, A. Estimating the uncertainty of video-based flow velocity and discharge measurements due to the conversion of field to image coordinates. Hydrol. Process. 2021, 35, e14169. [Google Scholar] [CrossRef]
- Peña-Haro, S.; Ljubičić, R.; Strelnikova, D. Geometric correction and stabilization of images collected by UASs in river monitoring. In Unmanned Aerial Systems for Monitoring Soil, Vegetation, and Riverine Environments 2023; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar] [CrossRef]
- Muste, M.; Fujita, I.; Hauet, A. Large-scale particle image velocimetry for measurements in riverine environments. Water Resour. Res. 2008, 44, 1–14. [Google Scholar] [CrossRef]
- Le Coz, J.; Jodeau, M.; Hauet, A.; Marchand, B.; Le Boursicaud, R. Image-based velocity and discharge measurements in field and laboratory river engineering studies using the free Fudaa-LSPIV software. In Proceedings of the River Flow, Lausanne, Switzerland, 3–5 September 2014. [Google Scholar]
- Fujita, I.; Notoya, Y.; Tani, K.; Tateguchi, S. Efficient and accurate estimation of water surface velocity in STIV. Environ. Fluid Mech. 2018, 19, 1363–1378. [Google Scholar] [CrossRef]
- Patalano, A.; García, C.M.; Rodríguez, A. Rectification of Image Velocity Results (RIVeR): A simple and user-friendly toolbox for large scale water surface Particle Image Velocimetry (PIV) and Particle Tracking Velocimetry (PTV). Comput. Geosci. 2017, 109, 323–330. [Google Scholar] [CrossRef]
- Leitão, J.P.; Peña-Haro, S.; Lüthi, B.; Scheidegger, A.; de Vitry, M.M. Urban overland runoff velocity measurement with consumer-grade surveillance cameras and surface structure image velocimetry. J. Hydrol. 2018, 565, 791–804. [Google Scholar] [CrossRef]
- Cao, L.; Weitbrecht, V.; Li, D.; Detert, M. Airborne Feature Matching Velocimetry for surface flow measurements in rivers. J. Hydraul. Res. 2020, 59, 637–650. [Google Scholar] [CrossRef]
- Jodeau, M.; Hauet, A.; Le Coz, J.; Faure, J.; Bodart, G. Fudaa-LSPIV Version 1.9.2 User Manual. EDF and INRAE 2022, Lyon, France. Available online: https://forge.irstea.fr/attachments/download/3031/User%20Manual%20Fudaa-LSPIV%201.9.2.pdf (accessed on 19 October 2023).
- Hydro Technology Institute Ltd. Hydro-STIV Operation Manual; Hydro Technology Institute Ltd.: Osaka, Japan, 2023. [Google Scholar]
- Patalano, A. River-STIV Software (Released 2018). Available online: https://riverdischarge.blogspot.com/p/download-river.html (accessed on 19 October 2023).
- Perks, M.T. KLT-IV v1.0: Image velocimetry software for use with fixed and mobile platforms. Geosci. Model Dev. 2020, 13, 6111–6130. [Google Scholar] [CrossRef]
- Winsemius, H.; Annor, F.; Hagenaars, R.; Luxemburg, W.; Van den Munckhoff, G.; Heeskens, P.; Dominic, J.; Waniha, P.; Mahamudu, Y.; Abdallah, H.; et al. OpenRiverCam, open-source operational discharge monitoring with low-cost cameras. In Proceedings of the EGU General Assembly, Online, 19–30 April 2021. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Kinzel, P.J. The Toolbox for River Velocimetry using Images from Aircraft (TRiVIA). River Res. Appl. 2023, 39, 1457–1468. [Google Scholar] [CrossRef]
- Randall, M. National Industry Guidelines for Hydrometric Monitoring—Part 11: Application of Surface Velocity Methods for Velocity and Open Channel Discharge Measurements; Bureau of Meteorology Publication: Melbourne, Australia, 2021. [Google Scholar]
- Biggs, H. Drone Flow User Guide v1.1-River Remote Sensing and Surface Velocimetry; National Institute of Water and Atmospheric Research (NIWA) Report 2022; NIWA: Christchurch, New Zealand, 2022. [Google Scholar] [CrossRef]
- Jolley, M.J.; Russell, A.J.; Quinn, P.F.; Perks, M.T. Considerations When Applying Large-Scale PIV and PTV for Determining River Flow Velocity. Front. Water 2021, 3, 709269. [Google Scholar] [CrossRef]
- Detert, M. How to Avoid and Correct Biased Riverine Surface Image Velocimetry. Water Resour. Res. 2021, 57, e2020WR027833. [Google Scholar] [CrossRef]
- Smart, G.M.; Biggs, H.J. Remote gauging of open channel flow: Estimation of depth averaged velocity from surface velocity and turbulence. In Proceedings of the River Flow, Delft, The Netherlands, 6–10 July 2020. [Google Scholar] [CrossRef]
- Turnipseed, D.; Sauer, V. Discharge measurements at gaging stations (No. 3-A8). In United States Geological Survey Report; United States Geological Survey: Reston, VA, USA, 2010. [Google Scholar] [CrossRef]
- Hauet, A.; Morlot, T.; Daubagnan, L. Velocity profile and depth-averaged to surface velocity in natural streams: A review over a large sample of rivers. In Proceedings of the River Flow, Lyon, France, 5–8 September 2018. [Google Scholar]
- Fujita, I. Principles of surface velocity gaugings. In Proceedings of the 4th IAHR-WMO-IAHS Training Course on Stream Gauging, Lyon, France, 5–8 September 2018. [Google Scholar]
- Biggs, H.J.; Nikora, V.I.; Gibbins, C.N.; Cameron, S.M.; Papadopoulos, K.; Stewart, M.; Fraser, S.; Vettori, D.; Savio, M.; O’Hare, M.T.; et al. Flow interactions with an aquatic macrophyte: A field study using stereoscopic particle image velocimetry. J. Ecohydraulics 2019, 4, 113–130. [Google Scholar] [CrossRef]
- Biggs, H.; Smart, G.; Doyle, M.; Holwerda, H.; McDonald, M.; Ede, M. River discharge from surface velocity measurements—A field guide for selecting alpha. In Envirolink Advice Report 2021; Envirolink: Christchurch, New Zealand, 2021. [Google Scholar] [CrossRef]
- Lennermark, M.; Hauet, A. Developing a post-processing software for ADCP discharge measurement piloted by an international and inter-agency group: A unique, ambitious experience… and one that works! In Proceedings of the EGU General Assembly, Vienna, Austria, 23–27 May 2022. [Google Scholar] [CrossRef]
- Keulegan, G.H. Laws of turbulent flow in open channels. J. Res. Natl. Bur. Stand. 1938, 21, 707. [Google Scholar] [CrossRef]
- Smart, G. A base for the log law and von Karman’s constant problem. J. Hydraul. Res. 2022, 60, 935–943. [Google Scholar] [CrossRef]
- Dietrich, J.T. Bathymetric Structure-from-Motion: Extracting shallow stream bathymetry from multi-view stereo photogrammetry. Earth Surf. Process. Landf. 2017, 42, 355–364. [Google Scholar] [CrossRef]
- Johnson, E.D.; Cowen, E.A. Remote monitoring of volumetric discharge employing bathymetry determined from surface turbulence metrics. Water Resour. Res. 2016, 52, 2178–2193. [Google Scholar] [CrossRef]
- Jin, T.; Liao, Q. Application of large scale PIV in river surface turbulence measurements and water depth estimation. Flow Meas. Instrum. 2019, 67, 142–152. [Google Scholar] [CrossRef]
- Polcyn, F.; Brown, W.; Sattinger, I. The measurement of water depth by remote sensing techniques. In Report for the Spacecraft Oceanography Project 1970; The University of Michigan: Ann Arbour, MI, USA, 1970. [Google Scholar]
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef]
- Legleiter, C.J. The optical river bathymetry toolkit. River Res. Appl. 2021, 37, 555–568. [Google Scholar] [CrossRef]
- Dolcetti, G.; Hortobágyi, B.; Perks, M.; Tait, S.J.; Dervilis, N. Using Noncontact Measurement of Water Surface Dynamics to Estimate River Discharge. Water Resour. Res. 2022, 58, e2022WR032829. [Google Scholar] [CrossRef]
- Melcher, N.B.; Costa, J.E.; Haeni, F.P.; Cheng, R.T.; Thurman, E.M.; Buursink, M.; Spicer, K.R.; Hayes, E.; Plant, W.J.; Keller, W.C.; et al. River discharge measurements by using helicopter-mounted radar. Geophys. Res. Lett. 2002, 29, 41. [Google Scholar] [CrossRef]
- Hong, J.-H.; Guo, W.-D.; Wang, H.-W.; Yeh, P.-H. Estimating discharge in gravel-bed river using non-contact ground-penetrating and surface-velocity radars. River Res. Appl. 2017, 33, 1177–1190. [Google Scholar] [CrossRef]
- Mandlburger, G.; Pfennigbauer, M.; Schwarz, R.; Flöry, S.; Nussbaumer, L. Concept and Performance Evaluation of a Novel UAV-Borne Topo-Bathymetric LiDAR Sensor. Remote Sens. 2020, 12, 986. [Google Scholar] [CrossRef]
- Kinzel, P.J.; Legleiter, C.J.; Grams, P.E. Field evaluation of a compact, polarizing topo-bathymetric lidar across a range of river conditions. River Res. Appl. 2021, 37, 531–543. [Google Scholar] [CrossRef]
- Aberle, J. Spatially averaged near-bed flow field over rough armor layers. In Proceedings of the River Flow, Lisbon, Portugal, 6–8 September 2006. [Google Scholar]
- Smart, G.M.; Plew, D.; Gateuille, D. Eddy Educed Entrainment. In Proceedings of the River Flow, Braunschweig, Germany, 8–10 September 2010. [Google Scholar]
- Smart, G.M.; Biggs, H.J. Effects of shallow flows on the ratio of depth averaged velocity to water surface velocity. In Proceedings of the Weathering the Storm: NZHS, NZ Rivers Group & NZFSS Conference, Invercargill, New Zealand, 1–4 December 2020. [Google Scholar]
- Coles, D. The law of the wake in the turbulent boundary layer. J. Fluid Mech. 1956, 1, 191–226. [Google Scholar] [CrossRef]
- Muste, M.; Lyn, D.A.; Admiraal, D.; Ettema, R.; Nikora, V.I.; García, M.H. (Eds.) Experimental Hydraulics: Methods, Instrumentation, Data Processing and Management: Volume I: Fundamentals and Methods; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Eickelberg, N. Investigations of Velocity Profiles in Open Channel Flow Streams with Particular Focus on the Effects of Water Surface Wind. Master’s Thesis, Technical University of Braunschweig, Braunschweig, Germany, 2023. [Google Scholar]
- Detert, M. Hydrodynamic Processes at the Water-Sediment Interface of Streambeds. Ph.D. Thesis, University of Karlsruhe, Karlsruhe, Germany, 2008. [Google Scholar]
- Johnson, E.D.; Cowen, E.A. Remote determination of the velocity index and mean streamwise velocity profiles. Water Resour. Res. 2017, 53, 7521–7535. [Google Scholar] [CrossRef]
- Smart, G.M. Turbulent Velocity Profiles and Boundary Shear in Gravel Bed Rivers. J. Hydraul. Eng. 1999, 125, 106–116. [Google Scholar] [CrossRef]
- Le Coz, J.; Duby, P.; Dramais, G.; Camenen, B.; Laronne, J.; Zamler, D.; Zolezzi, G. Use of emerging non-intrusive techniques for flood discharge measurements. In Proceedings of the 5th International Conference on Flood Management, Tokyo, Japan, 27–29 September 2011. [Google Scholar]
- Smart, G.M. Is delta alpha uniform charlie? In Proceedings of the International Surface Velocimetry Workshop, Hull, UK, 4–6 May 2021. [Google Scholar]
- Hicks, D.M.; Mason, P. Roughness characteristics of New Zealand Rivers: A handbook for assigning hydraulic roughness coefficients to river reaches by the “visual comparison” approach. In Water Resources Survey; DSIR Marine and Freshwater: Wellington, New Zealand, 1991. [Google Scholar]
- Hinze, J.O. Turbulence—An Introduction to Its Mechanism and Theory; McGraw–Hill: New York, NY, USA, 1959. [Google Scholar]
- Clauser, F.H. The turbulent boundary layer. Adv. Appl. Mech. 1956, 4, 1–51. [Google Scholar] [CrossRef]
- Nowell, A.R.; Church, M. Turbulent flow in a depth-limited boundary layer. J. Geophys. Res. Oceans 1979, 84, 4816–4824. [Google Scholar] [CrossRef]
- Johnson, E.D.; Cowen, E.A. Estimating bed shear stress from remotely measured surface turbulent dissipation fields in open channel flows. Water Resour. Res. 2017, 53, 1982–1996. [Google Scholar] [CrossRef]
- Nezu, I.; Nakagawa, H. Turbulence in Open Channel Flows; Balkema: Boca Raton, FL, USA, 1993. [Google Scholar]
- Cameron, S.M.; Nikora, V.I.; Stewart, M.T. Very-large-scale motions in rough-bed open-channel flow. J. Fluid Mech. 2017, 814, 416–429. [Google Scholar] [CrossRef]
- Peña-Haro, S.; Lüthi, B.; Lukes, R.; Carrel, M. Wind effect on image-based river surface velocity measurements. In Proceedings of the EGU General Assembly, Vienna, Austria, 3–8 May 2020. [Google Scholar]
- Fujita, I.; Shibano, T.; Tani, K. Application of masked two-dimensional Fourier spectra for improving the accuracy of STIV-based river surface flow velocity measurements. Meas. Sci. Technol. 2020, 31, 094015. [Google Scholar] [CrossRef]
- Sun, X.; Shiono, K.; Chandler, J.H.; Rameshwaran, P.; Sellin, R.H.; Fujita, I. Discharge estimation in small irregular river using LSPIV. Proc. Inst. Civ. Eng.-Water Manag. 2010, 163, 247–254. [Google Scholar] [CrossRef]
- Gunawan, B.; Sun, X.; Sterling, M.; Shiono, K.; Tsubaki, R.; Rameshwaran, P.; Knight, D.; Chandler, J.; Tang, X.; Fujita, I. The application of LS-PIV to a small irregular river for inbank and overbank flows. Flow Meas. Instrum. 2012, 24, 1–12. [Google Scholar] [CrossRef]
- Kim, Y. Uncertainty Analysis for Non-Intrusive Measurement of River Discharge Using Image Velocimetry. Ph.D. Thesis, University of Iowa, Iowa City, IA, USA, 2006. [Google Scholar]

| Normal | Smooth | Rough | Very Rough | Extreme Cases | |
|---|---|---|---|---|---|
| m | 6–7 | 10 | 4 | 2–3 | |
| M | 0.143–0.167 | 0.1 | 0.25 | 0.333–0.5 | |
| α | 0.86–0.87 | 0.91 | 0.8 | 0.67–0.75 | 0.6–1.2 |
| H/d84 | m | M | α |
|---|---|---|---|
| >30 | 6.25 | 0.16 | 0.86 |
| 10–30 | 5.26 | 0.19 | 0.84 |
| 2–10 | 1.72 | 0.58 | 0.63 |
| <2 | 0.63 | 1.59 | 0.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biggs, H.; Smart, G.; Doyle, M.; Eickelberg, N.; Aberle, J.; Randall, M.; Detert, M. Surface Velocity to Depth-Averaged Velocity—A Review of Methods to Estimate Alpha and Remaining Challenges. Water 2023, 15, 3711. https://doi.org/10.3390/w15213711
Biggs H, Smart G, Doyle M, Eickelberg N, Aberle J, Randall M, Detert M. Surface Velocity to Depth-Averaged Velocity—A Review of Methods to Estimate Alpha and Remaining Challenges. Water. 2023; 15(21):3711. https://doi.org/10.3390/w15213711
Chicago/Turabian StyleBiggs, Hamish, Graeme Smart, Martin Doyle, Niklas Eickelberg, Jochen Aberle, Mark Randall, and Martin Detert. 2023. "Surface Velocity to Depth-Averaged Velocity—A Review of Methods to Estimate Alpha and Remaining Challenges" Water 15, no. 21: 3711. https://doi.org/10.3390/w15213711





