Research on the Performance Characteristics and Unsteady Flow Mechanism of a Centrifugal Pump under Pitch Motion
Abstract
:1. Introduction
2. Materials and Methods
2.1. Centrifugal Pump Model
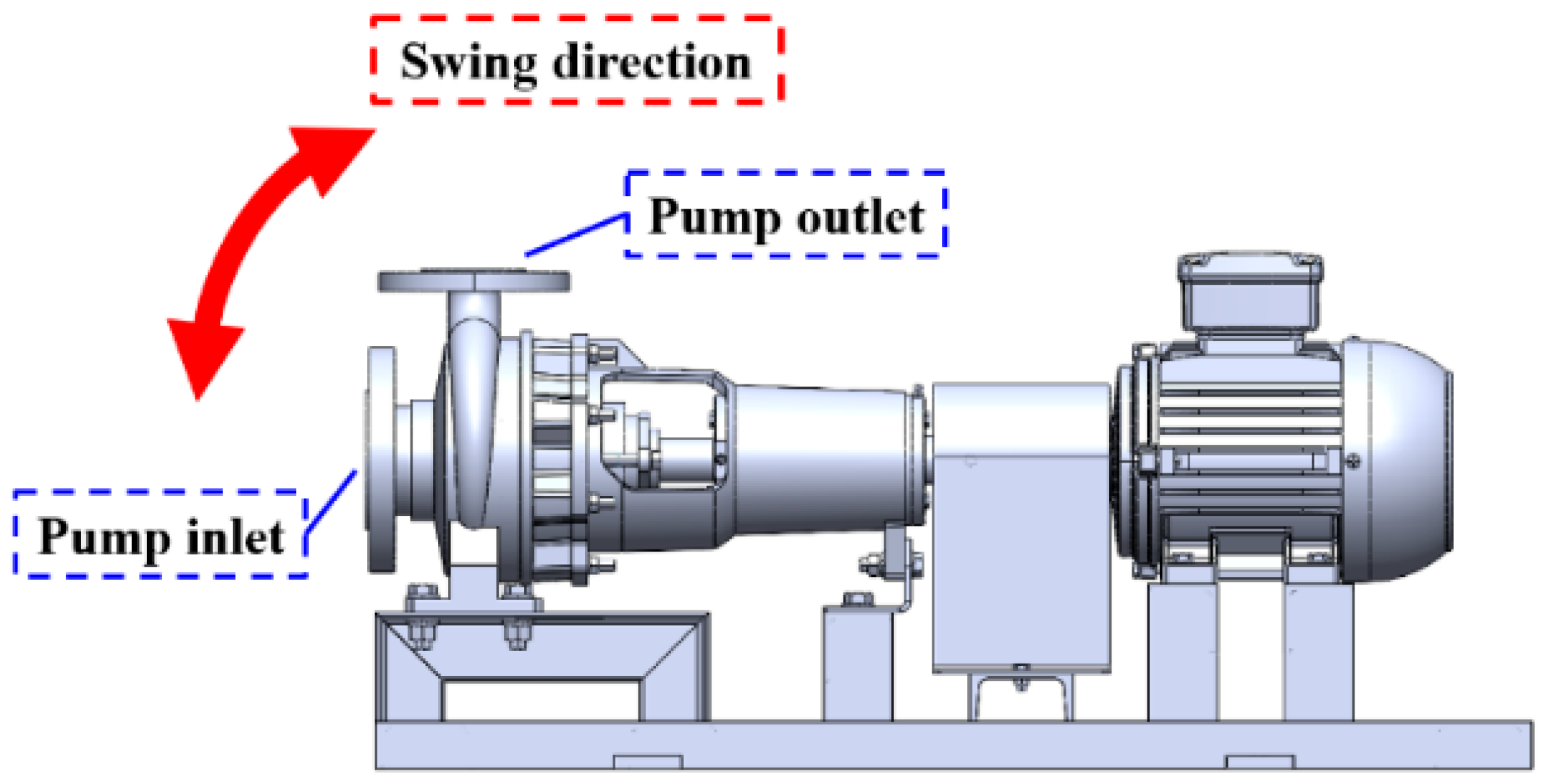
2.2. Experimental Devices and Methods
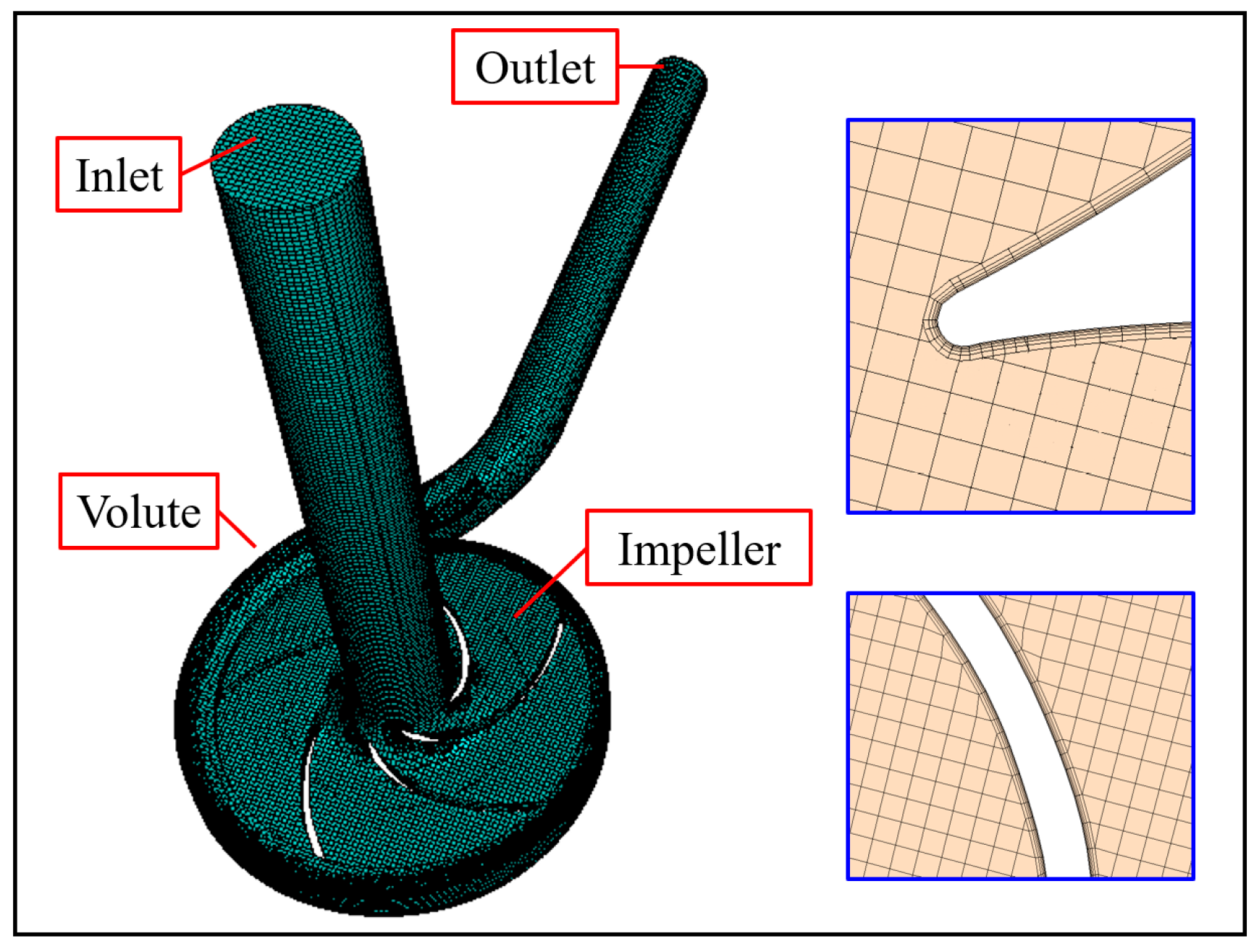
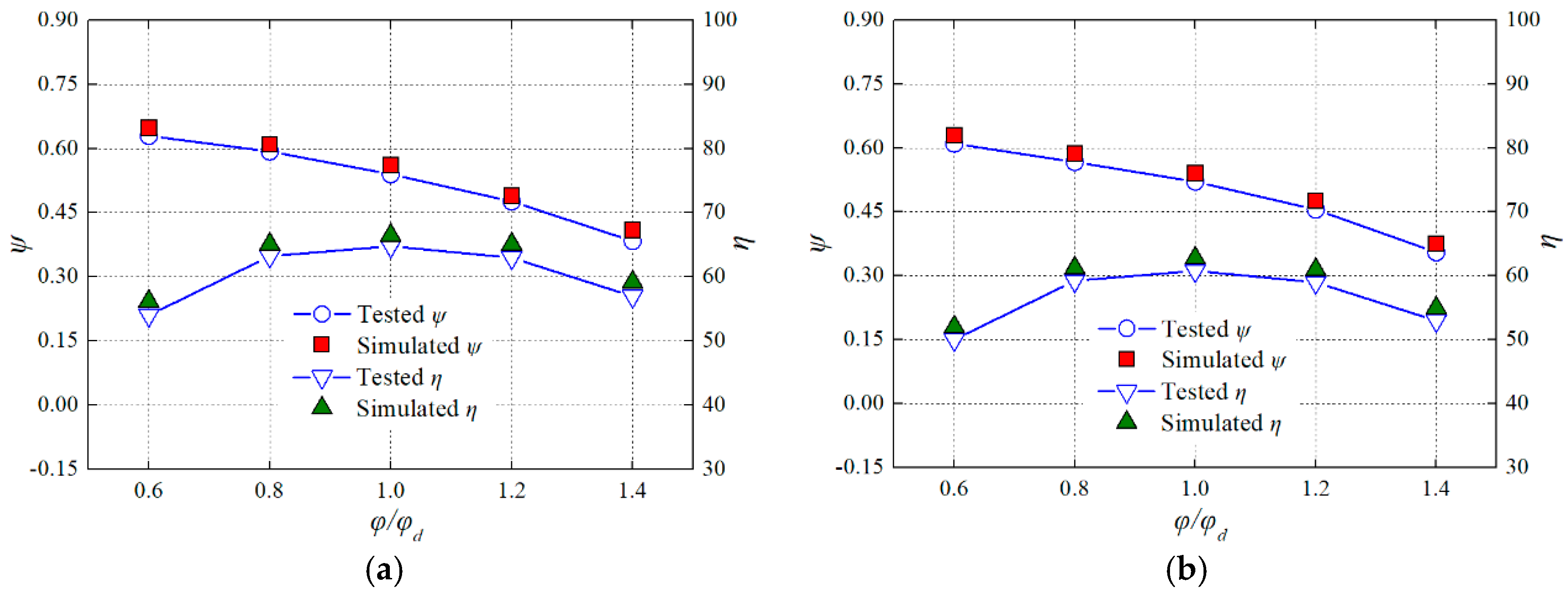
2.3. CFD Methodology
3. Result and Discussion
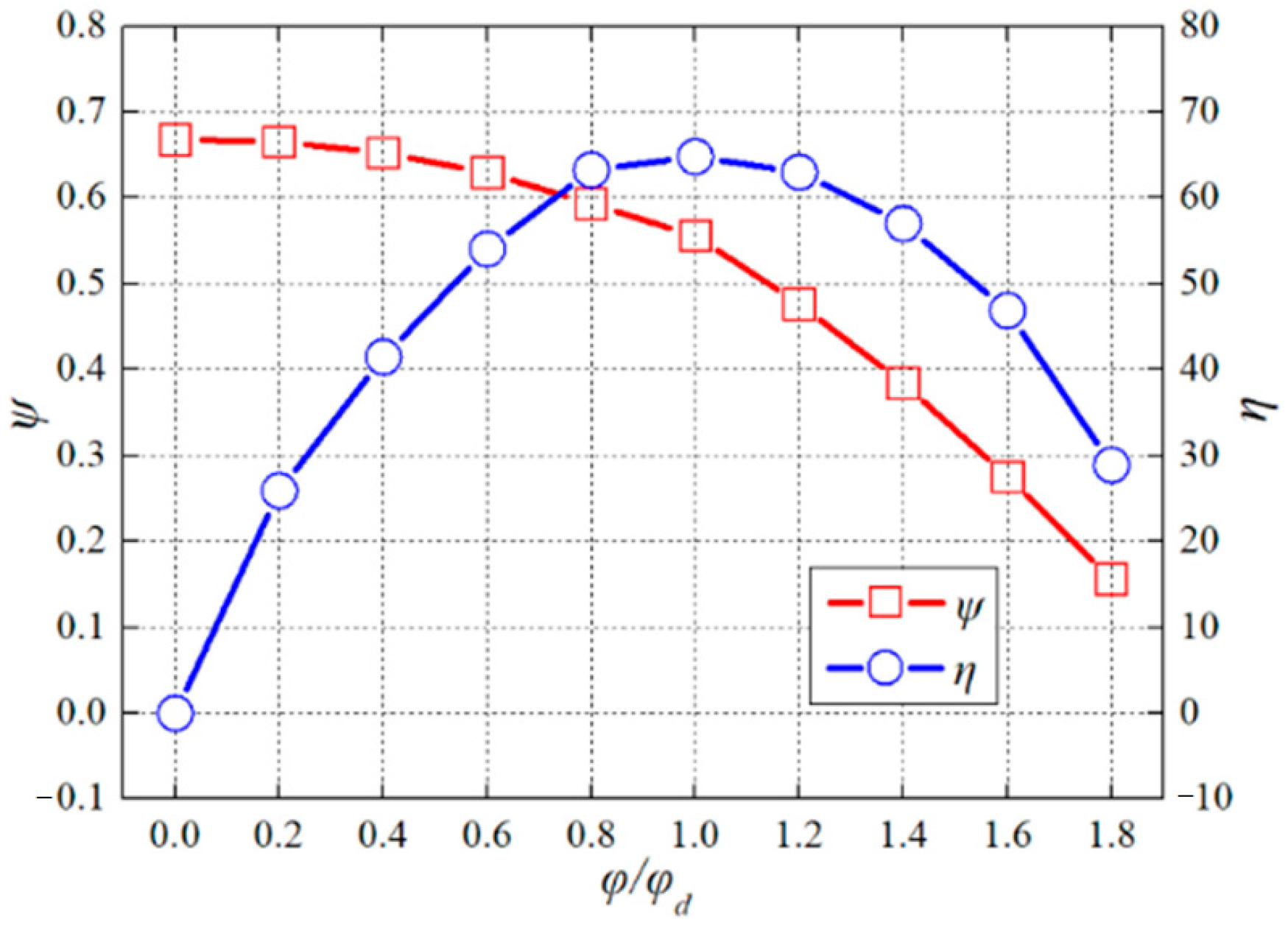
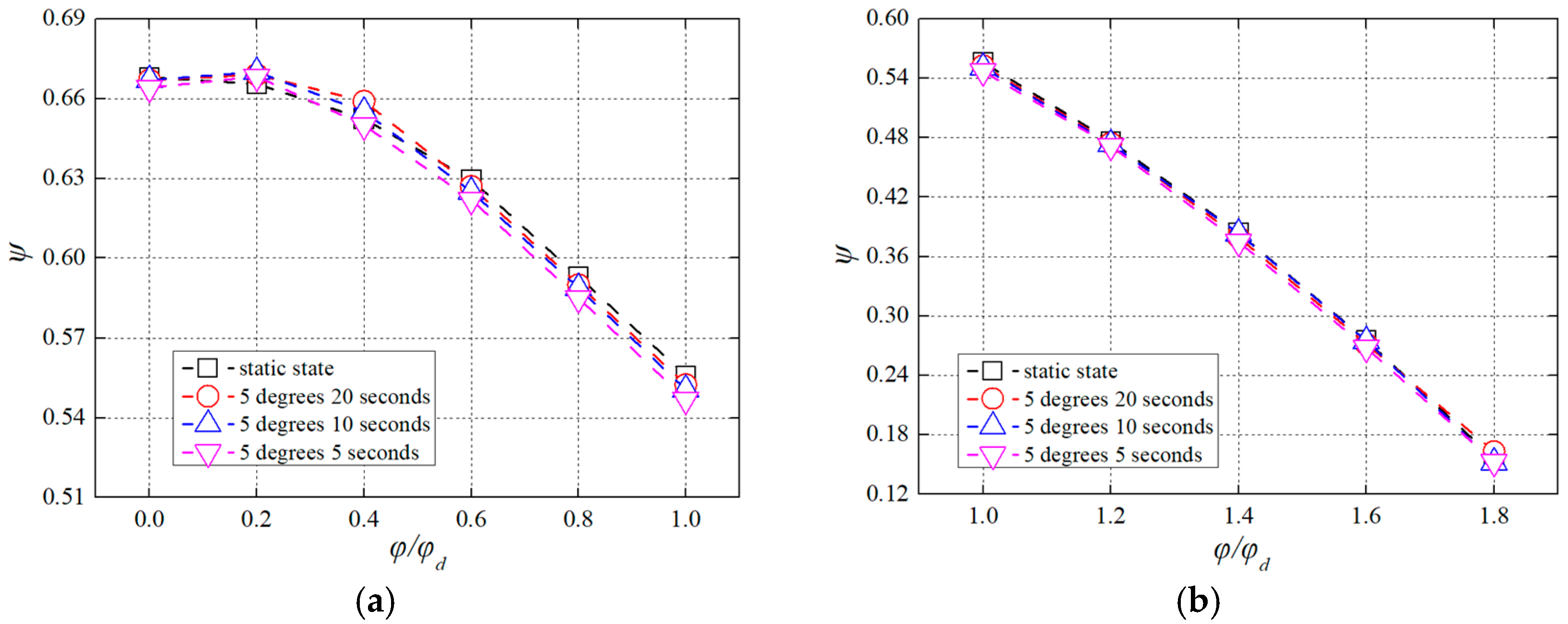
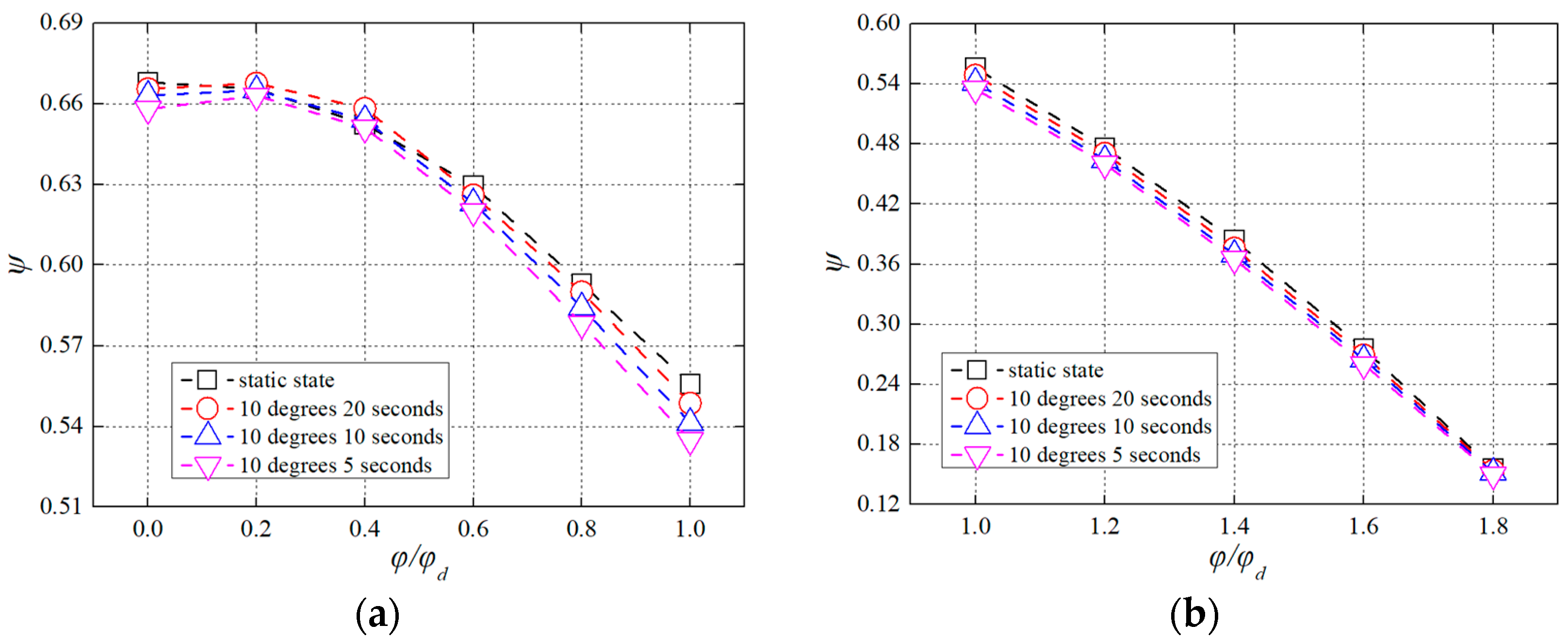
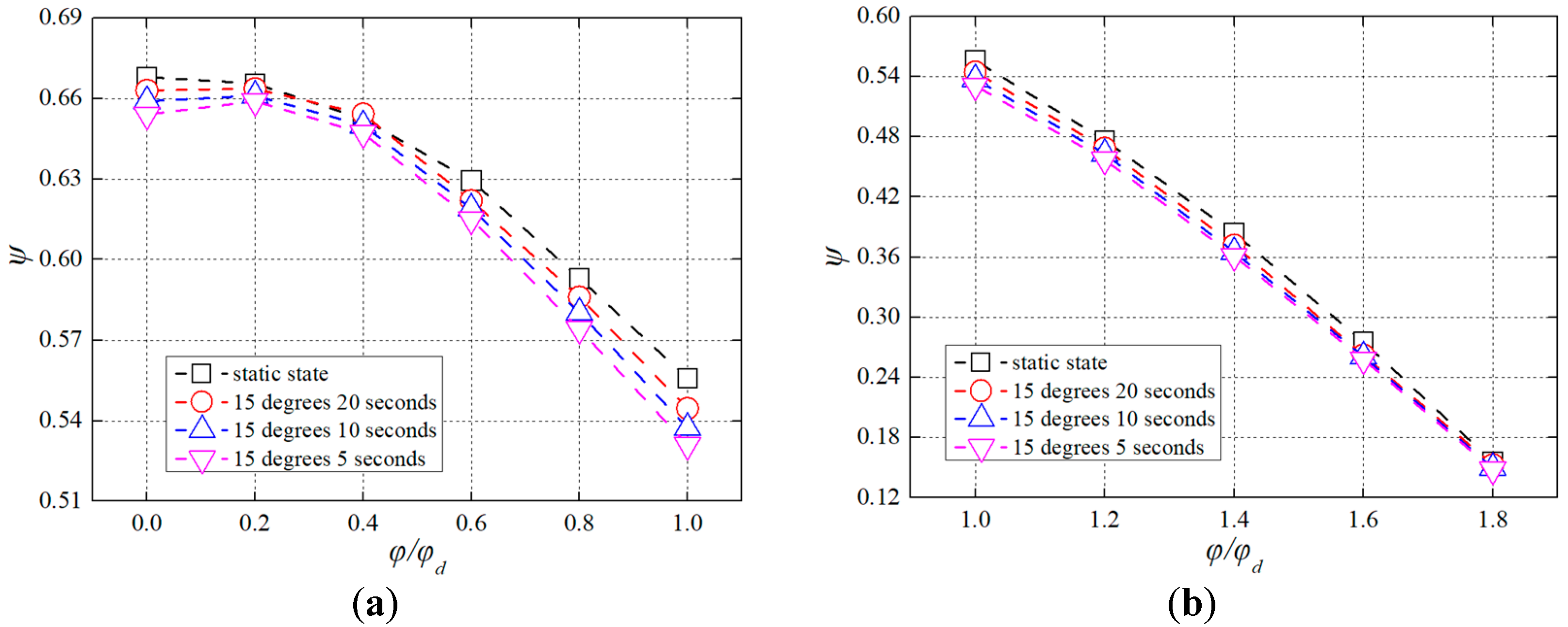
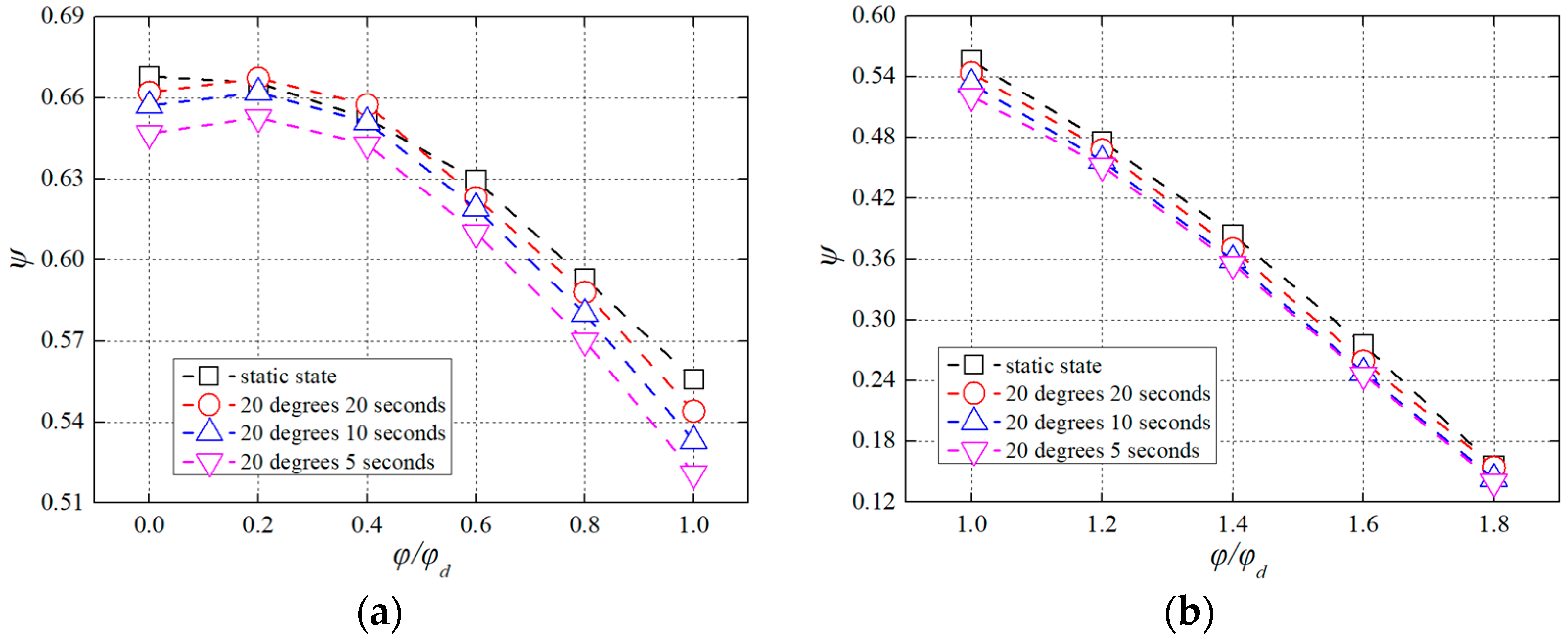
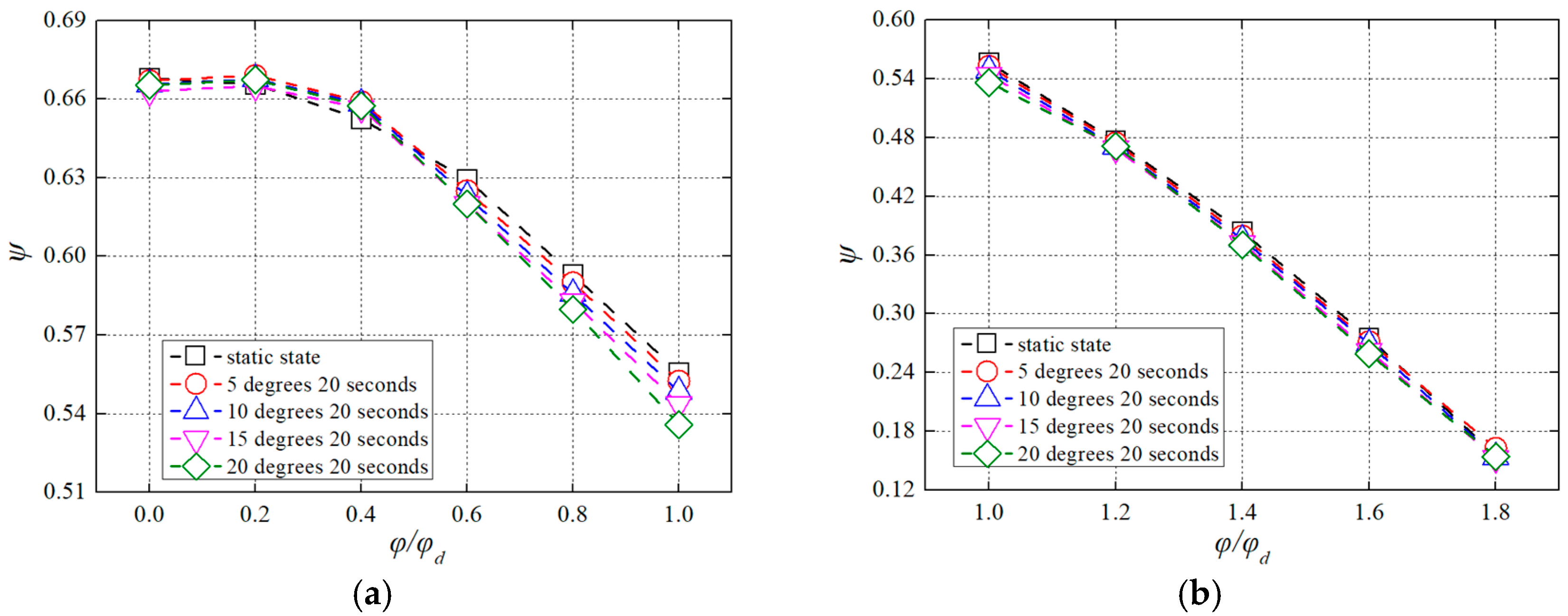
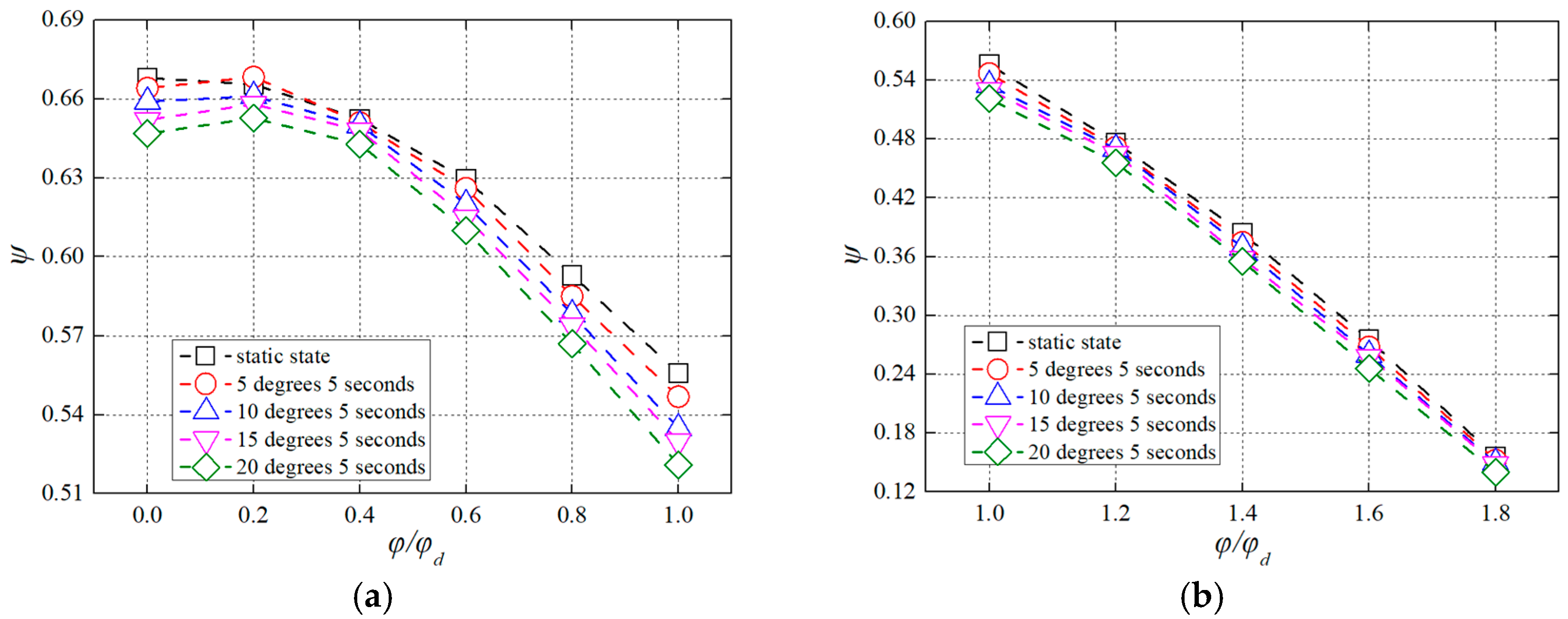
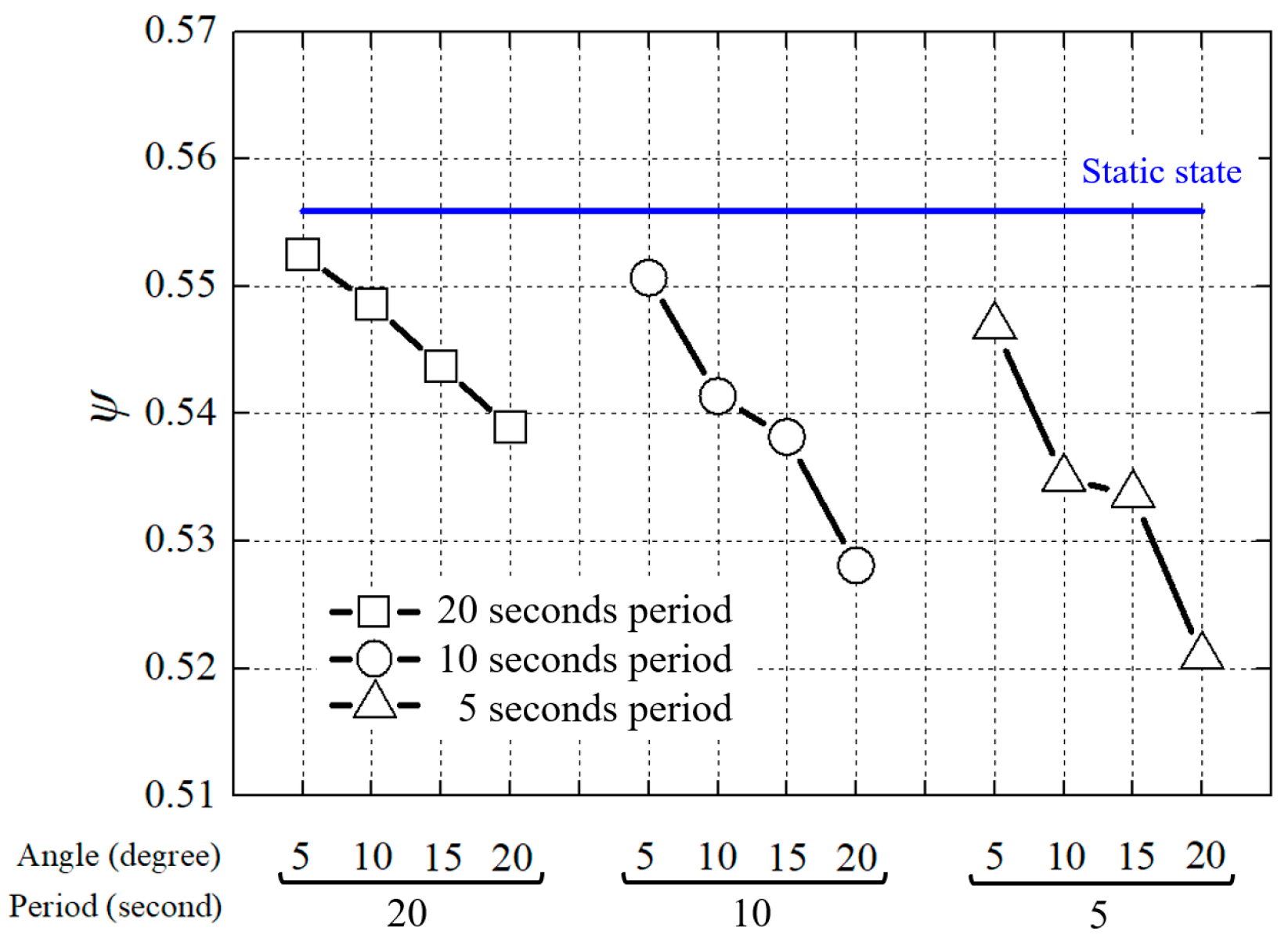
3.1. Pump Test Performances under Pitch Conditions
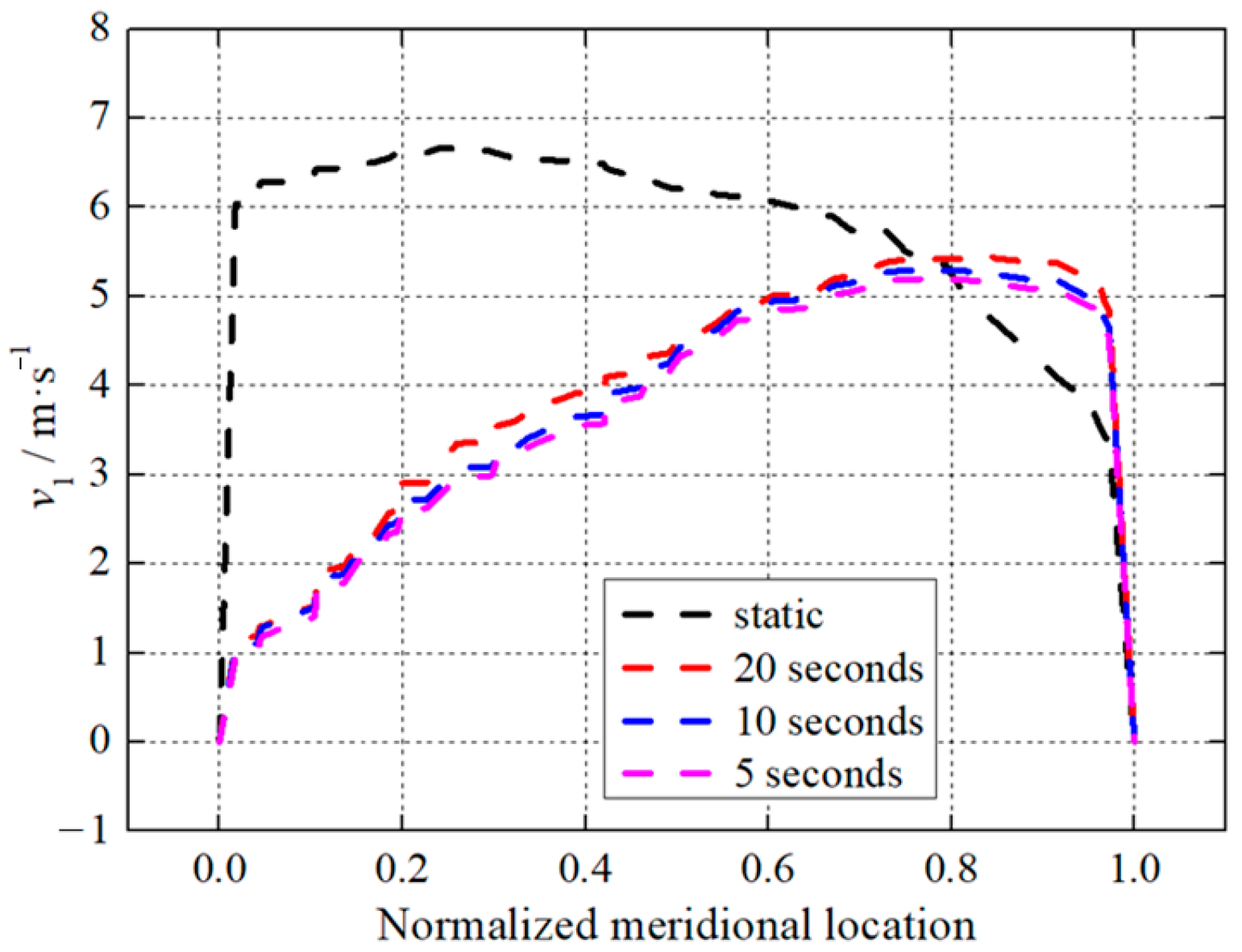
3.2. Flow Characteristics under Pitch Motion
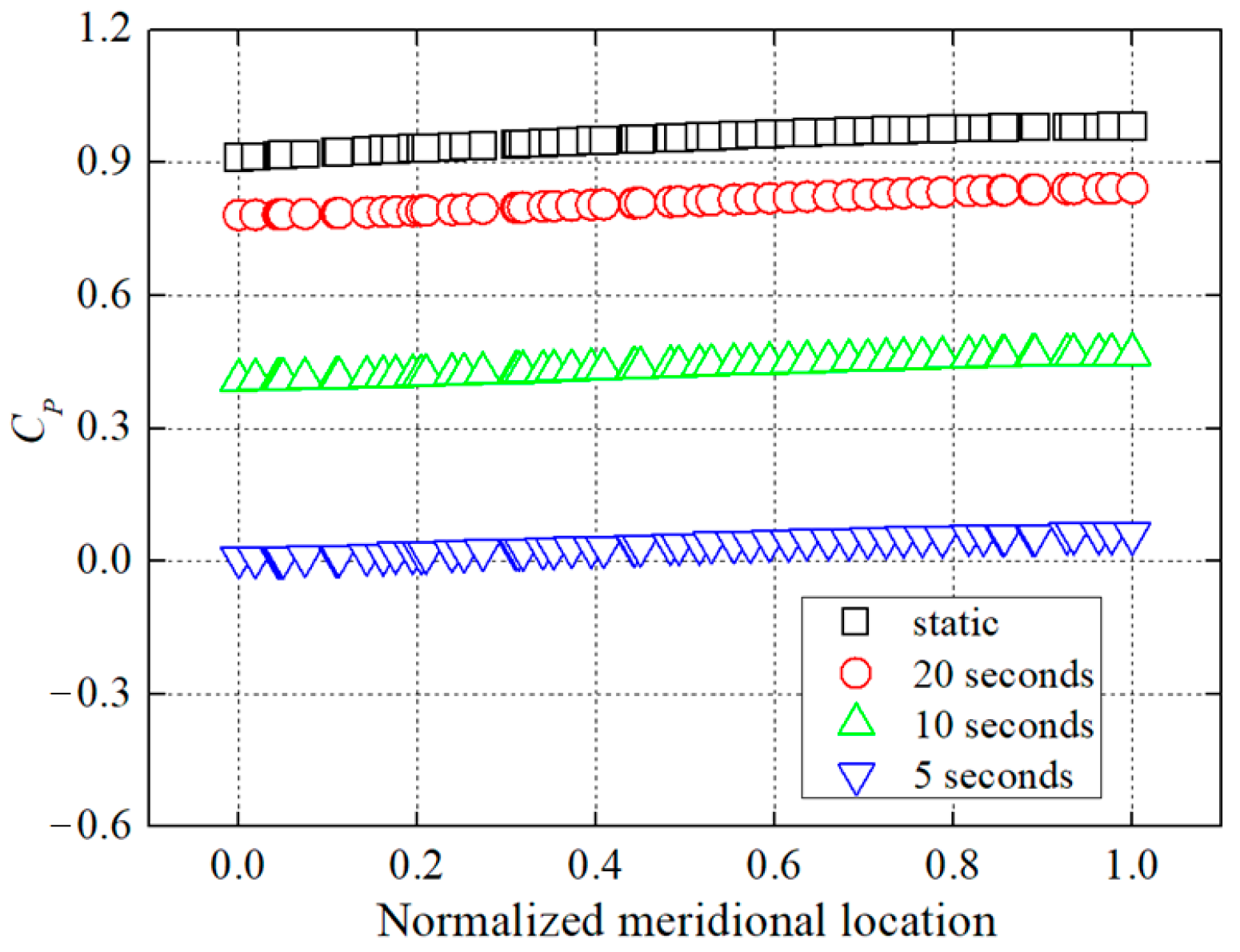
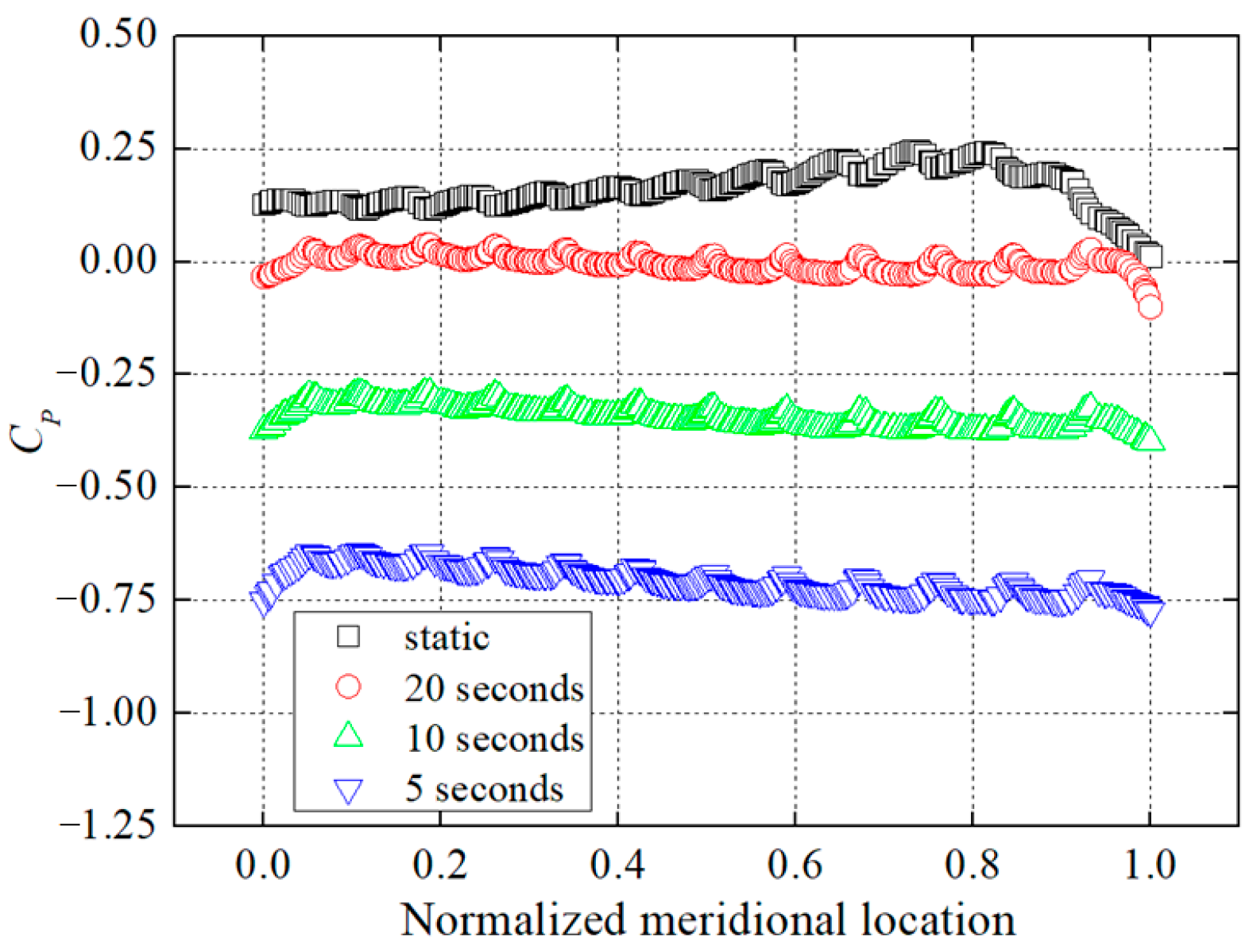
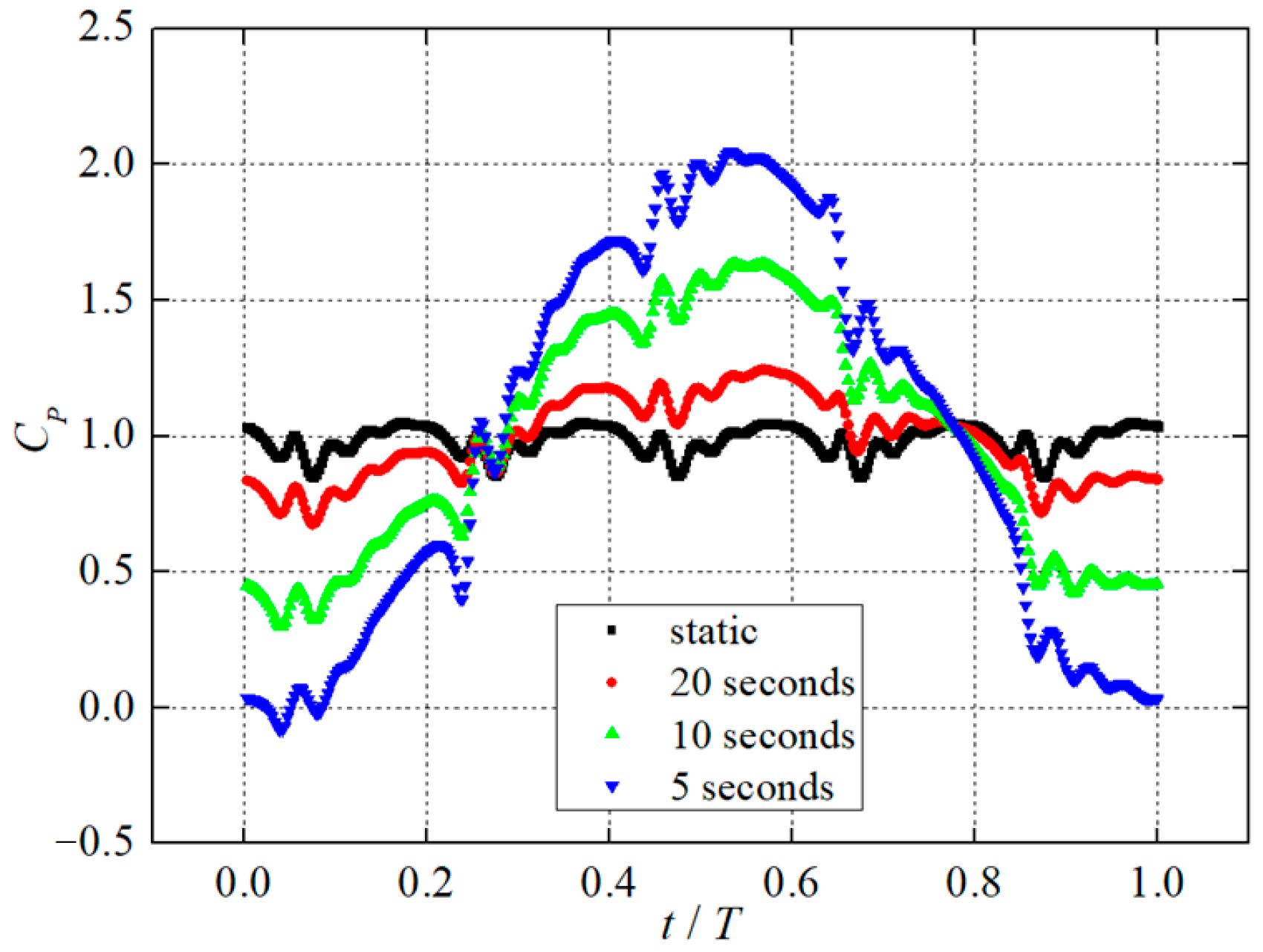
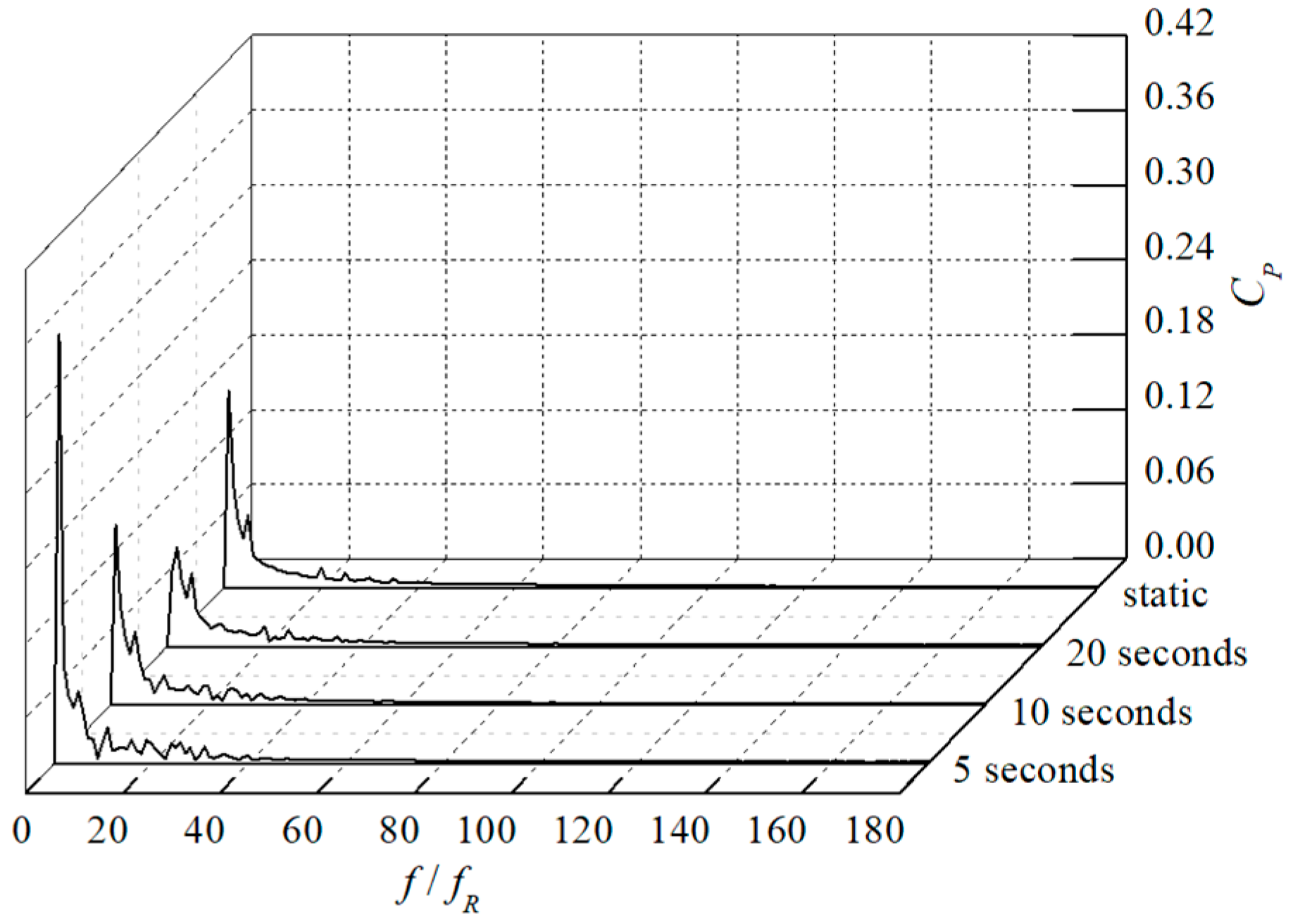
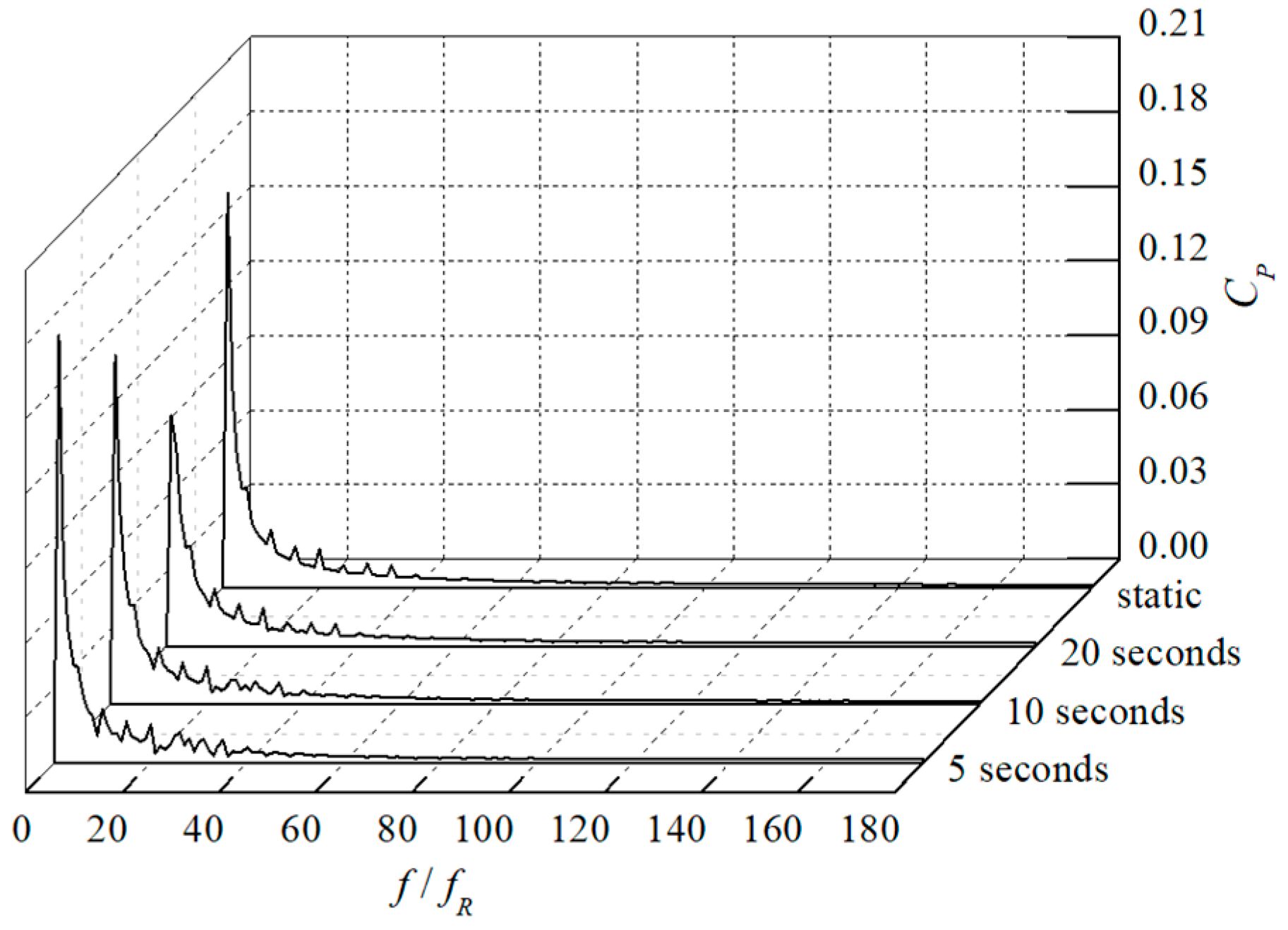
3.3. Unsteady Pressure Characteristics
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ghamkhar, K.; Ebrahimi, A.; Shariloo, K. Wavelet analysis of the flow field around an oscillating airfoil undergoing pure pitching motion at low Reynolds number. Phys. Fluids 2023, 35, 063607. [Google Scholar] [CrossRef]
- Xu, B.; Kang, H.; Shen, X.; Li, Z.; Cai, X.; Hu, Z. Aerodynamic analysis of a downwind offshore floating wind turbine with rotor uptilt angles in platform pitching motion. Ocean Eng. 2023, 281, 114951. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, X.; Mei, Y.; Ye, Z.; Guo, X. Effect of coupled platform pitch-surge motions on the aerodynamic characters of a horizontal floating offshore wind turbine. Renew. Energy 2022, 196, 278–297. [Google Scholar] [CrossRef]
- Chang, S.W.; Chen, Z.C. Hydrothermal performance of turbulent channel flow enhanced by spirally finned tube bundle in pitching and rolling motions. Therm. Sci. Eng. Prog. 2023, 37, 101567. [Google Scholar] [CrossRef]
- Yan, B.H. Review of the nuclear reactor thermal hydraulic research in ocean motions. Nucl. Eng. Des. 2017, 313, 370–385. [Google Scholar] [CrossRef]
- Hwang, J.; Lee, Y. Characteristics of critical heat flux under rolling condition for flow boiling in vertical tube. Nucl. Eng. Des. 2012, 252, 153–162. [Google Scholar] [CrossRef]
- Jin, G.; Yan, C.; Sun, L.; Xing, D. Effect of rolling motion on transient flow resistance of two-phase flow in a narrow rectangular duct. Ann. Nucl. Energy 2014, 64, 135–143. [Google Scholar] [CrossRef]
- Wang, Z.; He, Y.; Duan, Z.; Huang, C.; Yuan, Y.; Li, M.; Liu, S. Effects of rolling motion on transient flow behaviors of gas-liquid two-phase flow in horizontal pipes. Ocean Eng. 2022, 255, 111482. [Google Scholar] [CrossRef]
- Tan, S.; Wang, Z.; Wang, C.; Lan, S. Flow fluctuations and flow friction characteristics of vertical narrow rectangular channel under rolling motion conditions. Exp. Therm. Fluid Sci. 2013, 50, 69–78. [Google Scholar] [CrossRef]
- Abdelsalam, S.I.; Alsharif, A.M.; Elmaboud, Y.A.; Abdellateef, A.I. Assorted kerosene-based nanofluid across a dual-zone vertical annulus with electroosmosis. Heliyon 2023, 5, e15916. [Google Scholar] [CrossRef]
- Chen, C.; Gao, P.; Tan, S.; Huang, D.; Yu, Z. Effect of rolling motion on two-phase frictional pressure drop of boiling flows in a rectangular narrow channel. Ann. Nucl. Energy 2015, 83, 125–136. [Google Scholar] [CrossRef]
- Yuan, Y.; Fang, Y.; Tang, L. Effects of non-uniform elbow inflow on the unsteady flow and energy development characteristics of a centrifugal pump. Phys. Fluids 2023, 35, 015152. [Google Scholar] [CrossRef]
- Yuan, Y.; Yuan, S.; Tang, L. Investigation on the effect of complex impeller on vibration characteristics for a high-speed centrifugal pump. Proc. Inst. Mech. Eng. Part A J. Power Energy 2020, 234, 611–624. [Google Scholar] [CrossRef]
- Tang, L.; Yuan, S.; Tang, Y.; Qiu, Z. Optimization of impulse water turbine based on GA-BP neural network arithmetic. J. Mech. Sci. Technol. 2019, 33, 241–253. [Google Scholar] [CrossRef]
- Zhu, Z.; Liu, H. Dynamic Pressure Test and Analysis of Marine Ballasted Centrifugal Pump under Rapid Changing Conditions. J. Mar. Sci. Eng. 2021, 9, 1299. [Google Scholar] [CrossRef]
- Zhang, H.; Kong, F.; Zhu, A.; Zhao, F.; Xu, Z. Effect of Blade Outlet Angle on Acoustics of Marine Centrifugal Pump. Acoust. Aust. 2020, 48, 419–430. [Google Scholar] [CrossRef]
- Abdelsalam, S.I.; Magesh, A.; Tamizharasi, P.; Zaher, A.Z. Versatile response of a Sutterbynanofluid under activationenergy: Hyperthermia therapy. Int. J. Numer. Heat Fluid Flow 2023, 7, 0961–5539. [Google Scholar]
- Ye, C.; Tang, Y.; An, D.; Wang, F.; Zheng, Y.; van Esch, B.P.M. Investigation on stall characteristics of marine centrifugal pump considering transition effect. Ocean Eng. 2023, 280, 114823. [Google Scholar] [CrossRef]
- Alawadhi, K.; Alzuwayer, B.; Alrahmani, M.; Murad, A. Evaluation of the Erosion Characteristics for a Marine Pump Using 3D RANS Simulations. Appl. Sci. 2021, 11, 7364. [Google Scholar] [CrossRef]
- Xing, D.; Yan, C.; Sun, L.; Wang, C. Effect of rolling motion on single-phase laminar flow resistance of forced circulation with different pump head. Ann. Nucl. Energy 2013, 54, 141–148. [Google Scholar] [CrossRef]
- Abdelsalam, S.I.; Bhatti, M.M. Unraveling the nature of nano-diamonds and silica in a catheterized tapered artery: Highlights into hydrophilic traits. Sci. Rep. 2023, 13, 5684. [Google Scholar] [CrossRef]
- Xiao, H.L.; Luo, J.S. Shear-modified sub-grid model and its applications to turbulent channel flow. J. Aerosp. Power 2010, 25, 123–128. [Google Scholar]
- Shim, H.S.; Kim, K.Y. Effects of the number of blades on impeller-volute interaction and flow instability of a centrifugal pump. Proc. Inst. Mech. Eng. Part A J. Power Energy 2022, 236, 1500–1517. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, L. Tip clearance on pressure fluctuation intensity and vortex characteristic of a mixed flow pump as turbine at pump mode. Renew. Energy 2018, 129, 606–615. [Google Scholar] [CrossRef]
- Meng, Q.; Shen, X.; Zhao, X.; Yang, G.; Zhang, D. Numerical Investigation on Cavitation Vortex Dynamics of a Centrifugal Pump Based on Vorticity Transport Method. J. Mar. Sci. Eng. 2023, 11, 1424. [Google Scholar] [CrossRef]
- Silveira, N.; Meghoe, A.; Tinga, T. Integration of multiple failure mechanisms in a life assessment method for centrifugal pump impellers. Adv. Mech. Eng. 2023, 15, 16878132231175755. [Google Scholar] [CrossRef]
- Oro, J.M.F.; Perotti, R.B.; Vega, M.G.; González, J. Effect of the radial gap size on the deterministic flow in a centrifugal pump due to impeller-tongue interactions. Energy 2023, 278 Pt A, 127820. [Google Scholar]
- Capurso, T.; Bergamini, L.; Torresi, M. Performance analysis of double suction centrifugal pumps with a novel impeller configuration. Energy Convers. Manag. X 2022, 14, 100227. [Google Scholar] [CrossRef]










| impeller inlet diameter/m | 0.04 |
| impeller outlet diameter/m | 0.16 |
| blade outlet width/m | 0.006 |
| blade number | 5 |
| blade wrap angle/° | 120 |
| blade inlet angle/° | 22 |
| blade outlet angle/° | 24 |
| volute base circle diameter/m | 0.162 |
| volute outlet diameter/m | 0.032 |
| Parameters | Values | |
|---|---|---|
| Number of elements | N1/N2/N3 | 9.4 × 106/1.2 × 107/2.1 × 107 |
| Computed head coefficients (ψ) corresponding to N1, N2 and N3 | ψ1/ψ2/ψ3 | 0.565/0.561/0.559 |
| Apparent order | p | 1.32 |
| Grid convergence index corresponding to N1, N2 and N3 | GCI1/GCI2/GCI3 | 3.08%/2.12%/1.93% |
| Level 1 | Level 2 | Level 3 | Level 4 | |
|---|---|---|---|---|
| θmax/degree | 5 | 10 | 15 | 20 |
| k/second | 5 | 10 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Y.; Gong, W.; Wang, G.; Wang, J. Research on the Performance Characteristics and Unsteady Flow Mechanism of a Centrifugal Pump under Pitch Motion. Water 2023, 15, 3706. https://doi.org/10.3390/w15203706
Yuan Y, Gong W, Wang G, Wang J. Research on the Performance Characteristics and Unsteady Flow Mechanism of a Centrifugal Pump under Pitch Motion. Water. 2023; 15(20):3706. https://doi.org/10.3390/w15203706
Chicago/Turabian StyleYuan, Ye, Weihong Gong, Guojun Wang, and Jun Wang. 2023. "Research on the Performance Characteristics and Unsteady Flow Mechanism of a Centrifugal Pump under Pitch Motion" Water 15, no. 20: 3706. https://doi.org/10.3390/w15203706
APA StyleYuan, Y., Gong, W., Wang, G., & Wang, J. (2023). Research on the Performance Characteristics and Unsteady Flow Mechanism of a Centrifugal Pump under Pitch Motion. Water, 15(20), 3706. https://doi.org/10.3390/w15203706





