Application of the Monte-Carlo Method to Assess the Operational Reliability of a Household-Constructed Wetland with Vertical Flow: A Case Study in Poland
Abstract
:1. Introduction
2. Materials and Methods
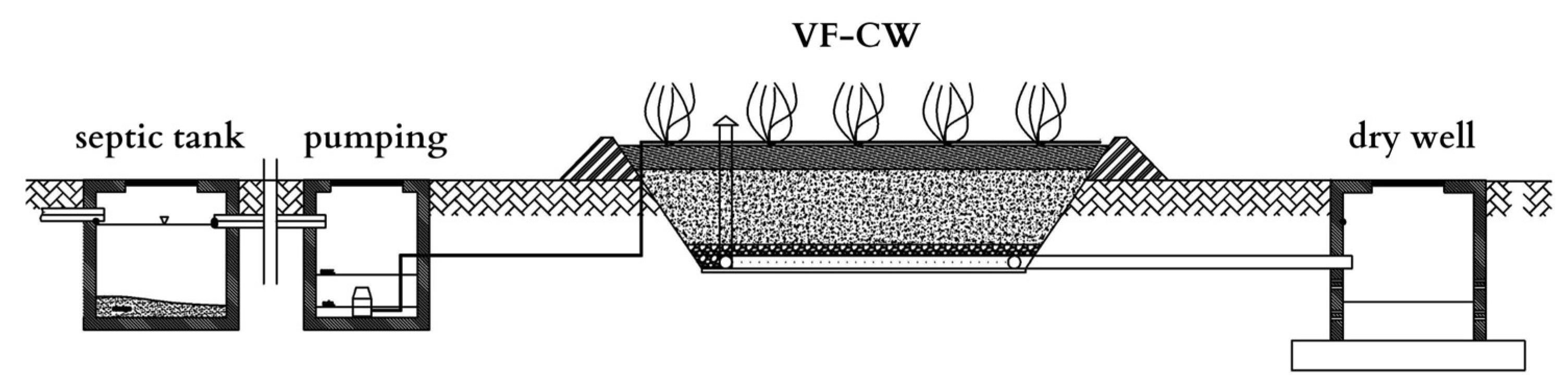
2.1. Description of Study Object
2.2. Preliminary Data Analysis
2.3. Theoretical Distribution Fitting
2.4. Indication of the Best-Fit Theoretical Distributions
2.5. Modelling of Pollutant Indicator Values
2.6. Determination of Reliability Coefficients for the Operation of the CW System
3. Results and Discussion
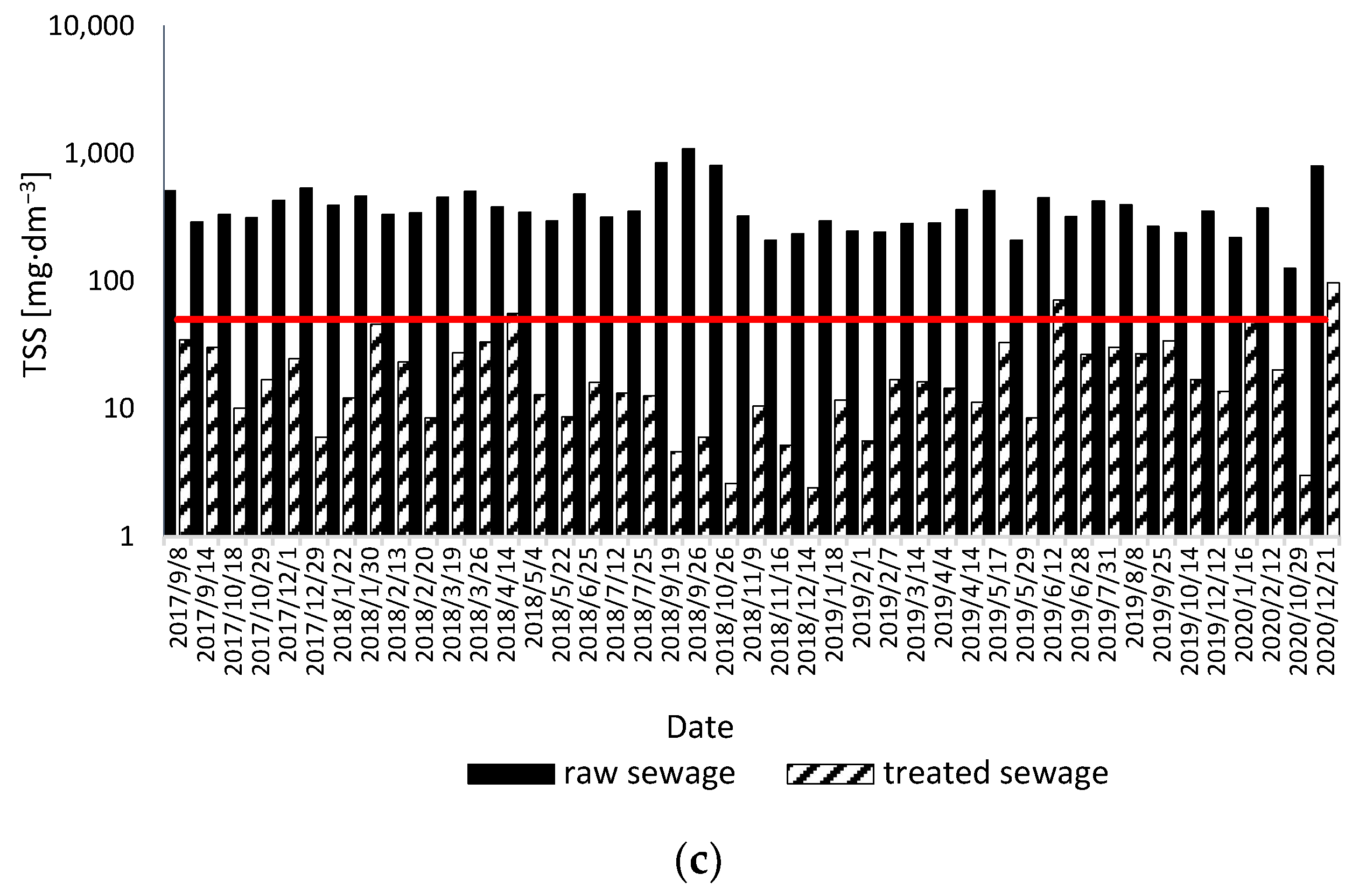
3.1. Preliminary Analysis
3.2. Fitting the Theoretical Distributions
3.3. Indication of the Best-Fit Probability Distribution
3.4. Determination of Reliability Coefficients for the Operation of VF-CW
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Steer, D.; Fraser, L.; Boddy, B.; Seibert, B. Efficiency of small constructed wetlands for subsurface treatment of single-family domestic effluent. Ecol. Eng. 2002, 18, 429–440. [Google Scholar] [CrossRef]
- Brix, H.; Arias, C.A. The use of vertical flow constructed wetlands for on-site treatment of domestic wastewater: New Danish guidelines. Ecol. Eng. 2005, 25, 491–500. [Google Scholar] [CrossRef]
- Seo, D.C.; DeLaune, R.D.; Park, W.Y.; Lim, J.S.; Seo, J.Y.; Lee, J.; Cho, J.S.; Heo, J.S. Evaluation of a hybrid constructed wetland for treating domestic sewage from individual housing units surrounding agricultural villages in South Korea. J. Environ. Monit. 2009, 11, 134–144. [Google Scholar] [CrossRef] [PubMed]
- Mikosz, J. Wastewater management in small communities in Poland. Desaliation Water Treat. 2013, 51, 2461–2466. [Google Scholar] [CrossRef]
- Jóźwiakowski, K.; Mucha, Z.; Generowicz, A.; Baran, S.; Bielińska, J.; Wójcik, W. The use of multi-criteria analysis for selection of technology for a household WWTP compatible with sustainable development. Arch. Environ. Prot. 2015, 41, 76–82. [Google Scholar] [CrossRef]
- Pawełek, J.; Bugajski, P. The development of household wastewater treatment plants in Poland—Advantages and disadvantages. Acta Sci. Pol. Form. Circumiectus 2017, 16, 3–14. (In Polish) [Google Scholar] [CrossRef]
- GUS. Municipal Infrastructure in 2020; Rocznik Statystyczny Rzeczypospolitej Polskiej; Główny Urząd Statystyczny: Warszawa, Poland, 2021. (In Polish)
- Mucha, Z.; Mikosz, J. Rational application of small wastewater treatment plants according to sustainability criteria. Czas. Tech. Sr. 2009, 106, 91–100. (In Polish) [Google Scholar]
- Martín, I.; Betancort, J.R.; Pidre, J.R. Contribution of non-conventional technologies for sewage treatment to improve the quality of bathing waters (ICREW project). Desalination 2007, 215, 82–89. [Google Scholar] [CrossRef]
- Bugajski, P.; Kaczor, G. The assessment of working sewage treatment plant at Wadowice before the modernization. Przemysł Chem. 2008, 87, 44–426. (In Polish) [Google Scholar]
- Orlik, T.; Jóźwiakowski, K. Evaluation of two BATEX wastewater treatment plants with a filtration outlet. Inżynieria Rol. 2003, 3, 109–119. (In Polish) [Google Scholar]
- Keffala, C.; Ghrabi, A. Nitrogen and bacterial removal in constructed wetlands treating domestic waste water. Desalination 2005, 185, 383–389. [Google Scholar] [CrossRef]
- De Filippis, L.F. Role of Phytoremediation in Radioactive Waste Treatment. In Soil Remediation and Plants; Academic Press: San Diego, CA, USA, 2015; pp. 207–254. [Google Scholar]
- Yeh, T.Y.; Chou, C.C.; Pan, C.T. Heavy metal removal within pilot-scale constructed wetlands receiving river water contaminated by confined swine operations. Desalination 2009, 249, 368–373. [Google Scholar] [CrossRef]
- Sheoran, A.S.; Sheoran, V. Heavy metal removal mechanism of acid mine drainage in wetlands: A critical review. Miner. Eng. 2006, 19, 105–116. [Google Scholar] [CrossRef]
- Arivoli, A.; Mohanraj, R.; Seenivasan, R. Application of vertical flow constructed wetland in treatment of heavy metals from pulp and paper industry wastewater. Environ. Sci. Pollut. Res. 2015, 22, 13336–13343. [Google Scholar] [CrossRef]
- Hendy, I.; Zelenakova, M.; Pietrucha-Urbanik, K.; Salama, Y.; Abu-hashim, M. Decentralized Constructed Wetlands for Wastewater Treatment in Rural and Remote Areas of Semi-arid Regions. Water 2023, 15, 2281. [Google Scholar] [CrossRef]
- Haynes, R.J. Use of industrial wastes as media in constructed wetlands and filter beds—Prospects for removal of phosphate and metals from wastewater streams. Crit. Rev. Environ. Sci. Technol. 2015, 45, 1041–1103. [Google Scholar] [CrossRef]
- Hua, T.; Haynes, R.J.; Zhou, Y.F.; Boullemant, A.; Chandrawana, I. Potential for use of industrial waste materials as filter media for removal of Al, Mo, As, V and Ga from alkaline drainage in constructed wetlands—Adsorption studies. Water Resour. 2015, 71, 32–41. [Google Scholar] [CrossRef] [PubMed]
- Młyński, D.; Chmielowski, K.; Młyńska, A. The assesment of the efficency and stability of work sewage treatment plant in Zabajka. Inżynieria Ekol. 2016, 47, 123–130. (In Polish) [Google Scholar] [CrossRef]
- Olyaei, M.A.; Karamouz, M.; Asce, F.; Farmani, R. Framework for assessing flood reliability and resilience of wastewater treatment plants. J. Environ. Eng. 2018, 144, 1–14. [Google Scholar] [CrossRef]
- Bugajski, P.; Almeida, M.A.A.; Kurek, K. Reliablity of sewage treatment plants processing sewage from school buildings located in non-urban areas. Infrastruct. Ecol. Rural. Areas 2016, 4, 1547–1557. [Google Scholar]
- Marzec, M. Reliability of removal of selected pollutants in different technological solutions of household wastewater treatment plants. J. Water Land Dev. 2017, 35, 141–148. [Google Scholar] [CrossRef]
- Jóźwiakowski, K.; Bugajski, P.; Mucha, Z.; Wójcik, W.; Jucherski, A.; Nastwany, M.; Siwiec, T.; Mazur, A.; Obroślak, R.; Gajewska, M. Reliability and efficiency of pollution removal during long-term operation of a one-stage constructed wetland system with horizontal flow. Sep. Purif. Technol. 2017, 187, 60–66. [Google Scholar] [CrossRef]
- Młyński, D.; Bugajski, P.; Młyńska, A. Application of the mathematical simulation methods for the assessment of the wastewater treatment plant operation work reliability. Water 2019, 11, 873. [Google Scholar] [CrossRef]
- Mitrenga, D. Methodological Basis of the Monte Carlo Stochastic Simulation. Stud. Ekon. Uniw. Ekon. W Katowicach 2014, 204, 164–180. (In Polish) [Google Scholar]
- Ferson, S. What Monte Carlo methods cannot do. Hum. Ecol. Risk Assess. Int. J. 1996, 4, 990–1007. [Google Scholar] [CrossRef]
- PN-C-04620-02:1974; Water and Sewage—Sampling—General Provision and Scope of the Standard. Polski Komitet Normalizacji, Miar i Jakości: Warszawa, Poland, 1975. (In Polish)
- PN-EN 25667-2:1999; Water Quality—Sampling—Guidance on Sampling Techniques. Polski Komitet Normalizacyjny: Warszawa, Poland, 1999. (In Polish)
- Water Quality—Determination of Biochemical Oxygen Demand after n Days (BOD)—Part 1: Dilution and Vaccination Method with the Addition of Allythiourea; Polski Komitet Normalizacyjny: Warszawa, Poland, 2002. (In Polish)
- Water Quality—Determination of the Chemical Oxygen Demand Index (ST-COD)—Small-Scale Sealed-Tube Method; Polski Komitet Normalizacyjny: Warszawa, Poland, 2005. (In Polish)
- Water Quality—Determination of Suspended Solids—Method by Filtration trough Filters; Polski Komitet Normalizacyjny: Warszawa, Poland, 2007. (In Polish)
- Regulation of the Minister of Environment of November 18, 2014 Laying down Conditions for the Introduction of Sewage into Water or Soil and Substances Particularly Harmful to the Aquatic Environments (No 2014 Item 1800). Available online: https://isap.sejm.gov.pl/isap.nsf/download.xsp/WDU20140001800/O/D20141800.pdf (accessed on 10 September 2023). (In Polish)
- Rozporządzenie Ministra Gospodarki Morskiej i Żeglugi Śródlądowej z dnia 12 lipca 2019 r.w Sprawie Substancji Szczególnie Szkodliwych dla Środowiska Wodnego Oraz Warunków, Jakie Należy Spełnić przy Wprowadzaniu do wód lub do Ziemi ścieków, a Także przy Odprowadzaniu wód Opadowych lub Roztopowych do wód lub do Urządzeń Wodnych. Regulation of the Minister of Maritime Economy and Inland Navigation of 12 July 2019 on Substances Particularly Harmful to the Aquatic Environment and Conditions to Be Met during Sewage Discharge into the Water or into the Ground and during Rainwater or Snowmelt Discharge into the Water or into the Water Devices. Available online: https://isap.sejm.gov.pl/isap.nsf/download.xsp/WDU20190001311/O/D20191311.pdf (accessed on 10 September 2023). (In Polish)
- Jagiełło, R.; Beker, C.; Jagodziński, A.M. Goodness of fit evaluation of the breast height diameter distributions of beech stands differing in age with selected theoretical distributions. Sylwan 2016, 160, 107–119. (In Polish) [Google Scholar]
- Glickman, T.S.; Xu, F. The distribution of the product of two random variables. Stat. Probab. Lett. 2008, 78, 2821–2826. [Google Scholar] [CrossRef]
- Wang, X. Vehicle Noise and Vibration Refinement; Woodhead Publishing: Cambridge, UK, 2010. [Google Scholar]
- Zoran, D.; Weiss, Y. From learning models of natural image patches to whole image restoration. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 479–486. [Google Scholar]
- Yu, G.; Sapiro, G.; Mallat, S. Solving inverse problems with piecewise linear estimators: From gaussian mixture models to structured sparsity. IEEE Trans. Image Process. 2012, 21, 2481–2499. [Google Scholar]
- Wałęga, A.; Rutkowska, A.; Policht-Latawiec, A. Sensitivity of beta and Weibull synthetic unit hydrographs to input parameter changes. Pol. J. Environ. Stud. 2014, 1, 221–229. [Google Scholar]
- Alam, M.A.; Emuro, K.; Farnham, C.; Yuan, J. Best-fit probability distributions and return periods for maximum monthly rainfall in Bangladesh. Climate 2018, 6, 9–25. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, D.; Wu, J. Evaluating the three methods of goodness of fit test for frequency analysis. J. Risk Anal. Crisis Response 2015, 5, 178–187. [Google Scholar] [CrossRef]
- Evans, D.L.; Drew, J.H.; Leemis, L.M. The distribution of the Kolmogorov–Smirnov, Cramer–von Mises, and Anderson–Darling test statistics for exponential populations with estimated parameters. Comput. Probab. Appl. 2017, 247, 165–190. [Google Scholar]
- Jäntschi, L.; Bolboacă, S.D. Computation of probability associated with Anderson–Darling statistic. Mathematics 2018, 6, 88–104. [Google Scholar] [CrossRef]
- Ajmal, M.; Waseem, M.; Kim, D.; Kim, T.W. A Pragmatic Slope-Adjusted Curve Number Model to Reduce Uncertainty in Predicting Flood Runoff from Steep Watersheds. Water 2020, 12, 1469. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Yuan, Y.; Nie, J.; McCutcheon, S.C.; Taguas, E.V. Initial abstraction and curve numbers for semiarid watersheds in south eastern Arizona. Hydrol. Process. 2014, 28, 774–783. [Google Scholar] [CrossRef]
- Archibald, J.A.; Buchanan, B.; Fuka, D.R.; Georgakakos, C.B.; Lyon, S.W.; Walter, M.T. A simple, regionally parameterized model for predicting nonpoint source areas in the northeastern US. J. Hydrol. Reg. Stud. 2014, 1, 74–91. [Google Scholar] [CrossRef]
- Donigian, A.S.; Imhoff, J.C.; Bicknell, B.R. Predicting water quality resulting from agricultural nonpoint-source pollution via simulation: HSPF. In Agricultural Management and Water Quality; Iowa State University Press: Ames, IA, USA, 1983; pp. 200–249. [Google Scholar]
- Singh, J.; Knapp, H.V.; Arnald, J.G.; Demissie, M. Hydrologic modeling of the Iroquois River watershed using HSPF and SWAT. J. Am. Water Resour. Assoc. 2004, 41, 343–360. [Google Scholar] [CrossRef]
- Van Liew, M.W.; Arnold, J.G.; Garbrecht, J.D. Hydrologic simulation on agricultural watersheds: Choosing between two models. Trans. ASAE 2003, 46, 1539–15512. [Google Scholar] [CrossRef]
- Halton, J.H. A retrospective and prospective survey of the Monte Carlo method. SIAM Rev. 1970, 12, 1–63. [Google Scholar] [CrossRef]
- Schauberger, G.; Piringer, M.; Baumann-Stanzer, K.; Knauder, W.; Petz, E. Use of a Monte Carlo technique to complete a fragment set of H2S emission rates from a wastewater treatment plant. J. Hazard. Mater. 2013, 263, 694–701. [Google Scholar] [CrossRef] [PubMed]
- Hendren, C.O.; Badireddy, A.R.; Casman, E.; Wiesner, M.R. Modeling nanomaterial fate in wastewater treatment: Monte Carlo simulation of silver nanoparticles (nano-Ag). Sci. Total Environ. 2013, 449, 418–425. [Google Scholar] [CrossRef] [PubMed]
- Barton, L.E.; Auffan, M.; Durenkamp, M.; McGrath, S.; Bottero, J.; Wiesner, M.R. Monte Carlo simulations of the transformation and removal of Ag, TiO2, and ZnO nanoparticles in wastewater treatment and land application of biosolids. Sci. Total Environ. 2015, 511, 535–543. [Google Scholar] [CrossRef] [PubMed]
- Andraka, D.; Dzienis, L. Modeling of risk in the operation of wastewater treatment plants. Rocz. Ochr. Sr. 2013, 15, 1111–1125. [Google Scholar]
- Kurek, K.; Bygajski, P.; Operacz, A.; Młyński, D.; Wałęga, A. Technological reliability of sewage treatment plant with the Pomiltek Mann type bioreactor. J. Water Land Dev. 2020, 46, 146–152. [Google Scholar]
- Kaczor, G. Concentrations of the pollutants in the sewage drained from the rural sewerage systems in lesser Poland voivodeship. Infrastrukt. Ekol. Teren. Wiej. 2009, 9, 97–104. (In Polish) [Google Scholar]
- Jóźwiakowski, K.; Bugajski, P.; Kurek, K.; Carvalho, F.; Almeida, A.; Siwiec, T.; Borowski, G.; Czekała, W.; Dach, J.; Gajewska, M. The efficiency and technological reliability of biogenic compounds removal during long-term operation of a one-stage subsurface horizontal flow constructed wetland. Sep. Purif. Technol. 2018, 202, 216–226. [Google Scholar] [CrossRef]
- Jucherski, A.; Nastawny, M.; Walczowski, A.; Jóźwiakowski, K.; Gajewska, M. Assessment of the technological reliability of a hybrid constructed wetland for wastewater treatment in a mountain eco-tourist farm in Poland. Water Sci. Technol. 2017, 75, 2649–2658. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Liu, Y.D.; Shen, Y.W.; Liu, H.; Xiong, Y. Effect of limited artificial aeration on constructed wetland treatment of domestic wastewater. Desalination 2010, 250, 915–920. [Google Scholar] [CrossRef]
- Wałęga, A.; Chmielowski, K.; Młyński, D. Influence of the Hybrid Sewage Treatment Plant’s Exploitation on Its Operation Effectiveness in Rural Areas. Sustainability 2018, 10, 2689. [Google Scholar] [CrossRef]
- Lu, S.; Pei, L.; Bai, X. Study on method of domestic wastewater treatment through new-type multi-layer artificial wetland. Int. J. Hydrogen Energy 2015, 40, 11207–11214. [Google Scholar] [CrossRef]
- Kuschk, P.; Wiener, A.; Kappelmeyer, U.; Weissbrodt, E.; Kästner, M.; Stottmeister, U. Annual cycle of nitrogen removal by a pilot-scale subsurface horizontal flow in a constructed wetland under moderate climate. Water Resour. 2003, 37, 4236–4242. [Google Scholar] [CrossRef] [PubMed]
- Kadlec, R.H.; Reddy, K. Temperature Effects in Treatment Wetlands. Water Environ. Res. 2001, 73, 543–557. [Google Scholar] [CrossRef]
- Stein, W.; Keblis, M. A new method to simulate the triangular distribution. Math. Comput. Model. 2009, 49, 1143–1147. [Google Scholar] [CrossRef]
- Pereira, E.J.S.; Pinho, J.T.; Galhardo, M.A.B.; Macêdo, W.M. Methodology of risk analysis by Monte Carlo Method applied to power generation with renewable energy. Renew. Energy 2014, 69, 347–355. [Google Scholar] [CrossRef]
- Młyński, D.; Młyńska, A.; Chmielowski, K.; Pawełek, J. Investigation of the Wastewater Treatment Plant Processes Efficiency Using Statistical Tools. Sustainability 2020, 12, 10522. [Google Scholar] [CrossRef]
- Vymazal, J. The use of sub-surface constructed wetlands for wastewater treatment in the Czech Republic: 10 years experience. Ecol. Eng. 2002, 18, 633–646. [Google Scholar] [CrossRef]
- Abdelhakeem, S.G.; Aboulroos, S.A.; Kamel, M.M. Performance of a vertical subsurface flow constructed wetland under different operational conditions. J. Adv. Res. 2016, 7, 803–814. [Google Scholar] [CrossRef]
- Ilyas, H.; Masih, I. The performance of the intensified constructed wetlands for organic matter and nitrogen removal: A review. J. Environ. Manag. 2017, 198, 372–383. [Google Scholar] [CrossRef]
- Sehar, S.; Sumera, S.; Naeem, I.; Perveen, N.; Ahmed, S. A comparative study of macrophytes influences on wastewater treatment through subsurface flow hybrid constructed wetland. Ecol. Eng. 2015, 81, 62–69. [Google Scholar] [CrossRef]
- Zhu, D.; Suna, C.; Zhang, H.; Wub, Z.; Jia, B.; Zhang, Y. Roles of vegetation, flow type and filled depth on livestock wastewater treatment through multi-level mineralized refuse-based constructed wetlands. Ecol. Eng. 2012, 39, 7–15. [Google Scholar] [CrossRef]
- Gajewska, M. Złoża hydrofitowe z pionowym przepływem ścieków charakterystyka procesów i zastosowań. Wydaw. Pol. Akad. Nauk. 2019, 150, 1–309. Available online: https://kis.pan.pl/images/stories/pliki/pdf/Monografie/Monografia-M-Gajewska-vol-150.pdf (accessed on 10 September 2023). (In Polish).
- Soroko, M. Annual Treatment Of Wastewater From Small Fruit And Vegetable Processing Plant In The Reed Bed System with Vertical Flow. Woda Sr. Obsz. Wiej. 2011, 11, 289–298. [Google Scholar]
- Wu, H.; Fan, J.; Zhang, J.; Ngo, H.H.; Guo, W.; Hu, Z.; Liang, S. Decentralized domestic wastewater treatment using intermittently aerated vertical flow constructed wetlands: Impact of influent strengths. Bioresour. Technol. 2015, 176, 163–168. [Google Scholar] [CrossRef]
- Wu, S.; Kuschk, P.; Brix, H.; Vymazal, J.; Dong, R. Development of constructed wetlands in performance intensifications for wastewater treatment: A nitrogen and organic matter targeted review. Water Resour. 2014, 57, 40–55. [Google Scholar] [CrossRef]

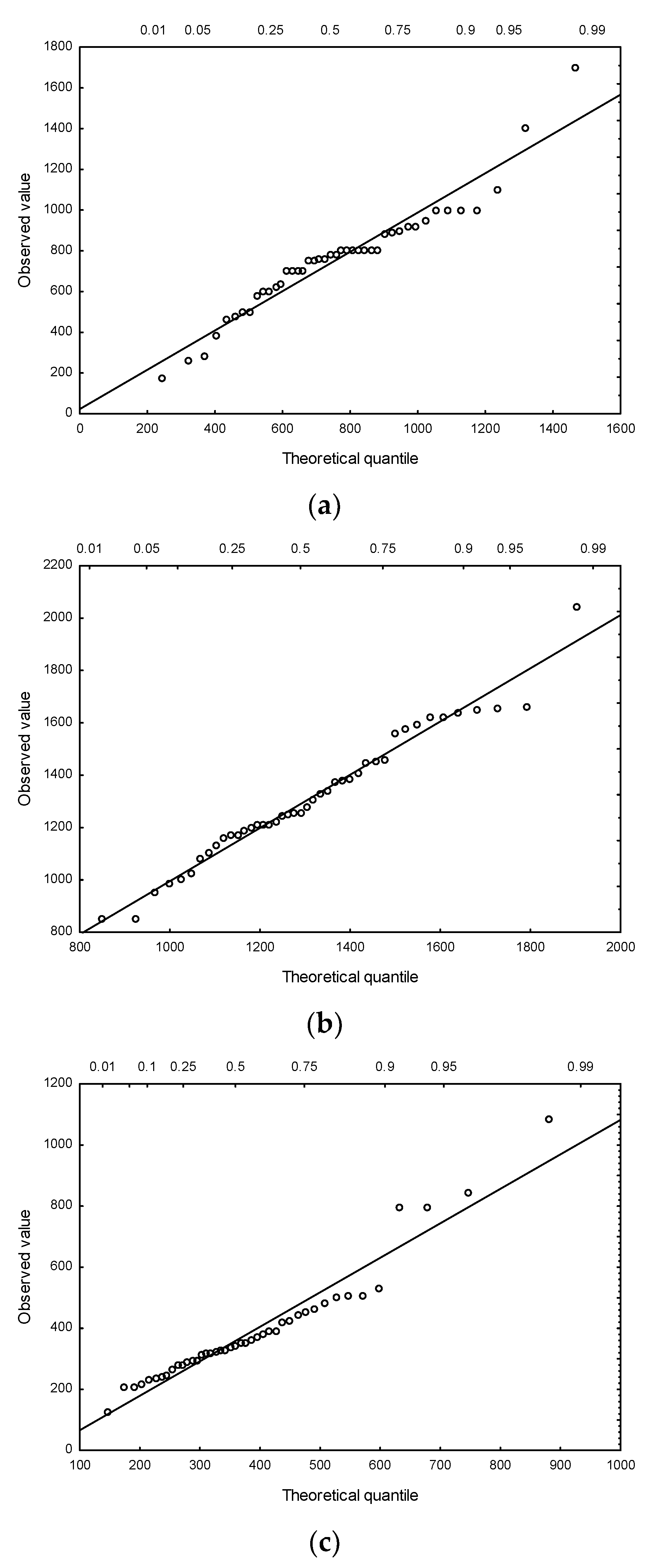
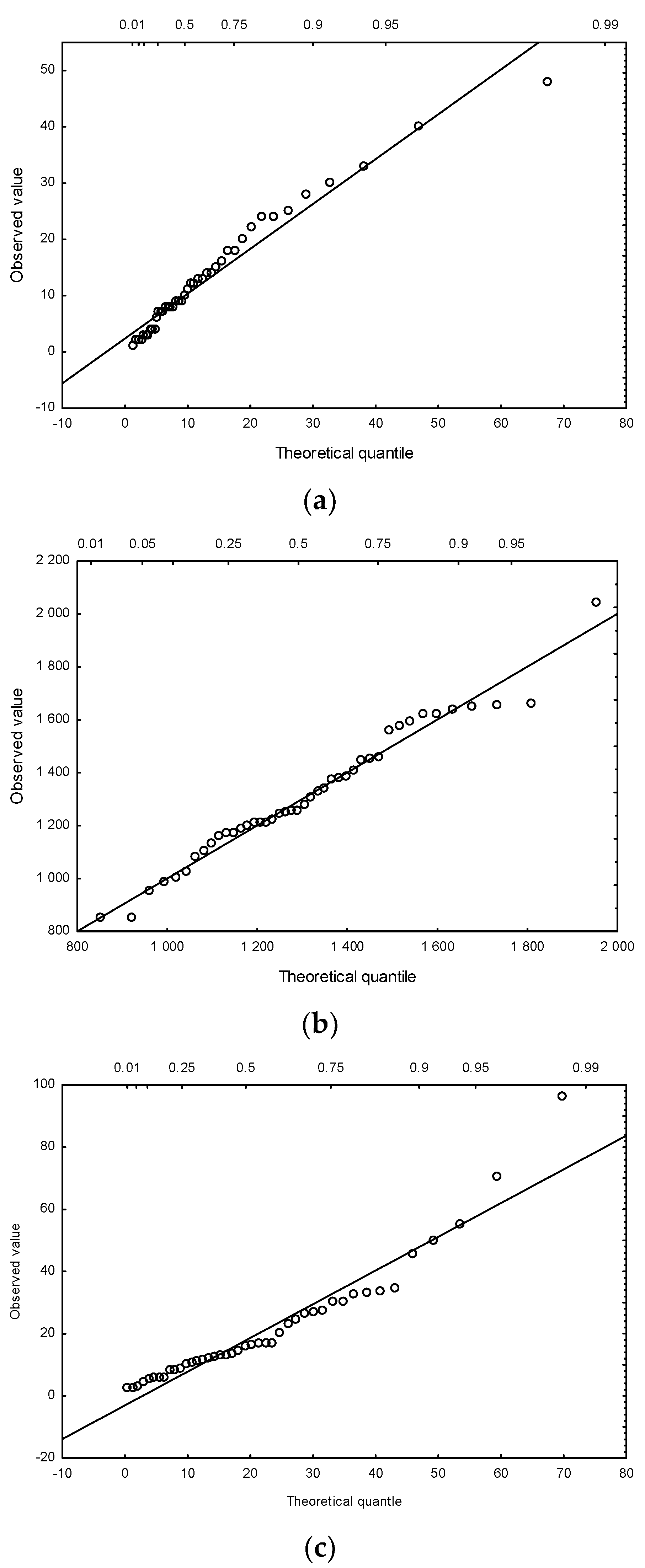
| Type of Indicator | Unit | Descriptive Statistics | |||||
|---|---|---|---|---|---|---|---|
| Raw Sewage | |||||||
| Min | Max | Mean | Median | s | Cs | ||
| BOD5 | mgO2∙dm−3 | 172.0 | 1700.0 | 760.7 | 780.0 | 10.6 | 0.79 |
| CODCr | mgO2∙dm−3 | 848.0 | 2041.0 | 1314.1 | 1257.0 | 245.9 | 0.19 |
| TSS | mg∙dm−3 | 125.0 | 1084.0 | 393.2 | 343.0 | 184.2 | 0.47 |
| Treated Sewage | |||||||
| BOD5 | mgO2∙dm−3 | 1.0 | 48.0 | 13.3 | 10.0 | 10.6 | 0.79 |
| CODCr | mgO2∙dm−3 | 114.0 | 304.0 | 162.0 | 150.0 | 41.2 | 0.25 |
| TSS | mg∙dm−3 | 2.4 | 96.0 | 21.5 | 16.0 | 18.8 | 0.87 |
| Distribution | BOD5 | CODCr | TSS | |||
|---|---|---|---|---|---|---|
| A–D | p | A–D | p | A–D | p | |
| Raw sewage | ||||||
| Johnson SB | 0.621 | 0.628 | 0.315 | 0.927 | N/A | N/A |
| Weibull | 1.045 | 0.334 | 0.701 | 0.557 | 1.939 | 0.099 |
| Gaussian | 0.344 | 0.901 | 0.313 | 0.928 | 0.233 | 0.979 |
| GEV | 0.945 | 0.387 | 0.322 | 0.921 | 0.353 | 0.893 |
| Half-normal | 7.914 | 0.000 | 13.698 | 0.000 | 5.948 | 0.001 |
| Log-normal | 1.692 | 0.137 | 0.322 | 0.921 | 0.584 | 0.662 |
| Pareto | 5.689 | 0.001 | 11.054 | 0.000 | 5.295 | 0.002 |
| Normal | 0.859 | 0.440 | 0.427 | 0.821 | 2.483 | 0.051 |
| Triangular | 4.399 | 0.006 | 2.863 | 0.032 | 6.563 | 0.001 |
| Rayleigh | 3.117 | 0.024 | 8.236 | 0.000 | 2.153 | 0.076 |
| Treated sewage | ||||||
| Johnson SB | 0.185 | 0.994 | 0.106 | 1.000 | 0.802 | 0.479 |
| Weibull | 0.223 | 0.982 | 1.612 | 0.152 | 0.411 | 0.837 |
| Gaussian | 0.287 | 0.947 | 0.195 | 0.992 | 0.433 | 0.814 |
| GEV | 0.296 | 0.941 | 0.209 | 0.988 | 0.208 | 0.988 |
| Half-normal | 0.388 | 0.860 | 11.495 | 0.000 | 0.934 | 0.393 |
| Log-normal | 0.394 | 0.854 | 0.649 | 0.602 | 0.203 | 0.990 |
| Pareto | 0.473 | 0.773 | 7.641 | 0.000 | 0.860 | 0.439 |
| Normal | 1.541 | 0.167 | 1.350 | 0.217 | 2.314 | 0.062 |
| Triangular | 4.667 | 0.004 | 6.915 | 0.000 | 9.779 | 0.000 |
| Rayleigh | 4.821 | 0.003 | 6.021 | 0.001 | 6.603 | 0.001 |
| Distribution | PBIAS [%] | |||||
|---|---|---|---|---|---|---|
| BOD5 | CODCr | TSS | ||||
| Raw | Treated | Raw | Treated | Raw | Treated | |
| Johnson SB | −1.276 | −0.185 | −0.026 | 0.184 | - | −2.551 |
| Weibull | 0.521 | −0.506 | 0.783 | 1.341 | 1.922 | 1.014 |
| Gaussian | 0.648 | 4.318 | −0.089 * | 0.045 | −0.197 | 8.392 |
| GEV | −1.648 * | −0.629 | −0.083 | 0.218 | −0.269 | −0.550 |
| Half-normal | - | 1.106 | - | 27.211 | - | −4.032 * |
| Log-normal | −1.097 | −0.987 * | −0.038 | −0.132 * | −0.359 * | −0.422 |
| Pareto | - | 8.085 | - | - | - | 11.007 |
| Normal | −0.048 | 38.029 | −0.036 | 0.038 | 2.575 | 42.708 |
| Rayleigh | - | - | - | - | 6.071 | - |
| Reliability Coefficient | Pollutant Indicator | ||
|---|---|---|---|
| BOD5 | CODCr | TSS | |
| CR | 0.33 | 1.10 | 0.46 |
| R | 0.98 | 0.49 | 0.91 |
| Re | 0.00 | 1.00 | 0.00 |
| η | 0.98 | 0.82 | 0.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Migdał, K.; Jóźwiakowski, K.; Czekała, W.; Śliz, P.; Tavares, J.M.R.; Almeida, A. Application of the Monte-Carlo Method to Assess the Operational Reliability of a Household-Constructed Wetland with Vertical Flow: A Case Study in Poland. Water 2023, 15, 3693. https://doi.org/10.3390/w15203693
Migdał K, Jóźwiakowski K, Czekała W, Śliz P, Tavares JMR, Almeida A. Application of the Monte-Carlo Method to Assess the Operational Reliability of a Household-Constructed Wetland with Vertical Flow: A Case Study in Poland. Water. 2023; 15(20):3693. https://doi.org/10.3390/w15203693
Chicago/Turabian StyleMigdał, Karolina, Krzysztof Jóźwiakowski, Wojciech Czekała, Paulina Śliz, Jorge Manuel Rodrigues Tavares, and Adelaide Almeida. 2023. "Application of the Monte-Carlo Method to Assess the Operational Reliability of a Household-Constructed Wetland with Vertical Flow: A Case Study in Poland" Water 15, no. 20: 3693. https://doi.org/10.3390/w15203693





