Modeling Method for Aerobic Zone of A2O Based on KPCA-PSO-SCN
Abstract
:1. Introduction
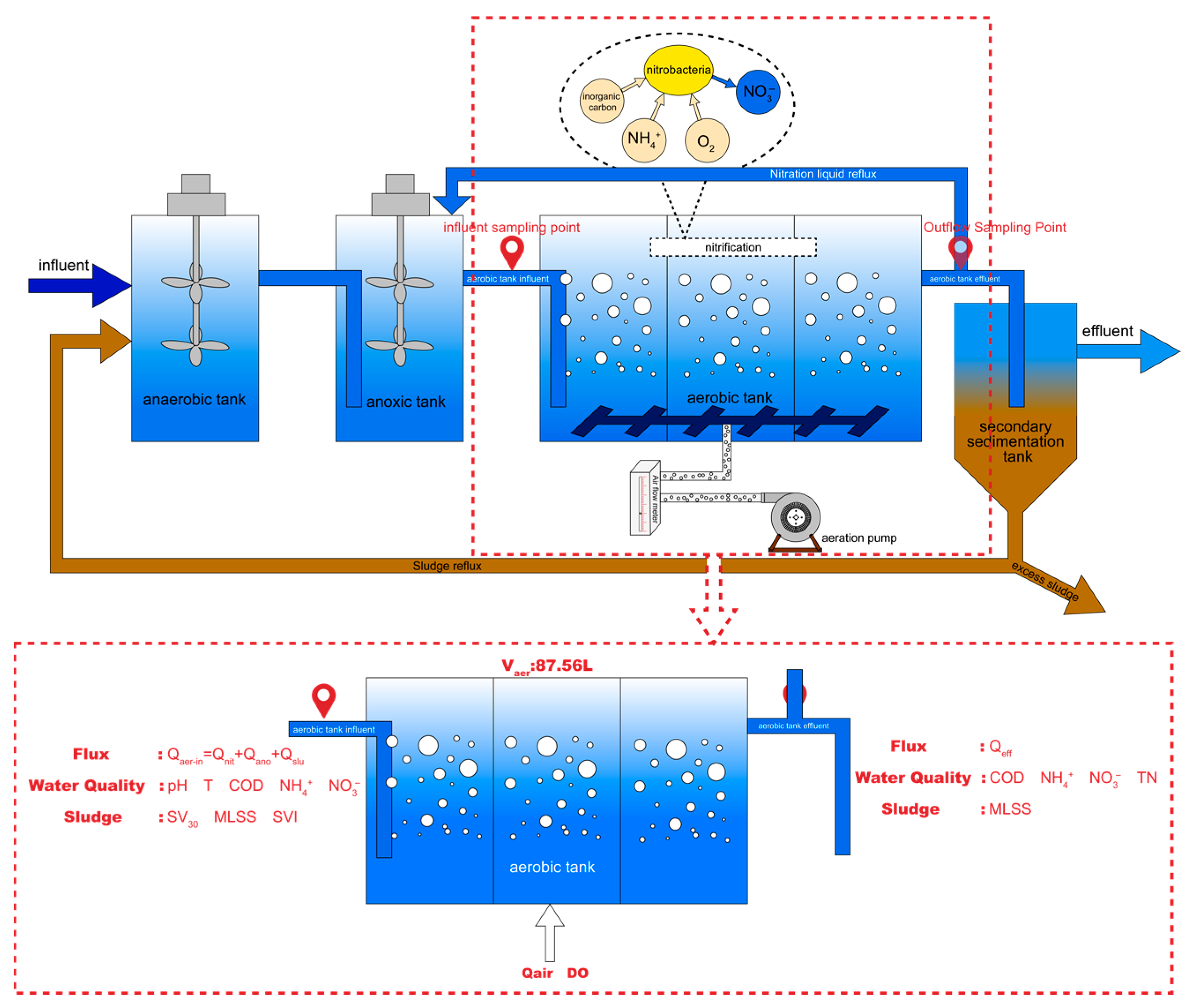
2. Selection and Treatment of Auxiliary Variables in A2O Aerobic Zone
- Nitration of ammonia nitrogen;
- Degradation of organic matter.
2.1. Data Collection and Selection
- COD;
- 2.
- NH4+;
- 3.
- NO3−;
- 4.
- pH;
- 5.
- T;
- 6.
- MLSS;
- 7.
- DO;
- 8.
- HRT.
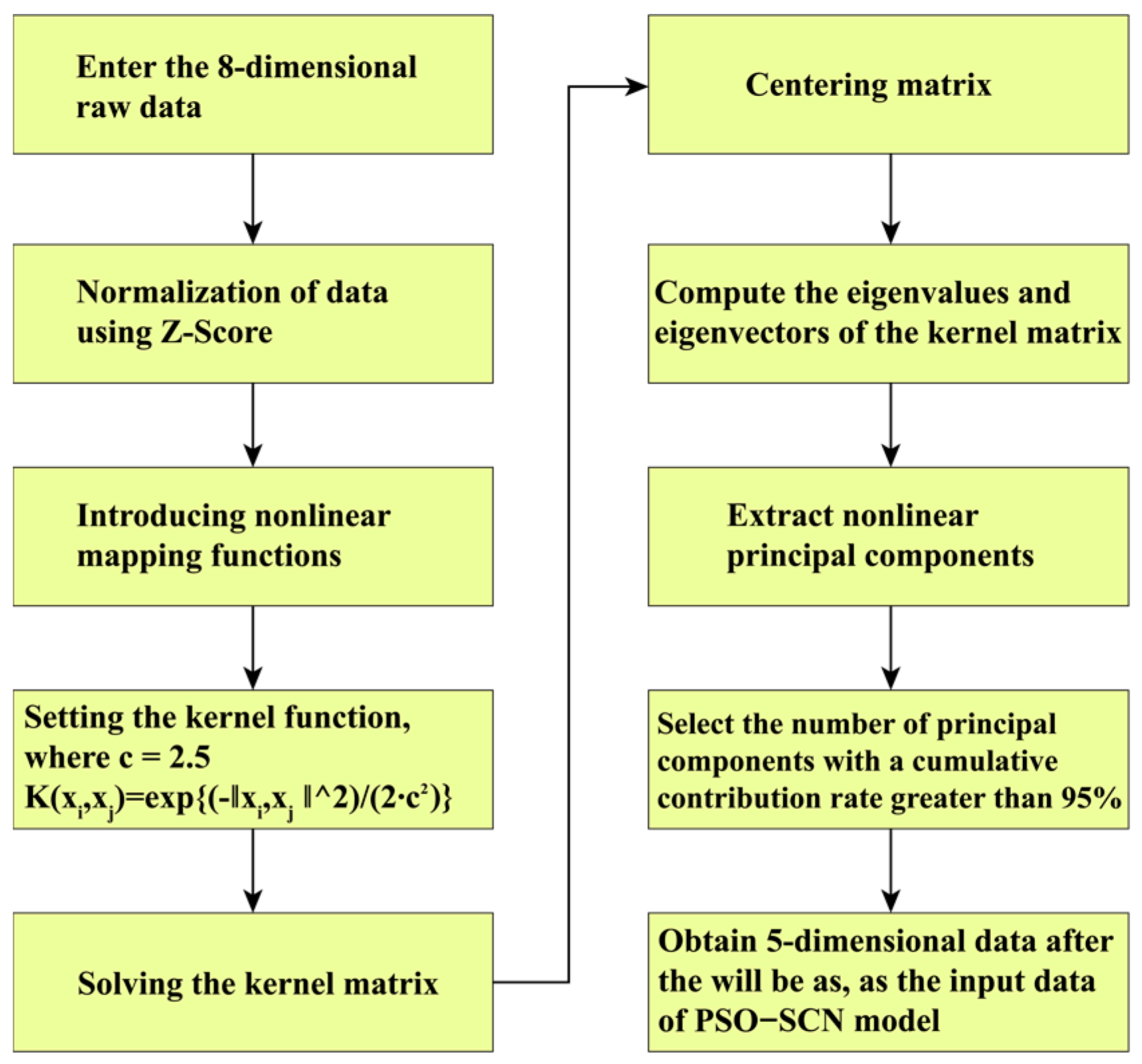
2.2. Data Dimensionality Reduction Based on KPCA
- Given a set of input vectors X as the feature matrix, it is mapped to a high-dimensional space using a Gaussian kernel function, .
- 2.
- Calculate the covariance matrix C in the high-order space Rk.
- 3.
- Calculate eigenvalues λ and eigenvectors ω through iterative algorithms.
- 4.
- Obtain the projection of xi from high-dimensional space to low-dimensional space.
- 5.
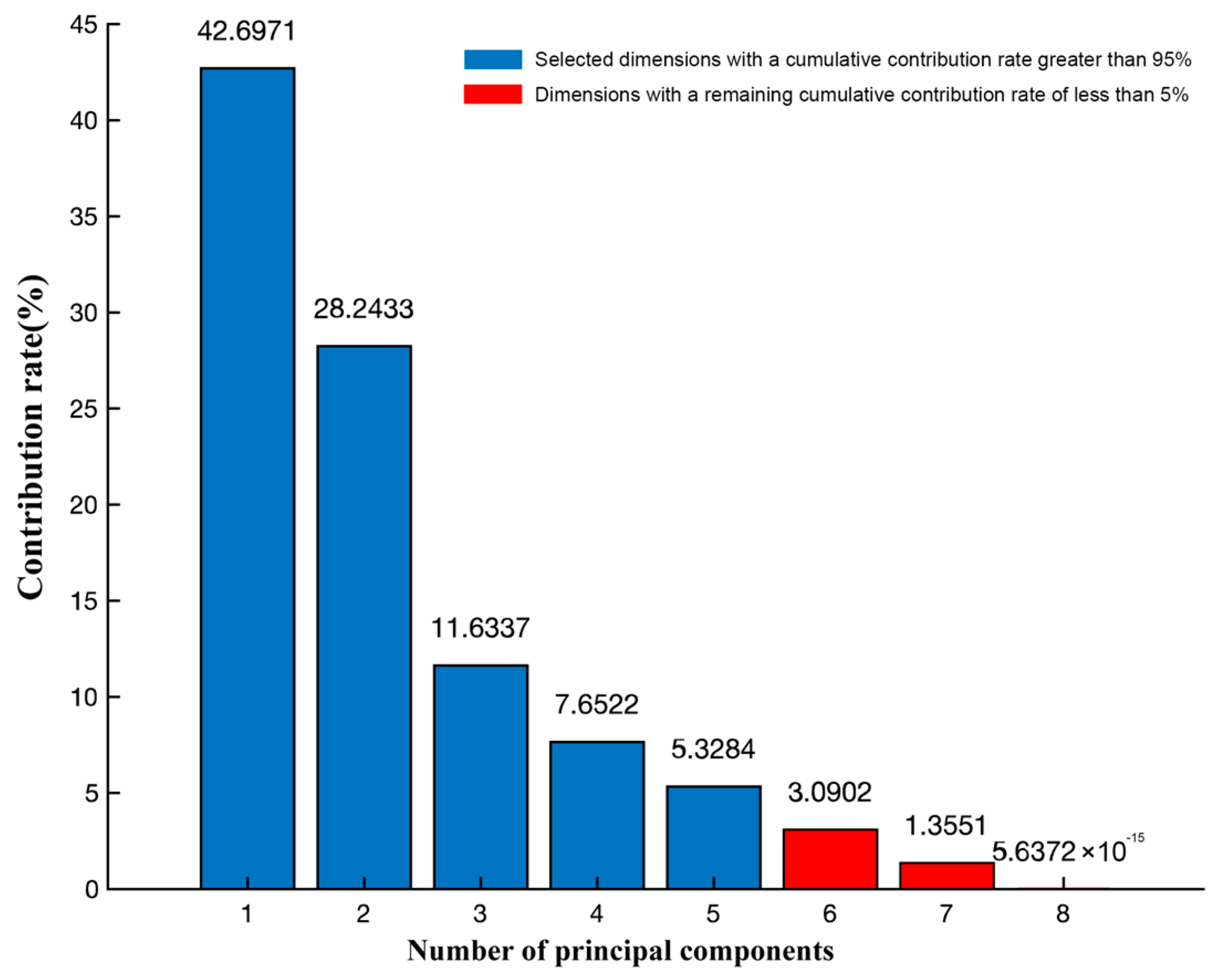
- Sort the feature vectors according to the size of their eigenvalues, and take the dimensionality-reduced matrix P composed of the first few rows with a cumulative contribution rate greater than 95%.
3. Modeling of A2O Aerobic Zone Based on PSO-SCN
3.1. PSO Principle
- Initialize the particle swarm. In D-dimensional space, each particle swarm has two attributes: velocity vector Vi and position vector Xi. Random initialization is performed for Vi and Xi.
- Obtaining the optimal position. The objective function is computed by the Vi and Xi of the particle to obtain the particle optimal position Pbest and the global optimal position Gbest in the space.
- Speed and position update.
- 4.
- After reaching the maximum number of iterations, obtain the final Pbest and Gbest.
3.2. SCN Principle
3.3. PSO Optimized SCN Model
- According to the SCN characteristics, randomly initialize the weights and bias, and obtain the weight and bias matrices.
- Take the error (Root Mean Square Error, RMSE) of the SCN model as the objective function, and use the PSO algorithm to optimize the weights and bias matrix, so that the error reaches the required range.
- The optimized weights and bias matrices are put through the selection operation by the supervision mechanism to check whether the network output meets the requirements. If no, increase the hidden layer network nodes and return to step 2 to optimize the optimized weights and bias matrix again. If yes, end.
- Output model.
- The specific optimization process of the PSO-SCN model is shown in Figure 5.
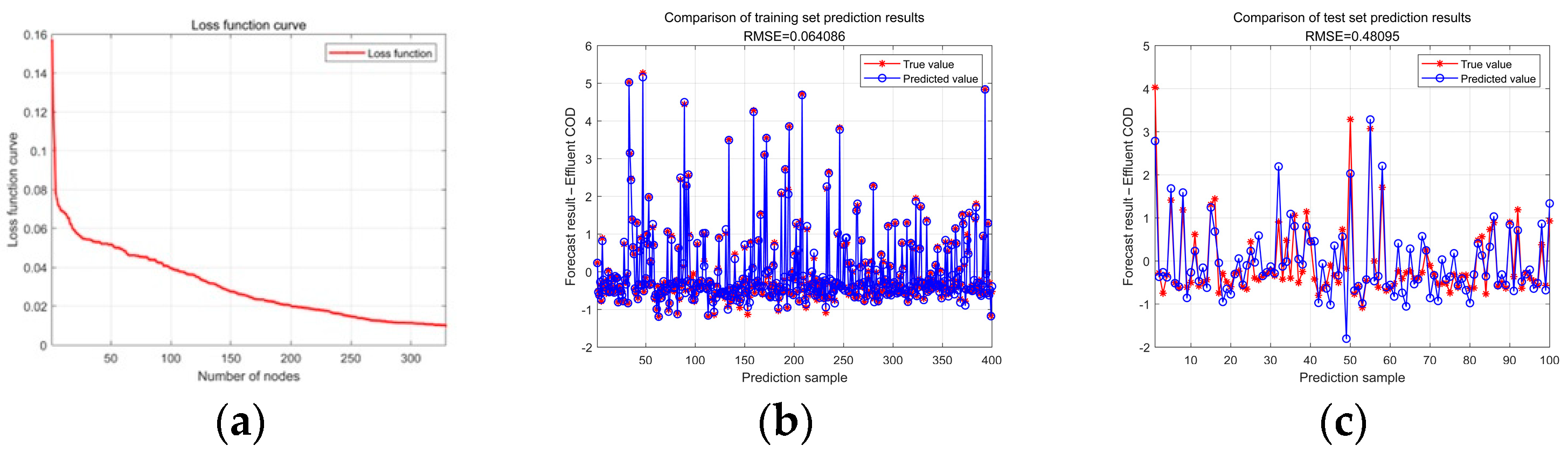
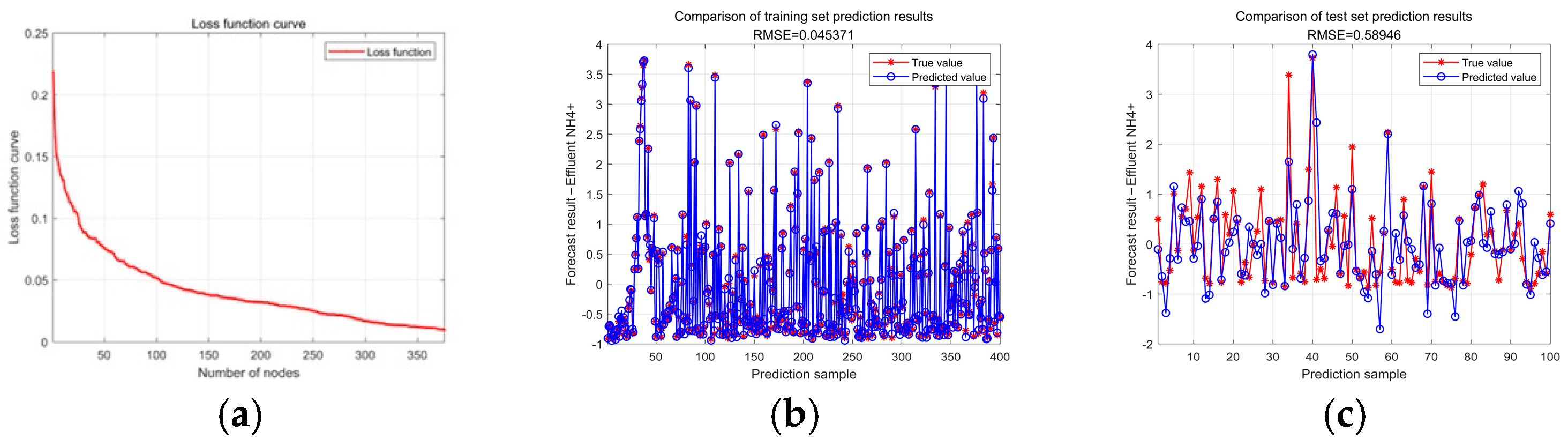
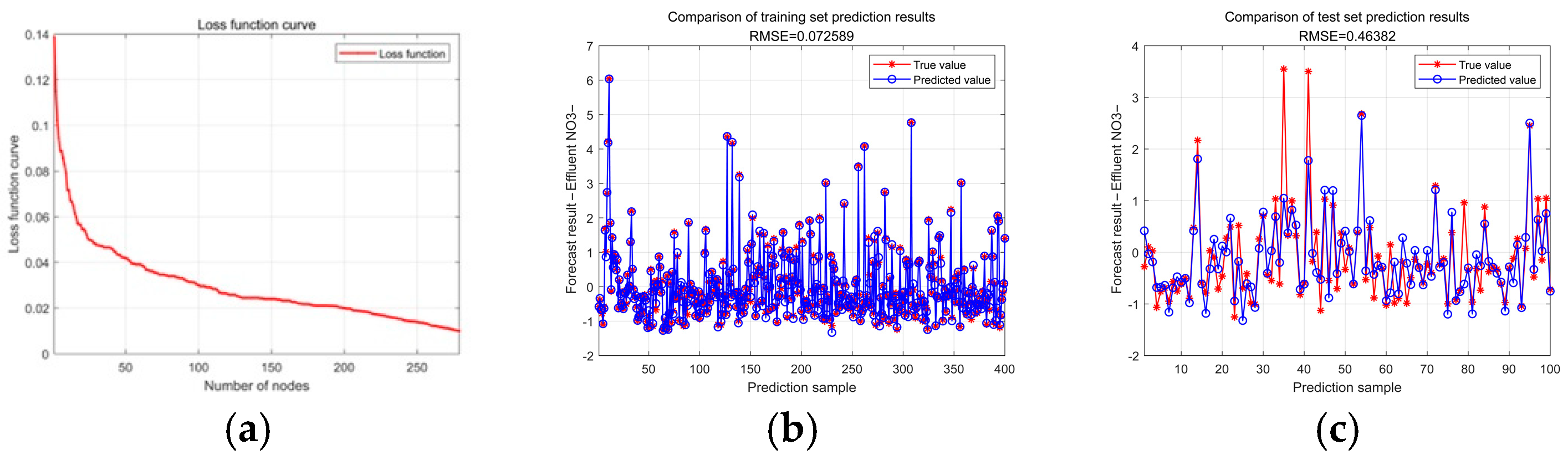
4. Experimental Results and Analysis
5. Conclusions
- Eight auxiliary variables that have a large impact on the effluent results were identified through the mechanistic reaction process in the aerobic zone. The KPCA method based on the Gaussian kernel function was used to downscale the sample data of the auxiliary variables, and the number of principal components with a cumulative contribution rate of more than 95% was selected to downscale the eight-dimensional data to five dimensions, which preserved the sample characteristics and improved the running speed and efficiency of the PSO-SCN algorithm.
- For the characteristics of the SCN algorithm with less manual intervention and more general approximation, but insufficient optimization of node weights and biases, the particle swarm optimization algorithm with smaller computational cost and faster convergence speed is selected to optimize the weights and bias of the SCN algorithm. The effectiveness of the algorithm was verified by experimental data.
- The classical water quality prediction algorithms such as SCN, PSO-BP, RBF, and PSO-RBF were compared, and the superiority of the PSO-SCN algorithm was verified in terms of RMSE, NSE and prediction time.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. 2021 Urban-Rural Construction Statistical Yearbook; China Planning Press: Beijing, China, 2021. [Google Scholar]
- Khan, A.U.; Rehman, M.U.; Zahoor, M.; Shah, A.B.; Zekker, I. Biodegradation of Brown 706 Dye by Bacterial Strain Pseudomonas aeruginosa. Water 2021, 13, 2959. [Google Scholar] [CrossRef]
- Ikram, M.; Naeem, M.; Zahoor, M.; Hanafiah, M.M.; Oyekanmi, A.A.; Ullah, R.; Farraj, D.A.A.; Elshikh, M.S.; Zekker, I.; Gulfam, N. Biological Degradation of the Azo Dye Basic Orange 2 by Escherichia coli: A Sustainable and Ecofriendly Approach for the Treatment of Textile Wastewater. Water 2022, 14, 2063. [Google Scholar] [CrossRef]
- Zekker, I.; Rikmann, E.; Tenno, T.; Vabamäe, P.; Kroon, K.; Loorits, L.; Saluste, A.; Tenno, T. Effect of concentration on anammox nitrogen removal rate in a moving bed biofilm reactor. Environ. Technol. 2012, 33, 2263–2271. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.H.; Yang, W.N.; Ngo, H.H.; Guo, W.S.; Jin, P.K.; Dzakpasu, M.; Yang, S.J.; Wang, Q.; Wang, X.C.; Ao, D. Current status of urban wastewater treatment plants in China. Environ. Int. 2016, 92–93, 11–22. [Google Scholar] [CrossRef]
- Eckenfelder, W.W.; Conor, D. Biological Waste Treatment; Pergamon Press: New York, NY, USA, 1961. [Google Scholar]
- Mckinney, R.E. Mathematics of complete-mixing activated sludge. J. Sanit. Eng. Divis. 1962, 88, 87–114. [Google Scholar] [CrossRef]
- Henze, M.; Grady, C.P.; Gujor, W.; Marais, G.V.R.; Matsuo, T. Activated Sludge Model No. 1; Scientific and Technical Reports; International Association on Water Pollution Research and Control: London, UK, 1986. [Google Scholar]
- Henze, M.; Gujer, W.; Mino, T.; Matsuo, T.; Wentzel, M.C.; Marais, G.V.R. Activated Sludge Model No. 2; Scientific and Technical Report No. 3; International Association on Water Pollution Research and Control: London, UK, 1995. [Google Scholar]
- Gujer, W.; Henze, M.; Mino, T.; Loosdrecht, M. Activated sludge model No. 3. Water Sci. Technol. 1999, 39, 183–193. [Google Scholar] [CrossRef]
- Iacopozzi, I.; Innocenti, V.; Marsili-Libelli, S.; Giusti, E. A modified activated sludge model No. 3 (ASM3) with two-step nitrification-denitrification. Environ. Model. Softw. 2007, 22, 847–861. [Google Scholar] [CrossRef]
- Rieger, L.; Koch, G.; Kühni, M.; Gujer, W.; Siegrist, H. The EAWAG Bio-P module for activated sludge model No. 3. Water Res. 2001, 35, 3887–3903. [Google Scholar] [CrossRef]
- Jeppsson, U.; Rosen, C.; Alex, J.; Copp, J.; Gernaey, K.V.; Pons, M.N.; Vanrolleghem, P.A. Towards benchmark simulation model for plant-wide control strategy performance evaluation of WWTPs. Water Sci. Technol. 2006, 53, 287–295. [Google Scholar] [CrossRef]
- Jeppsson, U.; Pons, M.N.; Nopens, I.; Alex, J.; Copp, J.B.; Gernaey, K.V.; Rosen, C.; Steyer, J.P.; Vanrolleghem, P.A. Benchmark simulation model No. 2: General protocol and exploratory case studies. Water Sci. Technol. 2007, 56, 67–78. [Google Scholar] [CrossRef]
- Flores-Alsina, X.; Corominas, L.; Snip, L.; Vanrolleghem, P.A. Including greenhouse gas emissions during benchmarking of wastewater treatment plant control strategies. Water Res. 2011, 45, 4700–4710. [Google Scholar] [CrossRef] [PubMed]
- Wan, J.; Huang, M.; Ma, Y.; Guo, W.; Wang, Y.; Zhang, H.; Li, W.; Sun, X. Prediction of effluent quality of a paper mill wastewater treatment using an adaptive network-based fuzzy inference system. Appl. Soft Comput. 2011, 11, 3238–3246. [Google Scholar] [CrossRef]
- Han, H.G.; Qiao, J.F. Prediction of activated sludge bulking based on a self-organizing RBF neural network. J. Process Control 2012, 22, 1103–1112. [Google Scholar] [CrossRef]
- Qiao, J.F.; Han, H.G. A repair algorithm for radial basis function neural network and its application to chemical oxygen demand modeling. Int. J. Neural Syst. 2010, 20, 63–74. [Google Scholar] [CrossRef]
- Yang, Y.; Kim, K.R.; Kou, R.; Li, Y.; Fu, J.; Zhao, L.; Liu, H. Prediction of effluent quality in a wastewater treatment plant by dynamic neural network modeling. Process Saf. Environ. Protect. 2022, 158, 515–524. [Google Scholar] [CrossRef]
- Kusiak, A.; Zeng, Y.; Zhang, Z. Modeling and analysis of pumps in a wastewater treatment plant: A data-mining approach. Eng. Appl. Artif. Intell. 2013, 26, 1643–1651. [Google Scholar] [CrossRef]
- Canete, J.F.D.; Sazorozco, P.D.; Baratti, R.; Mulas, M.; Ruano, A. Soft-sensing estimation of plant effluent concentrations in a biological wastewater treatment plant using an optimal neural network. Expert Syst. Appl. 2016, 63, 8–19. [Google Scholar] [CrossRef]
- Bagheri, M.; Mirbagheri, S.A.; Bagheri, Z. Modeling and optimization of activated sludge bulking for a real wastewater treatment plant using hybrid artificial neural networks-genetic algorithm approach. Process Saf. Environ. Protect. 2015, 95, 12–25. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, W.; Xie, J.; Huang, W.; Xin, K. LSTM-Based Model-Predictive Control with Rationality Verification for Bioreactors in Wastewater Treatment. Water 2023, 15, 1779. [Google Scholar] [CrossRef]
- Ren, X.; Wang, F.; Zhang, Y.; Wang, J.; Miao, H. Characterization and Disinfection by Product Formation of Dissolved Organic Matter in Anaerobic–Anoxic–Oxic Membrane Bioreactor (AAO-MBR) Process. Water 2023, 15, 1076. [Google Scholar] [CrossRef]
- Li, X.; Jia, R.; Zhang, R.; Yang, S.; Chen, G. A KPCA-BRANN based data-driven approach to model corrosion degradation of subsea oil pipelines. Reliab. Eng. Syst. Saf. 2022, 219, 108231. [Google Scholar] [CrossRef]
- Huang, Y.; Xiang, Y.; Zhao, R.; Chen, Z. Air quality prediction using improved PSO-BP neural network. IEEE Access 2020, 8, 99346–99353. [Google Scholar] [CrossRef]
- Yang, X.; Maihemuti, B.; Simayi, Z.; Saydi, M.; Na, L. Prediction of Glacially Derived Runoff in the Muzati River Watershed Based on the PSO-LSTM Model. Water 2022, 14, 2018. [Google Scholar] [CrossRef]
- Wang, D.; Li, M. Stochastic configuration networks: Fundamentals and algorithms. IEEE Trans. Cybern. 2017, 47, 3466–3479. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Li, M. Deep stochastic configuration networks with universal approximation property. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]


| Carbon Source | Nitrogen Source | |||
|---|---|---|---|---|
| Raw Material (g/L) | COD Content (mg/L) | Raw Material (g/L) | Nitrogen Content (mg/L) | |
| Glucose | 0.3 | 250 | - | |
| Milk powder | 0.3 | 250 | Trace neglect | |
| (NH4)2SO4 | - | 1.18 | 25 | |
| Total | - | 500 | - | 25 |
| Indicator Symbols | Unit | Description | ||
|---|---|---|---|---|
| Model Input Variables | Aerobic tank influent water quality indicators | ICOD | mg/L | COD concentration of influent water |
| INH4+ | mg/L | Influent ammonia nitrogen concentration | ||
| INO3− | mg/L | Concentration of nitrate nitrogen in influent water | ||
| Water quality indicators in aerobic tanks | pH | - | - | |
| T | °C | Temperature | ||
| MLSS | g/L | Mixed liquor suspended solid | ||
| DO | mg/L | Dissolved oxygen concentration | ||
| other | HRT | h | hydraulic retention time | |
| Model Output Variables | Aerobic tank effluent water quality indicators | ECOD | mg/L | COD concentration of effluent |
| ENH4+ | mg/L | Ammonia nitrogen concentration in effluent | ||
| ENO3− | mg/L | Nitrate nitrogen concentration in effluent |
| ICOD | INH4+ | INO3− | pH | T | MLSS | DO | HRT | ECOD | ENH4+ | ENO3− |
|---|---|---|---|---|---|---|---|---|---|---|
| 46.50 | 0.76 | 13.49 | 6.97 | 17.50 | 3.50 | 7.53 | 7 | 40.3 | 0.28 | 13.75 |
| 45.60 | 1.82 | 10.31 | 6.74 | 17.60 | 4.30 | 7.78 | 8 | 38.6 | 1.01 | 10.64 |
| 46.4 | 2.62 | 13.40 | 6.81 | 18.30 | 3.30 | 8.15 | 6 | 41.4 | 0.79 | 18.44 |
| 42.1 | 2.39 | 24.31 | 6.54 | 19.00 | 3.20 | 7.62 | 8 | 36.8 | 1.43 | 25.37 |
| 56.2 | 4.19 | 32.70 | 6.30 | 19.80 | 3.80 | 7.52 | 9 | 46.8 | 2.71 | 33.69 |
| 60.3 | 7.75 | 14.44 | 7.14 | 20.00 | 4.20 | 7.29 | 11 | 59.2 | 4.67 | 14.44 |
| … | … | |||||||||
| 40.5 | 4.35 | 4.70 | 7.08 | 20.60 | 4.52 | 7.02 | 13 | 39.2 | 1.66 | 5.43 |
| 41 | 7.65 | 13.66 | 6.93 | 19.50 | 4.21 | 7.14 | 12 | 38.7 | 5.27 | 12.58 |
| Symbol | Description | Value | Unit |
|---|---|---|---|
| c | Kernel function parameters | 2.5 | - |
| Con | Accumulated contribution rate | 95 | % |
| Model Parameter | Value | |
|---|---|---|
| SCN | Maximum number of hidden nodes | 500 |
| Maximum number of random configurations | 250 | |
| Training tolerance | 0.01 | |
| Random weight range | [0.5, 1,5, 10, 30, 50, 100, 150, 200, 250] | |
| PSO | Particle swarm dimension | 10 |
| Number of particles | 20 | |
| Evolutionary frequency | 50 |
| Model | RMSE | NSE | Prediction Time (s) | ||||
|---|---|---|---|---|---|---|---|
| ECOD | ENH4+ | ENO3− | ECOD | ENH4+ | ENO3− | ||
| SCN | 2.3458 | 1.0974 | 1.6535 | −1.51918 | −0.72963 | −0.30092 | 8.83 |
| PSO-BP | 0.35598 | 0.61494 | 0.52357 | 0.85265 | 0.64262 | 0.784922 | 12.71 |
| RBF | 0.59504 | 0.82213 | 0.51919 | 0.846274 | 0.29246 | 0.60818 | 2.55 |
| PSO-RBF | 0.5821 | 0.7833 | 1.0526 | 0.60607 | 0.2546 | 0.69002 | 38.08 |
| PSO-SCN | 0.43999 | 0.58946 | 0.46382 | 0.72875 | 0.95011 | 0.72875 | 3.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Tian, X.; Ma, Y.; Guan, Y.; Liu, L.; Shi, L. Modeling Method for Aerobic Zone of A2O Based on KPCA-PSO-SCN. Water 2023, 15, 3692. https://doi.org/10.3390/w15203692
Lu W, Tian X, Ma Y, Guan Y, Liu L, Shi L. Modeling Method for Aerobic Zone of A2O Based on KPCA-PSO-SCN. Water. 2023; 15(20):3692. https://doi.org/10.3390/w15203692
Chicago/Turabian StyleLu, Wenxia, Xueyong Tian, Yongguang Ma, Yinyan Guan, Libo Liu, and Liwei Shi. 2023. "Modeling Method for Aerobic Zone of A2O Based on KPCA-PSO-SCN" Water 15, no. 20: 3692. https://doi.org/10.3390/w15203692
APA StyleLu, W., Tian, X., Ma, Y., Guan, Y., Liu, L., & Shi, L. (2023). Modeling Method for Aerobic Zone of A2O Based on KPCA-PSO-SCN. Water, 15(20), 3692. https://doi.org/10.3390/w15203692





