Incipient Motion of Bed Material in a Channel with Varying Width and Vegetated Channel Walls
Abstract
:1. Introduction
2. Materials and Methods
- -
- The flows are steady and non-uniform;
- -
- The change of the channel width in the streamwise direction is symmetric;
- -
- The diameters of all reed elements are the same;
- -
- The density of inflexible vegetation on the sidewalls is kept as constant.
3. Results and Discussion
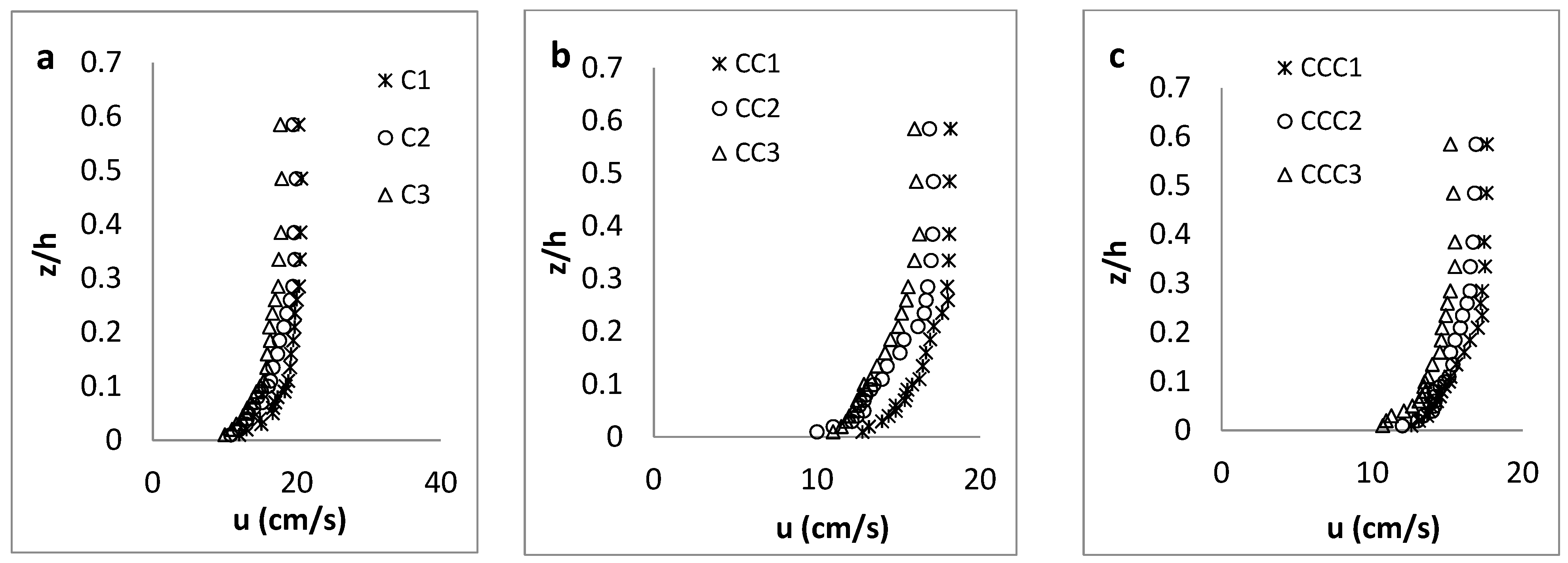
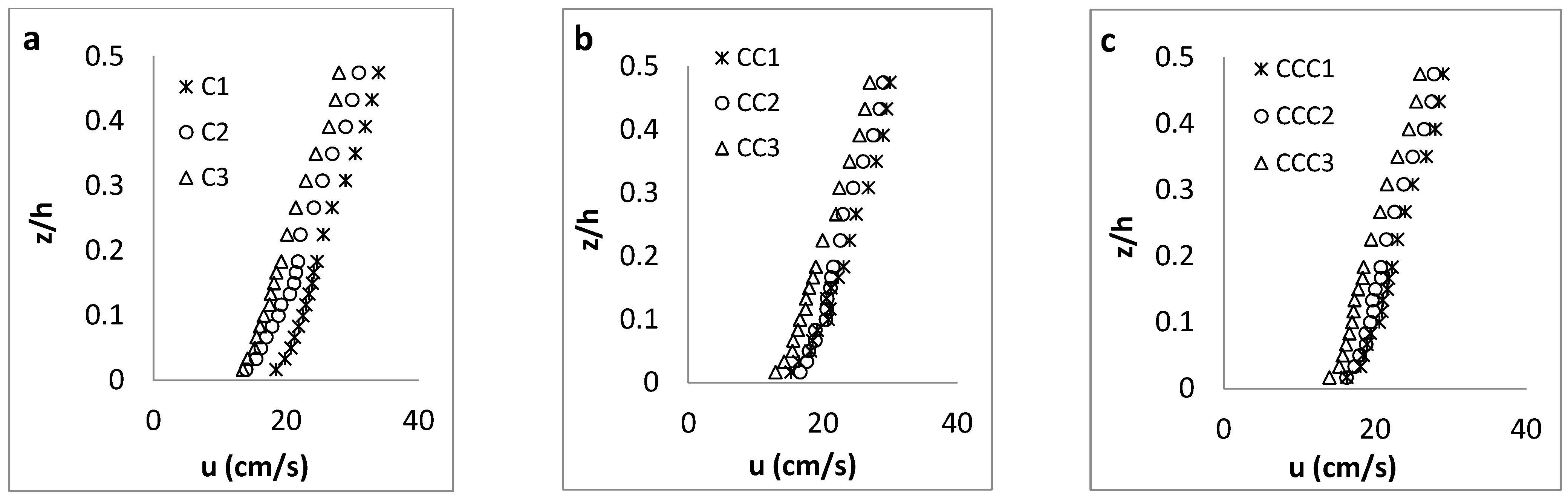
3.1. Results in the Flat Channel
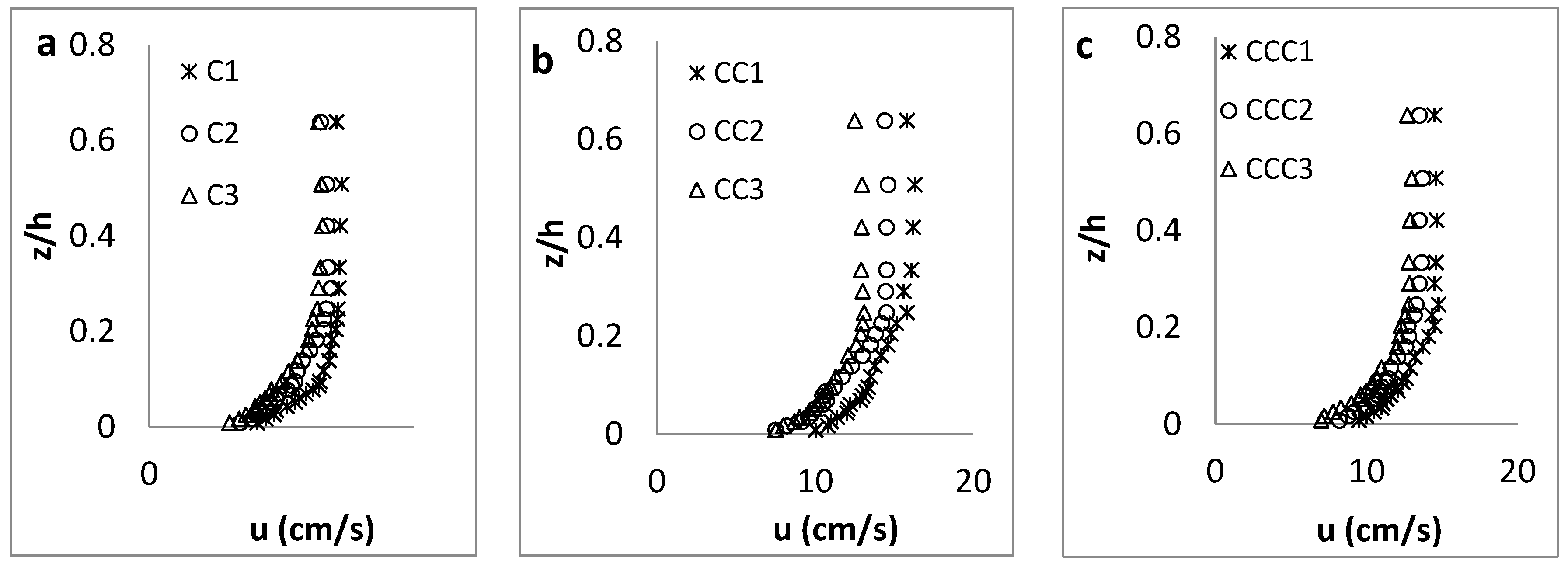
3.1.1. Streamwise Velocity Distribution
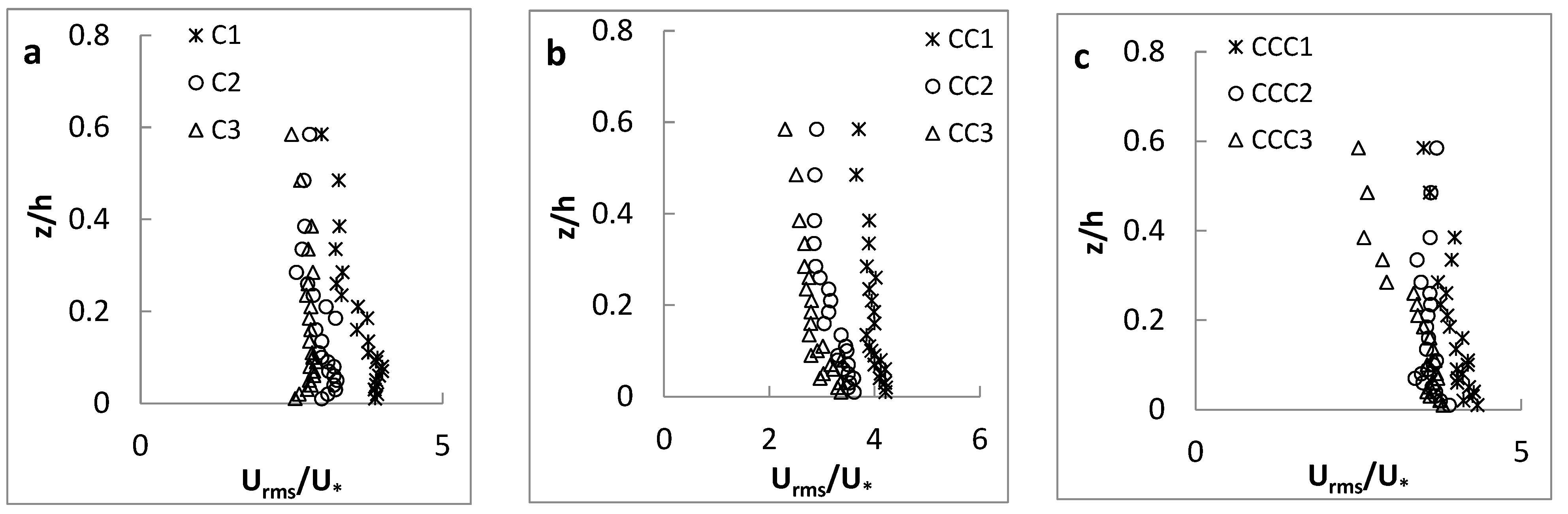
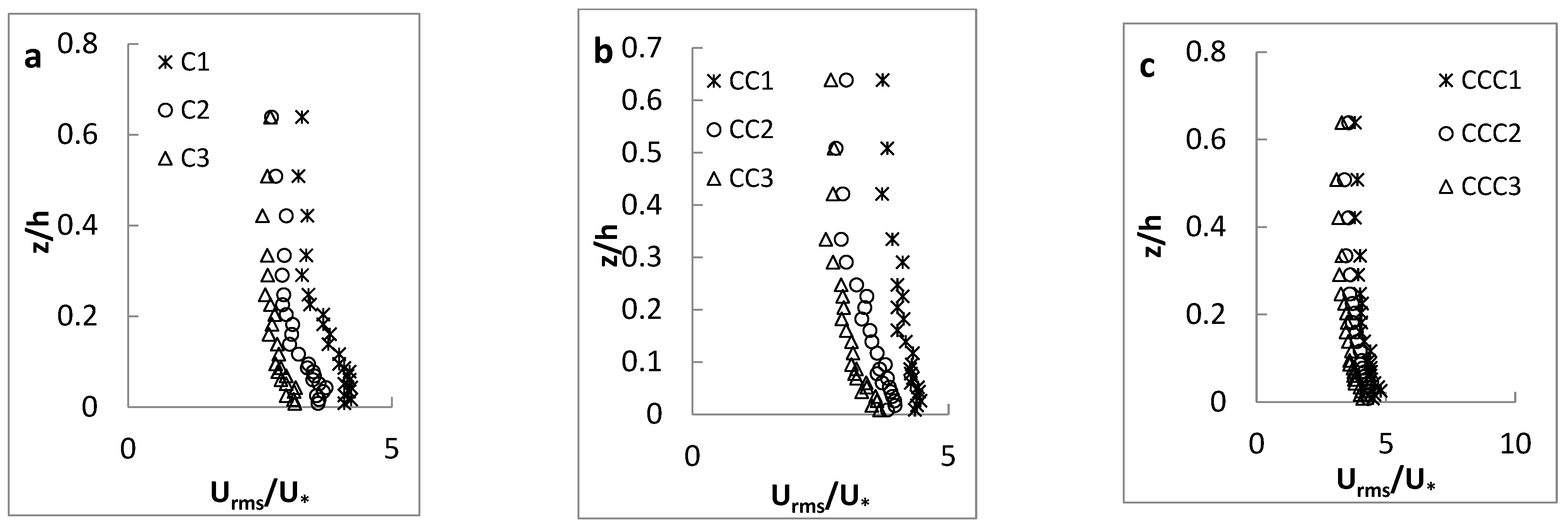
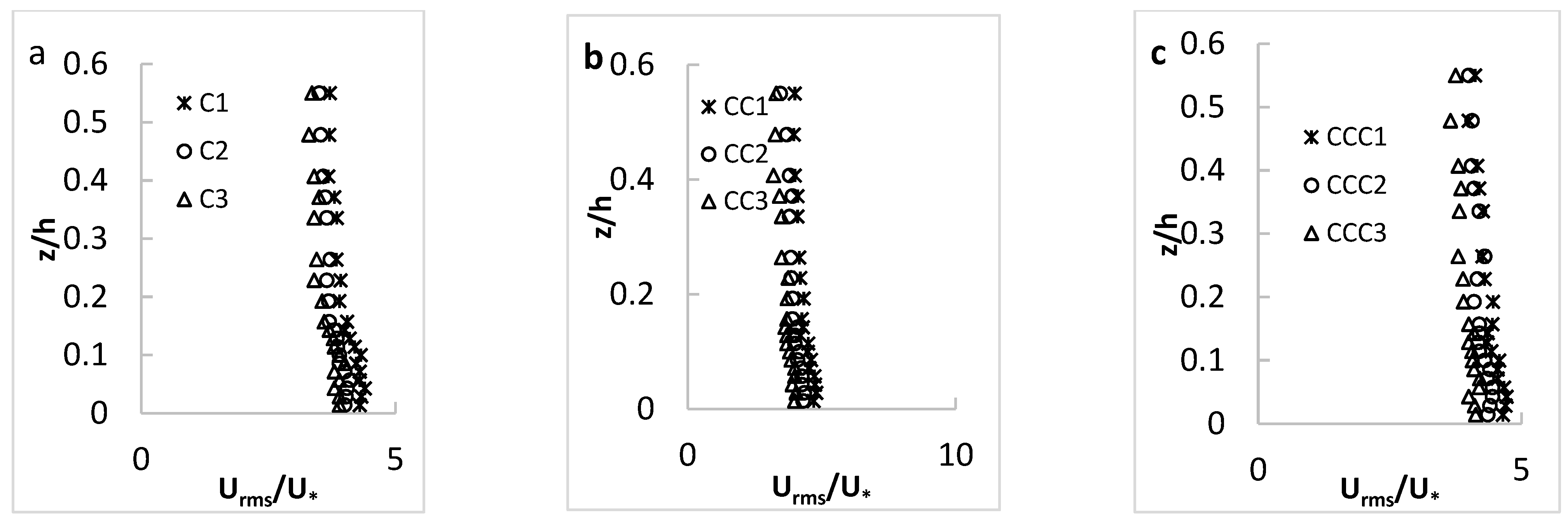
3.1.2. Turbulence Intensity Distribution
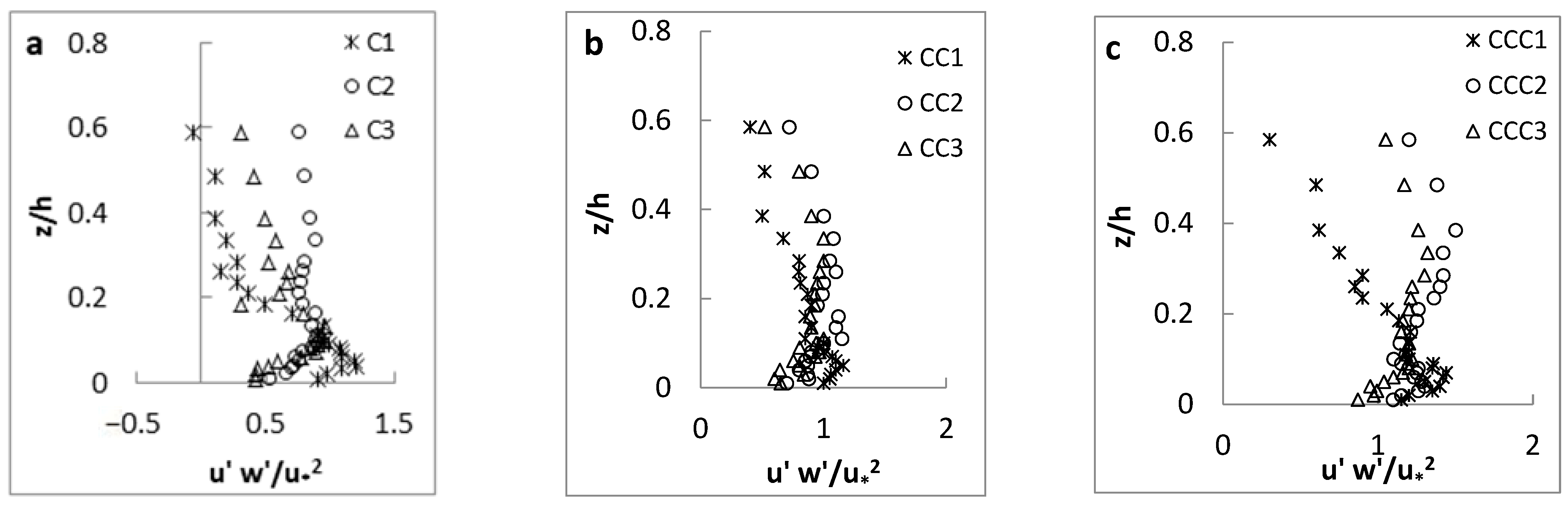
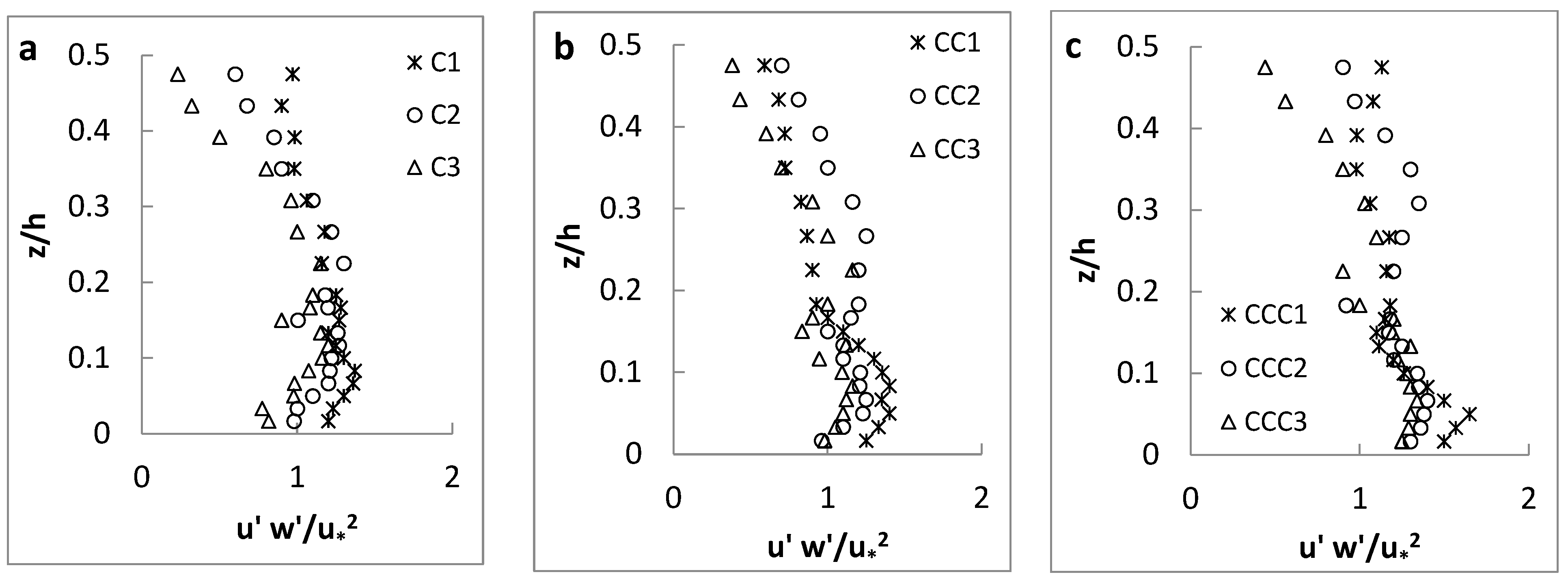
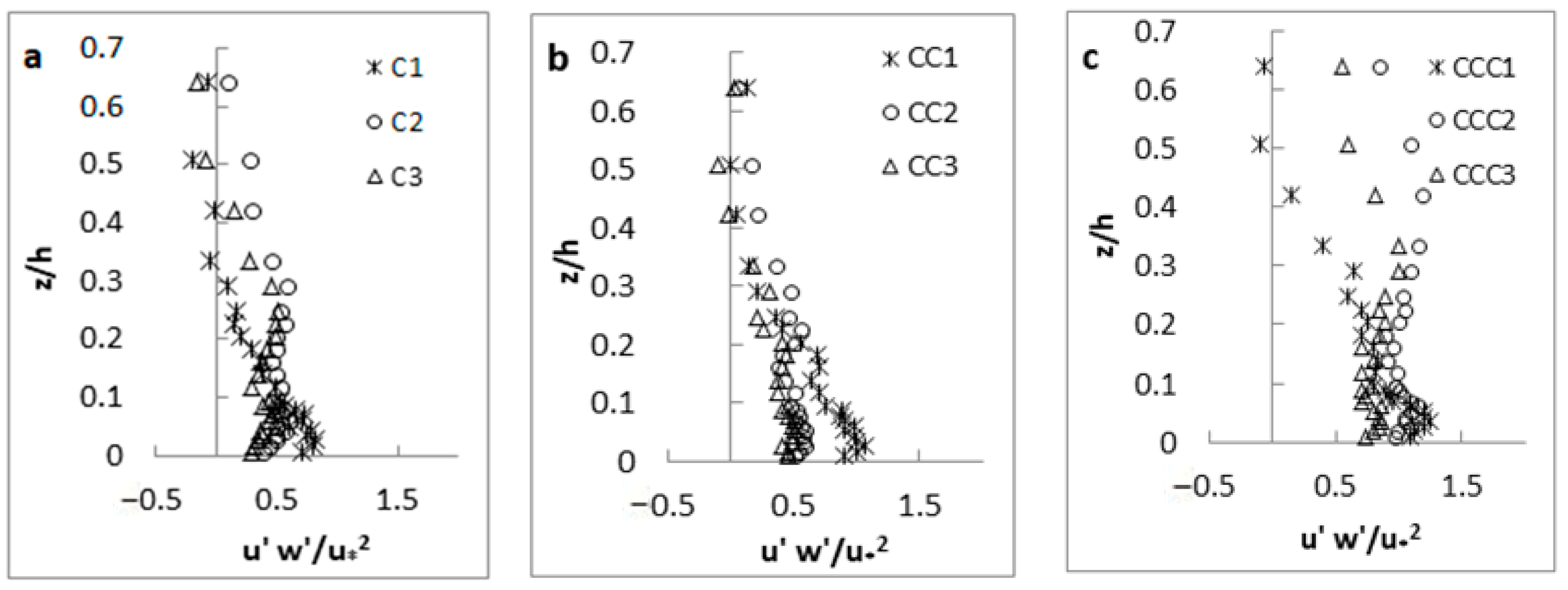
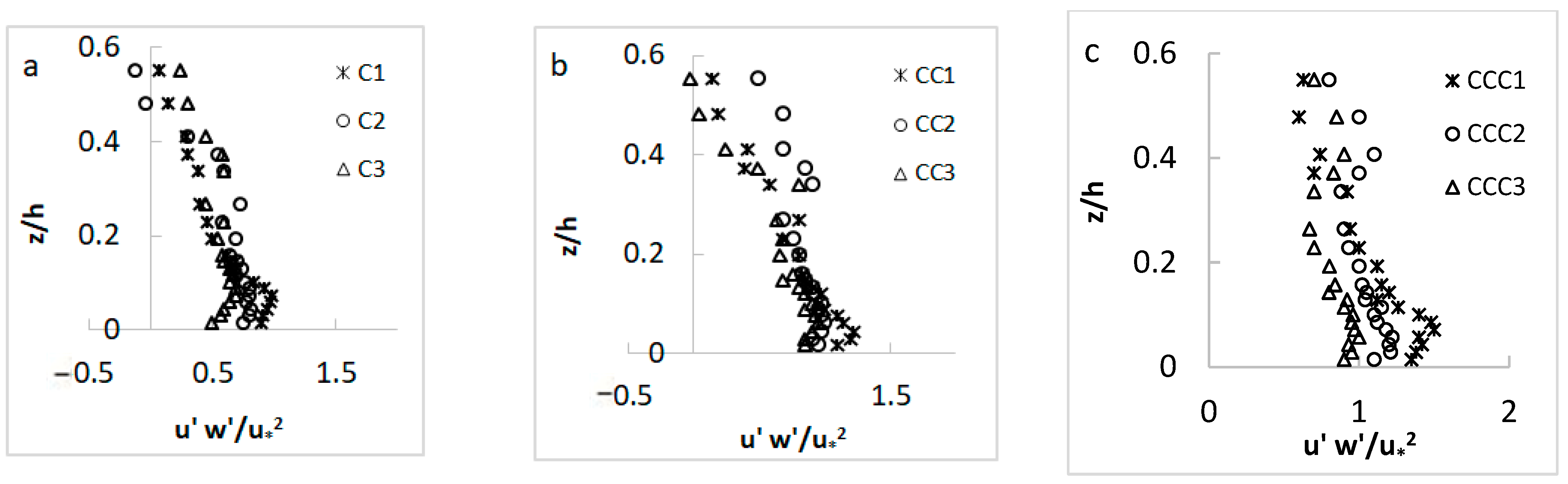
3.1.3. Reynolds Shear Stress
3.2. Results in the Steepest Channel
3.2.1. Streamwise Velocity Distribution
3.2.2. Turbulence Intensity Distribution
3.2.3. Reynolds Shear Stress
3.3. Determination of Incipient Near-Bed Velocity and Shear Stress
3.4. Estimation of Shields Parameter
- (1)
- The difference between the definitions of the threshold condition: Shields employed the general motion criteria of the Kramer method in his research [41]. In the present work, however, the medium transport criterion of the Kramer approach was applied, without formation of any bedforms. Different approaches for assessing the incipient motion of bed material may lead to various critical shear stress values. Generally, the presence of bedforms affects the bed near-bed shear stress and sediment transport by exerting more turbulence and drag force [42]. In previous studies, it was proved that the negligible differences in water level over the bedforms may cause some overestimation of shear stress [42,43,44]. Furthermore, the dissipation of bed shear stress due to presence of bedforms leads to a remarkable overestimation in determining bed shear stress.
- (2)
- Different experimental setups: experiments in Shields’ study were carried out in a prism channel without any changes in the channel width and without presence of vegetation. These changes in the present work led to an increase in turbulence intensities, which play a key role in lifting particles from the channel bed. Hence, the bed shear stress needed to render the bed particles’ motion decreases significantly.
- (3)
- Characteristics of bed particle: Shields used four types of sub-angular to very angular particles in his experiments. On the other hand, naturally rounded quartz particles were applied in the current research. Angular particles used in the Shields’ study led to more resistance to incipient movements, owing to producing more friction [15], and thus a significant increase in the critical shear stress.
- (4)
- Accuracy of measurement: The measuring tools for experiments in this study are more advanced and accurate, compared to those employed by Shields a long time ago. Resultantly, it is expected to estimate the critical shear stress more precisely comparing to that reported by Shields [14].
4. Conclusions
- (1)
- As expected, the streamwise velocity had its maximum and minimum values at the narrowest CS (CS-1) and widest CS (CS-3), respectively, along all axes (C-axis, CC-axis and CCC-axis). Additionally, in cases with an aspect ratio of w/h < 5, the maximum velocity occurred below the water surface (“dip” phenomenon), owing to the presence of secondary currents.
- (2)
- The turbulence intensity started from a non-zero value, increased until reached its maximum value at a distance near the bed, and then had a descending trend towards the water surface. The presence of vegetation on the channel sidewalls resulted in an increasing trend of the turbulence intensity while moving from the central C-axis to the channel sidewalls.
- (3)
- The distribution of Reynolds shear stress had a Z-shape profile at all measurement points, due to presence of vegetation on the channel sidewalls. The maximum values of the Reynolds shear stress at CS-2 and CS-3 occurred at the flow depth of 0.3 < z/h < 0.4 from the channel bed, where the flow decelerated along this channel section from CS-2 to CS-3.
- (4)
- The incipient near-bed velocity and shear stress increased by increasing the particle size. On the other hand, the estimated near-bed velocity and shear stress decreased with the increase in the bed slope, which represents the dominance of the gravity effect over the pressure gradient effect. It can be inferred that the variation of the channel width and the presence of vegetation on the channel sidewalls remarkably influences the turbulence intensity and Reynolds shear stress distributions.
- (5)
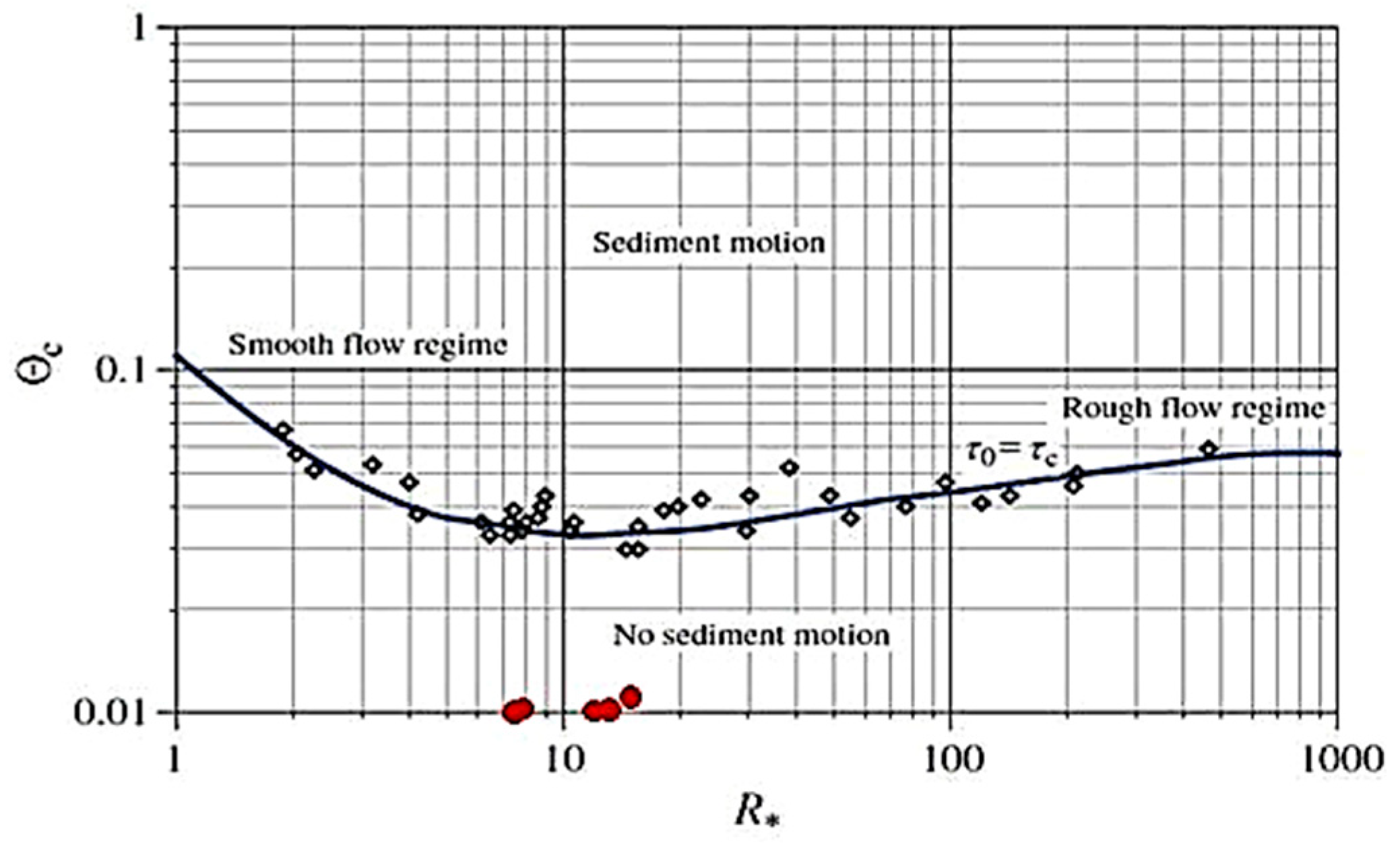
- By locating the critical shear Reynolds number and Shields parameter values on the Shields diagram, it was observed that all estimated data points were placed below the Shields curve in the range for “no sediment motion”, indicating the invalidity of the Shields approach for assessing the incipient motion in this research with the presence of varying channel width and vegetated channel sidewalls.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Sui, J.; Karney, B.W. Incipient motion of non-cohesive sediment under ice cover-an experimental study. J. Hydrodyn. 2008, 20, 117–124. [Google Scholar] [CrossRef]
- Church, M.; Hassan, M. Upland gravel-bed rivers with low sediment transport. In 643 Catchment Dynamics and River Processes, Mediterranean and other Climate Regions 644, Developments in Earth Surface Processes; Elsevier: Amsterdam, The Netherlands, 2005; Volume 7, pp. 141–168. [Google Scholar]
- Garcia, C.; Laronne, J.B.; Sala, M. Variable source areas of bedload in a gravel652 bed stream. J. Sediment. Res. 1999, 69, 2–31. [Google Scholar] [CrossRef]
- Dey, S. Fluvial Hydrodynamics: Hydrodynamic and Sediment Transport Phenomena; Springer: Berlin/Heidelberg, Germany, 2014; pp. 158–162. [Google Scholar]
- Buffington, J.M.; Montgomery, D.R. A systematic analysis of eight decades of incipient motion studies, with special reference to gravel-bedded rivers. Water Resour. Res. 1997, 33, 1993–2029. [Google Scholar] [CrossRef]
- Wilcock, P.R. Methods for estimating the critical shear stress of individual fractions in mixed-size sediment. Water Resour. Res. 1988, 24, 1127–1135. [Google Scholar] [CrossRef]
- Kramer, H. Sand mixtures and sand movement in fluvial model. Trans. Am. Soc. Civ. Eng. 1935, 100, 798–838. [Google Scholar] [CrossRef]
- Dey, S.; Sarkar, S.; Solari, L. Near-bed turbulence characteristics at the entrainment threshold of sediment beds. J. Hydraul. Eng. 2011, 137, 945–958. [Google Scholar] [CrossRef]
- Shahmohammadi, R.; Afzalimehr, H.; Sui, J. Impacts of turbulent flow over a channel bed with a vegetation patch on the incipient motion of sediment. Can. J. Civ. Eng. 2018, 9, 803–816. [Google Scholar] [CrossRef]
- Garde, R.J. Initiation of motion on a hydrodynamically rough surface-Critical velocity 654 approach. J. Irrig. Power 1970, 27, 271–282. [Google Scholar]
- Mavis, F.T.; Laushey, L.M. Discussion of “Sediment transportation mechanics: 662 Initiation of motion”. ASCE J. Hydraul. Div. 1966, 92, 288–291. [Google Scholar]
- Wang, H.; Tang, H.W.; Zhao, H.Q.; Zhao, X.Y.; Lu, S.Q. Incipient motion of 675 sediment in presence of submerged flexible vegetation. Water Sci. Eng. 2015, 676, 63–67. [Google Scholar] [CrossRef]
- Zanke, U.C.E. Neuer ansatz zur berechnung des transportbeginns von sedimenten unter 683 stromungseinfluss. Mitteilungen Des Franzius-Inst. Tech. Univ. Hann. 684 Heft 1977, 46, 156–178. [Google Scholar]
- Shields, A.F. Application of Similarity Principles and Turbulence Research to Bed-Load Movement; Mitteilungen der Preussischen Versuchsanstalt für Wasserbau und Schiffbau: Berlin, Germany, 1936; Volume 26, pp. 5–24. [Google Scholar]
- Bolhassani, R.; Afzalimehr, H.; Dey, S. Effects of relative submergence and bed slope on sediment incipient motion under decelerating flows. J. Hydrol. Hydromech. 2015, 63, 295–302. [Google Scholar] [CrossRef]
- Emadzadeh, A.; Meng Chiew, Y.; Afzalimehr, H. Effect of accelerating and decelerating flows on incipient motion in sand bed streams. Adv. Water Resour. 2010, 33, 1094–1104. [Google Scholar] [CrossRef]
- King, A.T.; Tinoco, R.O.; Cowen, E.A. A k–ε turbulence model based on the scales of vertical shear and stem wakes valid for emergent and submerged vegetated flows. J. Fluid Mech. 2012, 701, 1–39. [Google Scholar] [CrossRef]
- Mofrad, M.R.; Afzalimehr, H.; Parvizi, P.; Ahmad, S. Comparison of Velocity and Reynolds Stress Distributions in a Straight Rectangular Channel with Submerged and Emergent Vegetation. Water 2023, 15, 24–35. [Google Scholar] [CrossRef]
- Tang, H.W.; Wang, H.; Liang, D.F.; Lv, S.Q.; Yan, L. Incipient motion of sediment in the presence of emergent rigid vegetation. J. Hydro-Environ. Res. 2012, 7, 1–7. [Google Scholar]
- Yang, J.; Chung, H.; Nepf, H. The onset of sediment transport in vegetated channels predicted by turbulent kinetic energy. Geophys. Res. Lett. 2016, 43, 11, 261–268. [Google Scholar] [CrossRef]
- Soltani, N.; Afzalimehr, H.; Tabarestani, E.S.; Eftekhari, A.; Khabari, M.; Nazari-Sharabian, M.; Karakouzian, M. Turbulence Characteristics in Mild and Steep Entrance Slopes of Pool-Riffle Sequences. Water 2023, 15, 720. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, W.; Zhang, X.; Long, G.; Fan, J.; Chen, H.; Deng, L. A novel fractal solution for permeability and Kozeny-Carman constant of fibrous porous media made up of solid particles and porous fibers. Powder Technol. 2019, 1, 92–98. [Google Scholar] [CrossRef]
- Xiao, B.; Zhu, H.; Chen, F.; Long, G.; Li, Y. A fractal analytical model for Kozeny-Carman constant and permeability of roughened porous media composed of particles and converging-diverging capillaries. Powder Technol. 2023, 15, 118256. [Google Scholar] [CrossRef]
- Nelson, P.A.; Brew, A.K.; Morgan, J.A. Morphodynamic response of a variable- width channel to changes in sediment supply. Water Resour. Res. 2015, 51, 5717–5734. [Google Scholar] [CrossRef]
- Morgan, J.A. The Effects of Sediment Supply, Width Variations, and Unsteady Flow on Riffle- Pool Dynamics. Ph.D. Thesis, Department of Civil and Environmental Engineering, Colorado State University, Fort Collins, CO, USA, 2018. [Google Scholar]
- Shahiri Tabarestani, E.; Afzalimehr, H.; Sui, J. Assessment of Annual Erosion and Sediment Yield Using Empirical Methods and Validating with Field Measurements—A Case Study. Water 2022, 14, 1602. [Google Scholar] [CrossRef]
- Repetto, R.; Tubino, M.; Paola, C. Planimetric instability of channels with variable width. J. Fluid Mech. 2002, 457, 79–109. [Google Scholar] [CrossRef]
- Chartrand, S.M.; Jellinek, A.M.; Hassan, M.A.; Ferrer-Boix, C. Morphodynamics of a width-variable gravel bed stream: New insights on pool-riffle formation from physical experiments. J. Geophys. Res. Earth Surf. 2018, 123, 2735–2766. [Google Scholar] [CrossRef]
- Shahiri Tabarestani, E.; Afzalimehr, H.; Pham, Q.B. Flow structure investigation over a pool-riffle sequence in a variable width river. Acta Geophys. 2022, 70, 713–727. [Google Scholar] [CrossRef]
- Viparelli, E.; Gaeuman, D.; Wilcock, P.; Parker, G. A model to predict the evolution of a gravel bed river under an imposed cyclic hydrograph and its application to the Trinity River. Water Resour. Res. 2011, 47, 1–22. [Google Scholar] [CrossRef]
- PPace, K.M.; Tullos, D.; Walter, C.; Lancaster, S.; Segura, C. Sediment Pulse Behaviour Following Dam Removal in Gravel-Bed Rivers. River Res. Appl. 2017, 33, 102–112. [Google Scholar] [CrossRef]
- Nelson, P.A.; Venditti, J.G.; Dietrich, W.E.; Kirchner, J.W.; Ikeda, H.; Iseya, F.; Sklar, L.S. Response of bed surface patchiness to reductions in sediment supply. J. Geophys. Res. Earth Surf. 2009, 114, 1–18. [Google Scholar] [CrossRef]
- Maturana, O.; Tonina, D.; McKean, J.A.; Buffington, J.M.; Luce, C.H.; Caama˜no, D. Modeling the effects of pulsed versus chronic sand inputs on salmonid spawning habitat in a low-gradient gravel-bed river. Earth Surf. Process. Landf. 2014, 39, 877–889. [Google Scholar] [CrossRef]
- Parker, G. 1D Sediment Transport Morphodynamics with Applications to Rivers and Turbidity Currents. 2006. Available online: https://csdms.colorado.edu/wiki/1D_Sediment_Transport_Morphodynamics_with_applications_to_Rivers_and_Turbidity_Currents (accessed on 13 April 2006).
- Absi, R. An ordinary differential equation for velocity distribution and dip-phenomenon in open channel flows. J. Hydraul. Res. 2011, 49, 82–89. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Dey, S. Influence of bank vegetation and gravel bed on velocity and Reynolds stress distributions. Int. J. Sediment Res. 2009, 24, 236–246. [Google Scholar] [CrossRef]
- Grass, A.J. Structural features of turbulent flow over smooth and rough boundaries. J. Fluid Mech. 1971, 50, 233–255. [Google Scholar] [CrossRef]
- Hadian, S.; Afzalimehr, H.; Ahmad, S. Effects of Channel Width Variations on Turbulent Flow Structures in the Presence of Three-Dimensional Pool-Riffle. Sustainability 2023, 15, 7829. [Google Scholar] [CrossRef]
- Nepf, H.M.; Vivoni, E.R. Turbulence structure in depth-limited vegetated flow: Transition between emergent and submerged regimes. In Proceedings of the 28th IAHR Congress, Graz, Austria, August 1999; pp. 1–8. [Google Scholar]
- Nikora, V.I.; Goring, D.G. ADV measurements of turbulence: Can we improve their interpretation? J. Hydraul. Eng. 1998, 124, 630–634. [Google Scholar] [CrossRef]
- Kennedy, J.F. The Albert Shields story. J. Hydraul. Eng. 1995, 121, 766–772. [Google Scholar] [CrossRef]
- Buffington, J.M. The legend of AF Shields. J. Hydraul. Eng. 1999, 125, 376–387. [Google Scholar] [CrossRef]
- Parker, G.; Peterson, A.W. Bar resistance of gravel-bed streams. J. Hydraul. Div. 1980, 106, 1559–1575. [Google Scholar] [CrossRef]
- Hey, R.D. Bar form resistance in gravel-bed rivers. J. Hydraul. Eng. 1988, 114, 1498–1508. [Google Scholar] [CrossRef]
- Dey, S.; Papanicolaou, A. Sediment threshold under stream flow: A state-of-the-art review. KSCE J. Civ. Eng. 2008, 12, 45–60. [Google Scholar] [CrossRef]
- Paphitis, D. Sediment movement under unidirectional flows: An assessment of empirical threshold curves. Coast Eng. 2001, 43, 227–245. [Google Scholar] [CrossRef]
- Diplas, P. Bed load transport in gravel-bed streams. J. Hydraul. Eng. 1987, 113, 277–292. [Google Scholar] [CrossRef]

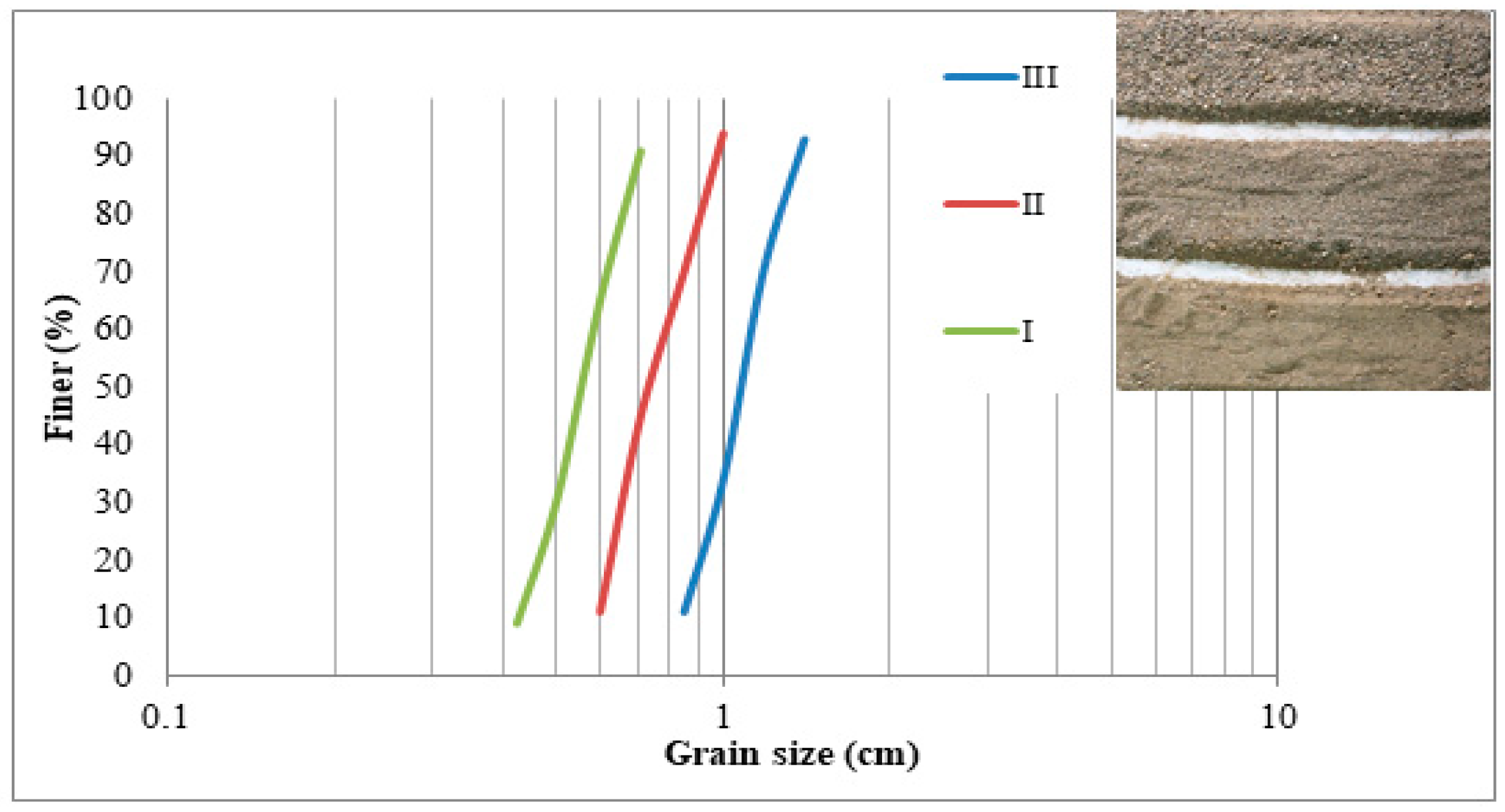
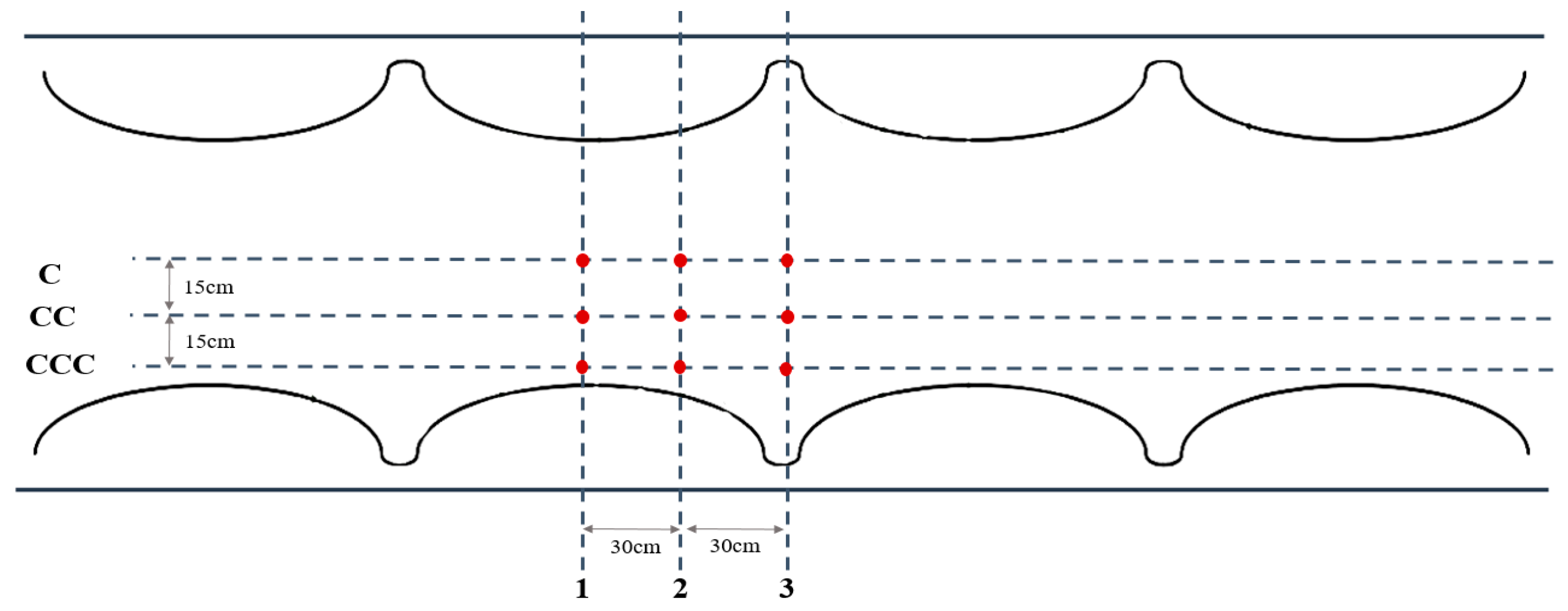


| Experimental Setup | Hydraulic Parameters | |||
|---|---|---|---|---|
| Discharge (lit/s) | Water Depth (cm) | Froude Number (Fr) | Reynolds Number Re × 105 | |
| d50 = 0.56 mm, S = 0 | 27 | 20 | 0.12 | 0.35 |
| d50 = 0.74 mm, S = 0 | 27 | 14 | 0.21 | 0.34 |
| d50 = 1.08 mm, S = 0 | 27 | 12 | 0.26 | 0.34 |
| d50 = 0.56 mm, S = 0.0075 | 27 | 22 | 0.11 | 0.34 |
| d50 = 0.74 mm, S = 0.0075 | 27 | 16 | 0.17 | 0.35 |
| d50 = 1.08 mm, S = 0.0075 | 27 | 13 | 0.23 | 0.34 |
| d50 = 0.56 mm, S = 0.015 | 27 | 23 | 0.1 | 0.35 |
| d50 = 0.74 mm, S = 0.015 | 27 | 21 | 0.11 | 0.35 |
| d50 = 1.08 mm, S = 0.015 | 27 | 14 | 0.21 | 0.34 |
| Sand Types | Locations | Equations | R2 |
|---|---|---|---|
| I | C1 | 0.9733 | |
| C2 | 0.9354 | ||
| C3 | 0.9306 | ||
| CC1 | 0.9432 | ||
| CC2 | 0.9404 | ||
| CC3 | 0.9305 | ||
| CCC1 | 0.9391 | ||
| CCC2 | 0.9304 | ||
| CCC3 | 0.9221 | ||
| II | C1 | 0.9542 | |
| C2 | 0.9606 | ||
| C3 | 0.9471 | ||
| CC1 | 0.9325 | ||
| CC2 | 0.94103 | ||
| CC3 | 0.9564 | ||
| CCC1 | 0.9567 | ||
| CCC2 | 0.9378 | ||
| CCC3 | 0.9422 | ||
| III | C1 | 0.963 | |
| C2 | 0.9343 | ||
| C3 | 0.9321 | ||
| CC1 | 0.9507 | ||
| CC2 | 0.9434 | ||
| CC3 | 0.9352 | ||
| CCC1 | 0.9391 | ||
| CCC2 | 0.9737 | ||
| CCC3 | 0.934 |
| Methods | Bed Slope: S = 0 | Bed Slope: S = 0.015 | ||||
|---|---|---|---|---|---|---|
| Particles | ||||||
| I | II | III | I | II | III | |
| Experimental results | 9.14 | 12.43 | 15.54 | 6.56 | 9.19 | 12.06 |
| Garde (1970) | 14.4 | 16.7 | 20 | 14.4 | 16.7 | 20 |
| Error | 36% | 25% | 22% | 54% | 44% | 39% |
| Mavis & Laushey (1966) | 11.8 | 13.3 | 15.8 | 11.8 | 13.3 | 15.8 |
| Error | 22% | 6% | 1.6% | 36% | 30% | 23% |
| Bed Slope | Particle I: d50 = 0.56 mm | Particle II: d50 = 0.74 mm | Particle III: d50 = 1.08 mm | |||
|---|---|---|---|---|---|---|
| uoc (cm/s) | τoc (N/m2) | uoc (cm/s) | τoc (N/m2) | uoc (cm/s) | τoc (N/m2) | |
| S = 0 | 9.14 | 0.071 | 12.43 | 0.099 | 15.54 | 0.195 |
| S = 0.0075 | 7.54 | 0.067 | 10.21 | 0.092 | 13.28 | 0.172 |
| S = 0.015 | 6.56 | 0.061 | 9.19 | 0.085 | 12.06 | 0.166 |
| Bed Slope | Particle I: d50 = 0.56 mm | Particle II: d50 = 0.74 mm | Particle III: d50 = 1.08 mm | |||
|---|---|---|---|---|---|---|
| S = 0 | 0.007 | 4.70 | 0.008 | 7.33 | 0.011 | 15.01 |
| S = 0.0075 | 0.007 | 4.58 | 0.008 | 7.09 | 0.010 | 14.15 |
| S = 0.015 | 0.0067 | 4.37 | 0.007 | 6.82 | 0.009 | 13.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hadian, S.; Afzalimehr, H.; Sui, J. Incipient Motion of Bed Material in a Channel with Varying Width and Vegetated Channel Walls. Water 2023, 15, 3691. https://doi.org/10.3390/w15203691
Hadian S, Afzalimehr H, Sui J. Incipient Motion of Bed Material in a Channel with Varying Width and Vegetated Channel Walls. Water. 2023; 15(20):3691. https://doi.org/10.3390/w15203691
Chicago/Turabian StyleHadian, Sanaz, Hossein Afzalimehr, and Jueyi Sui. 2023. "Incipient Motion of Bed Material in a Channel with Varying Width and Vegetated Channel Walls" Water 15, no. 20: 3691. https://doi.org/10.3390/w15203691
APA StyleHadian, S., Afzalimehr, H., & Sui, J. (2023). Incipient Motion of Bed Material in a Channel with Varying Width and Vegetated Channel Walls. Water, 15(20), 3691. https://doi.org/10.3390/w15203691






