Research on Threshold Selection Method in Wave Extreme Value Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. POT Method
2.2. Threshold Determination Using the Detrended Fluctuation Analysis Method
- (1)
- Determine the maximum and minimum values of the time series .
- (2)
- Determine the central point of the sequence , you can either take the average of all data points or choose a median value that lies between the maximum and minimum values.
- (3)
- Starting from the maximum value of , sequentially discard data points within intervals until reaching the central point . In this process, a series of new sequence is obtained, where is the interval size.
- (4)
- Calculate the fractal exponent for each new sequence and observe how it changes with the discarded interval size .
- (5)
- When the change in starts to become smooth and converges to the original DFA exponent of the data , take the corresponding value as the threshold for extreme events in the sequence . The degree of convergence to the original value is not unique and may fluctuate slightly around the original exponent. Therefore, to determine the convergence point, the variance of the sequence of exponents can be calculated. Variance can be defined as follows:
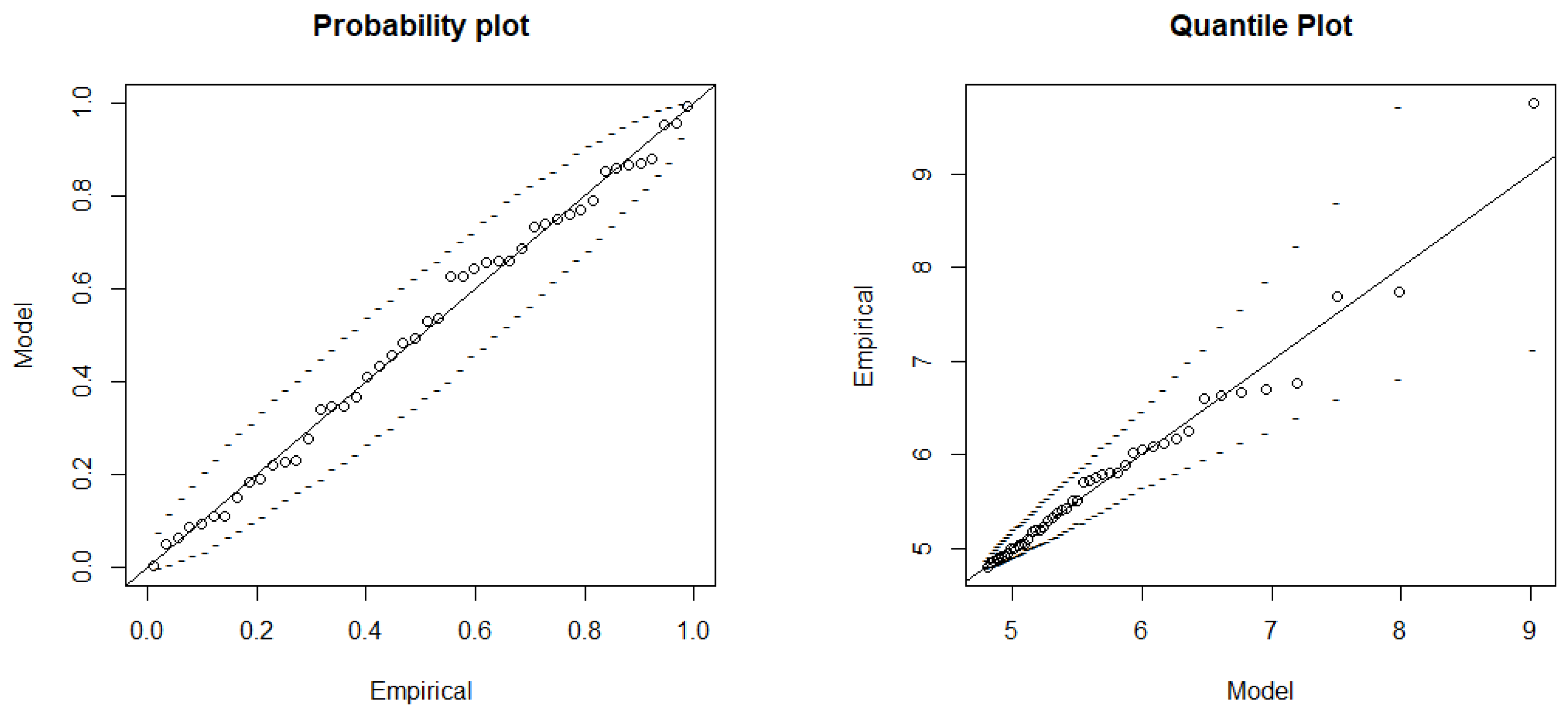
2.3. Method Validation
2.4. The Study Area and Data
3. Results
3.1. The Long-Range Correlation of the Significant Wave Height Series
3.2. Threshold Determination
3.3. Return Period
3.4. Comparison with Other Threshold Selection Methods
3.4.1. The Mean Residual Life Plot
3.4.2. Parameter Stability Plot
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cai, Y.; Reeve, D.E. Extreme value prediction via a quantile function model. Coast. Eng. 2013, 77, 91–98. [Google Scholar] [CrossRef]
- Sartini, L.; Besio, G.; Cassola, F. Spatio-temporal modelling of extreme wave heights in the Mediterranean Sea. Ocean Model. 2017, 117, 52–69. [Google Scholar] [CrossRef]
- Gao, J.; Shi, H.; Zang, J.; Liu, Y. Mechanism analysis on the mitigation of harbor resonance by periodic undulating topography. Ocean Eng. 2023, 281, 114923. [Google Scholar] [CrossRef]
- Gao, J.-L.; Chen, H.-Z.; Mei, L.-L.; Liu, Z.; Liu, Q. Statistical analyses of wave height distribution for multidirectional irregular waves over a sloping bottom. China Ocean Eng. 2021, 35, 504–517. [Google Scholar] [CrossRef]
- Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frequency distribution of the largest or smallest member of a sample. Math. Proc. Camb. Philos. Soc. 1928, 24, 180–190. [Google Scholar] [CrossRef]
- Muraleedharan, G.; Lucas, C.; Soares, C.G. Regression quantile models for estimating trends in extreme significant wave heights. Ocean Eng. 2016, 118, 204–215. [Google Scholar] [CrossRef]
- Pickands, J., III. Statistical inference using extreme order statistics. Ann. Stat. 1975, 3, 119–131. Available online: https://www.jstor.org/stable/2958083 (accessed on 1 January 2021).
- Tawn, J.A. An extreme-value theory model for dependent observations. J. Hydrol. 1988, 101, 227–250. [Google Scholar] [CrossRef]
- Weibull, W. A statistical theory of the strength of materials. Proc. Royal Swedish Inst. Eng. Res. 1939, 151, 1–45. [Google Scholar]
- Balkema, A.A.; De Haan, L. Residual life time at great age. Ann. Probab. 1974, 2, 792–804. [Google Scholar] [CrossRef]
- Soares, C.G.; Scotto, M. Application of the r largest-order statistics for long-term predictions of significant wave height. Coast. Eng. 2004, 51, 387–394. [Google Scholar] [CrossRef]
- Goda, Y.; Konagaya, O.; Takeshita, N.; Hitomi, H.; Nagai, T. Population distribution of extreme wave heights estimated through regional analysis. In Coastal Engineering 2000. Presented at the 27th International Conference on Coastal Engineering (ICCE), Copenhagen, Sydney, Australia, 16–21 July 2000; American Society of Civil Engineers: Sydney, Australia, 2001; pp. 1078–1091. [Google Scholar] [CrossRef]
- Davies, G.; Callaghan, D.P.; Gravois, U.; Jiang, W.; Hanslow, D.; Nichol, S.; Baldock, T. Improved treatment of non-stationary conditions and uncertainties in probabilistic models of storm wave climate. Coast. Eng. 2017, 127, 1–19. [Google Scholar] [CrossRef]
- Mazas, F.; Hamm, L. A multi-distribution approach to POT methods for determining extreme wave heights. Coast. Eng. 2011, 58, 385–394. [Google Scholar] [CrossRef]
- Shamji, V.; Aboobacker, V.; Vineesh, T. Extreme value analysis of wave climate around Farasan Islands, southern Red Sea. Ocean Eng. 2020, 207, 107395. [Google Scholar] [CrossRef]
- Coles, S.; Bawa, J.; Trenner, L.; Dorazio, P. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001; Volume 208, Available online: https://www.springer.com/gp/book/9781852334598 (accessed on 1 January 2021).
- Hill, B.M. A simple general approach to inference about the tail of a distribution. Ann. Stat. 1975, 3, 1163–1174. [Google Scholar] [CrossRef]
- Beirlant, J.; Goegebeur, Y.; Segers, J.; Teugels, J.L. Statistics of Extremes: Theory and Applications; John Wiley and Sons Ltd.: Chichester, UK, 2004. [Google Scholar]
- Carreau, J.; Bengio, Y. A hybrid Pareto model for asymmetric fat-tailed data: The univariate case. Extremes 2009, 12, 53–76. [Google Scholar] [CrossRef]
- Eastoe, E.F.; Tawn, J.A. Statistical models for overdispersion in the frequency of peaks over threshold data for a flow series. Water Resour. Res. 2010, 46, 1–12. [Google Scholar] [CrossRef]
- Solari, S.; Losada, M. A unified statistical model for hydrological variables including the selection of threshold for the peak over threshold method. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Chen, B.-Y.; Zhang, K.-Y.; Wang, L.-P.; Jiang, S.; Liu, G.-L. Generalized extreme value-pareto distribution function and its applications in ocean engineering. China Ocean Eng. 2019, 33, 127–136. [Google Scholar] [CrossRef]
- Niroomandi, A.; Ma, G.; Ye, X.; Lou, S.; Xue, P. Extreme value analysis of wave climate in Chesapeake Bay. Ocean Eng. 2018, 159, 22–36. [Google Scholar] [CrossRef]
- Vanem, E. Uncertainties in extreme value modelling of wave data in a climate change perspective. J. Ocean Eng. Mar. Energy 2015, 1, 339–359. [Google Scholar] [CrossRef]
- Thompson, P.; Cai, Y.; Reeve, D.; Stander, J. Automated threshold selection methods for extreme wave analysis. Coast. Eng. 2009, 56, 1013–1021. [Google Scholar] [CrossRef]
- Liang, B.; Shao, Z.; Li, H.; Shao, M.; Lee, D. An automated threshold selection method based on the characteristic of extrapolated significant wave heights. Coast. Eng. 2019, 144, 22–32. [Google Scholar] [CrossRef]
- Shao, Z.; Liang, B.; Gao, H. Extracting independent and identically distributed samples from time series significant wave heights in the Yellow Sea. Coast. Eng. 2020, 158, 103693. [Google Scholar] [CrossRef]
- Scarrott, C.; MacDonald, A. A review of extreme value threshold estimation and uncertainty quantification. REVSTAT-Stat. J. 2012, 10, 33–60. [Google Scholar] [CrossRef]
- Ozger, M. Scaling characteristics of ocean wave height time series. Phys. A Stat. Mech. Its Appl. 2011, 390, 981–989. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Du, H.; Wu, Z.; Zong, S.; Meng, X.; Wang, L. Assessing the characteristics of extreme precipitation over northeast China using the multifractal detrended fluctuation analysis. J. Geophys. Res. Atmos. 2013, 118, 6165–6174. [Google Scholar] [CrossRef]
- Liu, B.; Chen, J.; Chen, X.; Lian, Y.; Wu, L. Uncertainty in determining extreme precipitation thresholds. J. Hydrol. 2013, 503, 233–245. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, G.; Fu, B.; Wang, C.; Gupta, H.V.; Zhang, X.; Li, R. A universal multifractal approach to assessment of spatiotemporal extreme precipitation over the Loess Plateau of China. Hydrol. Earth Syst. Sci. 2020, 24, 809–826. [Google Scholar] [CrossRef]
- Du, H.; Wu, Z.; Li, M.; Jin, Y.; Zong, S.; Meng, X. Characteristics of extreme daily minimum and maximum temperature over Northeast China, 1961–2009. Theor. Appl. Climatol. 2013, 111, 161–171. [Google Scholar] [CrossRef]
- Naseef, T.M.; Kumar, V.S. Influence of tropical cyclones on the 100-year return period wave height—A study based on 39-year long ERA5 reanalysis data. Int. J. Climatol. 2020, 40, 2106–2116. [Google Scholar] [CrossRef]
- Sreelakshmi, S.; Bhaskaran, P.K. Wind-generated wave climate variability in the Indian Ocean using ERA-5 dataset. Ocean Eng. 2020, 209, 107486. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Wang, Y.; Liao, Z.; Sun, P. Spatiotemporal variations and extreme value analysis of significant wave height in the South China Sea based on 71-year long ERA5 wave reanalysis. Appl. Ocean Res. 2021, 113, 102750. [Google Scholar] [CrossRef]
- Méndez, F.J.; Menéndez, M.; Luceño, A.; Losada, I.J. Estimation of the long-term variability of extreme significant wave height using a time-dependent peak over threshold (pot) model. J. Geophys. Res. Ocean. 2006, 111, 1–13. [Google Scholar] [CrossRef]
- Luceño, A.; Menéndez, M.; Méndez, F.J. The effect of temporal dependence on the estimation of the frequency of extreme ocean climate events. Proc. R. Soc. A Math. Phys. Eng. Sci. 2006, 462, 1683–1697. [Google Scholar] [CrossRef]











| Location | Lat. (° N) | Lon. (° E) | Water Depth (m) | Maximum Wave Height (m) |
|---|---|---|---|---|
| P1 | 14 | 110 | 1274 | 9.75 |
| P2 | 11 | 116 | 2671 | 5.74 |
| P3 | 20 | 119 | 3032 | 12.65 |
| P4 | 17 | 114 | 3053 | 9.55 |
| P5 | 20 | 108 | 49 | 9.97 |
| P6 | 21 | 116 | 128 | 10.54 |
| Turning Point | n | Significance Test | |||
|---|---|---|---|---|---|
| 5.19 | 52 | 50.03 | 64.3 | 38.56 | No |
| 5.12 | 56 | 71.14 | 68.8 | 42.06 | Yes |
| 4.87 | 74 | 90.6 | 88.85 | 58.01 | Yes |
| 4.76 | 83 | 140.27 | 98.78 | 66.08 | Yes |
| 4.44 | 112 | 121.82 | 130.47 | 92.38 | No |
| 4.35 | 121 | 113.72 | 140.23 | 100.62 | No |
| Return Periods | 3 Days | 4 Days | 5 Days | 6 Days | 7 Days |
|---|---|---|---|---|---|
| 50 year (m) | 8.53 | 8.53 | 8.53 | 8.53 | 8.53 |
| 100 year (m) | 9.15 | 9.15 | 9.13 | 9.13 | 9.13 |
| 150 year (m) | 9.51 | 9.51 | 9.47 | 9.47 | 9.47 |
| 200 year (m) | 9.77 | 9.77 | 9.71 | 9.71 | 9.71 |
| Locactions\Return Periods | 50 Year (m) | 100 Year (m) | 150 Year (m) | 200 Year (m) |
|---|---|---|---|---|
| P1 | 8.53 | 9.13 | 9.47 | 9.71 |
| P2 | 6.17 | 6.24 | 6.28 | 6.31 |
| P3 | 11.38 | 12.32 | 12.87 | 13.26 |
| P4 | 9.84 | 10.42 | 10.75 | 10.99 |
| P5 | 8.73 | 9.38 | 9.74 | 10.01 |
| P6 | 10.67 | 11.42 | 11.85 | 12.14 |
| Return Periods | Stable Threshold Range (m) | Return Period Significant Wave Heights (m) | The Average of Wave Height (m) |
|---|---|---|---|
| 50 year | (4.60, 5.65) | (8.50, 8.55) | 8.53 |
| 100 year | (4.60, 5.55) | (9.09, 9.22) | 9.16 |
| 150 year | (4.60, 5.55) | (9.43, 9.61) | 9.52 |
| 200 year | (4.60, 5.55) | (9.65, 9.90) | 9.78 |
| Return Periods | Stable Threshold Range (m) | Range of Differences (m) | Width of Differences (m) |
|---|---|---|---|
| 50 year | (4.60, 5.65) | (−0.01, 0.09) | 0.10 |
| 100 year | (4.60, 5.55) | (−0.05, 0.06) | 0.11 |
| 150 year | (4.60, 5.55) | (−0.08, 0.10) | 0.18e |
| 200 year | (4.60, 5.55) | (−0.10, 0.14) | 0.24 |
| Locations | P1 | P2 | P3 | P4 | P5 | P6 |
|---|---|---|---|---|---|---|
| Stable threshold range (m) | (4.65, 5.55) | (3.75, 4.95) | (5.90, 6.35) | (4.70, 5.70) | (4.10, 5.15) | (4.80, 5.55) |
| Locations | MF-DFA (m) | Mean Excess Function (m) | Parameter Stability Plot (m) |
|---|---|---|---|
| P1 | 5.12 | (4.80, 5.40) | (4.85, 5.40) |
| P2 | 3.96 | (3.90, 4.70) | (3.95, 4.40) |
| P3 | 6.06 | (4.90, 6.50) | (5.80, 6.10) |
| P4 | 5.59 | (4.70, 6.00) | (4.80, 5.60) |
| P5 | 4.45 | (3.60, 4.50) | (4.10, 4.50) |
| P6 | 5.15 | (4.98, 5.35) | (4.90, 5.20) |
| Return Periods | MF-DFA (m) | Mean Excess Function (m) | Parameter Stability Plot (m) |
|---|---|---|---|
| 50 year | 8.53 | 8.54 | 8.55 |
| 100 year | 9.13 | 9.19 | 9.22 |
| 150 year | 9.47 | 9.58 | 9.61 |
| 200 year | 9.71 | 9.85 | 9.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Yang, F.; Wang, H. Research on Threshold Selection Method in Wave Extreme Value Analysis. Water 2023, 15, 3648. https://doi.org/10.3390/w15203648
Liu H, Yang F, Wang H. Research on Threshold Selection Method in Wave Extreme Value Analysis. Water. 2023; 15(20):3648. https://doi.org/10.3390/w15203648
Chicago/Turabian StyleLiu, Huashuai, Fan Yang, and Hongchuan Wang. 2023. "Research on Threshold Selection Method in Wave Extreme Value Analysis" Water 15, no. 20: 3648. https://doi.org/10.3390/w15203648






