Study on the Snowmelt Flood Model by Machine Learning Method in Xinjiang
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collection
2.3. Modeling Approaches
2.3.1. Element Screening
- (1)
- Pearson coefficient
- (2)
- Principal component analysis
- (3)
- Factor analysis
2.3.2. Machine Learning Methods
- (1)
- Support Vector Regression (SVR)
- (2)
- Random Forest (RF)
- (3)
- K-Nearest Neighbor (KNN)
- (4)
- Artificial Neural Network (ANN)
- (5)
- Recurrent Neural Network (RNN)
- (6)
- Long Short-Term Memory Neural Network (LSTM)
2.3.3. Evaluation Criteria
3. Result and Discussion
3.1. Element Screening
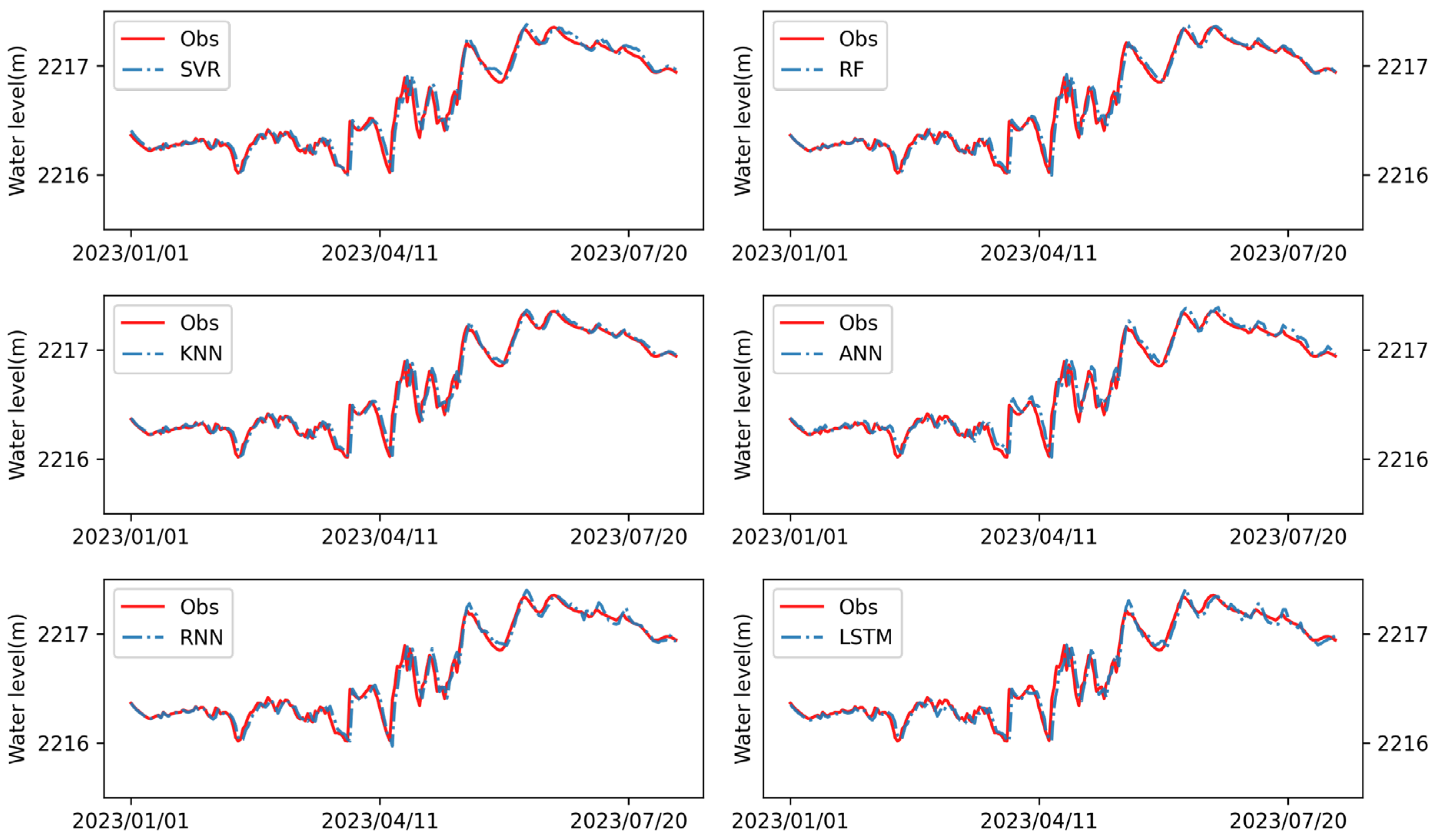
3.2. Machine Learning Results
3.3. Selection of Hyperparameters
3.4. Result Analysis
4. Conclusions
- (1)
- We used Pearson coefficient, principal component analysis, and factor analysis to screen input elements, screen 14 kinds of meteorological observation data from JINGHE and BAYANBULAK stations, and finally select 5 kinds of elements for modeling, including average sea level pressure, average wind speed, snow cover depth of JINGHE and average station pressure, and snow cover depth of BAYANBULAK. From the perspective of Pearson coefficient, the average temperature, average dew point, and average sea level pressure had a very high linear correlation. When constructing the model, we approximated that they were equivalent and only retained one.
- (2)
- SVR, RF, KNN, ANN, RNN, and LSTM were selected to construct 24 sets of models with different hyperparameters. Among all the models, LSTM had the best results, and the RMSEs in the training period and the testing period were respectively 0.011 and 0.071, and R2 values were 0.999 and 0.970, respectively. Next best were the results of RF, whose RMSEs in the training period and the test period were 0.012 and 0.072, respectively; R2 values were 0.999 and 0.969, respectively. Compared to other models, LSTM performed best, but it had more hyperparameters to optimize. From an application point of view, RF may be a better choice, because as long as the number of classifiers is set large enough, a model with good performance can be obtained. The LSTM model requires more work on model structure design and parameter optimization.
- (3)
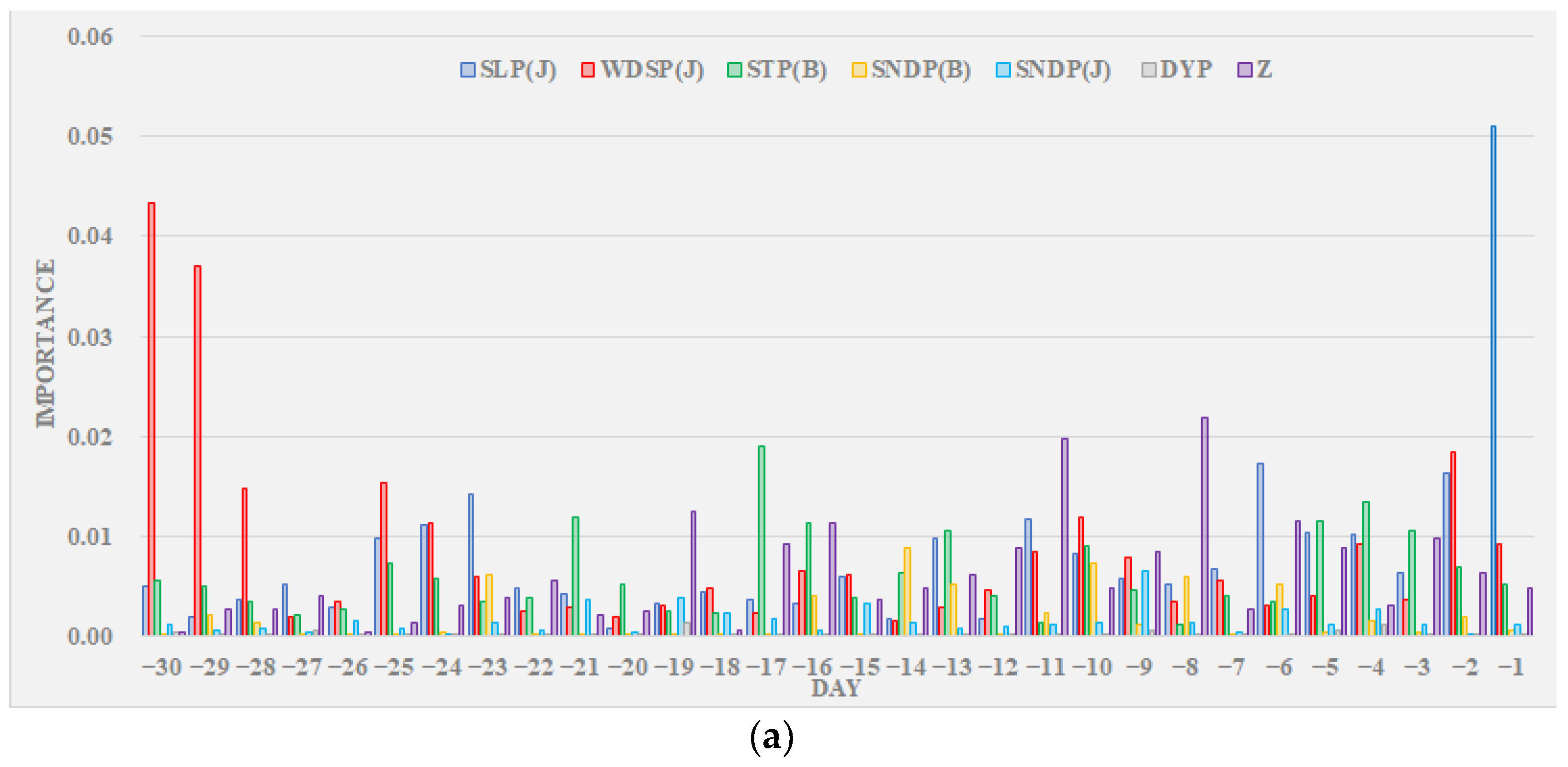
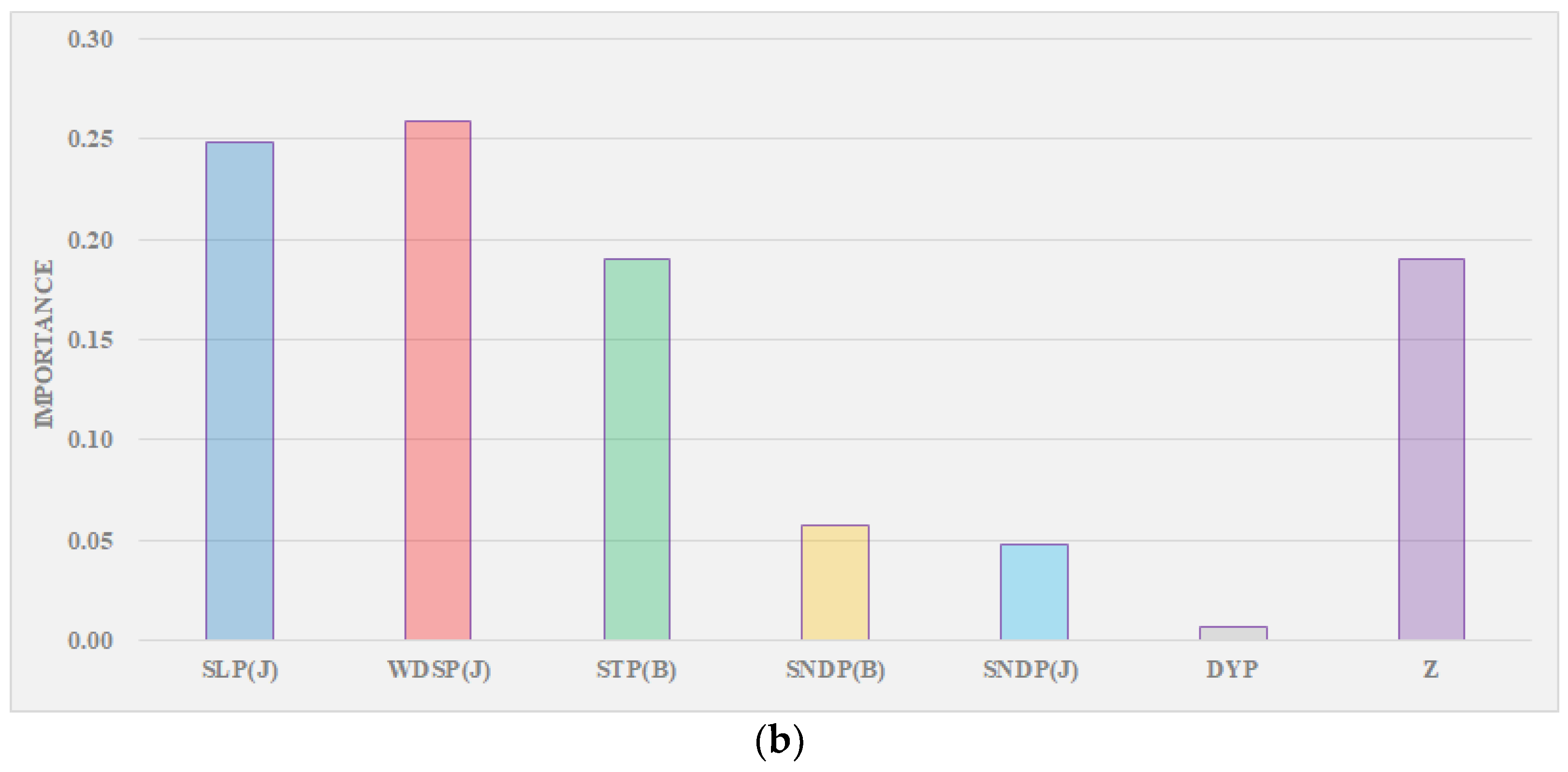
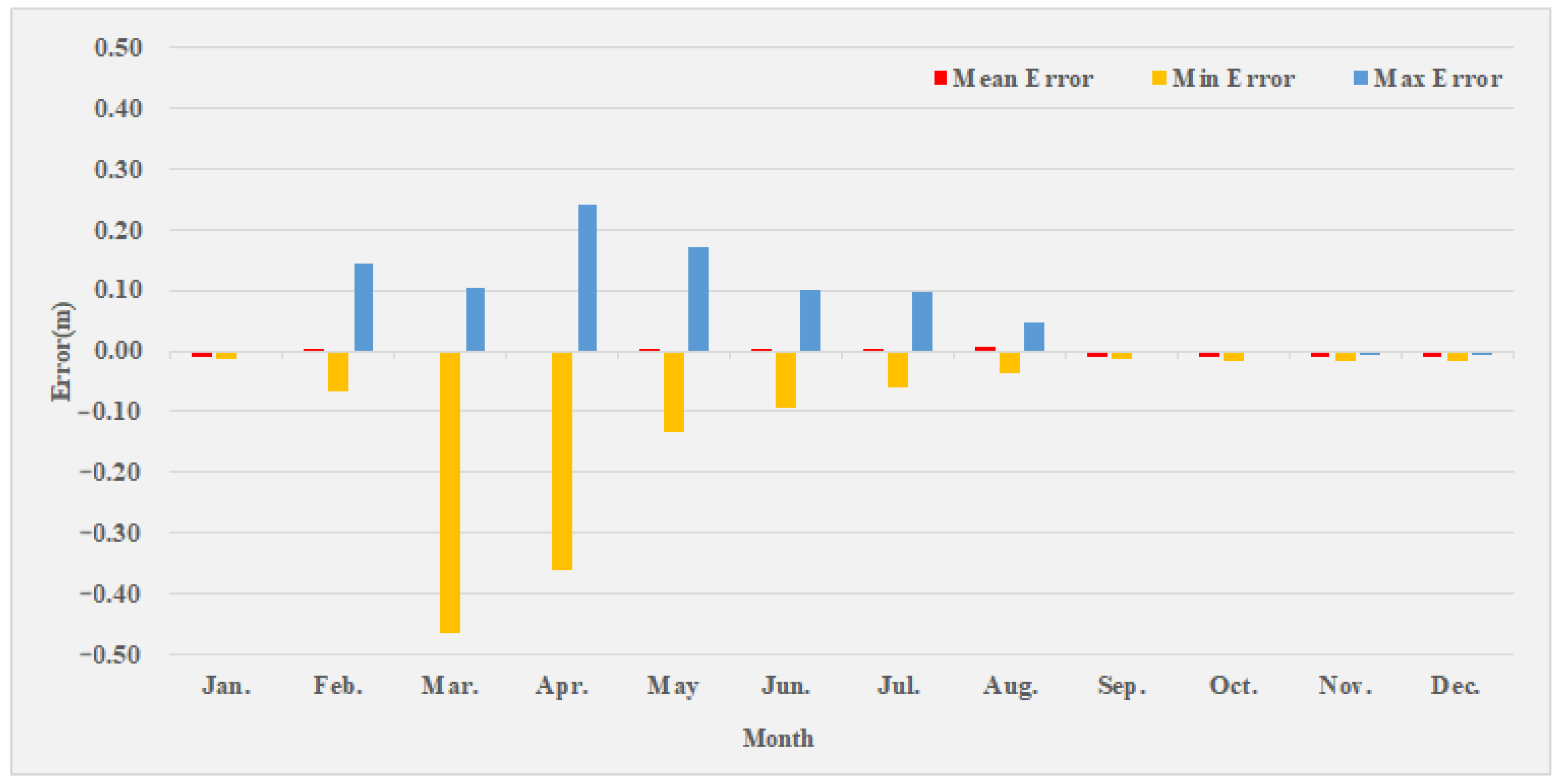
- From the contribution rate results of the RF model, when the model made predictions, the contribution of meteorological elements was higher, and the contribution of rainfall in the basin was lower. From the prediction results of LSTM, the average error of each month was relatively stable, most of which did not exceed ±0.01 m, and the errors fluctuated greatly in March and April. The selection of fitting data is very important when modeling. The results obtained by directly fitting the water level were not ideal. Adjusting the model to try to fit the water level residuals (i.e., the difference between future water levels and known water levels), and calculating future water levels based on the predicted residuals, would significantly improve the accuracy of the simulation.
- (4)
- The purpose of this study was to explore a hydrological forecast method that can be used in practical work under limited data conditions. Hydrological sensors have been widely constructed in Xinjiang, and as time goes by, more and more hydrological data will be available for modeling. For areas with rich hydrological data, there are more and better choices when modeling. Physical models, distributed models, or combinations of different types of models can obtain richer conclusions and results. Therefore, the method proposed in this study is a temporary solution when hydrological data are limited, and subsequent research on snowmelt models and forecasting and early warning technologies in Xinjiang should be continued.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Deng, X.L.; Li, Q.; Yang, Q.; Huo, W. Characteristics of the Extreme Precipitation Events in the Tianshan Mountains in Relation to Climate Change. J. Glaciol. Geocryol. 2010, 32, 927–934. [Google Scholar]
- Xu, L.P.; Li, P.H.; Li, Z.Q.; Zhang, Z.Y.; Wang, P.Y.; Xu, C.H. Advances in research on changes and effects of glaciers in Xinjiang mountains. Adv. Water Sci. 2020, 31, 946–959. [Google Scholar] [CrossRef]
- Chen, Y.N.; Li, Z.; Fang, G.H. Changes of key hydrological elements and research progress of water cycle in the Tianshan Mountains, Central Asia. Arid. Land Geogr. 2022, 45, 1–8. [Google Scholar]
- Cui, M.Y.; Zhou, G.; Zhang, D.H.; Zhang, S.Q. Global snowmelt flood disasters and their impact from 1900 to 2020. J. Glaciol. Geocryol. 2022, 44, 1898–1911. [Google Scholar]
- Wei, T.F.; Liu, Z.H.; Wang, Y. Effect on Snowmelt Water Outflow of Snow-covered Seasonal Frozen Soil. Arid. Zone Res. 2015, 32, 435–441. [Google Scholar] [CrossRef]
- Wu, S.F.; Liu, Z.H.; Qiu, J.H. Analysis of the Characteristics of Snowmelt Flood and Previous Climate Snow Condition in North Xinjiang. J. China Hydrol. 2006, 26, 84–87. [Google Scholar]
- Huai, B.J.; Li, Z.Q.; Sun, M.P.; Xiao, Y. Snowmelt runoff model applied in the headwaters region of Urumqi River. Arid Land Geogr. 2013, 36, 41–48. [Google Scholar] [CrossRef]
- Muattar, S.; Ding, J.L.; Abudu, S.; Cui, C.L.; Anwar, K. Simulation of Snowmelt Runoff in the Catchments on Northern Slope of the Tianshan Mountains. Arid Zone Res. 2016, 33, 636–642. [Google Scholar] [CrossRef]
- Yu, Q.Y.; Hu, C.H.; Bai, Y.G.; Lu, Z.L.; Cao, B.; Liu, F.Y.; Liu, C.S. Application of snowmelt runoff model in flood forecasting and warning in Xinjiang. Arid Land Geogr. 2023, 1–15. [Google Scholar]
- Dang, S.Z.; Liu, C.M. Modification of SNTHERM Albedo Algorithm and Response from Black Carbon in Snow. Adv. Mat. Res. 2011, 281, 147–150. [Google Scholar] [CrossRef]
- Bartelt, P.; Lehning, M. A physical SNOWPACK model for the Swiss avalanche warning. Cold Reg. Sci. Technol. 2002, 35, 123–145. [Google Scholar] [CrossRef]
- Wang, W.C.; Zhao, Y.W.; Tu, Y.; Dong, R.; Ma, Q.; Liu, C.J. Research on Parameter Regionalization of Distributed Hydrological Model Based on Machine Learning. Water 2023, 15, 518. [Google Scholar] [CrossRef]
- Vafakhah, M.; Sedighi, F.; Javadi, M.R. Modeling the Rainfall-Runoff Data in Snow-Affected Watershed. Int. J. Comput. Electr. Eng. 2014, 6, 40. [Google Scholar] [CrossRef]
- Thapa, S.; Zhao, Z.; Li, B.; Lu, L.; Fu, D.; Shi, X.; Tang, B.; Qi, H. Snowmelt-Driven Streamflow Prediction Using Machine Learning Techniques (LSTM, NARX, GPR, and SVR). Water 2020, 12, 1734. [Google Scholar] [CrossRef]
- Himan, S.; Ataollah, S.; Somayeh, R.; Shahrokh, A.; Binh, T.P.; Fatemeh, M.; Marten, G.; John, J.C.; Dieu, T.B. Flash flood susceptibility mapping using a novel deep learning model based on deep belief network, back propagation and genetic algorithm. Geosci. Front. 2021, 12, 101100. [Google Scholar] [CrossRef]
- Wang, G.; Hao, X.; Yao, X.; Wang, J.; Li, H.; Chen, R.; Liu, Z. Simulations of Snowmelt Runoff in a High-Altitude Mountainous Area Based on Big Data and Machine Learning Models: Taking the Xiying River Basin as an Example. Remote Sens. 2023, 15, 1118. [Google Scholar] [CrossRef]
- Yang, R.; Zheng, G.; Hu, P.; Liu, Y.; Xu, W.; Bao, A. Snowmelt Flood Susceptibility Assessment in Kunlun Mountains Based on the Swin Transformer Deep Learning Method. Remote Sens. 2022, 14, 6360. [Google Scholar] [CrossRef]
- Zhou, G.; Cui, M.Y.; Li, Z.; Zhang, S.Q. Dynamic evaluation of the risk of the spring snowmelt flood in Xinjiang. Arid Zone Res. 2021, 38, 950–960. [Google Scholar]
- Waldmann, P. On the Use of the Pearson Correlation Coefficient for Model Evaluation in Genome-Wide Prediction. Front. Genet. 2019, 10, 899. [Google Scholar] [CrossRef]
- Jackson, J.E. A User’s Guide to Principal Components; Wiley: Hoboken, NJ, USA, 1992. [Google Scholar]
- Horn, J.L. A rationale and test for the number of factors in factor analysis. Psychnmetrica 1965, 30, 179–185. [Google Scholar] [CrossRef]
- Okkan, U.; Serbes, Z.A. Rainfall–runoff modeling using least squares support vector machines. Environmetrics 2012, 23, 549–564. [Google Scholar] [CrossRef]
- Panahi, M.; Sadhasivam, N.; Pourghasemi, H.R.; Rezaie, F.; Lee, S. Spatial prediction of groundwater potential mapping based on convolutional neural network (CNN) and support vector regression (SVR). J. Hydrol. 2020, 588, 125033. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Li, X.N.; Zhang, Y.J.; She, Y.J.; Chen, L.W.; Chen, J.X. Estimation of impervious surface percentage of river network regions using an ensemble leaning of CART analysis. Remote Sens. Land Resour. 2013, 25, 174–179. [Google Scholar]
- Juna, A.; Umer, M.; Sadiq, S.; Karamti, H.; Eshmawi, W.; Mohamed, A.; Ashraf, I. Water Quality Prediction Using KNN Imputer and Multilayer Perceptron. Water 2022, 14, 2592. [Google Scholar] [CrossRef]
- Lippmann, R.P. An introduction to computing with neural nets. IEEE Assp. Mag. 1988, 4, 4–22. [Google Scholar] [CrossRef]
- Robert, H.N. Theory of the backpropagation neural network. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Washington, DC, USA, 18–22 June 1988. [Google Scholar]
- Wang, S.S.; Xu, P.B.; Hu, S.Y.; Wang, K. Research on a Deep Learning Based Model for Predicting Mountain Flood Water Level in Small Watersheds. Comput. Knowl. Technol. 2022, 18, 89–91. [Google Scholar] [CrossRef]
- Gao, W.L.; Gao, J.X.; Yang, L.; Wang, M.J.; Yao, W.H. A Novel Modeling Strategy of Weighted Mean Temperature in China Using RNN and LSTM. Remote Sens. 2021, 13, 3004. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, N.; Guo, J.Y.; Guo, B. Prediction of monthly precipitation over the Tibetan Plateau based on LSTM neural network. J. Geo-Inf. Sci. 2020, 22, 1617–1629. [Google Scholar] [CrossRef]

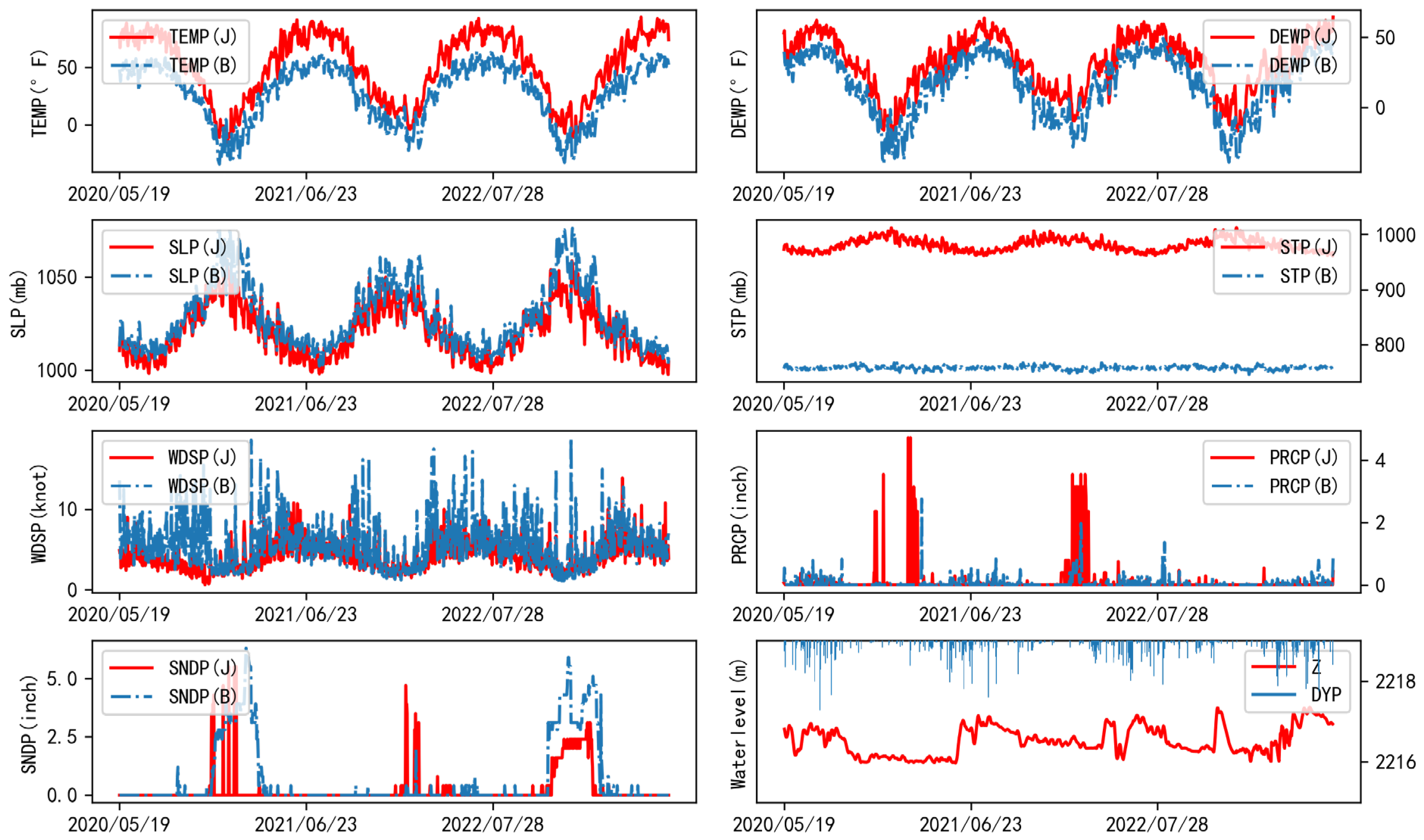

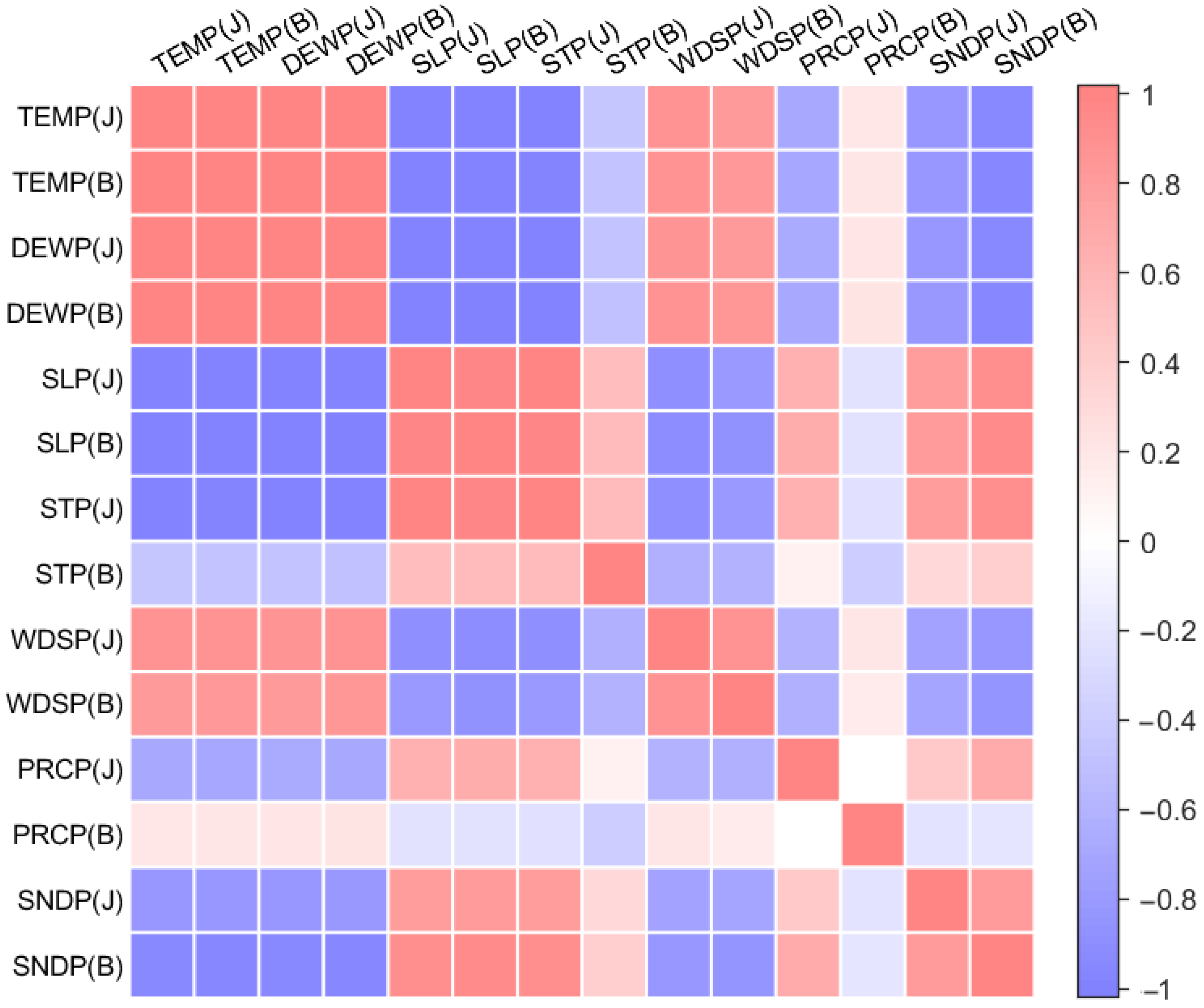
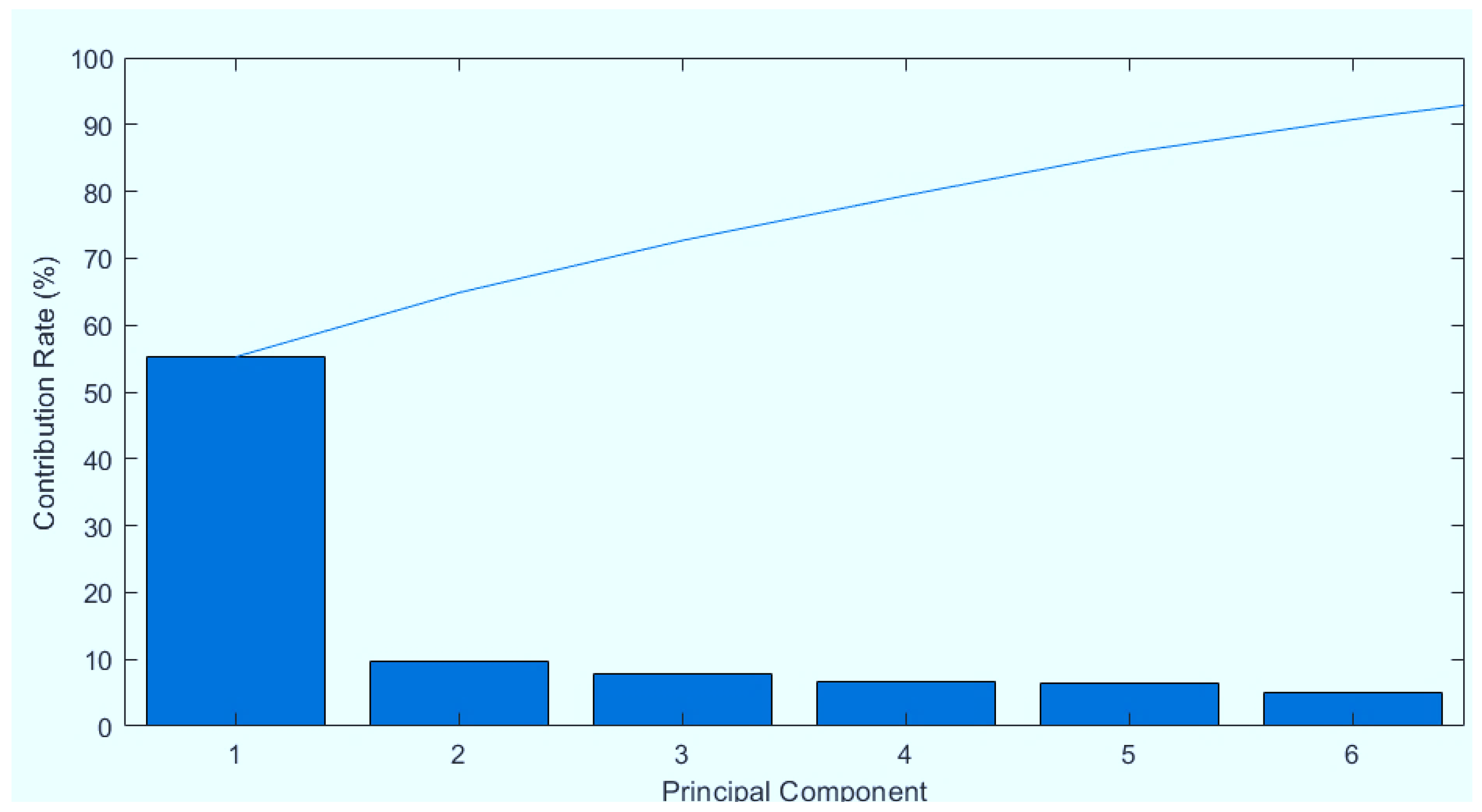
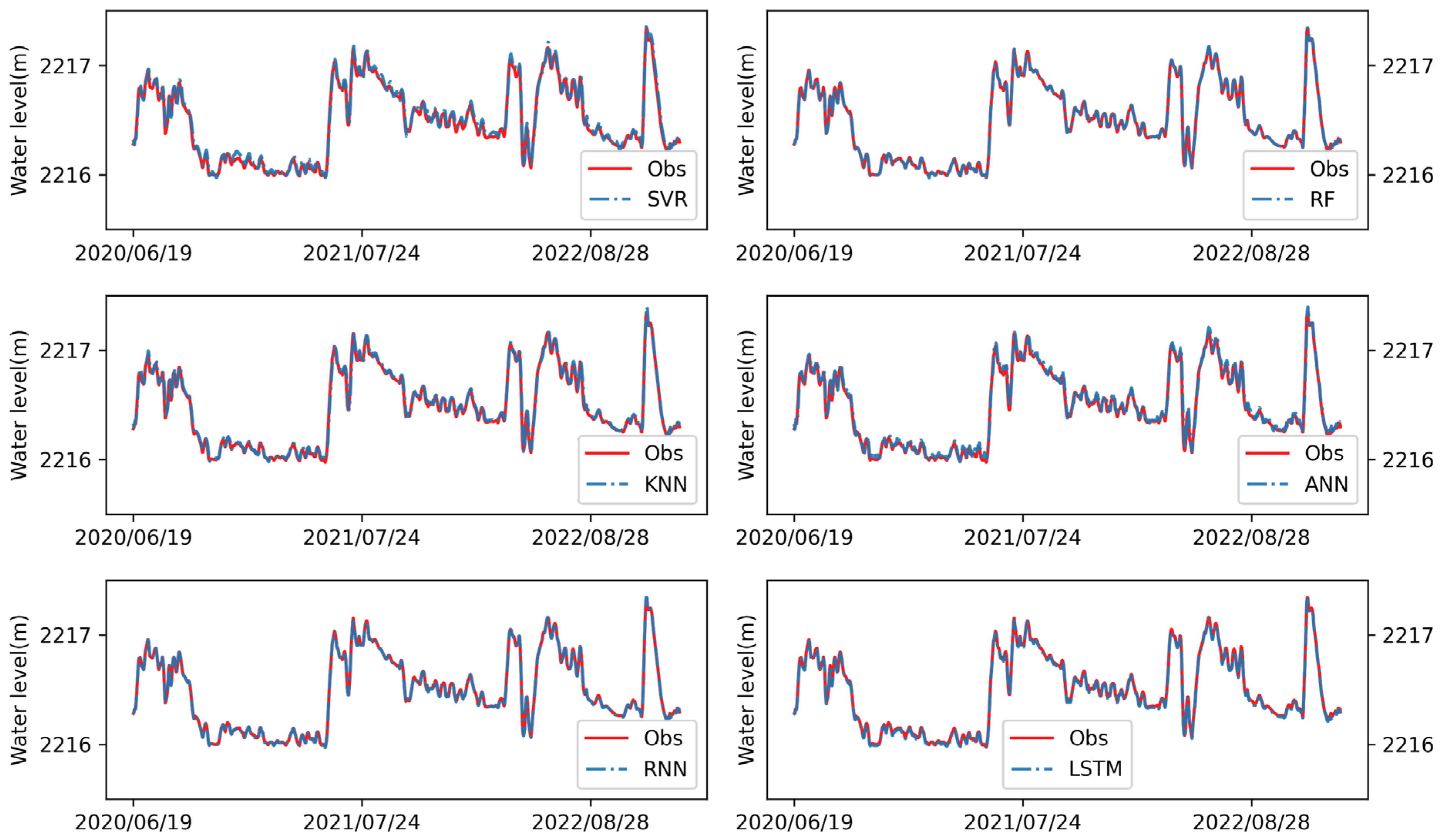

| Station | Data Source | Item | Desc | Mean Value | Precision and Unit |
|---|---|---|---|---|---|
| Lianggoushan | Hydrological department | Z | Water level | 2216.56 | 0.01 m |
| DYP | Precipitation | 1.8 | 0.1 mm | ||
| JINGHE | GSOD | TEMP(J) | Average temperature | 49.4 | 0.1 °F |
| DEWP(J) | Average dew point | 30.0 | 0.1 °F | ||
| SLP(J) | Average sea level pressure | 1021.2 | 0.1 mb | ||
| STP(J) | Average station pressure | 981.2 | 0.1 mb | ||
| WDSP(J) | Average wind speed | 4.1 | 0.1 knots | ||
| PRCP(J) | Daily precipitation | 0.14 | 0.01 inches | ||
| SNDP(J) | Snow cover depth | 0.2 | 0.1 inches | ||
| BAYANBULAK | GSOD | TEMP(B) | Average temperature | 26.1 | 0.1 °F |
| DEWP(B) | Average dew point | 15.0 | 0.1 °F | ||
| SLP(B) | Average sea level pressure | 1029.2 | 0.1 mb | ||
| STP(B) | Average station pressure | 758.2 | 0.1 mb | ||
| WDSP(B) | Average wind speed | 5.6 | 0.1 knots | ||
| PRCP(B) | Daily precipitation | 0.05 | 0.01 inches | ||
| SNDP(B) | Snow cover depth | 1.0 | 0.1 inches |
| Item | Com1 | Com 2 | Com 3 | Com 4 | Com 5 |
|---|---|---|---|---|---|
| TEMP(J) | 0.91 | 0.26 | 0.11 | −0.21 | −0.16 |
| TEMP(B) | 0.85 | 0.28 | 0.04 | −0.41 | −0.15 |
| DEWP(J) | 0.90 | 0.21 | 0.05 | −0.14 | −0.15 |
| DEWP(B) | 0.85 | 0.30 | 0.01 | −0.36 | −0.13 |
| SLP(J) | −0.95 | −0.16 | 0.16 | 0.08 | 0.12 |
| SLP(B) | −0.82 | −0.32 | 0.19 | 0.40 | 0.14 |
| STP(J) | −0.95 | −0.13 | 0.22 | 0.05 | 0.11 |
| STP(B) | −0.11 | −0.16 | 0.97 | −0.02 | −0.03 |
| WDSP(J) | 0.35 | 0.70 | −0.08 | 0.00 | −0.05 |
| WDSP(B) | 0.18 | 0.62 | −0.14 | −0.25 | −0.09 |
| PRCP(J) | −0.24 | −0.14 | −0.14 | 0.23 | −0.14 |
| PRCP(B) | 0.05 | 0.03 | −0.06 | 0.01 | −0.02 |
| SNDP(J) | −0.26 | −0.10 | −0.03 | 0.09 | 0.78 |
| SNDP(B) | −0.45 | −0.14 | 0.00 | 0.58 | 0.21 |
| Algorithm | Setting Items | Hyperparameter | Training | Testing | ||
|---|---|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | |||
| SVR | Kernel function | kernel = linear | 0.041 | 0.985 | 0.082 | 0.960 |
| kernel= rbf | 0.033 | 0.990 | 0.075 | 0.967 | ||
| kernel = poly | 0.036 | 0.988 | 0.078 | 0.964 | ||
| kernel = sigmoid | 5884 | −3.2 × 108 | 3251 | −6.2 × 108 | ||
| RF | Estimator number | Estimators = 10 | 0.014 | 0.998 | 0.073 | 0.969 |
| Estimators = 50 | 0.013 | 0.998 | 0.072 | 0.969 | ||
| Estimators = 100 | 0.012 | 0.999 | 0.072 | 0.970 | ||
| Estimators = 500 | 0.012 | 0.999 | 0.072 | 0.969 | ||
| KNN | Neighbor number | Neighbors = 2 | 0.016 | 0.997 | 0.071 | 0.970 |
| Neighbor = 10 | 0.029 | 0.992 | 0.071 | 0.970 | ||
| Neighbor = 30 | 0.033 | 0.990 | 0.070 | 0.971 | ||
| Neighbor = 100 | 0.035 | 0.989 | 0.070 | 0.971 | ||
| ANN | Number of neurons and layers | 16 × 16 | 0.038 | 0.986 | 0.074 | 0.968 |
| 32 × 32 | 0.040 | 0.985 | 0.078 | 0.964 | ||
| 64 × 64 | 0.031 | 0.991 | 0.075 | 0.967 | ||
| 256 × 256 | 0.022 | 0.995 | 0.075 | 0.967 | ||
| RNN | Number of neurons and layers | 1024 | 0.011 | 0.999 | 0.083 | 0.959 |
| 64 × 32 | 0.010 | 0.999 | 0.076 | 0.966 | ||
| 128 × 64 × 32 | 0.012 | 0.999 | 0.076 | 0.966 | ||
| 256 × 128 × 64 × 32 | 0.011 | 0.999 | 0.075 | 0.967 | ||
| LSTM | Number of neurons and layers | 1024 | 0.013 | 0.998 | 0.076 | 0.966 |
| 64 × 32 | 0.012 | 0.999 | 0.072 | 0.969 | ||
| 128 × 64 × 32 | 0.012 | 0.999 | 0.073 | 0.968 | ||
| 256 × 128 × 64 × 32 | 0.010 | 0.999 | 0.071 | 0.970 | ||
| Algorithm | Training | Testing | ||
|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | |
| SVR | 0.033 | 0.990 | 0.075 | 0.967 |
| RF | 0.012 | 0.999 | 0.072 | 0.969 |
| KNN | 0.016 | 0.997 | 0.071 | 0.970 |
| ANN | 0.022 | 0.995 | 0.075 | 0.967 |
| RNN | 0.011 | 0.999 | 0.075 | 0.967 |
| LSTM | 0.010 | 0.999 | 0.071 | 0.970 |
| Month | Mean Water Level (m) | Error of LSTM Model | ||
|---|---|---|---|---|
| Mean | Min | Max | ||
| Jan. | 2216.29 | −0.009 | −0.014 | 0.000 |
| Feb. | 2216.24 | 0.001 | −0.068 | 0.144 |
| Mar. | 2216.22 | −0.005 | −0.465 | 0.102 |
| Apr. | 2216.47 | −0.003 | −0.361 | 0.240 |
| May | 2216.45 | 0.000 | −0.132 | 0.171 |
| Jun. | 2216.97 | 0.004 | −0.092 | 0.101 |
| Jul. | 2216.92 | 0.002 | −0.061 | 0.096 |
| Aug. | 2216.74 | 0.008 | −0.037 | 0.048 |
| Sep. | 2216.59 | −0.009 | −0.014 | −0.003 |
| Oct. | 2216.33 | −0.010 | −0.015 | −0.004 |
| Nov. | 2216.33 | −0.011 | −0.018 | −0.007 |
| Dec. | 2216.53 | −0.010 | −0.017 | −0.007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, M.; Lu, W.; Ma, Q.; Wang, H.; He, B.; Liang, D.; Dong, R. Study on the Snowmelt Flood Model by Machine Learning Method in Xinjiang. Water 2023, 15, 3620. https://doi.org/10.3390/w15203620
Zhou M, Lu W, Ma Q, Wang H, He B, Liang D, Dong R. Study on the Snowmelt Flood Model by Machine Learning Method in Xinjiang. Water. 2023; 15(20):3620. https://doi.org/10.3390/w15203620
Chicago/Turabian StyleZhou, Mingqiang, Wenjing Lu, Qiang Ma, Han Wang, Bingshun He, Dong Liang, and Rui Dong. 2023. "Study on the Snowmelt Flood Model by Machine Learning Method in Xinjiang" Water 15, no. 20: 3620. https://doi.org/10.3390/w15203620






