A New Multi-Objective Genetic Programming Model for Meteorological Drought Forecasting
Abstract
:1. Introduction
2. Study Area and Data Collection
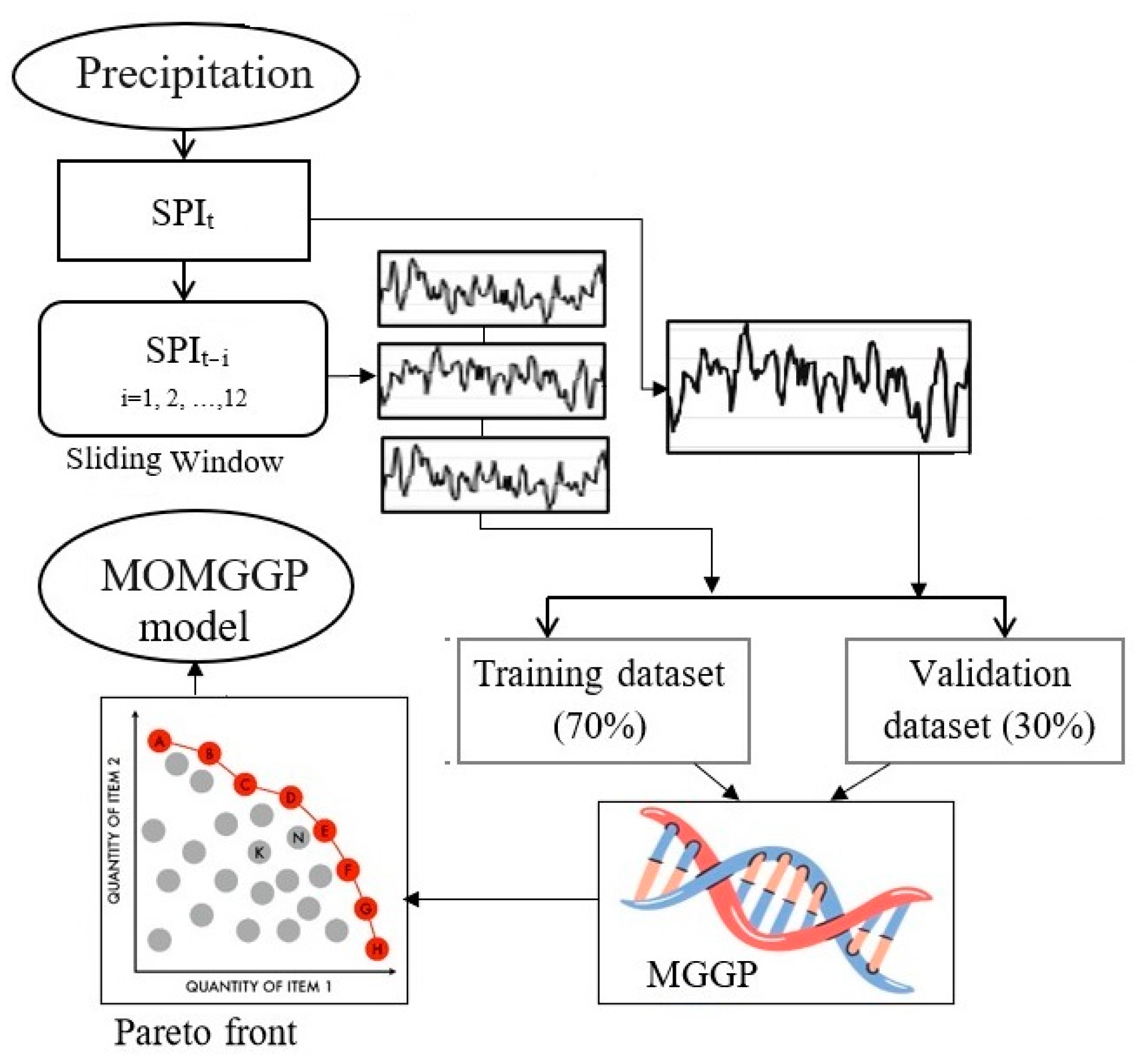
3. Methods
3.1. The Standardized Precipitation Index
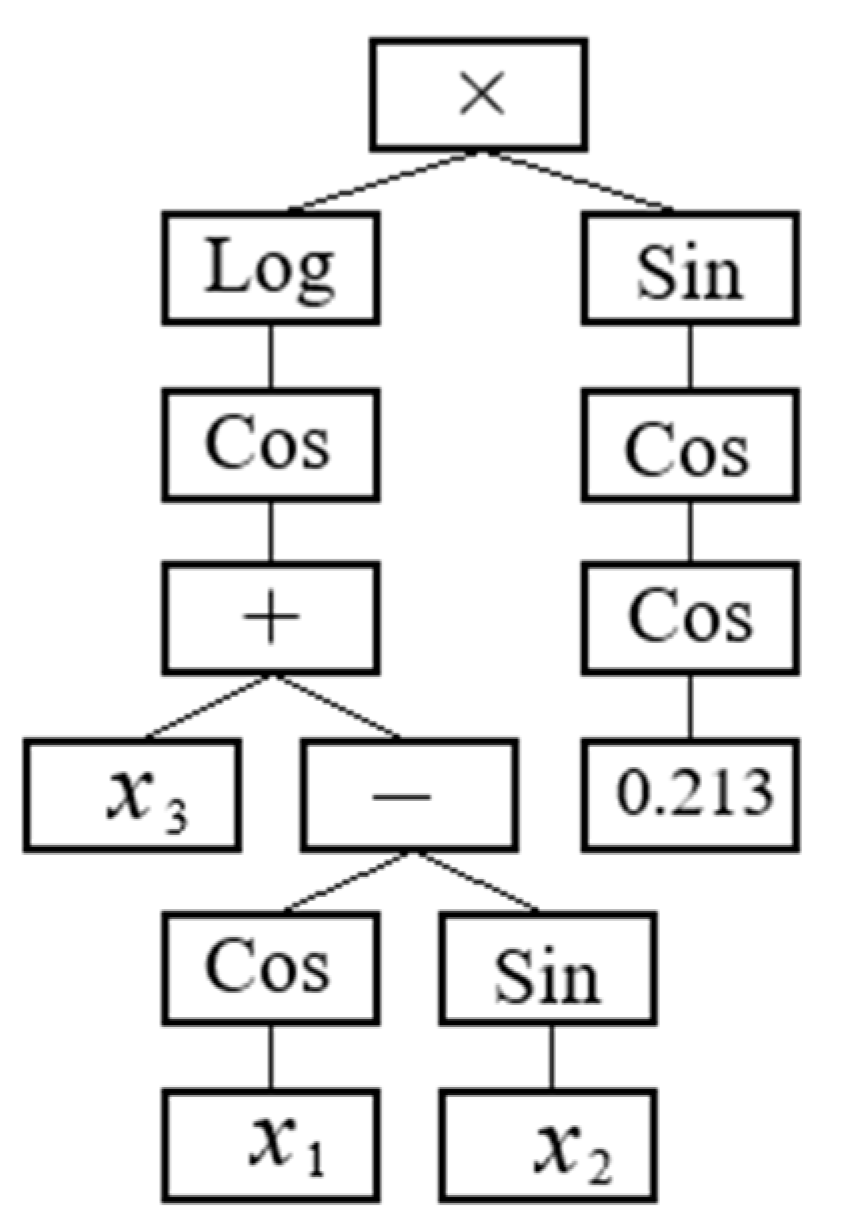
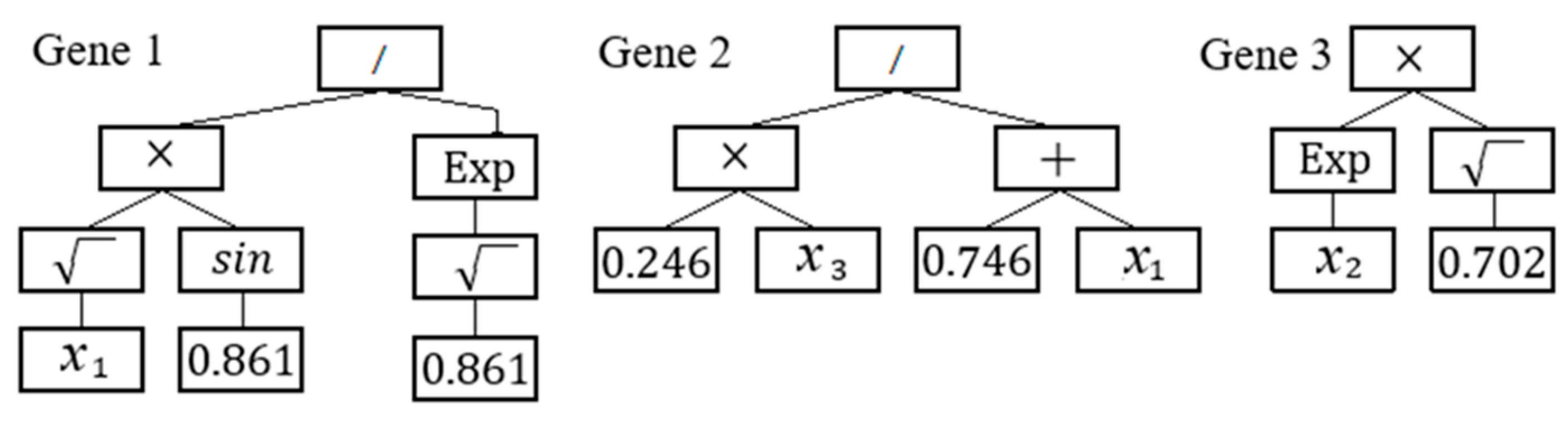
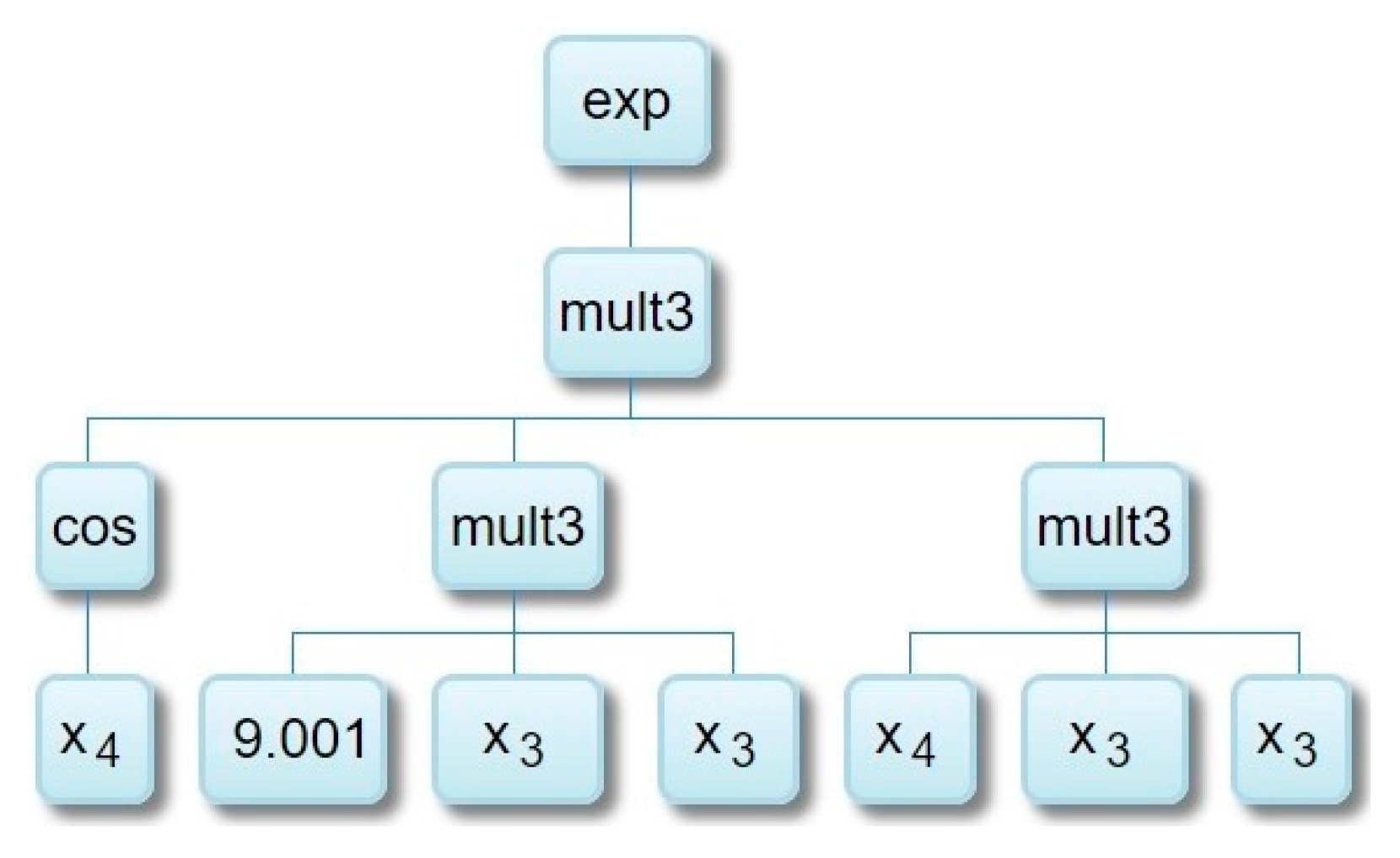
3.2. Overview of GP and MGGP
3.3. State-of-the-Art MOMGGP Algorithm
3.4. Performance Evaluation
4. Results and Discussion
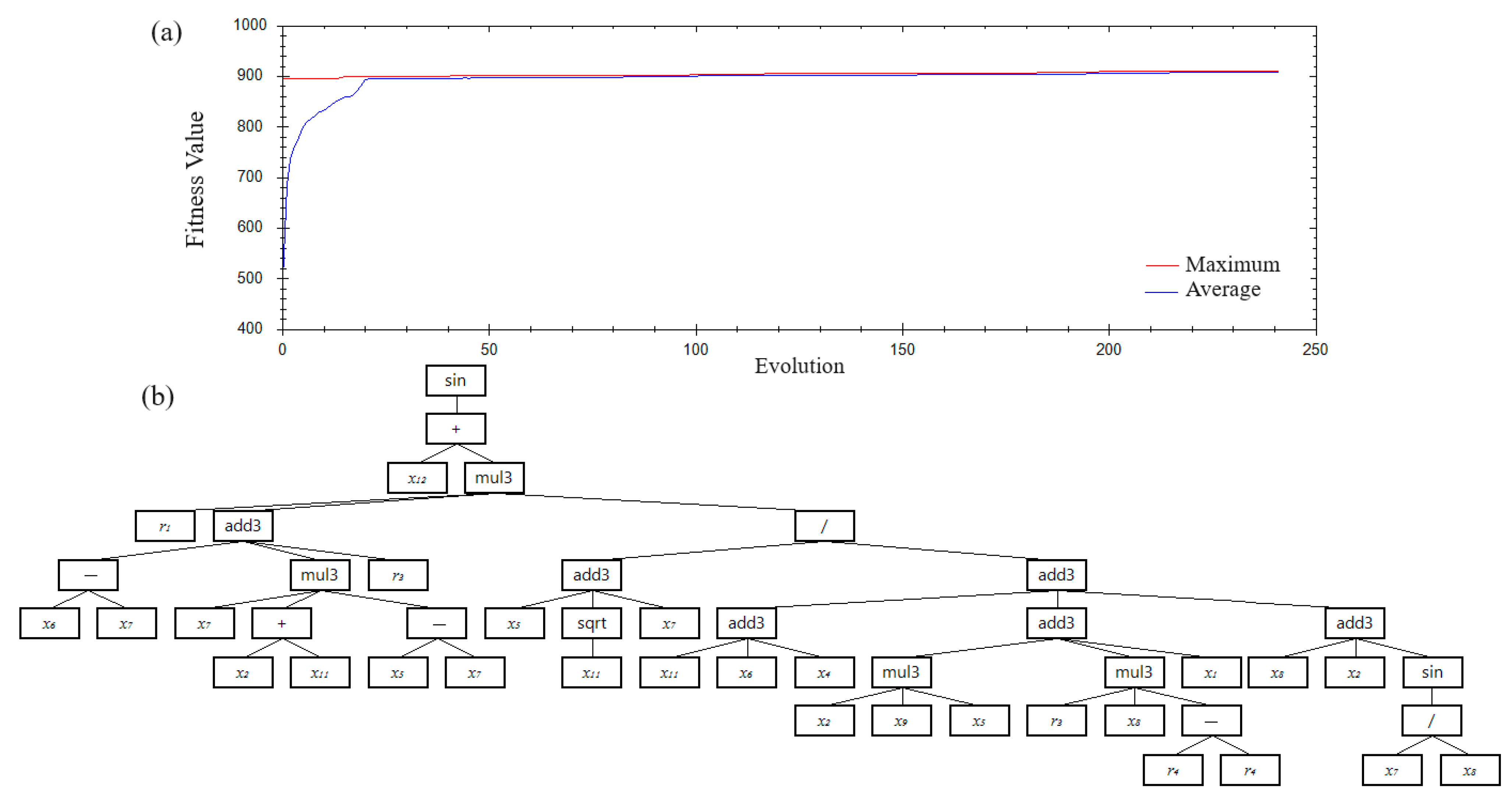
The Best GP, MGGP, and MOMGGP Solutions
- RMSE was applied as the objective function in both tools. The smaller the RMSE, the better the forecasting accuracy;
- arithmetic operations (+, −, ×, and /), exponential function (Exp), three argument addition multiplication, square, and trigonometric functions (including sin and cos) with the same selection probability were used as arbitrary functions;
- SPI lags (from lag 1 to lag 12) together with a set of random numbers in the range of −10 to 10 were used in the terminal set;
- the maximum tree depth for GP and MGGP solution was set to nine and four, respectively;
- the maximum number of genes for MGGP solution was set to five,
- ramped half and half initialization of individuals with the population size of 300 at each run were used;
- the run is configured to proceed for 500 generations or to terminate when a fitness (RMSE) of 0.002 is achieved.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Berbel, J.; Esteban, E. Droughts as a catalyst for water policy change. Analysis of Spain, Australia (MDB), and California. Glob. Environ. Change 2019, 58, 101969. [Google Scholar] [CrossRef]
- Barker, L.J.; Hannaford, J.; Chiverton, A.; Svensson, C. From meteorological to hydrological drought using standardised indicators. Hydrol. Earth Syst. Sci. 2016, 20, 2483–2505. [Google Scholar] [CrossRef]
- Ntano, M.M.; Busico, G.; Mastrocicco, M.; Kazakis, N. The impacts of drought on groundwater resources in the Upper Volturno basin, Southern Italy. In Proceedings of the 16th International Congress of Geological Society of Greece, Patra, Greece, 17–19 October 2022. [Google Scholar]
- Jehanzaib, M.; Sattar, M.N.; Lee, J.H.; Kim, T.W. Investigating effect of climate change on drought propagation from meteorological to hydrological drought using multi-model ensemble projections. Stoch. Environ. Res. Risk Assess. 2020, 34, 7–21. [Google Scholar] [CrossRef]
- Han, P.; Wang, P.X.; Zhang, S.Y. Drought forecasting based on the remote sensing data using ARIMA models. Math. Comput. Model. 2010, 51, 1398–1403. [Google Scholar] [CrossRef]
- Achite, M.; Bazrafshan, O.; Azhdari, Z.; Wałęga, A.; Krakauer, N.; Caloiero, T. Forecasting of SPI and SRI using multiplicative ARIMA under climate variability in a Mediterranean Region: Wadi Ouahrane Basin, Algeria. Climate 2022, 10, 36. [Google Scholar] [CrossRef]
- Moghimi, M.M.; Zarei, A.R.; Mahmoudi, M.R. Seasonal drought forecasting in arid regions, using different time series models and RDI index. J. Water Clim. Change 2020, 11, 633–654. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J. Drought forecasting using new machine learning methods. J. Water Land Dev. 2013, 18, 3–12. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Ali, M.; Sharafati, A.; Al-Ansari, N.; Shahid, S. Forecasting standardized precipitation index using data intelligence models: Regional investigations of Bangladesh. Sci. Rep. 2021, 11, 3435. [Google Scholar] [CrossRef]
- Deo, R.C.; Kisi, O.; Singh, V.P. Drought forecasting in eastern Australia using multivariate adaptive regression spline, least square support vector machine and M5Tree model. Atmos. Res. 2017, 184, 149–175. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P.; Xia, Y. Seasonal drought prediction: Advances, challenges, and future prospects. Rev. Geophys. 2018, 56, 108–141. [Google Scholar] [CrossRef]
- Vidyarthi, V.K.; Jain, A. Knowledge extraction from trained ANN drought classification model. J. Hydrol. 2020, 585, 124804. [Google Scholar] [CrossRef]
- Danandeh Mehr, A. Drought classification using gradient boosting decision tree. Acta Geophysica 2021, 69, 909–918. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar]
- Anshuka, A.; van Ogtrop, F.F.; Willem Vervoort, R. Drought forecasting through statistical models using standardised precipitation index: A systematic review and meta-regression analysis. Nat. Hazards 2019, 97, 955–977. [Google Scholar] [CrossRef]
- Fung, K.F.; Huang, Y.F.; Koo, C.H.; Soh, Y.W. Drought forecasting: A review of modelling approaches 2007–2017. J. Water Clim. Change 2020, 11, 771–799. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Pan, B.; Mazdiyasni, O.; Sadegh, M.; Jiwa, S.; Zhang, W.; Love, C.A.; Madadgar, S.; Papalexiou, S.M.; Davis, S.J.; et al. Status and prospects for drought forecasting: Opportunities in artificial intelligence and hybrid physical–statistical forecasting. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2022, 380, 20210288. [Google Scholar] [CrossRef]
- Danandeh Mehr, A.; Reihanifar, M.; Alee, M.M.; Vazifehkhah Ghaffari, M.A.; Safari MJ, S.; Mohammadi, B. VMD-GP: A New Evolutionary Explicit Model for Meteorological Drought Prediction at Ungauged Catchments. Water 2023, 15, 2686. [Google Scholar] [CrossRef]
- Yalçın, S.; Eşit, M.; Çoban, Ö. A new deep learning method for meteorological drought estimation based-on standard precipitation evapotranspiration index. Eng. Appl. Artif. Intell. 2023, 124, 106550. [Google Scholar] [CrossRef]
- Xu, X.; Lin, Z.; Li, X.; Shang, C.; Shen, Q. Multi-objective robust optimisation model for MDVRPLS in refined oil distribution. Int. J. Prod. Res. 2022, 60, 6772–6792. [Google Scholar] [CrossRef]
- Cao, B.; Zhao, J.; Gu, Y.; Ling, Y.; Ma, X. Applying graph-based differential grouping for multiobjective large-scale optimization. Swarm Evol. Comput. 2020, 53, 100626. [Google Scholar] [CrossRef]
- Cao, B.; Zhao, J.; Yang, P.; Gu, Y.; Muhammad, K.; Rodrigues, J.J.P.C.; de Albuquerque, V.H.C. Multiobjective 3-D Topology Optimization of Next-Generation Wireless Data Center Network. IEEE Trans. Ind. Inform. 2020, 16, 3597–3605. [Google Scholar] [CrossRef]
- Danandeh, M.e.h.r.; Nourani, V. A Pareto-optimal moving average-multigene genetic programming model for rainfall-runoff modelling. Environ. Model. Softw. 2017, 92, 239–251. [Google Scholar] [CrossRef]
- Tercan, E.; Dereli, M.A.; Tapkın, S. A GIS-based multi-criteria evaluation for MSW landfill site selection in Antalya, Burdur, Isparta planning zone in Turkey. Environ. Earth Sci. 2020, 79, 246. [Google Scholar] [CrossRef]
- Soylu Pekpostalci, D.; Tur, R.; Danandeh Mehr, A.; Vazifekhah Ghaffari, M.A.; Dąbrowska, D.; Nourani, V. Drought monitoring and forecasting across Turkey: A contemporary review. Sustainability 2023, 15, 6080. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology 1993, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Koza, J.R. Genetic Programming as a Means for Programming Computers by Natural Selection. Stat Comput 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Tür, R. Maximum wave height hindcasting using ensemble linear-nonlinear models. Theor. Appl. Climatol. 2020, 141, 1151–1163. [Google Scholar] [CrossRef]
- Herath HM, V.V.; Chadalawada, J.; Babovic, V. Genetic programming for hydrological applications: To model or to forecast that is the question. J. Hydroinform. 2021, 23, 740–763. [Google Scholar] [CrossRef]
- Hrnjica, B.; Danandeh Mehr, A. Optimized Genetic Programming Applications: Emerging Research and Opportunities; IGI Global: Hershey, PA, USA, 2018; p. 310. [Google Scholar] [CrossRef]
- Eray, O.; Mert, C.; Kisi, O. Comparison of multi-gene genetic programming and dynamic evolving neural-fuzzy inference system in modeling pan evaporation. Hydrol. Rese. 2018, 49, 1221–1233. [Google Scholar] [CrossRef]
- Searson, D.P. GPTIPS 2: An Open-Source Software Platform for Symbolic Data Mining. In Handbook of Genetic Programming Applications; Springer: Berlin/Heidelberg, Germany, 2015; pp. 551–573. [Google Scholar] [CrossRef]
- Liu, Q.Y.; Li, D.Q.; Tang, X.S.; Du, W. Predictive Models for Seismic Source Parameters Based on Machine Learning and General Orthogonal Regression Approaches. Bull. Seismol. Soc. Am. 2023. [Google Scholar] [CrossRef]
- Omidvar, E.; Tahroodi, Z.N. Evaluation and prediction of meteorological drought conditions using time-series and genetic programming models. J. Earth Sys. Sci. 2019, 128, 73. [Google Scholar] [CrossRef]
- Khan MM, H.; Muhammad, N.S.; El-Shafie, A. Wavelet based hybrid ANN-ARIMA models for meteorological drought forecasting. J. Hydrol. 2020, 590, 125380. [Google Scholar] [CrossRef]
- Alquraish, M.; Ali Abuhasel, K.; SAlqahtani, A.; Khadr, M. SPI-Based Hybrid Hidden Markov–GA, ARIMA–GA, and ARIMA–GA–ANN Models for Meteorological Drought Forecasting. Sustainability 2021, 13, 12576. [Google Scholar] [CrossRef]
- Gholizadeh, R.; Yılmaz, H.; Danandeh Mehr, A. Multitemporal Meteorological Drought Forecasting Using Bat-ELM. Acta Geophysica 2022, 70, 917–927. [Google Scholar] [CrossRef]
- Zhu, C. Machine Reading Comprehension: Algorithms and Practice; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Yang, D.; Qiu, H.; Ye, B.; Liu, Y.; Zhang, J.; Zhu, Y. Distribution and Recurrence of Warming-Induced Retrogressive Thaw Slumps on the Central Qinghai-Tibet Plateau. J. Geophys. Res. Earth Surface 2023, 128, e2022JF007047. [Google Scholar] [CrossRef]
- Chen, J.; Liu, Z.; Yin, Z.; Liu, X.; Li, X.; Yin, L.; Zheng, W. Predict the effect of meteorological factors on haze using BP neural network. Urban Clim. 2023, 51, 101630. [Google Scholar] [CrossRef]
- Wu, X.; Feng, X.; Wang, Z.; Chen, Y.; Deng, Z. Multi-source precipitation products assessment on drought monitoring across global major river basins. Atmos. Res. 2023, 295, 106982. [Google Scholar] [CrossRef]

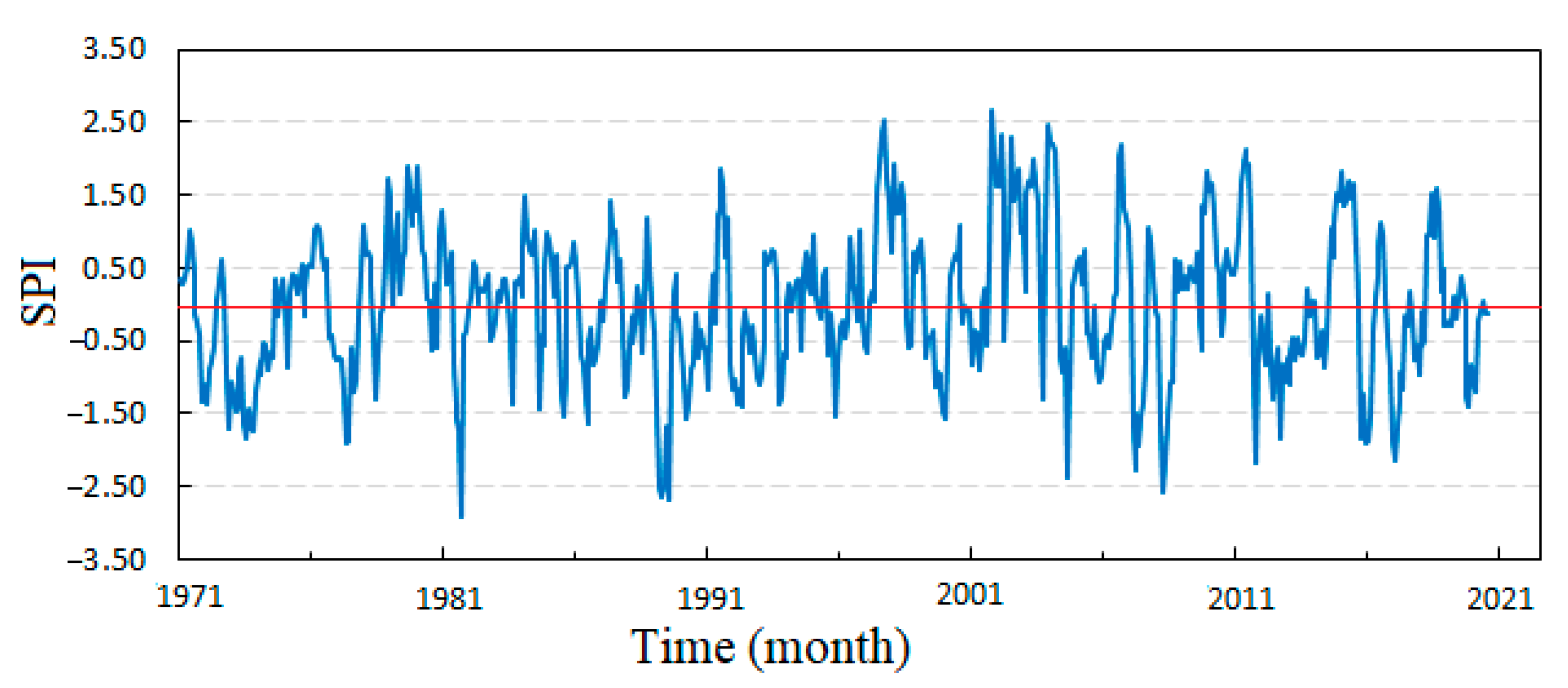




| Station | Dataset | Mean | Min | Max | SD * |
|---|---|---|---|---|---|
| Burdur | Entire | 0.00 | −2.91 | 2.65 | 1.005 |
| Training | 0.02 | −2.91 | 2.65 | 0.987 | |
| Testing | −0.04 | −2.58 | 2.20 | 1.046 |
| State | Threshold |
|---|---|
| No drought | 0.0 ≤ SPI |
| Mild drought | −1.0 ≤ SPI ≤ 0.0 |
| Moderate drought | −1.5 ≤ SPI < −1.0 |
| Severe drought | −2.0 ≤ SPI < −1.5 |
| Extreme drought | SPI < −2.0 |
| Training | Testing | ||||
|---|---|---|---|---|---|
| Models | Complexity | RMSE | NSE | RMSE | NSE |
| GP | 190 | 0.550 | 0.689 | 0.548 | 0.726 |
| MGGP | 195 | 0.504 | 0.740 | 0.555 | 0.717 |
| MOGGP | 128 | 0.522 | 0.721 | 0.542 | 0.731 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reihanifar, M.; Danandeh Mehr, A.; Tur, R.; Ahmed, A.T.; Abualigah, L.; Dąbrowska, D. A New Multi-Objective Genetic Programming Model for Meteorological Drought Forecasting. Water 2023, 15, 3602. https://doi.org/10.3390/w15203602
Reihanifar M, Danandeh Mehr A, Tur R, Ahmed AT, Abualigah L, Dąbrowska D. A New Multi-Objective Genetic Programming Model for Meteorological Drought Forecasting. Water. 2023; 15(20):3602. https://doi.org/10.3390/w15203602
Chicago/Turabian StyleReihanifar, Masoud, Ali Danandeh Mehr, Rifat Tur, Abdelkader T. Ahmed, Laith Abualigah, and Dominika Dąbrowska. 2023. "A New Multi-Objective Genetic Programming Model for Meteorological Drought Forecasting" Water 15, no. 20: 3602. https://doi.org/10.3390/w15203602








