Stochastic Precipitation Generation for the Xilingol League Using Hidden Markov Models with Variational Bayes Parameter Estimation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Sources
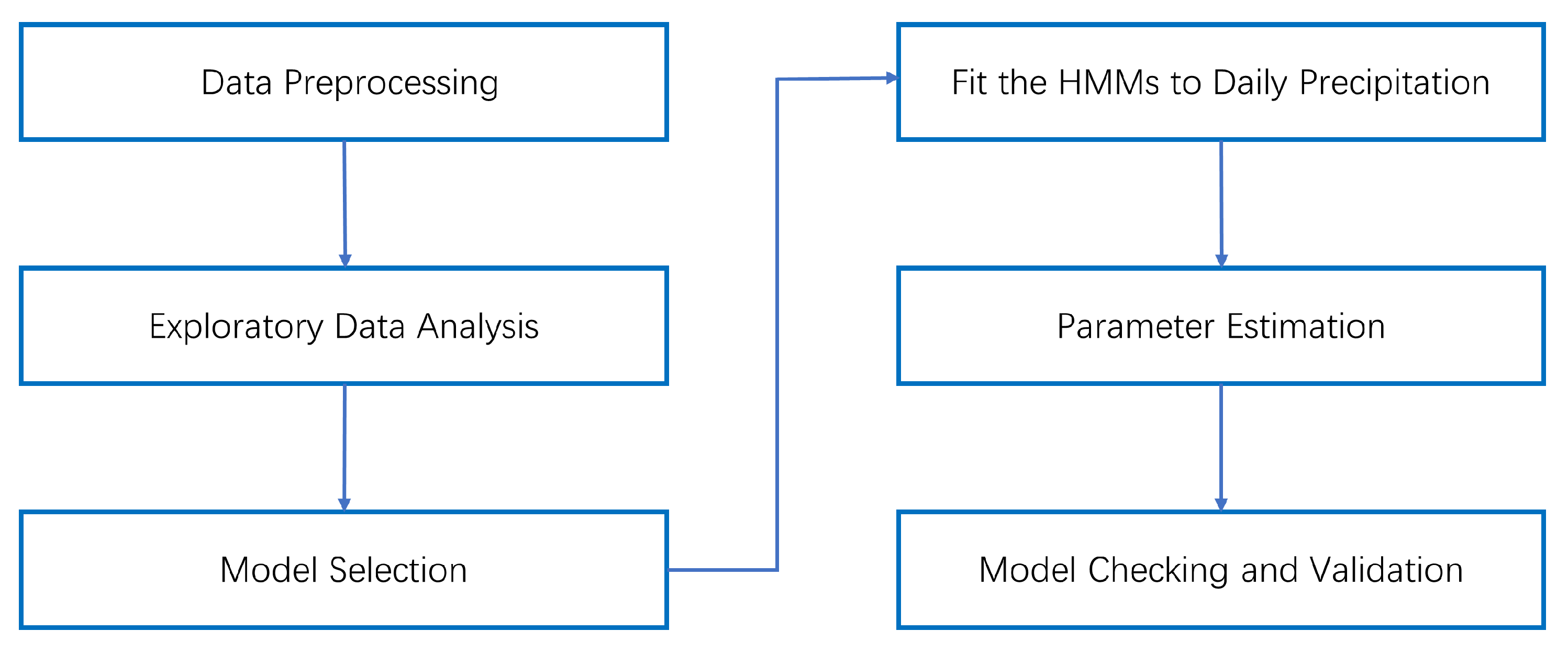
2.2. Methodology Workflow
2.3. The HMM for Precipitation
2.4. VB Parameter Estimation for the HMM
| Algorithm 1 VBEM algorithm for HMMs |
|
| Algorithm 2 Stochastic Variational Bayes for HMMs |
|
3. Results
3.1. Simulation Study
3.1.1. BIC Scores for Daily Precipitation
3.1.2. RMSE for Heavy Precipitation Weather
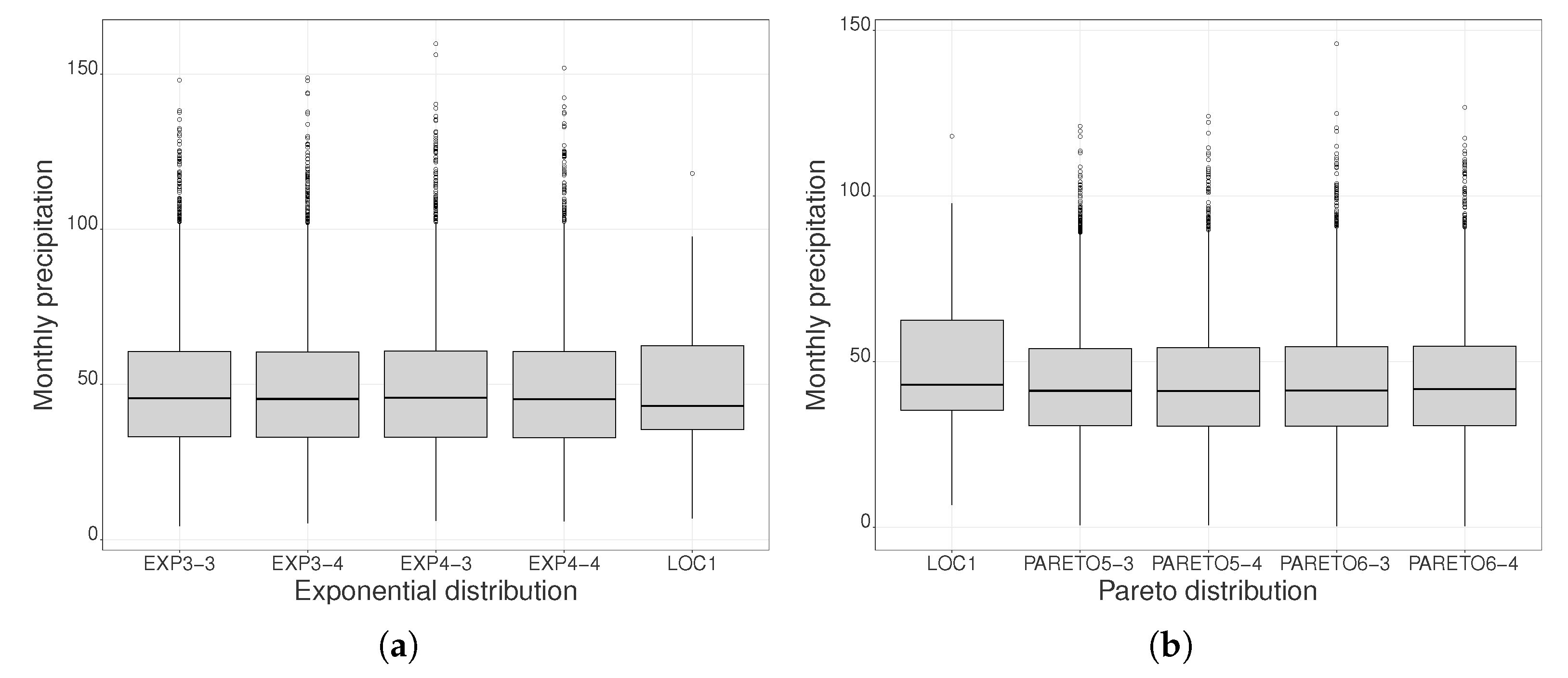
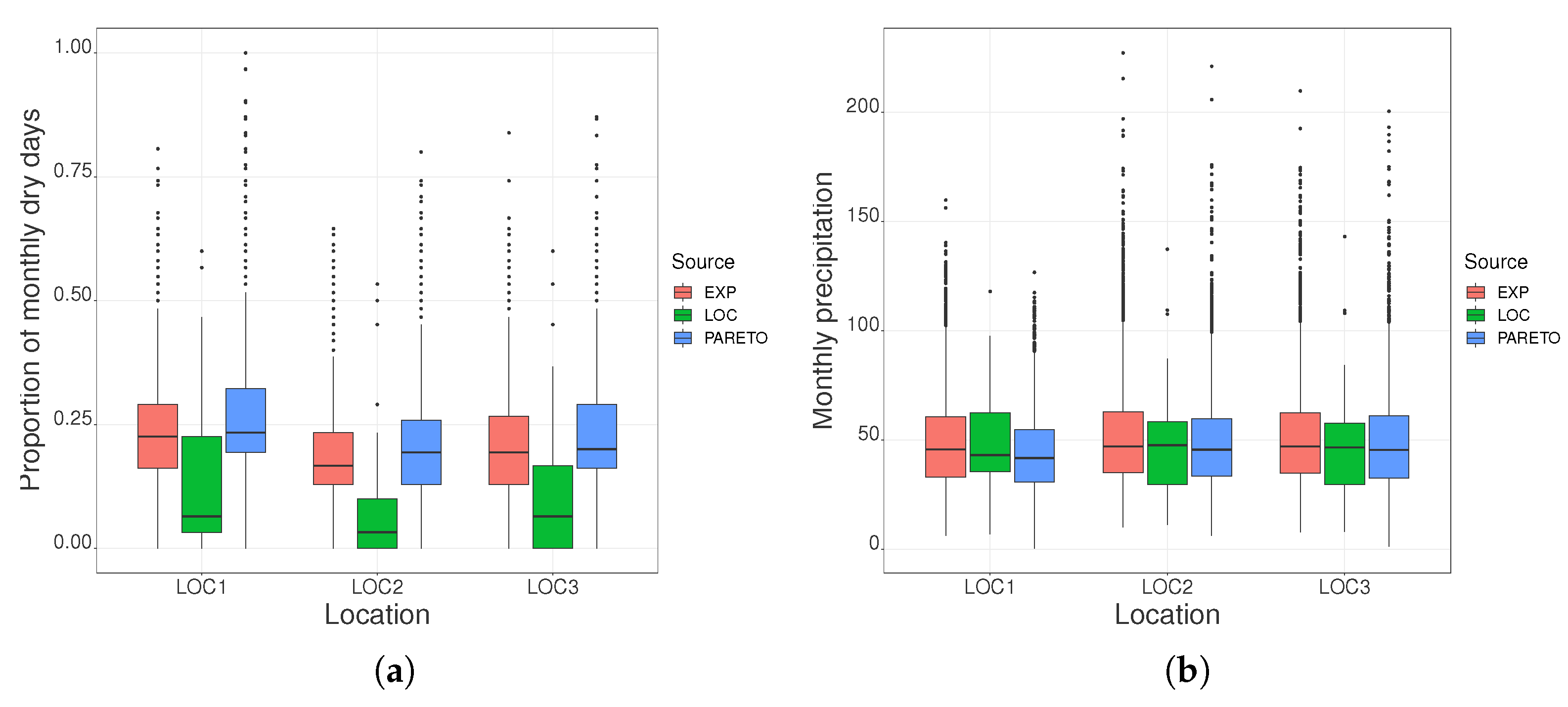
3.1.3. Scatter Plot Regression of Daily Precipitation
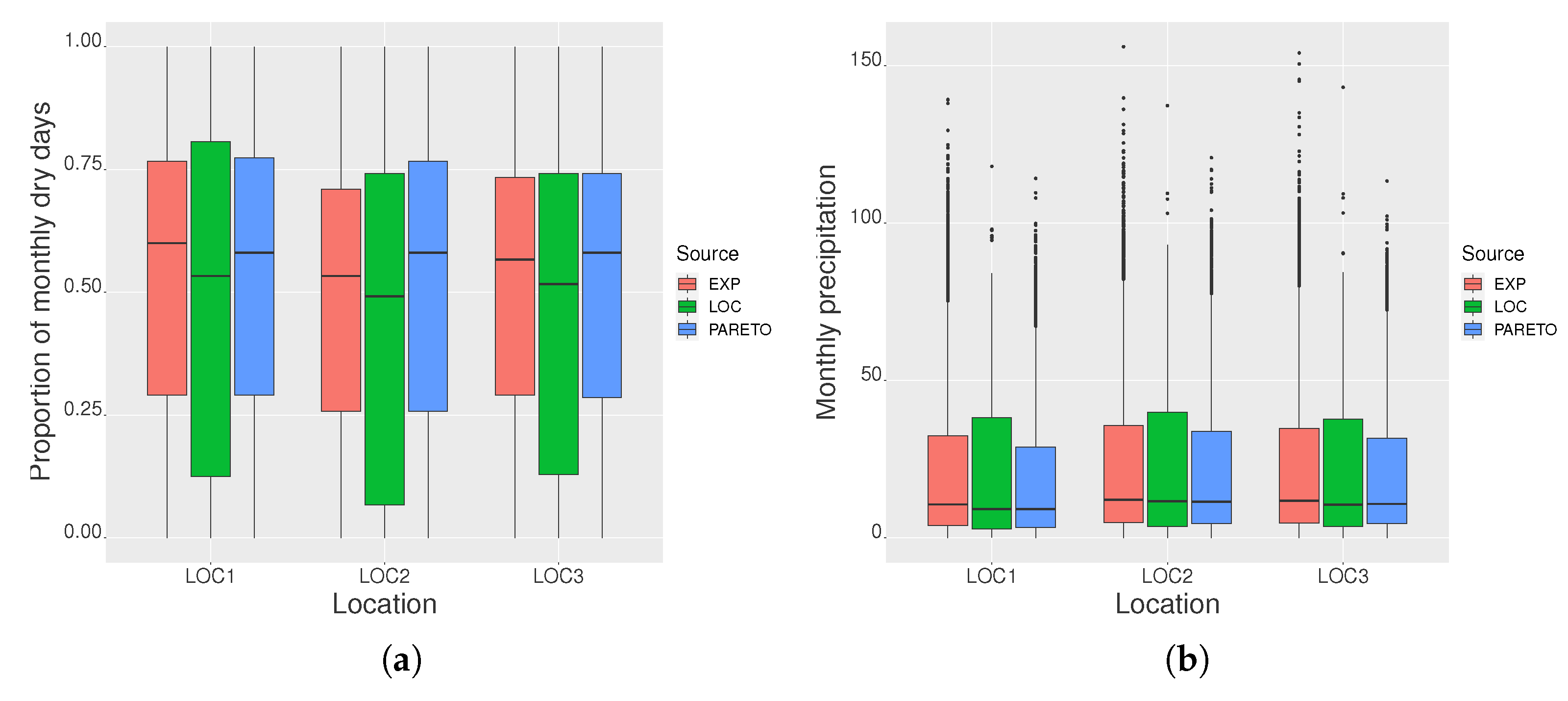
3.2. Analysis of Daily Precipitation in the Xilingol League
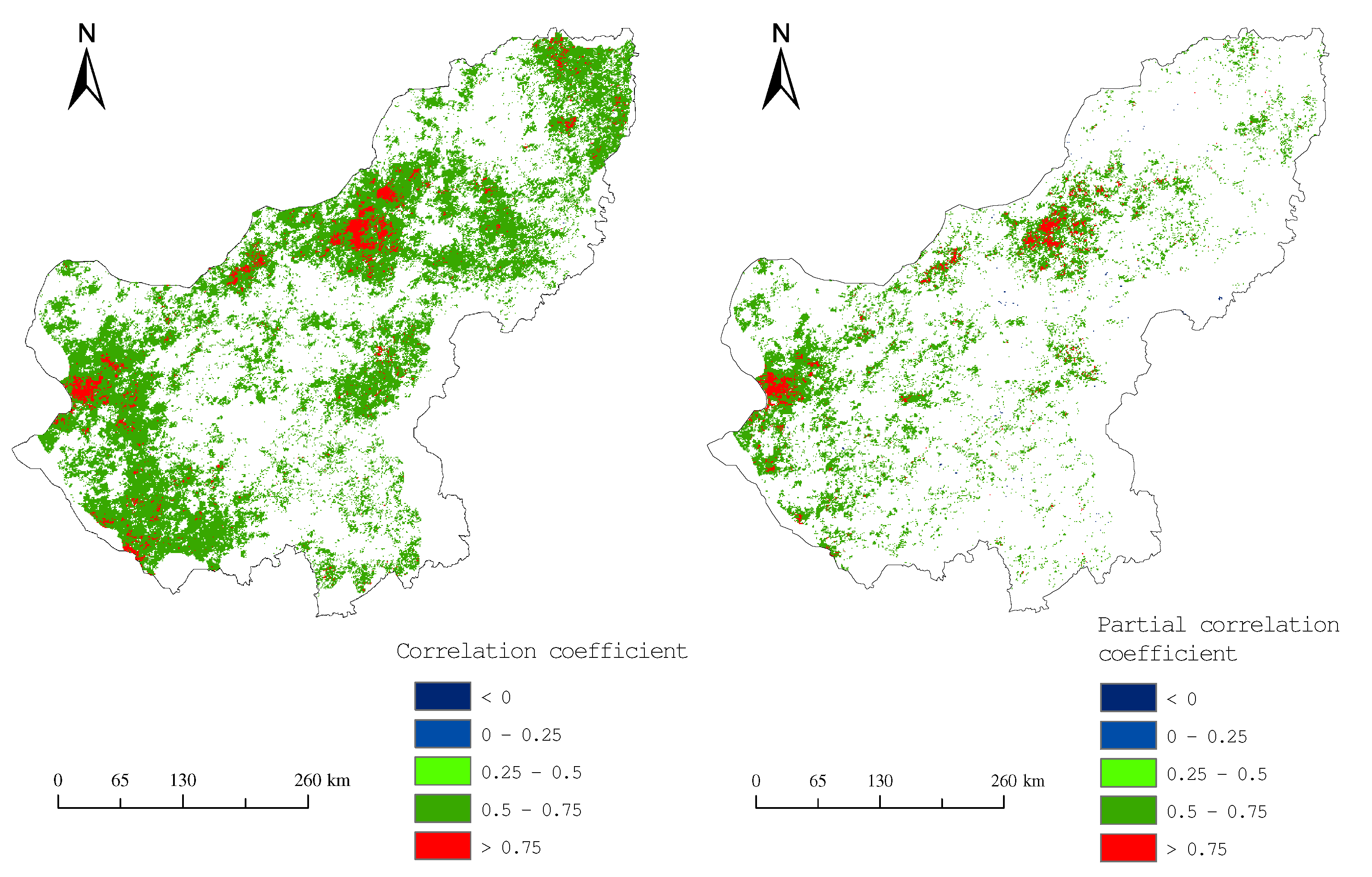
3.2.1. Annual Precipitation and NDVI Correlation Analysis
3.2.2. Seasonal Precipitation Sequences
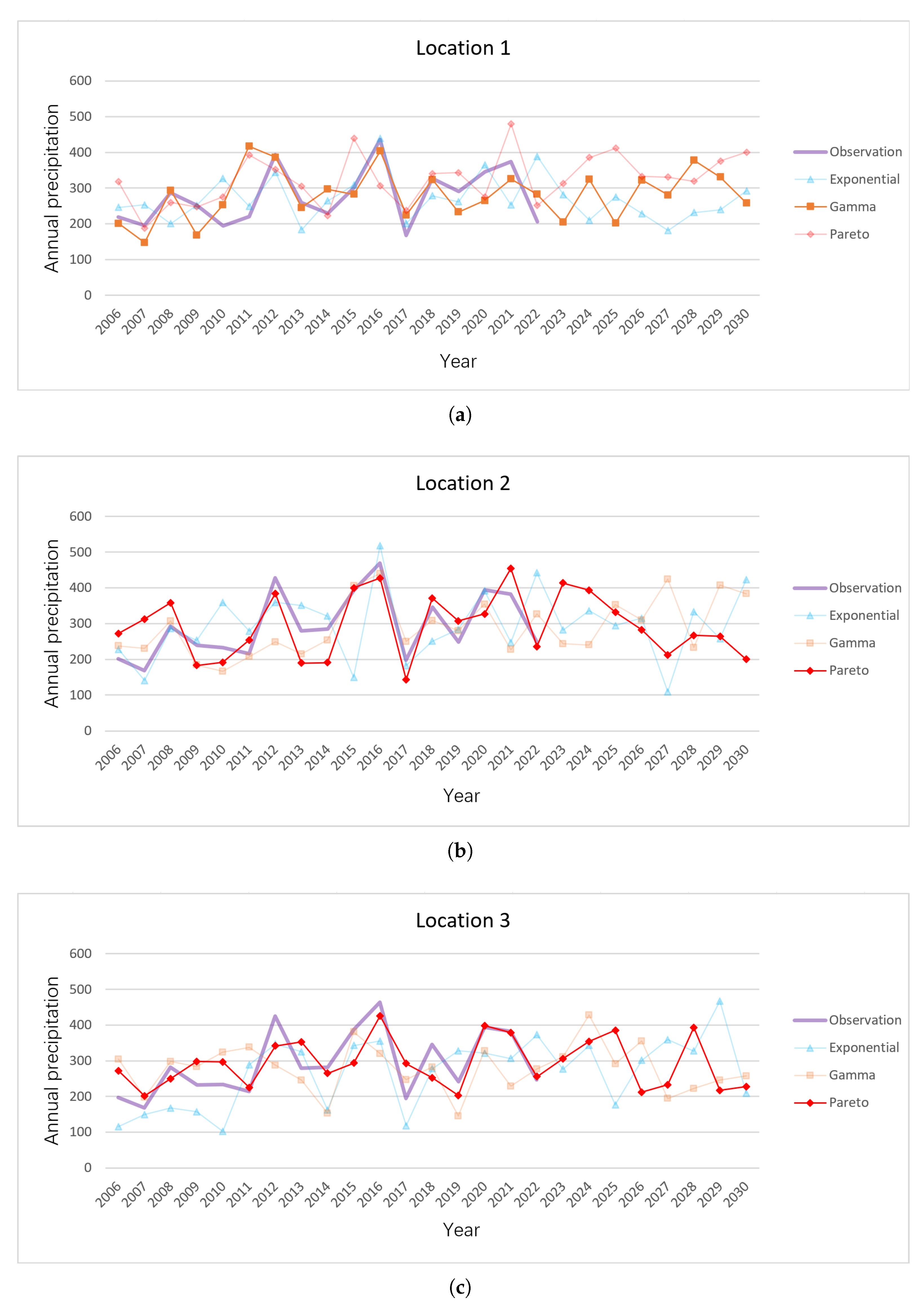
3.2.3. Annual Precipitation Sequence
3.2.4. Analysis of Annual Precipitation Trends
4. Conclusions
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. VBEM Algorithm
Appendix B. Hyperparameter Update for SVB Algorithm
Appendix C. Variational Forward–Backward Algorithm
Appendix D. Analytic Formula for KL Divergence
Appendix E. Bayesian Information Criterion
References
- Wilks, D.S. Interannual variability and extreme-value characteristics of several stochastic daily precipitation models. Agric. For. Meteorol. 1999, 93, 153–169. [Google Scholar] [CrossRef]
- Kou, X.; Ge, J.; Wang, Y.; Zhang, C. Validation of the weather generator CLIGEN with daily precipitation data from the Loess Plateau, China. J. Hydrol. 2007, 347, 347–357. [Google Scholar] [CrossRef]
- Wilks, D.S. Multisite generalization of a daily stochastic precipitation generation model. J. Hydrol. 1998, 210, 178–191. [Google Scholar] [CrossRef]
- Rabiner, L.R. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Hughes, J.P.; Guttorp, P. Incorporating spatial dependence and atmospheric data in a model of precipitation. J. Appl. Meteorol. Climatol. 1994, 33, 1503–1515. [Google Scholar] [CrossRef]
- Robertson, A.W.; Kirshner, S.; Smyth, P. Downscaling of daily rainfall occurrence over northeast Brazil using a hidden Markov model. J. Clim. 2004, 17, 4407–4424. [Google Scholar] [CrossRef]
- Kirshner, S. Modeling of Multivariate Time Series Using Hidden Markov Models. Ph.D. Thesis, University of California, Irvine, CA, USA, 2005. [Google Scholar]
- Robertson, A.W.; Kirshner, S.; Smyth, P.; Charles, S.P.; Bates, B.C. Subseasonal-to-interdecadal variability of the Australian monsoon over North Queensland. Q. J. R. Meteorol. Soc. A J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2006, 132, 519–542. [Google Scholar] [CrossRef]
- Bellone, E.; Hughes, J.P.; Guttorp, P. A hidden Markov model for downscaling synoptic atmospheric patterns to precipitation amounts. Clim. Res. 2000, 15, 1–12. [Google Scholar] [CrossRef]
- Li, Z.; Brissette, F.; Chen, J. Assessing the applicability of six precipitation probability distribution models on the Loess Plateau of China. Int. J. Climatol. 2014, 34, 462–471. [Google Scholar] [CrossRef]
- Breinl, K.; Di Baldassarre, G.; Girons Lopez, M.; Hagenlocher, M.; Vico, G.; Rutgersson, A. Can weather generation capture precipitation patterns across different climates, spatial scales and under data scarcity? Sci. Rep. 2017, 7, 5449. [Google Scholar] [CrossRef]
- Attias, H. Inferring parameters and structure of latent variable models by variational Bayes. arXiv 2013, arXiv:1301.6676. [Google Scholar]
- Holsclaw, T.; Greene, A.M.; Robertson, A.W.; Smyth, P. A Bayesian hidden Markov model of daily precipitation over South and East Asia. J. Hydrometeorol. 2016, 17, 3–25. [Google Scholar] [CrossRef]
- Scott, S.L. Bayesian methods for hidden Markov models: Recursive computing in the 21st century. J. Am. Stat. Assoc. 2002, 97, 337–351. [Google Scholar] [CrossRef]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- MacKay, D.J. Ensemble Learning for Hidden Markov Models; Technical Report; Cavendish Laboratory, University of Cambridge: Cambridge, UK, 1997. [Google Scholar]
- Ghahramani, Z.; Beal, M. Propagation algorithms for variational Bayesian learning. Adv. Neural Inf. Process. Syst. 2000, 13. [Google Scholar]
- Beal, M.J. Variational Algorithms for Approximate Bayesian Inference. Ph.D. Thesis, Gatsby Computational Neuroscience Unit, University College London, London, UK, 2003. [Google Scholar]
- Ji, S.; Krishnapuram, B.; Carin, L. Variational Bayes for continuous hidden Markov models and its application to active learning. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 522–532. [Google Scholar]
- McGrory, C.A.; Titterington, D.M. Variational Bayesian analysis for hidden Markov models. Aust. N. Z. J. Stat. 2009, 51, 227–244. [Google Scholar] [CrossRef]
- Kroiz, G.C.; Basalyga, J.N.; Uchendu, U.; Majumder, R.; Barajas, C.A.; Gobbert, M.K.; Kel, M.; Amita, M.; Neerchal, N.K. Stochastic Precipitation Generation for the Potomac River Basin Using Hidden Markov Models; UMBC Physics Department: Baltimore, MD, USA, 2020. [Google Scholar]
- Majumder, R.; Neerchal, N.K.; Mehta, A. Stochastic Precipitation Generation for the Chesapeake Bay Watershed using Hidden Markov Models with Variational Bayes Parameter Estimation. arXiv 2022, arXiv:2210.04305. [Google Scholar]
- Hoffman, M.D.; Blei, D.M.; Wang, C.; Paisley, J. Stochastic variational inference. J. Mach. Learn. Res. 2013, 14, 1303–1347. [Google Scholar]
- Foti, N.; Xu, J.; Laird, D.; Fox, E. Stochastic variational inference for hidden Markov models. arXiv 2014, arXiv:1411.1670. [Google Scholar]
- Qin, R.; Zhao, Z.; Xu, J.; Ye, J.S.; Li, F.M.; Zhang, F. HRLT: A high-resolution (1 day, 1 km) and long-term (1961–2019) gridded dataset for temperature and precipitation across China. Earth Syst. Sci. Data Discuss. 2022, 14, 4793–4810. [Google Scholar] [CrossRef]
- Huffman, G.J.; Stocker, E.F.; Bolvin, D.T.; Nelkin, E.J.; Tan, J. GPM IMERG Final Precipitation L3 1 Day 0.1 Degree × 0.1 Degree V07, Edited by Andrey Savtchenko, Greenbelt, MD, Goddard Earth Sciences Data and Information Services Center (GES DISC). Available online: https://disc.gsfc.nasa.gov/datasets/GPM_3IMERGDF_07/summary (accessed on 15 September 2023).
- Zheng, C.; Jia, L.; Zhao, T. A 21-year dataset (2000–2020) of gap-free global daily surface soil moisture at 1-km grid resolution. Sci. Data 2023, 10, 139. [Google Scholar] [CrossRef] [PubMed]
- Muñoz Sabater, J. ERA5-Land Monthly Averaged Data from 1950 to Present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2019. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.68d2bb30?tab=overview (accessed on 29 March 2023).
- Neath, A.A.; Cavanaugh, J.E. The Bayesian information criterion: Background, derivation, and applications. Wiley Interdiscip. Rev. Comput. Stat. 2012, 4, 199–203. [Google Scholar] [CrossRef]
- Bellone, E. Nonhomogeneous Hidden Markov Models for Downscaling Synoptic Atmospheric Patterns to Precipitation Amounts. Ph.D. Thesis, Department of Statistics, University of Washington, Seattle, WA, USA, 2000. [Google Scholar]
- Majumder, R.; Mehta, A.; Neerchal, N.K. Copula-Based Correlation Structure for Multivariate Emission Distributions in Hidden Markov Models; UMBC Faculty Collection; UMBC Mathematics and Statistics Department: Baltimore, MD, USA, 2020. [Google Scholar]
- Nyongesa, A.M.; Zeng, G.; Ongoma, V. Non-homogeneous hidden Markov model for downscaling of short rains occurrence in Kenya. Theor. Appl. Climatol. 2020, 139, 1333–1347. [Google Scholar] [CrossRef]




| Precipitation Level | Daily Precipitation Amounts Ranges |
|---|---|
| Light Precipitation | <10 mm |
| Moderate Precipitation | [10 mm, 25 mm] |
| Heavy Precipitation | [25 mm, 50 mm] |
| Torrential Precipitation | [50 mm, 100 mm] |
| Heavy Storms | [100 mm, 200 mm] |
| Torrential Storms | >200 mm |
| Number of Hidden States | Exponential Distribution | Gamma Distribution | Pareto Distribution | |||
|---|---|---|---|---|---|---|
| C = 3 | C = 4 | C = 3 | C = 4 | C = 3 | C = 4 | |
| 3 | 6124.92 | 6118.54 | 6490.61 | 6503.58 | 5679.57 | 5680.50 |
| 4 | 6131.62 | 6120.89 | 6465.26 | 6519.02 | 5711.61 | 5700.50 |
| 5 | 6624.81 | 6493.07 | 6617.57 | 6626.71 | 5690.45 | 5691.82 |
| 6 | 6595.85 | 6472.56 | 6669.12 | 6619.91 | 5695.55 | 5692.39 |
| Number of Hidden States | Exponential Distribution | Gamma Distribution | Pareto Distribution | |||
|---|---|---|---|---|---|---|
| C = 3 | C = 4 | C = 3 | C = 4 | C = 3 | C = 4 | |
| 3 | 44.94 | 44.79 | 67.01 | 68.61 | 21.70 | 21.74 |
| 4 | 45.05 | 44.36 | 64.09 | 68.79 | 25.30 | 23.94 |
| 5 | 82.85 | 73.09 | 72.80 | 76.05 | 3.15 | 4.84 |
| 6 | 80.58 | 71.87 | 78.19 | 80.80 | 4.45 | 3.11 |
| Location | Longitude | Latitude | Correlation Coefficient | Partial Correlation Coefficient |
|---|---|---|---|---|
| 1 | E | N | 0.90 | 0.90 |
| 2 | E | N | 0.91 | 0.93 |
| 3 | E | N | 0.93 | 0.90 |
| Location | Distribution | Daily Precipitation | Monthly Precipitation | Annual Precipitation |
|---|---|---|---|---|
| 1 | Exponential | 2.76 | 35.66 | 154.59 |
| 1 | Gamma | 0.83 | 26.82 | 63.63 |
| 1 | Pareto | 0.55 | 35.21 | 81.64 |
| 2 | Exponential | 2.38 | 46.38 | 167.72 |
| 2 | Gamma | 1.25 | 36.54 | 123.8 |
| 2 | Pareto | 0.68 | 36.14 | 110.97 |
| 3 | Exponential | 2.34 | 39.82 | 68.9 |
| 3 | Gamma | 1.52 | 34.32 | 50.95 |
| 3 | Pareto | 0.85 | 32.72 | 6.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Tuerde, M.; Hu, X. Stochastic Precipitation Generation for the Xilingol League Using Hidden Markov Models with Variational Bayes Parameter Estimation. Water 2023, 15, 3600. https://doi.org/10.3390/w15203600
Zhang S, Tuerde M, Hu X. Stochastic Precipitation Generation for the Xilingol League Using Hidden Markov Models with Variational Bayes Parameter Estimation. Water. 2023; 15(20):3600. https://doi.org/10.3390/w15203600
Chicago/Turabian StyleZhang, Shenyi, Mulati Tuerde, and Xijian Hu. 2023. "Stochastic Precipitation Generation for the Xilingol League Using Hidden Markov Models with Variational Bayes Parameter Estimation" Water 15, no. 20: 3600. https://doi.org/10.3390/w15203600





