Extraction of Spatiotemporal Distribution Characteristics and Spatiotemporal Reconstruction of Rainfall Data by PCA Algorithm
Abstract
:1. Introduction
2. Materials and Methods
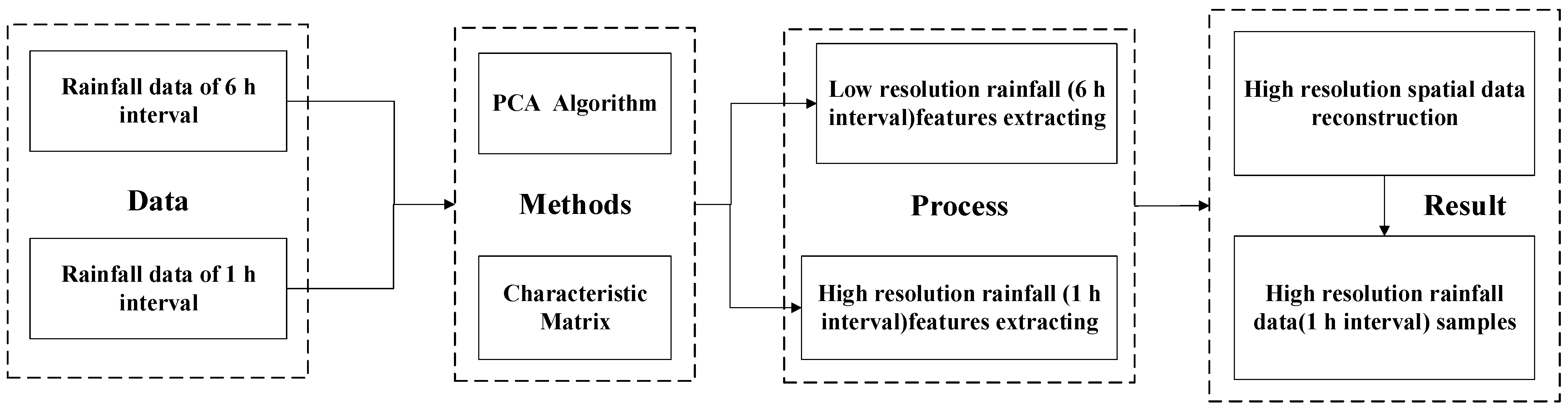
2.1. Technical Processes
2.2. Methods
2.2.1. Constructing a Dynamic Characteristics Matrix of the Spatial and Temporal Distribution of Heavy Rainfall
2.2.2. Dimensionality Reduction and Feature Extraction
2.2.3. Dynamic Clustering Analysis
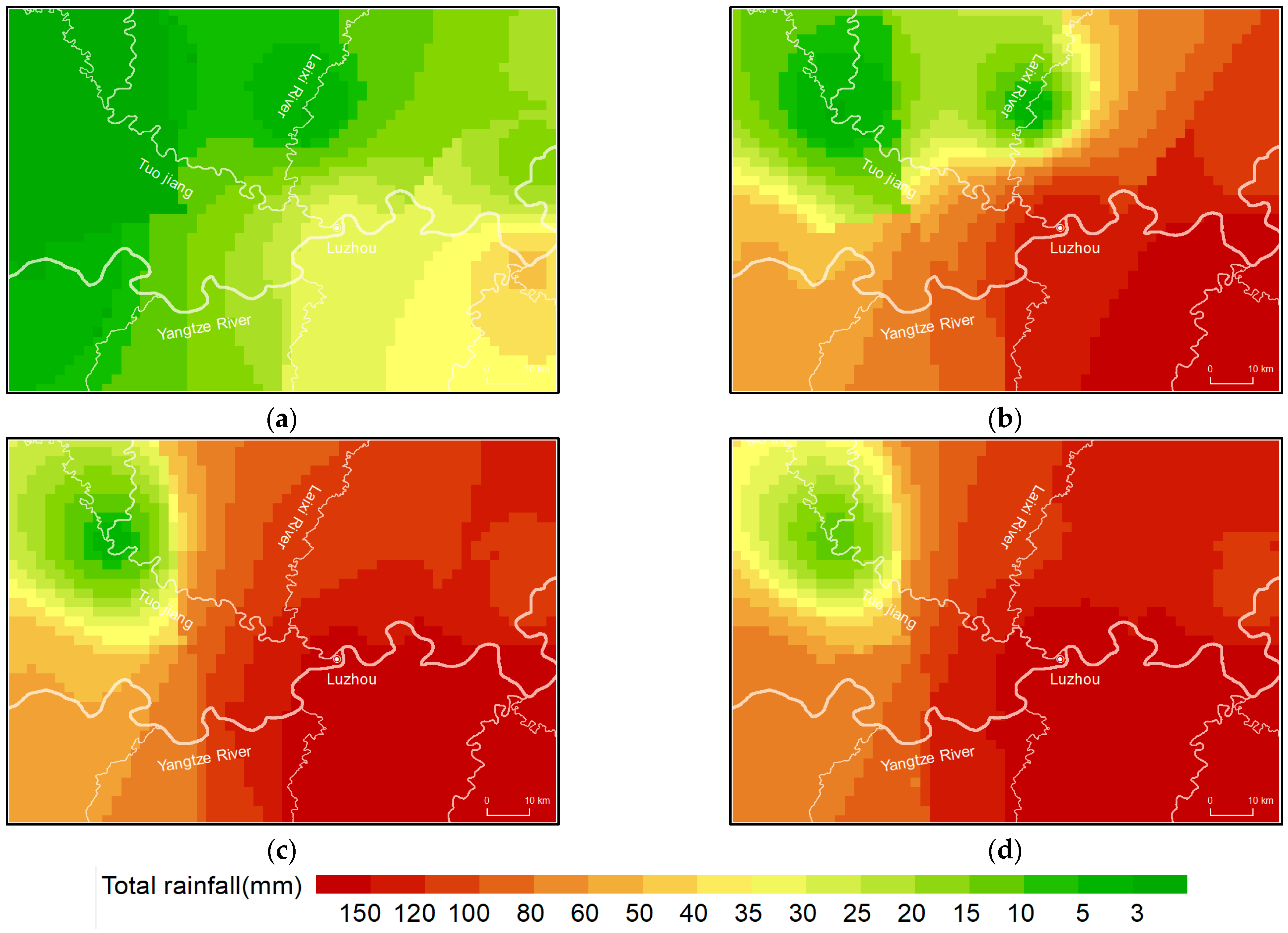
2.2.4. Reconstruction of High-Resolution Spatial Data
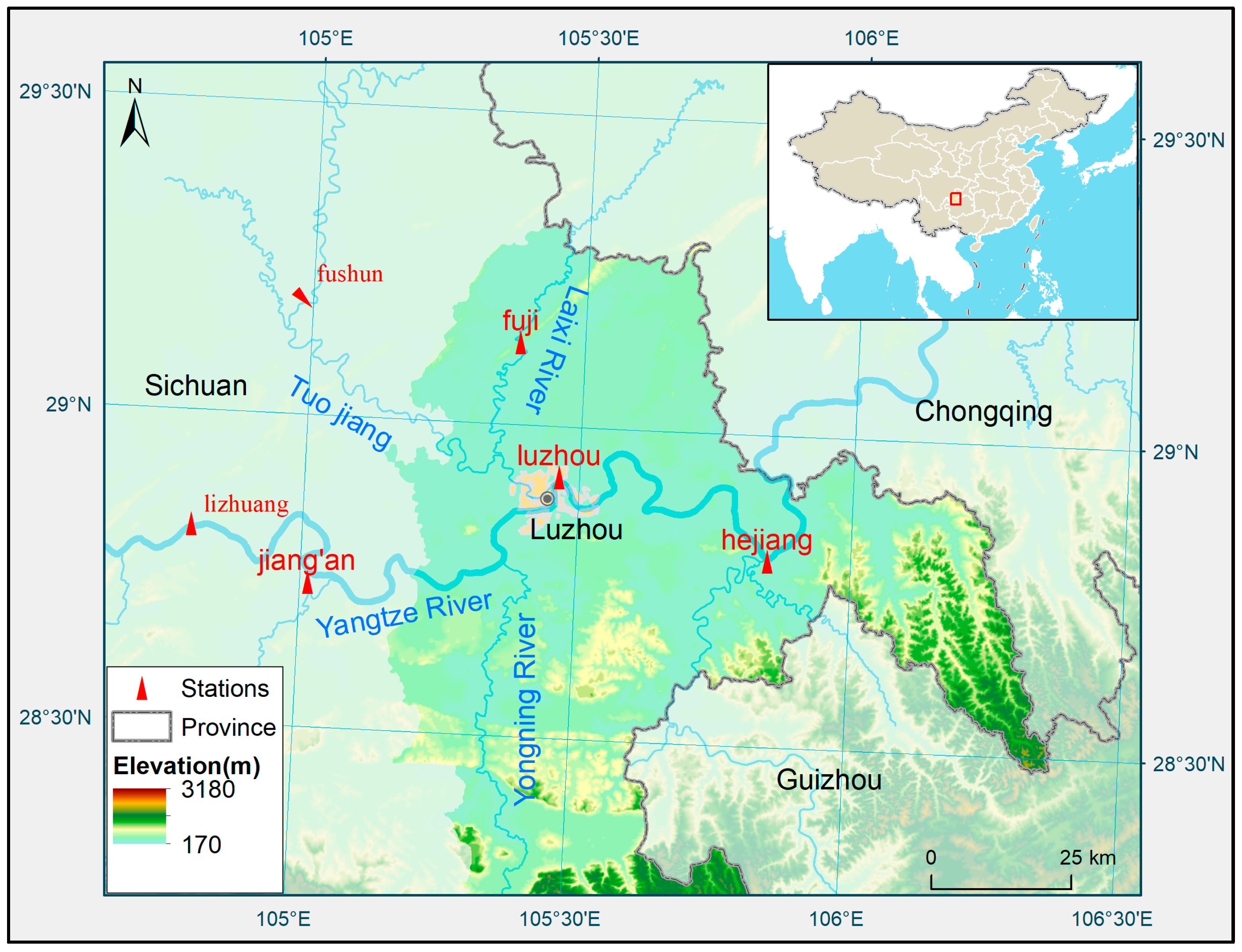
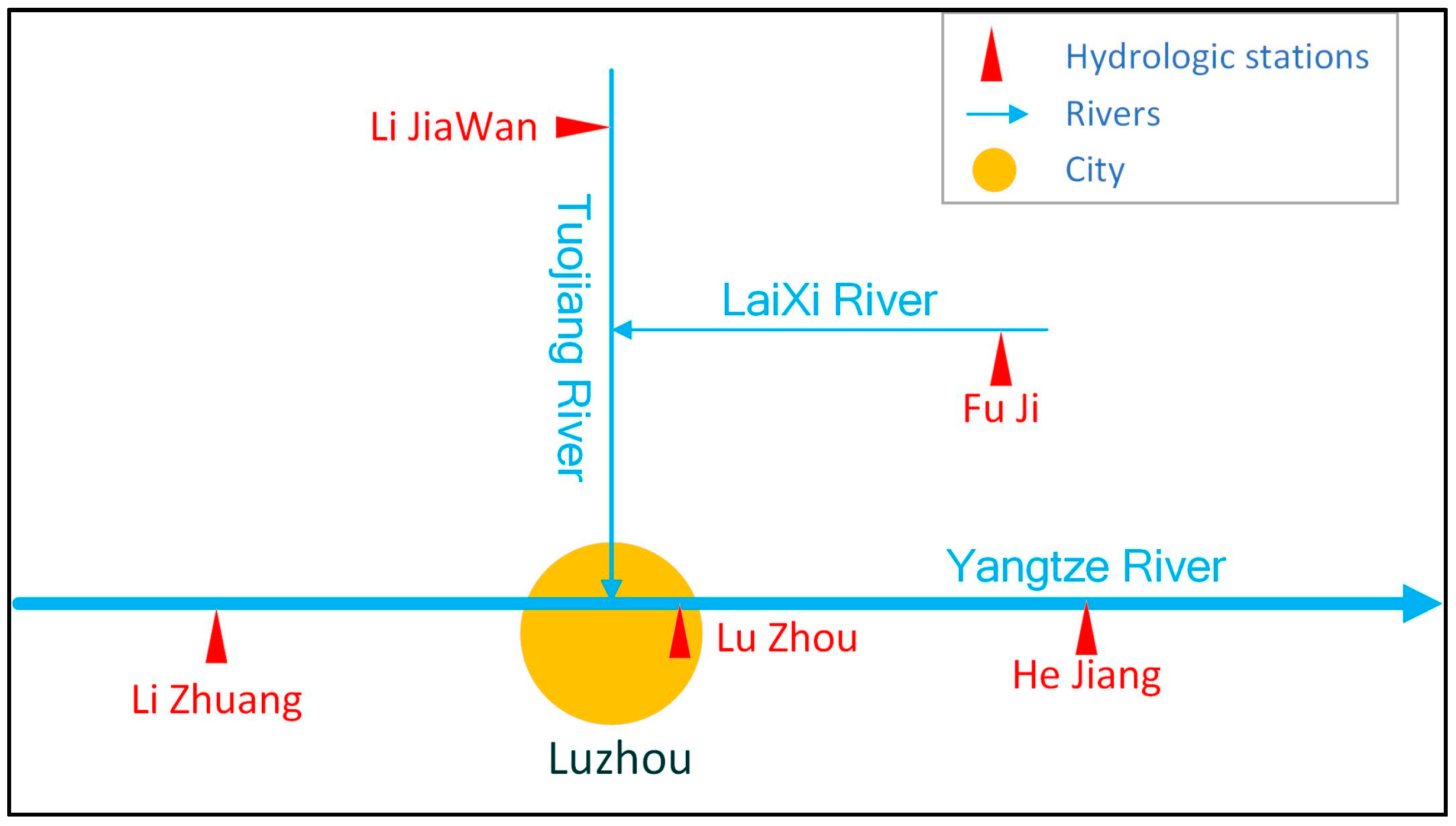
2.3. Regional Overview
2.4. Data
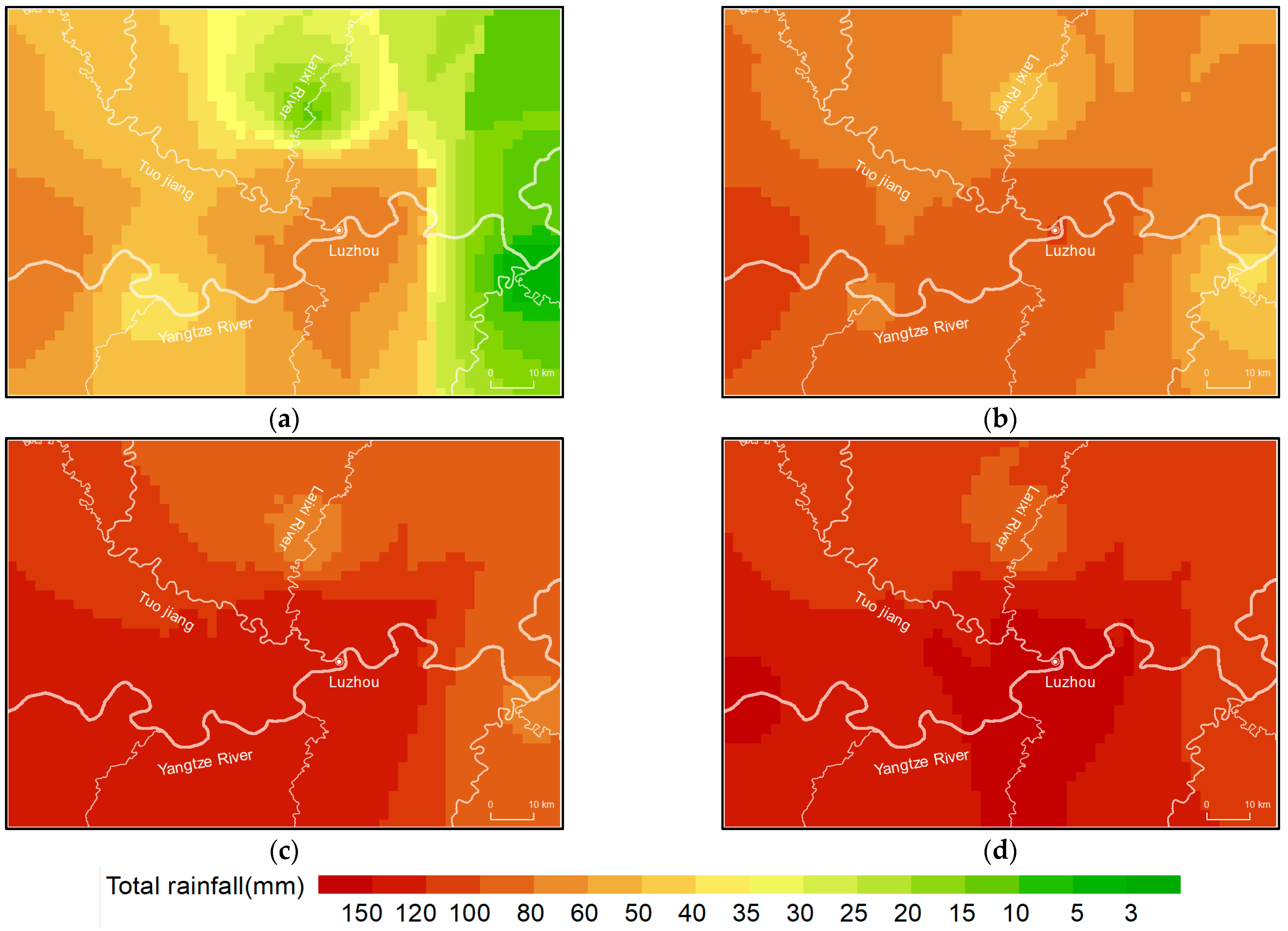
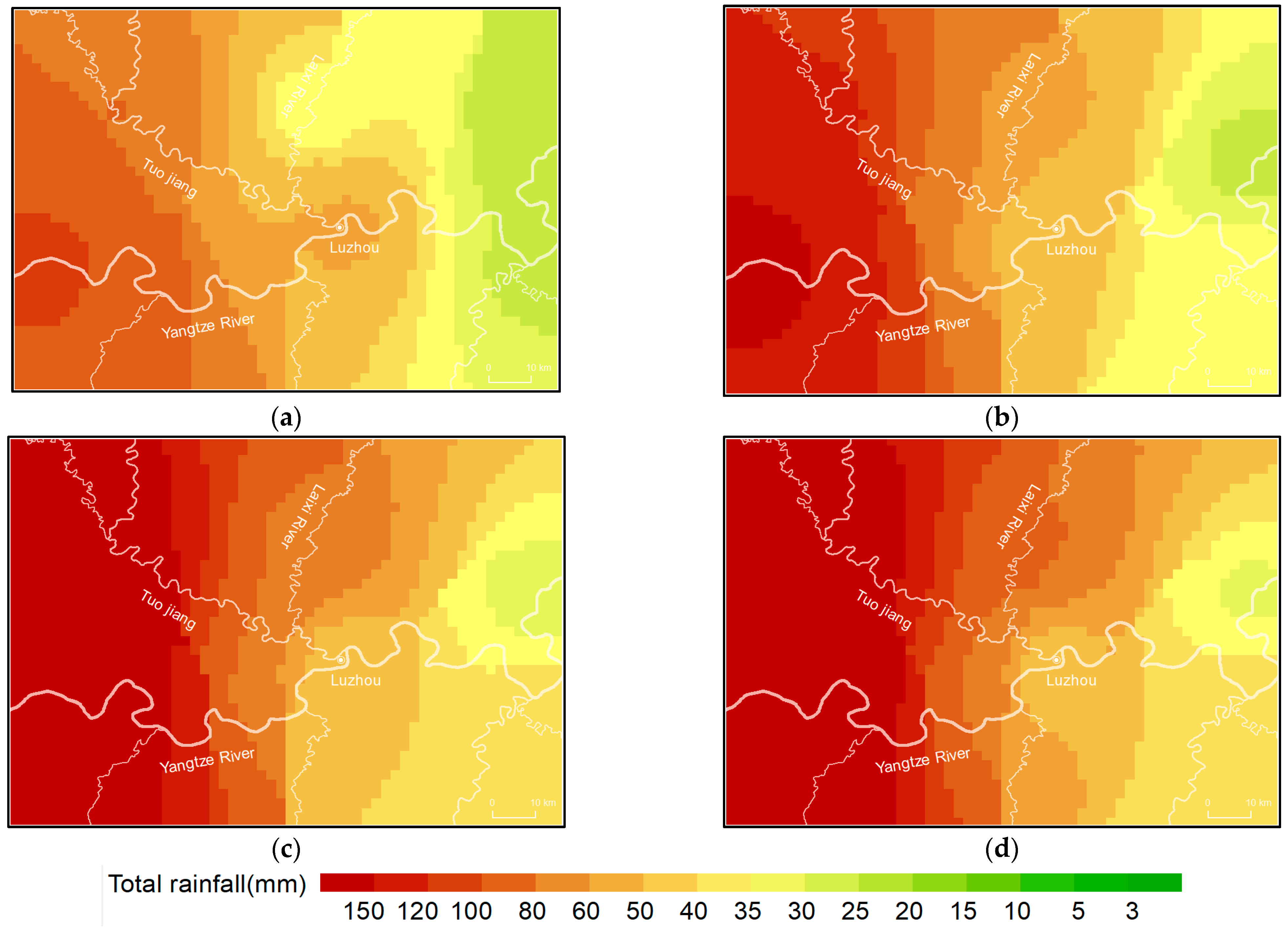
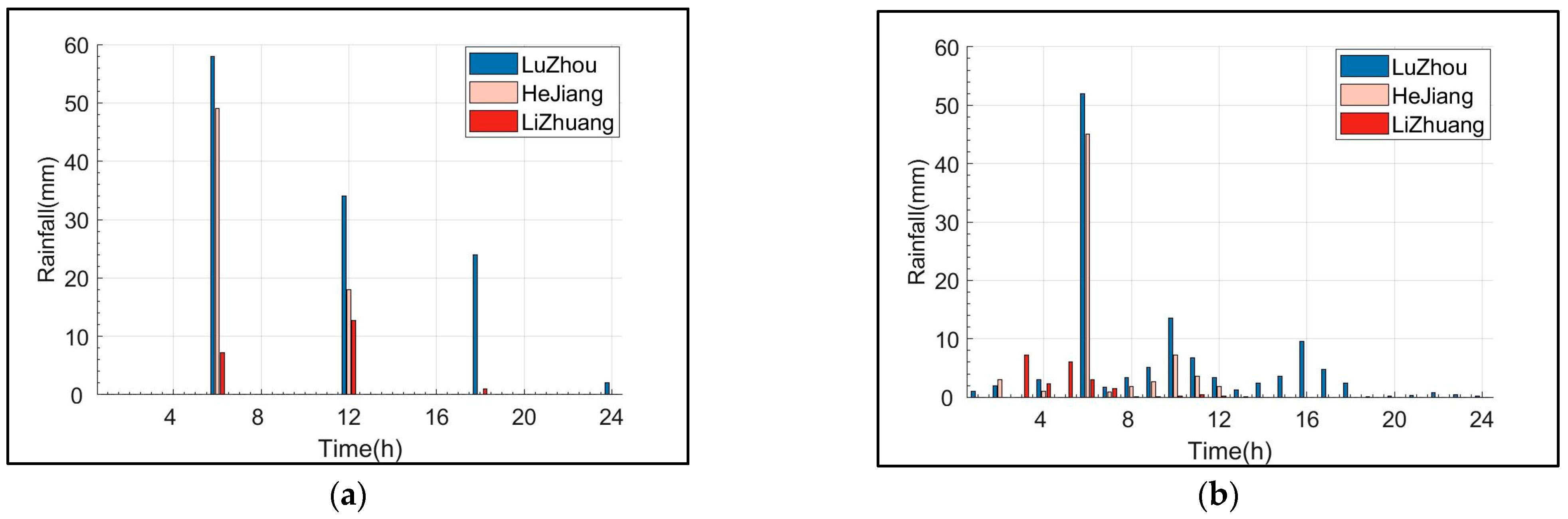
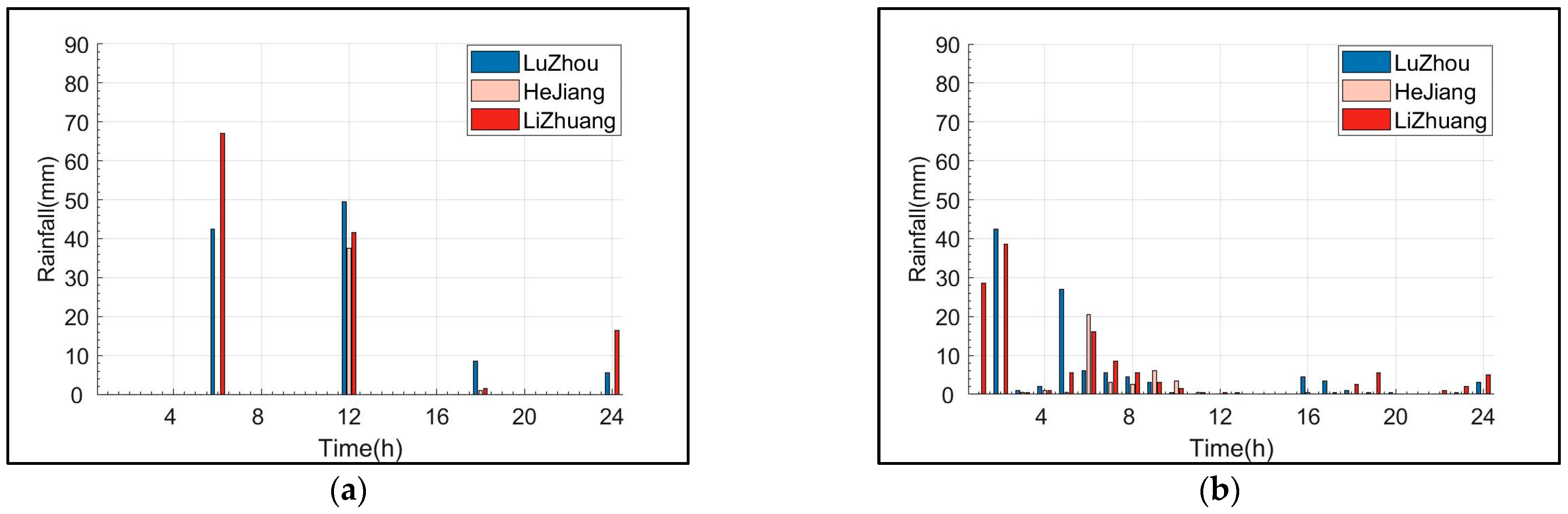
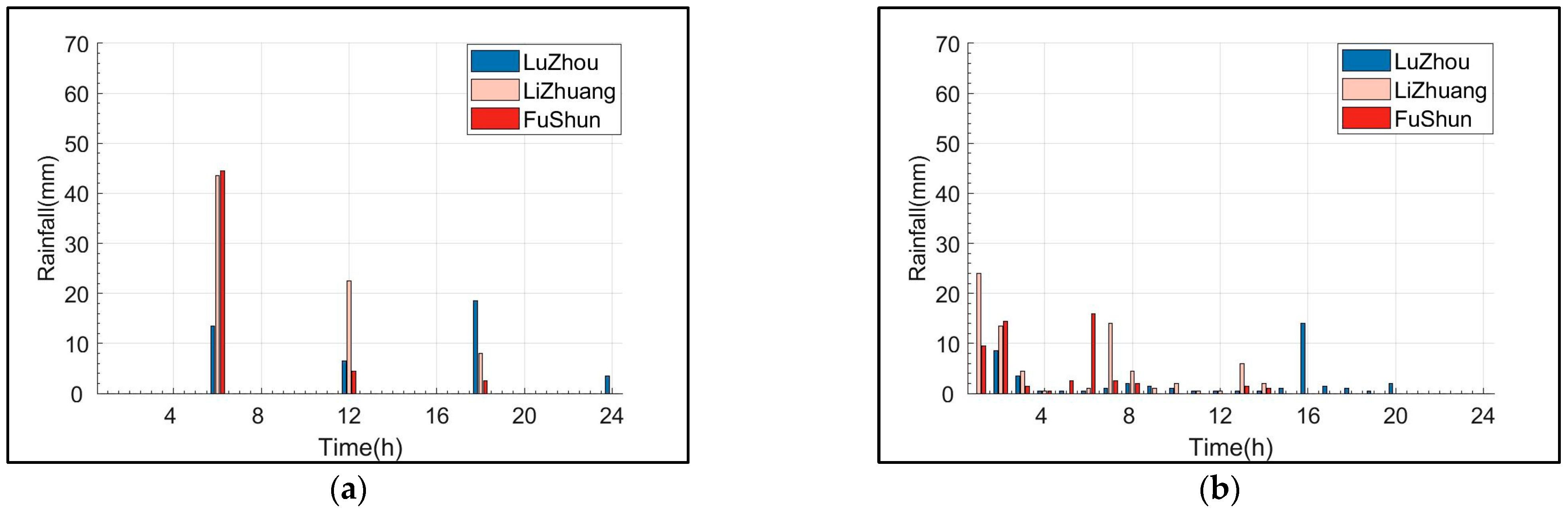
3. Results and Discussion
4. Conclusions
- The PCA algorithm was successfully applied for data reconstruction with spatio-temporal attributes. Reconstruction from low-dimensional to high-dimensional data was consistent with spatiotemporal variation characteristics. The reconstructed data better reflected the concentrated rainfall process and spatiotemporal distribution characteristics of the rainfall.
- Machine learning algorithms can extract clear features of the three types of rainfall that match the climatic characteristics of the region. The extracted features quantitatively described the dynamic spatiotemporal distribution characteristics of the various types of rainfall.
- Compared with average interpolated data, the reconstructed data had a 45–85% reduction in error in high-value areas and a 10–40% reduction in low-value areas. The refined rainfall process of the reconstruction effectively reduced the error in high and low-value areas.
- Although the types of rainfall identified in this study are specific to Luzhou, the proposed method can be universally applied. This study used hourly rainfall spatial data. In the future, feature matrices could be extracted at the minute level to achieve a more precise reconstruction of historical rainfall data. Precise rainfall data can assist in managing urban flash flood risks, including dispatching flood prevention, emergency personnel, and material resources.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tingsanchali, T. Urban flood disaster management. Procedia Eng. 2012, 32, 25–37. [Google Scholar] [CrossRef]
- Liu, Z. Analysis of characteristics and cause of urban storm runoff change and discussion on some issues. J. China Hydrol. 2009, 29, 3. [Google Scholar]
- Xi, C.; Zhu, Z.; Xie, Y.; Kai, L. The changing pattern of urban flooding in Guangzhou, China. Sci. Total Environ. 2017, 394, 622–623. [Google Scholar]
- Wang, G.Y.; Sun, G.R.; Li, J.K.; Li, J. The experimental study of hydrodynamic characteristics of the overland flow on a slope with three-dimensional Geomat. J. Hydrodyn. 2018, 30, 153–159. [Google Scholar] [CrossRef]
- Rafieeinasab, A.; Norouzi, A.; Kim, S.; Habibi, H.; Nazari, B.; Seo, D.-J.; Lee, H.; Cosgrove, B.; Cui, Z. Toward High-Resolution Flash Flood Prediction in Large Urban Areas—Analysis of Sensitivity to Spatiotemporal Resolution of Rainfall Input and Hydrologic Modeling. J. Hydrol. 2015, 531, 370–388. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Rainfall disaggregation methods: Theory and applications (Conference Presentation). In Proceedings, Workshop on Statistical and Mathematical Methods for Hydrological Analysis; Università di Roma “La Sapienza”: Rome, Italy, 2003. [Google Scholar]
- Takhellambam, B.S.; Srivastava, P.; Lamba, J.; McGehee, R.P.; Kumar, H.; Tian, D. Temporal disaggregation of hourly precipitation under changing climate over the Southeast United States. Sci. Data 2022, 9, 211. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D.; Potter, A.; Daniell, J.J. Application of machine learning methods to spatial interpolation of environmental variables. Environ. Model. Softw. 2011, 26, 1647–1659. [Google Scholar] [CrossRef]
- Han, L.; Cui, J.; Lin, H.; Ji, Z.; Cao, Z.; Li, Y.; Chen, Y. Recent progresses in the application of machine learning approach for predicting protein functional class independent of sequence similarity. Proteomics 2010, 6, 4023–4037. [Google Scholar] [CrossRef]
- Jian, Y.; David, Z.; Frangi, A.F.; Yang, J.Y. Two-dimensional PCA: A new approach to appearance-based face representation and recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 131–137. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Liu, H.W.; Huo, F.L. An application of machine learning on examining spatial and temporal distribution of short duration rainstorm. J. Hydraul. Eng. 2019, 50, 773–779. [Google Scholar]
- Onyutha, C.; Willems, P. Influence of Spatial and Temporal Scales on Statistical Analyses of Rainfall Variability in the River Nile Basin. Dyn. Atmos. 2017, 77, 26–42. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Liu, Y.S.; Zheng, J.W. Intelligent rapid prediction method of urban flooding based on BP neural network and numerical simulation model. J. Hydraul. Eng. 2022, 53, 284–295. [Google Scholar]
- Bai, G.G.; Hou, J.M.; Han, H.; Xia, J.Q.; Li, B.Y.; Zhang, Y.W.; Wei, Z.H. Intelligent monitoring method for road inundation based on deep learning. Water Resour. Prot. 2021, 37, 75–80. [Google Scholar]
- Liu, Y.Y.; Li, L.; Liu, Y.-S.; Chan, P.-W.; Zhang, W.-H.; Zhang, L. Estimation of precipitation induced by tropical cyclones based on machine-learning-enhanced analogue identification of numerical prediction. Meteorol. Appl. 2021, 28, e1978. [Google Scholar] [CrossRef]
- Ngongondo, C.; Xu, C.-Y.; Gottschalk, L.; Alemaw, B. Evaluation of Spatial and Temporal Characteristics of Rainfall in Malawi: A Case of Data Scarce Region. Theor. Appl. Climatol. 2011, 106, 79–93. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Qi, H.; Hu, Z.; Chen, Z.; Yang, R.; Qiao, H. Deep learning–enhanced T1 mapping with spatial-temporal and physical constraint. Magn. Reson. Med. 2021, 86, 1647–1661. [Google Scholar] [CrossRef]
- De Vittori, A.; Cipollone, R.; Di Lizia, P. Real-time space object tracklet extraction from telescope survey images with machine learning. Astrodynamics 2022, 6, 205–218. [Google Scholar] [CrossRef]
- Ravishankar, S.; Ye, J.C.; Fessler, J.A. Image Reconstruction: From Sparsity to Data-Adaptive Methods and Machine Learning. Proc. IEEE 2020, 108, 86–109. [Google Scholar] [CrossRef]
- Singh, C.V. Pattern characteristics of Indian monsoon rainfall using principal component analysis (PCA). Atmos. Res. 2006, 79, 317–326. [Google Scholar] [CrossRef]
- Huang, S.; Yang, D.; Ge, Y.X.; Zhang, X.H. Combined supervised information with PCA via discriminative component selection. Inf. Process. Lett. 2015, 115, 812–816. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Everitt, B.S.; Landau, S.; Leese, M.; Stahl, D. Cluster Analysis, 5th ed.; John Wiley & Sons, Ltd.: London, UK, 2011. [Google Scholar]
- Kumar, R.; Makkapati, V. Encoding of multispectral and hyperspectral image data using wavelet transform and gain shape vector quantization. Image Vis. Comput. 2005, 23, 721–729. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 100–108. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Liu, Y.; Liu, S.; Ren, H.; Tian, P.; Yang, N. Extraction of Spatiotemporal Distribution Characteristics and Spatiotemporal Reconstruction of Rainfall Data by PCA Algorithm. Water 2023, 15, 3596. https://doi.org/10.3390/w15203596
Liu Y, Liu Y, Liu S, Ren H, Tian P, Yang N. Extraction of Spatiotemporal Distribution Characteristics and Spatiotemporal Reconstruction of Rainfall Data by PCA Algorithm. Water. 2023; 15(20):3596. https://doi.org/10.3390/w15203596
Chicago/Turabian StyleLiu, Yuanyuan, Yesen Liu, Shu Liu, Hancheng Ren, Peinan Tian, and Nana Yang. 2023. "Extraction of Spatiotemporal Distribution Characteristics and Spatiotemporal Reconstruction of Rainfall Data by PCA Algorithm" Water 15, no. 20: 3596. https://doi.org/10.3390/w15203596




