1. Introduction
Hydrological models are able to effectively approximate the complex hydrological phenomena that occur in natural watersheds. However, real-world hydrological processes are innately imbued with uncertainties arising from the combined impact of climate forcing and underlying surface conditions [
1]. Basin characteristics with random properties are often described in hydrological models on the basis of their parameters. This randomness leads to the phenomenon of “equifinality”. This phenomenon may have negative impacts on the accuracy and reliability of hydrological simulations and basin management decisions [
2]. Therefore, it is crucial to quantify the uncertainty associated with the hydrological model parameters and evaluate the impact of parameter uncertainty on the model simulations [
3,
4].
To perform uncertainty analysis on hydrological model parameters, it is necessary to repeatedly run the hydrological model and to generate a number of parameter–objective data points, which are usually called sample points [
5]. The samples are usually generated using parameter optimization algorithms, otherwise referred to as parameter calibration algorithms. Since the 1920s and 1930s, the development of watershed hydrological models has progressed rapidly owing to the maturity of runoff production and flow concentration theories, as well as advancements in computer science and technology [
6,
7,
8]. Until recently, popular hydrological models such as the Soil and Water Assessment Tool (SWAT), the Topography-based Hydrological Model (TOPMODEL), and the MIKE System Hydrological European (MIKE SHE) and Xin’anjiang models have been widely applied to perform watershed hydrological simulation [
9]. Among these models, the Xin’anjiang model (abbreviated as XAJ in this paper) is the most commonly used hydrological model in China [
10,
11]. When generating samples or calibrating the parameters of the XAJ model in order to perform uncertainty analysis under unconstrained conditions, two problems often arise. The first problem is that in long-term hydrological simulation, negative soil moisture values usually occur. Many researchers have addressed this issue by simply resetting the negative soil moisture values to zero. Apparently, this treatment introduces extra water into the model simulations, leading to an imbalance in water quantity. The second problem is that the flow concentration parameters of the XAJ model have clear physical meanings, and their magnitude reflects the flow velocity of different runoff components. However, many scholars fail to consider the relationship between the magnitudes of the flow concentration parameters, such as
CG,
CI, and
CS, in parameter calibration. Given the practical considerations involved in optimizing hydrological model parameters, it is crucial to include constraints in the calibration process. Nevertheless, there has been a notable lack of research in this domain.
To quantify the uncertainty associated with hydrological model parameters, scholars have conducted extensive research. Beven (1992) introduced the Generalized Likelihood Uncertainty Estimation (GLUE) method [
12], which employs Monte Carlo sampling to generate parameter sample points, screens the samples with a likelihood criterion, and analyzes the posterior distribution of the parameters. This method is simple in principle and has been widely used to study parameter uncertainty in hydrological models [
13,
14,
15,
16,
17]. However, Mantovan et al. [
18] pointed out that the likelihood function does not strictly follow a probability distribution, and the posterior probability distribution of the inferred parameters may not have statistically significant characteristics. The Markov Chain Monte Carlo (MCMC) technique is an alternative approximate Bayesian approach that enables the sampling of intricate posterior distributions, obviating the “pseudo-Bayesian” dilemma associated with the GLUE method [
19]. The Metropolis–Hastings algorithm stands as the quintessential method in the realm of machine learning, founded on the principle of “rejection sampling”, which provides an approximation of the posterior distribution. Theoretically, the Metropolis–Hastings algorithm has the potential to estimate the posterior distribution of parameters; nonetheless, for intricate models, limited prior knowledge results in sluggish convergence of the algorithm. To enhance the effectiveness of MCMC, Vrugt et al. [
20] proposed the SCEM-UA algorithm [
21], which merges the improved Shuffled Complex Evolution developed at University of Arizona (SCE-UA) algorithm with the Metropolis–Hastings algorithm. The improved SCE-UA algorithm utilizes the random walk method to facilitate population evolution, whereas the Metropolis algorithm decides whether the sample points in the offspring are acceptable as points on the Markov chain. Ter Braak [
22] introduced the Differential Evolution Markov Chain (DE-MC), an innovative algorithm that merges the fundamental principles of Differential Evolution (DE) and MCMC. The DE algorithm is employed to accomplish population evolution, thereby addressing the pivotal issue of selecting the appropriate scale and direction for the jump distribution in MCMC [
23]. Furthermore, the Metropolis algorithm ascertains whether the sample points in the offspring qualified as points on a Markov chain. The SCEM-UA algorithm and the DE-MC algorithm are both MCMC techniques that permit the implementation of multiple chains running in parallel. They possess the advantage of rapid optimization and convergence, in contrast to traditional MCMC approaches, and therefore are suitable for examining uncertainty in studies on hydrological model parameters. However, both techniques rely on single-objective population evolutionary algorithms to generate their sampling results. Numerous studies have demonstrated that such sampling procedures tend to prioritize “exploitation” over “exploration”, leading to a loss of diversity within the sampled population [
24,
25,
26]. In this context, “exploitation” refers to the utilization and improvement of good existing solutions to enhance their fitness, while “exploration” involves searching for new solutions in unexplored regions. Therefore, it is crucial to enhance the exploratory nature of uncertainty analysis methods.
The main contribution of this paper lies in addressing two key challenges in the parameter uncertainty analysis of hydrological models. Firstly, existing parameter optimization methods often overlook the physical significance and constraints of model parameters and state variables, leading to unreliable optimization results and unrealistic simulation outcomes. Secondly, existing parameter optimization methods often focus on single-objective optimization, resulting in a lack of diversity in the sampling results as the population is concentrated in a specific region.
The proposed constrained multi-objective intelligent optimization algorithm effectively addresses the aforementioned difficulties in parameter optimization and uncertainty analysis. By employing a penalty function based on constraints, the algorithm guides the optimization process to avoid unreasonable regions and ensures the reliability of the sampling results. The inclusion of a multi-objective optimization algorithm in the sampling process further enhances the diversity of the obtained optimization result population, preventing concentration in a narrow region and promoting a more comprehensive distribution of solutions.
For the problem of imposing constraints in the optimization process, we analyzed the principles of the XAJ model and the physical meaning of the parameters. After that, we designed numerical simulation experiments to explore the relationship between the model parameters and the positive and negative values of soil moisture, before proposing a penalty function method for dealing with the case of negative values of soil moisture, and guiding the parameter optimization algorithm to find the combination of model parameters that corresponded to non-negative soil moisture. Regarding the flow concentration parameters, another penalty function was designed to ensure that they satisfied the magnitude relationship CG > CI > CS, and the optimization algorithm was guided in order for reasonable parameter values to be obtained. To address the issue of sample diversity deterioration, this study incorporates the double-objective and triple-objective NSGA-II methods, in contrast to the single-objective evolutionary algorithms typically utilized in existing uncertainty analysis methods. The numerical simulation results demonstrate the effectiveness of the proposed algorithm in addressing the limitations of existing methods. The proposed approach not only avoids the issue of negative soil moisture values and yields more reasonable model parameters, it also significantly improves the property of sample diversity. These findings highlight the value of the proposed algorithm in achieving more accurate and robust results in hydrological modeling and uncertainty analysis.
In summary, in this study, a new element is introduced by adding constraints to the hydrological model and a multi-objective optimization approach to the parametric optimization sampling method. By doing so, not only are the reliability and diversity of the sampling results improved, but a distinction is also made with respect to the results of previous publications that did not address these aspects.
2. Materials and Methods
2.1. XAJ Model
In the 1980s, Renjun Zhao et al. introduced the XAJ model, with three runoff components [
27], and this has since been employed extensively for flood simulation and forecasting in the humid and semi-humid regions of China. The XAJ model calculates the total runoff generated by rainfall using saturation excess theory, and divides the runoff components into saturated surface runoff, interflow, and groundwater runoff. The XAJ model uses the lag and route method for river network flow concentration computation and the Muskingum method for river channel routing.
The XAJ model holds significant importance in the field of hydrology, particularly in flood forecasting for the wet areas of China. With its extensive usage and effectiveness, solving the challenges associated with the XAJ model has far-reaching implications. Successful resolution of these issues would not only benefit the XAJ basin but also contribute to improved flood forecasting in a significant portion of China.
The significance of solving the issues related to the XAJ model extends beyond its use in a specific region. Solving these issues will play a pivotal role in improving flood forecasting capabilities and enhancing water management strategies for a significant portion of China, making it a matter of great importance in the field of hydrology.
2.1.1. The Structure of the XAJ Model
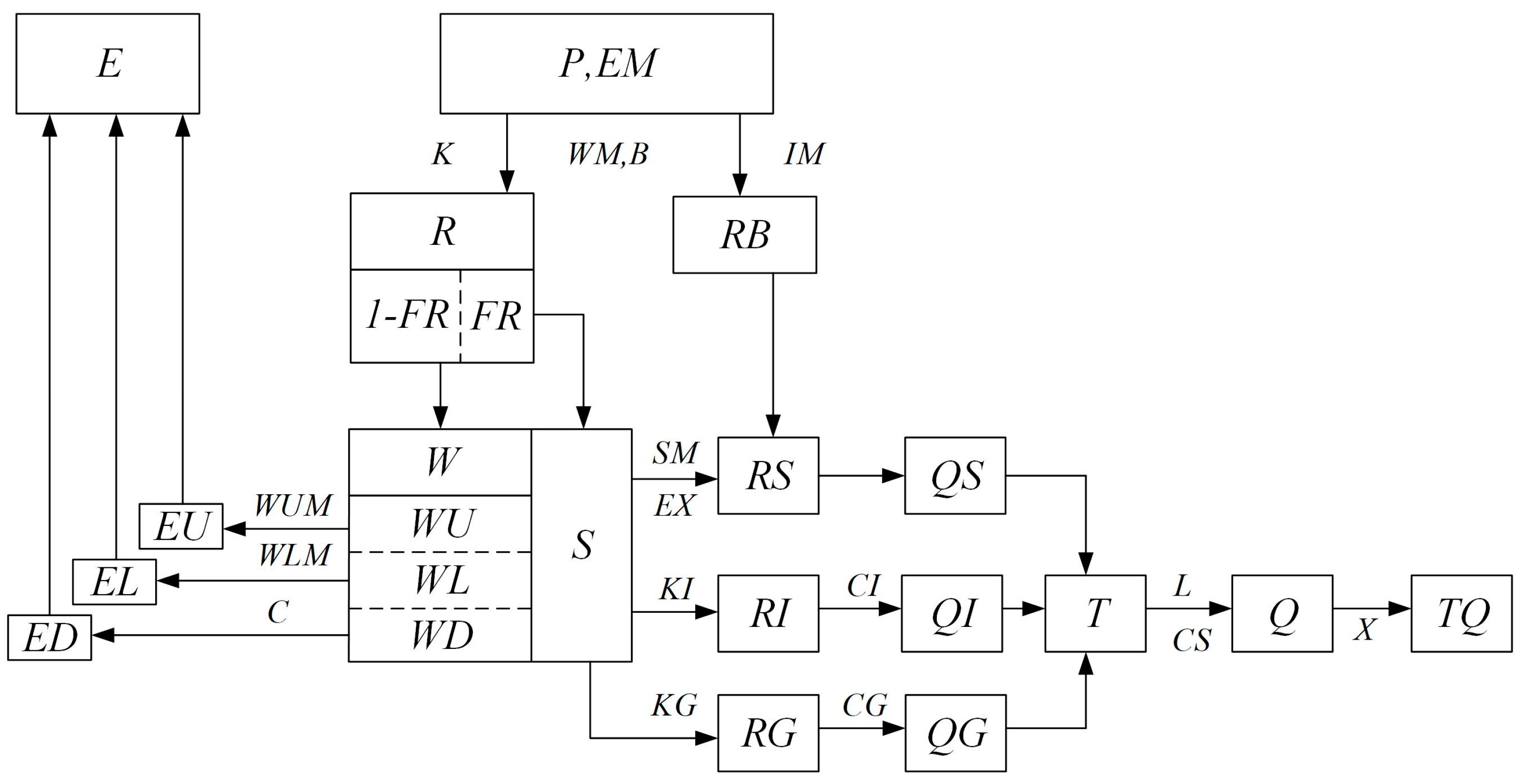
The watershed is partitioned into a collection of sub-basins, wherein the discharge hydrograph from each sub-basin is initially simulated and subsequently directed along the channels to the outlet of the watershed.
A flowchart of the XAJ model is depicted in
Figure 1. The symbols representing inputs, outputs, and state variables are indicated within the blocks in
Figure 1. On the other hand, the symbols representing parameters (constants specific to each sub-basin) are displayed outside the corresponding blocks.
The model takes in two inputs: P, representing the measured areal mean rainfall depth in the sub-basin, and EM, denoting the measured pan evaporation. The outputs consist of the discharge, Q, from each sub-basin, the outlet discharge from the entire basin, TQ, and the actual evapotranspiration from the entire basin, E. The actual evapotranspiration is obtained by summing the evapotranspiration from the upper (EU), lower (EL), and deepest (ED) soil layers, respectively.
The state variables encompass various components: W, which represents the areal mean tension water storage, comprising WU, WL, and WD for the upper, lower, and deep layers, respectively. Additionally, S stands for the areal mean free water storage. R accounts for the pervious area’s runoff, comprising RS, RI, and RG for surface, interflow, and groundwater runoff, respectively. Similarly, RB represents the runoff from the impervious area IM. FR denotes the runoff producing area, while T stands for the total sub-basin inflow to the channel network, encompasses QS, QI, and QG for surface runoff, interflow, and groundwater, respectively.
2.1.2. Parameters of the XAJ Model
The model involves the optimization of 16 parameters (see
Table 1).
2.2. Data Sources
The model is applied in the Chengcun watershed (see
Figure 2). Choosing the Chengcun watershed for this study is a safe and logical choice as it is a typical wet watershed and the birthplace of the XAJ model. This allows for a comprehensive analysis and enhances the reliability of research outcomes.
The watershed is located in a subtropical monsoon climate zone with considerable intra- and inter-annual runoff variability. The Chengcun watershed possesses characteristics consistent with those typical of humid regions. The basin has a total area of 298 km2 and encompasses 10 rainfall gauges, including Chengcun, Wangcun, Zuolong, and Tianli, etc. Chengcun station serves as the basin’s outlet hydrological station.
For runoff simulation, daily data covering a period of 14 years (1986–1999) were utilized to study the watershed. The limited availability of rainfall runoff information in China, constrained by policy and confidentiality requirements, restricts the time frame for data collection to between 1986 and 1999. However, based on the basin survey, it was found that the rainfall runoff characteristics of the basin remained relatively stable. Therefore, the selected information is still applicable to the XAJ model, and its limited availability does not impact the validity of this study.
The Chengcun watershed was divided into 10 sub-basins using the Thiessen polygon method, and the area weights of each sub-basin are presented in
Table 2. Due to the relatively small size of the watershed, the number of Muskingum segments between each sub-basin and the basin outlet is set to zero in this study, meaning that no Muskingum routing is needed. As a result, the Muskingum method parameter
X is not included in the optimization process. To ensure the stability of the optimization results and to avoid the bad impact of parameter correlation, a structural constraint of
KG +
KI = 0.7 is introduced. Consequently, the total number of parameters to be optimized in this study is reduced to 14.
2.3. Framework for Constrained Multi-Objective Intelligent Optimization Algorithm
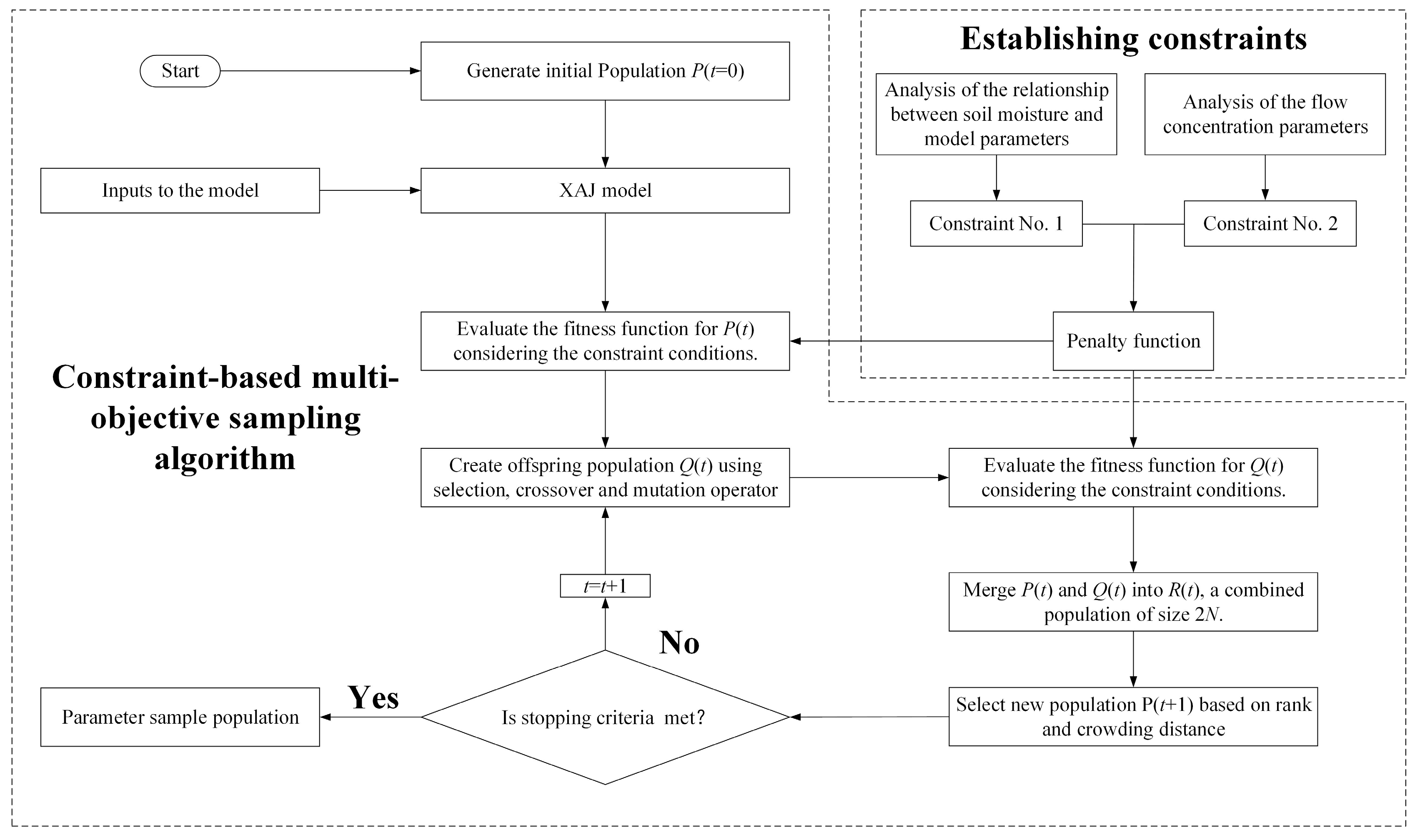
This study introduces a novel constraint-based multi-objective intelligent optimization algorithm, designed to maintain the diversity of sample points while eliminating ‘unreasonable’ samples during the sampling process. It aims to strike a balance between “local exploitation” and “global exploration”. The framework of the proposed methodology involves two main steps.
(1) Establishing constraints: First, two constraints are established for optimizing the parameters of the XAJ model. The first constraint ensures that the soil water content remains greater than 0 throughout the simulated hydrological process. The second constraint enforces the condition CG > CI > CS.
Negative soil moisture values are commonly encountered in long-term hydrological simulations. Unfortunately, many researchers address this issue by simply resetting the negative soil moisture to zero, without taking the physical implications of such an approach into consideration. This can lead to sampling results that lack physical sense and reliability.
Furthermore, another important aspect that is often overlooked is the specific size relationships among the parameters CG, CI, and CS in hydrological models. Neglecting these relationships can further compromise the physical sense of the sampling results.
This is in fact irresponsible, and this treatment can result in samples that lack physical meaning in the sampling results. This study addresses this issue by employing a penalty function method.
Penalty functions are formulated to accommodate the parametric optimization algorithm, taking into account the aforementioned constraints. Penalty functions are employed during the optimization of the model parameters to ascertain the guiding and constraining role of the established constraints in the process of parameter optimization.
(2) Constraint-based multi-objective sampling algorithm: Finally, by applying the NSGA-II algorithm, which takes into account the constraints, to the process of multi-objective sampling, this method ensures that the generated samples not only adhere to the specified constraints, but also achieve a balance between “global exploration” and “local exploitation”.
The core tasks are explained below and illustrated in
Figure 3.
3. Parameter Optimization in Consideration of Constraints
3.1. Relationship between Soil Moisture and Model Parameters
During long-term hydrological simulation, an infeasible combination of parameters could lead to negative values of soil moisture. As soil moisture is produced by the runoff generation module of the XAJ model, it must be related to the model’s runoff generation parameters, provided that the rainfall data and initial state variables of the basin remain fixed. Among the runoff generation parameters, the value of
IM is relatively constant and has a negligible impact on soil moisture. The parameter
K reflects the relationship between pan evapotranspiration and real evapotranspiration, where higher values of
K imply lower soil moisture, and conversely, lower values of
K imply higher soil moisture. The parameters
WM,
B, and
C have more complex effects on soil moisture and are interrelated, as noted in Zhao’s paper [
28]. Thus, these parameters were selected for further investigation, while the other parameters were held constant. The values of
WM,
B, and
C were sampled, and a numerical simulation was performed using the model to analyze their influence on soil moisture.
In this study, it is assumed that the model parameters used are the same as those in the previous research conducted by Zhao et al. [
29]. This is based on the fact that the model and the research basin in Zhao’s paper are identical to those used in the current study. The parameters of the XAJ model were set as shown in the following table (
Table 3).
In this section, we explore the impact of different combinations of
WM,
WUM,
WLM,
B, and
C on the soil moisture simulation results. We use the Latin hypercube sampling algorithm [
30] to randomly sample
WM,
WUM,
WLM,
B, and
C. The generated parameter sets, along with other fixed parameters, are used as parameters for the XAJ model simulations. The model’s output is examined for negative soil moisture values, and the spatial distribution of parameter combinations is analyzed. Following the approach described above, 100,000 simulations of the flooding process were conducted randomly, and the spatial distribution of the parameter values, along with positive and negative values of soil moisture, are presented in
Figure 4. Parameter combinations resulting in negative soil moisture are plotted with red dots, whereas those yielding positive soil moisture are represented by blue dots.
It can be inferred from the above figure that there exists a law describing the relationship between parameter combinations and the soil moisture values in the data. Under the fixed rainfall conditions and initial state variables in the data related to the Chengcun watershed, negative soil moisture values can be avoided in the simulation results when WM is sufficiently large. Furthermore, it can be observed from the plots on the upper right and lower left that increases in the value of C are associated with higher probabilities of negative soil moisture values being obtained, as evidenced by the increased density of the concentration of red dots. These results are consistent with the physical mechanism of transpiration in deep soil layers, where increasing C exacerbates soil drying in deep soil layers and increases the possibility of negative soil moisture values being obtained. Additionally, the results obtained at the sampling points indicate that the parameter B alone does not demonstrate a discernible law describing its relationship with the positivity or negativity of the soil moisture.
To further investigate the law mentioned above, we created a histogram of parameters for cases in which negative soil moisture values were observed. The vertical axis of the histogram indicates the relative frequency of parameter groups with negative soil moisture values, while the horizontal axis shows the parameter values. The resulting histogram is presented in
Figure 5. Through observation, the law becomes even more apparent. The figure demonstrates that negative values of soil moisture occur uniformly across the entire range of parameter
B. With increasing
WM or decreasing
C, the probability of the occurrence of negative soil moisture values decreases. In the Chengcun watershed,
WM values exceeding 171.16 ensure that the soil moisture will never fall below zero.
This comprehensive analysis demonstrates that the impact of WM on soil moisture is significant, with a clear law emerging. Parameter C also exhibits some degree of regularity in its influence on soil moisture, while parameter B does not show any obvious regularity. The graph clearly shows that increasing the value of WM leads to a decreased likelihood of the occurrence of negative soil moisture values. This relationship can be useful in the design of an objective function when incorporating constraints into the process of parameter optimization.
3.2. Analysis of the Flow Concentration Parameters
The parameters
CS,
CI, and
CG represent the flow concentration velocity of surface runoff, interflow runoff, and groundwater runoff, respectively. As stated by Zhao [
28], the recession coefficient is inversely proportional to the flow concentration velocity. The following law must be followed: the saturated surface runoff confluence velocity ≥ the interflow confluence velocity ≥ the groundwater confluence velocity in the same watershed. It can be inferred from this that in order for the confluence parameters to be consistent with their physical meaning, the constraint
CG ≥
CI ≥
CS must be complied with.
3.3. Construction of the Penalty Function for Constraints
Introducing constraints in the form of penalty functions into the objective function of the parameter optimization algorithm means that the optimization algorithm is modified to include the constraints as part of the objective function. The penalty function imposes a penalty on the objective function when the constraints are violated, thereby guiding the optimization algorithm to satisfy the constraints while finding the optimal values for the model parameters. This approach allows the optimization algorithm to take into account the physical meaning of the constraints and incorporate them into the optimization process, resulting in more reasonable and accurate parameter values for the model.
In an effort to integrate constraints into the optimization of model parameters, in this study, two penalty functions are introduced into the objective function of the parameter optimization algorithm. The penalty functions serve two crucial purposes. Firstly, they aim to reduce the competitive advantage of parameter combinations that do not meet the constraints during population evolution. Secondly, they indicate the degree of constraint violation carried out by unqualified parameter combinations. To fulfill these requirements, appropriate penalty functions were designed.
The penalty function was intelligently devised to assign higher objective function values (indicating poorer results) when the constraints related to CG, CI, CS or soil moisture content are violated. This design effectively guides the algorithm to avoid such regions and directs the search towards parameter intervals that adhere to the constraints. Moreover, the penalty function takes the magnitude of the constraint violation into consideration, with larger violations resulting in higher objective function values. This approach ensures that the algorithm prioritizes solutions that comply with the constraints and discourages solutions with significant violations.
To mitigate the influence of different units on the penalty function, a dimensionless approach was adopted. This approach aims to normalize the values of CG, CI, CS, and WM, thereby eliminating the impact of their magnitudes on the penalty function. By translating the parameters into a common scale, the penalty function is rendered independent of the original units of the parameters, enabling a fair and unbiased assessment of constraint violations. This dimensionless approach ensures that the penalty function focuses on the relative deviations from the constraints, rather than being skewed by the absolute values of the parameters.
If a negative value of soil moisture is calculated by the parameter sample, the objective function value is set to
where
λ is the penalty factor, which is determined based on the magnitude of the optimization objective;
WMmax represents the upper limit of parameter
WM; and
WMmin represents the lower limit of the parameter
WM. The remaining parameters are explained in the preceding sections.
- 2.
The penalty function guarantees the constraint of CG ≥ CI ≥ CS
If the parameter sample does not satisfy
CG ≥
CI ≥
CS, the objective function value is set to
where
CImax and
CImin represent the upper and lower limits of the parameter
CI, respectively;
CGmin represents the lower limit of the parameter
CG, and
CSmax represents the upper limit of the parameter
CS.
3.4. Comparison of Parameter Optimization Results
3.4.1. Analysis of Optimization Results
A comparison of the results of parameter optimization before and after the incorporation of constraints was carried out. The SCE-UA algorithm was applied to optimize the parameters of the XAJ model in Chengcun watershed [
31,
32]. In the absence of constraints, optimization was performed by setting the negative soil moisture value to zero whenever negative soil moisture values were detected.
Table 4 displays the statistics for the 20 optimization runs when the penalty function was not incorporated, while
Table 5 presents the statistics for the 20 optimization runs after the introduction of the penalty function. The “Result” column in the table indicates whether the value of soil moisture obtained from the flood simulation results was less than 0. A value of −1 indicates that the soil moisture was less than 0, while a value of 1 indicates that the soil moisture was greater than or equal to 0. The “NSE” column reflects the accuracy of the parameter optimization and flood simulation results, with higher values indicating greater accuracy. “REV” stands for relative error of runoff, with smaller values of REV indicating higher levels of accuracy. Only
KG is displayed in the table, as the condition of
KG +
KI = 0.7 is incorporated into the process of parameter optimization.
As can be seen from
Table 4 and
Table 5, prior to the implementation of the penalty function, all of the simulation outcomes indicated the detection of negative values of soil moisture. Furthermore, parameter groups 8, 9, 11, 12, and 20 exhibited the phenomenon
CI ≥
CG, which violates the expected relationship between the interflow runoff and groundwater runoff coefficients. After imposing the penalty function, all combinations of flow concentration parameters and simulation outcomes appeared to satisfy the requirements of physical plausibility, indicating that the penalty function was able to effectively enforce the constraints during the optimization process.
Table 6 provides the calculations for the mean, variance, and range (difference between the maximum and minimum values) of the Nash–Sutcliffe coefficient of efficiency (NSE) for the simulated runoff processes. It can be seen from the table that the mean NSE values for the two optimization algorithms are 0.8406 and 0.8400, respectively. These values are close to the Class A standard stipulated in the Standard for hydrological information and hydrological forecasting, indicating that both sets of simulated runoff processes exhibit high accuracy and are very close to one another. The values of NSE variance and range for both optimization algorithms are close to zero, implying a high level of stability in the quality of the simulated runoff for both approaches. This indicates that the performance of the algorithms consistently produces reliable and consistent results in terms of simulating the runoff process.
In summary, the constraints implemented in the optimization algorithm not only ensure the selection of physically meaningful model parameters, they also do not compromise the performance of the algorithm. The constraints effectively guide the parameter optimization process, resulting in a set of parameters that adhere to the specified constraints and maintain the algorithm’s ability to search for optimal solutions. Thus, the constraints contribute to both the meaningfulness of the parameter values and the effectiveness of the optimization algorithm.
3.4.2. Analysis of the Stability of the Algorithm
Euclidean distance is a metric that measures the absolute distance between two points in a multidimensional space. In the context of this study, it is used to assess the stability of the algorithm by examining the mean and variance of the Euclidean distance among all samples within an experimental group.
Table 7 presents the statistical values of the Euclidean distance for the two algorithms. Smaller mean Euclidean distance values indicate less variation between the samples, implying greater stability in the algorithm’s performance. Similarly, smaller variance in Euclidean distance signifies less variability in the Euclidean distance among the samples.
According to the information provided in
Table 7, it can be observed that the mean and variance of the Euclidean distance for the constrained SCE-UA algorithm are lower than those of the SCE-UA algorithm. This indicates that the constrained SCE-UA algorithm produces optimization results that are closer to each other, resulting in improved stability of the algorithm.
3.4.3. Analysis of Runoff Relative Error
The figure below illustrates a comparison of the runoff relative errors in the hydrological simulation before and after the introduction of constraints (based on 20 separate parameter optimization and model runs).
As shown in
Figure 6 and
Table 8, the application of constraints led to a decrease in the relative error of the runoff volume in the hydrological simulation process when using the optimized parameter set. This suggests that the conventional method, where negative values of soil moisture are reset to zero, introduces unnecessary water and compromises the reliability of the simulation results. In contrast, the penalty function approach proposed in this study more effectively addresses this issue.
In conclusion, the constrained SCE-UA algorithm is proved to be a more reliable approach for parameter optimization. It not only ensures the performance of the optimization algorithm but also enhances the physical significance of model parameters and state variables. Additionally, it guarantees the water balance of the simulated runoff process and improves the accuracy of runoff simulation.
4. Sample Generation Based on Constrained Multi-Objective Intelligent Optimization
Currently, the commonly used methods for analyzing parametric uncertainty, such as the SCEM-UA, DE-MC, and DREAM algorithms, all utilize MCMC methods coupled with single-objective optimization algorithms as sample generation methods. However, traditional single-objective optimization algorithms tend to guide the samples in the search space towards a better solution, leading to a final outcome that converges on a small region or a single point [
29]. As a result, the exploration of regions in the parameter space with lower posterior density is unfortunately neglected, thus degrading the diversity property of the sample results. In fact, empirical evidence from hydrological model calibration has shown that a single objective function, no matter how well crafted, often falls short in sufficiently evaluating all significant observation properties. In order to ensure the representation—or, in other words, the exploration properties—of parameter populations in hydrological model uncertainty analysis, this study introduces a multi-objective optimization algorithm to generate a sample population. It is noteworthy that all parameter sample generation methods discussed in this section take into account the constraints introduced in
Section 2 of this study. In this study, the SCE-UA and DE algorithms were selected as benchmark methods for sample generation. These algorithms are widely recognized and are commonly used in the field, making them suitable for comparison and evaluation in the context of this research.
4.1. Sample Generation Based on Single-Objective/Multi-Objective Optimization Algorithms
4.1.1. Improved SCE-UA Algorithm
Vrugt et al. improved the SCE-UA algorithm by replacing the simplex downhill method with a simulated annealing random step method. The remaining procedures of the algorithm are similar to those of the original SCE-UA algorithm. This enhancement allows for better exploration of the parameter space and prevents the algorithm from converging solely towards an “optimal solution”, instead focusing on finding a set consisting of an optimal population [
33,
34]. Similar to the SCE algorithm, the improved SCE algorithm requires the definition of some initial settings, including the selection of algorithm parameters, the termination criterion of the program, and the selection of the objective function. In the algorithm parameters, the number of complexes p is set to 17 [
35]. The program’s termination criterion is determined by three parameters [
36]: the maximum number of calls to the XAJ model (
nmax = 5 × 10
6); the maximum number of allowable objective function improvement failures (
kmax = 50); the minimum objective function improvement rate (
TOLa = 0.001%); and the interval of parameter convergence (
TOLλ = 0.001%).
To ensure the overall accuracy of the daily rainfall–runoff simulation, the Nash–Sutcliffe efficiency coefficient was selected as the objective function, which is calculated using the following formula:
where
N represents the total number of data points of the time periods;
Qobs,t represents the measured flow value at time
t;
Qsim,t represents the simulated flow at time
t;
Qobs,mean represents the mean value of the measured flow. The closer the NSE value is to one, the better the simulation results. The penalty factor
λ is set to 10,000 for all parameters, with NSE as the optimization objective.
4.1.2. Differential Evolution Algorithm
The Differential Evolution algorithm (DE) is a type of stochastic search algorithm that is based on population differences and uses a combination of mutation, selection, and hybridization to simulate natural evolution processes [
37]. DE has a few configuration parameters, a simple principle, and high robustness, making it an effective global optimization method and a popular choice for parameter optimization [
38]. Additionally, DE has been used as the basis for developing other algorithms, such as the DEMC and DREAM algorithms, which are frequently used for uncertainty analysis.
To apply the DE algorithm to optimize the parameters of the XAJ model, several parameters of the algorithm need to be determined, such as population size, scaling factor, crossover probability, termination criterion, variation strategy, and objective function. In this study, a population size of NP = 500, a scaling factor of
F = 0.5, and a crossover probability of CR = 0.5 were used. The termination criterion was set as the maximum number of calls to the XAJ model,
nmax = 5,000,000. To uphold the diversity of the parameter population throughout the optimization process, Equation (4) is employed as the mutation strategy.
where
G is the number of the current iteration;
VG is the mutation point;
Xrj,G are mutually unequal random points; and
F is the scaling factor. NSE is used as the objective function for the DE optimization algorithm.
To guarantee the comprehensive accuracy of the daily rainfall runoff simulation results, the Nash–Sutcliffe coefficient of efficiency (NSE) was selected as the objective function, as indicated by Equation (3).
4.1.3. The NSGA-II Algorithm with Constraints
The NSGA-II algorithm is a non-dominated algorithm with both good distributivity and fast convergence. The algorithm is able to find the set of parameter populations that is as close as possible to the Pareto optimal domain, and has been widely used and validated in the field of hydrological simulation and forecasting. The NSGA-II algorithm achieves non-dominated ranking by calculating the Pareto rank and crowding distance of sample points, and then generates offspring through selection, crossover, and mutation, generates new parents using the elite strategy, and then repeats this process until convergence at the Pareto front [
39]. The algorithm has very good performance for two or three targets, and thus has the potential to improve the representativeness of the sampling results [
40]. Moreover, the algorithm can also ensure sufficient variability among the samples of the population, guaranteeing the diversity of the sampling results [
21]. The constraint conditions studied above (
Section 3.3) can also be applied in the multi-objective optimization algorithm. The computational procedure of the NSGA-II algorithm is shown in
Figure 7.
The NSGA-II algorithm, along with other methods like the Weighted Sum Method, the ε-constraint method, and the Weighted Metric Method, is commonly used in multi-objective optimization. However, the NSGA-II algorithm is distinguished by providing an optimal solution set instead of a single solution. The solution set generated using NSGA-II is evenly distributed in the solution space, offering better diversity and suitability for uncertainty analysis compared to methods that concentrate solutions in a narrow parameter space.
In addition to NSE, the coefficient of determination (R2) and the mean absolute error (MAE) are commonly used as objective functions in model parameter optimization. Their expressions are as follows:
- (1)
Coefficient of determination (R2)
- (2)
Mean absolute error (MAE)
Note that the optimization directions and value ranges of NSE, MAE, and R2 differ. The NSE ranges from −∞ to 1, with values closer to 1 indicating better optimization results. MAE ranges from 0 to +∞, with lower values indicating better optimization results. R2 ranges from 0 to 1, with values closer to 1 indicating better optimization results.
However, the NSGA-II algorithm is designed for the minimization of objective functions, while NSE and R2 are maximization metrics. Therefore, in this study, 1 − NSE, MAE, and 1 − R2 are used as the objective functions. By doing so, all three objective functions follow the rule of “the closer to 0, the better the optimization result”, thus making them suitable for the NSGA-II algorithm.
In this study, a sample size of 500 individuals was selected for the optimization process. The optimization was performed over 10,000 generations, resulting in approximately 5 × 106 iterations of the XAJ model. The penalty factor λ used in the optimization process was set to 10,000.
4.2. Evaluation Indicators for Sample-Generation Algorithms
4.2.1. Indicators for Assessing the Prediction Bounds
In this study, the optimization methods employed no longer produce a solitary set of parameter samples, but rather generate a population of parameter samples comprising multiple sets. Moreover, the output of the hydrological model at each time step is no longer restricted to a point estimate such as a single value of flow or water level, but encompasses an interval delineated by prediction bounds acquired using a specific confidence level
α (0 <
α < 1). This approach facilitates the predicted flow of uncertainty information. In such circumstances, the analysis of the obtained prediction bounds and the evaluation of their quality assume a crucial role in the study of model uncertainty [
41]. They are of paramount importance in fostering a comprehensive and objective understanding of model uncertainty [
42].
In addition to describing the characteristics of prediction bounds in hydrological models, these indices can also serve as criteria for comparing the prediction bounds generated using different uncertainty assessment methods or schemes.
The paper by L. H. Xiong [
42] provides a comprehensive summary of the indices used for evaluating the prediction range. In this study, the most widely used indices, namely, containing ratio (CR) and average bandwidth (AB), are employed to assess the performance of different optimization methods in generating parametric sample populations.
- (1)
Containing ratio (CR)
The containing ratio, as mentioned earlier, is defined as the ratio of the number of observed discharges that lie within the prediction bounds to the total number of observed discharges, presented as a percentage. Since the introduction of the GLUE method, this index has been employed extensively to evaluate the accuracy of prediction bounds. Higher values of CR indicate larger proportions of observed discharge points falling within the interval defined by the prediction bounds. It is always the objective to achieve a high CR for the estimated prediction bounds. The ideal, albeit unattainable, value for CR is 100%, which would signify that the entire observed discharge hydrograph is encompassed within the band formed by the lower and upper prediction bound trajectories. It is important to note that the confidence level α for this study is set at 95%.
- (2)
Average bandwidth (AB)
The average bandwidth (AB) of the prediction bounds for the entire discharge series is defined as follows:
with
where
bi is the bandwidth of the prediction bounds for the discharge at time
i;
Qusim,i and
Qlsim,i represent the lower and upper prediction bounds of discharge, respectively. For a specific confidence level
α, it is optimal for the bandwidth of the prediction bounds to be as narrow as possible. This enables the capture of crucial information regarding modeling uncertainty, making it more pertinent and valuable in relation to the forecasting concerns of the respective catchments.
4.2.2. The Performance Indicators for Different Parameter Populations
In addition to assessing the indicators for evaluating the predictive bounds of the hydrological model, it is also essential to evaluate the representativeness and diversity of the parameter populations themselves. In this study, the mean and variance of the Nash–Sutcliffe efficiency coefficient (NSE) were selected as indicators of representation, while the mean Euclidean distance was chosen as an indicator for the evaluation of diversity.
- (1)
Mean and variance of the Nash–Sutcliffe efficiency coefficient
The parameter population should ideally include as many “optimal solutions” as possible; therefore, higher average NSE values of simulated discharge within the population indicate greater representativeness. In this study, the accuracy of the simulation results is measured using NSE. To evaluate the representativeness of the parameter populations, the means and variances of the NSE are evaluated.
- (2)
Mean Euclidean distance
In order to explore the entire distribution and find as many optimal solutions as possible in the space, the parameter population should avoid converging around a small region of the “optimal solution”. Thus, in this study, we measured the diversity of the parameter population by calculating the mean Euclidean distances among the samples within the population. Larger values of mean Euclidean distance indicate greater diversity in the population, as they imply that the population samples are spread out across the entire distribution space, rather than being concentrated around a single “optimal solution”.
In evaluating the diversity of the solution set, the average Euclidean distance is considered the most appropriate indicator. It captures the requirement for sufficient distances between points and the dispersion of the points throughout the solution space. Other indicators may not be applicable or may not be as suitable for this particular study.
4.3. Results and Analysis of the Sample-Generation Algorithms
The posterior density distribution of each XAJ model parameter inferred for the samples generated using the sample-generation algorithms for the Chengcun watershed is illustrated in
Figure 8.
The posterior density distribution of each XAJ model parameter inferred from the samples generated using the improved SCE-UA algorithm for the Chengcun watershed is illustrated in
Figure 8a. Despite the fact that the histograms of
WM,
WLM,
C,
B,
SM, and
CG exhibit an approximate normal distribution, the histograms of the other model parameters also reveal the existence of alternative distribution patterns. This multimodal feature signifies that there exist numerous regions of attraction within the parameter space, validating the phenomenon of “equifinality” in parameter optimization. It can be noted that the dataset sampled using the modified SCE-UA algorithm is characterized by a narrow distribution, which suggests that the samples are tightly clustered in a small region around the optimal point.
Figure 8b illustrates the posterior density distribution of each parameter of the XAJ model that was inferred for the Chengcun watershed on the basis of the samples generated using the DE algorithm. It can be observed that, much like the SCE-UA algorithm, the DE algorithm also reveals that the parameters of the XAJ model adhere to diverse distribution patterns. The DE algorithm displays a narrower distribution of sample populations compared to the SCE-UA algorithm, thus indicating its limited spatial exploration capacity.
The histograms of the distribution of the parameter population generated using (1 − NSE)-MEA/(1 − NSE)-(1 − R
2), as the optimization objectives are demonstrated in
Figure 8c,d. As can be observed from the histogram, the multi-objective optimization algorithm displays a more intricate distribution pattern and a wider distribution range compared to the single-objective optimization algorithm. This result suggests that the sampled dataset is dispersed across multiple centers, and the multi-objective optimization approach is better able to simultaneously find multiple “good points” and explore the parameter space.
The histogram of the distribution of the parameter population generated using (1 − NSE)-MEA-(1 − R
2) as the optimization objectives is shown in
Figure 8e. The histogram displays a complex distribution pattern, and in comparison to the double-objective NSGA-II method, the parameter sample set obtained using the triple-objective NSGA-II method exhibits a broader distribution range. This indicates that the triple-objective NSGA-II method has a stronger ability to explore the parameter space.
The Pareto front for the parameter populations generated using (1 − NSE)-MEA and (1 − NSE)-(1 − R
2) as optimization objectives is shown in
Figure 9. It demonstrates the effective convergence of the NSGA-II algorithm towards the Pareto front of the double-objective optimization problem.
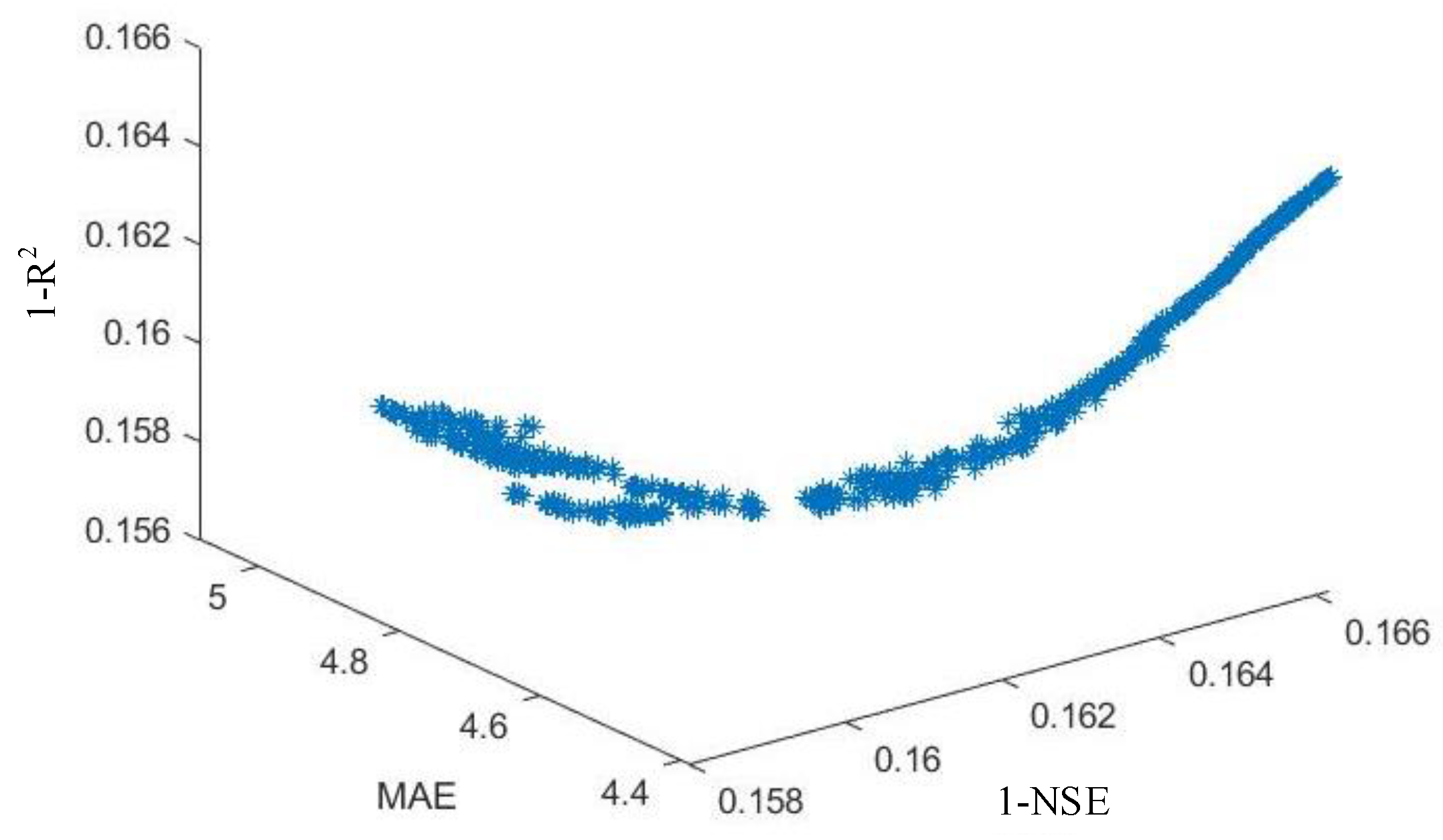
The Pareto front for the parameter populations generated using (1 − NSE)-MEA-(1 − R
2) as optimization objectives is shown in
Figure 10. As depicted in the figure, the set of parameter samples converges towards a three-dimensional Pareto front.
4.4. Containing Ratio (CR) and Average Bandwidth (AB) of Different Sample-Generation Algorithms
Table 9 and
Table 10 present the performance evaluation of various sample-generation algorithms in the realm of uncertainty analysis.
Table 9 and
Table 10 demonstrate that the “optimal” runoff simulation process attains a high level of accuracy for all five sample-generation algorithms, with a mean NSE of approximately 0.84.
Based on
Table 6, it is evident that the CR of the 95% confidence interval envelopes for the samples generated using the single-objective-based optimization algorithm is considerably low, while the AB is extremely low. As a result, the probabilistic predictions derived from the SCE-UA or DE algorithm lack sufficient information to serve as a reliable reference.
Table 10 depicts the performance of the multi-objective optimization algorithm in uncertainty analysis. It is evident that the CR of the samples generated using the double-objective NSGA-II algorithm is low, and the AB within the 95% confidence interval is low. Consequently, the probabilistic prediction outcomes obtained from the double-objective NSGA-II algorithm lack sufficient reference value.
According to
Table 10, the CR of the samples generated using the triple-objective NSGA-II algorithm is notably higher compared to that for samples generated using the single- and double-objective NSGA-II algorithms. Additionally, the average width of the samples generated using the triple-objective NSGA-II algorithm falls within an acceptable range. Therefore, the triple-objective NSGA-II algorithm proves to be the most suitable optimization algorithm for probabilistic forecasting and uncertainty analysis.
Figure 11 displays the hydrological simulation results obtained from the optimal parameters generated using different algorithms. Due to space constraints, only the hydrological simulation results for the period of 1996–1999 are presented. From
Figure 11, it is evident that the simulated hydrographs obtained from this method exhibit a strong correspondence with the measured hydrographs, indicating a satisfactory agreement between the model predictions and actual observations.
4.5. Performance Comparison of Different Sample Generation Methods
The numerical experiments conducted in this study demonstrate that the three methods mentioned above, namely, SCE-UA for single-objective optimization, DE for single-objective optimization, and NSGA-II for multi-objective optimization, are capable of generating parameter populations. In order to compare the advantages and disadvantages of these methods, it is essential to evaluate and compare the representativeness and diversity of the parameter populations.
4.5.1. Performance Indicators for Different Parameter Populations
The representativeness of the parameter populations generated using the three algorithms, SCE-UA for single-objective optimization, DE for single-objective optimization, and NSGA-II for multi-objective optimization, is evaluated using the mean and variance of the NSE values. The higher the average NSE value of the simulated discharge within the population, the greater the representativeness.
Table 11 illustrates the results of the evaluation of representativeness, specifically the mean and variance of the NSE values, for the parameter populations generated using the three algorithms. The table indicates that there is no noteworthy distinction in the representativeness of the parameter populations when comparing similar population sizes and maximum number of model runs. This suggests that all three algorithms possess the capability to generate parameter populations that are representative in nature.
4.5.2. Comparison of Diversity
In order to explore the entire distribution space and find as many optimal solutions in the space as possible, the parametric population should avoid converging around a small region of an “optimal solution”. Thus, in this study, we measured the diversity of the parametric population by calculating the mean Euclidean distance between the samples within the population. Larger mean Euclidean distances indicate better diversity in the population, as they imply that the population samples are spread out across the entire distribution space, rather than being concentrated around a single “optimal solution”.
Table 12 presents the diversity of the parameter populations generated using the three methods. It is evident that the multi-objective approach yields significantly higher diversity in the parameter samples compared to the single-objective approach, given similar population sizes and maximum number of model runs. It is important to note that the choice of objectives also influences the diversity of the parameter population. Specifically, the population with (1 − NSE)-MEA as the selected objectives exhibits greater diversity than the (1 − NSE)-(1 − R
2) combination, and the population with three objectives shows even better diversity than the population with two objectives.
5. Conclusions and Outlook
Based on the above study, four conclusions can be drawn:
- (1)
On the basis of the numerical experiments conducted, it was demonstrated that WM has a significant impact on the positivity and negativity of the soil moisture, when other variables are kept fixed. It was found in this study that increasing WM reduced the likelihood of negative soil moisture, while decreasing WM increased the possibility of negative soil moisture. Other parameters, such as C, also had an effect on the soil moisture, while the effect of parameter B was not obvious.
- (2)
The constraint of “soil moisture always non-negative” was introduced as a penalty function in the parameter optimization process. The penalty function penalized parameter sets that led to negative soil moisture, and thus the hydrological simulations with the optimized parameters did not have the phenomenon of “soil moisture less than zero”, and therefore achieved a better water balance.
- (3)
The physical meaning of the flow concentration parameters was incorporated into the parameter optimization process as a constraint by using a penalty function treatment. The simulation results showed that after incorporating the constraint, the physical meaning of the flow concentration parameters was maintained, and there was no significant negative impact on the accuracy of the simulation.
- (4)
Compared with the single-objective sample generation method, the sample population generated using the multi-objective method had better spatial exploration capability, while a similar degree of representativeness was maintained. The multi-objective method is a more suitable sample generation method for hydrological model parameter uncertainty analysis.
In this study, two novel and innovative improvements to previous research were presented. Firstly, the concept of constraints on hydrological models was introduced, and these were then incorporated into the parameter optimization sampling method. This inclusion ensured the preservation of the physical meaning of the model parameters and guaranteed the rationality of the state variable simulation results. This innovative approach addresses a gap in the existing literature by considering the constraints explicitly.
Secondly, the study incorporated multi-objective optimization techniques into the parameter optimization sampling method. This addition enhanced the diversity and reliability of the sampled parameter population, leading to more representative sampling results. This innovative extension represents an improvement upon previous studies, which have primarily focused on single-objective optimization, thereby offering a new perspective and contributing to the advancement of uncertainty analysis.
Overall, these two innovations set this study apart from the previous literature and offer valuable contributions to the field by improving the rationality and reliability of the sampling results in hydrological modeling.
The method proposed in this study effectively addresses the issues of parameter and state variable rationality in optimization, as well as the diversity of samples in the optimization algorithm. This can be considered a significant improvement in this research. While there may be other promising methods that require further exploration and improvement in future research, the method presented in this thesis demonstrates good application results, and can be considered the best approach available at this stage.
In the future, there are several aspects that still need to be addressed:
- (1)
It should be noted that the coverage and average width of the envelope of the NSGA-II-generated parameter populations should be further improved to fulfill the requirements of uncertainty analysis and ensemble flood forecasting, and there is still room for improvement with respect to this method in future studies.
- (2)
In this study, the sampling approach was based on a global optimization algorithm that prioritized “exploration” over “exploitation”. One area of improvement for the current algorithm would be to enhance its fine-grain search capability. This could be achieved by considering the introduction of gradient descent methods. Gradient descent is a popular optimization technique that iteratively adjusts the parameters in the direction of the steepest descent of the objective function. By incorporating gradient descent methods into the algorithm, it is possible to achieve a more precise and stable exploration of the parameter space, leading to improved optimization results.
- (3)
The process of sample generation can indeed be time consuming. Generating a large number of samples may require substantial time and computational resources. Future research could explore multi-thread CPU/CPU acceleration techniques for speeding up the calculation process of the multi-objective sampling algorithm used in XAJ model parameter optimization [
32,
43]. This area has received limited attention, and investigating acceleration methods could lead to improvements in computational efficiency and scalability. Such research would contribute to the field of hydrological modeling by providing faster and more efficient approaches for parameter optimization.
- (4)
In future research, expanding the scope of uncertainty analysis in hydrological modeling and prediction would be a valuable objective. While this paper focuses on uncertainty in model parameters, considering the uncertainty in model inputs and the hydrological model itself is crucial for a comprehensive analysis [
44,
45,
46]. By incorporating these sources of uncertainty, the accuracy of the study could be enhanced, and a more holistic understanding of uncertainty in hydrological modeling and prediction could be provided. This extension would contribute to advancing the field and improving the reliability of hydrological assessments and forecasts.