A Unified General Resistance Formula for Uniform Coarse Porous Media
Abstract
:1. Introduction and Objectives
2. State of the Art
2.1. Review of the Formulation and Conceptual Scheme
- Characteristic Length Lc
- Generalized dimensionless coefficients A1, linear and A2, quadratic.
2.2. Experimental Data from Previous Studies
3. The Unified Seepage Equation for Coarse Materials
3.1. Methodology
- (a)
- Selecting as characteristic length the average hydraulic diameter defined by Equation (11) with the physical parameters , , and . Equation (11), together with Equation (7), will result in a unified general equation that contemplates the unified dimensionless coefficients (linear) and (quadratic), equivalent to the coefficients and from generalized quadratic Equation (7). The rationale for this new formulation is developed in Section 3.2 below.
- (b)
- Collecting the experimental data duly selected according to the type of granular porous media, smooth spheres, rolled aggregates, and crushed aggregates, in order to calculate the linear term and the quadratic term of the Forchheimer equation (Equation (1)) that appear in Appendix A.
- (c)
- Analyzing with the available experimental data from Appendix A whether the linear and quadratic dimensionless coefficients for a granular porous media defined by a given geometry and size are constant for all non-Darcy flow regimes, nonlinear laminar, turbulent transition, and turbulent fully developed, as most research seems to confirm (J.C. López et al. [3]), or conversely, whether they need to be adjusted for each particular non-Darcy flow regime. This analysis is developed in Section 3.3 with the experimental data used, and in the absence of further research in this regard, we can consider as a hypothesis that the USEC can be applied to all non-Darcy flow regimes.
- (d)
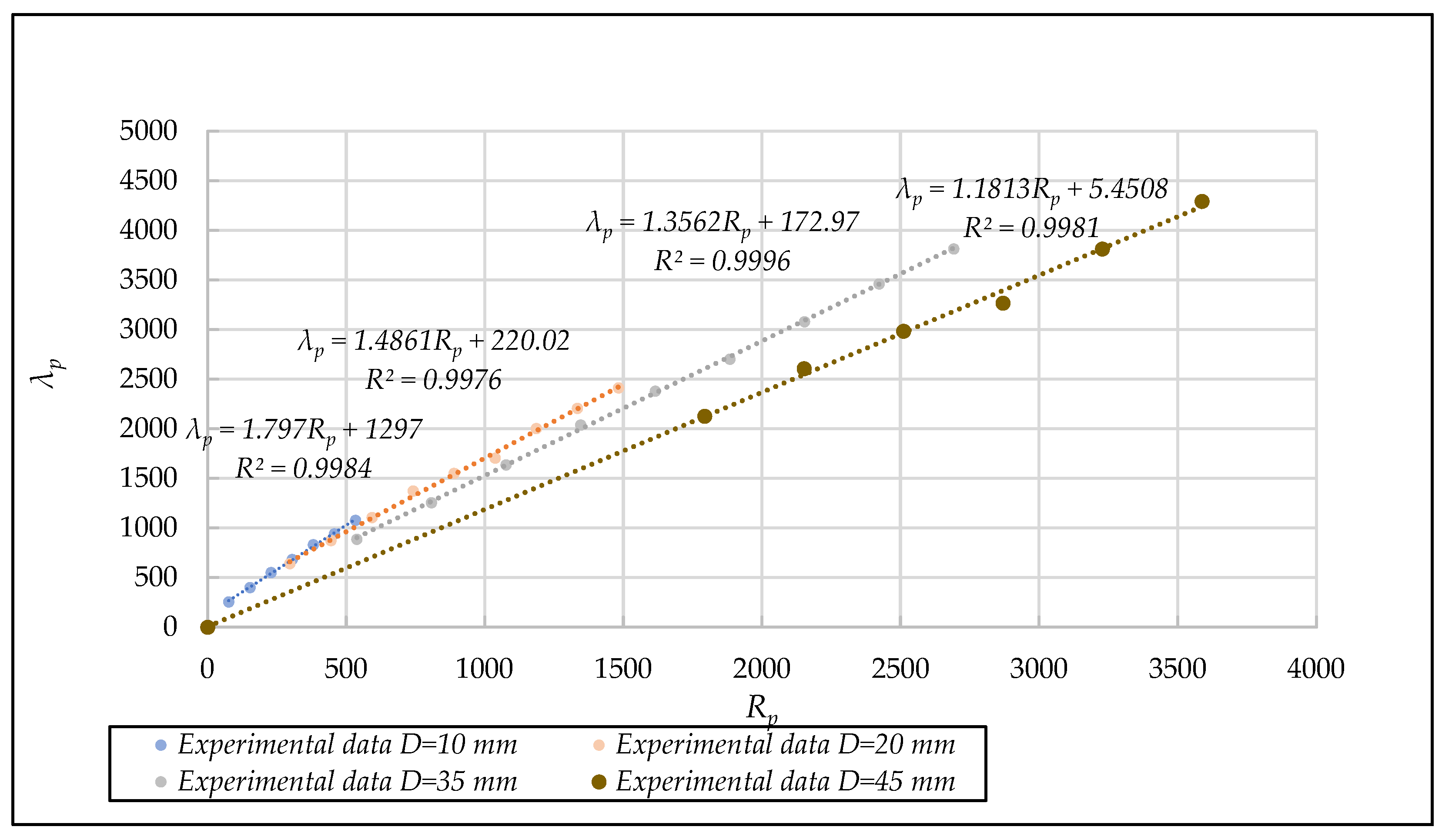
- Obtaining the empirical equations relating the dimensionless USEC coefficients and to the representative particle size for granular porous media included in Appendix A. These empirical equations have been grouped into three representative geometries, smooth spheres, rolled aggregates, and crushed aggregates, in order to analyze where there are similarities between them. The values obtained have been represented in the type [, ] and [, ] diagrams in order to analyze their evolution regarding the representative size of particles . Section 3.4 and Section 3.5 develop these aspects.
- (e)
- Finally, in Section 4, we have analyzed the results obtained by applying the newly developed USEC to the experimental data obtained in the tests carried out at the Hydraulics Laboratory of the Centro de Estudios Hidrográficos (CEDEX). The granular porous media used in these tests consist of crushed aggregates with uniform granulometry and are from the same limestone rock quarry, so the dispersions in the geometric properties of the same are minimal.
3.2. Justification for the New Formulation
3.3. Study of the Continuity of the Equation in Non-Laminar Flow Regimes
- Flow regimes: nonlinear laminar, turbulent transition
- Fully developed turbulent flow
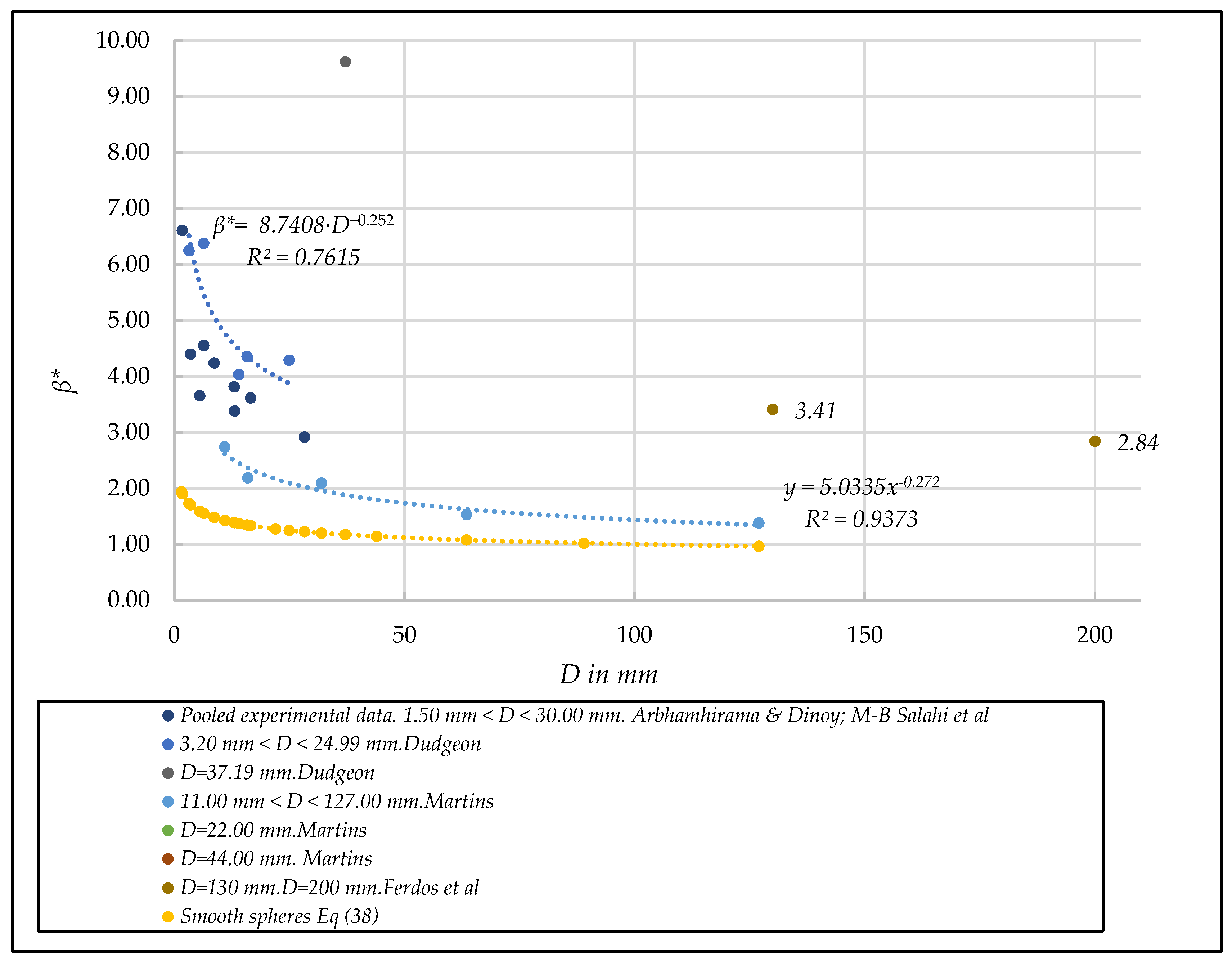
3.4. Analysis of the Effect of Representative Size on the Unified Coefficients α* and β*
- (a)
- For the same absolute pipe roughness , the friction coefficient can be fitted by a smooth curve . The friction coefficient decreases as the diameter of the pipe increases. For high values of , the friction coefficient tends to an asymptotic value.
- (b)
- As the roughness of the pipe decreases, curves approach the horizontal axis with lower values of the friction coefficients, , for the same diameter of the pipe, .
3.5. Analysis of the Effect of the Aggregate Type on the Unified Coefficients α* and β*
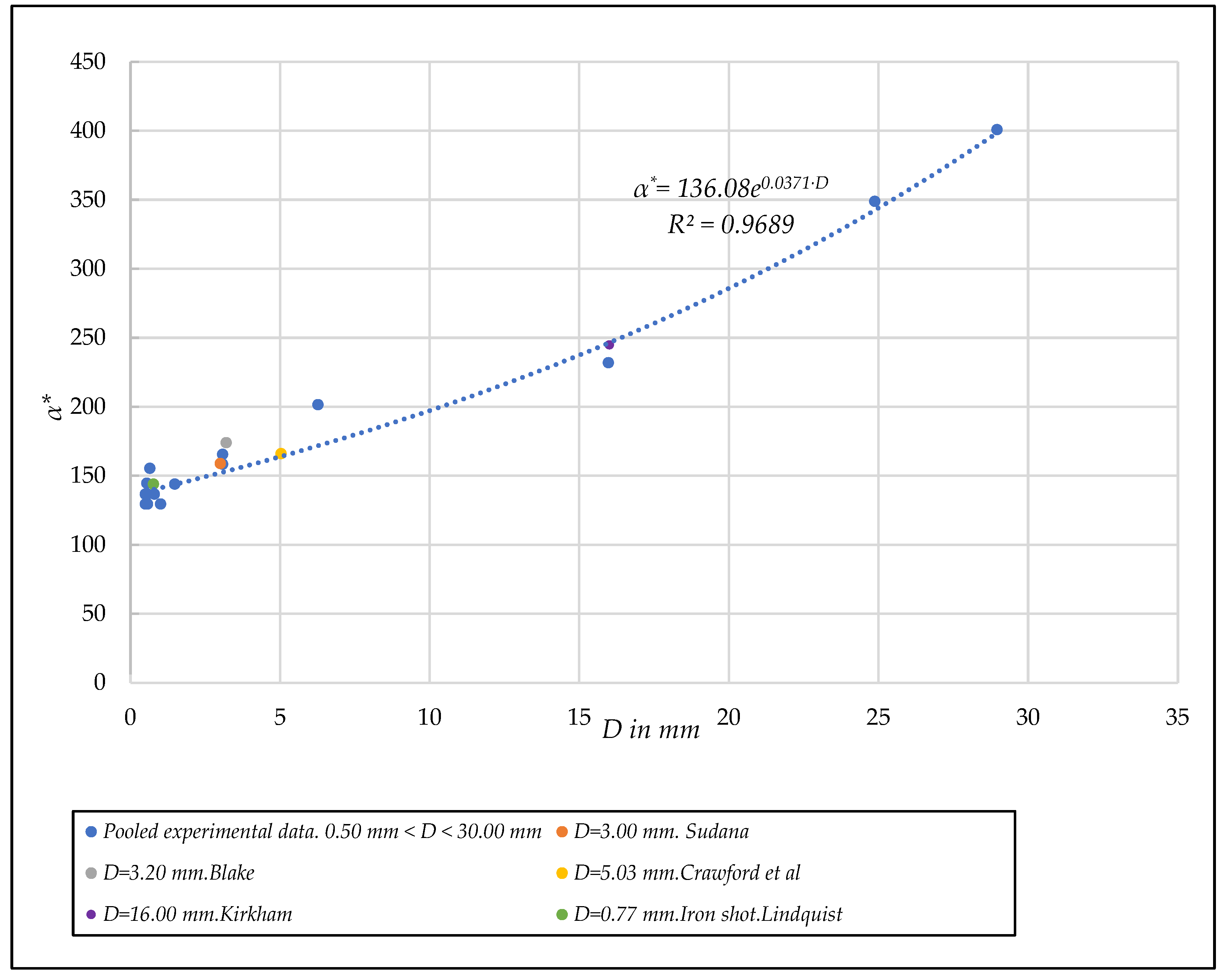
3.5.1. Tests with Smooth Spheres
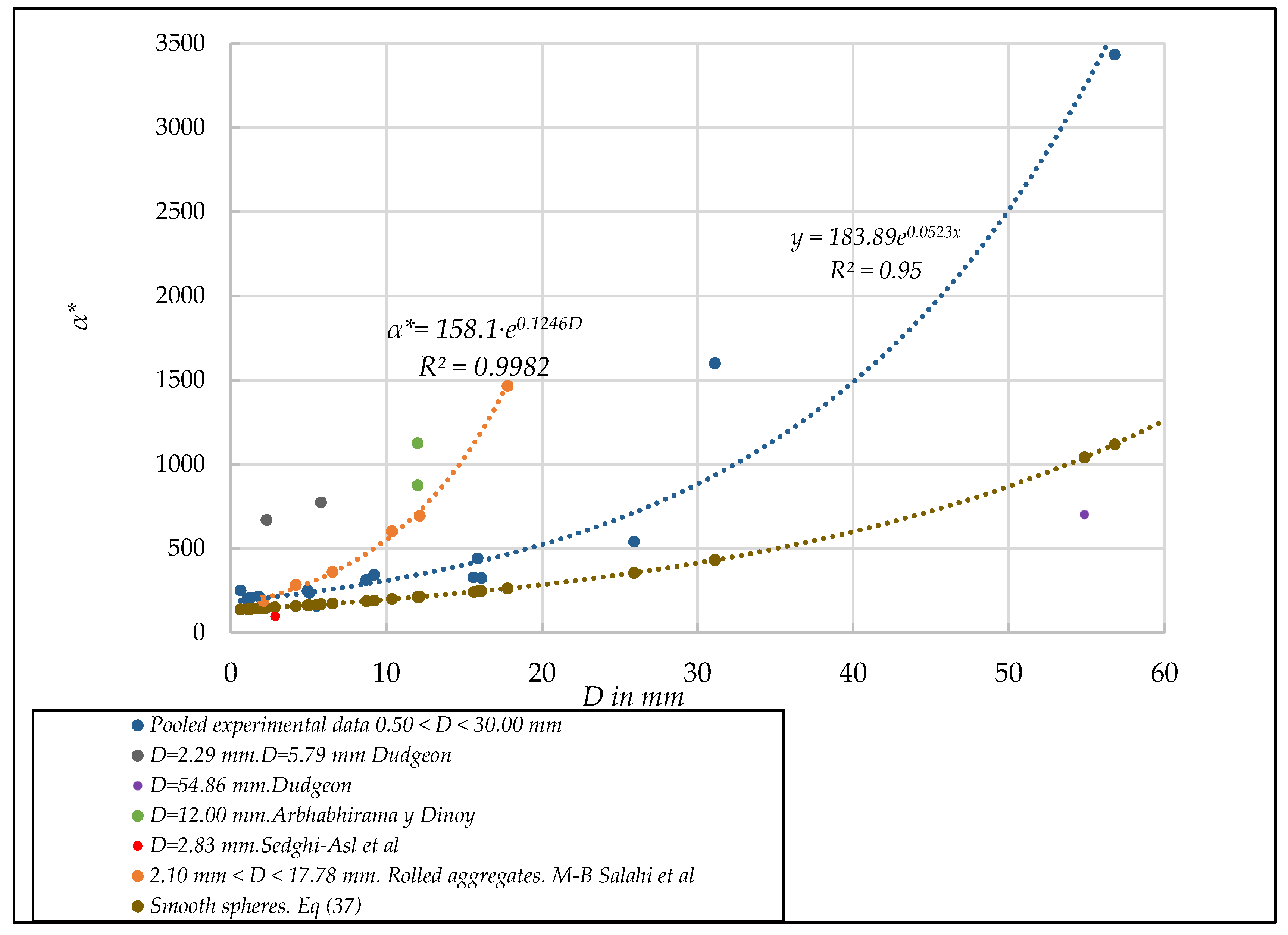
3.5.2. Tests with Rolled Aggregates
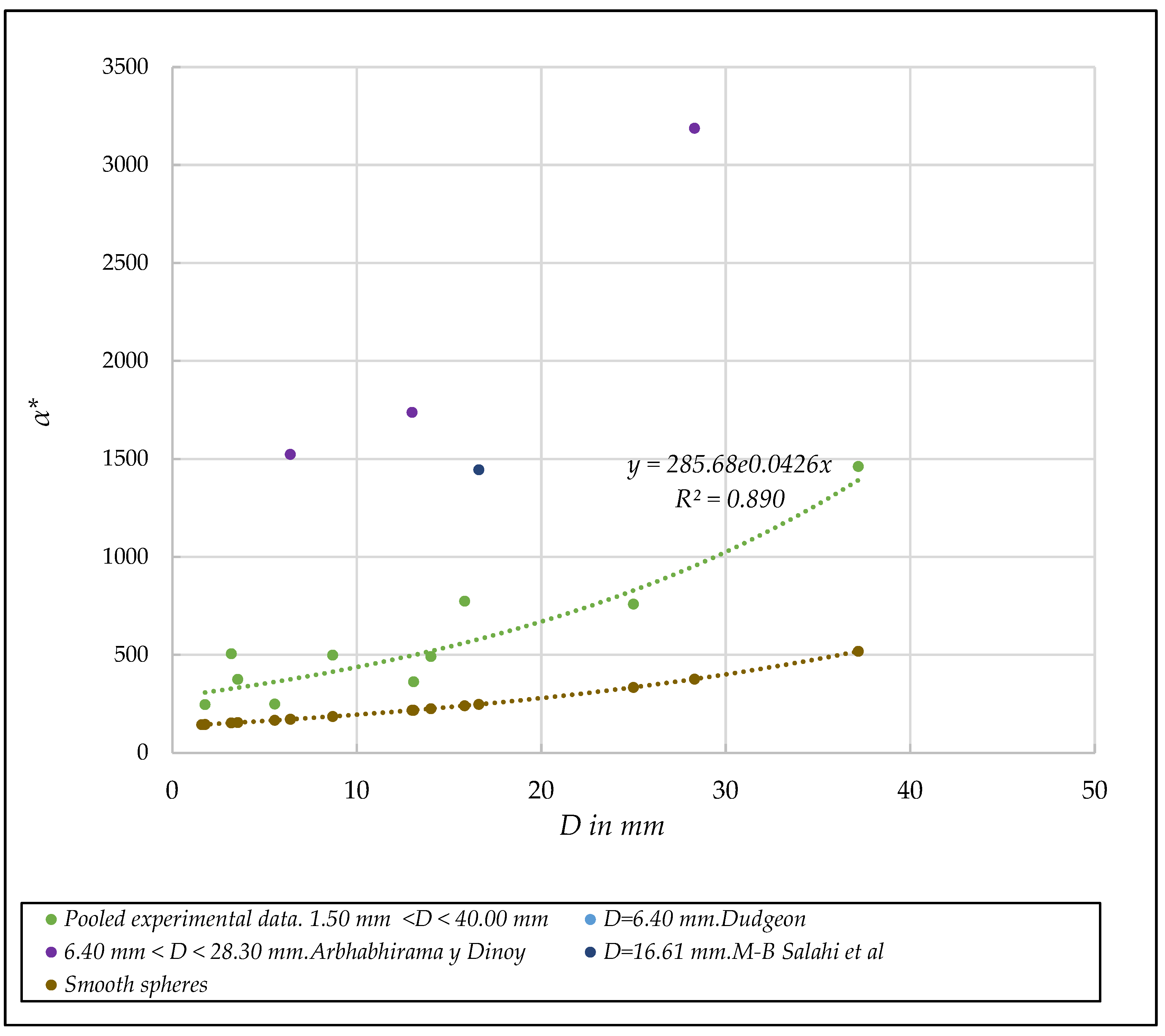
3.5.3. Tests with Crushed Aggregates
- (a)
- (b)
- (c)
4. Experimental Research
- (a)
- Obtain crushed aggregates from the same geological origin (limestone quarry in this case) with the intention of reducing the dispersion in the geometric properties of the selected porous media.
- (b)
- Select four sizes relatively close to each other ( = 1.00 mm; = 2.00 mm; = 3.50 mm; = 4.00 mm) in order to analyze the relationship of the unified dimensionless coefficients and with the representative particle size .
- (c)
- Test at least 10 different pressure gradients for each porous material tested in order to obtain a good fit of the and parameters from quadratic Equation (1).
- d)
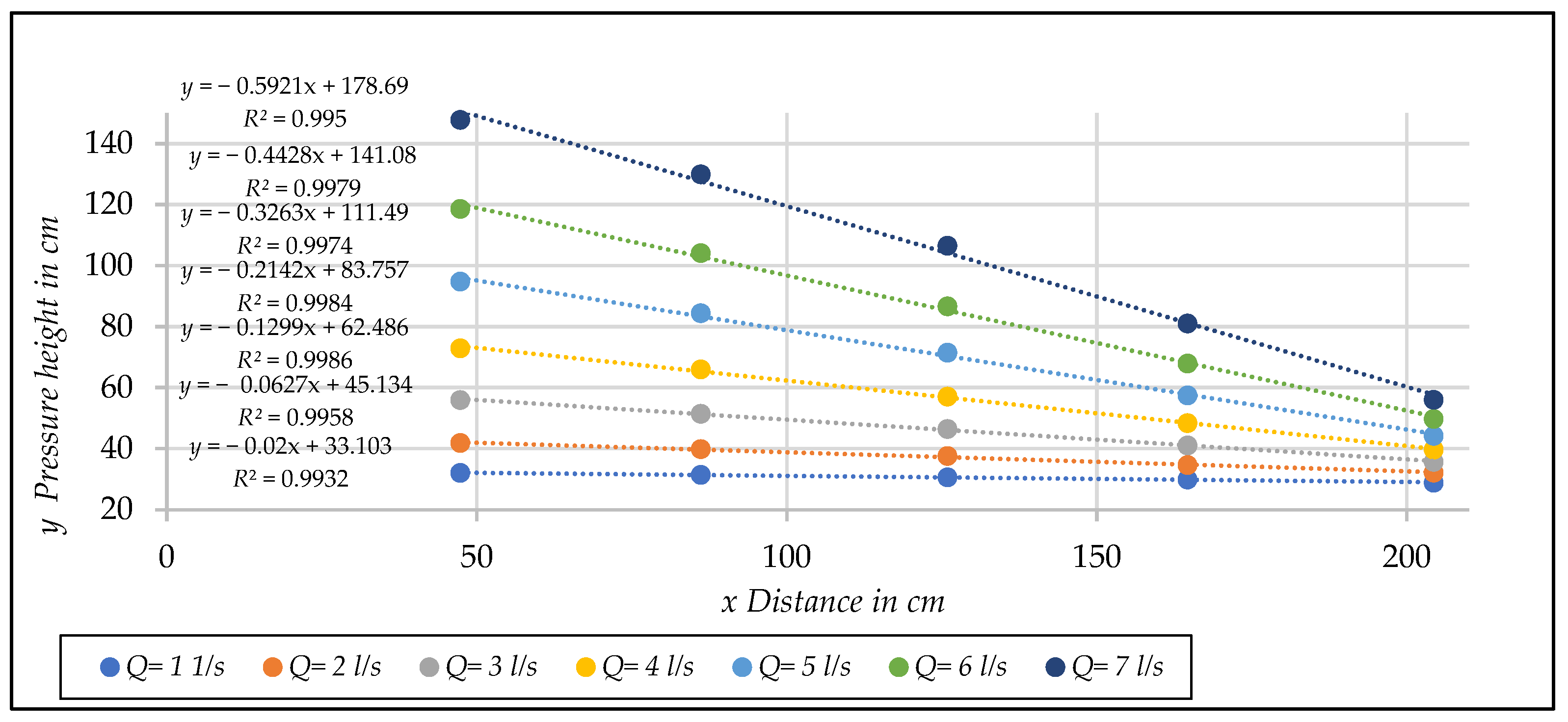
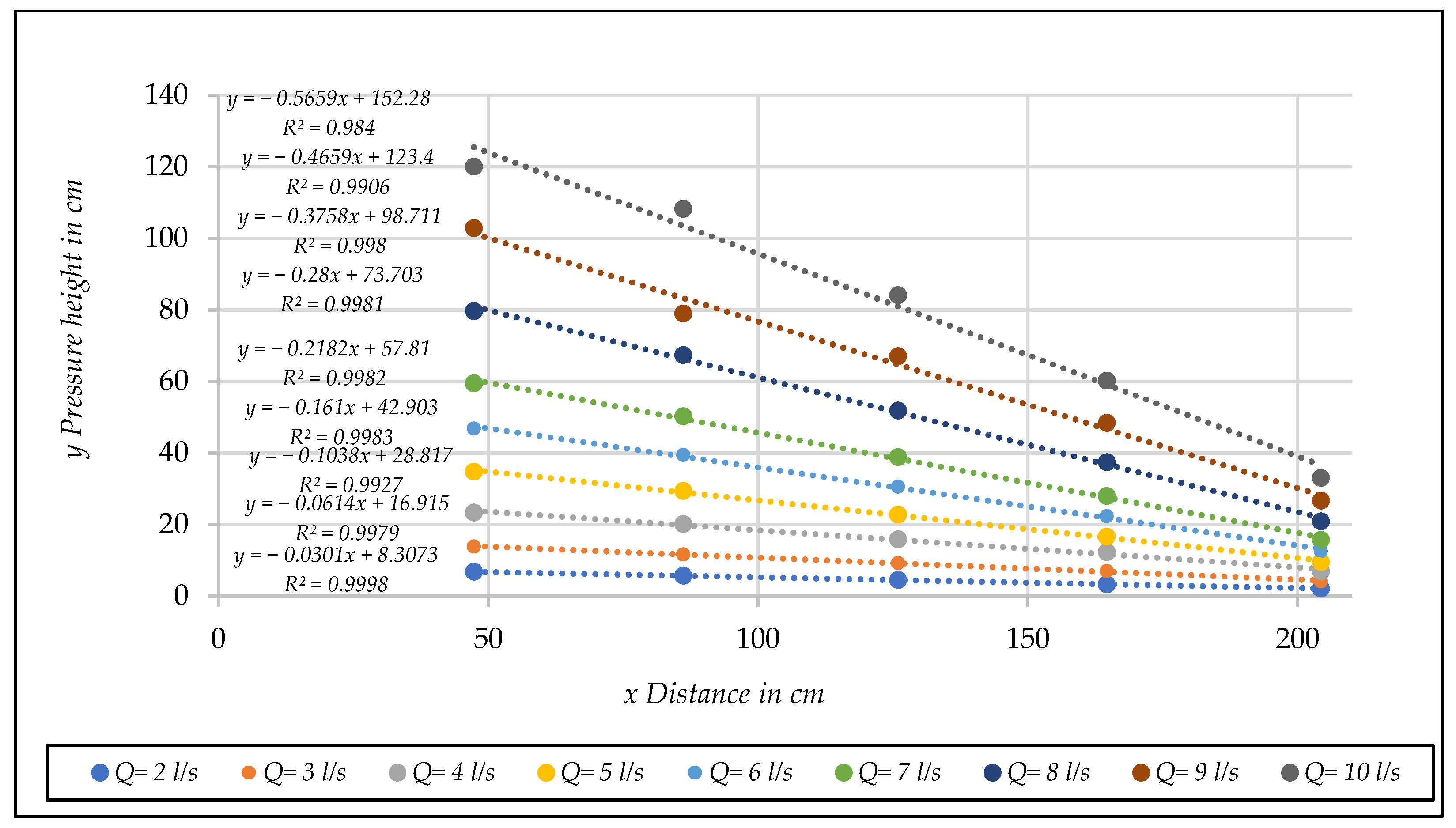
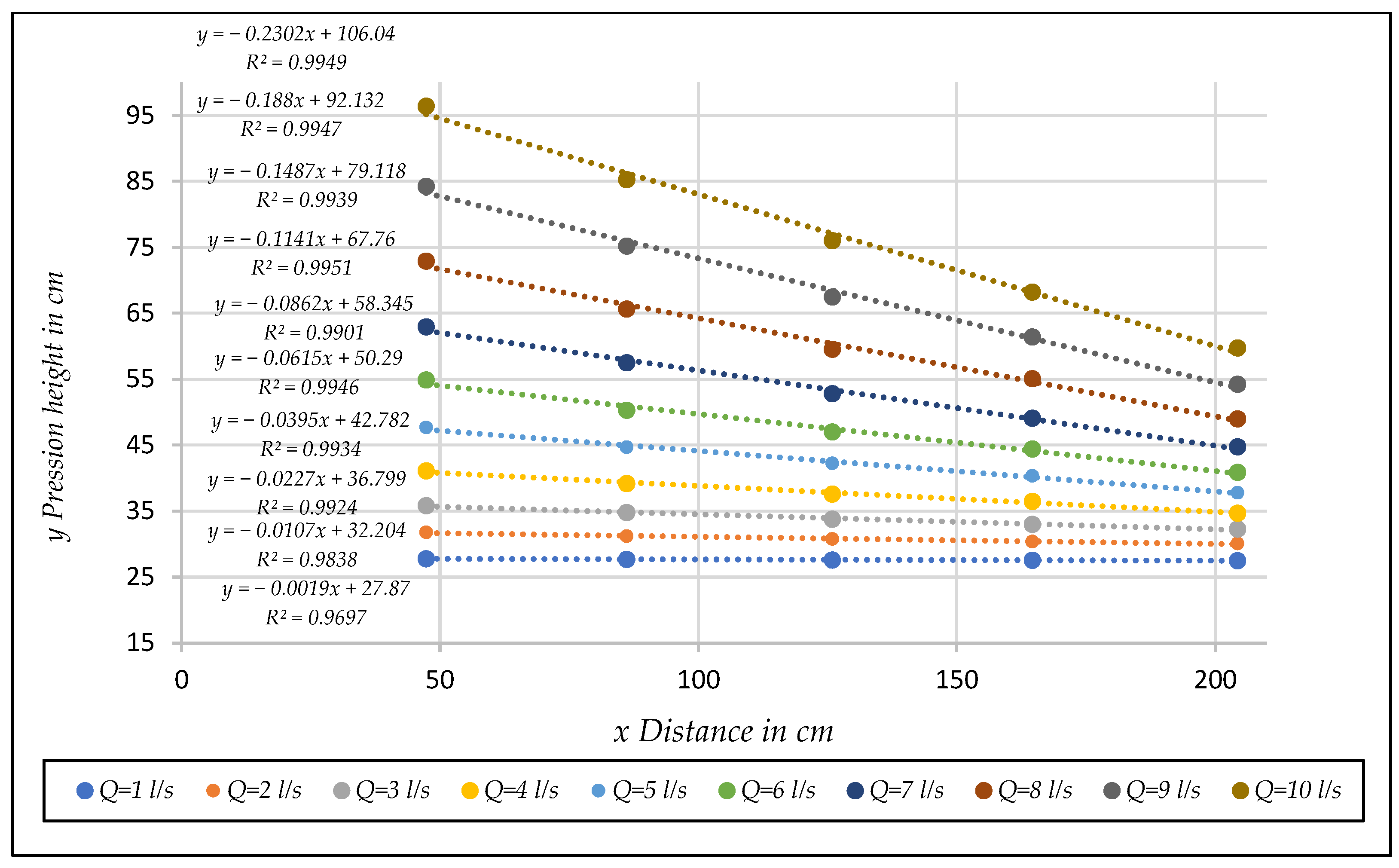
- Represent in a [] diagram the results obtained to verify that the experimental data corresponding to each porous material tested fall on the theoretical curve defined by Equation (26) for the whole range of non-Darcy flows tested.
- (e)
- Apply Equations (29), (32), and (33) to obtain the unified dimensionless coefficients and for each of the four porous media.
- (f)
- Represent in the [] and [] diagrams the obtained values of the and unified dimensionless coefficients for the four granular materials tested with the finality of observing their evolution with the representative size of particles .
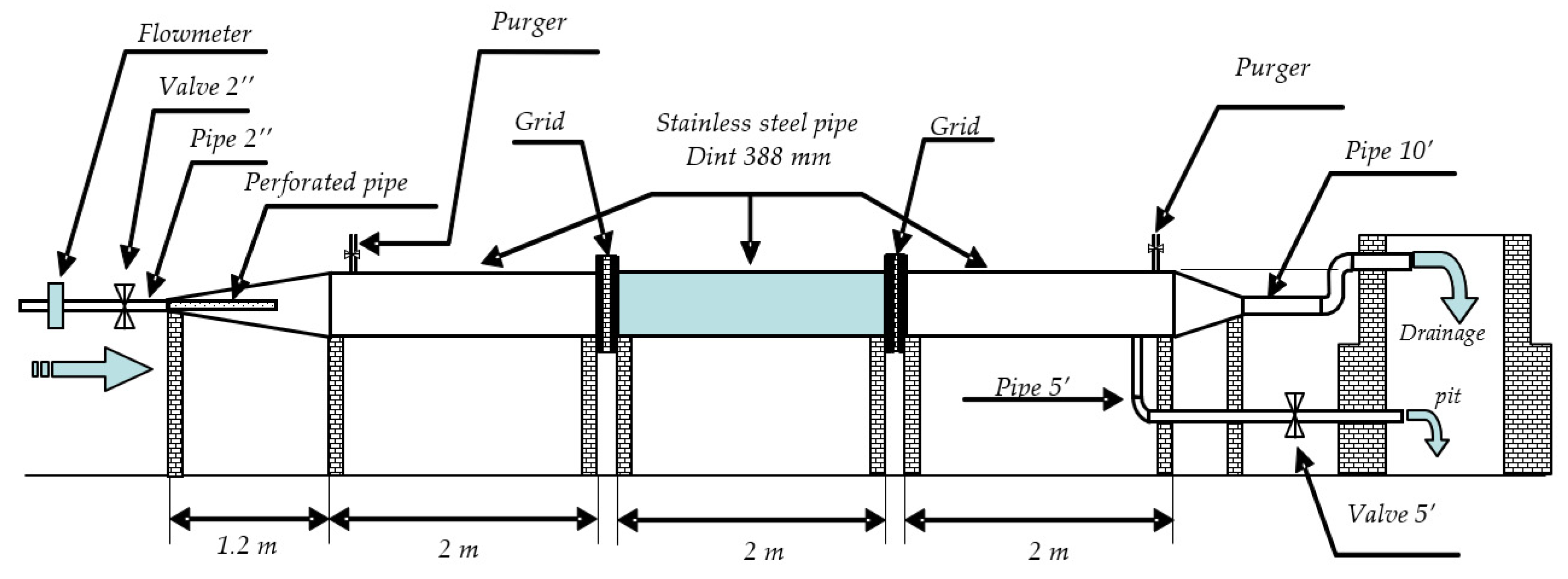
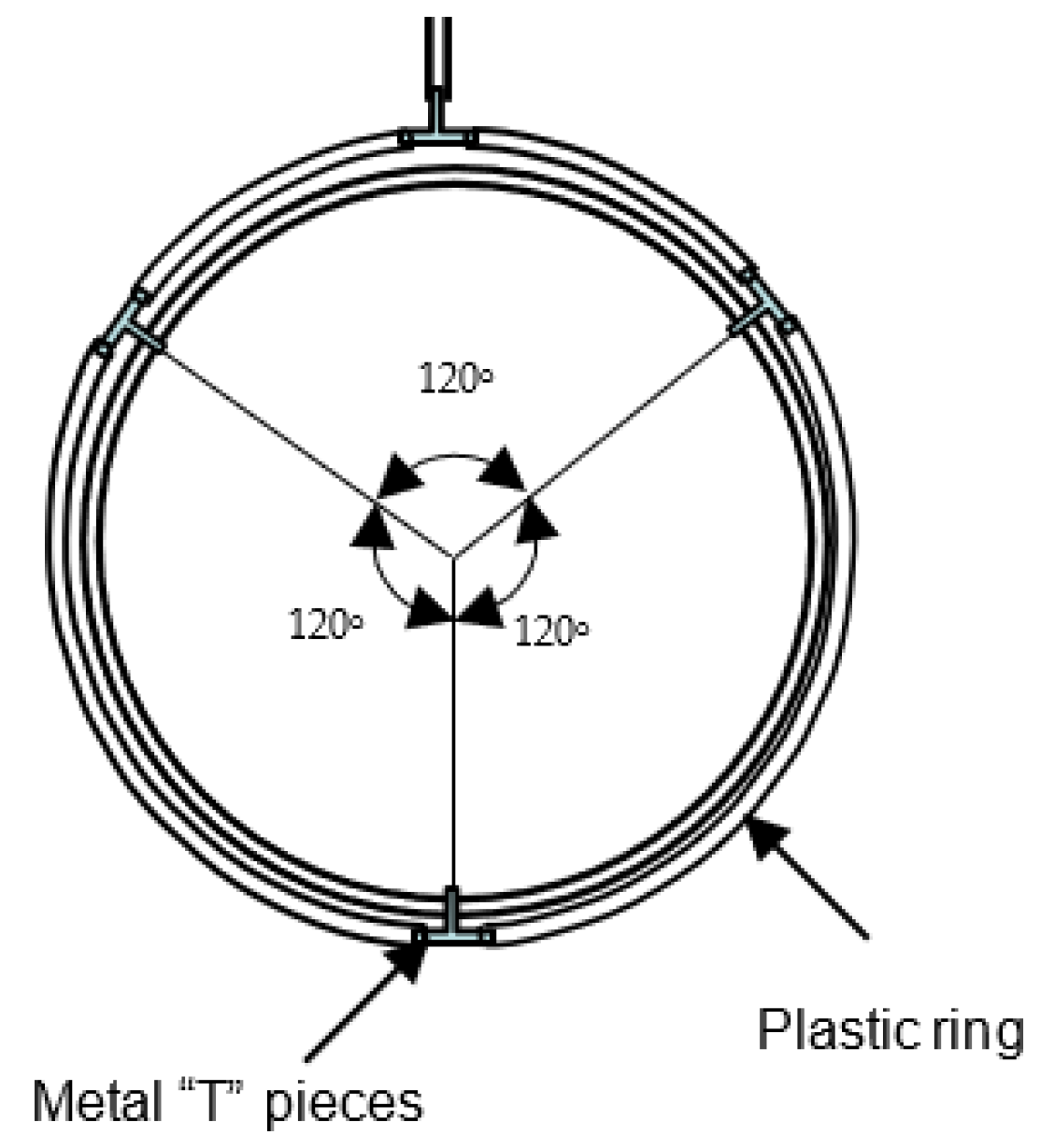
4.1. Description of Installation
4.2. Test Procedure
4.3. Materials
- Representative particle size D
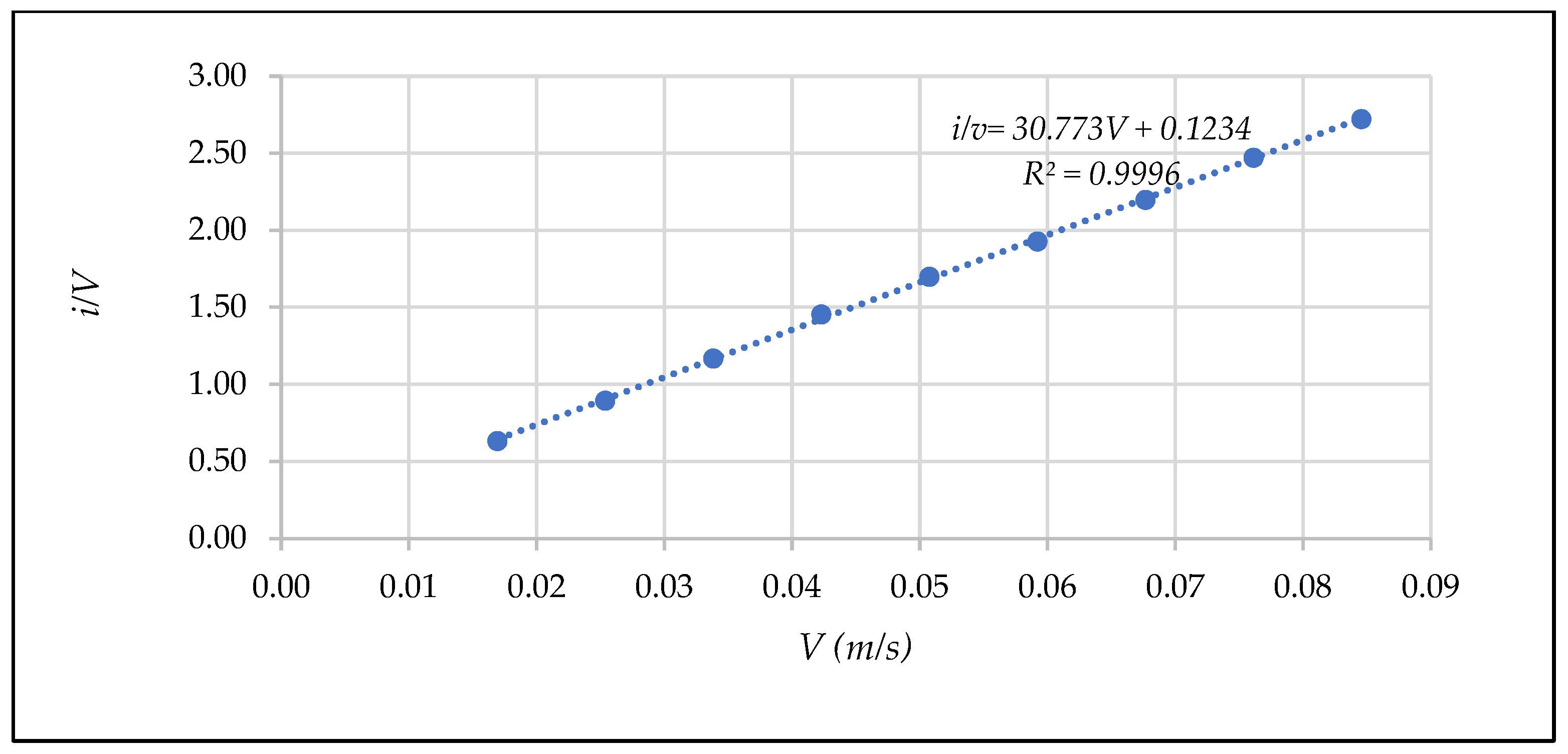
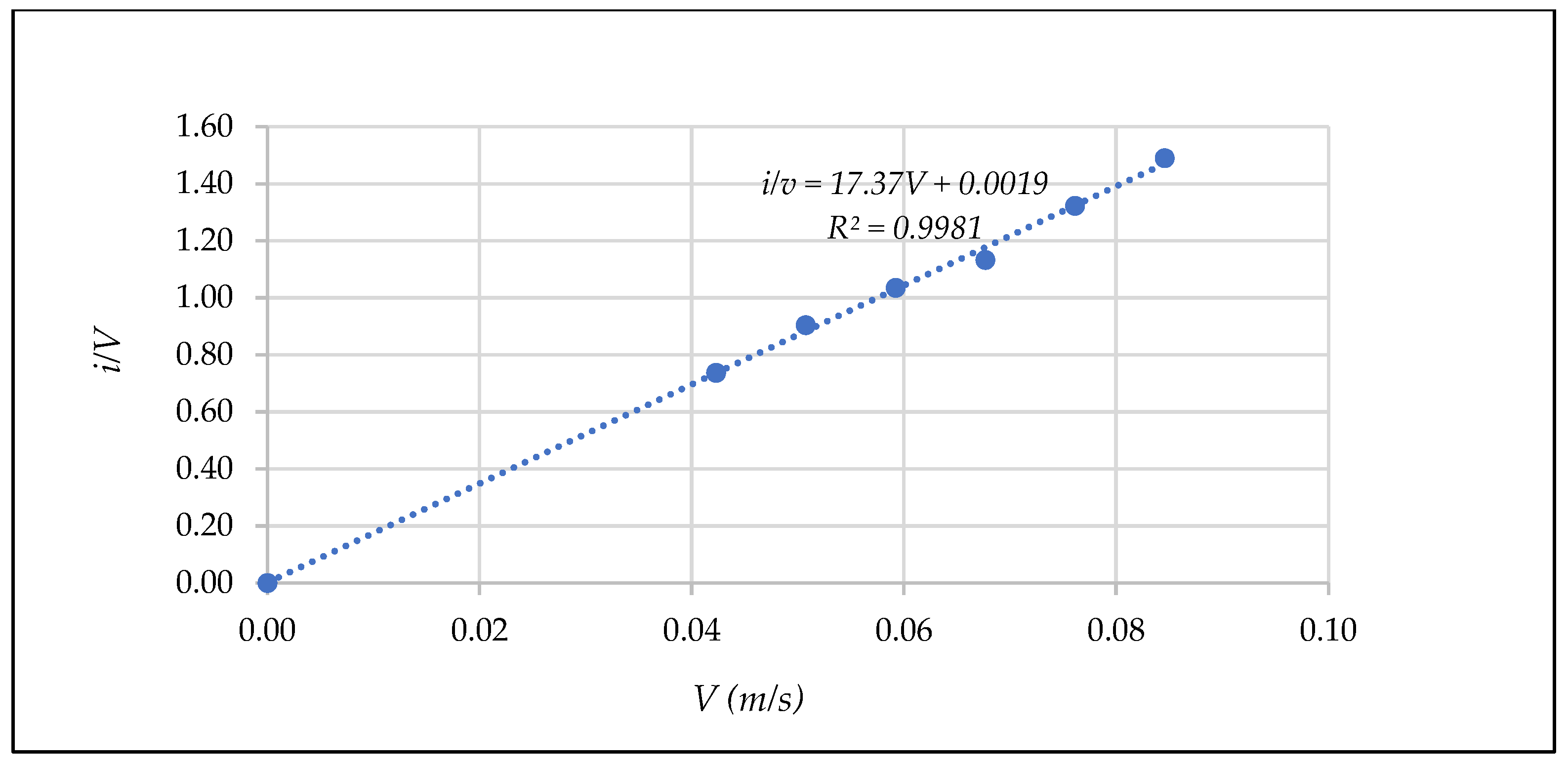
4.4. Tests Results and Discussion
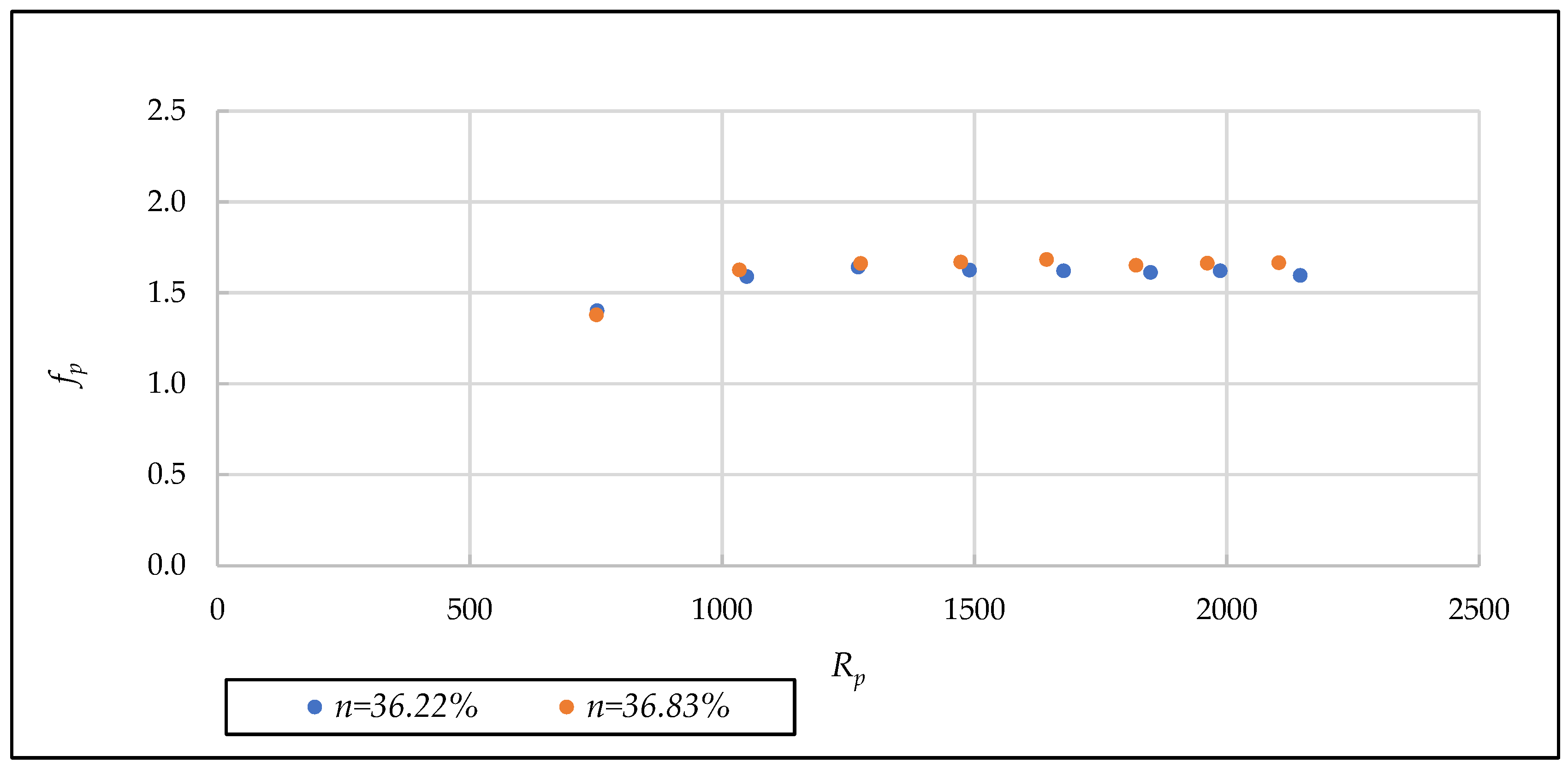
- Representation of the results in a [Rp, fp] diagram
- Obtaining coefficients α * and β *
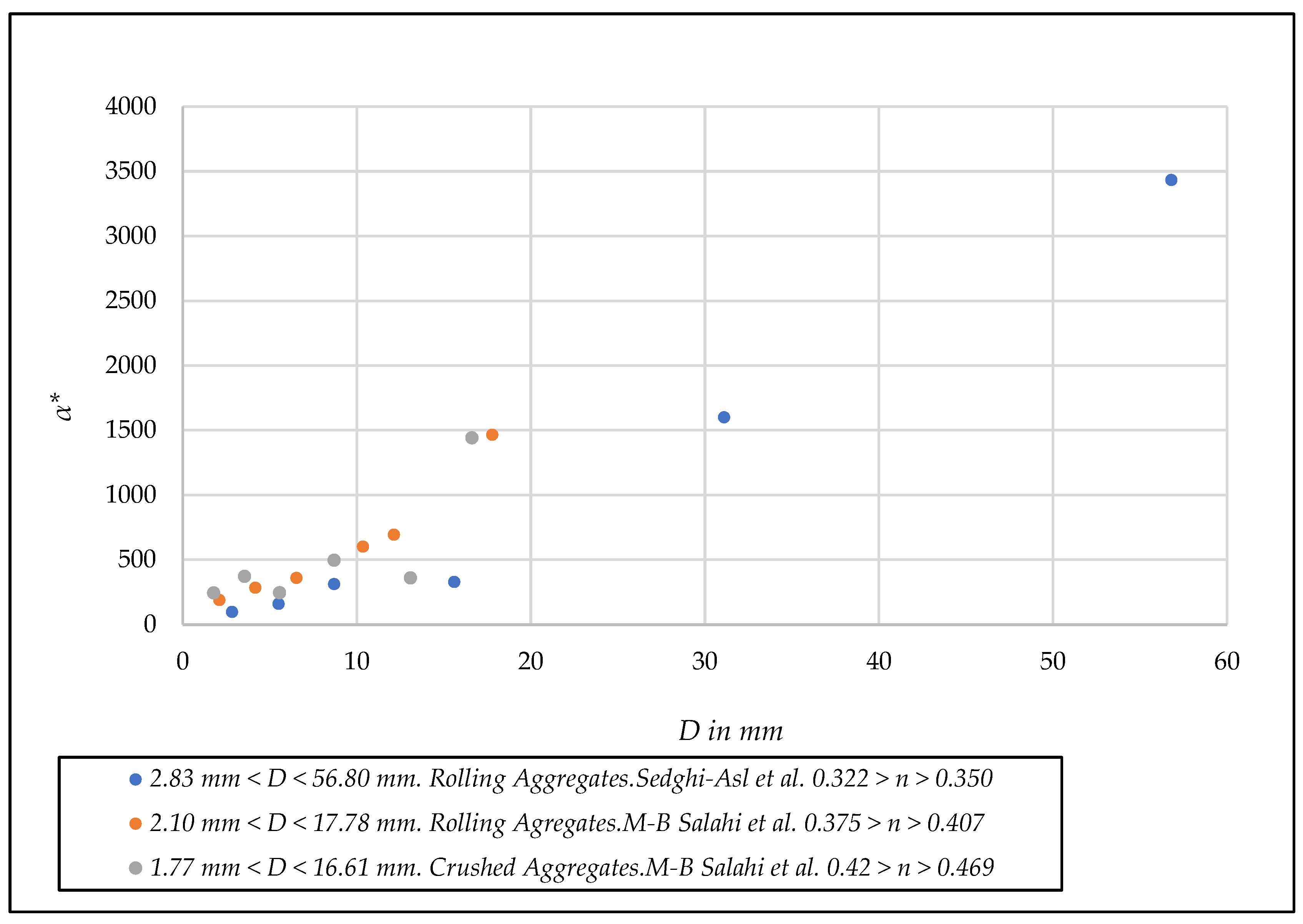
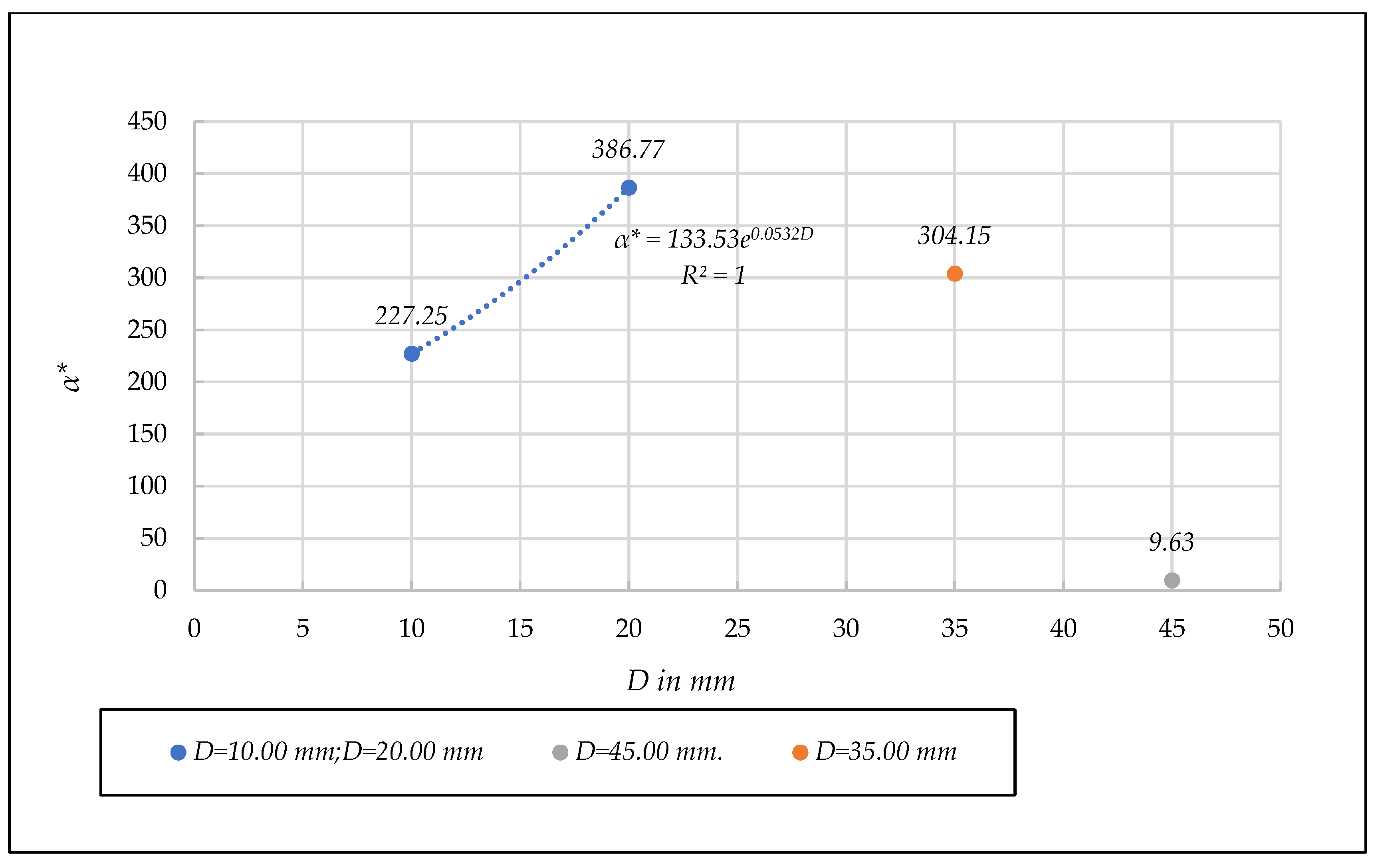
- Unified linear dimensionless coefficient α*. [D,α*] diagram
- (a)
- There is an increase in the unified dimensionless coefficient when going from the porous media = 10.00 mm to = 20.00 mm.
- (b)
- For the porous media = 45.00 mm, the reduced value of = 9.58 indicates that we are in the fully developed turbulent regime.
- (c)
- The value of the coefficient = 304.05 should be a matter for discussion. A possible explanation lies in the fact that in 6 of the 9 points the quadratic component of Equation (1) represents more than 90% of the total energy loss, so these 6 points are close to the fully developed turbulent flow, and consequently, the evolution of the dimensionless coefficient is decreasing as we approach the fully developed turbulent flow.
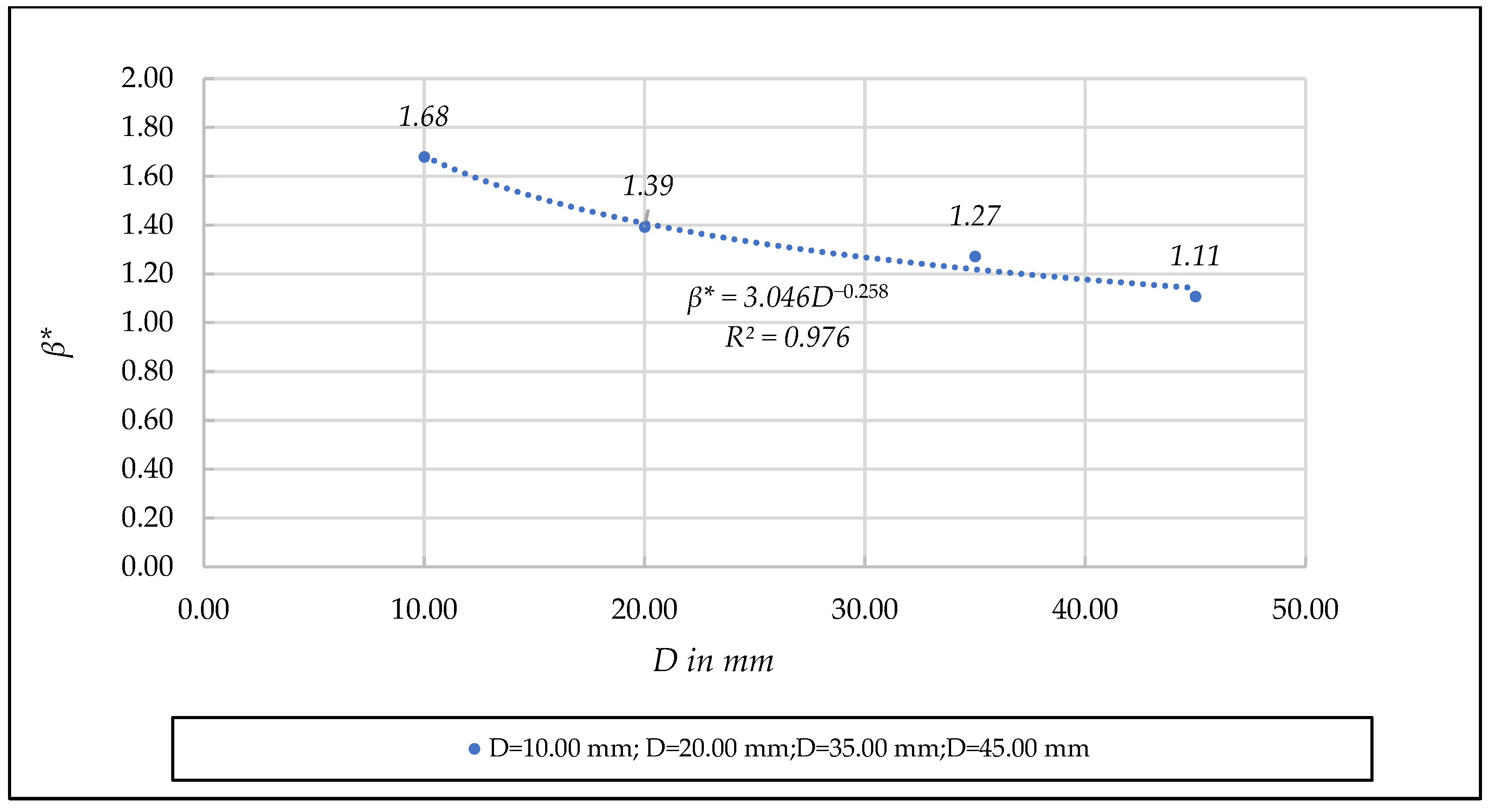
- Unified quadratic dimensionless coefficient β*. [D, β*] diagram
5. Conclusions
- (a)
- Verification of the existence of smooth curves in the [ diagram for all the sizes tested, adjusting to the general unified Equation (26).
- (b)
- Application of the linearized unified general Equation (29) to obtain the dimensionless linear and quadratic coefficients.
- (c)
- Verification of the asymptote for the fully developed turbulent flow reached with the largest size, D = 45.00 mm
- (d)
- No clear conclusions have been drawn for the linear unified dimensionless coefficient .
- (e)
- For the quadratic unified dimensionless coefficient , a good fit is observed (R2 = 0.9764) with values = 3.0653 and = 0.258.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Coefficient of the exponential equation that depends on the characteristics of the porous media and of the fluid | |
| USEC linear parameter depending on the geometry of the porous material | |
| Generalized dimensionless coefficient of the linear expression r | |
| Generalized dimensionless coefficient of the quadratic expression s | |
| Exponent of the exponential equation function of the flow conditions | |
| USEC quadratic parameter depending on the geometry of the porous material. | |
| Particle shape coefficient as set of R. D. Gupta | |
| Representative size of the particles in uniform materials | |
| Average consecutive sieve aperture | |
| Equivalent diameter or diameter of a sphere with the same volume as the particle | |
| Hydraulic mean diameter | |
| Pipe diameter | |
| Permeameter diameter of an installation | |
| Dimensionless coefficient that considers shape, angularity, and roughness of particles | |
| Relative specific weight of solid particles | |
| Generalized friction factor by Darcy–Weisbach | |
| Porosity function of hydraulic mean diameter | |
| Porosity function of the linear term of the USEC | |
| Porosity function of the quadratic term of the USEC | |
| Pore friction factor based on | |
| Pipe turbulent friction factor | |
| Gravitational acceleration | |
| Hydraulic gradient | |
| Intrinsic permeability of the porous media | |
| Generalized characteristic length of porous media | |
| Length of the permeameter | |
| Angularity as a set of aggregates defined by R. D. Gupta | |
| Number of tests performed | |
| Porosity | |
| R. D. Gupta exponent for the formula that defines the angularity η | |
| USEC linear exponent depending on the geometry of the granular porous media | |
| USEC quadratic exponent depending on the geometry of the granular porous media | |
| Mean permeameter flow rate (l/s) | |
| Linear coefficient of the Forchheimer equation of function of the characteristic of the porous media and fluid | |
| Correlation coefficient | |
| Generalized Reynolds number | |
| Pipe Reynolds number | |
| Hydraulic mean radius | |
| Pore Reynolds number based on | |
| Quadratic coefficient of the Forchheimer equation of function of the characteristic of the porous media | |
| Average specific surface area of solid particles | |
| Independent term of the USEC linearized equation | |
| Linear term of the USEC linearized equation | |
| Kinematic viscosity | |
| Average seepage velocity | |
| Fixed tank volume used for porosity calculation. | |
| Volume of equivalent sphere of one particle | |
| Total void volume of the reservoir for the porosity calculation | |
| Pore velocity | |
| Horizontal distance in cm to obtain pressure loss | |
| Measured pressure in cm to obtain pressure loss | |
| * | USEC unified linear dimensionless coefficient |
| * | USEC unified quadratic dimensionless coefficient |
| Particle surface roughness | |
| Pipe absolute roughness | |
| Specific weight of limestone rock | |
| p | Linearized USEC pore friction factor |
Appendix A
| Data By | Reference | Medium Type | Particle Size D(m) | Porosity n | ν (m2:s−1) | r (s2.m−2) | s (s2.m−2) | Ko (m2) | α | β | F | α* | β* | Rp | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lindquist (1933) | S.Ergun & A.A.Orning [13] | Glass beads | 0.000227 | 0.343 | * | * | 0.00 | * | 1.90 | 3.00 | 1.00 | 136.80 | 2.25 | * | * |
| Ward (1964) | Ward [30] | Glass beads | 0.000273 | 0.370 | * | * | * | 5.77 × 10−11 | * | * | 1.00 | 164.84 | * | * | * |
| Ward (1964) | Ward [30] | Glass beads | 0.000322 | 0.341 | * | * | * | 6.37 × 10−11 | * | * | 1.00 | 148.62 | * | * | * |
| Ward (1964) | Ward [30] | Glass beads | 0.000322 | 0.355 | * | * | * | 8.36 × 10−11 | * | * | 1.00 | 133.37 | * | * | * |
| Ward (1964) | Ward [30] | Glass beads | 0.000322 | 0.370 | * | * | * | 9.01 × 10−11 | * | * | 1.00 | 146.86 | * | * | * |
| Ward (1964) | Ward [30] | Glass beads | 0.000383 | 0.370 | * | * | * | 1.15 × 10−10 | * | * | 1.00 | 162.79 | * | * | * |
| Ward (1964) | Ward [30] | Glass beads | 0.000458 | 0.370 | * | * | * | 1.87 × 10−10 | * | * | 1.00 | 143.16 | * | * | * |
| Lindquist (1933) | S. Ergun & A. A. Orning [13] | Iron shot | 0.000472 | 0.375 | * | * | * | * | 2.00 | 2.50 | 1.00 | 144.00 | 1.88 | * | * |
| Lindquist (1933) | S. Ergun & A. A. Orning [13] | Iron shot | 0.000472 | 0.375 | * | * | * | * | 2.00 | 2.60 | 1.00 | 144.00 | 1.95 | * | * |
| Lindquist (1933) | S. Ergun & A. A. Orning [13] | Iron shot | 0.000472 | 0.375 | * | * | * | * | 1.80 | 2.50 | 1.00 | 129.60 | 1.88 | * | * |
| Lindquist (1933) | S. Ergun & A. A. Orning [13] | Lead shot | 0.000497 | 0.350 | * | * | * | * | 1.90 | 2.70 | 1.00 | 136.80 | 2.03 | * | * |
| Lindquist (1933) | S. Ergun & A. A. Orning [13] | Lead shot | 0.000497 | 0.350 | * | * | * | * | 1.80 | 3.10 | 1.00 | 129.60 | 2.33 | * | * |
| Ward (1964) | Ward [30] | Glass beads | 0.000545 | 0.370 | * | * | * | 2.62 × 10−10 | * | * | 1.00 | 144.68 | * | * | * |
| Lindquist (1933) | S. Ergun & A. A. Orning [13] | Lead shot | 0.000562 | 0.350 | * | * | * | * | 1.80 | 2.70 | 1.00 | 129.60 | 2.03 | * | * |
| Lindquist (1933) | S. Ergun & A. A. Orning [13] | Lead shot | 0.000562 | 0.352 | * | * | * | * | 1.80 | 3.10 | 1.00 | 129.60 | 2.33 | * | * |
| Lindquist (1933) | S. Ergun & A. A. Orning [13] | Glass beads | 0.000570 | 0.330 | * | * | * | * | 1.80 | 3.10 | 1.00 | 129.60 | 2.33 | * | * |
| Lindquist (1933) | S. Ergun & A. A. Orning [13] | Glass beads | 0.000570 | 0.330 | * | * | * | * | 1.90 | 2.80 | 1.00 | 136.80 | 2.10 | * | * |
| Ward (1964) | Ward [30] | Glass beads | 0.000650 | 0.370 | * | * | * | 3.47 × 10−10 | * | * | 1.00 | 155.39 | * | * | * |
| Lindquist (1933) | S. Ergun & A. A. Orning [13] | Iron shot | 0.000769 | 0.371 | * | * | * | * | 2.00 | 2.70 | 1.00 | 144.00 | 2.03 | ||
| Lindquist (1933) | S. Ergun & A. A. Orning [13] | Lead shot | 0.000798 | 0.364 | * | * | * | * | 1.90 | 3.30 | 1.00 | 136.80 | 2.48 | * | * |
| Lindquist (1933) | S. Ergun & A. A. Orning [13] | Lead shot | 0.000798 | 0.364 | * | * | * | * | 1.90 | 3.30 | 1.00 | 136.80 | 2.48 | * | * |
| Lindquist (1933) | S. Ergun & A.A. Orning [13] | Lead shot | 0.001004 | 0.366 | * | * | * | * | 1.80 | 2.90 | 1.00 | 129.60 | 2.18 | * | * |
| Burke and Plummer (1928) | S. Ergun & A. A. Orning [13] | Lead shot | 0.001478 | 0.375 | * | * | * | * | 2.00 | 2.60 | 1.00 | 144.00 | 1.95 | * | * |
| Sunada (1965) | Ahmed & Sunada [15] | Glass spheres | 0.003000 | 0.360 | 9.17 × 10−7 | 14.50 | 648.00 | 6.45 × 10−9 | * | * | 1.00 | 158.94 | 1.39 | * | * |
| Burke and Plummer (1928) | S. Ergun & A. A. Orning [13] | Lead shot | 0.003077 | 0.383 | * | * | * | * | 2.30 | 2.50 | 1.00 | 165.60 | 1.88 | * | * |
| Burke and Plummer (1928) | S. Ergun & A. A. Orning [13] | Lead shot | 0.003077 | 0.390 | * | * | * | * | 2.20 | 2.50 | 1.00 | 158.40 | 1.88 | * | * |
| Blake (1922) | Ahmed & Sunada [15] | Glass beads | 0.003200 | 0.360 | 9.79 × 10−7 | 14.90 | 623.00 | 6.70 × 10−9 | * | * | 1.00 | 174.09 | 1.43 | * | * |
| Crawford C.W et al. (1986) | Crawford C.W et al. [9] | Glass sheres | 0.005030 | 0.356 | * | * | * | * | * | * | 1.00 | 166.10 | 1.50 | * | * |
| Burke & Plummer (1928) | S. Ergun & A. A. Orning [13] | Lead shot | 0.006270 | 0.421 | * | * | * | * | 2.80 | 2.00 | 1.00 | 201.60 | 1.50 | ||
| Burke & Plummer (1928) | S. Ergun & A. A. Orning [13] | Lead shot | 0.006270 | 0.393 | * | * | * | * | 2.80 | 2.10 | 1.00 | 201.60 | 1.58 | ||
| Kirkham (1966) | Ahmed & Sunada [15] | Marble | 0.016000 | 0.360 | 1.04 × 10−6 | 0.90 | 117.00 | 1.19 × 10−7 | * | * | 1.00 | 245.04 | 1.34 | ||
| Dudgeon (1966) | McDonald I.F, et al. [44] | Marbles | 0.01597 | 0.369 | 1.28 × 10−6 | 1.1000 | 103.0000 | 1.19 × 10−7 | * | * | 1.00 | 232.01 | 1.26 | 3.21 | 3590.05 |
| Dudgeon (1966) | McDonald I.F, et al. [44] | Marbles | 0.01597 | 0.415 | 1.21 × 10−6 | 0.5000 | 63.0000 | 2.46 × 10−7 | * | * | 1.00 | 232.01 | 1.26 | 5.33 | 2342.52 |
| Dudgeon (1966) | McDonald I.F, et al. [44] | Marbles | 0.01597 | 0.372 | 1.15 × 10−6 | 0.7600 | 95.0000 | 1.55 × 10−7 | * | * | 1.00 | 232.01 | 1.26 | 29.16 | 2018.50 |
| Dudgeon (1966) | McDonald I.F, et al. [44] | Marbles | 0.02487 | 0.369 | 1.27 × 10−6 | 0.5800 | 66.0000 | 2.24 × 10−7 | * | * | 1.00 | 348.91 | 1.28 | 6.29 | 6669.85 |
| Dudgeon (1966) | McDonald I.F, et al. [44] | Marbles | 0.02896 | 0.385 | 1.11 × 10−6 | 0.3600 | 49.0000 | 3.16 × 10−7 | * | * | 1.00 | 400.87 | 1.29 | 33.47 | 9699.04 |
| Data By | Reference | Medium Type | Particle Size D (m) | Porosity n | ν (m2.s−1) | r (s2.m−1) | s (s2.m−2) | Ko (m2) | α* | β* | Rp | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sedghi-Asl M et al. (2013) | Sedghi-Asl M et al. [32] | Rounded alluvial materials | 0.00283 | 0.3200 | 9.12 × 10−7 | 16.242 | 887.200 | 5.72 × 10−9 | 99.16 | 1.19 | 4.46 | 213.90 |
| Sedghi-Asl M et al. (2013) | Sedghi-Asl M et al. [32] | Rounded alluvial materials | 0.00550 | 0.3300 | 8.80 × 10−7 | 5.906 | 508.830 | 1.52 × 10−8 | 159.51 | 1.47 | 28.04 | 651.29 |
| Sedghi-Asl M et al. (2013) | Sedghi-Asl M et al. [32] | Rounded alluvial materials | 0.00870 | 0.3500 | 8.72 × 10−7 | 3.622 | 274.880 | 2.46 × 10−8 | 312.78 | 1.55 | 55.94 | 1435.90 |
| Sedghi-Asl M et al. (2013) | Sedghi-Asl M et al. [32] | Rounded alluvial materials | 0.01560 | 0.3200 | 8.71 × 10−7 | 1.692 | 170.590 | 5.25 × 10−8 | 328.78 | 1.26 | 134.58 | 3493.76 |
| Sedghi-Asl M et al. (2013) | Sedghi-Asl M et al. [32] | Rounded alluvial materials | 0.03110 | 0.3600 | 8.78 × 10−7 | 1.301 | 47.046 | 6.88 × 10−8 | 1601.53 | 1.05 | 435.61 | 11,837.12 |
| Sedghi-Asl M et al. (2013) | Sedghi-Asl M et al. [32] | Rounded alluvial materials | 0.05680 | 0.4000 | 8.77 × 10−7 | 0.535 | 22.367 | 1.67*10−7 | 3433.40 | 1.33 | 2424.24 | 31,060.61 |
| M-B Salahi et al. (2015) | M-B Salahi et al. [23] | Rounded materials | 0.00210 | 0.3750 | 1.32 × 10−6 | 42.782 | 3548.800 | 3.15 × 10−9 | 189.29 | 6.17 | 12.61 | 34.91 |
| M-B Salahi et al. (2015) | M-B Salahi et al. [23] | Rounded materials | 0.00417 | 0.3790 | 1.33 × 10−6 | 15.678 | 854.850 | 8.62 × 10−9 | 284.72 | 3.07 | 73.20 | 162.01 |
| M-B Salahi et al. (2015) | M-B Salahi et al. [23] | Rounded materials | 0.00653 | 0.3830 | 1.32 × 10−6 | 7.712 | 501.490 | 1.74 × 10−8 | 360.69 | 2.93 | 152.25 | 376.21 |
| M-B Salahi et al. (2015) | M-B Salahi et al. [23] | Rounded materials | 0.01035 | 0.3864 | 1.32 × 10−6 | 4.924 | 440.700 | 2.73 × 10−8 | 602.16 | 4.21 | 286.44 | 703.25 |
| M-B Salahi et al. (2015) | M-B Salahi et al. [23] | Rounded materials | 0.01213 | 0.3978 | 1.32 × 10−6 | 3.658 | 242.700 | 3.68 × 10−8 | 694.30 | 3.02 | 415.65 | 1081.89 |
| M-B Salahi et al. (2015) | M-B Salahi et al. [23] | Rounded materials | 0.01778 | 0.4071 | 1.28 × 10−6 | 3.161 | 158.580 | 4.14 × 10−8 | 1465.41 | 3.15 | 729.85 | 1923.77 |
| Dudgeon (1966) | McDonald I.F, et al. [44] | River Gravel | 0.00229 | 0.418 | 1.30 × 10−6 | 78.9100 | 2232.0000 | 1.68 × 10−9 | 672.79 | 6.29 | 0.07 | 111.74 |
| Dudgeon (1966) | McDonald I.F, et al. [44] | River Gravel | 0.00579 | 0.392 | 1.32 × 10−6 | 19.0400 | 2174.0000 | 7.06 × 10−9 | 773.57 | 12.23 | 0.23 | 278.75 |
| Dudgeon (1966) | McDonald I.F, et al. [44] | Rivel Gravel | 0.01585 | 0.367 | 1.30 × 10−6 | 1.8900 | 262.0000 | 7.02 × 10−8 | 441.68 | 3.18 | 4.27 | 2239.85 |
| Dudgeon (1966) | McDonald I.F, et al. [44] | River Gravel | 0.02595 | 0.372 | 1.30 × 10−6 | 0.8200 | 145.0000 | 1.62 × 10−7 | 543.49 | 3.03 | 8.21 | 5016.46 |
| Dudgeon (1966) | McDonald I.F, et al. [44] | River Gravel | 0.05486 | 0.369 | 1.27 × 10−6 | 0.2400 | 51.0000 | 5.41 × 10−7 | 702.40 | 2.19 | 113.55 | 12,868.54 |
| Dudgeon (1966) | McDonald I.F, et al. [44] | River Gravel | 0.10973 | 0.406 | 1.27 × 10−6 | 0.0600 | 15.0000 | 2.16 × 10−6 | 1055.96 | 1.82 | 156.82 | 36,188.89 |
| Arbhabhirama & Dinoy (1973) | Arbhabhirama & Dinoy [31] | Sand | 0.001600 | 0.399 | 1.00 × 10−6 | 85.23 | 1750.86 | 1.196 × 10−6 | 376.43 | 2.90 | * | * |
| Arbhabhirama & Dinoy (1973) | Arbhabhirama & Dinoy [31] | Sand | 0.001600 | 0.391 | 1.00 × 10−6 | 95.18 | 1819.07 | 1.071 × 10−6 | 385.25 | 2.80 | * | * |
| Arbhabhirama & Dinoy (1973) | Arbhabhirama & Dinoy [31] | Gravel Round | 0.012000 | 0.373 | 1.00 × 10−6 | 6.04 | 207.10 | 1.6885 × 10−8 | 1125.78 | 2.02 | * | * |
| Arbhabhirama & Dinoy (1973) | Arbhabhirama &y Dinoy [31] | Gravel Round | 0.012000 | 0.357 | 1.00 × 10−6 | 5.63 | 187.82 | 1.8117× 10−8 | 874.70 | 1.56 | * | * |
| Ward (1964) | Ward [30] | Sand | 0.000625 | 0.407 | * | * | * | 2.98 × 10−10 | 251.31 | * | * | * |
| Ward (1964) | Ward [30] | Sand | 0.001260 | 0.400 | * | * | * | 1.36 × 10−9 | 207.53 | * | * | * |
| Ward (1964) | Ward [30] | Gravel | 0.001800 | 0.410 | * | * | * | 2.98 × 10−9 | 215.27 | * | * | * |
| Ward (1964) | Ward [30] | Gravel | 0.005040 | 0.389 | * | * | * | 1.69 × 10−8 | 237.00 | * | * | * |
| Ward (1964) | Ward [30] | Gravel | 0.009210 | 0.417 | * | * | * | 5.26 × 10−8 | 344.04 | * | * | * |
| Ward (1964) | Ward [30] | Gravel | 0.016100 | 0.422 | * | * | * | 1.80 × 10−7 | 323.94 | * | * | * |
| Lindquist (1933) | Ahmed & Sunada [15] | Sand | 0.001050 | 0.380 | 9.14 × 10−7 | 116.40 | 2920.00 | 8.00 × 10−10 | 196.72 | 2.66 | ||
| Lindquist (1933) | Ahmed & Sunada [15] | Sand | 0.004920 | 0.380 | 9.12 × 10−7 | 6.74 | 368.00 | 1.38 × 10−8 | 250.39 | 1.57 | ||
| Martins (1990) | Martins [11] | Rounded materials | 0.02200 | 0.3622 | 1.15 × 10−6 | * | * | * | * | 1.29 | 752.00 | 2146.00 |
| Martins (1990) | Martins [11] | Rounded materials | 0.02200 | 0.3683 | 1.15 × 10−6 | * | * | * | * | 1.29 | 751.00 | 2103.00 |
| Martins (1990) | Martins [11] | Rounded materials | 0.04400 | 0.3618 | 1.15 × 10−6 | * | * | * | * | 0.90 | 2631.00 | 6970.00 |
| Martins (1990) | Martins [11] | Rounded materials | 0.04400 | 0.3553 | 1.15 × 10−6 | * | * | * | * | 0.90 | 2583.00 | 7027.00 |
| Martins (1990) | Martins [11] | Rounded materials | 0.08900 | 0.3823 | 1.15 × 10−6 | * | * | * | * | 0.83 | 8881.00 | 23,359.00 |
| Martins (1990) | Martins [11] | Rounded materials | 0.08900 | 0.3884 | 1.15 × 10−6 | * | * | * | * | 0.83 | 10,765.00 | 25,430.00 |
| Farzad Ferdos et al. (2015) | Farzad Ferdos et al. [33] | Cobblestone | 0.13000 | 0.4680 | 1.00 × 10−6 | 3.71 × 10−13 | 10.079 | 2.74 × 10+5 | 0.00 | 2.48 | 9515.00 | 114,176.00 |
| Farzad Ferdos et al. (2015) | Farzad Ferdos et al. [33] | Cobblestone | 0.13000 | 0.4680 | 1.00 × 10−6 | 2.37 × 10−10 | 9.977 | 4.31 × 10+2 | 0.00 | 2.45 | 9515.00 | 114,176.00 |
| Farzad Ferdos et al. (2015) | Farzad Ferdos et al. [33] | Cobblestone | 0.13000 | 0.4450 | 1.00 × 10−6 | 2.00 × 10−10 | 11.697 | 5.09 × 10+2 | 0.00 | 2.37 | 3648.00 | 115,829.00 |
| Farzad Ferdos et al. (2015) | Farzad Ferdos et al. [33] | Cobblestone | 0.20000 | 0.5060 | 1.00 × 10−6 | 2.04 × 10−11 | 3.947 | 5.00 × 10+3 | 0.00 | 2.03 | 15,621.00 | 187,448.00 |
| Farzad Ferdos et al. (2015) | Farzad Ferdos et al. [33] | Cobblestone | 0.20000 | 0.5060 | 1.00 × 10−6 | 1.49 × 10−11 | 4.201 | 6.84 × 10+3 | 0.00 | 2.16 | 15,621.00 | 187,448.00 |
| Farzad Ferdos et al. (2015) | Farzad Ferdos et al. [33] | Cobblestone | 0.20000 | 0.4590 | 1.00 × 10−6 | 1.96 × 10−14 | 5.809 | 5.21 × 10−6 | 0.00 | 2.04 | 11,411.00 | 184,400.00 |
| Data By | Reference | Medium Type | Particle Size D (m) | Porosity n | ν (m2.s−1) | r (s.2m−1) | s (s2.m−2) | Ko (m2) | α* | β* | Rp | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M-B Salahi et al. (2015) | M-B Salahi et al. [23] | Crushed materials | 0.00177 | 0.4200 | 1.30 × 10−6 | 45.515 | 2978.800 | 2.91 × 10−9 | 236.98 | 6.61 | 7.66 | 25.29 |
| M-B Salahi et al. (2015) | M-B Salahi et al. [23] | Crushed materials | 0.00355 | 0.4210 | 1.30 × 10−6 | 15.665 | 979.710 | 8.46 × 10−9 | 331.59 | 4.40 | 42.22 | 109.77 |
| M-B Salahi et al. (2015) | M-B Salahi et al. [23] | Crushed materials | 0.00555 | 0.4225 | 1.30 × 10−6 | 4.550 | 514.300 | 2.91 × 10−8 | 239.14 | 3.66 | 130.06 | 278.60 |
| M-B Salahi et al. (2015) | M-B Salahi et al. [23] | Crushed materials | 0.00869 | 0.4284 | 1.30 × 10−6 | 3.508 | 361.700 | 3.78 × 10−8 | 481.05 | 4.24 | 178.06 | 471.97 |
| M-B Salahi et al. (2015) | M-B Salahi et al. [23] | Crushed materials | 0.01308 | 0.4392 | 1.30 × 10−6 | 1.066 | 174.420 | 1.24 × 10−7 | 370.88 | 3.38 | 460.45 | 1045.33 |
| M-B Salahi et al. (2015) | M-B Salahi et al. [23] | Crushed materials | 0.01661 | 0.4692 | 1.30 × 10−6 | 1.789 | 114.040 | 7.41 × 10−8 | 1365.18 | 3.62 | 617.94 | 1544.84 |
| Dudgeon (1966) | McDonald I.F. et al. [44] | Blue metal | 0.00320 | 0.477 | 1.31 × 10−6 | 16.61 | 959.00 | 8.04 × 10−9 | 505.38 | 6.25 | 0.97 | 221.45 |
| Dudgeon (1966) | McDonald I.F. et al. [44] | Blue metal | 0.00640 | 0.458 | 1.31 × 10−6 | 7.79 | 573.00 | 1.71 × 10−8 | 781.44 | 6.38 | 1.27 | 565.36 |
| Dudgeon (1966) | McDonald I.F. et al. [44] | Blue metal | 0.01402 | 0.428 | 1.29 × 10−6 | 1.43 | 220.00 | 9.20 × 10−8 | 512.21 | 4.15 | 3.09 | 1776.00 |
| Dudgeon (1966) | McDonald I.F. et al. [44] | Blue metal | 0.01402 | 0.515 | 1.14 × 10−6 | 0.51 | 97.00 | 2.28 × 10−7 | 500.92 | 3.76 | 6.87 | 1374.02 |
| Dudgeon (1966) | McDonald I.F. et al. [44] | Blue metal | 0.01585 | 0.455 | 1.16 × 10−6 | 1.15 | 162.00 | 1.03 × 10−7 | 774.83 | 4.35 | 1.83 | 2734.03 |
| Dudgeon (1966) | McDonald I.F. et al. [44] | Blue metal | 0.02499 | 0.438 | 1.31 × 10−6 | 0.61 | 117.00 | 2.19 × 10−7 | 758.94 | 4.29 | 22.99 | 4368.32 |
| Dudgeon (1966) | McDonald I.F. et al. [44] | Blue metal | 0.03719 | 0.483 | 1.29 × 10−6 | 0.33 | 121.00 | 3.98 × 10−7 | 1463.21 | 9.62 | 12.84 | 7100.78 |
| Arbhabhirama & Dinoy (1973) | Arbhabhirama & Dinoy [31] | Sand | 0.001600 | 0.399 | 1.00 × 10−6 | 85.23 | 1750.86 | 1.196 × 10−9 | 376.43 | 2.90 | * | * |
| Arbhabhirama & Dinoy (1973) | Arbhabhirama & Dinoy [31] | Sand | 0.001600 | 0.391 | 1.00 × 10−6 | 95.18 | 1819.07 | 1.071 × 10−9 | 385.25 | 2.80 | * | * |
| Arbhabhirama & Dinoy (1973) | Arbhabhirama & Dinoy [31] | Gravel Angular 1 | 0.006400 | 0.467 | 1.00 × 10−6 | 8.80 | 359.00 | 1.1581 × 10−8 | 1267.97 | 4.31 | * | * |
| Arbhabhirama & Dinoy (1973) | Arbhabhirama & Dinoy [31] | Gravel Angular 1 | 0.006400 | 0.470 | 1.00 × 10−6 | 11.98 | 390.07 | 8.51 × 10−9 | 1778.98 | 4.80 | * | * |
| Arbhabhirama & Dinoy (1973) | Arbhabhirama & Dinoy [31] | Gravel Angular 2 | 0.013000 | 0.461 | 1.00 × 10−6 | 2.96 | 176.91 | 3.4425 × 10−8 | 1655.53 | 4.10 | * | * |
| Arbhabhirama & Dinoy (1973) | Arbhabhirama & Dinoy [31] | Gravel Angular 2 | 0.013000 | 0.479 | 1.00 × 10−6 | 2.71 | 130.93 | 3.7585 × 10−8 | 1820.55 | 3.52 | * | * |
| Arbhabhirama & Dinoy (1973) | Arbhabhirama & Dinoy [31] | Gravel Angular 3 | 0.028300 | 0.465 | 1.00 × 10−6 | 1.16 | 55.93 | 8.8255 × 10−8 | 3187.75 | 2.92 | * | * |
| Martins (1990) | Martins [11] | Angular materials | 0.01100 | 0.462 | 1.15 × 10−6 | * | * | * | * | 2.74 | 236.00 | 683.00 |
| Martins (1990) | Martins [11] | Angular materials | 0.01100 | 0.460 | 1.15 × 10−6 | * | * | * | * | 2.74 | 243.00 | 692.00 |
| Martins (1990) | Martins [11] | Angular materials | 0.01600 | 0.428 | 1.15 × 10−6 | * | * | * | * | 2.19 | 382.00 | 1123.00 |
| Martins (1990) | Martins [11] | Angular materials | 0.01600 | 0.427 | 1.15 × 10−6 | * | * | * | * | 2.19 | 394.00 | 1101.00 |
| Martins (1990) | Martins [11] | Angular materials | 0.02200 | 0.431 | 1.15 × 10−6 | * | * | * | * | 1.72 | 647.00 | 2010.00 |
| Martins (1990) | Martins [11] | Angular materials | 0.02200 | 0.424 | 1.15 × 10−6 | * | * | * | * | 1.72 | 622.00 | 1945.00 |
| Martins (1990) | Martins [11] | Angular materials | 0.03200 | 0.429 | 1.15 × 10−6 | * | * | * | * | 2.10 | 1150.00 | 3146.00 |
| Martins (1990) | Martins [11] | Angular materials | 0.03200 | 0.436 | 1.15 × 10−6 | * | * | * | * | 2.10 | 1287.00 | 3405.00 |
| Martins (1990) | Martins [11] | Angular materials | 0.04400 | 0.397 | 1.15 × 10−6 | * | * | * | * | 1.37 | 1907.00 | 5176.00 |
| Martins (1990) | Martins [11] | Angular materials | 0.04400 | 0.395 | 1.15 × 10−6 | * | * | * | * | 1.37 | 1860.00 | 5188.00 |
| Martins (1990) | Martins [11] | Angular materials | 0.06350 | 0.414 | 1.15 × 10−6 | * | * | * | * | 1.53 | 3925.00 | 10,509.00 |
| Martins (1990) | Martins [11] | Angular materials | 0.06350 | 0.444 | 1.15 × 10−6 | * | * | * | * | 1.53 | 4623.00 | 12,210.00 |
| Martins (1990) | Martins [11] | Angular materials | 0.08900 | 0.474 | 1.15 × 10−6 | * | * | * | * | 2.04 | 8127.00 | 19,793.00 |
| Martins (1990) | Martins [11] | Angular materials | 0.08900 | 0.470 | 1.15 × 10−6 | * | * | * | * | 2.04 | 7695.00 | 19,820.00 |
| Martins (1990) | Martins [11] | Angular materials | 0.12700 | 0.481 | 1.15 × 10−6 | * | * | * | * | 1.38 | 16,581.00 | 43,687.00 |
| Martins (1990) | Martins [11] | Angular materials | 0.12700 | 0.475 | 1.15 × 10−6 | * | * | * | * | 1.38 | 15,658.00 | 41,238.00 |
| Farzad Ferdos et al. (2015) | Farzad Ferdos et al. [33] | Crushed rock | 0.13000 | 0.5060 | 1.00 × 10−6 | 8.96 × 10−15 | 10.869 | 1.14 × 10+7 | 0.00 | 3.64 | 8273.00 | 99,278.00 |
| Farzad Ferdos et al. (2015) | Farzad Ferdos et al. [33] | Crushed rock | 0.13000 | 0.5060 | 1.00 × 10−6 | 2.08 × 10−11 | 10.546 | 4.91 × 10+3 | 0.00 | 3.53 | 8273.00 | 99,278.00 |
| Farzad Ferdos et al. (2015) | Farzad Ferdos et al. [33] | Crushed rock | 0.13000 | 0.4970 | 1.00 × 10−6 | 4.20 × 10−10 | 9.860 | 2.43 × 10+2 | 0.00 | 3.07 | 3250.00 | 105,626.00 |
| Farzad Ferdos et al. (2015) | Farzad Ferdos et al. [33] | Crushed rock | 0.20000 | 0.4900 | 1.00 × 10−6 | 2.61 × 10−13 | 6.779 | 3.90 × 10+5 | 0.00 | 3.07 | 11,478.00 | 137,741.00 |
| Farzad Ferdos et al. (2015) | Farzad Ferdos et al. [33] | Crushed rock | 0.20000 | 0.4900 | 1.00 × 10−6 | 1.09 × 10−11 | 6.651 | 9.40 × 10+3 | 0.00 | 3.01 | 11,478.00 | 137,741.00 |
| Farzad Ferdos et al. (2015) | Farzad Ferdos et al. [33] | Crushed rock | 0.20000 | 0.4840 | 1.00 × 10−6 | 2.53 × 10−14 | 5.676 | 4.04 × 10+6 | 0.00 | 2.45 | 6807.00 | 147,484.00 |
References
- Forchheimer, P.H. Wasserbewegung durch Boden. Z. Vereines Dtsch. Ingenieure 1901, 50, 1781–1788. [Google Scholar]
- Izbash, S.V. O Filtracii v Krupnozernstom Materiale; Nauchno Issled. Inst. Gidrotechniki (NIIG): Saint Petersburg, Russia, 1931. [Google Scholar]
- López, J.C.; Toledo, M.Á.; Moran, R. A unified view of nonlinear resistance formulas for seepage flow in coarse granular media. Water 2021, 13, 1967. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluid in Porous Media; American Elsevier Publishing Company Inc.: New York, NY, USA, 1972. [Google Scholar]
- White, F.M. Fluid Mechanics, 5th ed.; McGraw-Hill, Inc.: Boston, MA, USA, 2003. [Google Scholar]
- Taylor, D.W. Fundamentals of Soil Mechanics; John Wiley & Sons Inc.: New York, NY, USA, 1948. [Google Scholar]
- Loudon, A.G. The computation of permeability from simple soil test. Geotechnique 1952, 3, 165–183. [Google Scholar] [CrossRef]
- Lindford, A.; Saunders, D.H. A Hydraulic Investigation of through and Overflow Rockfill Dams; British Hydromechanics Research Associations: Cranfield, UK, 1967. [Google Scholar]
- Crawford, C.W.; Plumb, O.A. The influence of surface roughness on resistance to flow through packed beds. J. Fluids Eng. 1986, 108, 343–347. [Google Scholar] [CrossRef]
- Martins, R.; Escarameria, M. Caracterizaçao dos Materiais Para o Estudo em Laboratorio do Escoamento de Percolaçao Turbulento; Springer: Lisbon, Portugal, 1989. [Google Scholar]
- Martins, R. Seepage Flow through Rockfill Dams. In Proceedings of the 17th International Congress on Large Dams, Vienna, Austria, 17–21 June 1991; Volume Q67R14. [Google Scholar]
- Sabin, G.C.; Hansen, D. The effects of particle shape and surface roughness on the hydraulic mean radius of a porous medium consisting of quarried rock. Geotech. Test. J. 1994, 17, 43–49. [Google Scholar]
- Ergun, S.; Orning, A.A. Fluid flow through randomly packed columns and fluidized beds. Ind. Eng. Chem. 1949, 41, 1179–1184. [Google Scholar] [CrossRef]
- Huang, H.; Ayoub, J. Applicability of the Forchheimer equation for non-Darcy flow in porous media. SPE J. 2007, 13, 112–122. [Google Scholar] [CrossRef]
- Ahmed, N.; Sunada, D.K. Nonlinear flow in porous media. J. Hydraul. Div. 1969, 95, 1847–1858. [Google Scholar] [CrossRef]
- Wright, D.E. Nonlinear flow through granular media. J. Hydraul. Div. 1968, 94, 851–872. [Google Scholar] [CrossRef]
- Panfilov, M.; Oltean, C.; Panfilova, I.; Buès, M. Singular nature of nonlineal macroscale effects in high-rate flow through porous media. Comtes Rendus Mec. 2003, 331, 41–48. [Google Scholar] [CrossRef]
- Fourar, M.; Radilla, G.; Lenormand, R.; Moyne, C. On the non-linear behavior of a laminar single-phase flow through two and three dimensional porous media. Adv. Water Resour. 2004, 27, 669–677. [Google Scholar] [CrossRef]
- Mccorquodale, J.A.; Hannoura, A.A.A.; Sam Nasser, M. Hydraulic conductivity of rockfill. Hydraul. Res. 1978, 16, 123–127. [Google Scholar] [CrossRef]
- Mulqueen, J. The flow of water through gravels. Ir. J. Agrucyltural Food Res. 2005, 44, 83–94. [Google Scholar]
- Terzaghi, K.; Peck, R.B. Soil Mechanics in Engineering Practice; John Wiley & Sons: Hoboken, NJ, USA, 1964. [Google Scholar]
- Engelund, F. On the laminar and turbulent flows of ground water through homogeneous sand. Hydraul. Lab. 1953, 4, 356–361. [Google Scholar]
- Salahi, M.-B.; Sedghi-Als, M.; Parvizi, M. Nonlinear flow through a packed-column experiment. J. Hydrol. Eng. 2015, 20, 04015003. [Google Scholar] [CrossRef]
- Fand, R.M.; Kim, B.Y.K.; Lam, A.C.C.; Phan, R.T. Resistance to the flow of fluids through simple and complex porous media whose matrices are composed of randomly packed spheres. J. Fluid Eng. 1987, 109, 268–273. [Google Scholar] [CrossRef]
- Barree, R.D.; Conway, M.W. Reply to Discussion of “Beyond Beta factors: A complete model for Darcy. Forchheimer and trans-Forchheimer flow in porous media”. J. Pet. Technol. 2005, 57, 73. [Google Scholar] [CrossRef]
- Gupta, R.D. Angularity of Aggregate Particles as a Measure of Their Shape and Hydraulic Resistance; Technical note 438; Water Engineering Group, Aligarh Muslim University: Aligarh, India, 1985; pp. 705–716. [Google Scholar]
- Shergold, F.A. The percentage voids in compacted gravel as a measure of its angularity. Mag. Concr. Res. 1953, 5, 3–10. [Google Scholar] [CrossRef]
- Dudgeon, R.D. An experimental study of the flow of water through coarse granular media. Houllie Blanche 1966, 7, 785–802. [Google Scholar] [CrossRef]
- Stephenson, D. Flow through rockfill. Dev. Geotech. Eng. 1979, 27, 19–37. [Google Scholar] [CrossRef]
- Ward, J.C. Turbulent flow in porous media. J. Hydraul. Div. 1964, 90. [Google Scholar] [CrossRef]
- Arbhabhirama, A.; Dinoy, A.A. Friction factor and Reynolds number in porous media Flow. J. Hydraul. Div. 1973, 99, 901–911. [Google Scholar] [CrossRef]
- Sedghi-Als, M.; Rihimi, H.; Salehi, R. Non-Darcy Flow of Water through a Packed-Column; Springer Science: Berlin, Germany, 2013; pp. 215–227. [Google Scholar] [CrossRef]
- Ferdos, F.; Wörman, A.; Ekström, I. Hydraulic conductivity of coarse Rockfill used in hydraulic structures. Trans. Porous Med. 2015, 108, 367–391. [Google Scholar] [CrossRef]
- Parkin, A.K. Through and overflow rockfill dams. In Advances in Rockfill Structures; Kluwer Academic Publishers: Alphen aan den Rijn, The Netherlands, 1991; pp. 571–592. [Google Scholar]
- Colebrook, C.F. Turbulent Flow in Pipes, with Particular Reference to the Transition Region between the Smooth and Rough Pipe Laws. J. Inst. Civ. Eng. 1939, 12, 393–422. [Google Scholar] [CrossRef]
- Blake, F.C. The Resistance of Packing to Fluid Flow; Read at the Richmond Meeting; American Institute of Chemical Engineers: New York, NY, USA, 1922; pp. 415–421. [Google Scholar]
- Burke, S.P.; Plummer, W.B. Gas flow through packed columns. Ind. Eng. Chem. 1928, 20, 1196–1200. [Google Scholar] [CrossRef]
- Lindquist, E. Premier Congrès des Grandes Banages; Stockholm, Sweden, 1933; Volume V, pp. 81–99. Available online: https://fr.wikipedia.org/wiki/Premier_Congr%C3%A8s_universel_des_races (accessed on 9 October 2023).
- Sunada, D.K. Laminar and Turbulent Flow of Water through Homogeneous Porous Media. Ph.D. Thesis, University of California at Berkeley, Berkeley, CA, USA, 1969. [Google Scholar]
- Kirkham, C.E. Turbulent Flow in Porous Media—An Analytical and Experimental Model Study. Ph.D. Thesis, University of Melbourne, Melbourne, Australia, 1966. [Google Scholar]
- Ahmed, N. Physical Properties of Porous Medium Affecting Laminal and Turbulent Flow of Water. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 1967. [Google Scholar]
- Francher, G.H.; Lewis, J.A. Flow of simple fluids through materials. Ind. Eng. Chem. 1933, 25, 1139–1147. [Google Scholar] [CrossRef]
- Brownell, L.E.; Kaltz, D.L. Flow of fluids through porous media. Chem. Eng. Prog. 1974, 43, 537–548. [Google Scholar]
- McDonald, I.F.; El-Sayed, M.S.; Mow, K.; Dillen, F.A.L. Flow through porous media-the Ergun equation revisited. Am. Chem. Soc. 1979, 18, 199–208. [Google Scholar] [CrossRef]
- Tyagi, A.K.; Tood, D.K. Discussion of Non-linear flow in porous media by N Ahmed and DK Sunada. J. Hydraul. Div. 1970, 96, 1734–1738. [Google Scholar] [CrossRef]


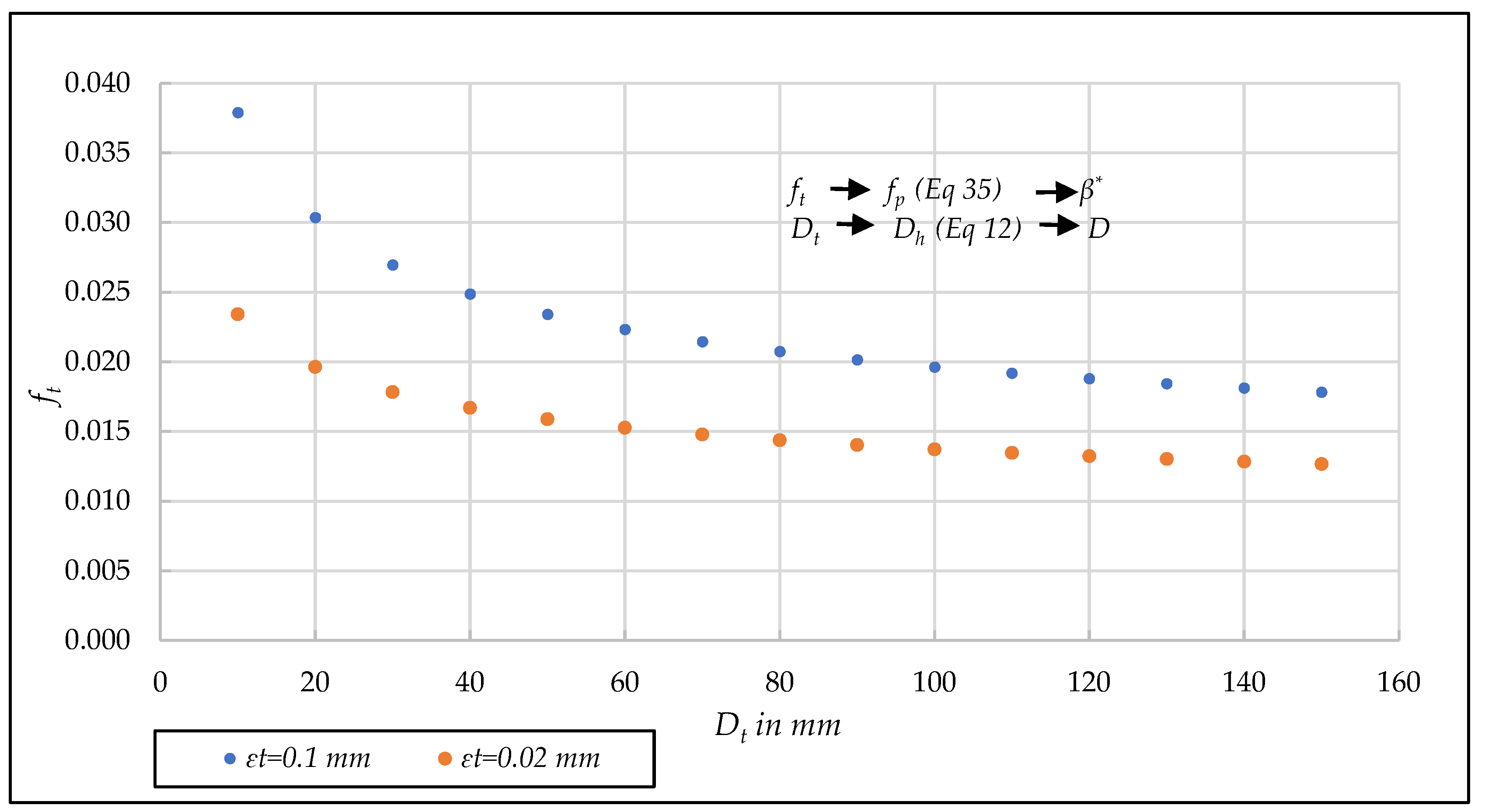





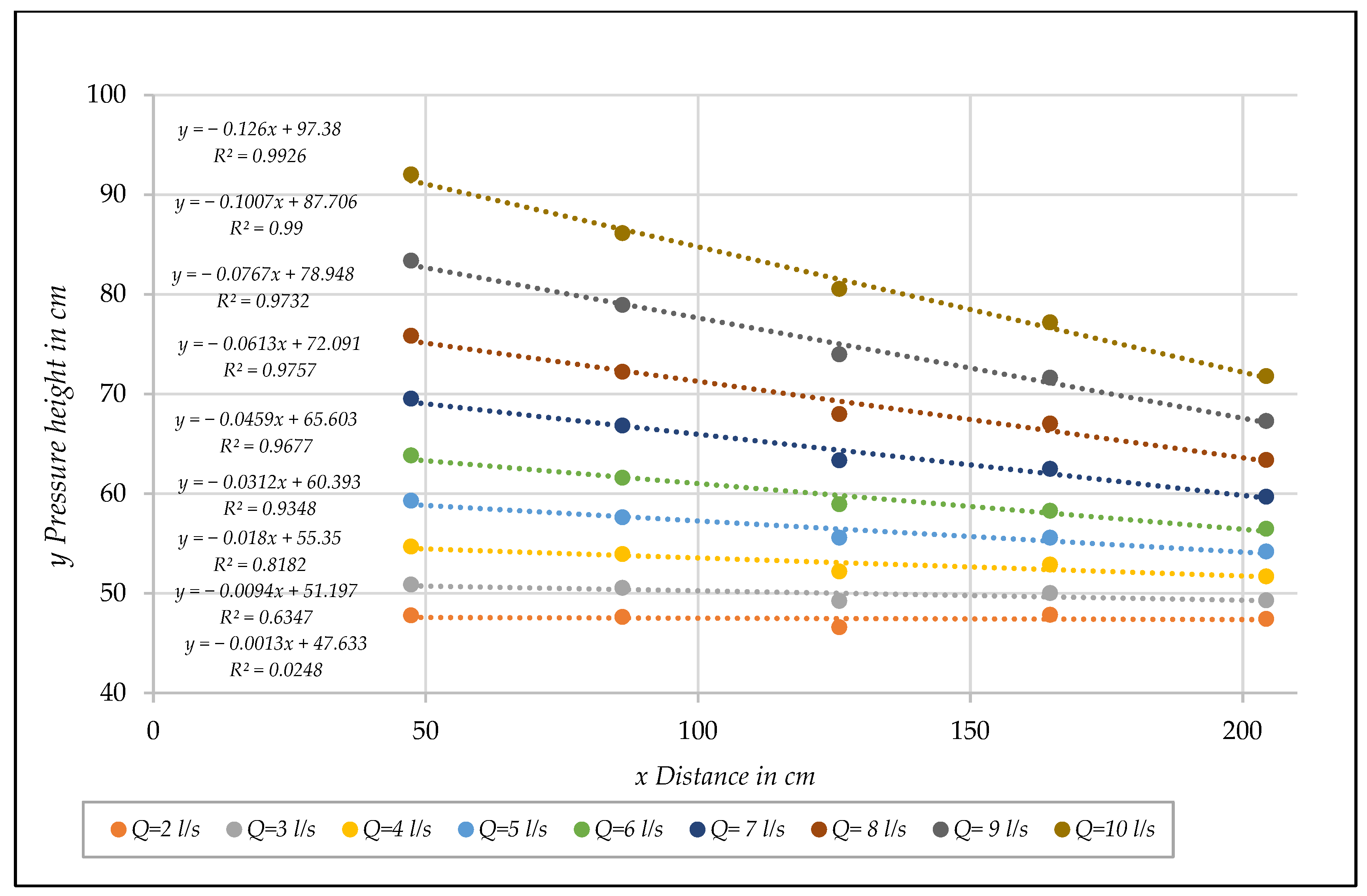
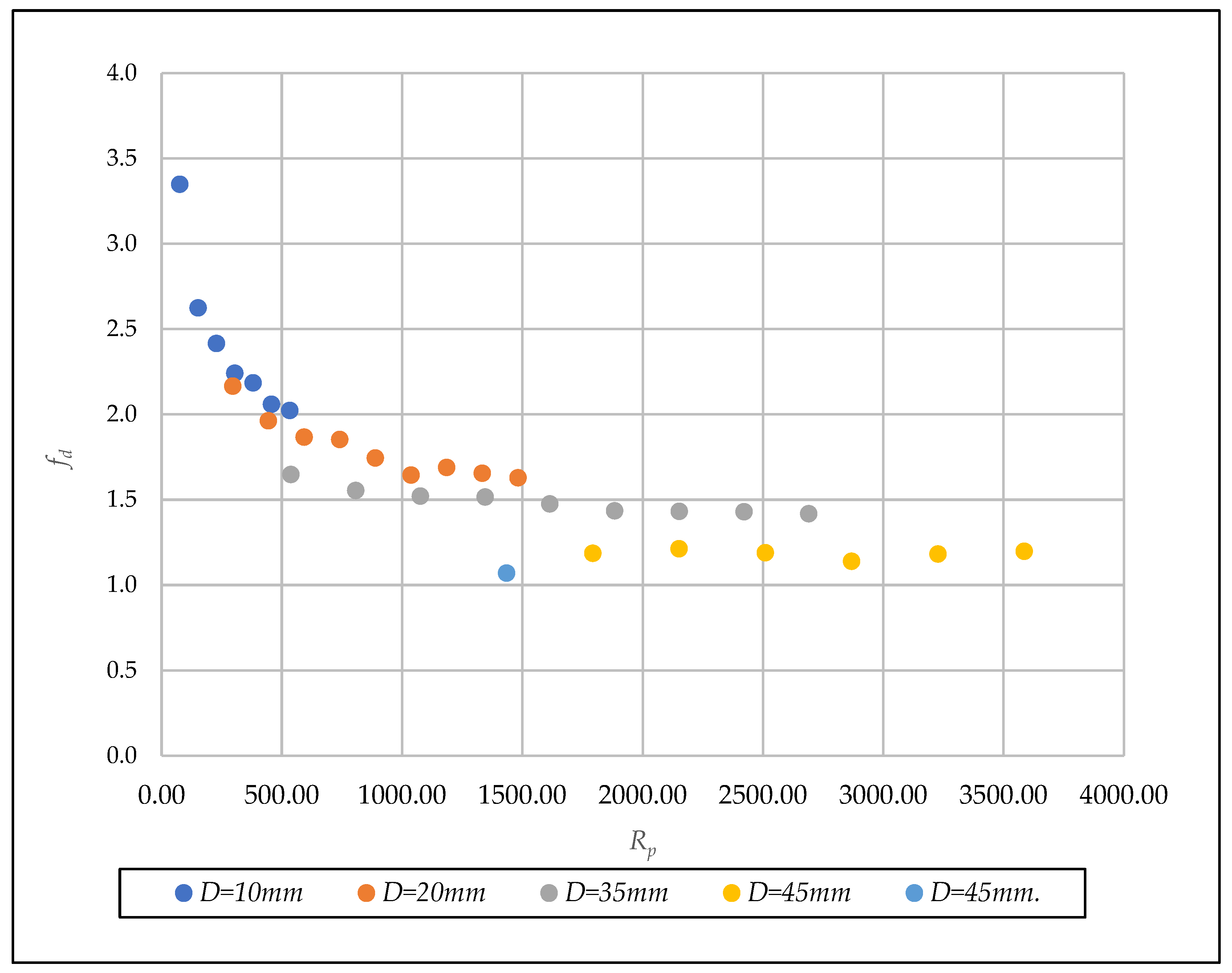
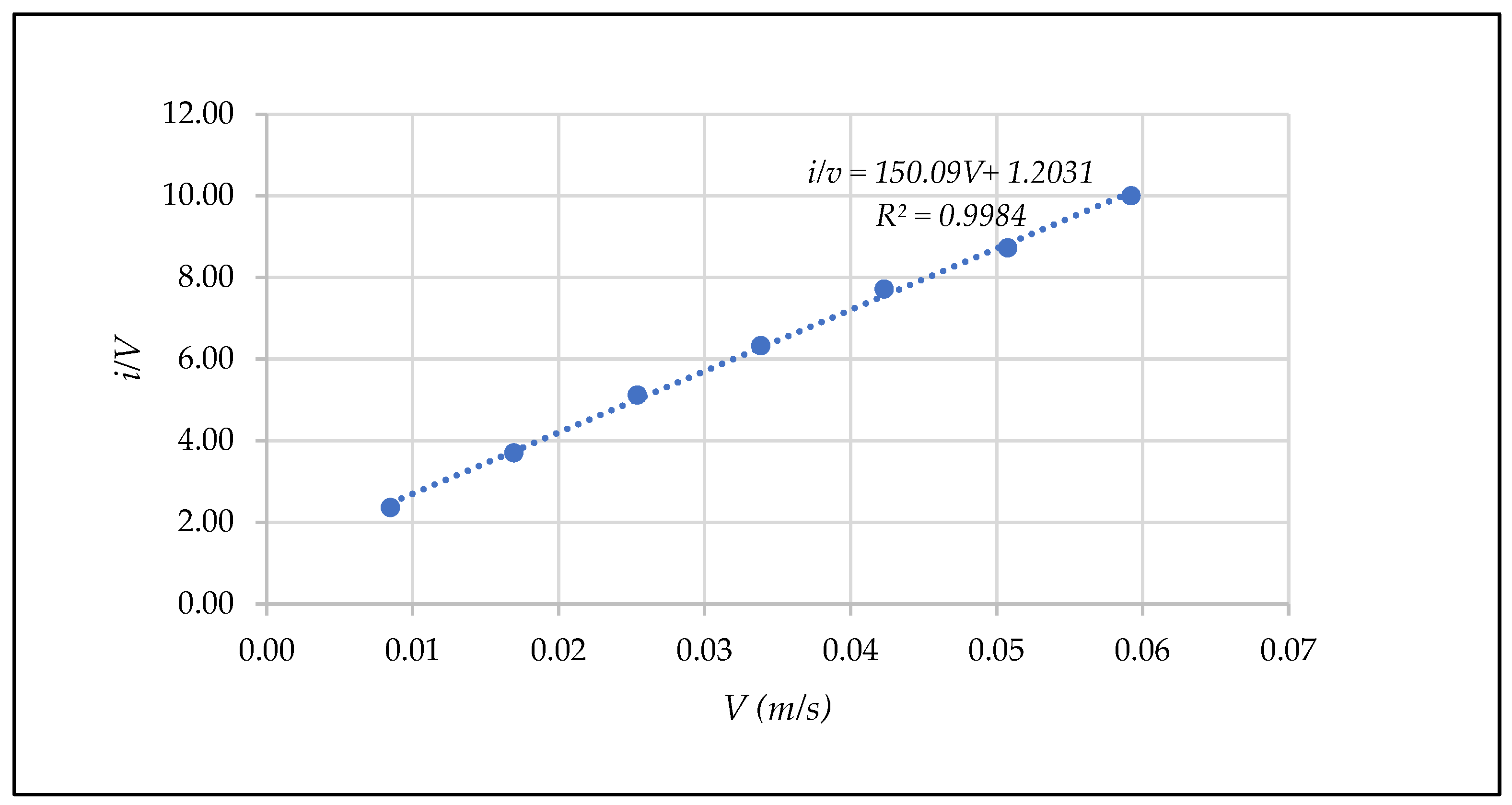

| D (mm) | Test | n | F | Rh/D | N | β* (Equation (35)) | N | (Equation (36)) | β* (Equation (33)) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 22.00 | A | 36.22% | 1.050 | 0.090 | 7 | 1049 | 1.615 | 1.272 | - | - | |
| 22.00 | B | 36.83% | 1.050 | 0.093 | 7 | 1034 | 1.660 | 1.308 | 14 | 1.639 | 1.290 |
| 44.00 | A | 36.18% | 1.050 | 0.090 | 5 | 4986 | 1.168 | 0.920 | - | - | |
| 44.00 | B | 35.53% | 1.050 | 0.087 | 5 | 5019 | 1.110 | 0.874 | 10 | 1.143 | 0.900 |
| 89.00 | A | 38.23% | 1.050 | 0.098 | 5 | 17,033 | 1.055 | 0.831 | - | - | |
| 89.00 | B | 38.84% | 1.050 | 0.101 | 5 | 18,097 | 1.035 | 0.815 | 10 | 1.052 | 0.828 |
| Q (ls−1) | (ms−1) | ||||
|---|---|---|---|---|---|
| Hydraulic Gradient | |||||
| 1 | 0.0085 | 0.0200 | (4) | 0.0019 | (4) |
| 2 | 0.0169 | 0.0627 | 0.0301 | 0.0107 | 0.0013 (1) |
| 3 | 0.0254 | 0.1299 | 0.0614 | 0.0227 | 0.0094 (2) |
| 4 | 0.0338 | 0.2142 | 0.1038 | 0.0395 | 0.0180 (3) |
| 5 | 0.0423 | 0.3263 | 0.1610 | 0.0615 | 0.0312 |
| 6 | 0.0507 | 0.4428 | 0.2182 | 0.0862 | 0.0459 |
| 7 | 0.0592 | 0.5921 | 0.2800 | 0.1141 | 0.0613 |
| 8 | 0.0677 | (4) | 0.3758 | 0.1487 | 0.0767 |
| 9 | 0.0761 | (4) | 0.4659 | 0.1880 | 0.1007 |
| 10 | 0.0846 | (4) | 0.5659 | 0.2302 | 0.1260 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López, J.C.; Toledo, M.Á.; Moran, R.; Balairón, L. A Unified General Resistance Formula for Uniform Coarse Porous Media. Water 2023, 15, 3578. https://doi.org/10.3390/w15203578
López JC, Toledo MÁ, Moran R, Balairón L. A Unified General Resistance Formula for Uniform Coarse Porous Media. Water. 2023; 15(20):3578. https://doi.org/10.3390/w15203578
Chicago/Turabian StyleLópez, Juan Carlos, Miguel Ángel Toledo, Rafael Moran, and Luis Balairón. 2023. "A Unified General Resistance Formula for Uniform Coarse Porous Media" Water 15, no. 20: 3578. https://doi.org/10.3390/w15203578





