Analytical Solution for Water Inflow into Deeply Buried Symmetrical Subsea Tunnels with Excavation Damage Zones
Abstract
:1. Introduction
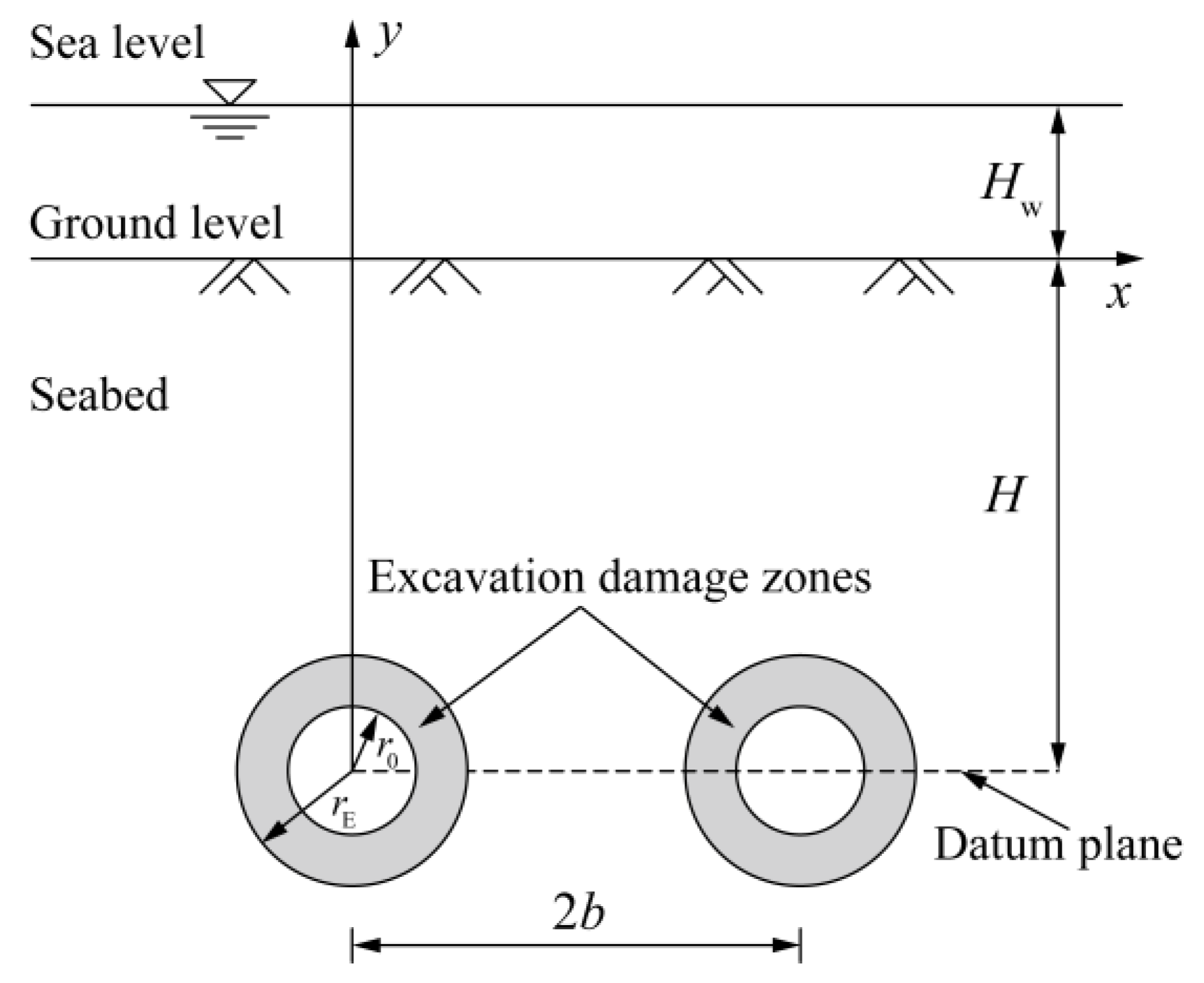
2. Problem Description
2.1. Theoretical Model and Assumptions
- (1)
- The seabed and EDZs are saturated, homogeneous, and isotropic.
- (2)
- (3)
- A steady and incompressible flow, which obeys Darcy’s law, is employed in this model. The hydraulic heads on the circumference of the tunnels and the EDZs are constant.
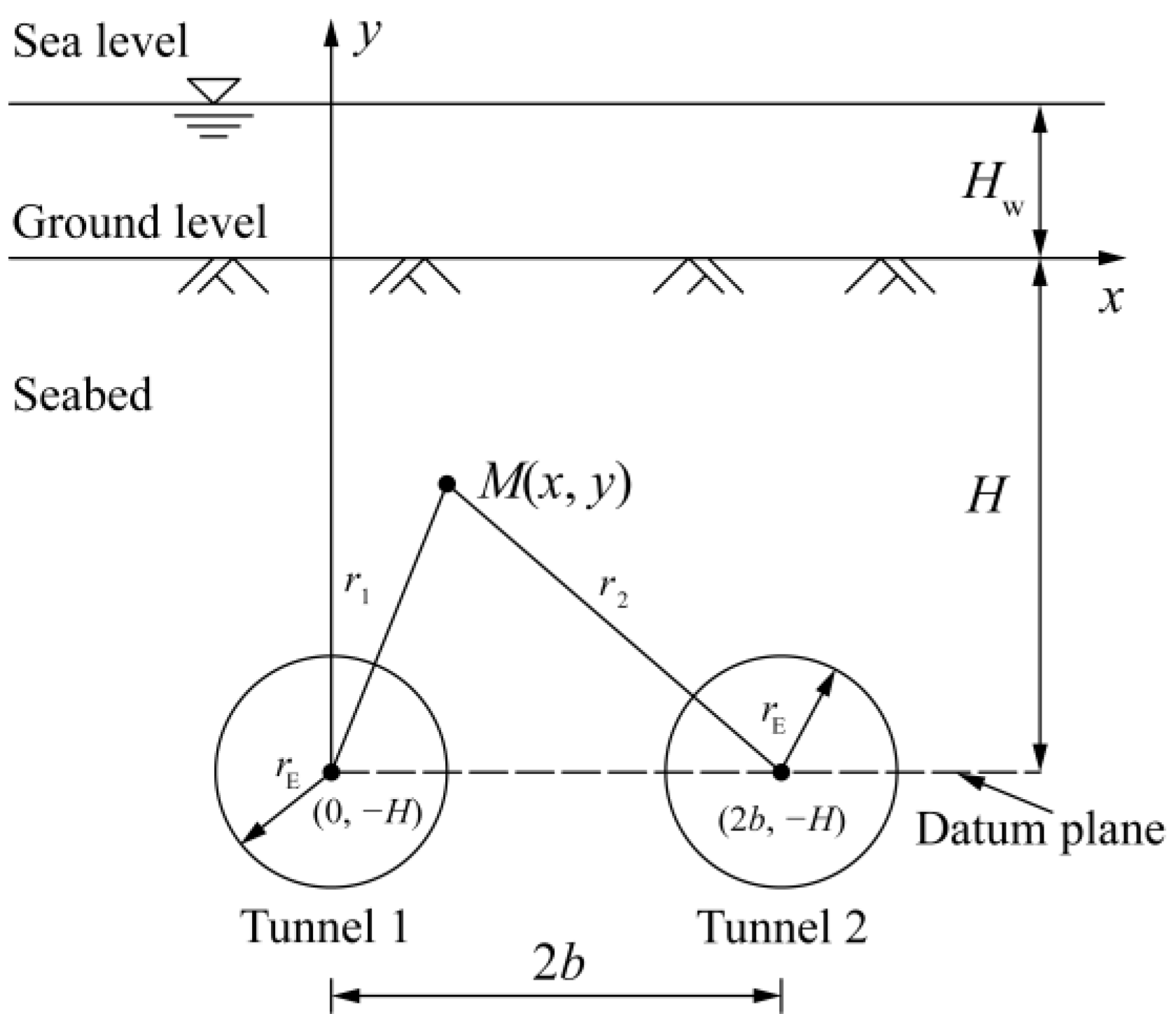
2.2. Governing Equation and Boundary Conditions
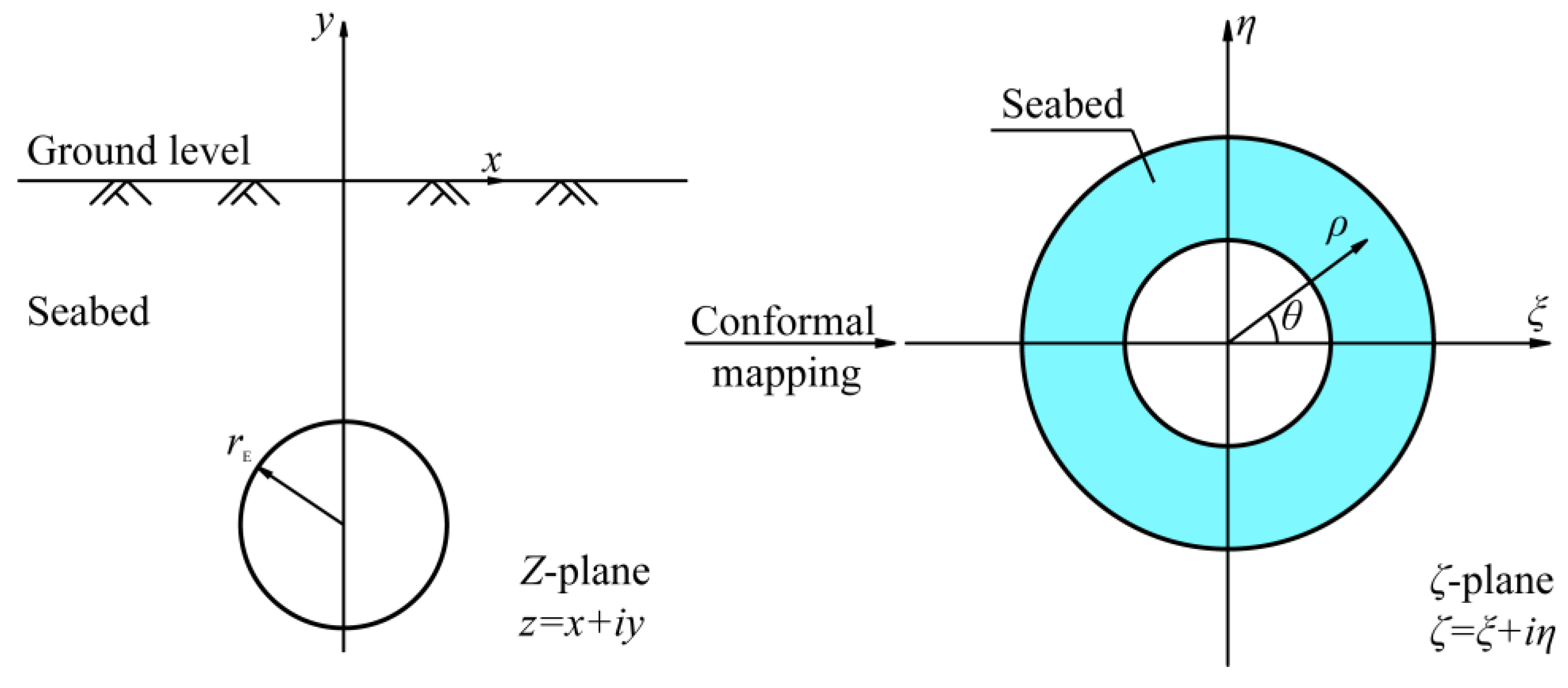
3. Analytical Solution
3.1. Seepage in the Seabed
3.2. Seepage in Excavation Damage Zones
3.3. Final Analytical Solution
4. Verification
4.1. Comparison with a Simplified Analytical Solution
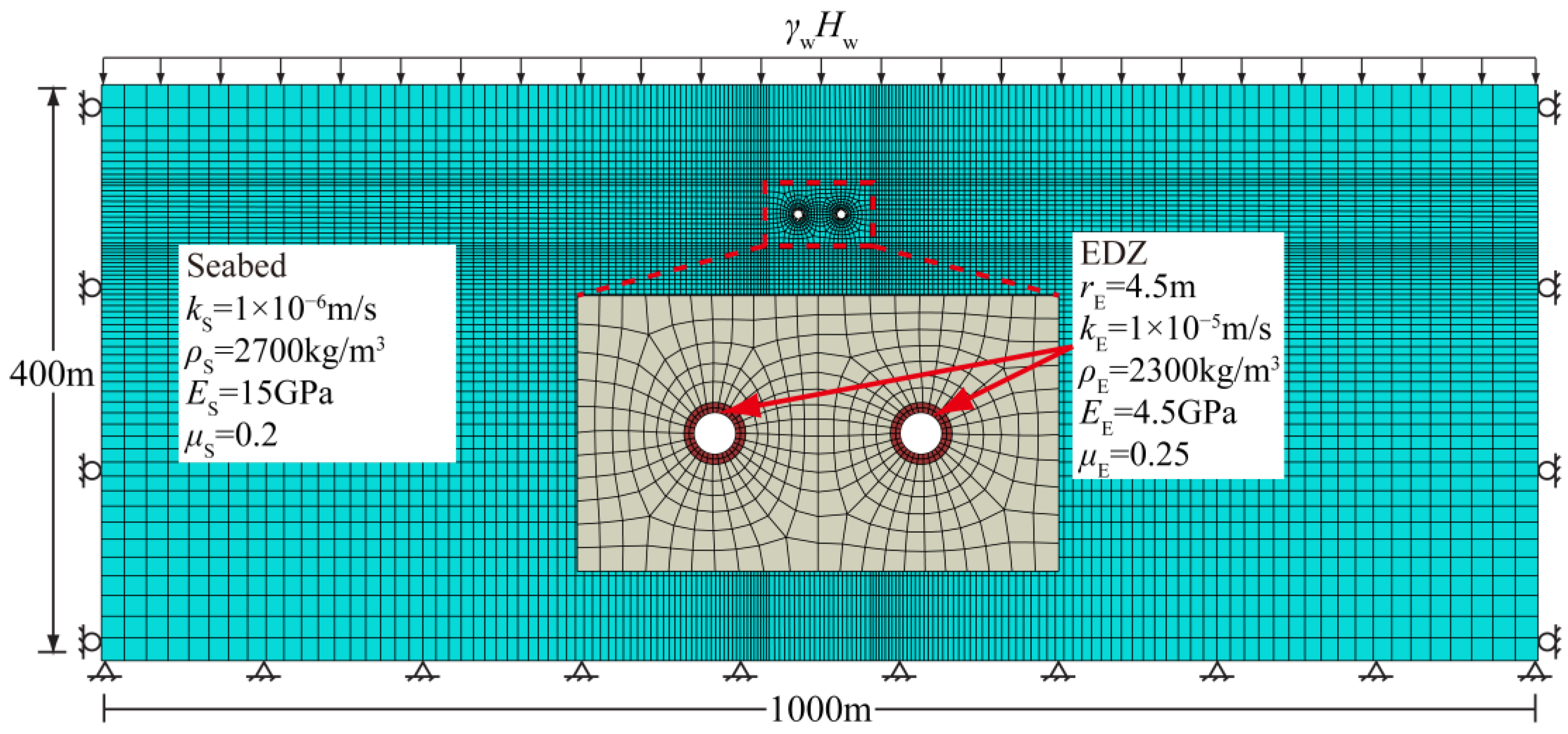
4.2. Comparison with the Numerical Solution
5. Discussion
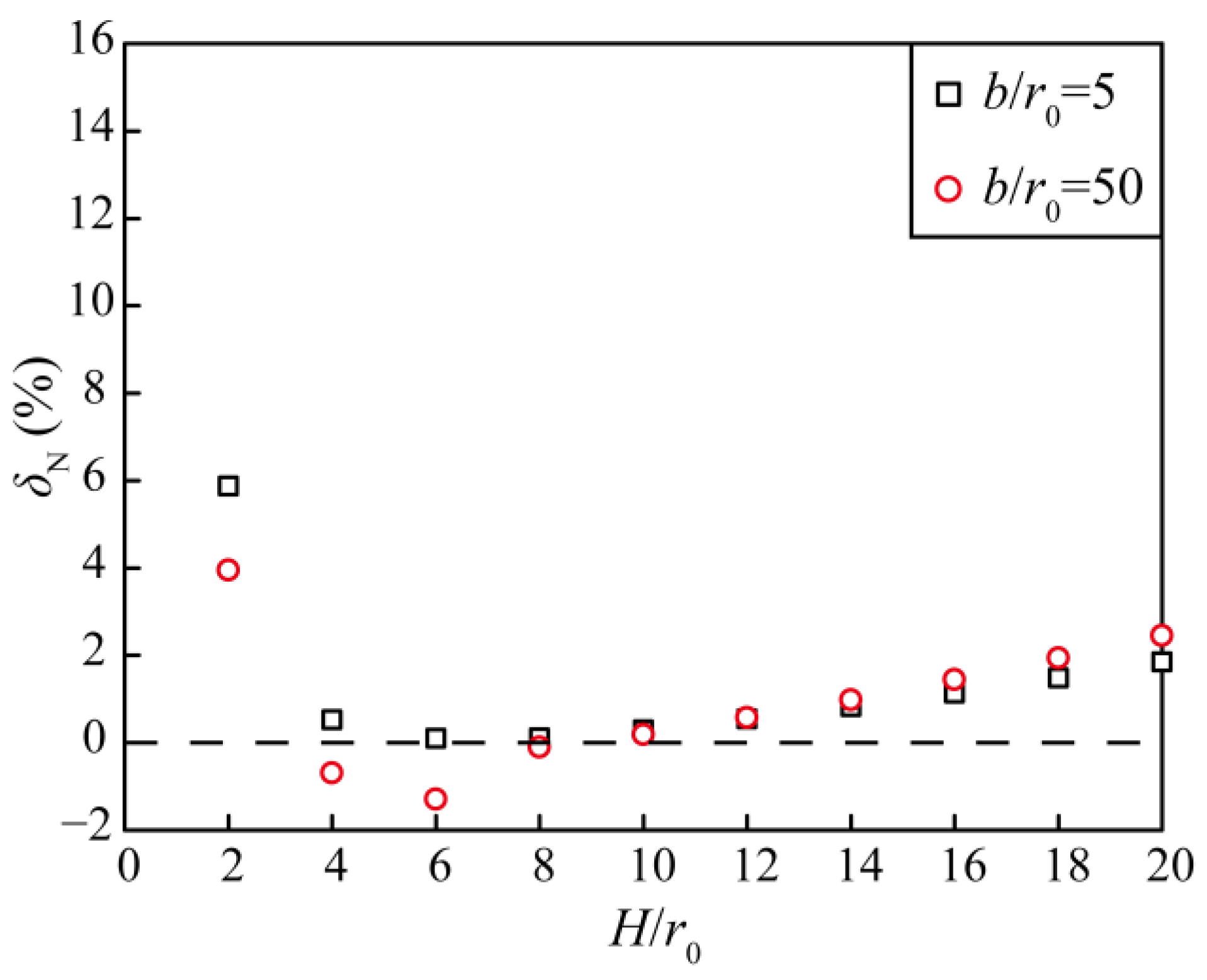
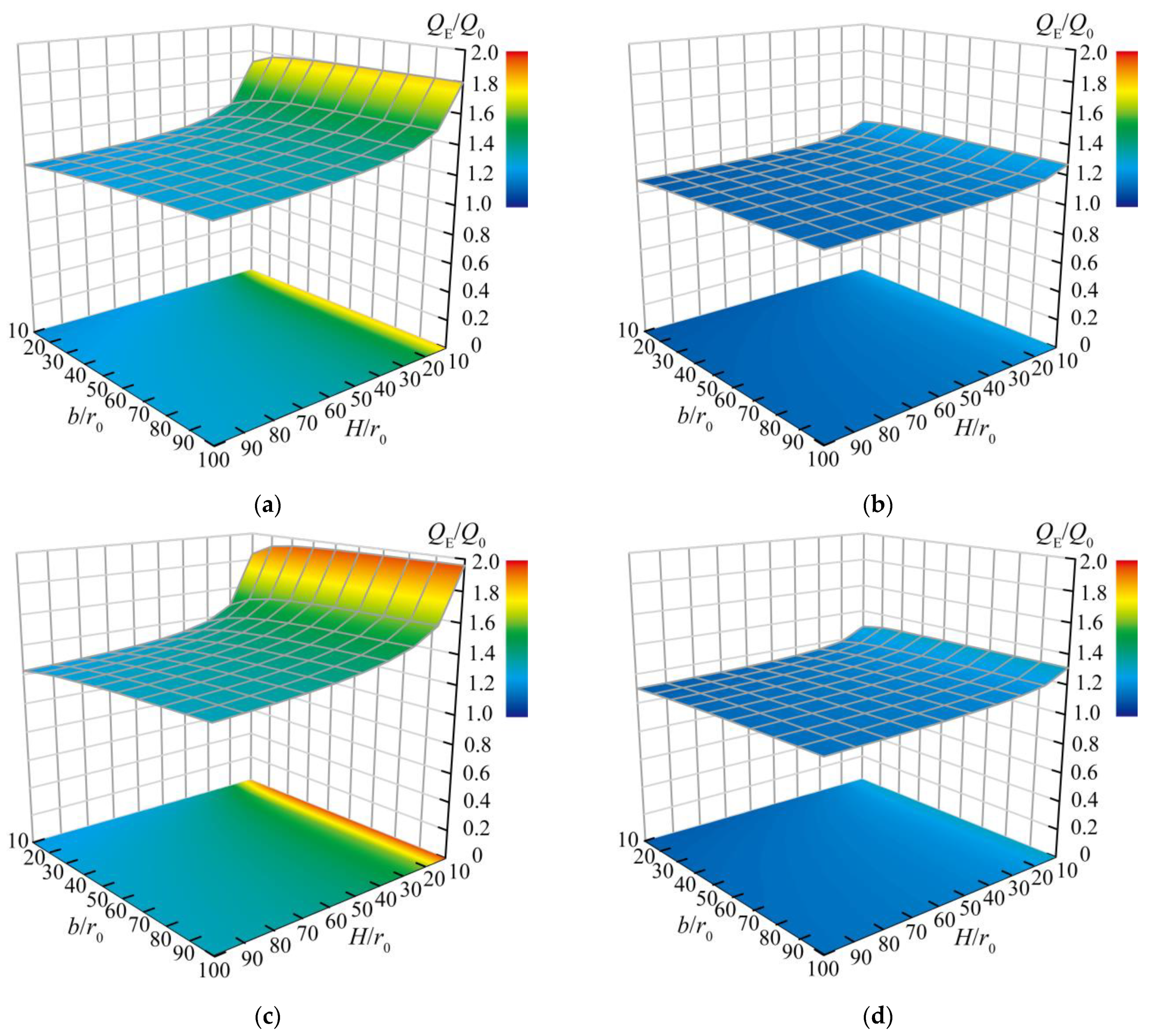
5.1. Effects of Excavation Damage Zones
5.2. Effects of Spatial Parameters
5.3. Comparison with Analytical Solution for Water Inflow into a Tunnel with an EDZ
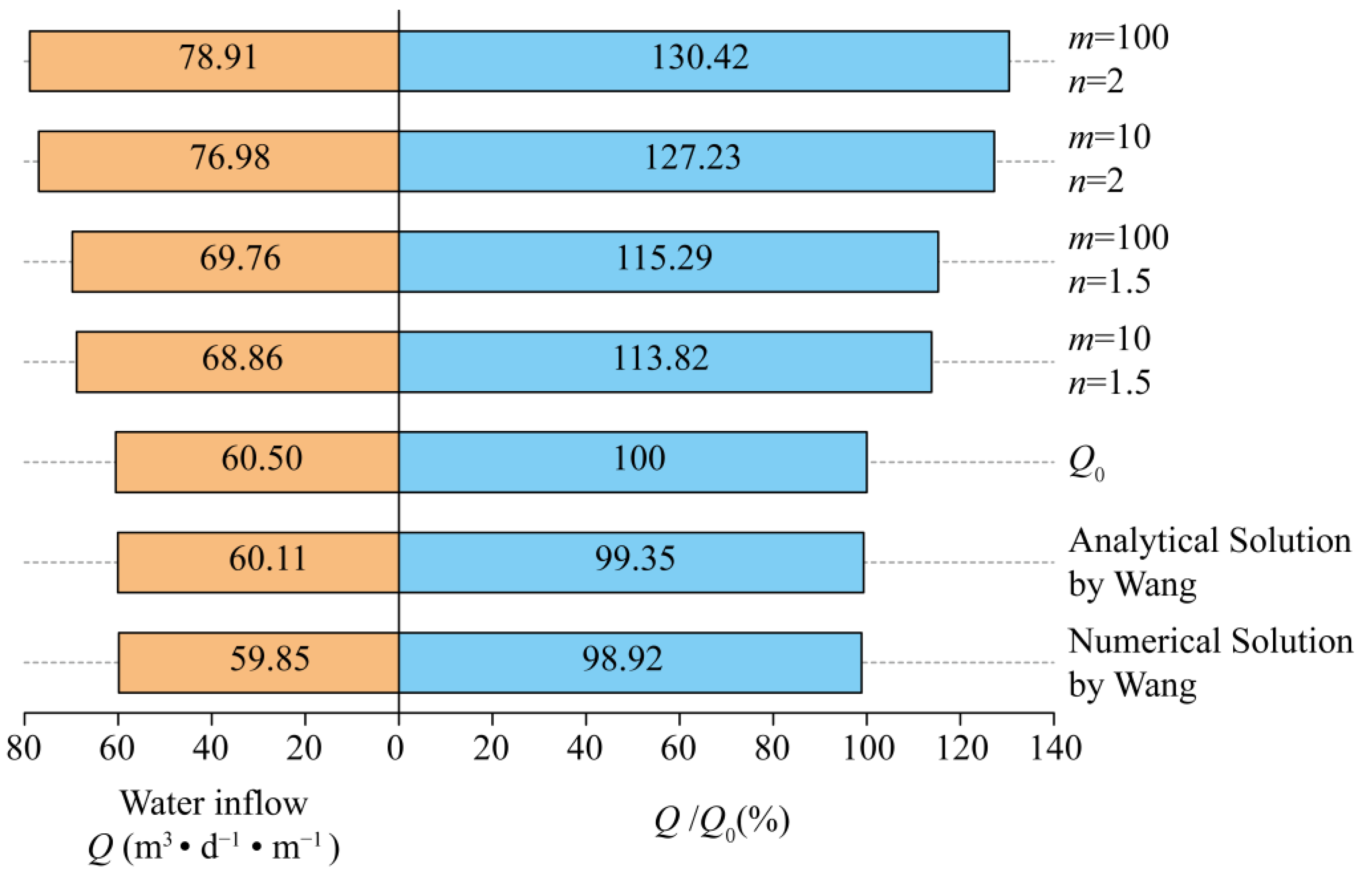
5.4. Application in an Engineering Case
6. Conclusions
- (1)
- The water inflow into the deeply buried symmetrical subsea tunnels with EDZs is related to parameters that include the permeability coefficients of the seabed and the EDZs (, ), the radii of the tunnels and the tunnels with EDZs (, ), the distance from the sea level to the ground level (), the distance from the ground level to the tunnel centre (), the distance between the two tunnel centres (2b), and the hydraulic head on the circumference of the tunnels ().
- (2)
- If the effects of the EDZs are neglected, the relative error between the proposed solution and an analytical solution for the water inflow into the symmetrical subsea tunnels without EDZs developed by Wang is always less than 2.5% when . If the effects of the EDZs are accounted for, the relative error between the proposed solution and the numerical solution is still always less than 2.5% when . The comparisons prove that the proposed solution is applicable to the evaluation of the water inflow into the deeply buried symmetrical subsea tunnels.
- (3)
- The effects of EDZs on the water inflow into the deeply buried symmetrical subsea tunnels were analysed based on the EDZ parameters m () and n (). Firstly, increases significantly at an early stage of increasing m and then gradually stabilizes as m increases further. Moreover, increases approximately linearly with n, which implies that the thickness of EDZs has a strong effect on the water inflow.
- (4)
- For spatial parameters, decreases as increases but increases as increases. The effects of the EDZs are more significant with smaller buried depths and greater distances between the two tunnel centres and this effect gradually stabilizes as buried depth and distance between the two tunnel centres increase. Changes in H affect the effects of EDZs more than changes in 2b.
- (5)
- Compared with a single subsea tunnel, there is a diverting effect between the symmetrical subsea tunnels. This diverting effect can be promoted by increasing the EDZ parameters and is more sensitive to the EDZ thickness than to the EDZ permeability coefficient. In addition, this diverting effect increases as the buried depth increases and the distance between the two tunnel centres decreases.
- (6)
- The application in the engineering case shows that the proposed solution has good reliability and that the effects of EDZs should be accounted for when assessing the water inflow into the deeply buried symmetrical subsea tunnels with EDZs. In this paper, for m = 100 and n = 2, the water inflow into tunnels considering EDZs is 30.42% higher than that without considering EDZs’ effects. Further efforts can be made to conduct relevant research on prevention methods to diminish the effects of EDZs and on analytical solutions for the water inflow into asymmetrical subsea tunnels with EDZs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nilsen, B. Characteristics of Water Ingress in Norwegian Subsea Tunnels. Rock Mech. Rock Eng. 2014, 47, 933–945. [Google Scholar] [CrossRef]
- Zhu, C.; Ying, H.; Gong, X.; Wang, X.; Wu, W. Analytical solution for wave-induced hydraulic response on subsea shield tunnel. Ocean Eng. 2021, 228, 108924. [Google Scholar] [CrossRef]
- Liu, X.; Wang, D.; Zhang, Y.; Jiang, A.; Fang, Q.; Zhang, R. Analytical solutions on non-Darcy seepage of grouted and lined subsea tunnels under dynamic water levels. Ocean Eng. 2023, 267, 113276. [Google Scholar] [CrossRef]
- Li, P.; Wang, F.; Long, Y.; Zhao, X. Investigation of steady water inflow into a subsea grouted tunnel. Tunn. Undergr. Sp. Technol. 2018, 80, 92–102. [Google Scholar] [CrossRef]
- Wang, H.; Chen, J.; Liu, H.; Guo, L.; Lu, Y.; Su, X.; Zhu, Y.; Liu, T. Study on the Influence of Mud Properties on the Stability of Excavated Face of Slurry Shield and the Quality of Filter Cake Formation. J. Mar. Sci. Eng. 2020, 8, 291. [Google Scholar] [CrossRef]
- Li, S.; Zhou, Z.; Li, L.; Xu, Z.; Zhang, Q.; Shi, S. Risk assessment of water inrush in karst tunnels based on attribute synthetic evaluation system. Tunn. Undergr. Sp. Technol. 2013, 38, 50–58. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, H.; Li, C.; He, X.; Tang, H.; Zhao, X. A semi-empirical model for water inflow into a tunnel in fractured-rock aquifers considering non-Darcian flow. J. Hydrol. 2021, 597, 126149. [Google Scholar] [CrossRef]
- Pan, Y.; Qi, J.; Zhang, J.; Peng, Y.; Chen, C.; Ma, H.; Ye, C. A Comparative Study on Steady-State Water Inflow into a Circular Underwater Tunnel with an Excavation Damage Zone. Water 2022, 14, 3154. [Google Scholar] [CrossRef]
- Liu, R.; Liu, Y.; Xin, D.; Li, S.; Zheng, Z.; Ma, C.; Zhang, C. Prediction of water inflow in subsea tunnels under blasting vibration. Water 2018, 10, 1336. [Google Scholar] [CrossRef]
- Zhao, J.; Tan, Z.; Ma, N. Development and application of a new reduction coefficient of water pressure on sub-sea tunnel lining. Appl. Sci. 2022, 12, 2496. [Google Scholar] [CrossRef]
- Zhao, J.; Tan, Z.; Zhou, Z. Discussion on the waterproof and drainage system of the coastal tunnel and analysis of water pressure law outside lining: A case study of the gongbei tunnel. Adv. Civ. Eng. 2021, 2021, 6610601. [Google Scholar] [CrossRef]
- Harr, M.E. Groundwater and Seepage. Soil Sci. 1963, 95, 289. [Google Scholar] [CrossRef]
- Goodman, R.E.; Moye, D.G.; Schalkwyk, A.; Javandel, I. Ground water inflow during tunnel driving. Eng. Geol. 1965, 2, 39–56. [Google Scholar]
- Qin, Z.; He, W.; Zhou, H. Analytical study on seepage field of subsea twin tunnels constructed by NATM. Ocean Eng. 2022, 264, 112345. [Google Scholar] [CrossRef]
- Wang, F.; Li, P. An Analytical Model of Seepage Field for Symmetrical Underwater Tunnels. Symmetry 2018, 10, 273. [Google Scholar] [CrossRef]
- Zhang, B. Analytical Solution for Seepage Field of Twin-parallel Tunnels in Semi-infinite Plane. J. China Railw. Soc. 2017, 39, 125–131. [Google Scholar]
- Guo, Y.; Wang, H.; Jiang, M. Analytical solutions of seepage field for underwater shallow-buried parallel twin tunnels. Chin. J. Geotech. Eng. 2021, 43, 1088–1096. [Google Scholar]
- Zhu, C.; Ying, H.; Gong, X.; Shen, H.; Wang, X. Analytical solutions to seepage field of underwater twin parallel tunnels. Chin. J. Geotech. Eng. 2019, 41, 355–360. [Google Scholar]
- Pan, Y.; Luo, Q.; Zhou, B.; Chen, J. Analytical study on seepage field of deep tunnel with grouting circle in half plane. J. Zhejiang Univ. Eng. Sci. 2018, 52, 1114–1122. [Google Scholar]
- Huangfu, M.; Wang, M.; Tan, Z.; Wang, X. Analytical solutions for steady seepage into an underwater circular tunnel. Tunn. Undergr. Sp. Technol. 2010, 25, 391–396. [Google Scholar] [CrossRef]
- Park, K.; Owatsiriwong, A.; Lee, J. Analytical solution for steady-state groundwater inflow into a drained circular tunnel in a semi-infinite aquifer: A revisit. Tunn. Undergr. Sp. Technol. 2008, 23, 206–209. [Google Scholar] [CrossRef]
- Kolymbas, D.; Wagner, P. Groundwater ingress to tunnels—The exact analytical solution. Tunn. Undergr. Sp. Technol. 2007, 22, 23–27. [Google Scholar] [CrossRef]
- El Tani, M. Circular tunnel in a semi-infinite aquifer. Tunn. Undergr. Sp. Technol. 2003, 18, 49–55. [Google Scholar] [CrossRef]
- Huang, Z.; Zhu, S.; Zhao, K.; Li, X.; Wu, R.; Wang, Y.; Wang, X. Influence of Structural Variation of Host Rock Induced by Engineering Activities on Water Inrush of Tunnels. Chin. J. Geotech. Eng. 2018, 40, 449–458. [Google Scholar]
- Yang, G.; Wang, X.; Wang, X.; Cao, Y. Analyses of seepage problems in a subsea tunnel considering effects of grouting and lining structure. Mar. Georesour. Geotec. 2016, 34, 65–70. [Google Scholar] [CrossRef]
- Wang, X.; Tan, Z.; Wang, M.; Zhang, M.; Ming, H. Theoretical and experimental study of external water pressure on tunnel lining in controlled drainage under high water level. Tunn. Undergr. Sp. Technol. 2008, 23, 552–560. [Google Scholar] [CrossRef]
- Hwang, J.; Lu, C. A semi-analytical method for analyzing the tunnel water inflow. Tunn. Undergr. Sp. Technol. 2007, 22, 39–46. [Google Scholar] [CrossRef]
- Farhadian, H.; Katibeh, H.; Huggenberger, P. Empirical model for estimating groundwater flow into tunnel in discontinuous rock masses. Environ. Earth Sci. 2016, 75, 471. [Google Scholar] [CrossRef]
- Farhadian, H.; Katibeh, H. New empirical model to evaluate groundwater flow into circular tunnel using multiple regression analysis. Int. J. Min Sci. Technol. 2017, 27, 415–421. [Google Scholar] [CrossRef]
- Nikvar Hassani, A.; Farhadian, H.; Katibeh, H. A comparative study on evaluation of steady-state groundwater inflow into a circular shallow tunnel. Tunn. Undergr. Sp. Technol. 2018, 73, 15–25. [Google Scholar] [CrossRef]
- Nikvar Hassani, A.; Katibeh, H.; Farhadian, H. Numerical analysis of steady-state groundwater inflow into Tabriz line 2 metro tunnel, northwestern Iran, with special consideration of model dimensions. B. Eng. Geol. Environ. 2016, 75, 1617–1627. [Google Scholar] [CrossRef]
- Farhadian, H.; Katibeh, H.; Huggenberger, P.; Butscher, C. Optimum model extent for numerical simulation of tunnel inflow in fractured rock. Tunn. Undergr. Sp. Technol. 2016, 60, 21–29. [Google Scholar] [CrossRef]
- Zhu, W.C.; Wei, J.; Zhao, J.; Niu, L.L. 2D numerical simulation on excavation damaged zone induced by dynamic stress redistribution. Tunn. Undergr. Sp. Technol. 2014, 43, 315–326. [Google Scholar] [CrossRef]
- Siren, T.; Kantia, P.; Rinne, M. Considerations and observations of stress-induced and construction-induced excavation damage zone in crystalline rock. Int. J. Rock Mech. Min. 2015, 73, 165–174. [Google Scholar] [CrossRef]
- Martino, J.B.; Chandler, N.A. Excavation-induced damage studies at the Underground Research Laboratory. Int. J. Rock Mech. Min. 2004, 41, 1413–1426. [Google Scholar] [CrossRef]
- Bossart, P.; Meier, P.M.; Moeri, A.; Trick, T.; Mayor, J. Geological and hydraulic characterisation of the excavation disturbed zone in the Opalinus Clay of the Mont Terri Rock Laboratory. Eng. Geol. 2002, 66, 19–38. [Google Scholar] [CrossRef]
- Souley, M.; Homand, F.; Pepa, S.; Hoxha, D. Damage-induced permeability changes in granite: A case example at the URL in Canada. Int. J. Rock Mech. Min. 2001, 38, 297–310. [Google Scholar] [CrossRef]



| Distance between Two Tunnel Centres (m) | Permeability Coefficient of Seabed (m/s) | Radii of Tunnels (m) | Distance from Sea Level to Ground Level (m) | Hydraulic Head on the Circumference of Tunnels (m) | Distance from Ground Level to Tunnel Centre (m) |
|---|---|---|---|---|---|
| 30 | 1 × 10−6 | 3 | 45 | 0 | 6–60 |
| 120 |
| Dimensional Parameters | Material Parameters | ||
|---|---|---|---|
| Radii of tunnels (m) | 3 | Permeability coefficient of seabed (m/s) | 1 × 10−6 |
| Distance from sea level to ground level (m) | 45 | Permeability coefficient of EDZs (m/s) | 1 × 10−5 |
| Distance from ground level to tunnel centre H (m) | 6–60 | Density of seabed (kg/m3) | 2700 |
| Hydraulic head on the circumference of tunnels (m) | 0 | Density of EDZs (kg/m3) | 2300 |
| Distance between two tunnel centres (m) | 30, 300 | Young’s modulus of seabed (GPa) | 15 |
| Radii of tunnels with EDZs (m) | 4.5 | Young’s modulus of EDZs (GPa) | 4.5 |
| Seabed thickness (m) | 400 | Poisson’s ratio of seabed (m/s) | 0.2 |
| Seabed width (m) | 1000 | Poisson’s ratio of EDZs (m/s) | 0.25 |
| Permeability Coefficient of Seabed (m/s) | Ratio of EDZ Permeability to Seabed Permeability m | Radii of Tunnels (m) | Ratio of Radii of Tunnels with EDZs to Radii of Tunnels n | Distance from Sea Level to Ground Level (m) | Distance between Two Tunnel Centres (m) | Distance from Ground Level to Tunnel Centre H (m) | Hydraulic Head on the Circumference of Tunnels (m) |
|---|---|---|---|---|---|---|---|
| 1 × 10−6 | 1–1000 | 3 | 1–5 | 45 | 60, 600 | 30, 300 | 0 |
| Permeability Coefficient of Seabed (m/s) | Ratio of EDZ Permeability to Seabed Permeability m | Radii of Tunnels (m) | Ratio of Radii of Tunnels with EDZs to Radii of Tunnels n | Distance from Sea Level to Ground Level (m) | Distance between Two Tunnel Centres (m) | Distance from Ground Level to Tunnel Centre H (m) | Hydraulic Head on the Circumference of Tunnels (m) |
|---|---|---|---|---|---|---|---|
| 1 × 10−6 | 10, 1000 | 3 | 2, 4 | 45 | 60–600 | 30–300 | 0 |
| Permeability Coefficient of Seabed (m/s) | Ratio of EDZ Permeability to Seabed Permeability m | Radii of Tunnels (m) | Ratio of Radii of Tunnels with EDZs to Radii of Tunnels n | Distance from Sea Level to Ground Level (m) | Distance between Two Tunnel Centres (m) | Distance from Ground Level to Tunnel Centre H (m) | Hydraulic Head on the Circumference of Tunnels (m) |
|---|---|---|---|---|---|---|---|
| 1 × 10−6 | 1–1000 | 3 | 1–5 | 45 | 60–600 | 30–300 | 0 |
| Permeability Coefficient of Seabed (m/s) | Ratio of EDZ Permeability to Seabed Permeability m | Radii of Tunnels (m) | Ratio of Radii of Tunnels with EDZs to Radii of Tunnels n | Distance from Sea Level to Ground Level (m) | Distance between Two Tunnel Centres (m) | Distance from Ground Level to Tunnel Centre H (m) | Hydraulic Head on the Circumference of Tunnels (m) |
|---|---|---|---|---|---|---|---|
| 5 × 10−6 | 10100 | 7.4 | 1.52 | 20 | 66.8 | 52.4 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Y.; Qi, J.; Zhang, J.; Xia, P.; Peng, Y. Analytical Solution for Water Inflow into Deeply Buried Symmetrical Subsea Tunnels with Excavation Damage Zones. Water 2023, 15, 3556. https://doi.org/10.3390/w15203556
Pan Y, Qi J, Zhang J, Xia P, Peng Y. Analytical Solution for Water Inflow into Deeply Buried Symmetrical Subsea Tunnels with Excavation Damage Zones. Water. 2023; 15(20):3556. https://doi.org/10.3390/w15203556
Chicago/Turabian StylePan, Yiheng, Jiarui Qi, Jinfeng Zhang, Peng Xia, and Yaxiong Peng. 2023. "Analytical Solution for Water Inflow into Deeply Buried Symmetrical Subsea Tunnels with Excavation Damage Zones" Water 15, no. 20: 3556. https://doi.org/10.3390/w15203556
APA StylePan, Y., Qi, J., Zhang, J., Xia, P., & Peng, Y. (2023). Analytical Solution for Water Inflow into Deeply Buried Symmetrical Subsea Tunnels with Excavation Damage Zones. Water, 15(20), 3556. https://doi.org/10.3390/w15203556






