A Machine Learning-Based Framework for Water Quality Index Estimation in the Southern Bug River
Abstract
:1. Introduction
2. Materials and Methods
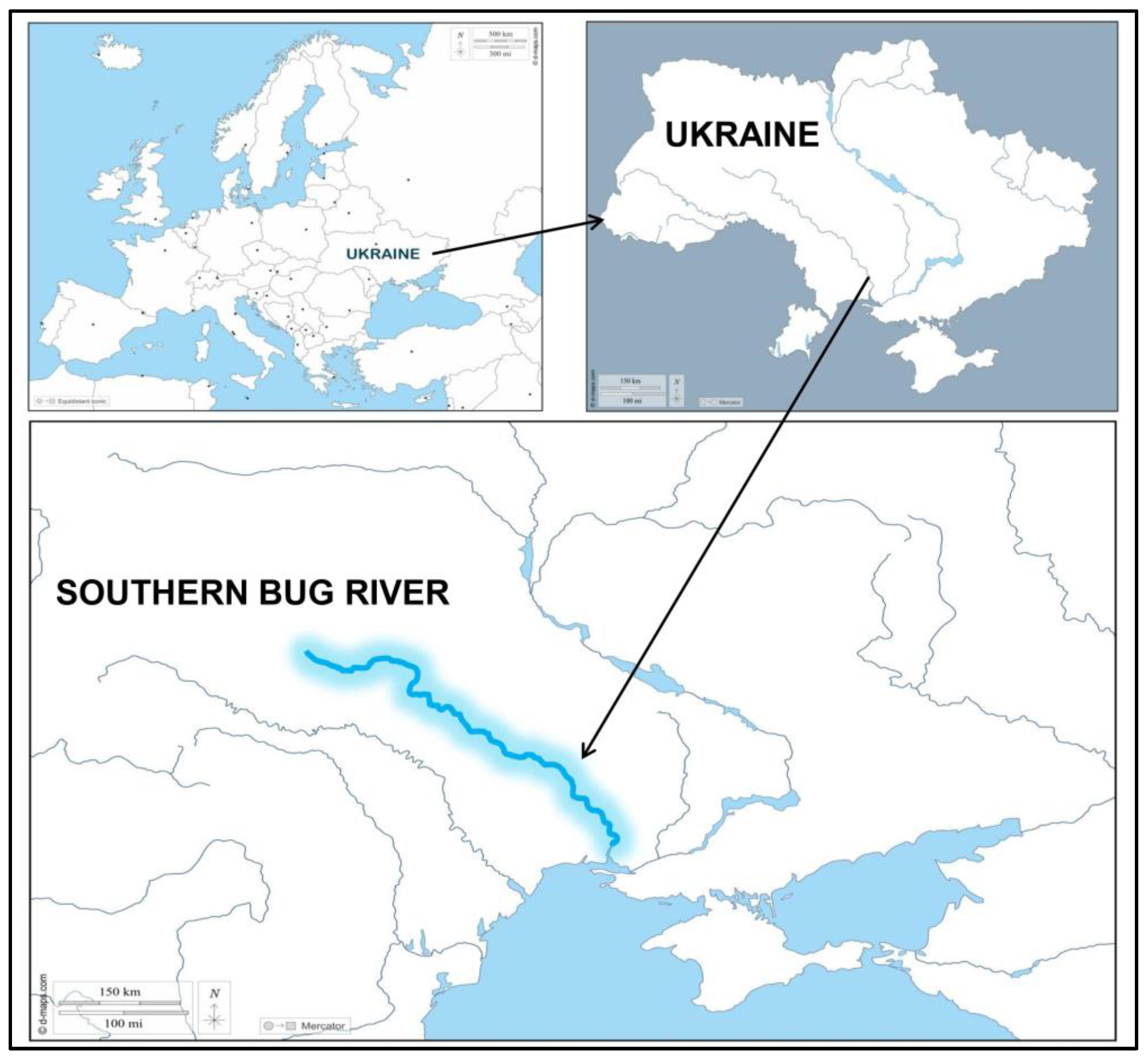
2.1. Study Area and Data Collection
2.2. Water Quality Index
- (1)
- To evaluate the overall quality of water, experts assigned weights (Awj) ranging from 1 to 4 to each chemical parameter. These weights, based on previous studies [18,19,20], were utilized to assess the impact of each parameter on the overall water quality assessment. The calculation of the relative weight (Rw) for this study was performed using the following Equation (1).
- (2)
- A quality rating scale (Qj) for each parameter is determined by dividing its annual mean concentration by its standard value [21].
- (3)
- To obtain the sub-indices (Sij), the assigned weight is multiplied by the relative weight. WQI is then calculated by summing up these sub-indices using Equation (4):
2.3. Machine Learning Models
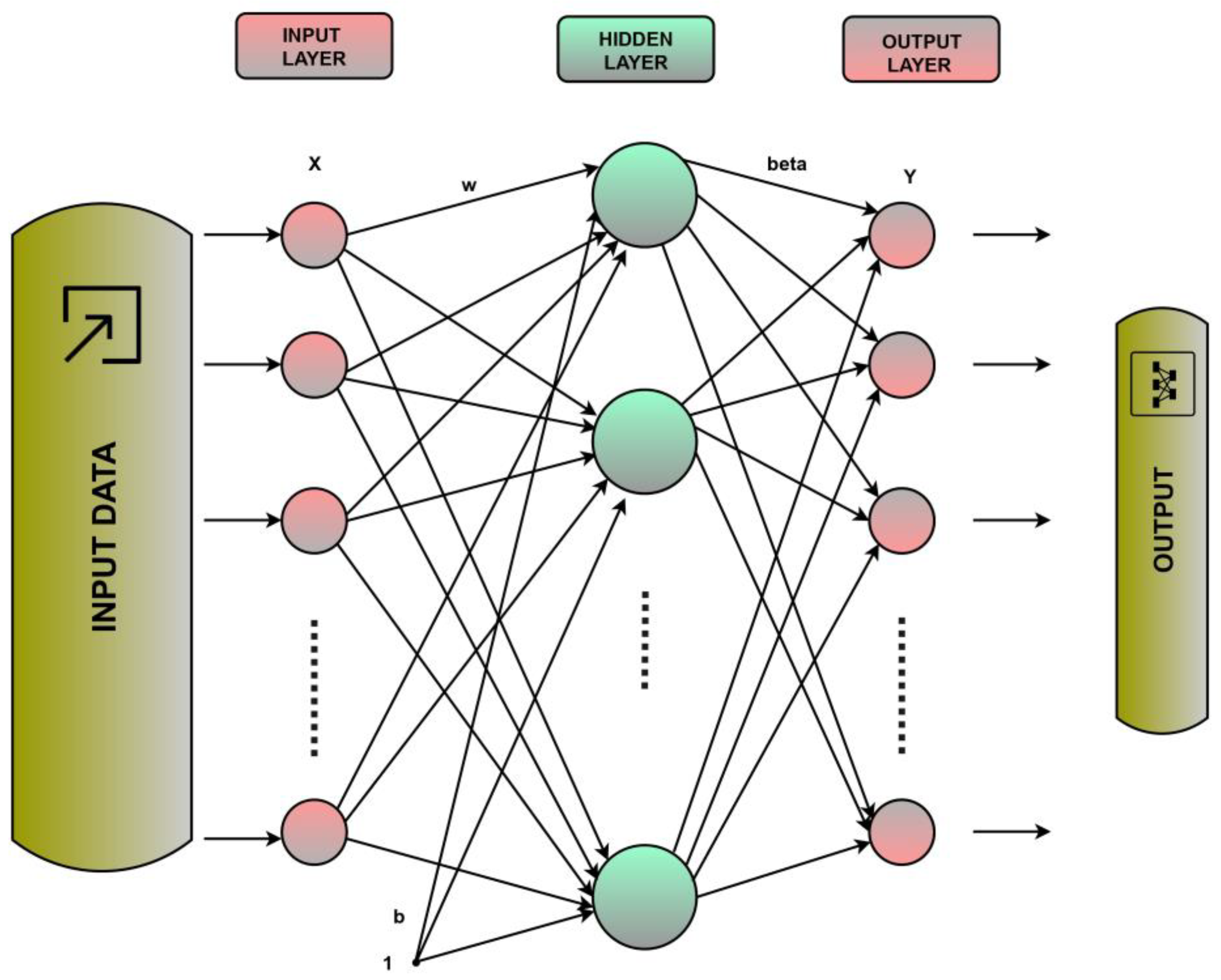
2.3.1. Artificial Neural Networks
2.3.2. Extreme Learning Machine
2.3.3. Decision Tree Regressor
2.3.4. Random Forest
2.3.5. Boosting-based Algorithms
2.3.6. Gaussian Process
2.3.7. K-Nearest Neighbors
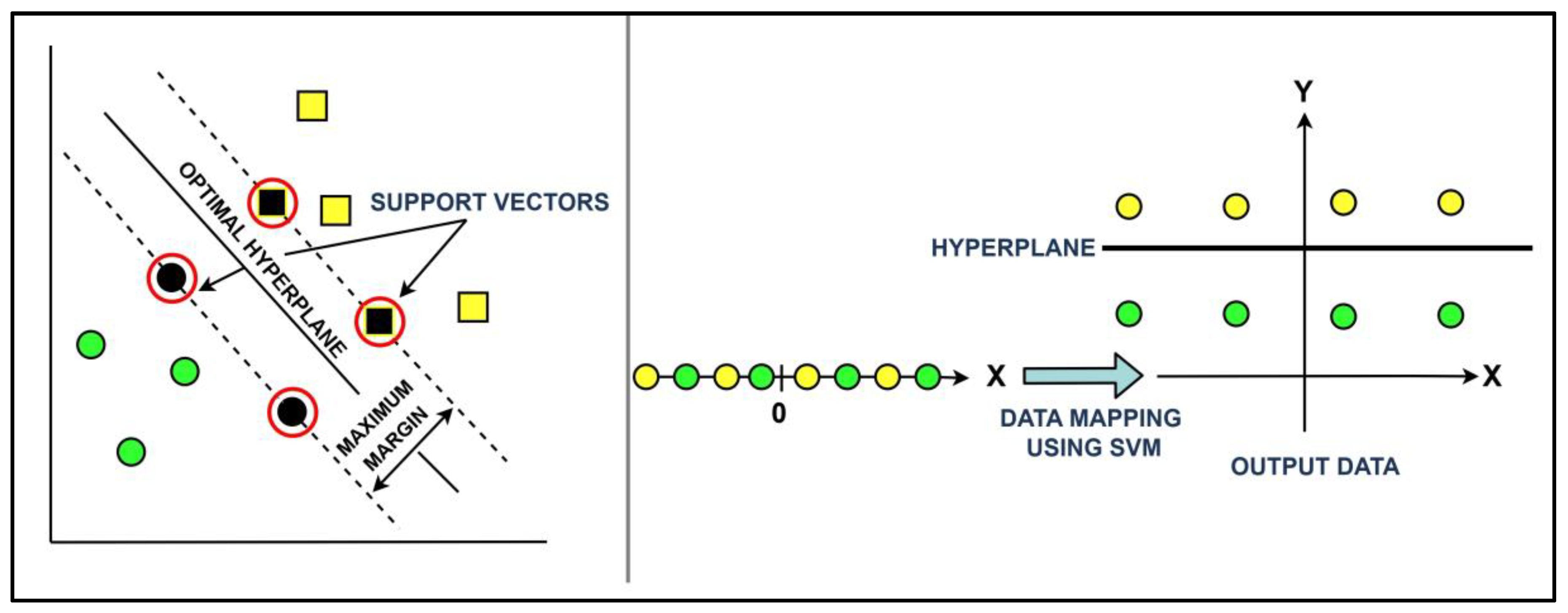
2.3.8. Support Vector Machine
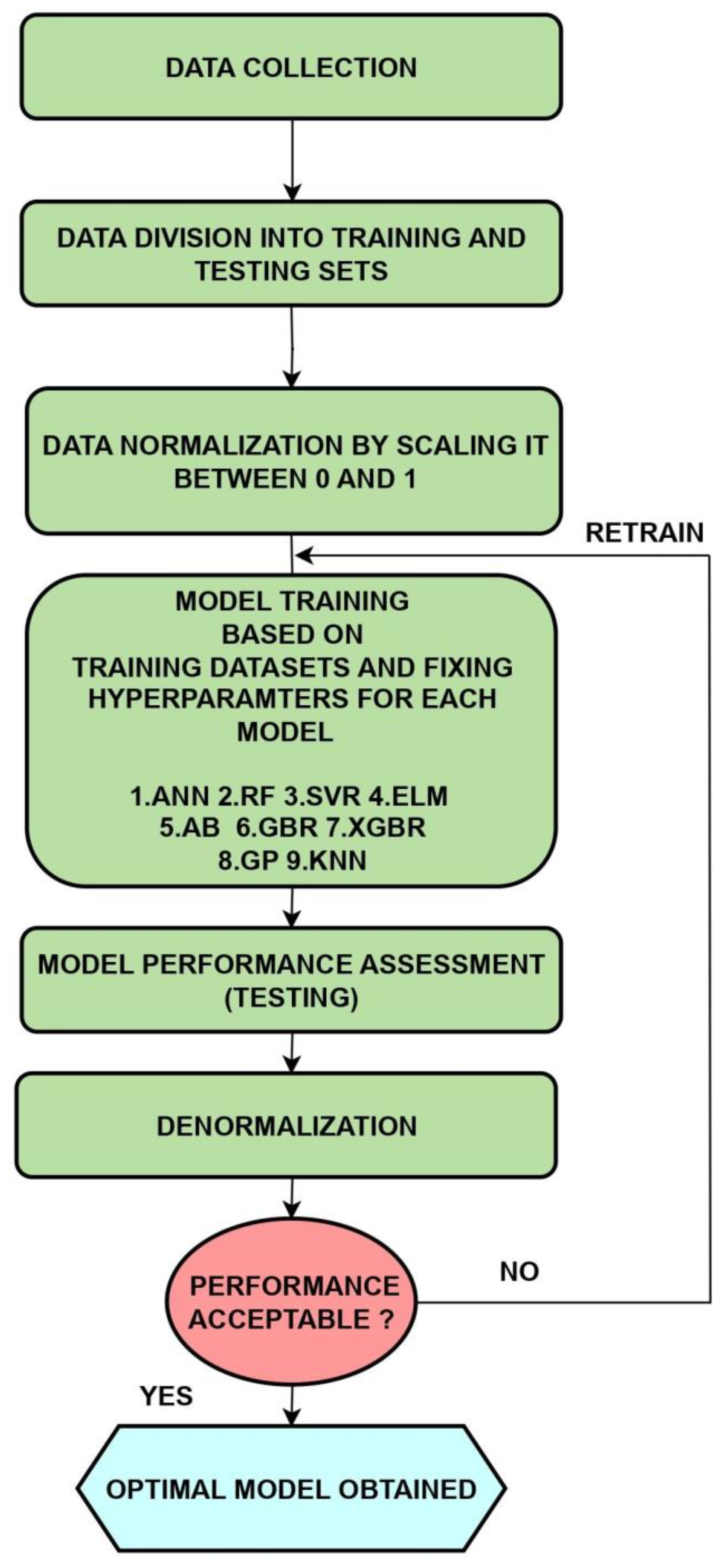
2.4. Model Development
2.5. Reliability Analysis
2.6. Performance Metrics
2.7. Ranking Scheme
3. Results
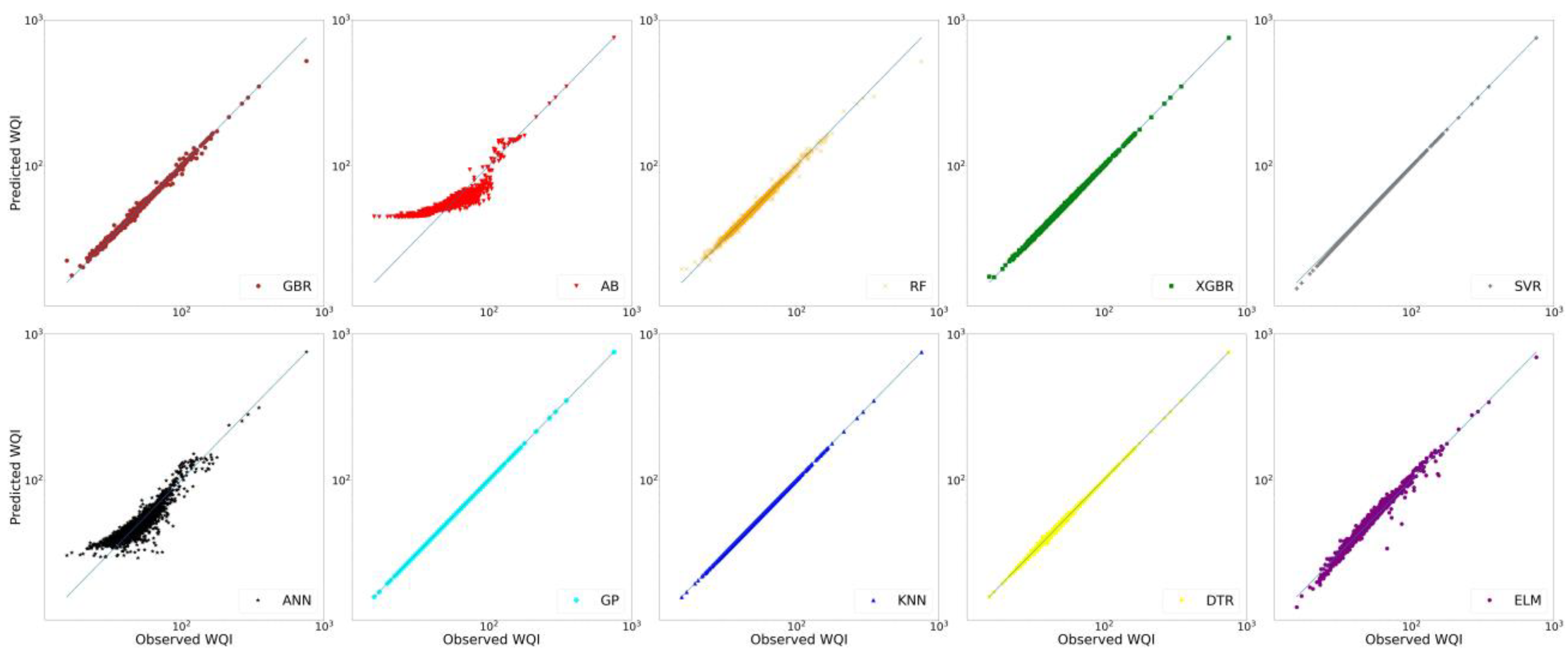
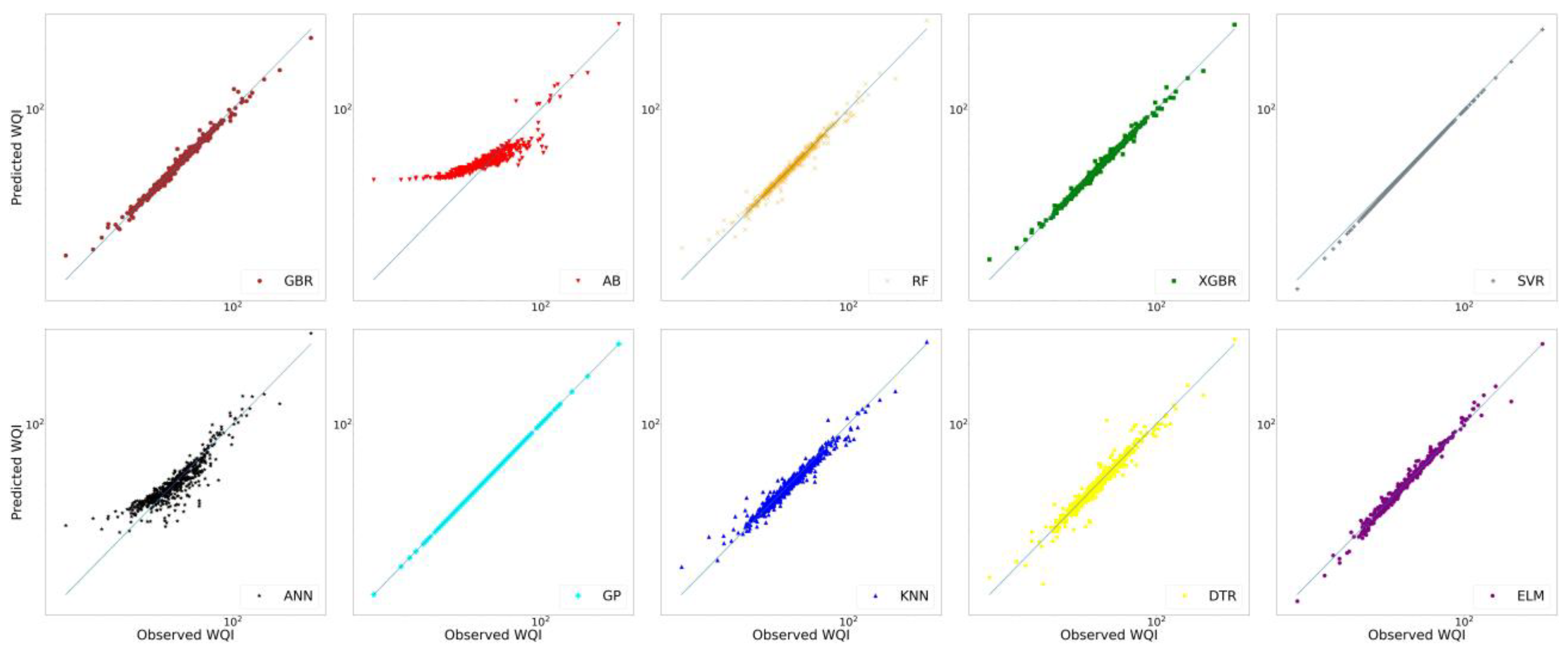
3.1. Results of WQI Estimated by ML Models
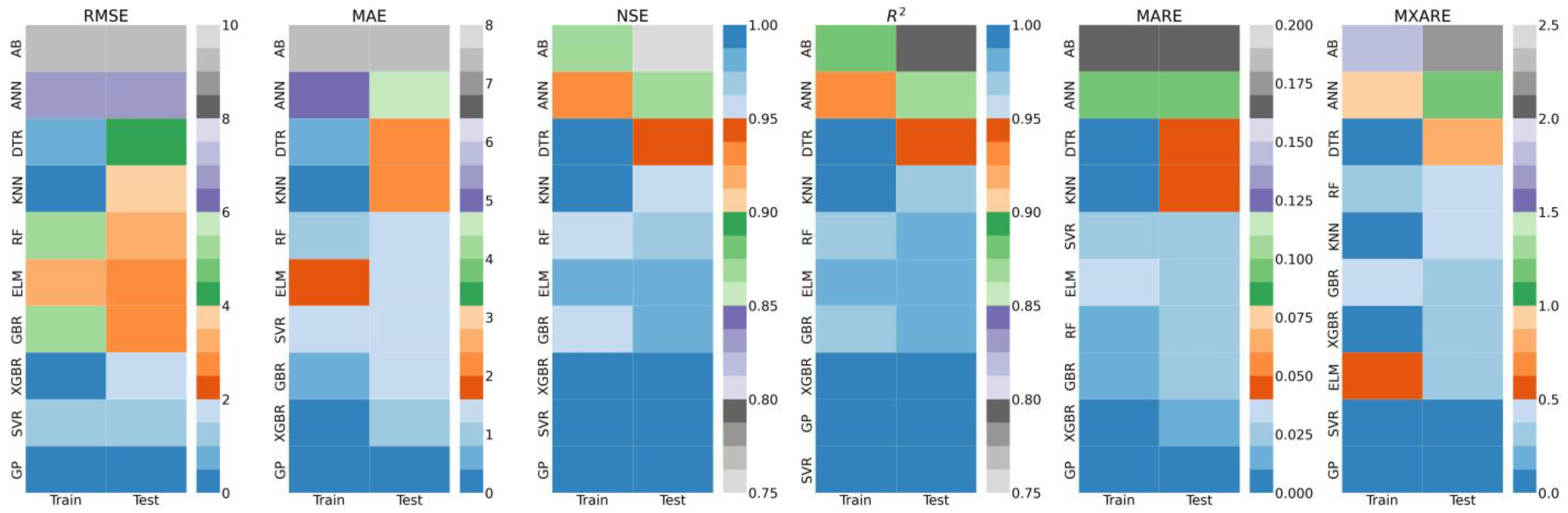
3.2. Metrics Results
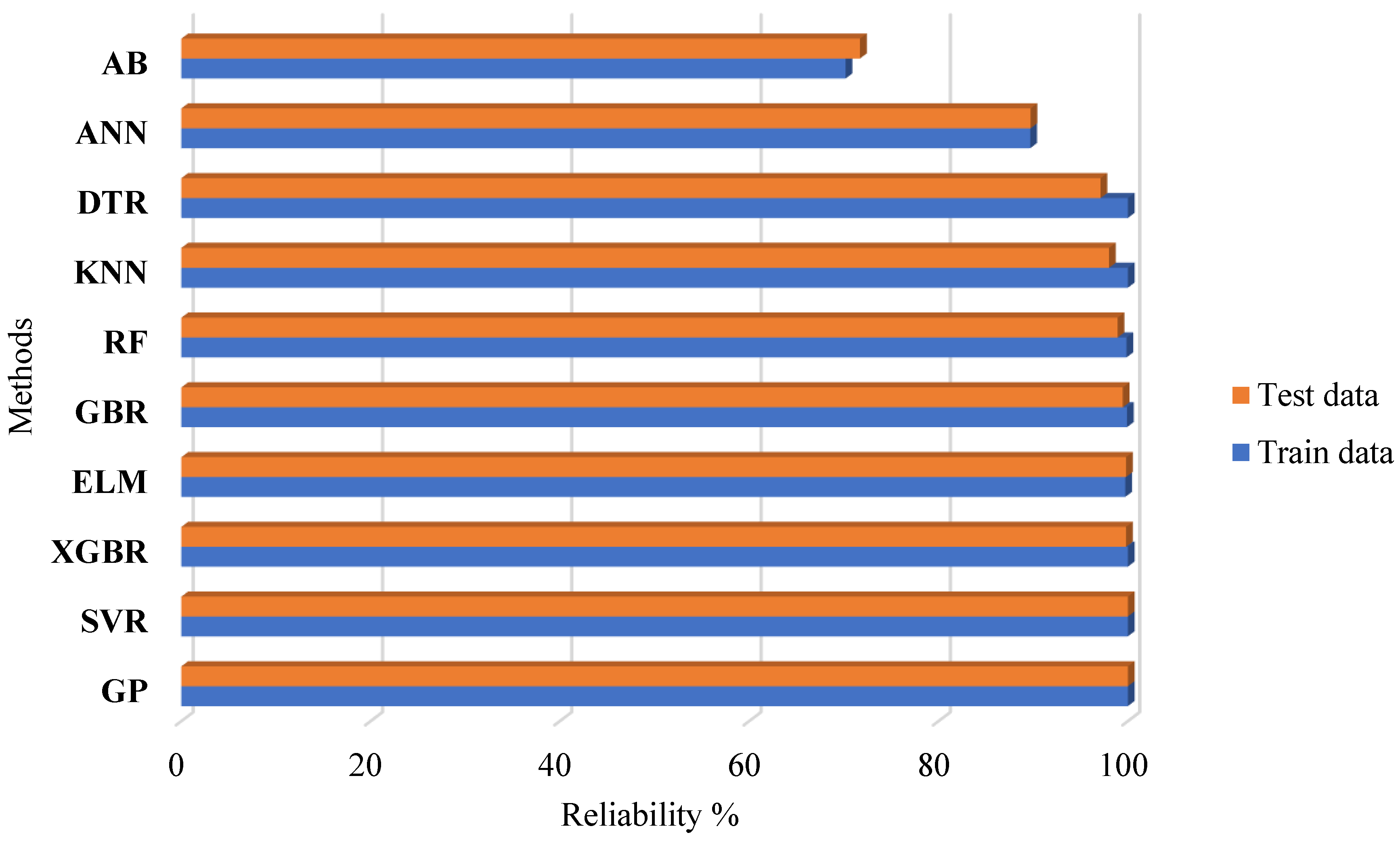
3.3. Results of the Reliability Analysis
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alam, J.B.; Islam, M.R.; Muyen, Z.; Mamun, M.; Islam, S. Archive of SID Water quality parameters along rivers Archive of SID. Int. J. Environ. Sci. Technol. 2007, 4, 159–167. [Google Scholar] [CrossRef]
- Khan, I.; Zakwan, M.; Mohanty, B. Water Quality Assessment for Sustainable Environmental Management. ECS Trans. 2022, 107, 10133. [Google Scholar] [CrossRef]
- Alizamir, M.; Sobhanardakani, S. An Artificial Neural Network—Particle Swarm Optimization (ANN- PSO) Approach to Predict Heavy Metals Contamination in Groundwater Resources. Jundishapur J. Health Sci. 2018, 10, e67544. [Google Scholar] [CrossRef]
- Ghobadi, A.; Cheraghi, M.; Sobhanardakani, S.; Lorestani, B.; Merrikhpour, H. Hydrogeochemical characteristics, temporal, and spatial variations for evaluation of groundwater quality of Hamedan–Bahar Plain as a major agricultural region, West of Iran. Environ. Earth Sci. 2020, 79, 428. [Google Scholar] [CrossRef]
- Khan, I.; Zakwan, M.; Pulikkal, A.K.; Lalthazula, R. Impact of unplanned urbanization on surface water quality of the twin cities of Telangana state, India. Mar. Pollut. Bull. 2022, 185, 114324. [Google Scholar] [CrossRef]
- Haghiabi, A.H.; Nasrolahi, A.H.; Parsaie, A. Water quality prediction using machine learning methods. Water Qual. Res. J. 2018, 53, 3–13. [Google Scholar] [CrossRef]
- Bui, D.T.; Khosravi, K.; Tiefenbacher, J.; Nguyen, H.; Kazakis, N. Improving prediction of water quality indices using novel hybrid machine-learning algorithms. Sci. Total Environ. 2020, 721, 137612. [Google Scholar] [CrossRef] [PubMed]
- El Bilali, A.; Taleb, A. Prediction of irrigation water quality parameters using machine learning models in a semi-arid environment. J. Saudi Soc. Agric. Sci. 2020, 19, 439–451. [Google Scholar] [CrossRef]
- Aldhyani, T.H.H.; Al-Yaari, M.; Alkahtani, H.; Maashi, M. Water Quality Prediction Using Artificial Intelligence Algorithms. Appl. Bionics Biomech. 2020, 2020, 6659314. [Google Scholar] [CrossRef]
- Tiyasha; Tung, T.M.; Yaseen, Z.M. A survey on river water quality modelling using artificial intelligence models: 2000–2020. J. Hydrol. 2020, 585, 124670. [Google Scholar] [CrossRef]
- Kouadri, S.; Elbeltagi, A.; Islam, A.R.M.T.; Kateb, S. Performance of machine learning methods in predicting water quality index based on irregular data set: Application on Illizi region (Algerian southeast). Appl. Water Sci. 2021, 11, 190. [Google Scholar] [CrossRef]
- Asadollah, S.B.H.S.; Sharafati, A.; Motta, D.; Yaseen, Z.M. River water quality index prediction and uncertainty analysis: A comparative study of machine learning models. J. Environ. Chem. Eng. 2021, 9, 104599. [Google Scholar] [CrossRef]
- Ahmed, M.; Mumtaz, R.; Anwar, Z.; Shaukat, A.; Arif, O.; Shafait, F. A multi–step approach for optically active and inactive water quality parameter estimation using deep learning and remote sensing. Water 2022, 14, 2112. [Google Scholar] [CrossRef]
- Uddin, M.G.; Nash, S.; Rahman, A.; Olbert, A.I. Performance analysis of the water quality index model for predicting water state using machine learning techniques. Process Saf. Environ. Prot. 2023, 169, 808–828. [Google Scholar] [CrossRef]
- Goodarzi, M.R.; Niknam, A.R.R.; Barzkar, A.; Niazkar, M.; Zare Mehrjerdi, Y.; Abedi, M.J.; Heydari Pour, M. Water Quality Index Estimations Using Machine Learning Algorithms: A Case Study of Yazd-Ardakan Plain, Iran. Water 2023, 15, 1876. [Google Scholar] [CrossRef]
- Shakhman, I.; Bystriantseva, A. Water Quality Assessment of the Surface Water of the Southern Bug River Basin by Complex Indices. J. Ecol. Eng. 2020, 22, 195–205. [Google Scholar] [CrossRef]
- Frank, A.J. UCI Machine Learning Repository. 2010. Available online: http://archive.ics.uci.edu/ml (accessed on 1 January 2023).
- Das Kangabam, R.; Bhoominathan, S.D.; Kanagaraj, S.; Govindaraju, M. Development of a water quality index (WQI) for the Loktak Lake in India. Appl. Water Sci. 2017, 7, 2907–2918. [Google Scholar] [CrossRef]
- Ismail, A.H.; Robescu, D. Assessment of water quality of the Danube river using water quality indices technique. Environ. Eng. Manag. J. 2019, 18, 1727–1737. [Google Scholar] [CrossRef]
- Pesce, S.F.; Wunderlin, D.A. Use of Water Quality Indices To Verify the Córdoba City (Argentina) on Suquía River. Wat. Res. 2000, 34, 2915–2926. [Google Scholar] [CrossRef]
- Cotruvo, J.A. 2017 Who guidelines for drinking water quality: First addendum to the fourth edition. J. Am. Water Work. Assoc. 2017, 109, 44–51. [Google Scholar] [CrossRef]
- Gaya, M.S.; Abba, S.I.; Abdu, A.M.; Tukur, A.I.; Saleh, M.A.; Esmaili, P.; Wahab, N.A. Estimation of water quality index using artificial intelligence approaches and multi-linear regression. IAES Int. J. Artif. Intell. 2020, 9, 126–134. [Google Scholar] [CrossRef]
- Gazzaz, N.M.; Yusoff, M.K.; Aris, A.Z.; Juahir, H.; Ramli, M.F. Artificial neural network modeling of the water quality index for Kinta River (Malaysia) using water quality variables as predictors. Mar. Pollut. Bull. 2012, 64, 2409–2420. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.; Singh, A.N.; Singhal, A. Application of ANN for water quality index. Int. J. Mach. Learn. Comput. 2019, 9, 688–693. [Google Scholar] [CrossRef]
- Yıldız, S.; Karakuş, C.B. Estimation of irrigation water quality index with development of an optimum model: A case study. Environ. Dev. Sustain. 2020, 22, 4771–4786. [Google Scholar] [CrossRef]
- Piraei, R.; Afzali, S.H.; Niazkar, M. Assessment of XGBoost to Estimate Total Sediment Loads in Rivers. Water Resour. Manag. 2023. [Google Scholar] [CrossRef]
- Piraei, R.; Niazkar, M.; Afzali, S.H.; Menapace, A. Application of Machine Learning Models to Bridge Afflux Estimation. Water 2023, 15, 2187. [Google Scholar] [CrossRef]
- Ebtehaj, I.; Bonakdari, H.; Moradi, F.; Gharabaghi, B.; Khozani, Z.S. An integrated framework of Extreme Learning Machines for predicting scour at pile groups in clear water condition. Coast. Eng. 2018, 135, 1–15. [Google Scholar] [CrossRef]
- Anmala, J.; Turuganti, V. Comparison of the performance of decision tree (DT) algorithms and extreme learning machine (ELM) model in the prediction of water quality of the Upper Green River watershed. Water Environ. Res. 2021, 93, 2360–2373. [Google Scholar] [CrossRef]
- Alomar, M.K.; Khaleel, F.; Aljumaily, M.M.; Masood, A.; Razali, S.F.M.; AlSaadi, M.A.; Al-Ansari, N.; Hameed, M.M. Data-driven models for atmospheric air temperature forecasting at a continental climate region. PLoS ONE 2022, 17, e0277079. [Google Scholar] [CrossRef]
- Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Niazkar, M.; Zakwan, M. Developing ensemble models for estimating sediment loads for different times scales. Environ. Dev. Sustain. 2023. [Google Scholar] [CrossRef]
- Mohammadpour, R.; Shaharuddin, S.; Chang, C.K.; Zakaria, N.A.; Ghani, A.A.; Chan, N.W. Prediction of water quality index in constructed wetlands using support vector machine. Environ. Sci. Pollut. Res. 2015, 22, 6208–6219. [Google Scholar] [CrossRef] [PubMed]
- Khoi, D.N.; Quan, N.T.; Linh, D.Q.; Nhi, P.T.T.; Thuy, N.T.D. Using machine learning models for predicting the water quality index in the La Buong River, Vietnam. Water 2022, 14, 1552. [Google Scholar] [CrossRef]

| Parameters | Unit | Mean | Minimum | Maximum | Standard Deviation | Variance | Range |
|---|---|---|---|---|---|---|---|
| BOD5 | mg/L | 4.31 | 0 | 50.90 | 2.97 | 8.84 | 39.42 |
| Suspended solids | mg/L | 12.93 | 0 | 595.00 | 16.54 | 273.67 | 595.00 |
| DO | mg/L | 9.50 | 0 | 90.00 | 4.42 | 19.60 | 90.00 |
| NO3 | mg/L | 4.31 | 0 | 133.40 | 6.88 | 47.35 | 133.40 |
| NO2 | mg/L | 0.24 | 0 | 109.00 | 2.18 | 4.76 | 109.00 |
| SO4 | mg/L | 59.36 | 0 | 3573.40 | 96.58 | 9328.20 | 3573.40 |
| PO4 | mg/L | 0.41 | 0 | 13.879 | 0.77 | 0.59 | 13.87 |
| Cl | mg/L | 93.73 | 0.02 | 5615.28 | 394.51 | 155,639.90 | 5615.26 |
| NH4 | mg/L | 0.75 | 0 | 39.42 | 2.48 | 6.18 | 39.42 |
| Model | Hyperparameter |
|---|---|
| SVR | Box constraint = 1 |
| Epsilon = 7.268 | |
| Kernel scale = 1 | |
| Solver = ISDA | |
| Iteration = 1000 | |
| KNN | Algorithm = auto Weights = distance n_neighbors = 3 p = 2 |
| GBR | loss = absolute_error n_estimators = 1600 max_depth = 3 learning_rate = 0.2 min_samples_split = 3 |
| XGBR | n_estimators = 400 reg_alpha = 0.4 reg_lambda = 1.6 learning_rate = 0.1 max_depth = 4 min_split_loss = 0.1 min_child_weight = 1 |
| AB | Criterion = squared_error loss = square n_estimators = 700 learning_rate = 1.5 |
| RFR | n_estimators = 100 max_depth = 12 min_samples_split = 3 |
| GP | kernel = Matern alpha = 0.001 |
| DTR | Criterion = friedman_mse |
| max_depth = 13 | |
| min_samples_split = 2 | |
| ANN | momentum = 0.2 |
| Learning rate = 0.1 | |
| Hidden layer = 2 | |
| Hidden neurons = 5 | |
| Max epochs = 50 | |
| ELM | Hidden nodes = 10 |
| RMSE | MAE | NSE | R2 | MARE | MXARE | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | |
| GP | 0.01 | 0.02 | 0.00 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| XGBR | 0.40 | 1.80 | 0.31 | 0.85 | 1.00 | 0.99 | 1.00 | 0.99 | 0.01 | 0.01 | 0.10 | 0.27 |
| SVR | 1.39 | 1.39 | 1.39 | 1.39 | 1.00 | 0.99 | 1.00 | 1.00 | 0.03 | 0.03 | 0.09 | 0.10 |
| KNN | 0.00 | 3.77 | 0.00 | 2.21 | 1.00 | 0.96 | 1.00 | 0.96 | 0.00 | 0.04 | 0.00 | 0.42 |
| GBR | 5.09 | 2.51 | 0.79 | 1.30 | 0.96 | 0.98 | 0.97 | 0.98 | 0.01 | 0.02 | 0.42 | 0.32 |
| ELM | 3.24 | 2.94 | 1.62 | 1.50 | 0.98 | 0.98 | 0.98 | 0.98 | 0.03 | 0.03 | 0.50 | 0.26 |
| DTR | 0.69 | 4.40 | 0.44 | 2.38 | 1.00 | 0.95 | 1.00 | 0.95 | 0.01 | 0.04 | 0.10 | 0.87 |
| RF | 5.34 | 3.04 | 0.93 | 1.53 | 0.96 | 0.97 | 0.97 | 0.98 | 0.01 | 0.03 | 0.31 | 0.44 |
| ANN | 6.83 | 6.90 | 4.81 | 4.75 | 0.93 | 0.87 | 0.93 | 0.87 | 0.10 | 0.09 | 0.93 | 1.23 |
| AB | 9.17 | 9.49 | 7.41 | 7.43 | 0.87 | 0.76 | 0.89 | 0.79 | 0.16 | 0.16 | 1.84 | 2.17 |
| RMSE | MAE | NSE | R2 | MARE | MXARE | Dataset Rank | Rank | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | ||
| GP | 2 | 1 | 2 | 1 | 2 | 1 | 3 | 2 | 2 | 1 | 2 | 1 | 2 | 1 | 1 |
| XGBR | 3 | 3 | 3 | 2 | 3 | 3 | 4 | 3 | 3 | 2 | 4 | 4 | 3 | 2 | 2 |
| SVR | 5 | 2 | 7 | 4 | 5 | 2 | 2 | 1 | 7 | 6 | 3 | 2 | 5 | 3 | 3 |
| KNN | 1 | 7 | 1 | 7 | 1 | 7 | 1 | 7 | 1 | 7 | 1 | 6 | 1 | 7 | 3 |
| GBR | 7 | 4 | 5 | 3 | 7 | 4 | 7 | 4 | 5 | 3 | 7 | 5 | 6 | 4 | 5 |
| ELM | 6 | 5 | 8 | 5 | 6 | 5 | 6 | 5 | 8 | 5 | 8 | 3 | 7 | 5 | 6 |
| DTR | 4 | 8 | 4 | 8 | 4 | 8 | 5 | 8 | 4 | 8 | 5 | 8 | 4 | 8 | 6 |
| RF | 8 | 6 | 6 | 6 | 8 | 6 | 8 | 6 | 6 | 4 | 6 | 7 | 8 | 6 | 8 |
| ANN | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| AB | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masood, A.; Niazkar, M.; Zakwan, M.; Piraei, R. A Machine Learning-Based Framework for Water Quality Index Estimation in the Southern Bug River. Water 2023, 15, 3543. https://doi.org/10.3390/w15203543
Masood A, Niazkar M, Zakwan M, Piraei R. A Machine Learning-Based Framework for Water Quality Index Estimation in the Southern Bug River. Water. 2023; 15(20):3543. https://doi.org/10.3390/w15203543
Chicago/Turabian StyleMasood, Adil, Majid Niazkar, Mohammad Zakwan, and Reza Piraei. 2023. "A Machine Learning-Based Framework for Water Quality Index Estimation in the Southern Bug River" Water 15, no. 20: 3543. https://doi.org/10.3390/w15203543








