Design of Drainage Downspouts Systems over a Road Embankment

Abstract

Numerous studies have examined the complex relationship between factors like embankment downspout spacing, height, slope, and rainfall characteristics in the quest to find the best spacing for embankment downspouts. Defining the correct spacing between road drainage elements is of utmost importance in minimizing water flow on roadways. This paper presents a methodology based on numerical methods for the design of road drainage systems using the Iber model. The objective of the work is to propose a tool and criteria for analyzing the hydraulic behavior of runoff on highways, determine the appropriate drainage behavior, and apply the methodology in a case study. This case study is based on a straight highway section with slopes up to 5%, according to Spanish road design regulations. Different dimensions are considered for the chute, drainage channel, collection nozzle, and downspout over the embankment. Tests are carried out to evaluate the separation between downspouts, the longitudinal slope, and the size of the nozzles. The results show the suitable hydraulic performance of the model, besides providing the absorption capacity of each downspout. The influence of the nozzle size, the slope, and the width of the causeway on the draughts and velocities is analyzed. The influence of downspout spacing and nozzle type on road drainage design is determined. In summary, this article presents a methodology and criteria for the design of road drainage systems and shows the results obtained in a case study using the Iber model. The results help in understanding the influence of different variables on the hydraulic behavior of road runoff and provide relevant information for proper drainage design.

1. Introduction

The impact of adverse weather conditions on traffic demand, traffic safety, and traffic flow is a well-documented phenomenon [1]. Generally, precipitation events, such as rainfall, exert a notable influence on travel dynamics. On average, they result in a reduction in travel speeds ranging from 1.2% to 18.4% and can lead to a decrease in traffic volume by approximately 1.1% to 16.5% [2]. Consequently, the presence of water on the road surface emerges as a pivotal factor in ensuring traffic safety. It not only affects drivers’ visibility but also predisposes the occurrence of hydroplaning [3,4]. The likelihood of hydroplaning is contingent upon several factors, including water depth, roadway geometry, vehicle speed, tread depth, tire inflation pressure, and the overall condition of the pavement surface [5].

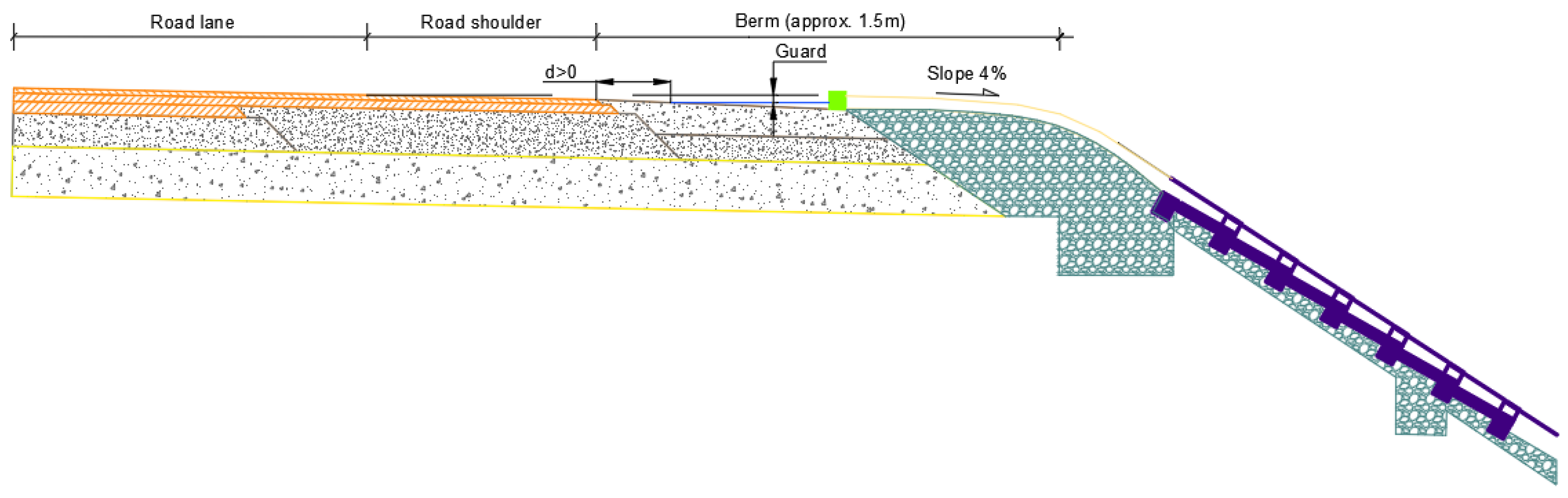
Various countries have established guidelines to ensure the efficient removal of runoff from road surfaces, aiming to prevent skidding, pooling, and related hazards. Notably, Spanish regulations govern road surface drainage [6] and delineate roadway protection within a specific cross-section. This protection is defined as the vertical difference in elevation between the lowest point of the roadway and the water level corresponding to the design flow rate. In accordance with these regulations, the drainage system for both the roadbed and shoulders must facilitate the collection, conveyance, and evacuation of runoff while adhering to the prescribed cross-sectional profile. That is, roadway protection greater than or equal to 0.05 m. Although the project may justify the adoption of a lower value, the water level must not reach the hard shoulder.

Within the context of Australian road design guidelines [7], specific criteria are prescribed for geometric road design, with a particular emphasis on drainage considerations. These criteria stipulate that road surface geometry should be configured to limit the drainage path to a maximum length of 60 m. For road sections where the operational or design speed exceeds 80 km/h, it is recommended to maintain a maximum water depth of 2.5 mm as desirable, with an absolute limit of 4.0 mm. In all other scenarios, both the desirable and absolute maximum allowable water depth are set at 5.0 mm. These guidelines play a crucial role in ensuring safe and efficient road design in Australia, addressing concerns related to water accumulation and road geometry.

In the United States, as per guidelines provided by the Federal Highway Administration [5], hydroplaning is acknowledged to potentially occur at speeds as low as 89 km/h when water depth reaches a mere 2 mm. However, the occurrence of hydroplaning is subject to a range of variables, which can lead to this phenomenon happening at even lower velocities and shallower water depths [8,9,10]. Consequently, in critical road sections, the risk of hydroplaning can be effectively mitigated through prudent highway geometry design, which involves reducing the drainage path length for water flowing over the pavement, thereby preventing the accumulation of water. Implementing such measures involves strategies like enhancing pavement surface texture depth, incorporating open-graded asphaltic pavements to channel water away from the tire contact area, or deploying drainage structures along the roadway to capture and expeditiously evacuate water flowing over the pavement [11].

In the pursuit of determining the optimal spacing for embankment downspouts, numerous studies have delved into the intricate interplay between factors such as embankment downspout spacing, embankment height, slope, and rainfall characteristics (e.g., [12,13,14]). Typically, these investigations leverage hydraulic and hydrologic models to simulate runoff patterns over embankments, facilitating the estimation of downspout spacing required to avert spillage and consequent erosion within the embankment. The findings of these studies offer valuable insights that can inform the design of road surface drainage systems and the development of overarching guidelines for embankment downspout spacing. Nonetheless, it is imperative to bear in mind that the optimal spacing remains contingent upon a multitude of variables, including localized climatic conditions and the construction material employed, necessitating case-specific adjustments for optimal results.

The precise definition of inlet spacing between road drainage elements holds paramount significance in the effort to minimize water flow on roadways. Diverse methodologies have been proposed by various authors in this context. Wong [12] introduced an approach founded on kinematic wave theory for determining road drainage inlet spacing under continuous grade conditions. This method correlates with the permissible maximum flood width, the physical attributes of the roadway, the empirical relationship between maximum discharge and intercepted flow, as well as the rainfall intensity–duration curve. Meanwhile, Nickow and Hellman [14] employed a genetic algorithm to present a decision-making framework for cost-effective stormwater inlet design within highway drainage systems. In this context, optimal design is defined as the most economical combination of inlet types, sizes, and locations that effectively drain a given length of pavement.

Ku et al. [13] presented a computational model designed for the optimal planning of road surface drainage facilities rooted in the varied flow theory. This model is specifically tailored to calculate flow profiles within linear drainage channels. It estimates the inflow from the road surface into the channel by considering rainfall intensity and road width as key variables. Notably, the inlet spacing determined through varied flow analysis tends to be greater than that derived from uniform flow analysis. However, this spacing diminishes with increasing slope. Consequently, a larger outlet spacing corresponds to a reduced number of outlets positioned along a road curb, illustrating the intricate relationship between design parameters and flow dynamics.

Kwak et al. [15] devised an optimal methodology for conducting a comprehensive analysis of road surface runoff, accounting for diverse road conditions to ensure a precise evaluation of the road’s drainage capacity. Factors taken into consideration encompass road width (set at 6 m) and slopes (ranging from a longitudinal road slope of 2% to 10%, a transverse road slope of 2%, and a transverse gutter slope of 2% to 7%). The analytical framework utilized essential parameters from the spatially varied flow module, with attention to basin geometry (simplified or modified basin), travel time (in the context of road surface flow or gutter flow), and the interception efficiency of the grate inlet. This approach enables a more comprehensive and accurate assessment of the road’s ability to manage surface runoff, accommodating various real-world road scenarios.

Han et al. [16] proposed a prediction model for water film depth (WFD) that hinges on the geometric attributes of road infrastructure and the effectiveness of drainage systems under varying rainfall intensities. Specifically, pavement WFD on rainy days is defined as the depth of water accumulation during short-duration (1 h) rainfall events. This research centers its attention on WFD at locations like water-retaining belts and curb stones. The interplay of different road configurations and combinations yields varied water depths, even when water accumulation remains constant. As such, constructing a WFD-based model entails a multi-faceted approach, encompassing rainfall calculations, the development of a water accumulation model, the determination of drainage facility displacement, and the derivation of WFD formulas for road surfaces through the application of the Manning equation, tailored to the distinct geometric characteristics of the road.

Li et al. [17] introduced an updated two-dimensional flow simulation program, FullSWOF [18], which constitutes a significant advancement in hydraulic modeling. This model comprehensively solves shallow water equations governing overland flow while incorporating submodules for modeling infiltration by zones and the interception of flow by grate inlets. In the context of this study, a comprehensive dataset comprising 1000 road-curb inlet modeling cases was established. These cases spanned a wide array of combinations involving 10 longitudinal slopes ranging from 0.1% to 1%, 10 cross slopes ranging from 1.5% to 6%, and 10 upstream inflow rates ranging from 6 L/s to 24 L/s, all aimed at determining inlet length. A second set of 1000 modeling cases, sharing the same longitudinal and cross slopes, explored 10 different curb inlet lengths, varying from 0.15 m to 1.5 m, with the goal of assessing inlet efficiency. Consequently, regression equations for inlet length and inlet efficiency were meticulously developed as functions of the input parameters, offering valuable insights into the design and optimization of road-curb inlets.

Aranda et al. [19] presented a novel approach grounded in hydraulic numerical simulation, harnessing the Iber model [20], to assess the efficacy of grate inlets. This method is well aligned with the design standards upheld in various countries. The methodology delineated in this study streamlines the process of conducting sensitivity analyses for diverse scupper configurations. It grants comprehensive control over the hydraulic performance of each individual grate inlet within a range of scenarios. The availability of detailed hydraulic data serves as the cornerstone for comparative evaluations of different solutions, thereby facilitating informed decision-making processes and ultimately culminating in the realization of efficiency-centric solutions.

This article introduces a methodology underpinned by numerical methods for the design of road drainage systems, achieved through the solution of 2D shallow water equations utilizing the Iber model. The primary objectives of this paper encompass the development of a tool and a set of criteria for the systematic analysis of the hydraulic dynamics of runoff on road surfaces, the formulation of a comprehensive methodology to ascertain the effectiveness and efficiency of road drainage systems, and the practical demonstration of the proposed methodology through an illustrative case study, offering a real-world application and validation of the approach.

2. Methodology

2.1. Design Hyetograph

Design hyetographs are used in conjunction with unit hydrographs to obtain peak discharge and hydrograph shape for hydraulic design [20]. Their definition is critical in drainage design since it determines the peak flooding volume in a catchment and the corresponding drainage capacity demand for a given return period [21]. Different synthetic unit hydrograph methods available in the hydrologic literature can be found in Bhunya et al. [22] or in Singh et al. [23].

For the construction of the design hyetograph, the Alternating Blocks Hyetograph Method [24] was selected, which is commonly used as a conservative method because it conducts the highest estimate of peak flows, creating critical flood situations [25].

2.2. Numerical Tool: Iber

Iber is a two-dimensional (2D) numerical tool for the simulation of free surface flows [26]. Initially originating from the academic realm, it was originally conceived for assessing hydrodynamics and sediment transport processes in river systems [27,28,29,30,31,32,33,34]. Presently, Iber boasts an integrated suite of calculation modules tailored to simulate a diverse array of environmental fluid phenomena. These encompass hydrological processes [35,36], pollutant transport [37,38], large-wood transport [39,40], dam-break scenarios [41,42,43], eco-hydraulics [44], urban drainage processes [45,46], as well as the release and propagation of snow avalanches [47,48].

When utilizing Iber for simulating surface urban drainage problems, the continuity equation’s source terms must account for rainfall intensity, the loss process, and flow sinks resulting from drainage inlets leading to the sewer system network. These considerations are crucial for the governing equations [49].

$$\begin{array}{c}\frac{\partial h}{\partial t}+\frac{\partial q_x}{\partial x}+\frac{\partial q_y}{\partial y}=R-f-f_i\\ \frac{\partial q_x}{\partial t}+\frac{\partial }{\partial x}\left(\frac{q_x^2}{h}+g\frac{h^2}{2}\right)+\frac{\partial }{\partial y}\left(\frac{q_x{q}_y}{h}\right)=gh\left(S_{o,x}-S_{f,x}\right)\\ \frac{\partial q_x}{\partial t}+\frac{\partial }{\partial x}\left(\frac{q_x{q}_y}{h}\right)+\frac{\partial }{\partial y}\left(\frac{q_y^2}{h}+g\frac{h^2}{2}\right)=gh\left(S_{o,y}-S_{f,y}\right)\end{array}$$

(1)

where h is the water depth, q_x and q_y denote the two components of the specific discharge, g is the gravitational acceleration, S_o,x and S_o,y are the two components of the bottom slope, and S_f,x and S_f,y are the two components of the friction slope, typically calculated using the Manning formula.

When it comes to hydrological modeling, the variable $R$ considers the impact of rainfall on the overland flow [49], while $f$ represents the rate of distributed hydrological losses, including infiltration, evapotranspiration, interception, and surface retention [35]. The term $f_i$ relates to the distributed losses of surface water as it is incorporated into the drainage system.

Iber solves two-dimensional shallow water equations (Equation (1)) using a conservative scheme based on the Finite Volume Method (FVM). It operates on unstructured, structured, or hybrid meh configurations, which may comprise triangles and/or quadrilaterals. To handle convective fluxes, Iber employs an explicit first-order Godunov-type upwind scheme [50], specifically the Roe Scheme [51].

Iber offers a range of functionalities that greatly simplify the process of calculating rainfall–runoff transformation processes. It can be effectively utilized as a distributed hydrological model based on the principles of 2D shallow water equations [35]. These functionalities include:

• Rainfall Field Definition: Iber allows users to define rainfall fields using data from rain gauges or raster files.
• Rainfall Loss Definition: Users can specify rainfall losses using various infiltration models, such as Green–Ampt, Horton, SCS, and constant infiltration, all of them constant or spatially distributed.
• Ad hoc Numerical Scheme: Iber incorporates a specialized numerical scheme known as the DHD scheme, purpose-built for hydrological applications.
• Digital Terrain Model Enhancement: Iber provides utilities to efficiently smooth Digital Terrain Models, even when they may have poor quality or unfavorable conditions.

2.3. Design Criteria

The design of the drainage elements of the highway platform requires the establishment of particular parameters according to the regulations in force in each state. In the author’s opinion, the most relevant parameters are as follows:

• Design storm. In this case study, rainfall is established for a return period of T = 25 years, as indicated in the Spanish Road Drainage Regulation (5.2-IC).
• Flow depth is circulating over the side gutter, encroaching into the shoulder. This parameter relates to the driver’s safety to the extent that a vehicle driving on the shoulder could present stability problems due to aquaplaning [4,16,19,52]. This parameter depends on the dimensions of the prefabricated element that limits the flow, generally a barrier kerb of 10 cm high.
• Flow depth in the downspout drain inlet and in the downspout. This parameter is related to the maintenance of the road embankment to the extent that hypothetical drain overflows on the embankment could affect its stability. The authors, based on their experience, consider that a minimum guard of 3 cm should be considered, bearing in mind the potential existence of obstacles or sediments.
• Cross-section choice. A standard section must be selected with the indications of the Project Technical Specifications. The analysis of the possible standard sections is beyond the scope of this research; instead, a methodology where any cross-section can be considered is presented. Nevertheless, generally speaking, there are currently two possible cross sections, with or without a side gutter. For the purposes of the present paper, the latter type of cross-section has been selected (Figure 1).

3. Case Study

3.1. Study Area

The case study presented in this paper is a synthetic stretch of highway fulfilling the characteristics indicated in the highway design regulations of the Spanish Ministry of Public Works and Transport (Instruction 3.1-IC).

The choice of a synthetic case was determined by the geometric needs of the cases to be modeled. In other words, it is a straight section with a slope varying between 0% and 5% (i.e., the maximum value allowed in the Spanish regulations for the design of highways). The curved section was not considered because the design radii of a dual carriageway are greater than 700 m, and the distance between the straight and curved sections is negligible.

The geometric characteristics of the straight highway section are based on the indications of Instruction 3.1-IC, which are summarized in

Table 1. Geometric characteristics of the section of highway modeled.

Inner Shoulder	Inner Road Lane	Outer Road Lane	Outer Shoulder	Berm	Cross Slope (it)	Long. Slope (il)
1.0 m	3.5 m	3.5 m	2.5 m	1.5 m	2%	0–5%

.

In addition to the above parameters, the gutter and platform drainage channel dimensions, the collection nozzle typology, and the embankment downspout spacing are involved. With regards to the gutter and platform drainage channel dimensions, two alternatives with a width of 20 and 30 cm were analyzed.

Nozzles collecting the roadway water and discharging it to the embankment downspouts were modeled for two sizes and two different shapes (i.e., symmetrical and asymmetrical) (see Figure 2). It should be noted that the hydraulic capacity of symmetric nozzles is lower than that of asymmetric ones, so their use would only be justified in alignment changes (concave agreements coinciding with slopes close to 0%) where flow reaches the nozzle from both directions.

Finally, regarding the dimensions of the embankment downspout itself, since these are prefabricated pieces, standard dimensions from the existing manufacturers were considered. From all of them, the smallest one (30 cm wide) was selected since, as it will be later verified, it is sufficient to satisfy the conditions of the Spanish regulations for the design of highways.

Following the above conditions, a set of 72 different models combining all possible configurations was analyzed. These can be summarized as follows:

• Separation between embankment downspouts: 25 m, 20, and 15 m (three models)
• Longitudinal slope: 0.5% to 5% (six models)
• Gutter width: 30 cm and 20 cm (two models)
• Type of nozzle, called large and reduced (see dimensions in Figure 2) (two models)

3.2. Climate Information

In the present study, the same design hyetograph as in Aranda et al. [19] was used. Due to their torrential intensity, a typical highly convective storm was selected by the Júcar River Basin Authority (CHJ) through the Júcar Automatic Hydrological Information System (SAIH). The design hyetograph was created from a dataset with 26 full years of 5-min precipitation records (1995–2020) at the Arquillo reservoir rain gauge located in Teruel (Spain).

3.3. Numerical Model and Domain Discretization

Regarding the model geometry, as commented above, it is a straight section of highway with the characteristics indicated in Table 1. However, for computing time purposes, it was necessary to find out the minimum length of the model to ensure its hydraulic stability. In this sense, a sensitivity analysis was carried out on the number of embankment downspouts and the minimum distance between them.

As shown in Figure 3, a minimum number of five embankment downspouts is needed since the first three (i.e., B3, B4, and B5) do not have a full receiving basin. B1 and B2 are justified by the need to compare at least two downspouts with the same receiving basin size and, thus, with a similar flow. Otherwise, the model would not be representative of the physical phenomenon to simulate, giving rise to each subsequent element having to capture the runoff from its basin plus the excess of the previous one.

Table 2. Drainage area for each embankment downspout (B) (m²) for a separation of 25 m, depending on the longitudinal slope of the road (i_l).

Slope (il)	B1	B2	B3	B4	B5
0.5%	262.75	262.75	262.75	262.75	40.17
1%	262.75	262.75	262.75	262.52	25.25
2%	262.75	262.75	262.75	246.31	11.52
3%	262.75	262.75	262.75	220.92	6.97
4%	262.75	262.75	262.75	193.22	4.73
5%	262.75	262.75	262.75	164.61	3.41

,

Table 3. Drainage area for each embankment downspout (B) (m²) for a separation of 20 m, depending on the longitudinal slope of the road (i_l).

Slope (il)	B1	B2	B3	B4	B5
0.5%	210.06	210.06	210.06	210.06	40.17
1%	210.06	210.06	210.06	210.06	25.25
2%	210.06	210.06	210.06	193.79	11.52
3%	210.06	210.06	210.06	168.40	6.97
4%	210.06	210.06	210.06	141.39	4.05
5%	210.06	210.06	209.53	113.00	3.40

and

Table 4. Drainage area for each embankment downspout (B) (m²) for a separation of 15 m, depending on the longitudinal slope of the road (i_l).

Slope (il)	B1	B2	B3	B4	B5
0.5%	157.55	157.55	157.55	157.55	40.17
1%	157.55	157.55	157.55	157.49	25.25
2%	157.55	157.55	157.55	141.28	11.52
3%	157.55	157.55	157.55	168.40	6.97
4%	157.55	157.55	156.86	88.75	4.73
5%	157.55	157.55	146.72	69.75	3.40

show the drainage area at each downspout for different longitudinal slopes and downspout separations.

According to Table 3 and Table 4, Figure 3, it can be seen that B3, B4, and B5 only capture the runoff from the full basin for certain longitudinal slopes, while B1 and B2 always receive the contribution of the entire basin. Therefore, with this model setup, at least there are always two downspouts in such a way that the runoff volume drained through them can be quantified.

With regard to other relevant model parameters, it should be noted that a constant roughness was adopted for the entire surface (bituminous hot mixture) estimated according to the Manning coefficient (i.e., n = 0.015). The SCS Curve Number Method was used as a rainfall–runoff model, with a curve number of 96. Finally, the mesh size of the hydraulic model is constant for all simulations: for the area corresponding to the receiving basin (highway roadway), the elements are 40 × 20 cm; 15 × 15 cm elements for the nozzles; and 20 × 30 cm elements were selected for the embankment downspouts (Figure 4).

Table 5. Geometric characteristics of hydraulic models.

Downspout Separation (m)	Longitude (m)	Width (m)	Surface Area (m2)	Volume (m3)
25	108	10.5	1134.3	171.2
20	88	10.5	924.27	140.04
15	68	10.5	714.21	109.06

summarizes the most relevant variables of the models used in this research according to downspout separation.

4. Results and Discussion

This section presents the results obtained through the 72 simulations conducted in the case study. The set of data obtained for each simulation corresponds to a two-dimensional model in such a way that information on flow depth, level, and velocity, as well as the Froude number, is available on each mesh element, thus being able to evaluate the design criteria according to the adopted regulations.

4.1. Hydraulic Performance

The aim of this analysis is to evaluate the hydraulic performance of the drainage element, verifying that each downspout is capable of absorbing all the flow collected by each nozzle. Otherwise, if a nozzle-downspout system is not capable of collecting all the flow coming from its basin, it would transfer additional flow to the next nozzle. This fact is aggravated as the length of the embankment increases.

Table 6. Percentage of evacuated volume of water with respect to the total volume for the 72 models analyzed for different downspout separations, gutter width, and nozzle type.

Downspout Separation		25 m				20 m				15 m
Gutter Width		20 cm		30 cm		20 cm		30 cm		20 cm		30 cm
Nozzle Type		RN	LN	RN	LN	RN	LN	RN	LN	RN	LN	RN	LN
Longitudinal slope (il)	0.5	* 99	* 99	100	100	100	100	100	100	100	100	100	100
	1	* 99	* 99	* 98	100	* 95	100	100	100	100	100	100	100
	2	* 96	* 99	* 96	100	* 95	100	* 97	100	* 99	100	100	100
	3	* 93	* 99	* 92	100	* 92	100	* 94	100	* 96	100	* 98	100
	4	* 89	* 98	* 88	100	* 88	100	* 91	100	* 94	100	* 98	100
	5	* 84	* 97	* 82	* 99	* 86	98	* 86	100	* 91	100	* 97	100

* Not suitable design; RN: Reduced nozzle; LN: Large nozzle.

shows the percentage of the evacuated volume of water with respect to the total volume for the 72 models analyzed for different downspout separations, gutter width, and nozzle type.

4.2. Nozzle Size

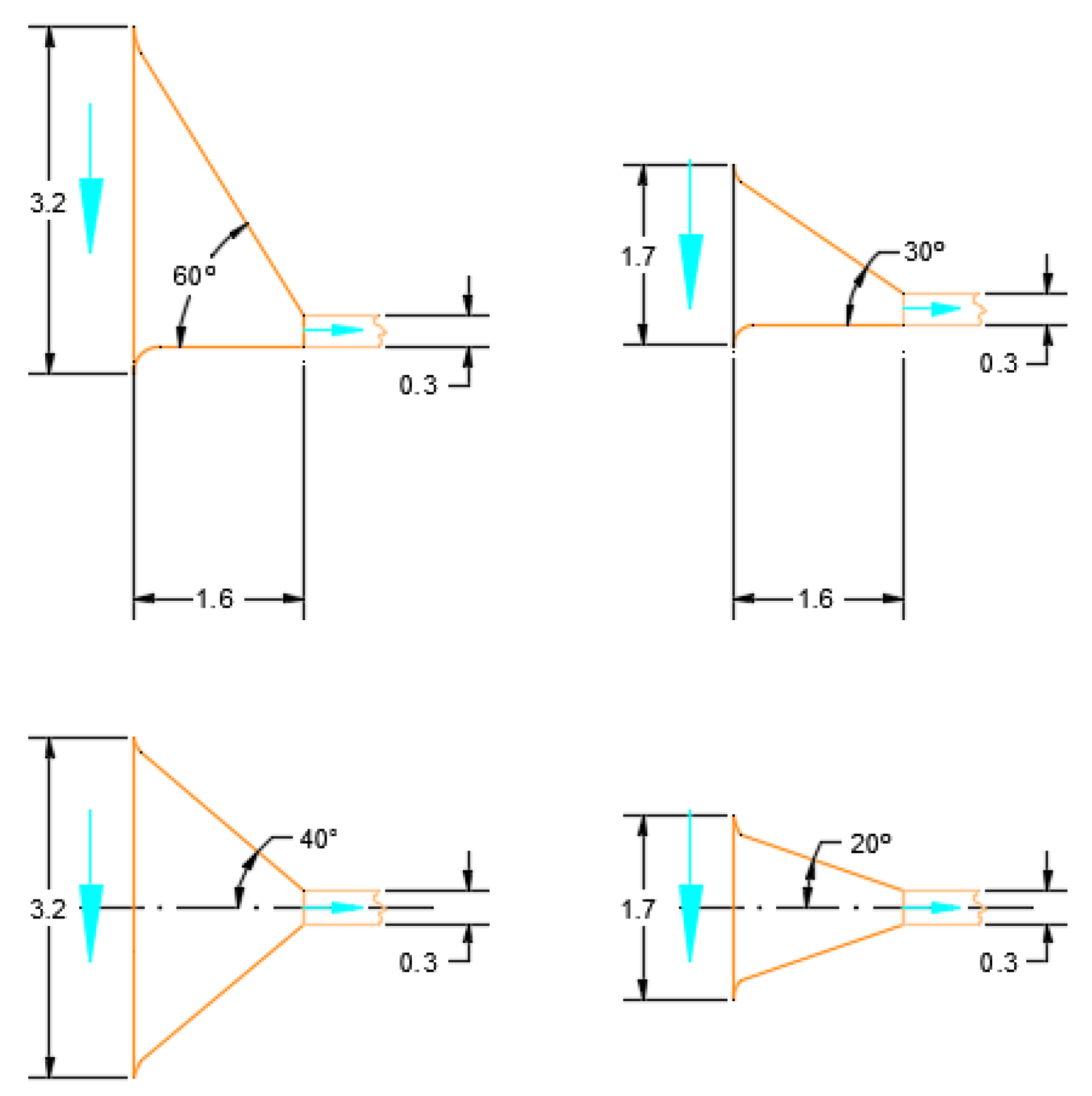
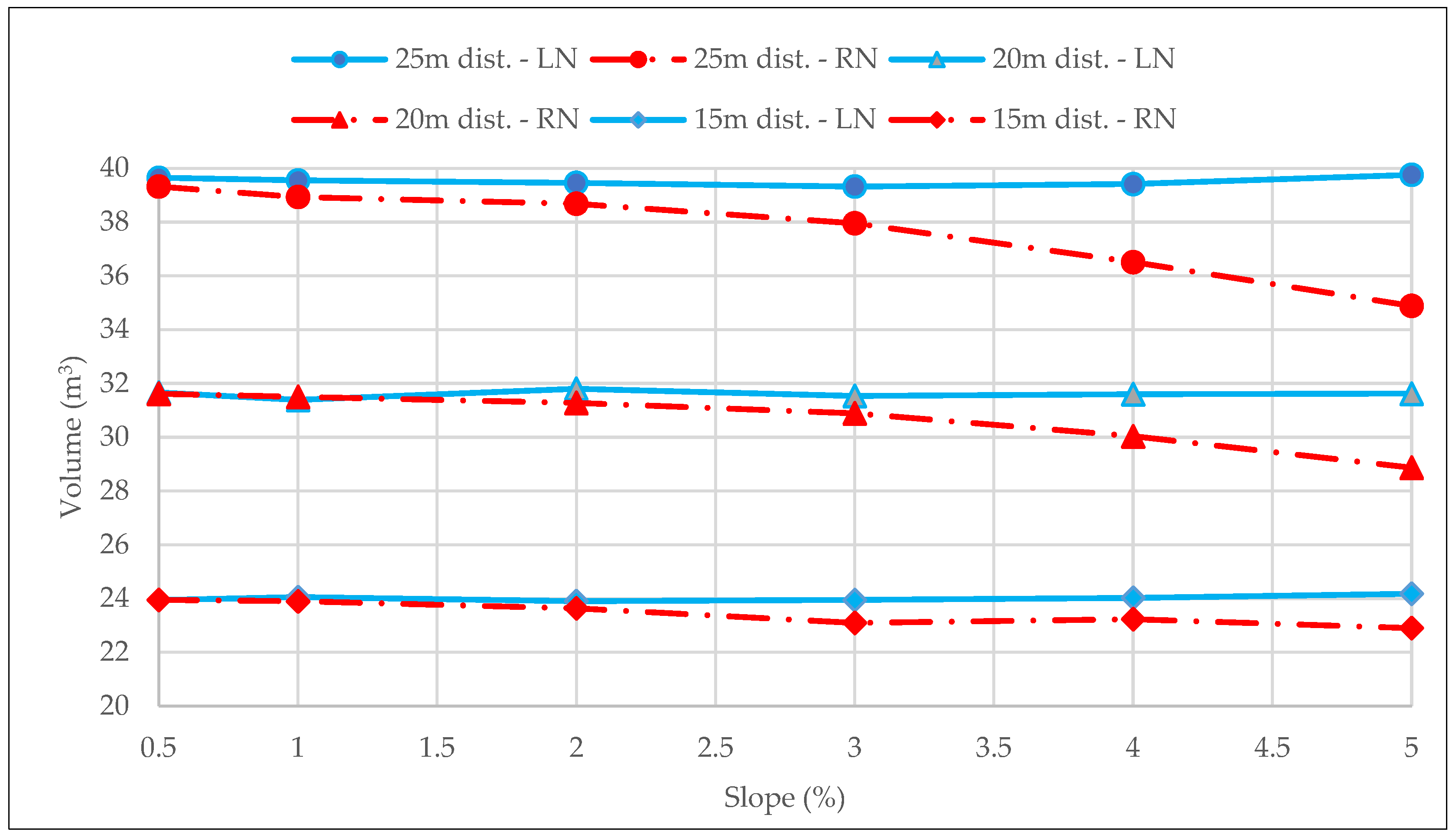
In this section, the effect of the size of the nozzle (Figure 2) is studied. Figure 5 and Figure 6 show the volume evacuated by each nozzle (considering equal drainage area) for both nozzle typologies and all longitudinally considered slopes.

As can be seen in Figure 5 and Figure 6, when the slope is equal to or less than 2%, both nozzles have equal hydraulic capacity. However, for slopes greater than 2%, the small nozzle presents a decrease in its hydraulic capacity that increases with the slope. This phenomenon can also be seen when comparing Figure 5 and Figure 6. For small nozzles, the volume evacuated by B1 is higher than B2 due to the lower hydraulic capacity of the reduced nozzle, which causes an increase in the gutter water level and, thus, in the flow evacuated by B1, since this is proportional to the water level.

4.3. Longitudinal Slope

This section shows the influence of the longitudinal slope on the elements that constitute the drainage of the platform: the gutter, nozzle, and downspout.

Table 7. Maximum water depths (in cm) for the different drainage elements of the platform with a large nozzle and a 30 cm wide gutter.

	25 m Downspout Separation			20 m Downspout Separation			15 m Downspout Separation
Slope	Gutter	Nozzle	Downspout	Gutter	Nozzle	Downspout	Gutter	Nozzle	Downspout
0.5%	7.5	8.2	6.6	6.5	7.5	6.1	5.4	7.0	5.0
1%	6.9	7.5	6.2	6.0	7.0	6.0	5.2	6.0	5.0
2%	6.0	7.0	6.0	5.6	6.7	5.6	5.0	6.0	5.0
3%	5.7	7.3	5.8	5.3	6.0	5.2	4.9	6.0	5.0
4%	5.3	7.1	5.7	4.8	5.9	5.0	4.6	5.0	4.0
5%	5.0	6.9	5.5	4.6	5.8	4.8	4.0	5.0	4.0

and

Table 8. Maximum water depths (in cm) for the different drainage elements of the platform with a reduced nozzle and a 30 cm wide gutter.

	25 m Downspout Separation			20 m Downspout Separation			15 m Downspout Separation
Slope	Gutter	Nozzle	Downspout	Gutter	Nozzle	Downspout	Gutter	Nozzle	Downspout
0.5%	7.9	7.1	3.8	7.0	6.1	3.3	5.3	4.8	2.6
1%	7.7	6.6	3.7	6.7	5.7	3.1	5.1	4.5	2.5
2%	7.5	7.4	3.8	6.5	6.1	3.0	5.0	4.5	2.6
3%	7.1	8.7	3.6	6.2	7.0	3.0	5.0	5.9	2.5
4%	6.8	9.7	3.4	5.8	7.8	3.0	4.7	6.4	2.3
5%	6.6	10.0	3.3	5.7	8.9	3.0	4.4	8.1	2.6

show the maximum water depth reached in the model with a 30 cm wider gutter, combining different longitudinal slopes and embankment downspout distancing for a large and a reduced nozzle, respectively.

Table 9. Maximum water depths (in cm) for the different drainage elements of the platform with a large nozzle and a 20 cm wide gutter.

	25 m Downspout Separation			20 m Downspout Separation			15 m Downspout Separation
Slope	Gutter	Nozzle	Downspout	Gutter	Nozzle	Downspout	Gutter	Nozzle	Downspout
0.5%	8.9	7.2	6.3	7.2	6.6	5.2	6.5	6.1	4.3
1%	7.8	6.4	5.5	6.8	6.3	4.8	6.0	5.4	4.6
2%	6.9	6.1	5.3	6.0	6.1	4.5	4.9	4.9	4.1
3%	6.3	6.0	5.3	5.2	6.0	4.4	4.3	4.4	4.1
4%	6.0	5.8	5.1	4.9	5.8	4.3	4.0	4.2	3.8
5%	5.8	6.2	4.9	4.7	5.6	4.2	3.9	4.1	3.8

and

Table 10. Maximum water depths (in cm) for the different drainage elements of the platform with a reduced nozzle and a 20 cm wide gutter.

	25 m Downspout Separation			20 m Downspout Separation			15 m Downspout Separation
Slope	Gutter	Nozzle	Downspout	Gutter	Nozzle	Downspout	Gutter	Nozzle	Downspout
0.5%	9.5	6.2	3.3	7.9	4.8	2.6	6.8	5.4	3.1
1%	9.3	6.2	3.6	7.8	5.2	3.0	6.5	4.5	2.4
2%	8.1	7.1	3.4	7.0	6.6	2.8	6.1	4.5	2.5
3%	7.6	8.0	3.3	6.6	7.0	3.0	5.4	5.3	2.3
4%	7.3	8.8	3.2	6.4	7.3	2.7	5.1	5.9	2.2
5%	7.2	9.5	3.1	6.3	7.9	2.6	5.2	7.4	2.8

show the maximum water depth reached in the model with a 20 cm wider gutter, combining different longitudinal slopes and embankment downspout distancing for a large and a reduced nozzle, respectively.

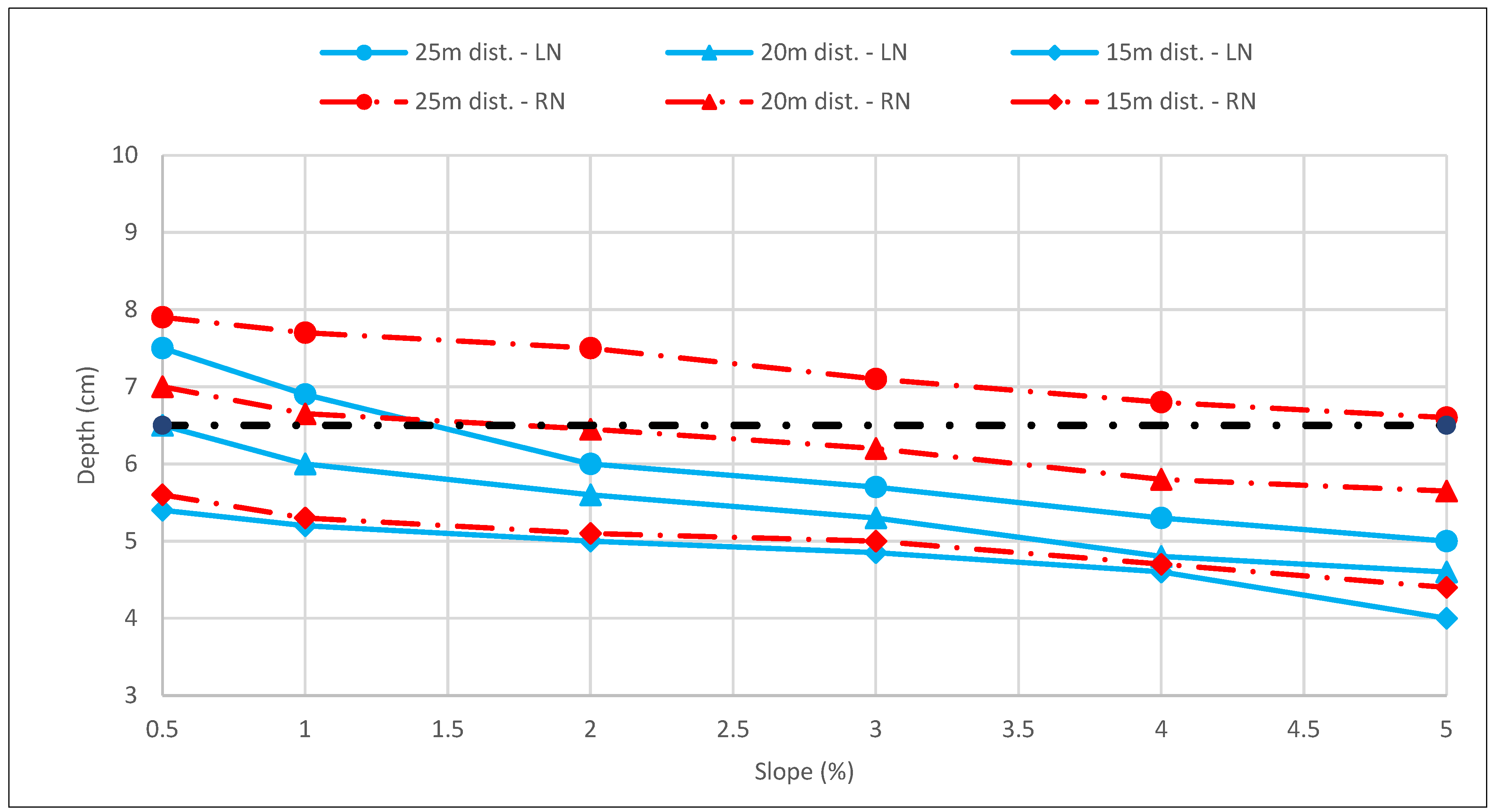
In view of the results, it can be concluded that the 30 cm wide downspout satisfactorily meets any type of design; that is, it is not a conditioning element, reaching maximum values of 6.3 cm for a minimum slope of 0.5%, a 20 cm wide gutter, and a large nozzle.

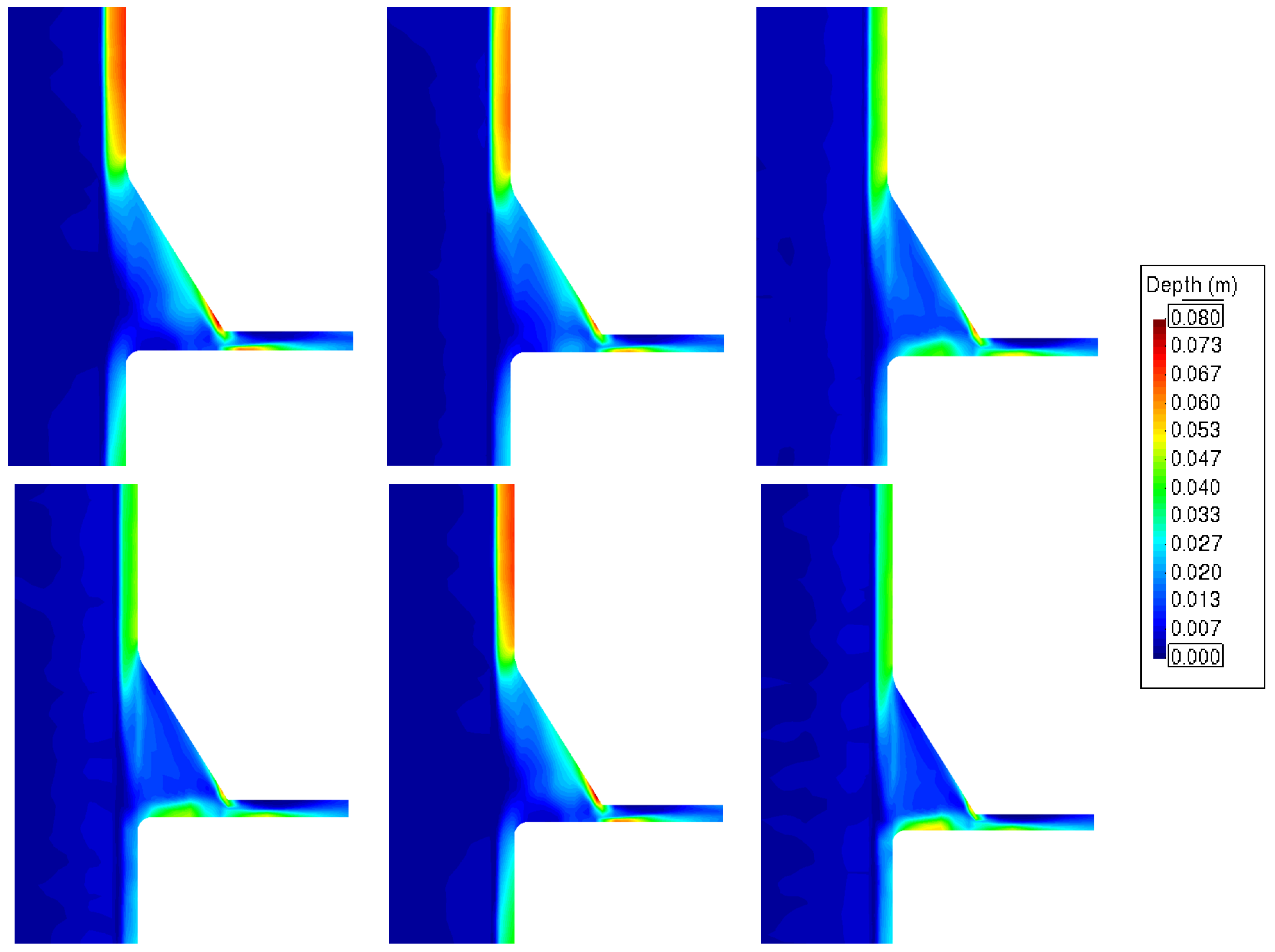
Finally, the slope considerably influences the nozzle water depths. For low slopes (<2%) and low velocities, the flow follows the edge of the nozzle inlet. However, for slopes greater than 3%, the flow is concentrated on the opposite edge of the inlet (Figure 7).

4.4. Gutter Width and Embankment Downspout Distancing

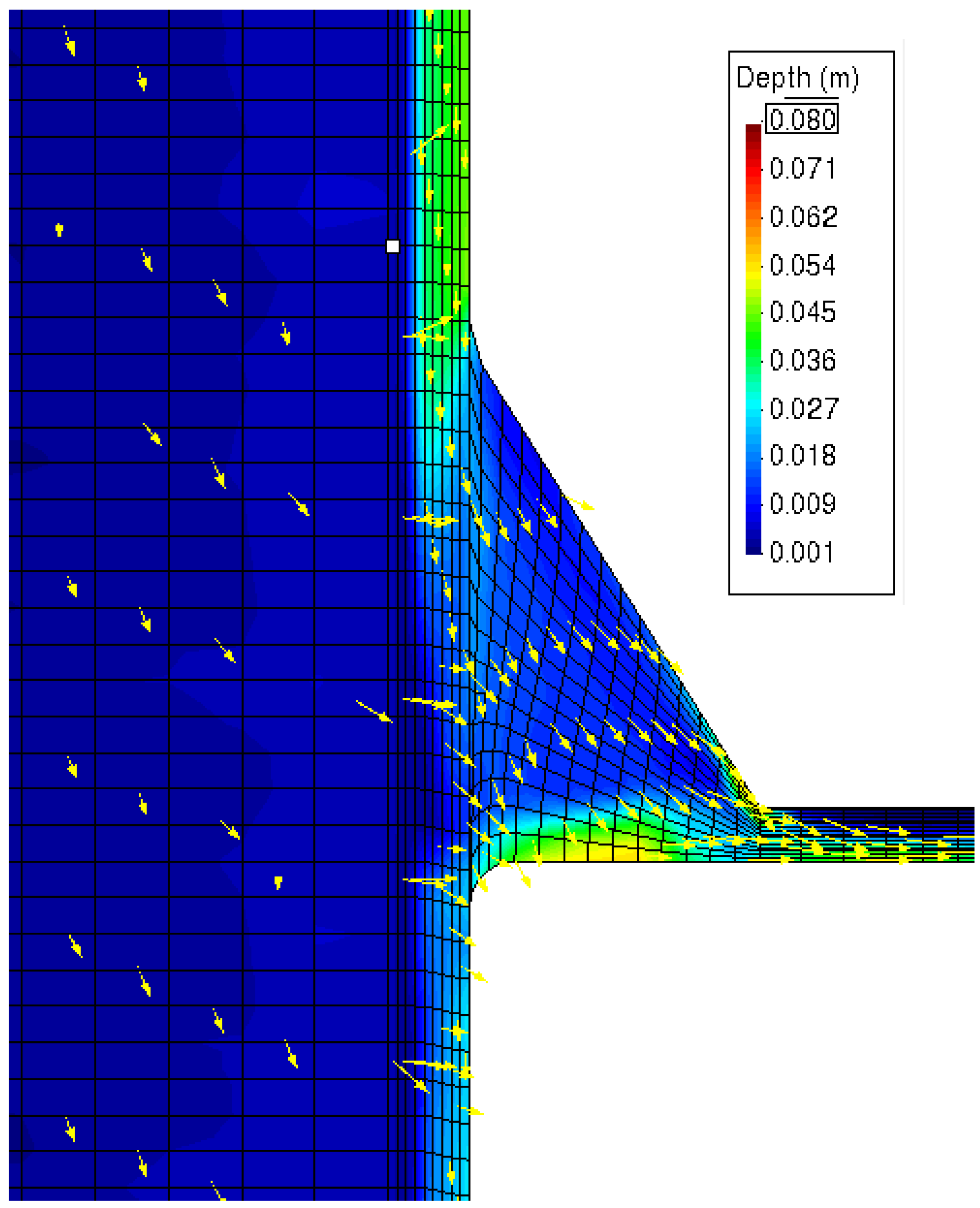
The influence of the gutter width and the embankment downspout distancing on the gutter are those associated with the flow velocity and depth in a channel. As the slope increases, there is a decrease in the water depth (Figure 8) and, consequently, an increase in velocity.

This information is relevant since it conditions the suitability of the design because, according to Instruction 5.2-IC, this maximum water depth must have a guard on the shoulder platform greater than 5 cm.

Thus, for a 30 cm wide gutter, the guard is variable depending on the slope. As a summary, it can be concluded that, for slopes of less than 1%, downspout separations of 15 m can be used for both reduced and large nozzles, and if the separation is 20 m, only large nozzles should be used. For slopes greater than 2%, downspouts must be installed every 15 or 20 m with reduced or large nozzles.

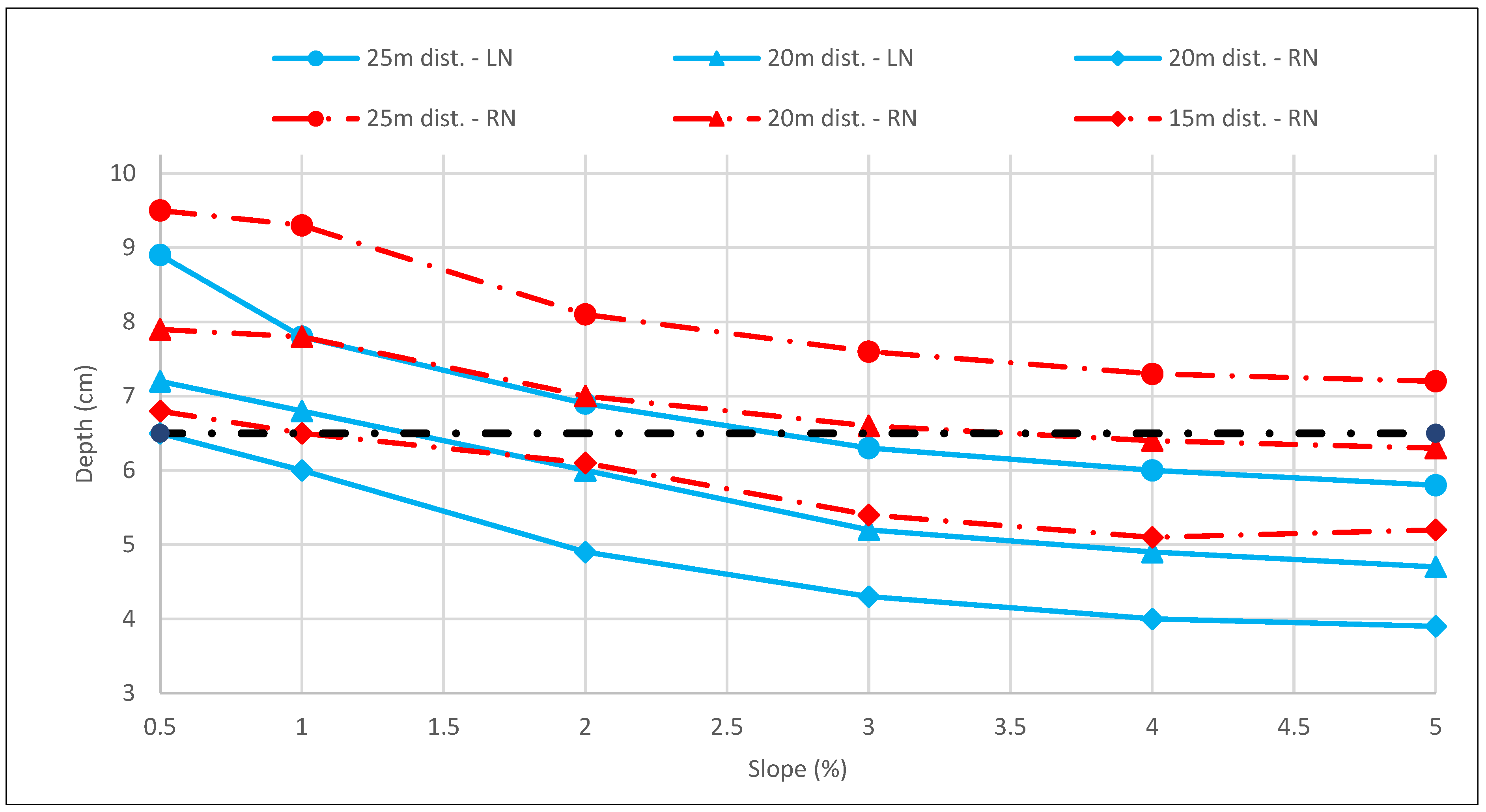
Notwithstanding, for a 20 cm wide gutter, the scenario is different (Figure 9). Separations of 15 m can be used with large nozzles for slopes of less than 1% and reduced nozzles for slopes between 1% and 5%. For separations of 20 m between downspouts, large nozzles can be used at 1.5% and reduced nozzles at slopes greater than 3.5%. Lastly, separations between downspouts of 25 m can only be used with large nozzles and with slopes greater than 2.5%.

4.5. Nozzle Type: Symmetrical and Asymmetrical

In this section, the influence of the nozzle type is analyzed: symmetrical vs. asymmetrical (Figure 2) performance was compared in a model with 3 m downspouts with a 20 m separation between them.

The results indicate that for slopes ≤ 1%, the hydraulic capacity obtained in both cases is practically the same. However, for greater slopes, the hydraulic capacity of the symmetrical nozzle decreases progressively (

Table 11. Flow deficit (l/s) between symmetrical (S) and asymmetrical (A) nozzles.

	20 m Downspout Distancing—30 cm Width Gutter
	% of Evacuated Volume		Gutter Water Depth		Nozzle Water Depth
Slope	S	A	S	A	S	A
0.5%	100	100	6.5	6.5	7.0	6.1
1%	100	100	6.0	6.3	7.3	6
2%	99	100	5.0	5.6	7.2	5.6
3%	93	100	5.2	5.3	7.5	5.2
4%	81	100	5.8	4.8	7.6	5
5%	66	100	6.2	4.6	8.1	4.8

). Figure 10 shows the comparison between the longitudinal profile in the gutter when symmetrical and asymmetrical nozzles are arranged for a longitudinal slope of 5%, where a considerable increase in the water depth is observed at the exit of the symmetrical nozzle compared to the asymmetrical one. The water depth in the gutter increases slightly on slopes ≥ 3%, and it presents a better distribution in the nozzle on the asymmetrical one for all slopes (Figure 11 and Figure 12).

For the application to a practical case, the authors recommend the creation of a synthetic model in accordance with the geometry and the hydrological characteristics of the site, such as a design hyetograph with a time resolution of five minutes (according to the concentration times of each downspout catchment). Regarding the former, it is necessary to highlight the importance of an adequate design of the width of the road, shoulders, gutter, and slope, which depends on the section. The variation in the slope is easily modifiable since once the model is available, it is only necessary to assign heights from an external file (e.g., raster or meshing point cloud).

With all the above, the proposed methodology is easily applicable to any type of road to be dimensioned. Furthermore, this methodology is also applicable for infrastructure already built in order to determine the degree of efficiency of the existing drainage system, thus anticipating future problems related to the road safety of the platform.

The methodology presented here addresses the problem of platform drainage through a rigorous mathematical model. The authors, experts in hydraulic calculation, have reviewed the current calculation methods, reaching the conclusion that the current methodologies are based on empirical formulas to obtain the water depth and flow in each of the designed downspouts. However, the methodology proposed here provides water depth, speed, and flow at any point of the model in a rigorous way.

5. Conclusions

This work explores the design of drainage downspout systems on road embankments through two-dimensional hydraulic modeling. A methodology that enables an efficient design of both the outlet and the spacing between downspouts was proposed, facilitating an optimal reduction in the runoff on the platform.

The application of this methodology revealed that the volume of runoff evacuated is greater with lower longitudinal slopes and with lower separations between downspouts. In all cases studied, a gutter width of 30 cm and a large nozzle ensure total runoff evacuation, even for separations of up to 30 m.

The influence of the longitudinal slope on the drainage elements has been studied, revealing that the 30 cm wide downspout satisfactorily meets the requirements in any design typology, while the depths of the nozzles vary depending on the slope. In such cases, the water depth reaches maximum values of 6.3 cm for a minimum longitudinal slope of 0.5%.

The influence of nozzle size shows that for slopes greater than 2%, smaller nozzles have lower hydraulic capacity than the larger ones. A 30 cm wide gutter with slopes lower than 1% and downspout separations of 15 m can be used for any size of nozzles, while a 20 m separation should be used only for large nozzles. Where slopes are greater than 2%, downspouts must be installed every 15–20 m. On the other hand, for a 20 cm wide gutter and a downspout separation of 15 m, large nozzles can be used for slopes lower than 1% and reduced nozzles for slopes between 1% and 5%. In the case of downspout separation of 20 m between, large nozzles can be used for slopes of 1.5% and reduced nozzles for slopes greater than 3.5%. Lastly, separations between downspouts of 25 m can only be used with large nozzles with slopes greater than 2.5%.