Optimum Coastal Slopes Exposed to Waves: Experimental and Numerical Study
Abstract
:1. Introduction
2. Experimental Wave Tank
2.1. Wave Generation
2.2. Wave Energy Dissipation
2.3. Wave Gauges
3. Simulation Method
3.1. Governing Equations
3.2. Numerical Method
Dynamic Mesh
| Algorithm 1 Computer programming codes provided for flap in Fluent software. |
| #include “udf.h” DEFINE_CG_MOTION (Case1, dt, vel, omega, time, dtime) { if (time < 14.0801) omega [2] = −0.3722 ∗ cos(5.7120 ∗ time−2 ∗ atan(1.0)); else if (time < 66) omega [2] = −0.3722 ∗ cos(5.7120 ∗ (time + 0.2199)−2 ∗ atan(1.0)); else omega [2] = 0; |
4. Simulation Results and Discussions
4.1. Mesh Independence
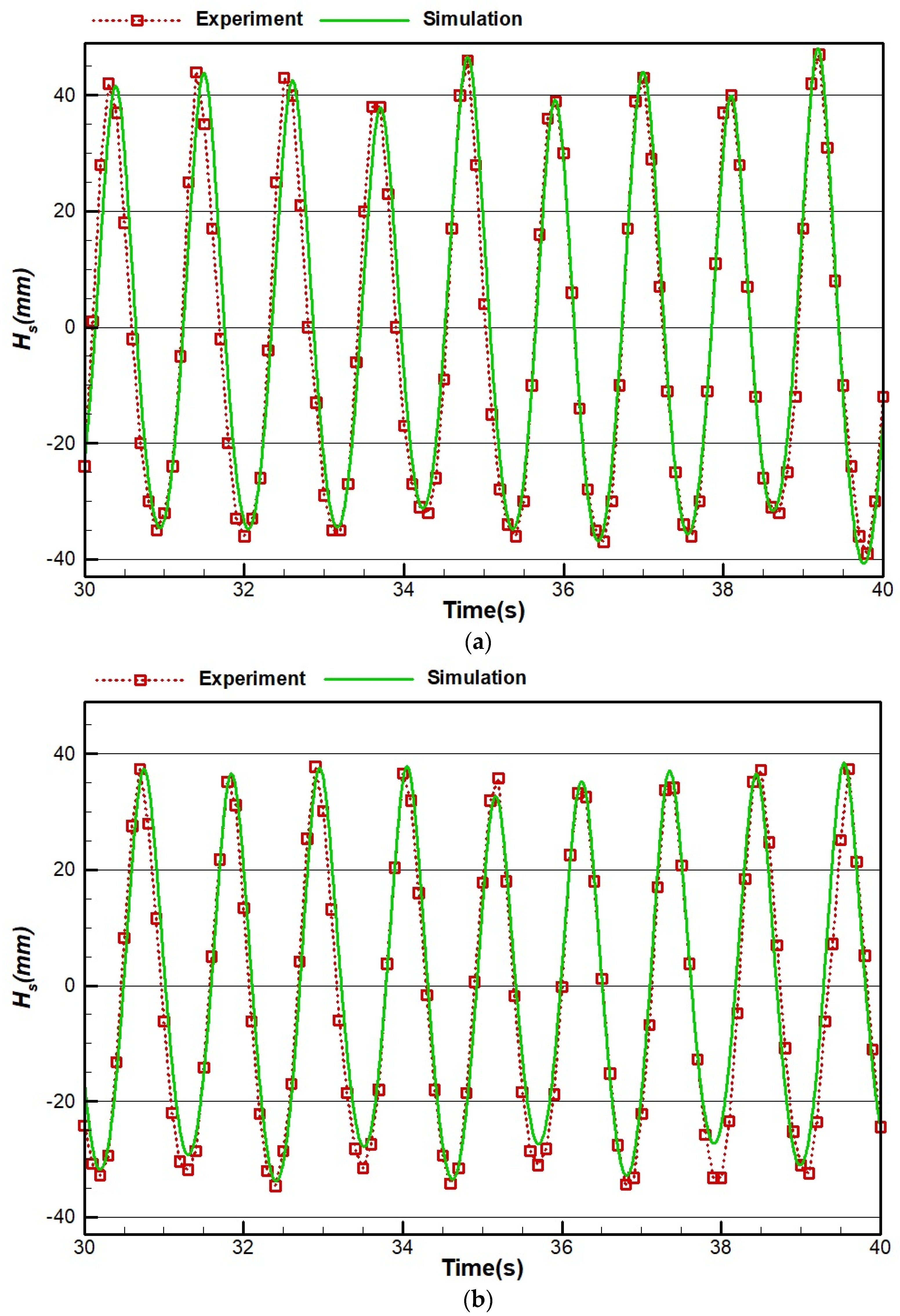
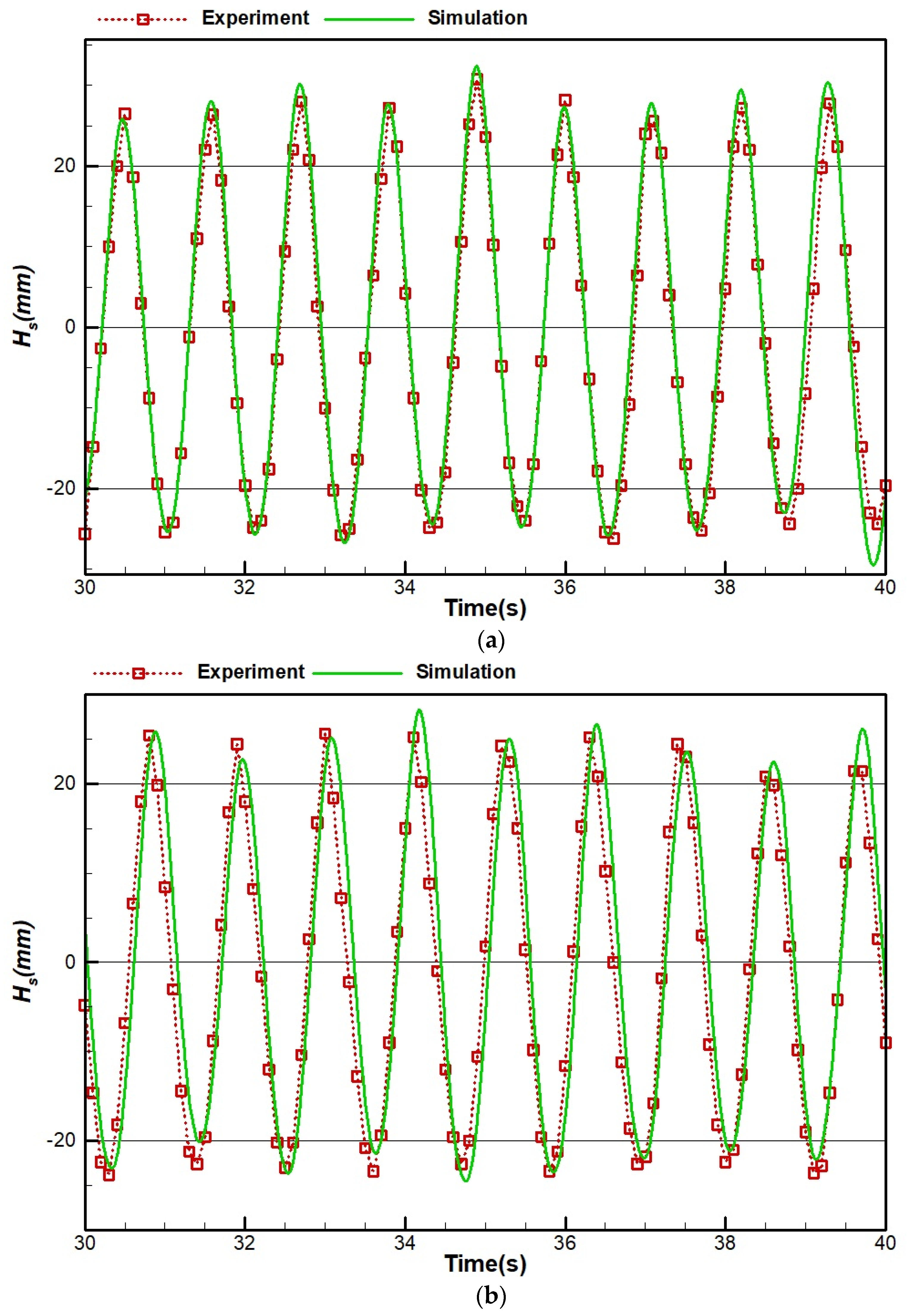
4.2. Model Validation
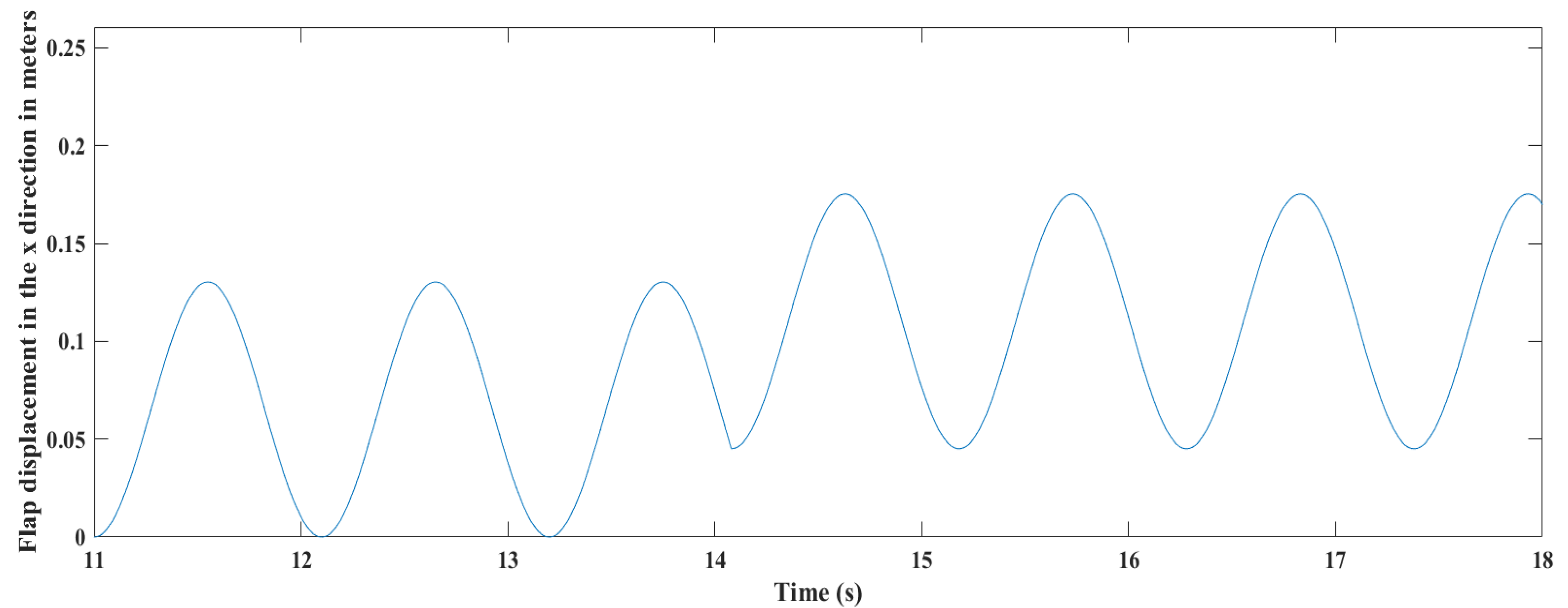
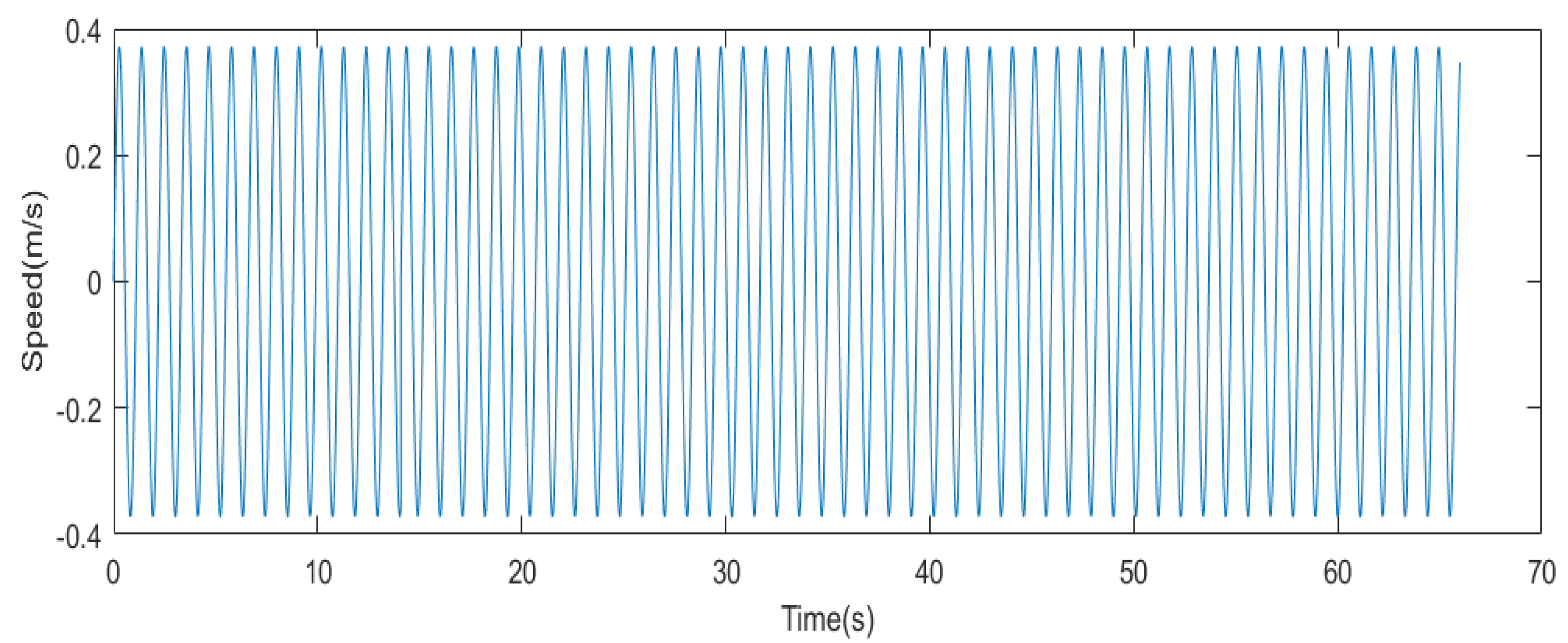
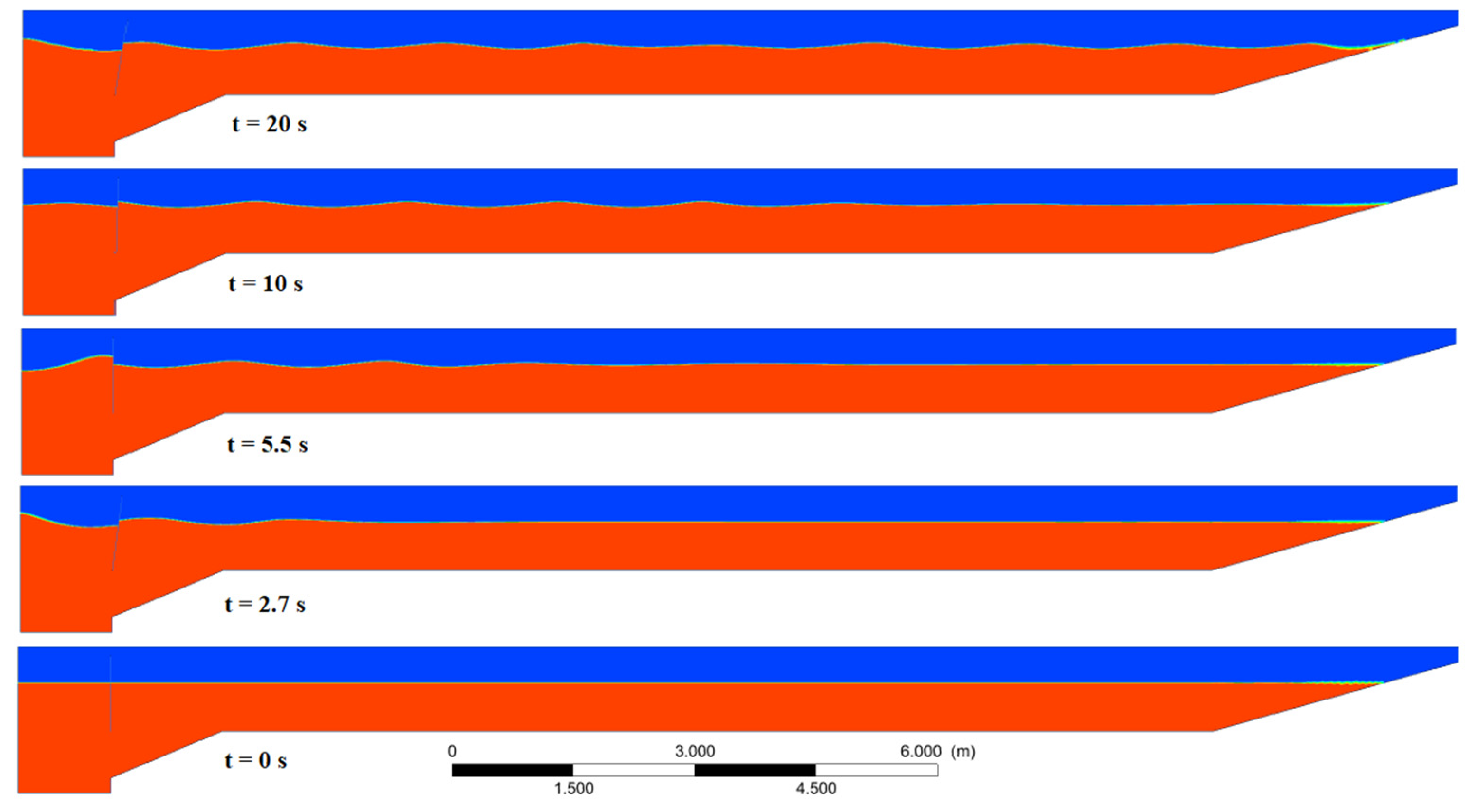
4.3. Wave Generation Results
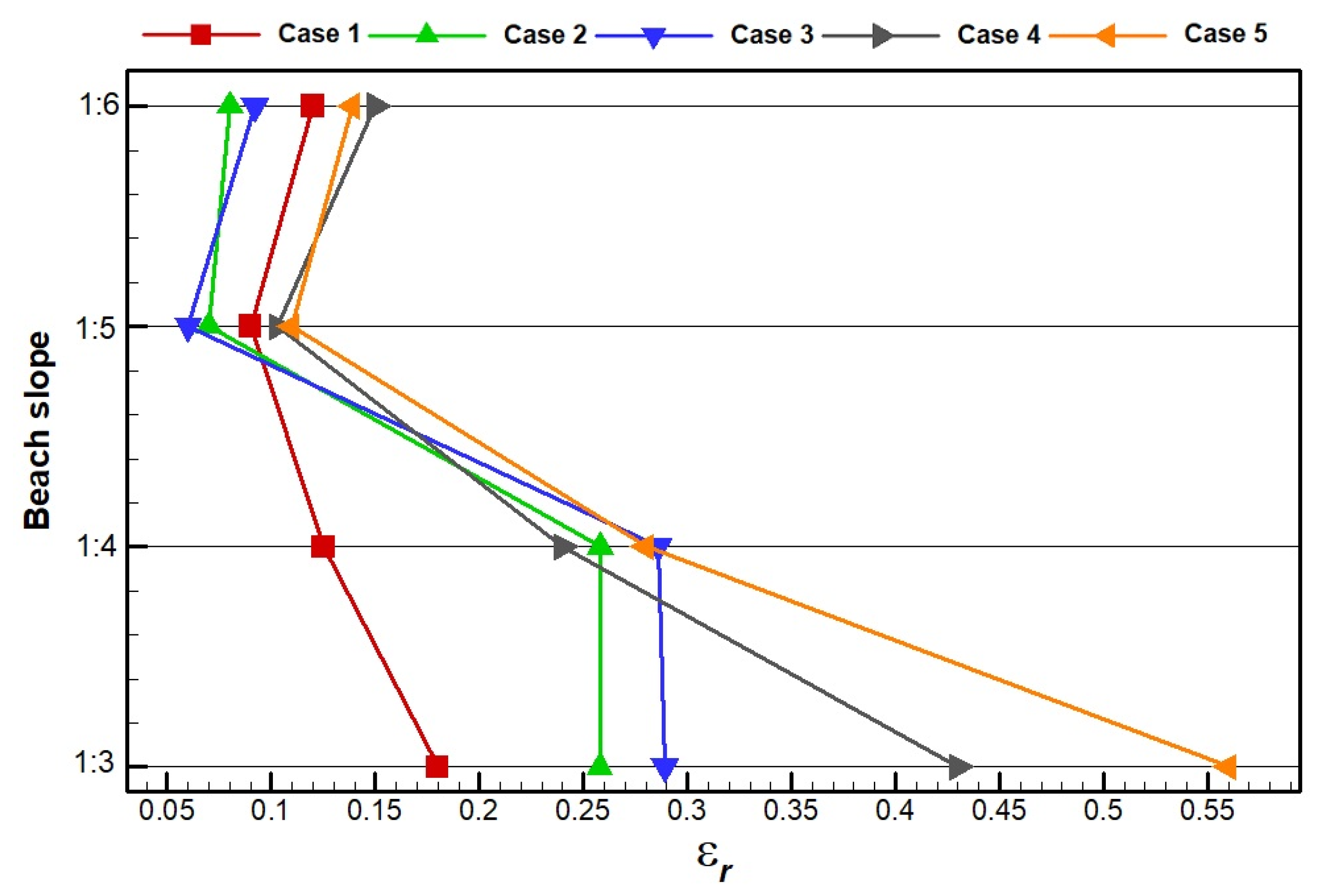
4.4. Study of the Beach Slope
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amanatidis, G. European Policies on Climate and Energy towards 2020, 2030 and 2050. Policy Department for Economic, Scientific and Quality of Life Policies. European Parliament. 2019. PE 631.047. Available online: https://policycommons.net/artifacts/1335288/european-policies-on-climate-and-energy-towards-2020-2030-and-2050/1941726/ (accessed on 29 December 2022).
- Pecher, A.; Kofoed, J.P. Handbook of Ocean Wave Energy, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Lal, A.; Elangovan, M. CFD Simulation and Validation of Flap Type Wave-Maker. Int. J. Math. Comput. Sci. 2008, 2, 708–714. [Google Scholar]
- Anbarsooz, M.; Passandideh-Fard, M.; Moghiman, M. Fully nonlinear viscous wave generation in numerical wave tanks. Ocean Eng. 2013, 59, 73–85. [Google Scholar] [CrossRef]
- Han, Z.; Liu, Z.; Shi, H. Numerical study on overtopping performance of a multi-level breakwater for wave energy conversion. Ocean Eng. 2008, 150, 94–101. [Google Scholar] [CrossRef]
- Collins, K.M.; Stripling, S.; Simmonds, D.J.; Greaves, D.M. Quantitative metrics for evaluation of wave fields in basins. Ocean Eng. 2018, 169, 300–314. [Google Scholar] [CrossRef] [Green Version]
- Alamian, R.; Shafaghat, R.; Ketabdari, M.J. Wave simulation in a numerical wave tank using BEM. Am. Inst. Phys. Conf. Proc. 1648, 2015, 770008. [Google Scholar]
- Wu, Y.T.; Hsiao, S.C. Generation of stable and accurate solitary waves in a viscous numerical wave tank. Ocean Eng. 2018, 167, 102–113. [Google Scholar] [CrossRef]
- Dao, M.H.; Chew, L.W.; Zhang, Y. Modeling physical wave tank with flap paddle and porous beach in OpenFOAM. Ocean Eng. 2018, 154, 204–215. [Google Scholar] [CrossRef]
- Houtani, H.; Waseda, T.; Fujimoto, W.; Kiyomatsu, K.; Tanizawa, K. Generation of a spatially periodic directional wave field in a rectangular wave basin based on higher-order spectral simulation. Ocean Eng. 2018, 169, 428–441. [Google Scholar] [CrossRef]
- Li, Z.; Deng, G.; Queutey, P.; Bouscasse, B.; Ducrozet, G.; Gentaz, L.; Ferrant, P. Comparison of wave modeling methods in CFD solvers for ocean engineering applications. Ocean Eng. 2019, 188, 106237. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, X.; Li, Y.; Li, X.; Qin, H. Numerical simulations of super rogue waves in a numerical wave tank. Ocean Eng. 2021, 229, 108929. [Google Scholar] [CrossRef]
- Lv, C.; Zhao, X.; Li, M.; Xie, Y. An improved wavemaker velocity boundary condition for generating realistic waves in the numerical wave tank. Ocean Eng. 2022, 261, 112188. [Google Scholar] [CrossRef]
- Westphalen, J.; Greaves, D.M.; Williams, C.J.K.; Hunt-Raby, A.C.; Zang, J. Focused waves and wave-structure interaction in a numerical wave tank. Ocean Eng. 2012, 45, 9–21. [Google Scholar] [CrossRef]
- Hu, Z.Z.; Greaves, D.; Raby, A. Numerical wave tank study of extreme waves and wave-structure interaction using OpenFoam®. Ocean Eng. 2016, 126, 329–342. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.Y.; Kim, K.M.; Park, J.C.; Jeon, G.M.; Chun, H.H. Numerical simulation of wave and current interaction with a fixed offshore substructure. Int. J. Nav. Archit. Ocean Eng. 2016, 8, 188–197. [Google Scholar] [CrossRef] [Green Version]
- Bruinsma, N.; Paulsen, B.T.; Jacobsen, N.G. Validation and application of a fully nonlinear numerical wave tank for simulating floating offshore wind turbines. Ocean Eng. 2018, 147, 647–658. [Google Scholar] [CrossRef]
- Tian, X.; Wang, Q.; Liu, G.; Deng, W.; Gao, Z. Numerical and experimental studies on a three-dimensional numerical wave tank. IEEE Access 2018, 6, 6585–6593. [Google Scholar] [CrossRef]
- Martínez-Ferrer, P.J.; Qian, L.; Ma, Z.; Causon, D.M.; Mingham, C.G. Improved numerical wave generation for modeling ocean and coastal engineering problems. Ocean Eng. 2018, 152, 257–272. [Google Scholar] [CrossRef] [Green Version]
- Anbarsooz, M.; Rashki, H.; Ghasemi, A. Numerical investigation of front-wall inclination effects on the hydrodynamic performance of a fixed oscillation water column wave energy converter. Proc. Inst. Mech. Eng. Part A J. Power Energy 2018, 233, 262–271. [Google Scholar] [CrossRef]
- Kim, S.J.; Kim, M. The nonlinear wave and current effects on fixed and floating bodies by a three-dimensional fully-nonlinear numerical wave tank. Ocean Eng. 2022, 245, 110458. [Google Scholar] [CrossRef]
- Finnegan, W.; Goggins, J. Numerical simulation of linear water waves and wave-structure interaction. Ocean Eng. 2012, 43, 23–31. [Google Scholar] [CrossRef] [Green Version]
- Zabihi, M.; Mazaheri, S.; Mazyak, A.R. Wave Generation in a Numerical Wave Tank. Int. J. Ocean Coast. Eng. 2015, 5, 33–43. [Google Scholar]
- Fathi-Moghadam, M.; Davoudi, L.; Motamedi-Nezhad, A. Modeling of solitary breaking wave force absorption by coastal trees. Ocean Eng. 2018, 169, 87–98. [Google Scholar] [CrossRef]
- Jiang, C.; Liu, X.; Yao, Y.; Deng, B. Numerical investigation of solitary wave interaction with a row of vertical slotted piles on a sloping beach. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 530–541. [Google Scholar] [CrossRef]
- Casella, F.; Aristodemo, F.; Filianoti, P. A comprehensive analysis of solitary wave run-up at sloping beaches using an extended experimental dataset. Appl Ocean Res. 2022, 126, 103283. [Google Scholar] [CrossRef]
- Lee, W.D.; Yeom, G.S.; Kim, J.; Lee, S.; Kim, T. Runup characteristics of a tsunami-like wave on a slope beach. Ocean Eng. 2022, 259, 111897. [Google Scholar] [CrossRef]
- Machado, F.M.M.; Lopes, A.M.G.; Ferreira, A.D. Numerical simulation of regular waves: Optimization of a numerical wave tank. Ocean Eng. 2018, 170, 89–99. [Google Scholar] [CrossRef]
- Prasad, D.D.; Ahmed, M.R.; Lee, Y.-H. Studies on the performance of Savonius rotors in a numerical wave tank. Ocean Eng. 2018, 158, 29–37. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; Advances Series on Ocean Engineering: Volume 2; World Scientific Publishing Company: Singapore, 1991. [Google Scholar]
- Ursell, F.; Dean, R.G.; Yu, Y.S. Forced small-amplitude water waves: A comparison of theory and experiment. J. Fluid Mech. 1960, 7, 33–52. [Google Scholar] [CrossRef]






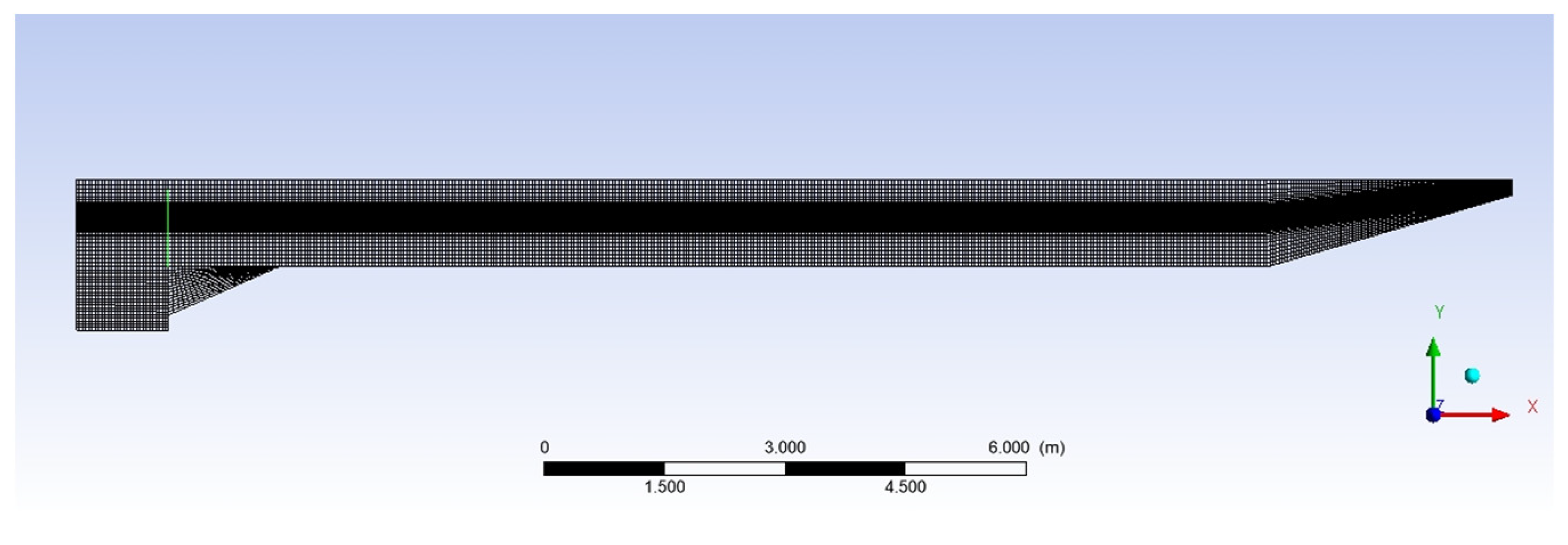





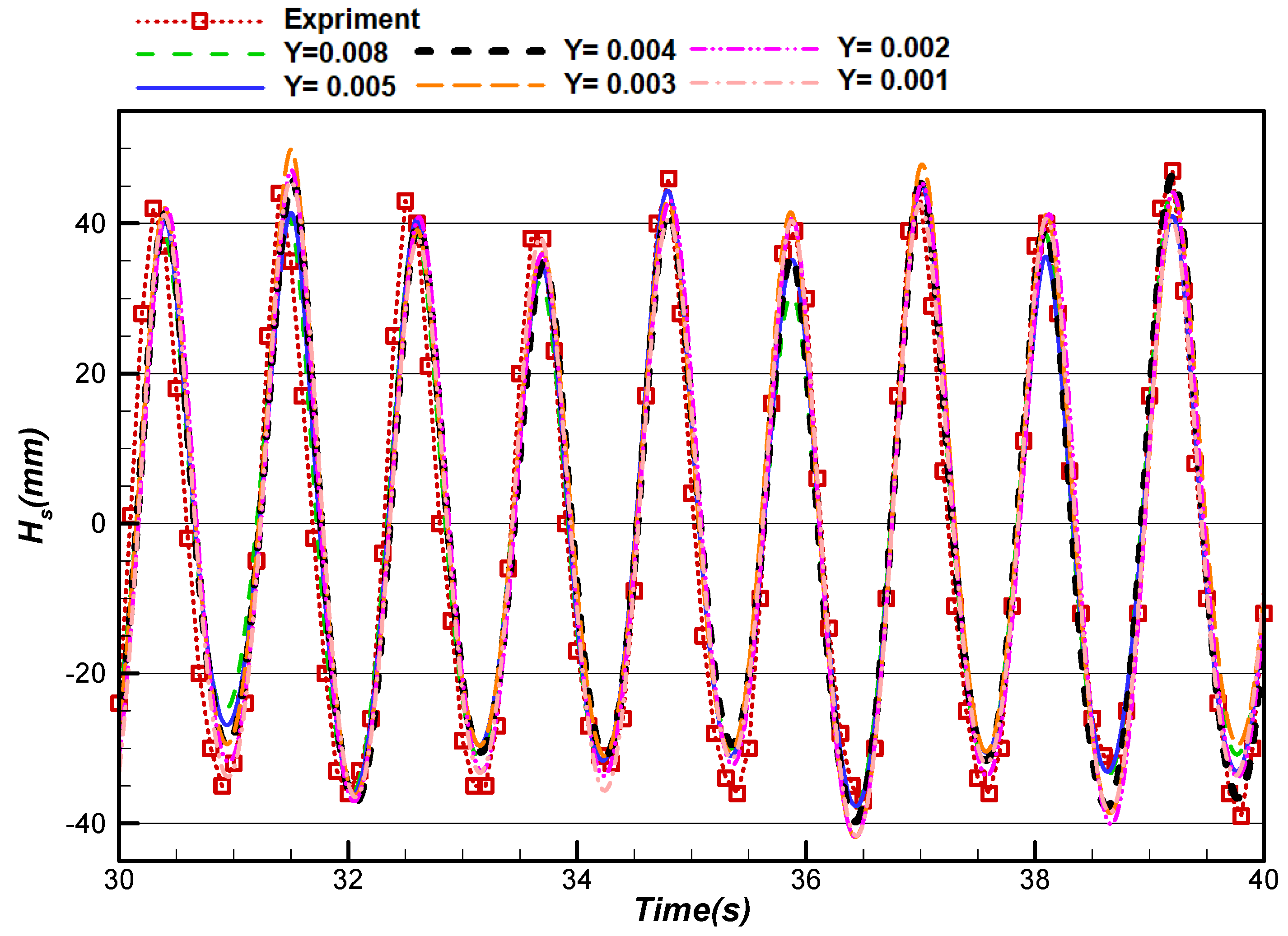






| Cell height (m) | 0.008 | 0.005 | 0.004 | 0.003 | 0.002 | 0.001 |
| Mesh number produced | 25,213 | 37,686 | 54,355 | 64,659 | 86,555 | 210,883 |
| Case Number | Period (s) | Stroke (cm) | Still Water Depth (m) | H/S | 2πd/L |
|---|---|---|---|---|---|
| Small wave steepness | |||||
| 1 | 2.1 | 8.45 | 0.3 | 0.25 | 0.5481 |
| 2 | 1.4 | 8.45 | 0.3 | 0.43 | 0.8746 |
| 3 | 1.05 | 3.15 | 0.45 | 0.88 | 1.7449 |
| 4 | 1.5 | 2.4 | 0.8 | 1.25 | 2.9351 |
| 5 | 1.4 | 8.57 | 0.5 | 0.65 | 1.2212 |
| High wave steepness | |||||
| 6 | 0.84 | 8.47 | 0.4 | 1.003 | 2.3242 |
| 7 | 1.05 | 8.45 | 0.3 | 0.67 | 1.2783 |
| 8 | 0.84 | 8.45 | 0.3 | 0.84 | 1.8051 |
| 9 | 1.05 | 6.3 | 0.9 | 1.3 | 3.2925 |
| 10 | 1.05 | 4.69 | 0.67 | 1.13 | 2.4789 |
| Case | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Hs (mm) | 90 | 60 | 40 | 60 | 40 |
| H (m) | 0.62 | 0.62 | 0.62 | 0.62 | 0.62 |
| Frequency (Hz) | 1.1 | 1.1 | 1.1 | 1.2 | 1.2 |
| Wave period (s) | 0.9 | 0.9 | 0.9 | 0.83 | 0.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zandi, R.; Lari, K.; Najafzadeh, M. Optimum Coastal Slopes Exposed to Waves: Experimental and Numerical Study. Water 2023, 15, 366. https://doi.org/10.3390/w15020366
Zandi R, Lari K, Najafzadeh M. Optimum Coastal Slopes Exposed to Waves: Experimental and Numerical Study. Water. 2023; 15(2):366. https://doi.org/10.3390/w15020366
Chicago/Turabian StyleZandi, Reza, Khosro Lari, and Mohammad Najafzadeh. 2023. "Optimum Coastal Slopes Exposed to Waves: Experimental and Numerical Study" Water 15, no. 2: 366. https://doi.org/10.3390/w15020366






