Hydrogeological Parameter Estimation of Confined Aquifer within a Rectangular Shaped Drop Waterproof Curtain
Abstract
:1. Introduction
2. Methods
2.1. Drawdown Solution for Flow in a Confined Aquifer of Infinite Extent
2.1.1. Mathematical Model
2.1.2. Solution
2.2. Drawdown Solution for Flow in a Confined Aquifer within a Fully Penetrated Waterproof Curtain
2.3. Estimation for Hydrogeologic Parameters
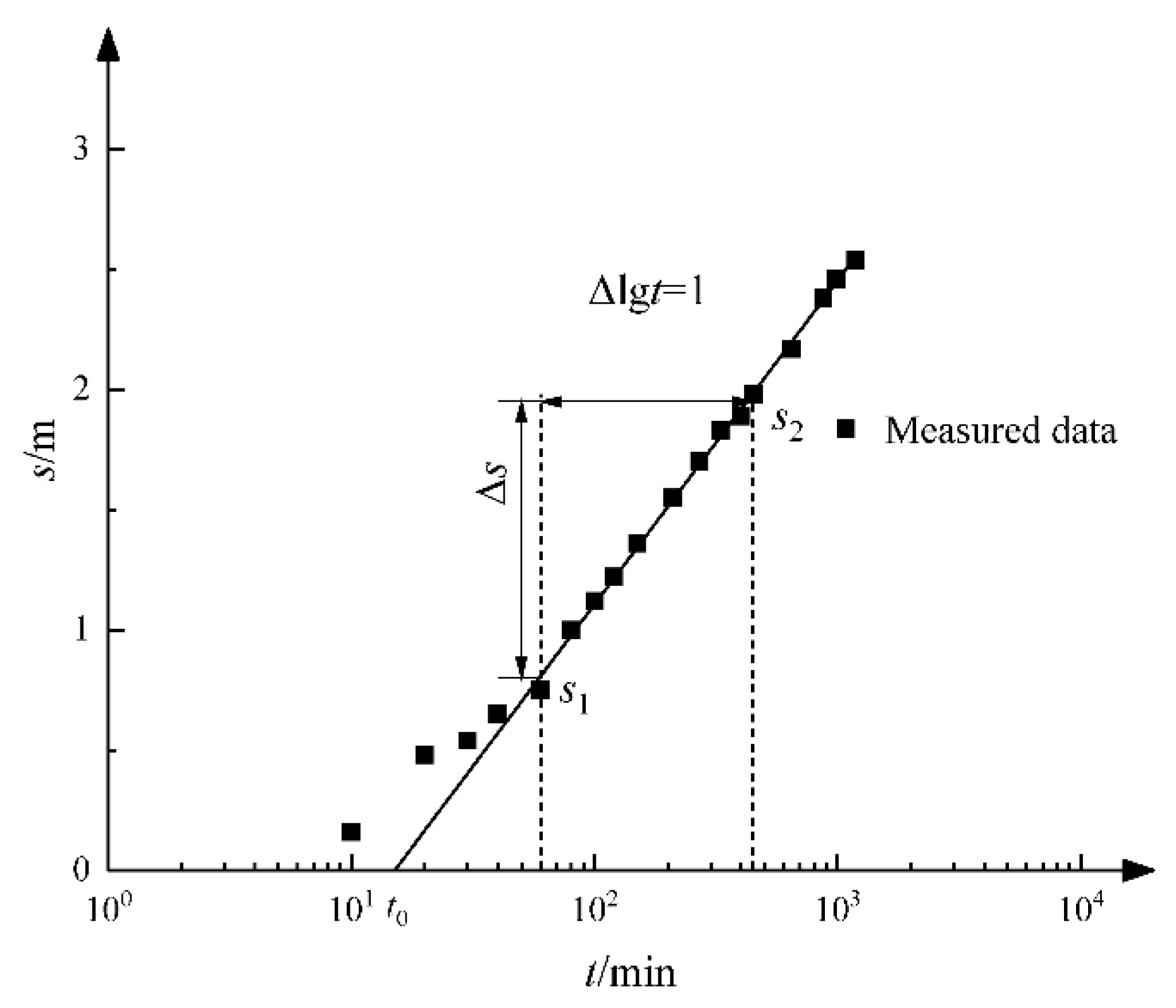
3. Application for Parameter Estimation Using Field Test Data
3.1. Study Area
3.2. Field Pumping Tests
3.3. Parameter Estimation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Theis, C.V. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using ground-water storage. Trans. Am. Geophys. Union 1935, 16, 519–524. [Google Scholar] [CrossRef]
- Hantush, M.S. Hydraulics of wells. Adv. Hydrosci. 1964, 1, 281–432. [Google Scholar]
- Neuman, S.P.; Witherspoon, P.A. Field determinations of the hydraulic properties of leaky multiple aquifer systems. Water Resour. Res. 1972, 8, 1184–1298. [Google Scholar] [CrossRef] [Green Version]
- Moench, A.F. Analytical and numerical analyses of an unconfined aquifer test considering unsaturated zone characteristics. Water Resour. Res. 2008, 44, W06409. [Google Scholar] [CrossRef] [Green Version]
- Feng, Q.; Liu, Z.; Zhan, H. Semi-analytical solutions for transient flow to a partially penetrated well with variable discharge in a general three-layer aquifer system. J. Hydrol. 2021, 598, 126329. [Google Scholar] [CrossRef]
- Xiong, F.; Sun, H.; Zhang, Q.; Wang, Y.; Jiang, Q. Preferential flow in three-dimensional stochastic fracture networks: The effect of topological structure. Eng. Geol. 2022, 309, 106856. [Google Scholar] [CrossRef]
- Xiong, F.; Zhu, C.; Feng, G.; Zheng, J.; Sun, H. A three-dimensional coupled thermos-hydro model for geothermal development in discrete fracture networks of hot dry rock reservoirs. Gondwana Res. 2023. [Google Scholar] [CrossRef]
- Li, F.; Yin, D.; Wang, F.; Jiang, N.; Li, X. Effects of combination mode on mechanical properties of bi-material samples consisting of rock and coal. J. Mater. Res. Technol.-JMRT 2022, 19, 2156–2170. [Google Scholar] [CrossRef]
- Yin, D.; Ding, Y.; Jiang, N.; Li, F.; Zhang, J.; Xu, H. Mechanical Properties and Damage Characteristics of Coal Samples under Water Immersion Pressure. Lithosphere 2022, 1, 1–16. [Google Scholar]
- Butler, J.J., Jr.; Tsou, M. Pumping-induced leakage in a bounded aquifer: An example of a scale-invariant phenomenon. Water Resour. Res. 2003, 39, 1344. [Google Scholar] [CrossRef]
- Yeh, H.D.; Chang, Y.C. Recent advances in modeling of well hydraulics. Adv. Water Resour. 2013, 51, 27–51. [Google Scholar] [CrossRef]
- Latinopoulos, P. Analytical solutions for periodic well recharge in rectangular aquifers with third-kind boundary conditions. J. Hydrol. 1985, 77, 293–306. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; Zhang, X.; Liu, Y.; Yang, T.; Feng, B. Field experiments and numerical simulations of confined aquifer response to multi-cycle recharge–recovery process through a well. J. Hydrol. 2012, 464, 328–343. [Google Scholar] [CrossRef]
- Lu, C.; Luo, J. Groundwater pumping in head-controlled coastal systems: The role of lateral boundaries in quantifying the interface toe location and maximum pumping rate. J. Hydrol. 2014, 512, 147–156. [Google Scholar] [CrossRef]
- Lu, C.; Xin, P.; Li, L.; Luo, J. Steady state analytical solutions for pumping in a fully bounded rectangular aquifer. Water Resour. Res. 2015, 51, 8294–8302. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.C.; Yang, S.Y.; Fen, C.S.; Yeh, H.D. A general analytical model for pumping tests in radial finite two-zone confined aquifers with Robin-type outer boundary. J. Hydrol. 2016, 540, 1162–1175. [Google Scholar] [CrossRef]
- Feng, Q.; Zhan, H. Constant-head test at a partially penetrating well in an aquifer-aquitard. J. Hydrol. 2019, 569, 495–505. [Google Scholar] [CrossRef]
- Dagan, G. A method of determining the permeability and effective porosity of unconfined anisotropic aquifers. Water Resour. Res. 1967, 3, 1059–1071. [Google Scholar] [CrossRef]
- Bear, J. Hydraulics of Groundwater; McGraw-Hill: Dover, NY, USA, 2007. [Google Scholar]
- Shen, S.L.; Wu, Y.X.; Xu, Y.S.; Hino, T.; Wu, H.N. Evaluation of hydraulic parameters from pumping tests in multi-aquifers with vertical leakage in Tianjin. Comput. Geotech. 2015, 68, 196–207. [Google Scholar] [CrossRef]
- Bateni, S.M.; Mortazavi-Naeini, M.; Ataie-Ashtiani, B.; Jeng, D.S.; Khanbilvardi, R. Evaluation of methods for estimating aquifer hydraulic parameters. Appl. Soft Comput. 2015, 28, 541–549. [Google Scholar] [CrossRef]
- Wang, C.T.; Yeh, H.D.; Tsai, C.S. Transient drawdown solution for a constant pumping test in finite two-zone confined aquifers. Hydrol. Earth Syst. Sci. 2012, 16, 441–449. [Google Scholar] [CrossRef] [Green Version]
- Amiri, V.; Asgari-Nejad, M. Hydrogeological assessment and estimation of groundwater inflow into the water transmission tunnel to Urmia Lake, Northwestern Iran. Bull. Eng. Geol. Environ. 2022, 81, 111. [Google Scholar] [CrossRef]
- Li, M.G.; Chen, J.J.; Xia, X.H.; Zhang, Y.Q.; Wang, D.F. Statistical and hydro-mechanical coupling analyses on groundwater drawdown and soil deformation caused by dewatering in a multi-aquifer-aquitard system. J. Hydrol. 2020, 589, 125365. [Google Scholar] [CrossRef]
- Feng, Q.; Zhan, H. Two-region flow caused by pumping at a partial penetration well in a leaky confined aquifer. Int. J. Numer. Anal. Methods Geomech. 2023, 1–19. [Google Scholar] [CrossRef]
- Liu, N.W.; Peng, C.X.; Li, M.G.; Chen, J.J. Hydro-mechanical behavior of a deep excavation with dewatering and recharge in soft deposits. Eng. Geol. 2022, 307, 106780. [Google Scholar] [CrossRef]
- Zeng, C.F.; Liao, H.; Xue, X.L.; Long, S.C.; Luo, G.J.; Diao, Y.; Li, M.G. Responses of groundwater and soil to dewatering considering the barrier effect of adjacent metro station on multi-aquifers. J. Hydrol. 2022, 612, 128117. [Google Scholar] [CrossRef]
- Batu, V. Aquifer Hydraulics: A Comprehensive Guide to Hydrogeologic Data Analysis; Wiley: Chichester, UK, 1998. [Google Scholar]
- Yeh, H.D.; Huang, Y.C. Parameter estimation for leaky aquifers using the extended Kalman filter, and considering model and data measurement uncertainties. J. Hydrol. 2005, 302, 28–45. [Google Scholar] [CrossRef]
- Li, P.; Qian, H.; Wu, J. Comparison of three methods of hydrogeological parameter estimation in leaky aquifers using transient flow pumping tests. Hydrol. Process. 2014, 28, 2293–2301. [Google Scholar] [CrossRef]
- Luo, N.; Illman, W.A. Automatic estimation of aquifer parameters using long-term water supply pumping and injection records. Hydrogeol. J. 2016, 24, 1443–1461. [Google Scholar] [CrossRef] [Green Version]
- Doherty, J.E. PEST, Model-Independent Parameter Estimation: User Manual, 7th ed.; Watermark: Brisbane, Australia, 2018. [Google Scholar]
- Zhuang, C.; Zhou, Z.; Zhan, H.; Wang, J.; Li, Y.; Dou, Z. New graphical methods for estimating aquifer hydraulic parameters using pumping tests with exponentially decreasing rates. Hydrol. Process. 2019, 33, 2314–2322. [Google Scholar] [CrossRef]
- Ha, D.; Zheng, G.; Zhou, H.; Zeng, C.; Zhang, H. Estimation of hydraulic parameters from pumping tests in a multiaquifer system. Undergr. Space 2020, 5, 210–222. [Google Scholar] [CrossRef]
- Amiri, V.; Sohrabi, N.; Li, P.; Shukla, S. Estimation of hydraulic conductivity and porosity of a heterogeneous porous aquifer by combining transition probability geostatistical simulation, geophysical survey, and pumping test data. Environ. Dev. Sustain. 2022, 1–24. [Google Scholar] [CrossRef]
- Cooper, H.H.; Jacob, C.E. A generalized graphical method for evaluating formation constants and summarizing well-field history. Eos Trans. Am. Geophys. Union 1946, 27, 526–534. [Google Scholar] [CrossRef]
- Corapcioglu, M.Y.; Borekci, O.; Haridas, A. Analytical solutions for rectangular aquifers with 3rd-kind (Cauchy) boundary conditions. Water Resour. Res. 1983, 19, 523–552. [Google Scholar] [CrossRef]
- Kuo, M.C.T.; Wang, W.L.; Lin, D.S.; Lin, C.C.; Chiang, C.J. An image-well method for predicting drawdown distribution in aquifers with irregularly shaped boundaries. Ground Water 1994, 32, 794–804. [Google Scholar] [CrossRef]
- Feng, Q.; Luo, Y.; Zhan, H. Three-dimensional response to a partially penetration well pumping in a general anisotropic three-layer aquifer system. J. Hydrol. 2020, 585, 124850. [Google Scholar] [CrossRef]
- Zhuang, C.; Li, Y.; Zhou, Z.; Illman, W.A.; Dou, Z.; Wang, J.; Yan, L. A Type-Curve Method for the Analysis of Pumping Tests with Piecewise-Linear Pumping Rates. Ground Water 2020, 58, 788–798. [Google Scholar] [CrossRef]

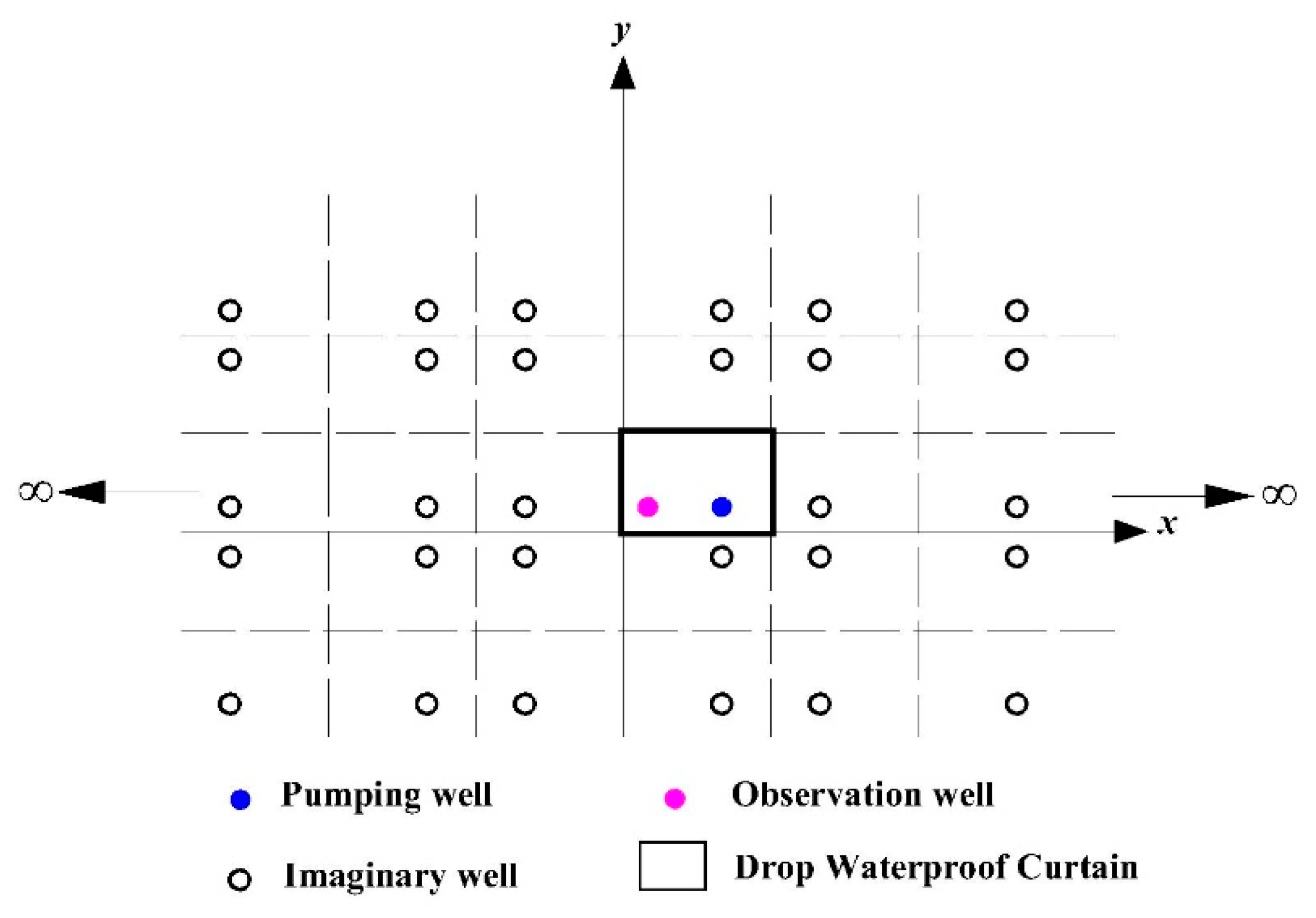
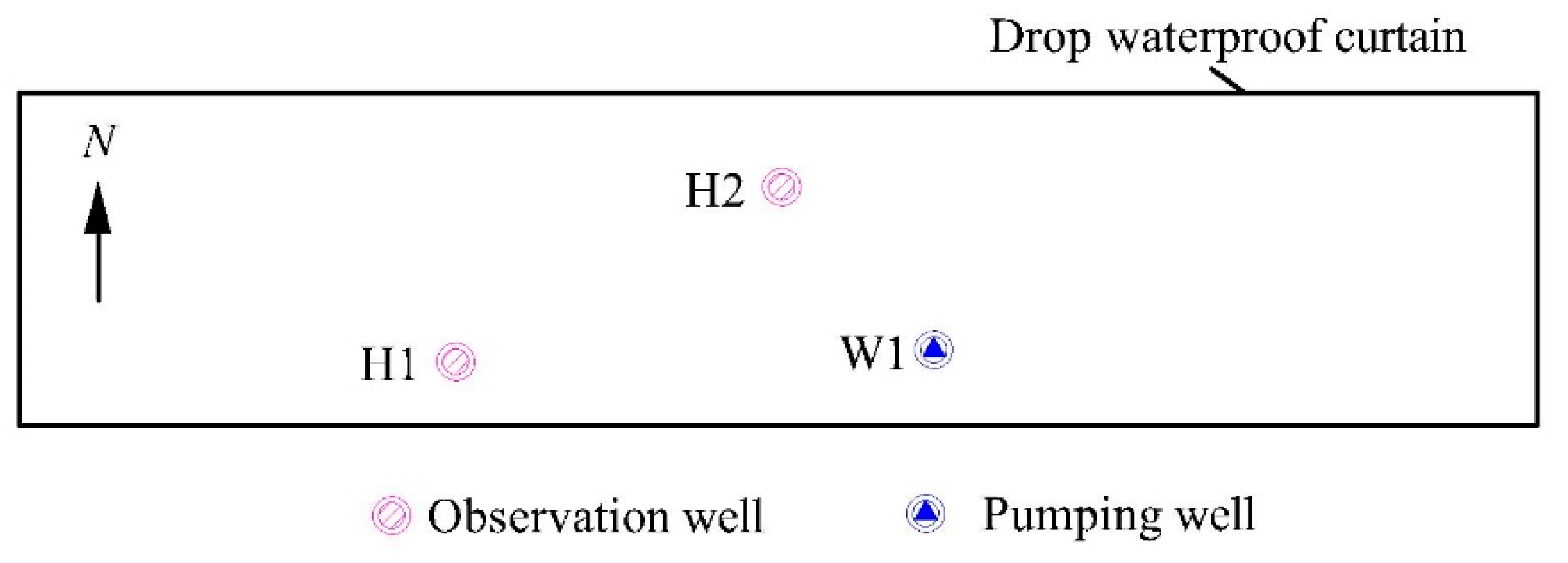
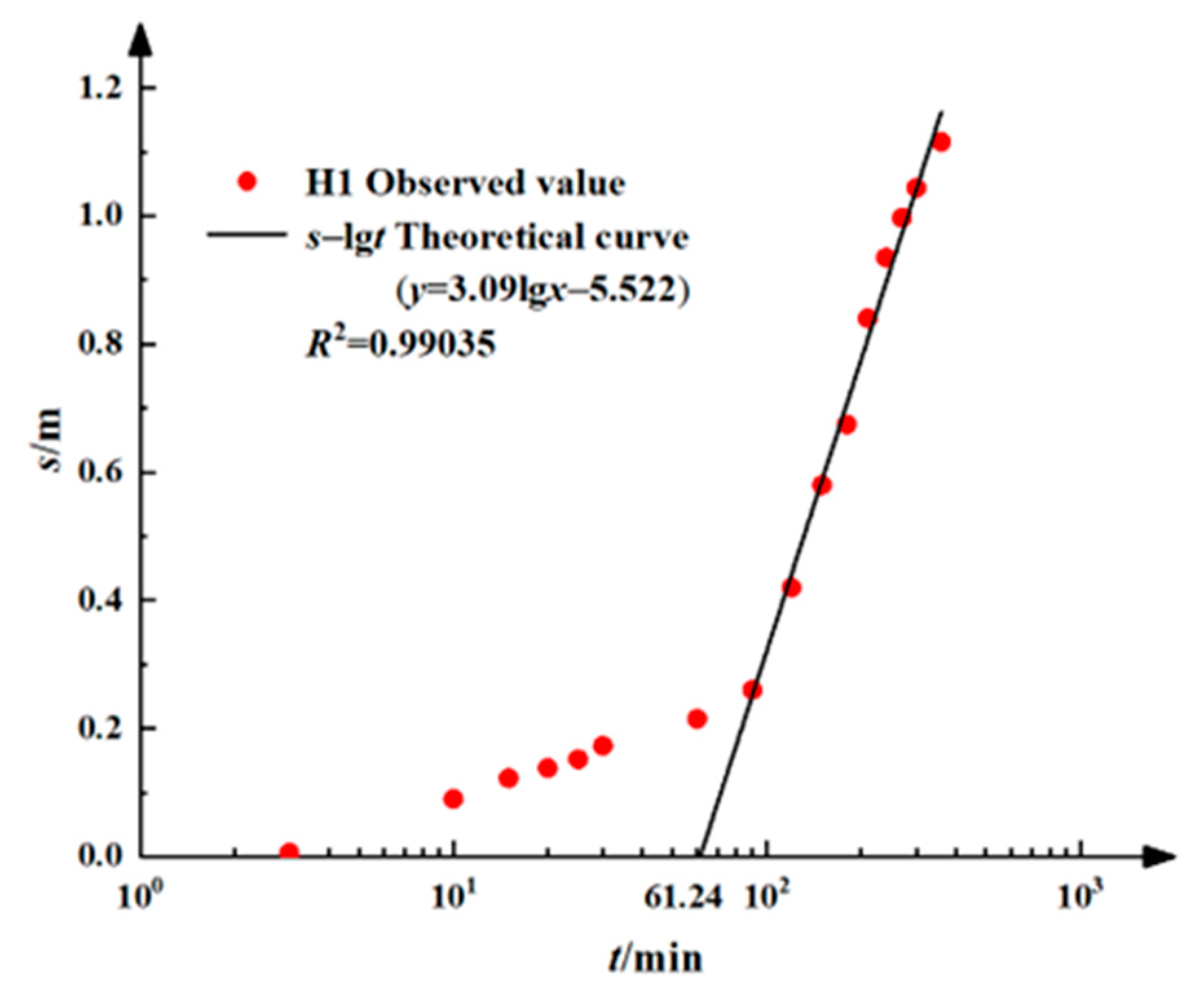
| Pumping Time (t/min) | Observation Well (H1) | Observation Well (H2) |
|---|---|---|
| Drawdown (s/m) | Drawdown (s/m) | |
| 0 | 0 | 0 |
| 3 | 0.006 | 0.04 |
| 10 | 0.09 | 0.06 |
| 15 | 0.122 | 0.07 |
| 20 | 0.138 | 0.08 |
| 25 | 0.152 | 0.1 |
| 30 | 0.173 | 0.11 |
| 60 | 0.215 | 0.17 |
| 90 | 0.26 | 0.3 |
| 120 | 0.42 | 0.5985 |
| 150 | 0.58 | 0.7801 |
| 180 | 0.675 | 0.8504 |
| 210 | 0.84 | 1.0529 |
| 240 | 0.935 | 1.2037 |
| 270 | 0.997 | 1.2545 |
| 300 | 1.044 | 1.2681 |
| l/M | r/M | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 1 | 1/3 | 0.1 | 1/30 | 0.01 | 0.005 | 0.002 | 0.001 | 0.0005 | |
| 0.1 | 0.00034 | 0.0130 | 0.4390 | 3.3949 | 8.6047 | 15.2123 | 19.1007 | 24.2574 | 28.1615 | 32.0661 |
| 0.3 | 0.0012 | 0.0383 | 0.5674 | 2.6123 | 5.6922 | 9.5087 | 11.7527 | 14.7297 | 16.9837 | 19.2382 |
| 0.5 | 0.0020 | 0.0630 | 0.8501 | 2.9352 | 5.3649 | 8.1824 | 9.8214 | 11.9919 | 13.6346 | 15.2775 |
| 0.7 | 0.0022 | 0.0702 | 0.9672 | 3.3991 | 6.1969 | 9.3944 | 11.2468 | 13.6980 | 15.5527 | 17.4075 |
| 0.9 | 0.0018 | 0.0570 | 0.7689 | 2.6914 | 4.9703 | 7.6265 | 9.1730 | 11.2214 | 12.7718 | 14.3223 |
| Group | r1 | r2 | r3 | r4 | r5 | r6 | r7 | r8 | r9 | r10 |
| No. 1 | 135.43 | 114.00 | 109.18 | 101.90 | 102.47 | 113.02 | 118.65 | 74.09 | 64.68 | 43.70 |
| No. 2 | 148.58 | 134.00 | 131.40 | 130.21 | 132.11 | 144.75 | 150.47 | 79.68 | 68.26 | 34.05 |
| r11 | r12 | r13 | r14 | r15 | r16 | r17 | r18 | r19 | r20 | |
| No. 1 | 57.71 | 66.38 | 98.75 | 267.42 | 257.23 | 255.13 | 252.11 | 252.34 | 256.80 | 259.33 |
| No. 2 | 31.16 | 40.78 | 76.04 | 241.96 | 233.30 | 231.81 | 231.14 | 232.22 | 239.63 | 243.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Xie, W.; Wang, H.; Peng, B.; Xiong, F.; Zhu, C. Hydrogeological Parameter Estimation of Confined Aquifer within a Rectangular Shaped Drop Waterproof Curtain. Water 2023, 15, 356. https://doi.org/10.3390/w15020356
Li Y, Xie W, Wang H, Peng B, Xiong F, Zhu C. Hydrogeological Parameter Estimation of Confined Aquifer within a Rectangular Shaped Drop Waterproof Curtain. Water. 2023; 15(2):356. https://doi.org/10.3390/w15020356
Chicago/Turabian StyleLi, Yi, Wentao Xie, Hongwei Wang, Bin Peng, Feng Xiong, and Chun Zhu. 2023. "Hydrogeological Parameter Estimation of Confined Aquifer within a Rectangular Shaped Drop Waterproof Curtain" Water 15, no. 2: 356. https://doi.org/10.3390/w15020356
APA StyleLi, Y., Xie, W., Wang, H., Peng, B., Xiong, F., & Zhu, C. (2023). Hydrogeological Parameter Estimation of Confined Aquifer within a Rectangular Shaped Drop Waterproof Curtain. Water, 15(2), 356. https://doi.org/10.3390/w15020356








