Impact of Geometrical Features on Solute Transport Behavior through Rough-Walled Rock Fractures
Abstract
1. Introduction
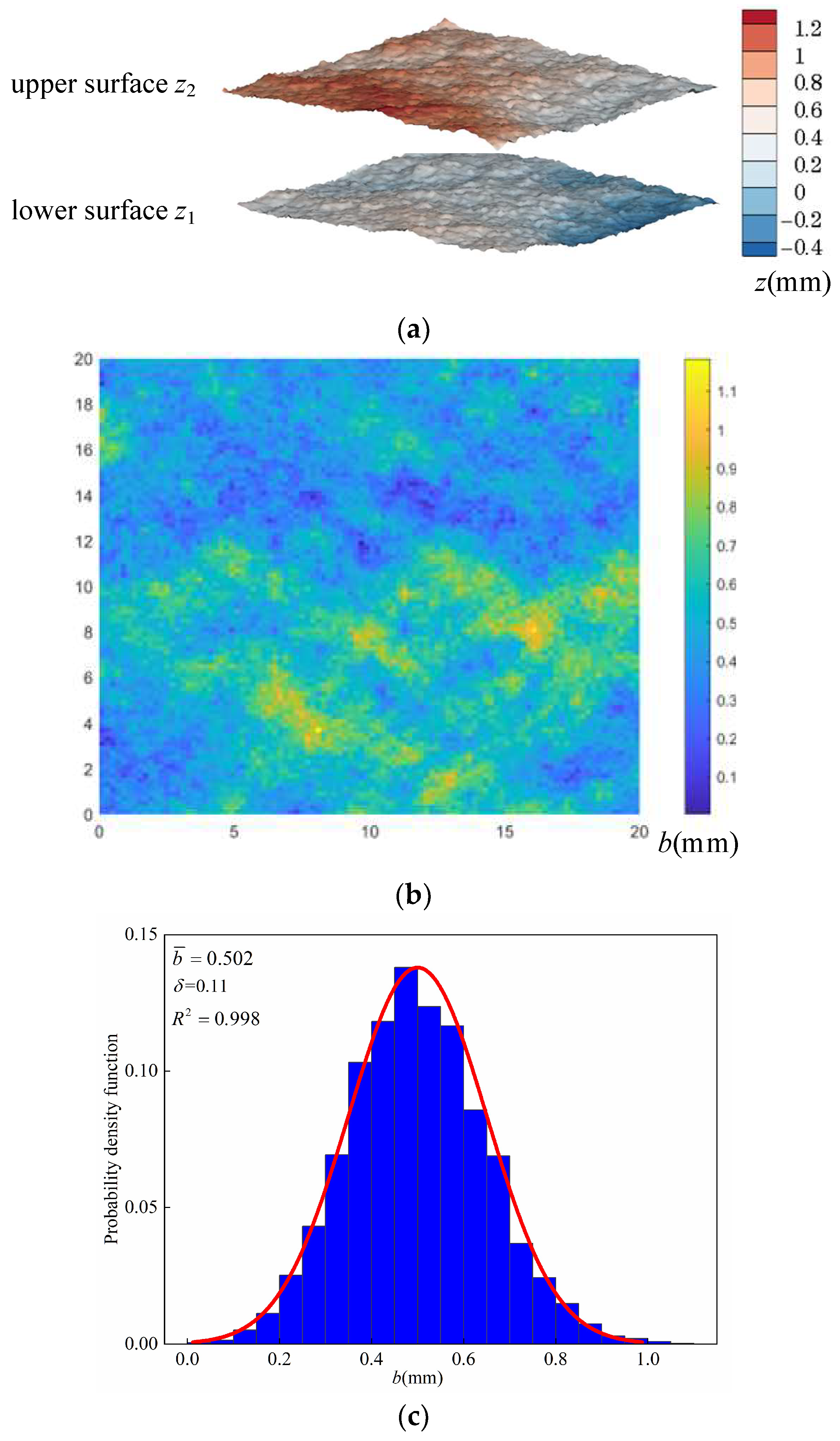
2. Generation of Rough-Walled Fracture
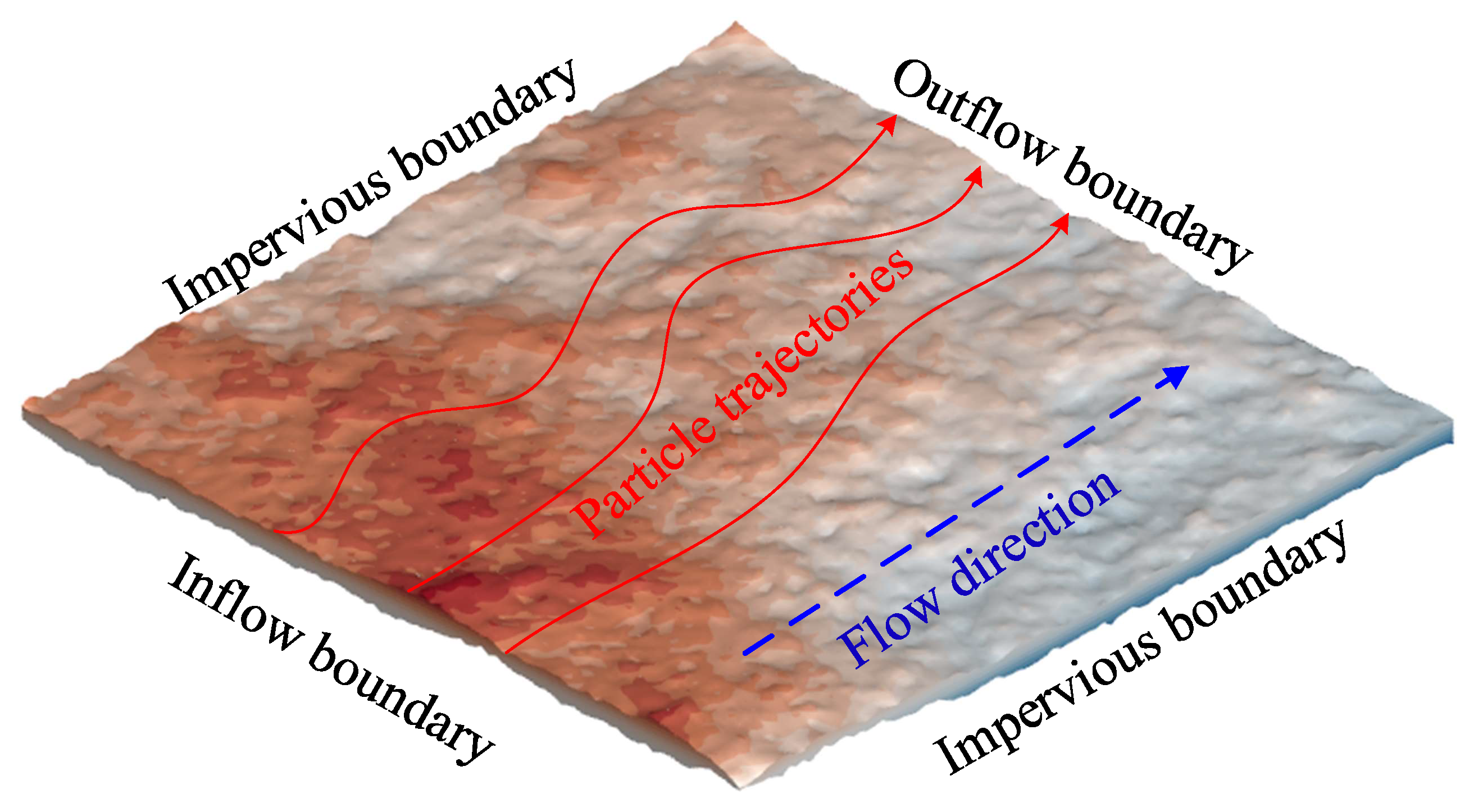
3. Solute Transport Model in Rough Fracture
4. Results and Analysis
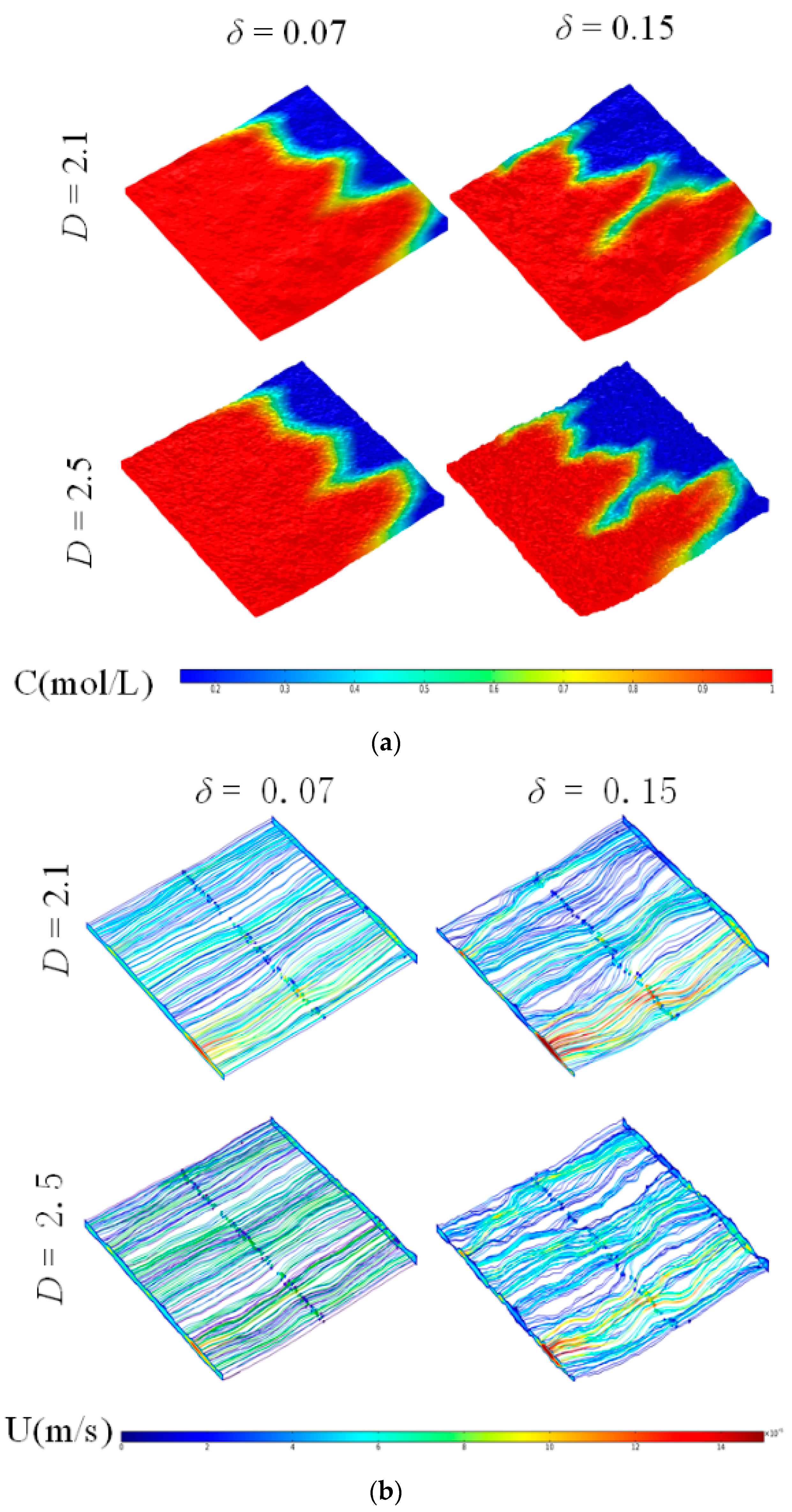
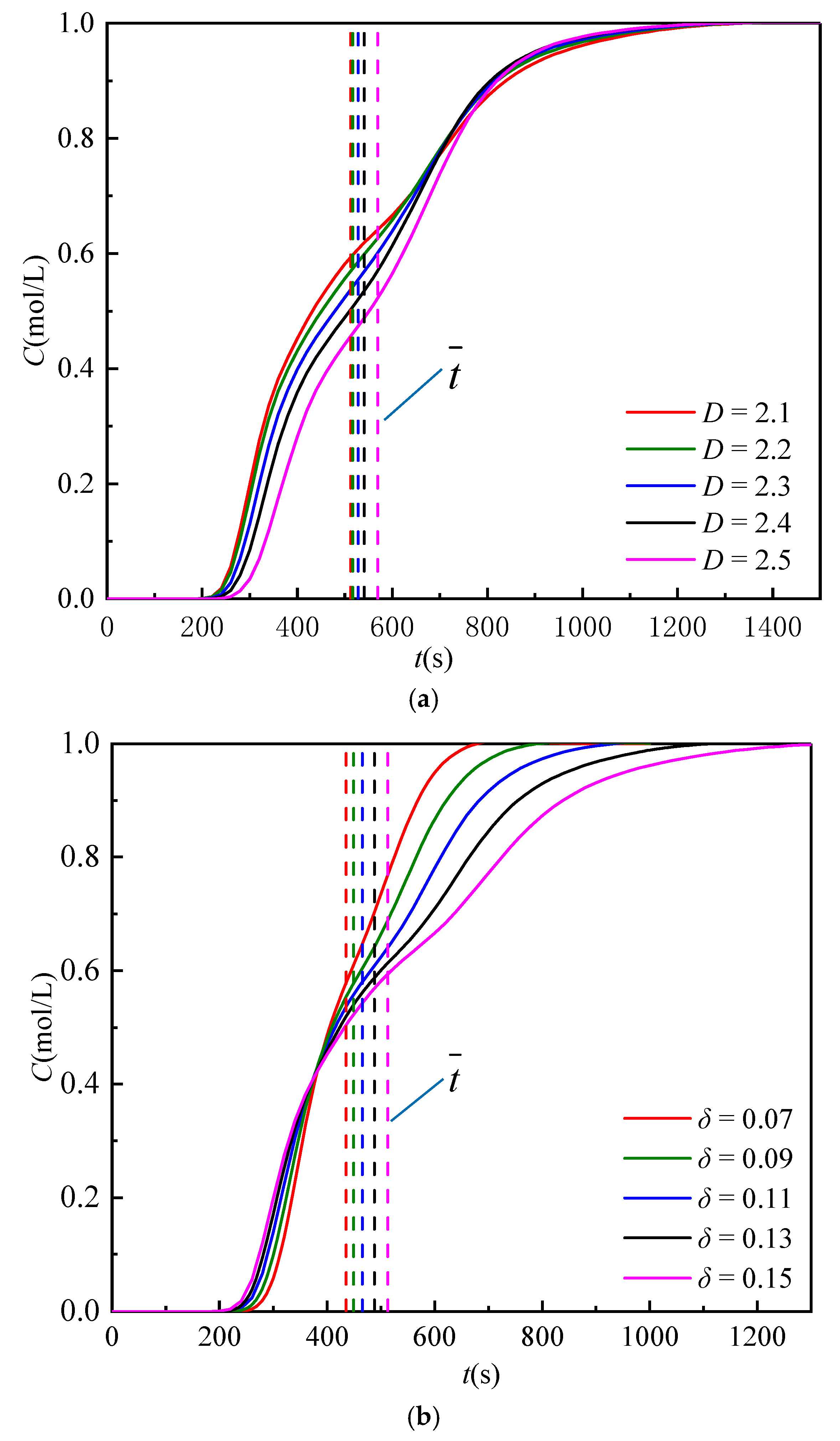
4.1. Concentration Distribution
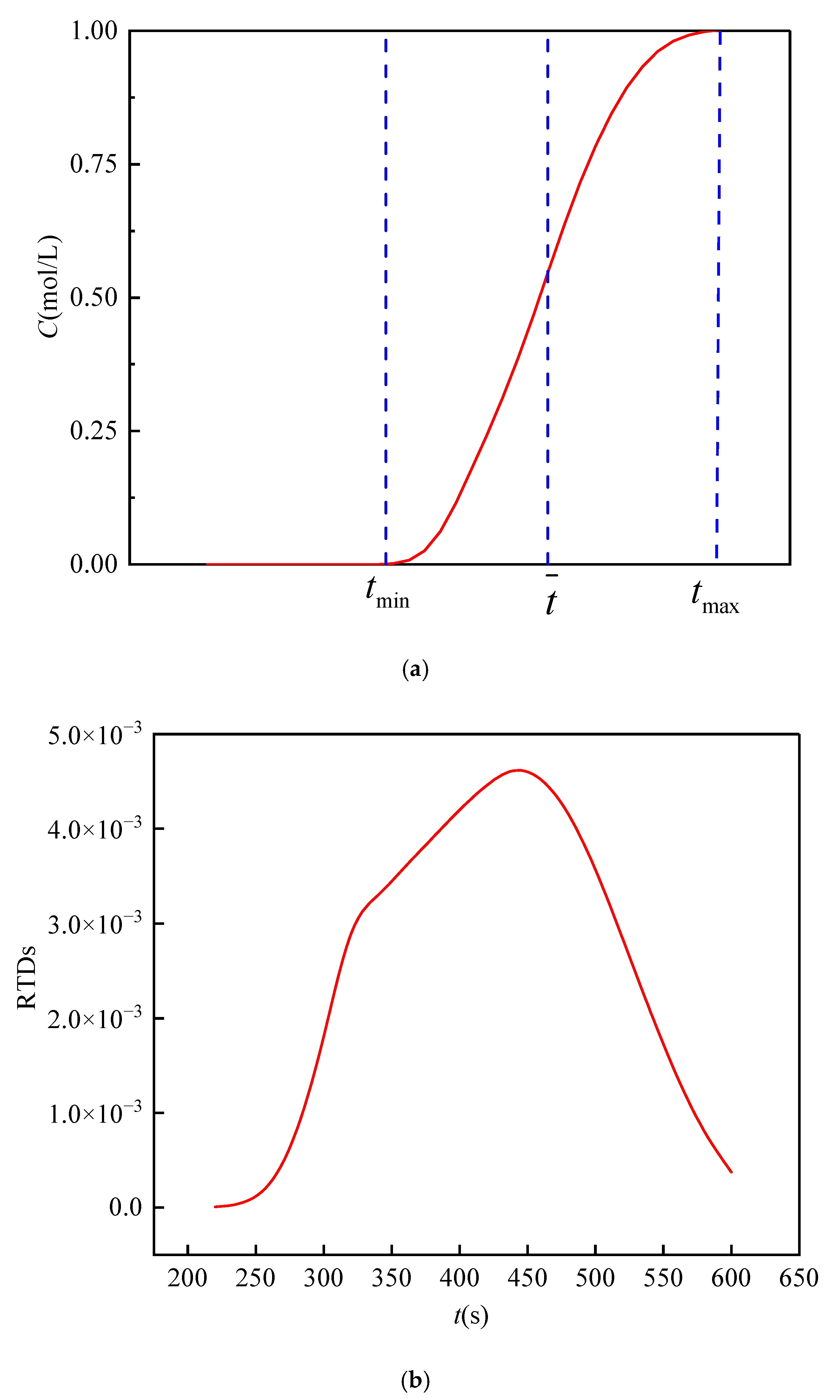
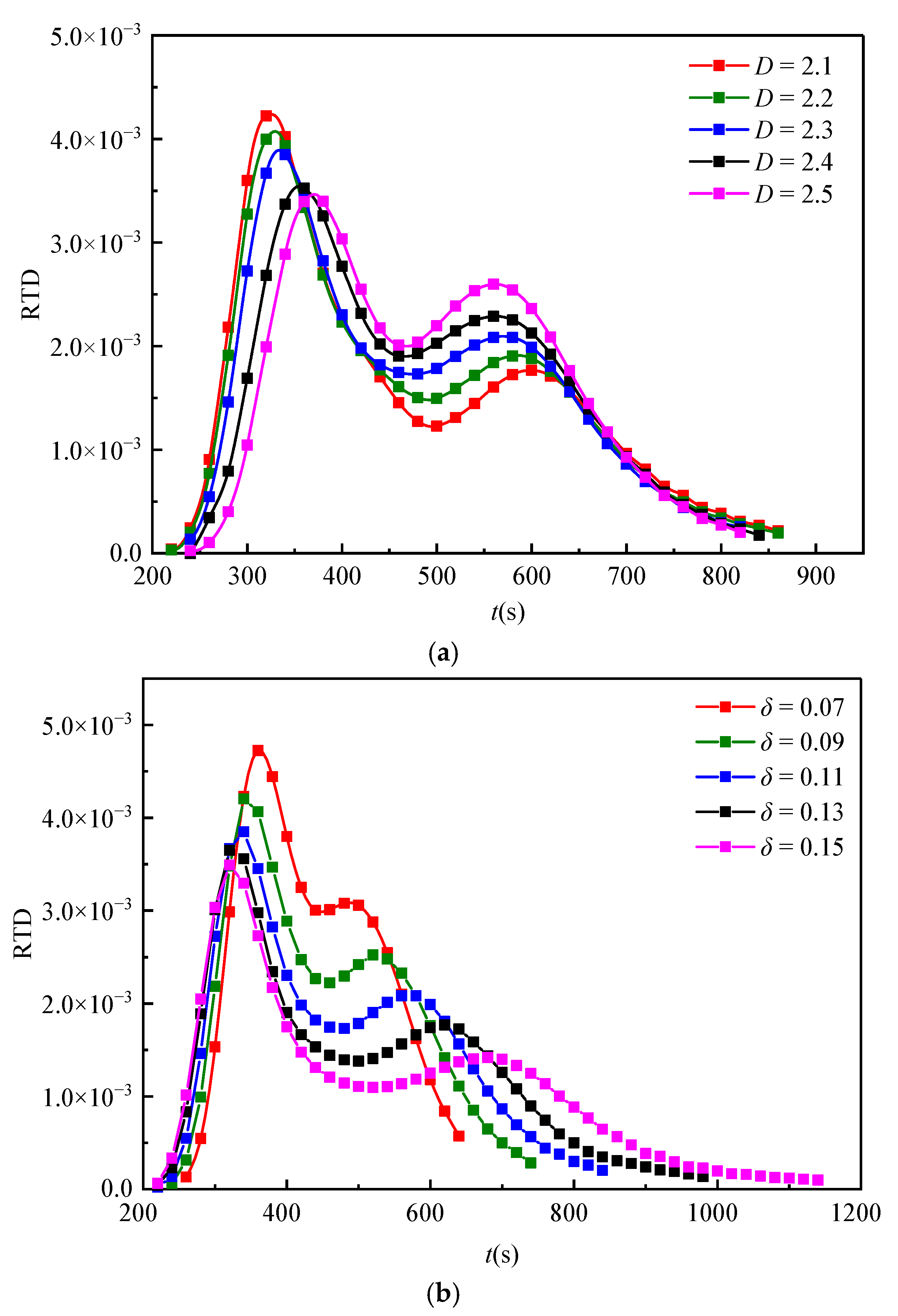
4.2. Breakthrough Curve
5. Conclusions
- (1)
- The geometric model of rough-walled fractures is successfully generated by the successive random addition method, which can guarantee consistency between the output and input values. With the increased fractal dimension and standard deviation, the fracture roughness becomes larger, and the aperture distribution becomes more scattered, which can make the streamline more tortuous, the flow distribution more uneven, and the concentration front more inhomogeneous.
- (2)
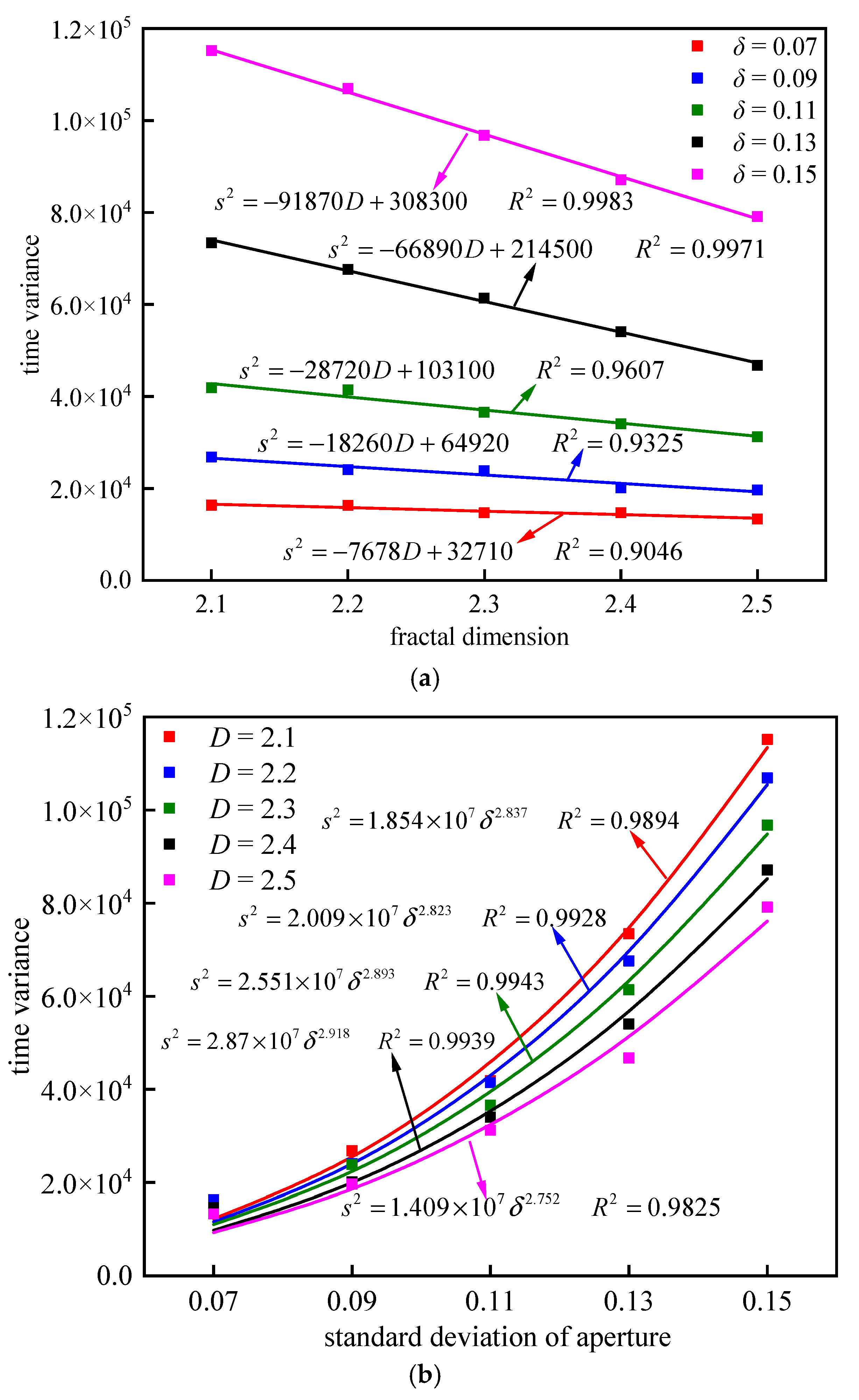
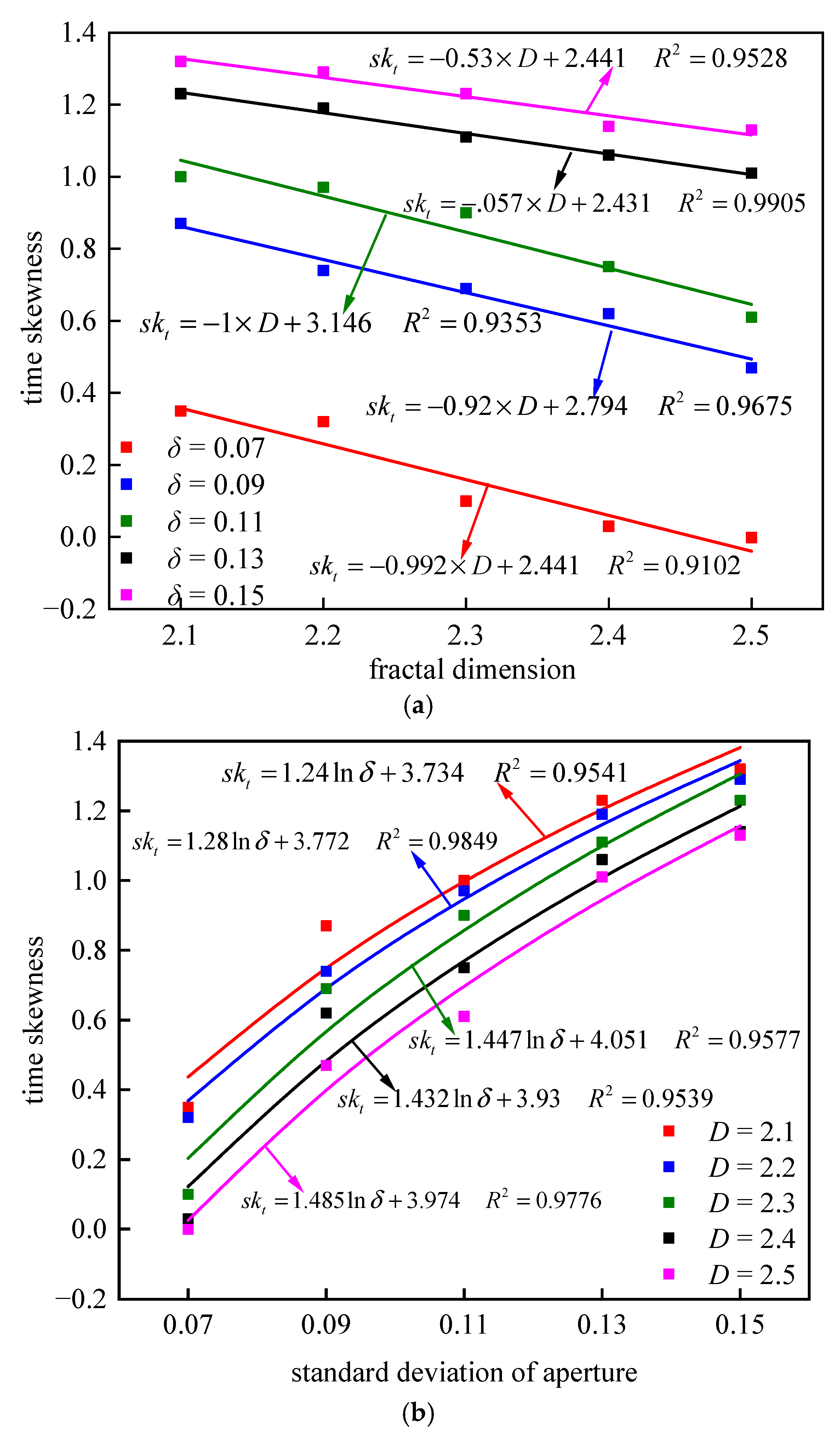
- With the growth of fractal dimensions, the average time of solute transport increases nonlinearly, and the time variance decreases linearly, respectively. The RTD curve skews more to the right, and the middle region turns to be more concentrated. The curve symmetry is enhanced, the tailing degree is weakened, and the time skewness is decreased.
- (3)
- With the increase of the standard deviation, the average time and the time variance of solute transport increase linearly and nonlinearly, respectively. The right part of RTD curves turns to be flatter with a larger range of time distribution, and the tailing degree is enhanced. Therefore, the curve symmetry is weakened while the skewness is increased.
- (4)
- Based on the curve fitting, the average time of solute transport linearly increases with the standard deviation and the fractal dimension by the power function. The time variance has a linear decreasing relationship with fractal dimension and a power function increasing relationship with standard deviation. The time skewness has a linear decreasing relationship with fractal dimension and a logarithmic increasing relationship with standard deviation.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cassiraga, E.F.; Fernàndez-Garcia, D.; Gómez-Hernández, J.J. Performance assessment of solute transport upscaling methods in the context of nuclear waste disposal. Int. J. Rock Mech. Min. Sci. 2005, 42, 756–764. [Google Scholar] [CrossRef]
- Zhang, H.J.; Jeng, D.S.; Seymour, B.R.; Barry, D.A.; Li, L. Solute transport in partially-saturated deformable porous media: Application to a landfill clay liner. Adv. Water Resource. 2012, 40, 1–10. [Google Scholar] [CrossRef]
- Hua, L.; Jing, W.; Shi, X.; Zi, X. Simulation of solute transport of groundwater at abandoned arsenic factory in downstream of Dehou reservoir in Yunnan based on GMS. J. Water Resource. Water Eng. 2014, 2(25), 209–217. [Google Scholar]
- Ye, Z.; Liu, H.; Jiang, Q.; Zhou, C. Two-phase flow properties of a horizontal fracture: The effect of aperture distribution. Adv. Water Resour. 2015, 76, 43–54. [Google Scholar] [CrossRef]
- Ye, Z.; Liu, H.; Jiang, Q.; Liu, Y.; Cheng, A. Two-phase flow properties in aperture-based fractures under normal deformation conditions: Analytical approach and numerical simulation. J. Hydrol. 2017, 545, 72–87. [Google Scholar] [CrossRef]
- Lee, J.; Babadagli, T. Effect of roughness on fluid flow and solute transport in a single fracture: A review of recent developments, current trends, and future research. J. Nat. Gas Sci. Eng. 2021, 91, 103971. [Google Scholar] [CrossRef]
- Xiong, X.; Li, B.; Jiang, Y.; Koyama, T.; Zhang, C. Experimental and numerical study of the geometrical and hydraulic characteristics of a single rock fracture during shear. Int. J. Rock Mech. Min. Sci. 2011, 48, 1292–1302. [Google Scholar] [CrossRef]
- Li, B.; Mo, Y.; Zou, L.; Liu, R.; Cvetkovic, V. Influence of surface roughness on fluid flow and solute transport through 3D crossed rock fractures. J. Hydrol. 2020, 582, 124284. [Google Scholar] [CrossRef]
- Ye, Z.; Fan, Q.; Huang, S.; Cheng, A. A one-dimensional line element model for transient free surface flow in porous media. Appl. Math. Comput. 2021, 392, 125747. [Google Scholar] [CrossRef]
- Ye, Z.; Fan, X.; Zhang, J.; Sheng, J.; Chen, Y.; Fan, Q.; Qin, H. Evaluation of connectivity characteristics on the permeability of two-dimensional fracture networks using geological entropy. Water Resour. Res. 2021, 57, e2020WR029289. [Google Scholar] [CrossRef]
- Ye, Z.; Yang, J.; Xiong, F.; Huang, S.; Cheng, A. Analytical relationships between normal stress and fluid flow for single fractures based on the two-part Hooke’s model. J. Hydrol. 2022, 608, 127633. [Google Scholar] [CrossRef]
- Wendland, E.; Himmelsbach, T. Transport simulation with stochastic aperture for a single fracture–comparison with a laboratory experiment. Adv. Water Resource. 2002, 25, 19–32. [Google Scholar] [CrossRef]
- Yu, C.; Lei, W. Simulation study on preferential channel of solute transport in rough single fracture. J. Chongqing Jiaotong Univ.: Nat. Sci. Ed. 2015, 34, 91–94. [Google Scholar]
- Xiong, F.; Sun, H.; Zhang, Q.; Yong, W.; Qing, J. Preferential flow in three-dimensional stochastic fracture networks: The effect of topological structure. Eng. Geol. 2022, 309, 106856. [Google Scholar] [CrossRef]
- Xiong, F.; Zhu, C.; Feng, G.; Zheng, J.; Sun, H. A three-dimensional coupled thermo-hydro model for geothermal development in discrete fracture networks of hot dry rock reservoirs. Gondwana Res. 2022, 1–17. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Z. Simulation of groundwater solute transport in fractured rock mass based on fractal theory. Chin. J. Rock Mech. Eng. 2004, 122–126. [Google Scholar]
- Jeong, W.; Song, J. A numerical study on flow and transport in a rough fracture with self-affine fractal variable apertures. Energy Sources 2008, 30, 606–619. [Google Scholar] [CrossRef]
- Zou, L.; Jing, L.; Cvetkovic, V. Modeling of Solute Transport in a 3D Rough-Walled Fracture–Matrix System. Transp. Porous Media 2017, 116, 1005–1029. [Google Scholar] [CrossRef]
- Stoll, M.; Huber, F.; Trumm, M.; Enzmann, F.; Meinel, D.; Wenka, A.; Schill, E.; Schäfer, T. Experimental and numerical investigations on the effect of fracture geometry and fracture aperture distribution on flow and solute transport in natural fractures. J. Contam. Hydrol. 2019, 221, 82–97. [Google Scholar] [CrossRef]
- Wang, L.; Cardenas, M.B. Transition from non-Fickian to Fickian longitudinal transport through 3-D rough fractures: Scale-(in)sensitivity and roughness dependence. J. Contam. Hydrol. 2017, 198, 1–10. [Google Scholar] [CrossRef]
- Wang, M.; Guo, Q.; Shan, P.; Cai, M.; Ren, F.; Dai, B. Numerical research of fluid flow and solute transport in rough fractures under different normal stress. Geofluids 2020, 2020, 1–17. [Google Scholar] [CrossRef]
- Hu, Y.; Xu, W.; Zhan, L.; Ye, Z.; Chen, Y. Non-fickian solute transport in rough-walled fractures: The effect of contact area. Water 2020, 12, 2049. [Google Scholar] [CrossRef]
- Zou, L.; Cvetkovic, V. Impact of normal stress-induced closure on laboratory-scale solute transport in a natural rock fracture. J. Rock Mech. Eng. 2020, 12, 1–10. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Zhou, C.; Li, C.; Xie, H. Retaining primary wall roughness for flow in rock fractures and implications on heat transfer and solute transport. Int. J. Heat Mass Transf. 2021, 176, 121488. [Google Scholar] [CrossRef]
- Zhou, X.; Sheng, J.; Lu, R.; Ye, Z.; Luo, W. Numerical simulation of the nonlinear flow properties in self-affine aperture-based fractures. Adv. Civ. Eng. 2021, 2021, 1–11. [Google Scholar] [CrossRef]
- Wang, J.S.Y.; Narasimhan, T.N.; Scholz, C.H. Aperture correlation of a fractal fracture. Geophys. Res: Solid Earth 1988, 93, 2216–2224. [Google Scholar] [CrossRef]
- Wang, L.; Cardenas, M.B.; Slottke, D.T.; Ketcham, R.A.; Sharp, J.M., Jr. Modification of the local cubic law of fracture flow for weak inertia, tortuosity, and roughness. Water Resour. Res. 2015, 51, 2064–2080. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, C.; Wang, F.; Li, C.; Xie, H. Channeling flow and anomalous transport due to the complex void structure of rock fractures. J. Hydrol. 2021, 601, 12624. [Google Scholar] [CrossRef]
- Bodin, J.; Delay, F.; Marsily, G.D. Solute transport in a single fracture with negligible matrix permeability: 1. fundamental mechanisms. Hydrogeol. J. 2003, 11, 418–433. [Google Scholar] [CrossRef]
- Bodin, J.; Delay, F.; Marsily, G.D. Solute transport in a single fracture with negligible matrix permeability: 2. mathematical formalism. Hydrogeol. J. 2003, 11, 434–454. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, Z. Heat transfer in a 3D rough rock fracture with heterogeneous apertures. Int. J. Rock Mech. Min. Sci. 2020, 134, 104445. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chuang, X.; Li, S.; Hu, Y.; Zhou, X. Impact of Geometrical Features on Solute Transport Behavior through Rough-Walled Rock Fractures. Water 2023, 15, 124. https://doi.org/10.3390/w15010124
Chuang X, Li S, Hu Y, Zhou X. Impact of Geometrical Features on Solute Transport Behavior through Rough-Walled Rock Fractures. Water. 2023; 15(1):124. https://doi.org/10.3390/w15010124
Chicago/Turabian StyleChuang, Xihong, Sanqi Li, Yingtao Hu, and Xin Zhou. 2023. "Impact of Geometrical Features on Solute Transport Behavior through Rough-Walled Rock Fractures" Water 15, no. 1: 124. https://doi.org/10.3390/w15010124
APA StyleChuang, X., Li, S., Hu, Y., & Zhou, X. (2023). Impact of Geometrical Features on Solute Transport Behavior through Rough-Walled Rock Fractures. Water, 15(1), 124. https://doi.org/10.3390/w15010124





