1. Introduction
Although many studies regarding the determination of flow velocity in gravel-bed rivers are available, some scientific and technical aspects still need to be clarified. For channels having gravel beds, the macro-scale roughness condition [
1,
2,
3] occurs when the mean flow depth
h is comparable with the bed roughness size, which is generally assumed equal to the median bed particle diameter
d50. According to some studies [
4,
5,
6,
7], if the hydraulic condition is defined by the ratio between
h and the bed particle diameter
d84 (i.e., diameter for which 84% of the particles are finer), a macro-scale occurs for
h/
d84 ≤ 4. Macro-scale roughness condition is characterized by different dissipative mechanisms as compared to micro-scale one. Mendicino and Colosimo [
7] stated that, for values higher than 100 of the depth/sediment ratio (i.e., the ratio between the hydraulic radius
R or
h and the particle diameter representing the characteristic roughness height), skin friction is due to drag effects related to the shape of each bed particle and viscous friction on its surfaces, and is also influenced by macro-scale bed-forms.
For low values of the relative submergence (i.e.,
h/
d84 ≤ 10, and in particular for
h/
d84 ~ 1), the resistance effects due to form drag and turbulent wakes caused by large roughness elements are high. When some elements protrude above the water surface, and the flow is locally supercritical, additional energy losses occur [
8,
9,
10]. According to Bathurst [
11], a channel can be defined with a “cobble and boulder bed” when
d50 > 64 mm, the flow resistance due to vegetation is negligible, and the occurring roughness condition is “transition” or “macro-scale”.
Since most of the studies available in the literature investigated the flow resistance of uniform open channel flows for micro-scale roughness conditions, there is a scientific need to widen the knowledge on the macro-scale condition.
The open-channel flow resistance equation was theoretically obtained [
12] for some known cross-section shapes (i.e., circular, and very wide rectangular) and established boundary conditions for which the velocity distribution is known. Integrating the flow-velocity profile, a semi-theoretical flow resistance equation [
12,
13,
14,
15,
16], which is a major tool required in studying open-channel flow hydraulics, can be obtained.
For micro and macro-scale roughness, Ferro and Pecoraro [
17], using measured distributions having the measured maximum velocity located at the free surface, deduced a power velocity profile using the incomplete self-similarity theory.
For macro-scale roughness condition (
h/
d84 ≤ 4), some authors [
18,
19] demonstrated that the velocity profile is S-shaped, with near-surface velocities higher than near-bed ones, and the logarithmic or power distribution can be assumed only for a bottom distance greater than the roughness size.
Ferro [
20] carried out flume experiments for transition and macro-scale roughness conditions using boulders, with concentrations varying from 0 to 83%, arranged on a quarry rubble bed. Ferro [
20] concluded that a skimming flow regime [
21] occurs for boulder concentrations higher than 50%. For this regime, the proximity of the roughness elements determines the confinement of the eddies, and the flow motion occurs on a surface placed at the top level of the elements.
To estimate the flow velocity, having the cross-section shape and sizes, depth, and bed slope, is still one of the most relevant topics in hydraulics [
22]. The Chezy, Manning, and Darcy–Weisbach uniform flow resistance formulas are the most applied [
12,
22]:
where
V is the cross-section average velocity,
C is the Chezy coefficient (m
1/2 s
−1), n is the Manning coefficient (m
−1/3 s),
s is the channel slope,
g is the gravitational acceleration,
f is the Darcy–Weisbach friction factor,
R is the hydraulic radius, and
, which is the shear velocity.
For a uniform turbulent open-channel flow, the vertical velocity profile distribution can be represented by the following equation [
23]:
in which
v is the local velocity,
y is the distance from the bottom,
νk is the kinematic viscosity, Γ is a function estimated by experimental velocity measurements, and
δ is an exponent calculated by the following relationship [
24]:
in which
Re =
V h/νk is the flow Reynolds number.
Integrating Equation (2), the following expression of the Darcy–Weisbach friction factor
f [
25] is obtained:
Hypothesizing that
y =
α h (i.e., the distance from the bottom where the local velocity is equal to the cross-section average velocity V), Equation (2) gives the following estimate Γ
v of the function Γ [
25]:
where
α < 1 is a coefficient which implies two conditions: (i) the average flow velocity
V occurs below the water surface and (ii) a single velocity profile is used to express the velocity distribution for the whole cross-section. Ferro [
25] theoretically deduced the following equation for calculating
α:
Ferro [
25] tested Equations (4) and (5) using field measurements of flow velocity, water depth, river width, and bed slope of some Canadian mountain streams [
6]. Moreover, this author [
25] empirically deduced the following relationship for the estimation of Γ function:
in which
F =
V/(gh)1/2 is the flow Froude number and
a,
b, and
c are coefficients to be estimated experimentally.
Equation (7) was calibrated by Ferro and Porto [
15] using 104 experimental measurements collected in Calabrian gravel-bed rivers with high boulder concentrations, and 101 literature data on gravel-bed reaches [
1,
2,
26,
27,
28,
29].
Ferro [
30] tested the applicability of Equation (7) by using gravel-bed flume measurements [
17,
31,
32,
33], and demonstrated that this theoretical approach can be applied to measurements carried out in gravel-bed rivers [
6] upscaling the equation calibrated by flume data by a scale factor equal to 0.7611.
Carollo and Ferro [
34] also positively tested Equation (7) using experimental data obtained for flume covered by hemispheric elements in different hydraulic conditions (i.e., partially submerged and completely submerged). These authors [
34] placed the elements with a square arrangement and a concentration,
Ch, in the range 4–64%. The results obtained by Carollo and Ferro [
34] showed that the two investigated hydraulic conditions gave the same exponents
b and
c of Equation (7), but a different scale factor
a. The results also highlighted that, for these hydraulic conditions, the scale factor has a different trend with the concentration. The variability of
a with
Ch was explained because of the variability with
Ch of the reference plane for the
h measurement.
For macro-scale roughness conditions, the shape and size of the roughness elements and their arrangement (position to flow streamlines, spacing between elements, and protrusion of the elements from the channel bed) influence flow resistance [
1,
3,
4,
29,
35,
36].
O’Laughlin and MacDonald [
35] performed flume experiments to evaluate the flow resistance for two bed roughnesses (cube and sand) characterized by different concentrations. The results highlighted that for high element concentrations (0.7), the regularity of the surface determines the development of skimming flow.
Lawrence [
3], using the data available in the literature for a wide range of
h/d, studied the overland flow resistance. Lawrence [
3] found a non-monotonic dependence between friction factor and
h/d and presented three flow regimes distinguished by the submergence ratio. The results also suggested that
h/d should be considered as the main dimensionless group affecting the hydraulics of overland flow on rough surfaces.
Lawrence [
37] conducted experimental runs on overland flow in a flume with the bed covered by hemispheric elements (0.2 ≤
h/d ≤ 7.5, and
Ch = 10, 18, and 39%). For
Re > 500, Lawrence [
37] found a relationship between
f and
h/d, especially for values of the ratio higher than 1. This author found that flow resistance increases for increasing
Ch.
For low values of
Ch, the distance among the roughness elements determines the dissipation of the wake generated by each element before approaching the next element along the flow direction (semi-smooth isolated roughness turbulent flow) [
21]. Instead, for high values of it, the vicinity of the elements determines that the wake cannot dissipate before approaching the next one (wake interference flow). As a consequence, the effect of roughness element concentration becomes predominant as compared to that determined by the arrangement of the elements.
To the best of our knowledge, there is a lack of investigations on the effects of the boulder arrangement on flow resistance for low values of
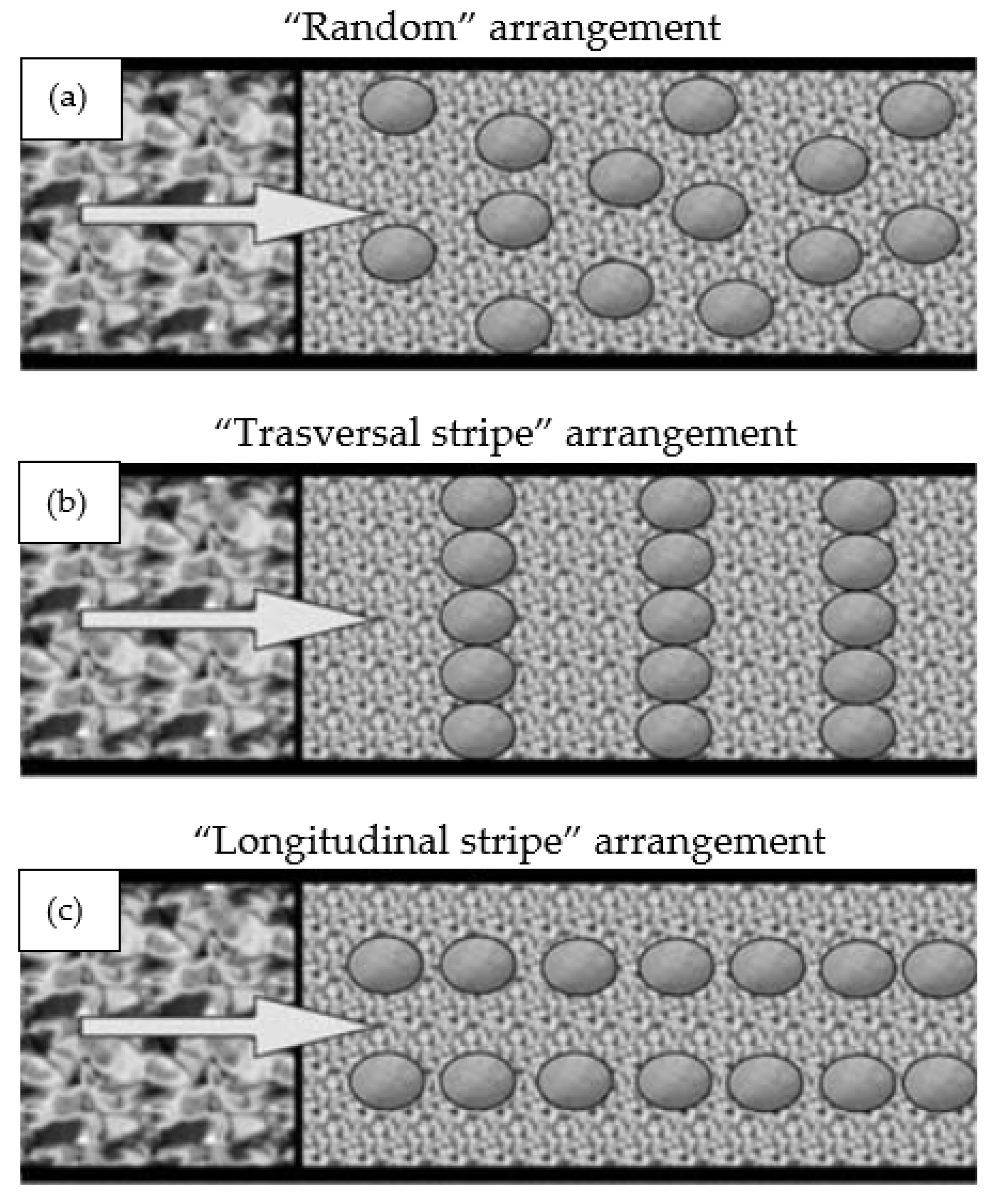
Ch in which this effect should be dominant. For this reason, this paper aims to investigate the effect of different boulder arrangements (i.e., “Random”, “Transversal stripe”, and “Longitudinal stripe”), with different concentrations, on flow resistance for macro-scale roughness conditions. In particular, the measurements available in the literature by Canovaro et al. [
38] and Ferro and Giordano [
31] allowed for (i) calibrating and testing the relationship between the velocity profile parameter Γ, the bed slope, and the flow Froude number, (ii) investigating the influence of the boulder concentration on flow resistance, and (iii) assessing the influence of the boulder arrangements on flow resistance for both low and high element concentration values.
3. Results
Considering that Ferro [
20] suggested that a skimming flow regime occurs for boulder concentrations higher than 50%, the 189 measurements carried out for the “Random” arrangement by Canovaro et al. [
38] were divided into two datasets distinguishing them by the boulder concentration threshold equal to 48% (84 data for
Ch < 48% and 105 data for
Ch ≥ 48%). These two datasets were used to calibrate Equation (7), obtaining the following result:
for
Ch < 48% and
for
Ch ≥ 48%. These equations are both characterized by a coefficient of determination of 0.999.
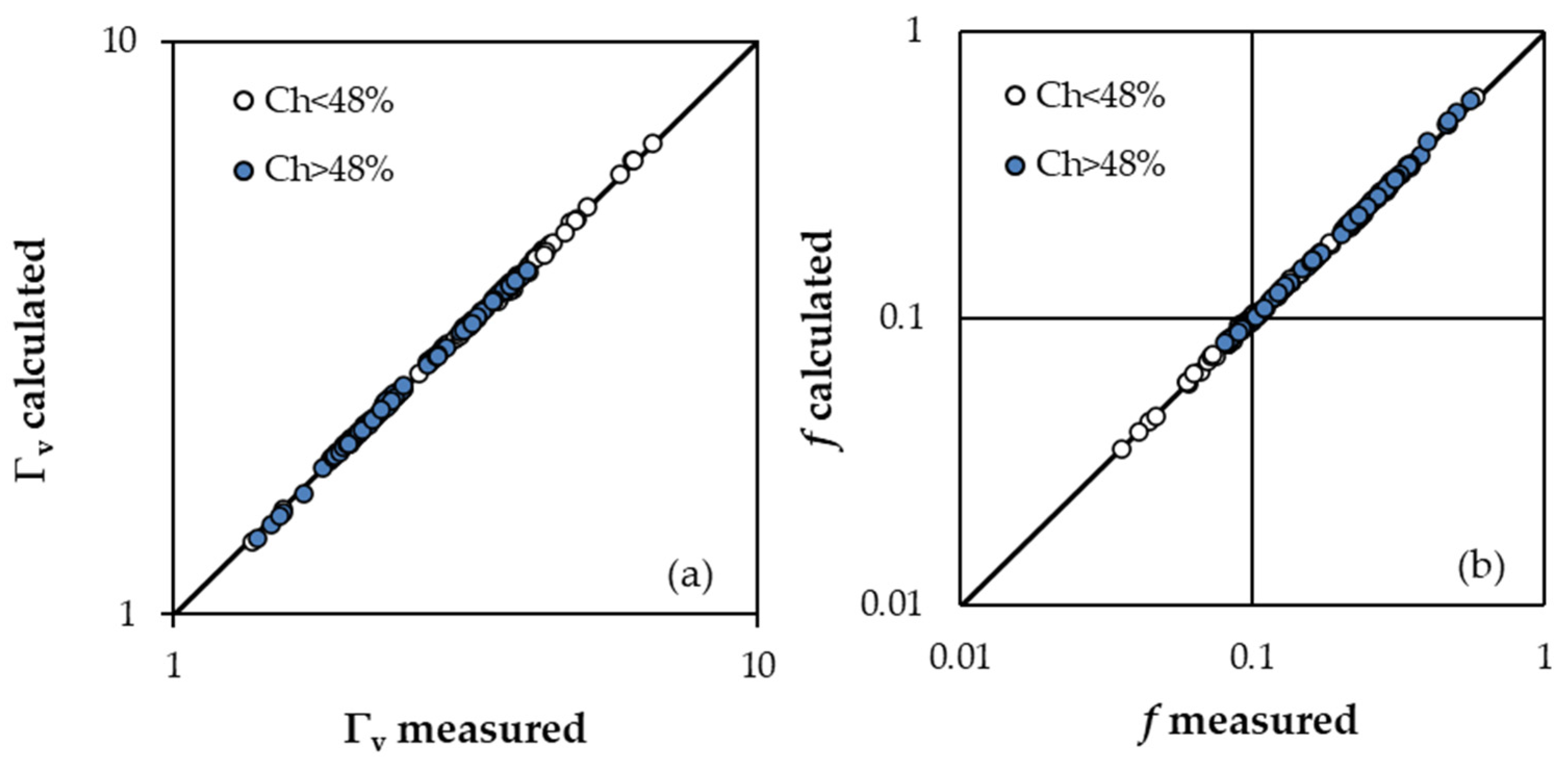
Figure 2a shows the comparison between the Γ
v values obtained by Equations (5) and (6), with those calculated by Equations (8a) and (8b).
Coupling Equations (8a) and (8b) and Equation (4), the following equations to estimate the Darcy–Weisbach friction factor are obtained:
Figure 2b shows the comparison between the measured
fm values and those calculated
fc by Equations (9a) and (9b) and remarks that an accurate estimate of the Darcy–Weisbach friction factor can be obtained by the proposed approach. The friction factor values calculated by Equations (9) are characterized by errors in estimate
E = (
fc −
fm)/
fm which are less than or equal to ±5% for 98.9% of cases and less than or equal to ±2.5% for 87.8% of cases.
Equation (9a) was tested using the 416 experimental data by Ferro and Giordano [
31], since these data were obtained for an overlapped range of element concentrations (0 ≤
Ch ≤ 44%).
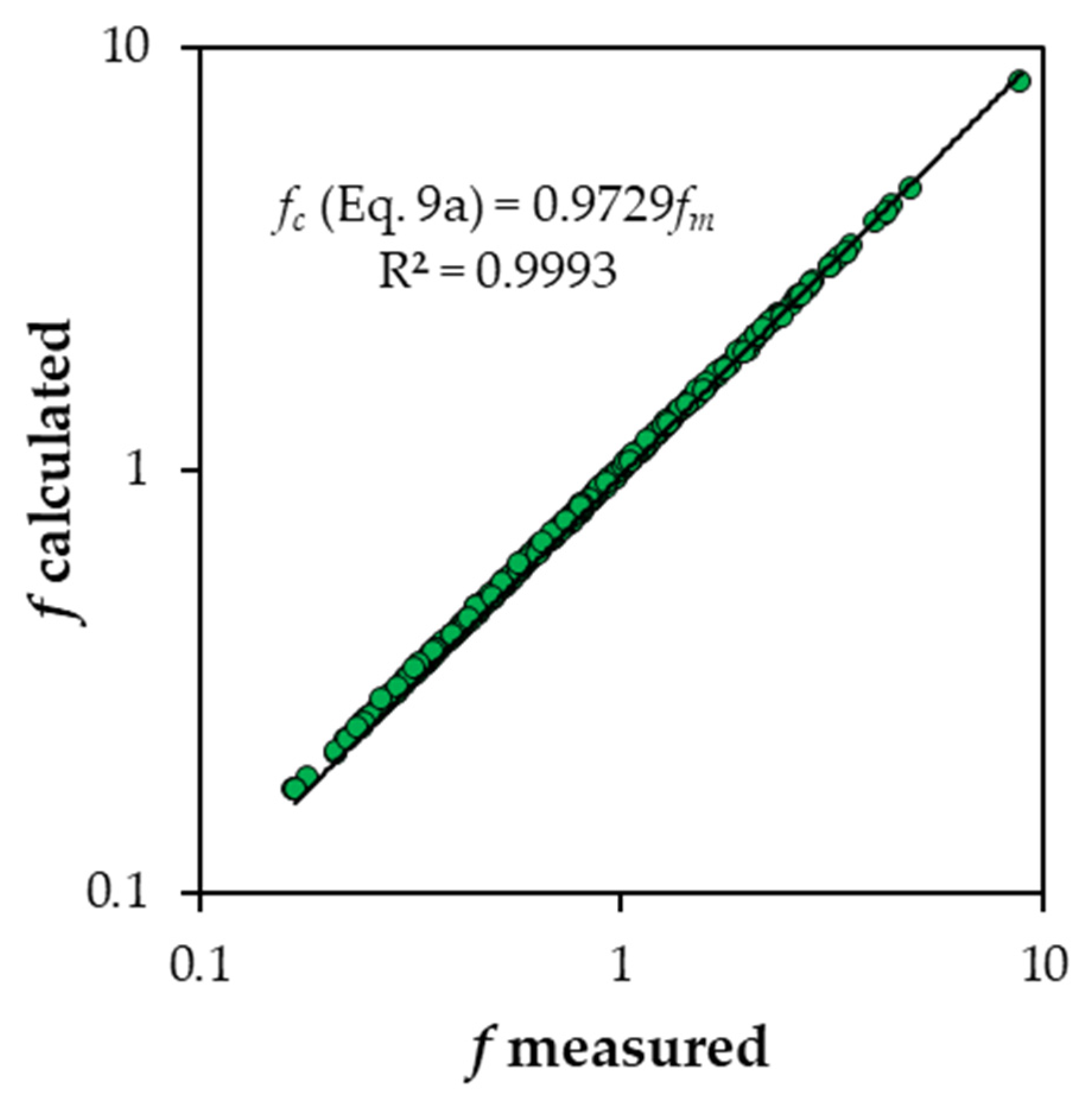
Figure 3 shows the comparison between the measured
f values and those calculated applying Equation (9a), obtained for the “Random” arrangement by Canovaro et al. [
38], to the dataset by Ferro and Giordano [
31]. For the dataset by Ferro and Giordano [
31], this figure shows that, on average, the Darcy–Weisbach friction factor values calculated by Equation (9a) are approximately equal to 0.97
fm. In other words, Equation (9a) systematically underestimates (−3%) the
f values measured by Ferro and Giordano [
31].
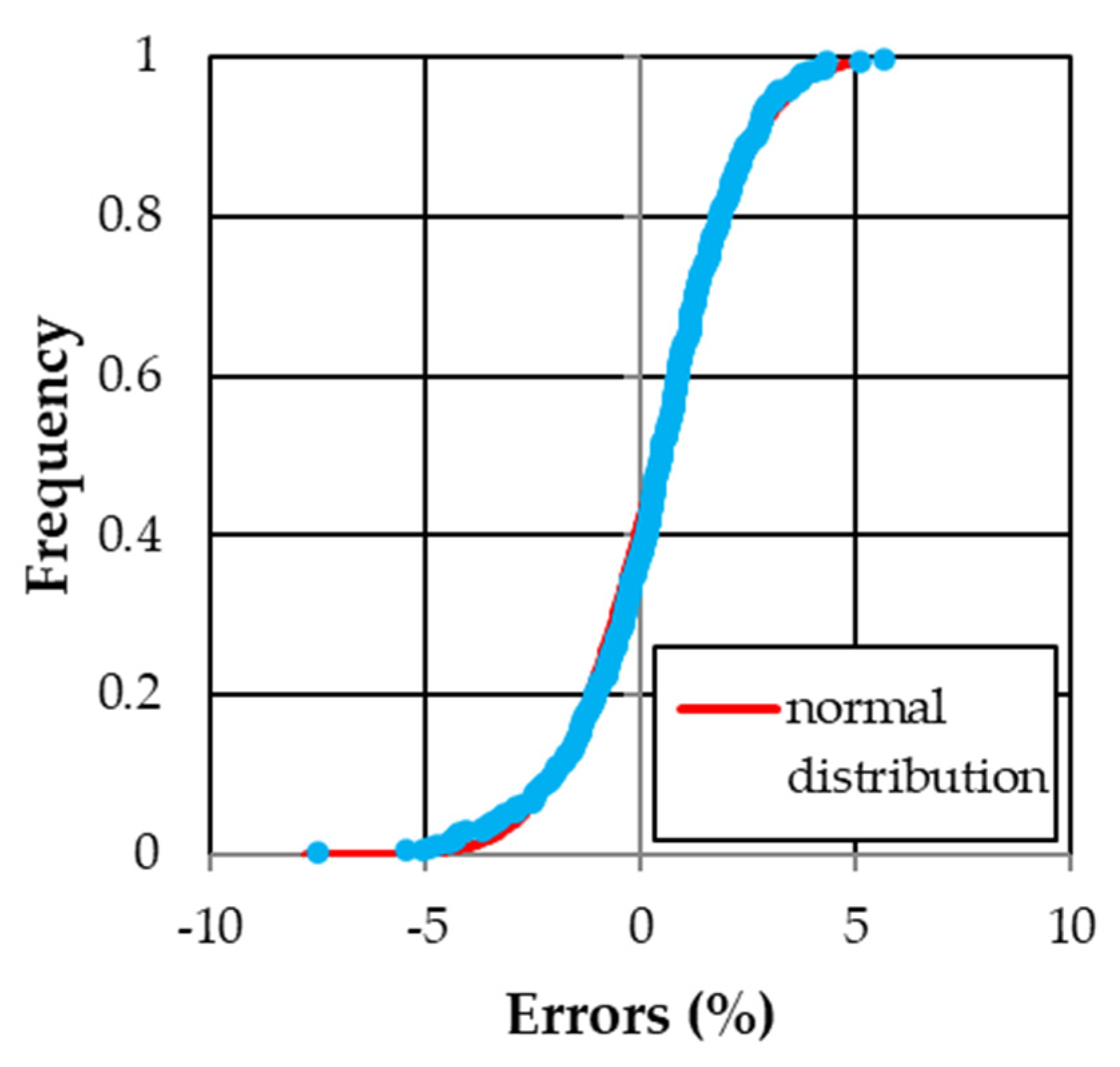
The friction factor values calculated applying Equation (9a) to this dataset are characterized by errors in estimate
E, which are distributed according to the normal law (
Figure 4), less than or equal to ±5% for 98.8% of cases and less than or equal to ±2.5% for 82.4% of cases.
Then, Equation (7) was also calibrated using the 160 measurements carried out for the “Trasversal stripe” arrangement by Canovaro et al. [
38]. The equation was calibrated for both
Ch ≤ 35% (140 data, Equation (10a)) and
Ch = 100% (20 data, Equation (10b)) and the following results were obtained:
Characterized by a coefficient of determination of 0.999. Coupling Equations (10a) and (10b) and Equation (4), the following equations to estimate the Darcy–Weisbach friction factor are obtained:
Figure 5 shows the comparison between the
f measured values and those calculated by Equations (11a) and (11b). The friction factor values calculated by these equations are characterized by errors in estimate
E which are less than or equal to ±5% for 97.5% of cases and less than or equal to ±2.5% for 85% of cases.
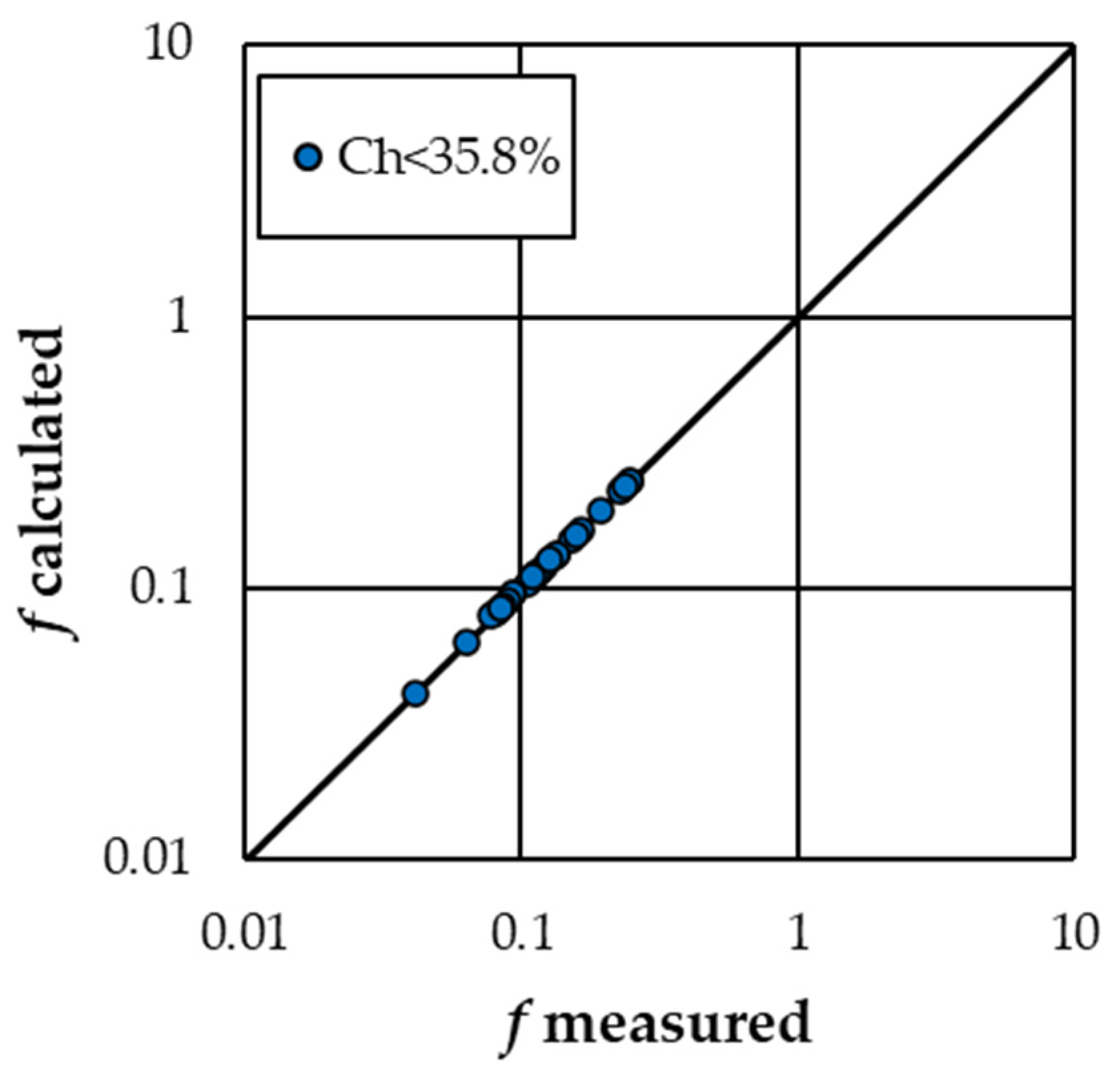
Finally, Equation (7) was also calibrated using the 30 measurements carried out for the “Longitudinal stripe” arrangement and
Ch ≤ 35.8% by Canovaro et al. [
38], and the following result was obtained:
Characterized by a coefficient of determination of 0.999. Coupling Equation (12) and Equation (4), the following equation to estimate the Darcy–Weisbach friction factor is obtained:
Figure 6 shows the comparison between the
f measured values and those calculated by Equation (13). The friction factor values calculated by Equation (13) are characterized by errors in estimate
E which are always less than or equal to ±5% and ±2.5%.
To investigate the effect of the boulder concentration on flow resistance, the trend of the Darcy–Weisbach friction factor values with
Ch was examined for both low (<48%) and high (≥48%) values of roughness concentrations.
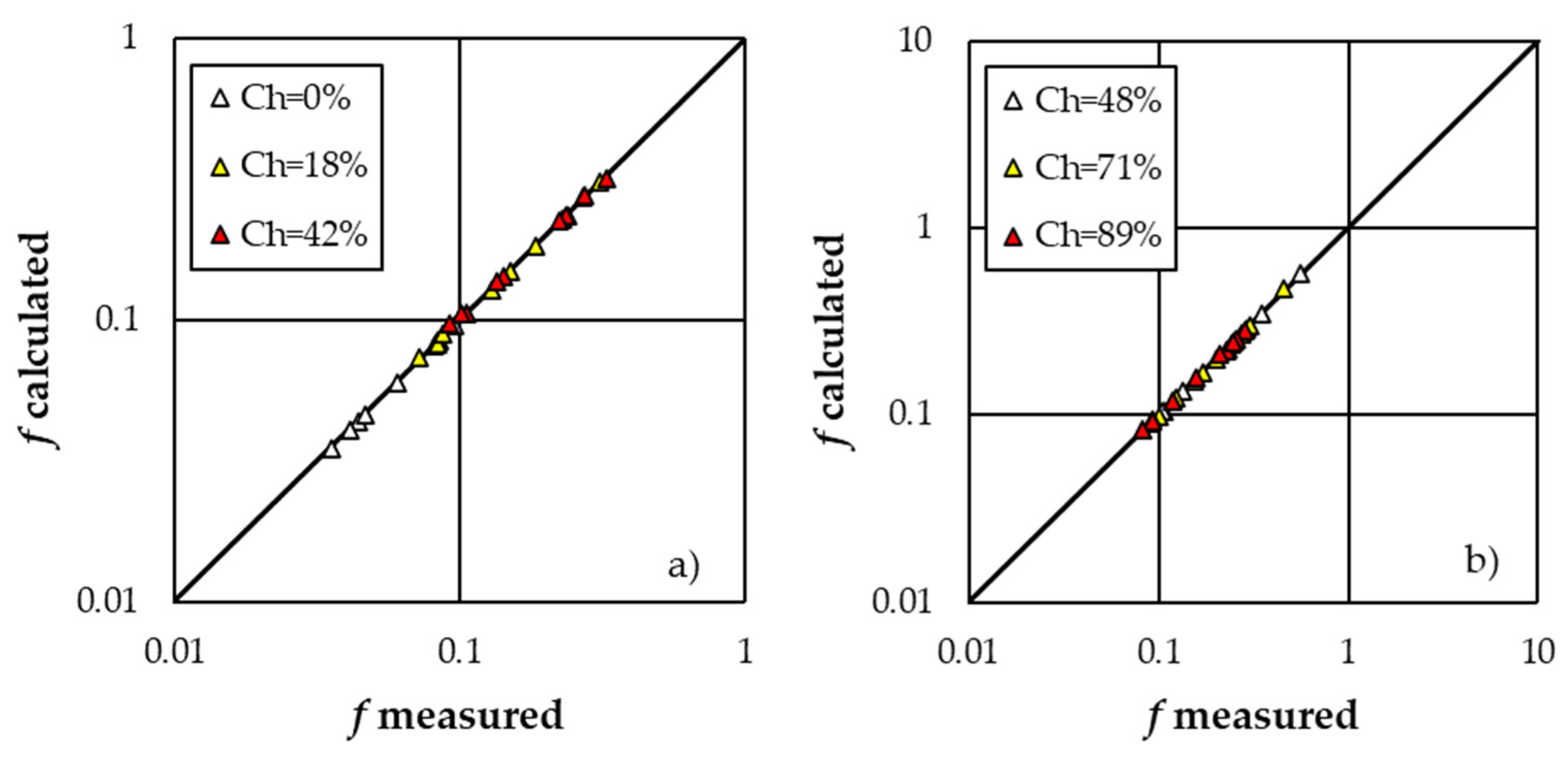
Figure 7a,b show, as an example for the “Random” arrangement, the trend of
f for three selected values of concentration for low (
Ch = 0, 18, and 42%) and high (
Ch = 48, 71, and 89%) values of roughness concentration, respectively.
For
Ch < 48%, since Equations (8a), (10a), and (12) presented similar values of the
b and
c coefficients, their mean values (
b = 1.078 and
c = 0.58) can be used to attribute to the
a coefficient the effect of the arrangements on flow resistance. For each arrangement, the behavior of the pairs (F
1.078s
−0.58, Γ) was investigated and a value of the
a coefficient, equal to the slope coefficient of the best-fit straight line passing through the origin of the axes, was obtained. In particular, the
a coefficient resulted equal to 0.3354 for the “Random” arrangement, 0.3372 for the “Transversal stripe” arrangement, and 0.335 for the “Longitudinal stripe” arrangement (
Table 2).
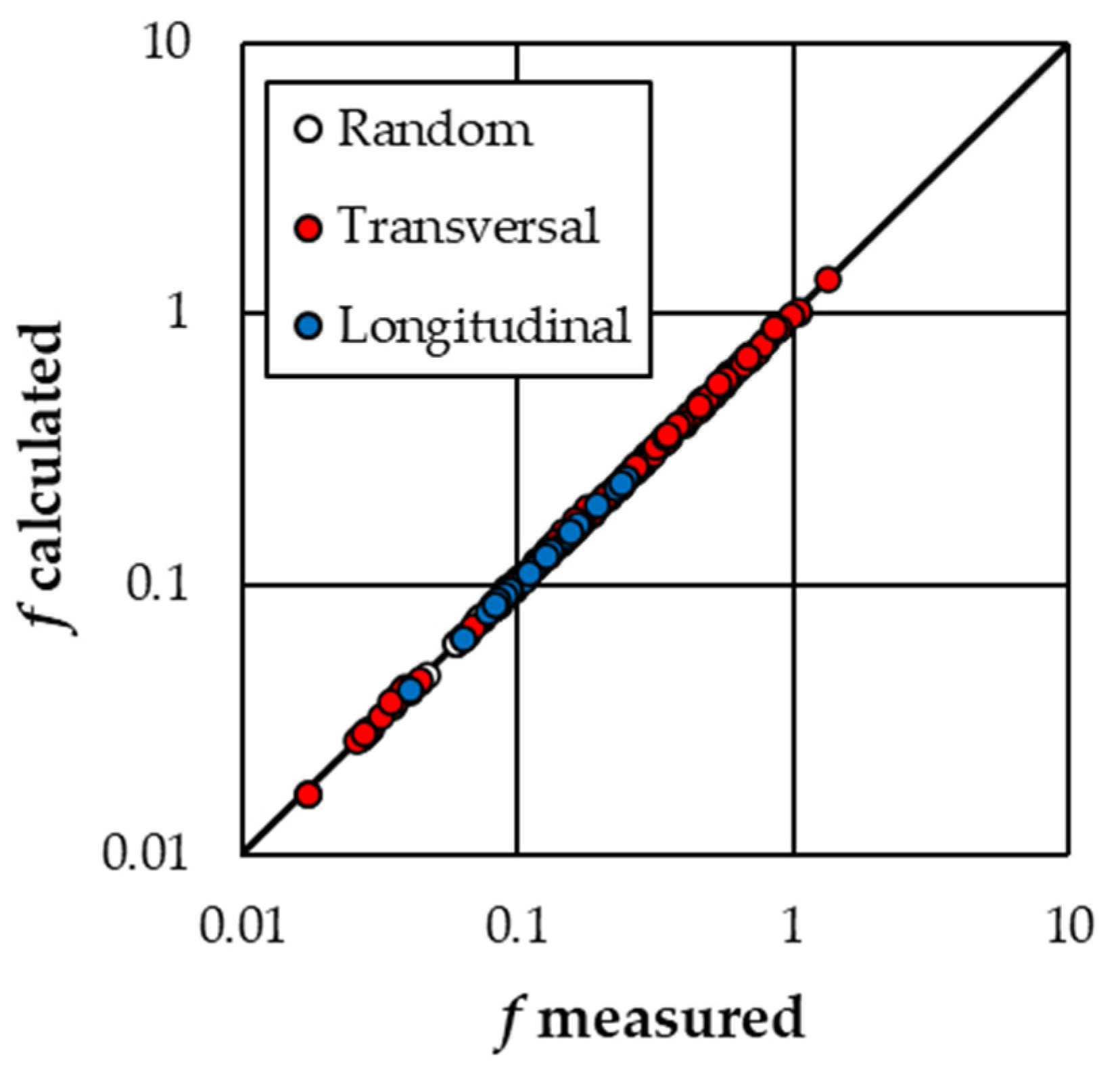
Figure 8 shows the comparison between the
f measured values and those calculated coupling Equations (4) and (7) with
b = 1.078,
c = 0.58, and
a varying with the arrangement. In this case, the errors
E in the estimate of the Darcy–Weisbach friction factor are less than or equal to ±5% for 96.8% of cases and less than or equal to ±2.5% for 88.2% of cases.
The same procedure was applied for the data with
Ch ≥ 48%, and the mean values of
b (1.1175) and
c (0.587) coefficients were used obtaining
a coefficient equal to 0.3356 for the “Random” arrangement, and 0.3366 for the “Transversal stripe” arrangement (
Table 2).
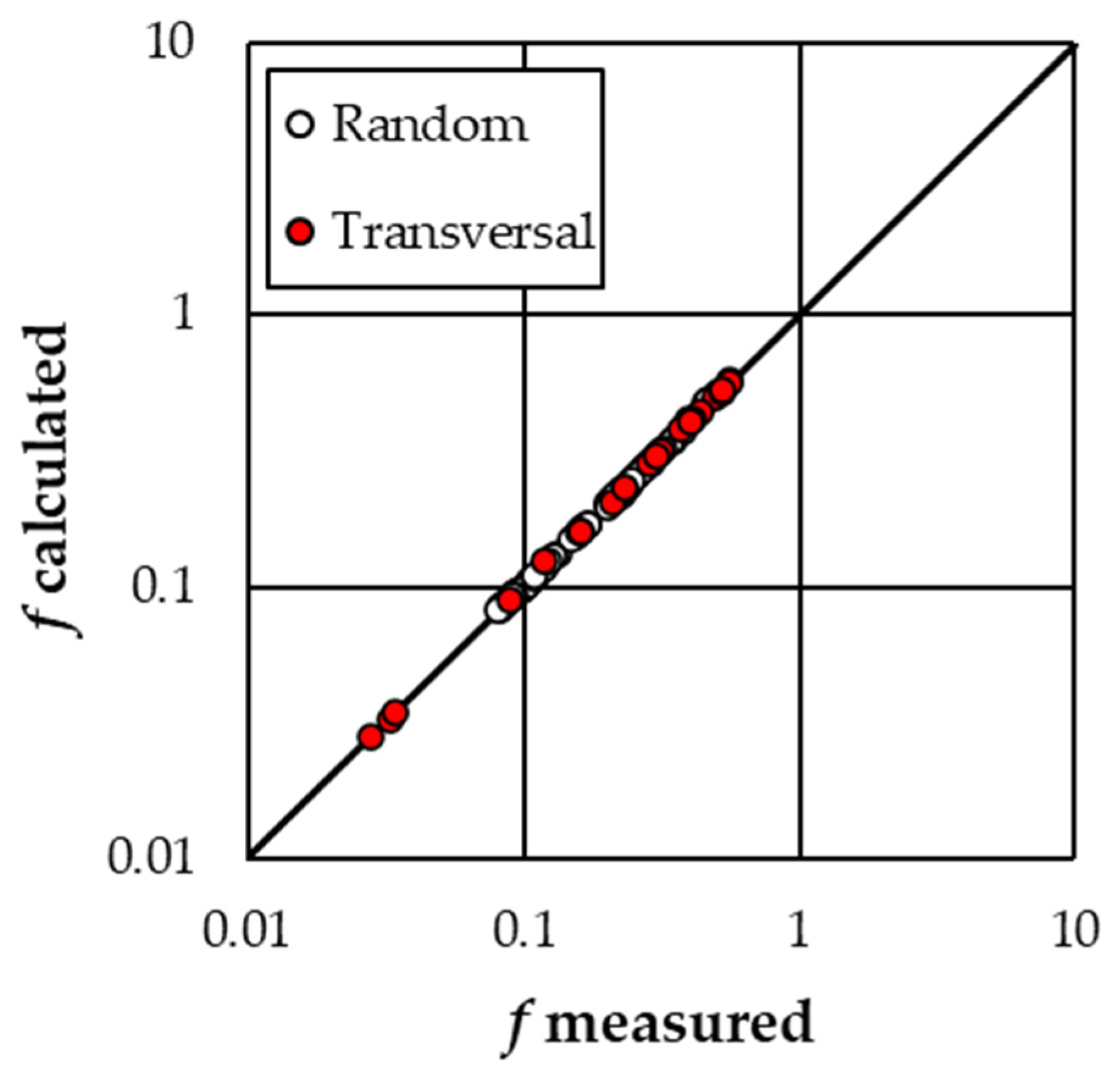
Figure 9 shows the comparison between the
f measured values and those calculated coupling Equations (4) and (7) with
b = 1.1175,
c = 0.587 and
a varying with the arrangement. In this case, the errors
E in the estimate of the Darcy–Weisbach friction factor are always less than or equal to ±5% and less than or equal to ±2.5% for 86.4% of cases.
4. Discussion
Figure 2b,
Figure 5, and
Figure 6 demonstrate that the presented theoretical approach guarantees a good estimate of the Darcy–Weisbach friction factor for both low (<48%) and high (≥48%) values of boulder concentration for all the three investigated arrangements. The reliability of the proposed approach is also confirmed by the fact that the equation (Equation (9a)), obtained for the “Random” arrangement by Canovaro et al. [
38] and
Ch < 48%, gave a good estimate of
f (
Figure 3 and
Figure 4) when applied to the dataset by Ferro and Giordano [
31], which falls into the same
Ch range (0–44%) and is characterized by the same arrangement. The systematic low underestimation (
Figure 3) can be justified considering that Canovaro et al. [
38] used smooth river pebbles as macro-roughness elements while Ferro and Giordano [
31] used rough quarry rubble boulders.
Figure 7 shows, as an example for the “Random” arrangement, that the Darcy–Weisbach friction factor values increase for increasing values of
Ch for concentrations lower than 48% (
Figure 7a), while no trend between
f and
Ch is detectable for boulder concentrations higher than or equal to 48% (
Figure 7b). These results can be justified by the circumstance that, according to the findings by Lawrence [
37], for low values of
Ch, the distance among the roughness elements determines the dissipation of the wake generated by each element before approaching the next element along the flow direction (semi-smooth isolated roughness turbulent flow) [
21], but for increasing concentrations the flow is increasingly disturbed as this distance diminishes determining an increase of flow resistance (wake interference flow). Instead, for high values of
Ch, the vicinity of the elements determines that a quasi-skimming flow occurs, and the flow resistance loses its dependence on boulder concentration. This result agrees with the findings by Carollo and Ferro [
34] who found that, for a square arrangement, the skimming flow occurs for element concentrations ≥50%, which is close to the threshold value of 48% used in this investigation.
Finally, the values (0.3354 for the “Random”, 0.3372 for the “Transversal stripe”, and 0.335 for the “Longitudinal stripe” arrangement) of the coefficient a obtained fixing b and c coefficients suggest that, for Ch < 48%, the “Random” and the “Longitudinal stripe” arrangements are characterized by similar values of f for fixed hydraulic conditions, while the “Transversal stripe” arrangement generates less flow resistance. For low values of concentration, the boulder arrangement influences the flow resistance. In fact, the position to flow streamlines change with the arrangement and determine a different behavior of the flow. The “Transversal stripe” arrangement is characterized by a position of the elements which allows the flow for dissipating the wake. In other words, the investigated transversal strips are so distant that energy loss due to each strip is independent from the previous and the next ones.
Instead, for
Ch ≥ 48% the obtained
a values (0.3356 for the “Random”, and 0.3366 for the “Transversal stripe” arrangement) fixing
b and
c coefficients, suggest that the arrangement slightly influences the flow resistance. This result seems to not agree with that obtained by Lawrence [
37], who suggested that, for high
Ch values, the effect of roughness element concentration becomes predominant as compared to that determined by the arrangement of the elements. This result can be justified considering that the analysis developed in the present study is influenced by the low number of available measurements for the “Transversal stripe” arrangement, and the circumstance that the runs for this arrangement were only performed for
Ch equal to 100%.
In any case, also the second applied procedure (i.e., fixing the
b and
c coefficients varying
a) guaranteed a reliable estimate of the Darcy–Weisbach friction factor for both low (
Figure 8) and high (
Figure 9) values of the boulder concentration.
The obtained results about the knowledge of the flow behavior for some known conditions can guide the decisions, for instance, in river management. The main limitations of this investigation are related to the concentration values used for the experimental runs of the “Transversal” and “Longitudinal” arrangements. Consequently, future studies can overcome the need for increasing the number of runs regarding these experimental conditions.