Regional Adaptability of Global and Regional Hydrological Forecast System
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Dataset
2.3. Methods
2.3.1. Hydrological Forecast Systems
Regional Hydrological Forecast System
Global Hydrological Forecast System
2.3.2. Modeled Design
Simulation
- RHFS-S was the simulation of the RHFS forced with meteorological observations, run separately in each year from 1 June to 31 October;
- GloFAS-S is short for GloFAS reanalysis, and was the reanalysis simulation generated by the global hydrological forecast system GloFAS, forced with ERA5 as proxy-observations. We used the pixel that best represented the study basin in the GloFAS river network at a resolution of 0.1° × 0.1°, located at 32.45° E, 115.55° N. The upstream area of this point in GloFAS was almost the same as the actual area of the basin (the former was 31,364 km2 and the latter was 30,630 km2);
- RHFS-S-ERA5 was produced by the RHFS forced with ERA5. This simulation, with the same hydrological forecast system as RHFS-S and the same input as GloFAS-S, was designed to study the effect of the input data as well as the modelling. The ERA5 basin–mean precipitation was calculated by applying IDW to the original grid precipitation of ERA5 and then used to force the RHFS system to produce RHFS-ERA5;
- RHFS-S-QM was the result of applying quantile mapping to RHFS-S;
- GloFAS-S-QM was the result of applying quantile mapping to GloFAS-S;
- RHFS-S-ERA5-QM was the result of applying quantile mapping to RHFS-S-ERA5.
Forecast
- RHFS-F used meteorological observations as initialization of the RHFS, and the input was basin–mean precipitation reforecasts, which were converted from raw daily gridded ECMWF precipitation reforecasts by IDW. Due to the gaps in the observation time series in the winter half-year of the evaluated years, the reforecasts of the RHFS system were initialized separately from 1 June of each year. For example, when the start day of the reforecast was 2 October 2008, the initialization period was from 1 June 2008 to 1 October 2008. This meant that the initialization period was different for each reforecast depending on the time of year, the period being shortest in June, and longest in October. Although this had some impact on the simulations, overall, we believe it did not alter the results;
- GloFAS-F is short for GloFAS reforecast and was the existing CEMS river discharge reforecast dataset from GloFAS, initialized with ERA5 and forced with ECMWF-ENS reforecasts [22]. GloFAS-F was downloaded for the same river pixel as GloFAS-S;
- RHFS-F-ERA5 had the same configuration as RHFS-F, but used ERA5 as initialization data; it is used to evaluate the impact of the model error and the initialization error;
- RHFS-F-QM was the result of applying quantile mapping to RHFS-F;
- GloFAS-F-QM was the result of applying quantile mapping to GloFAS-F;
- RHFS-F-ERA5-QM was the result of applying quantile mapping to RHFS-F-ERA5.
2.3.3. Quantile Mapping
2.3.4. Verification Metrics
3. Result
3.1. ERA5 Precipitation
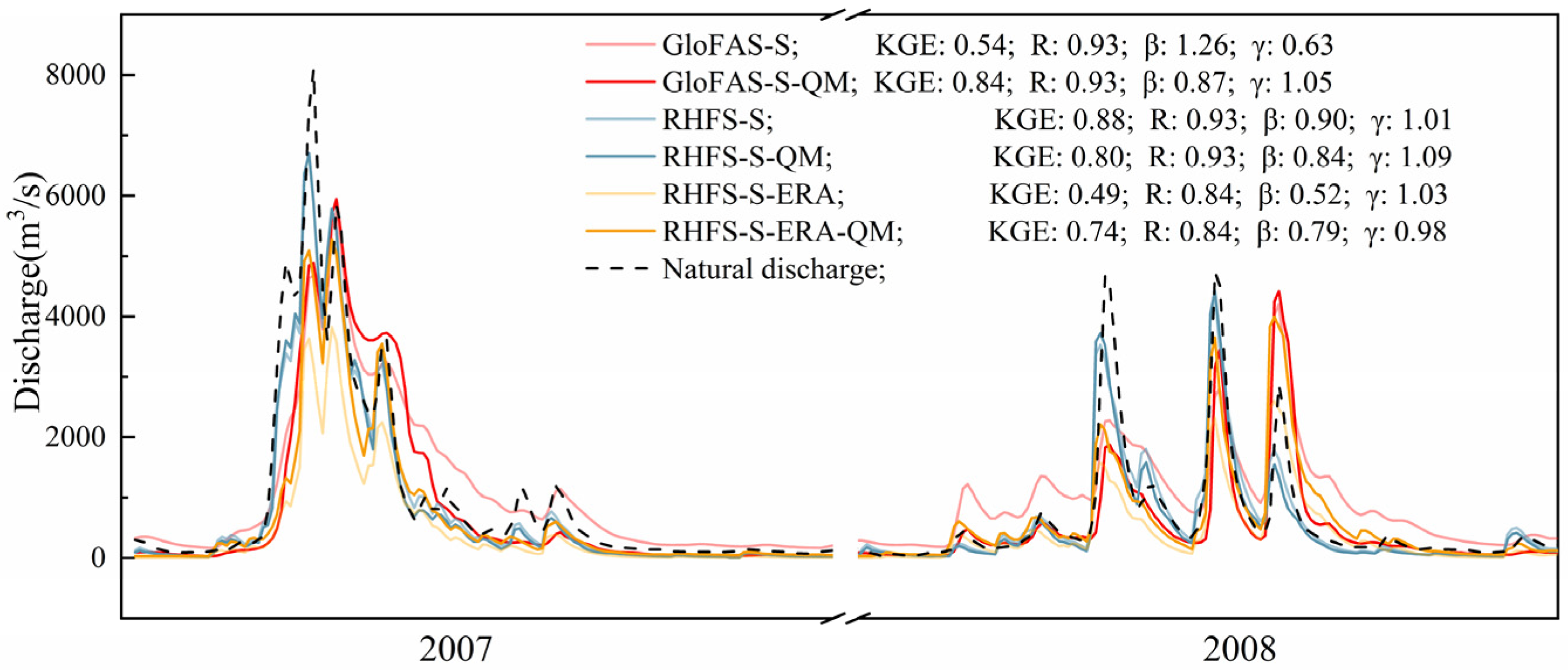
3.2. Discharge Simulation
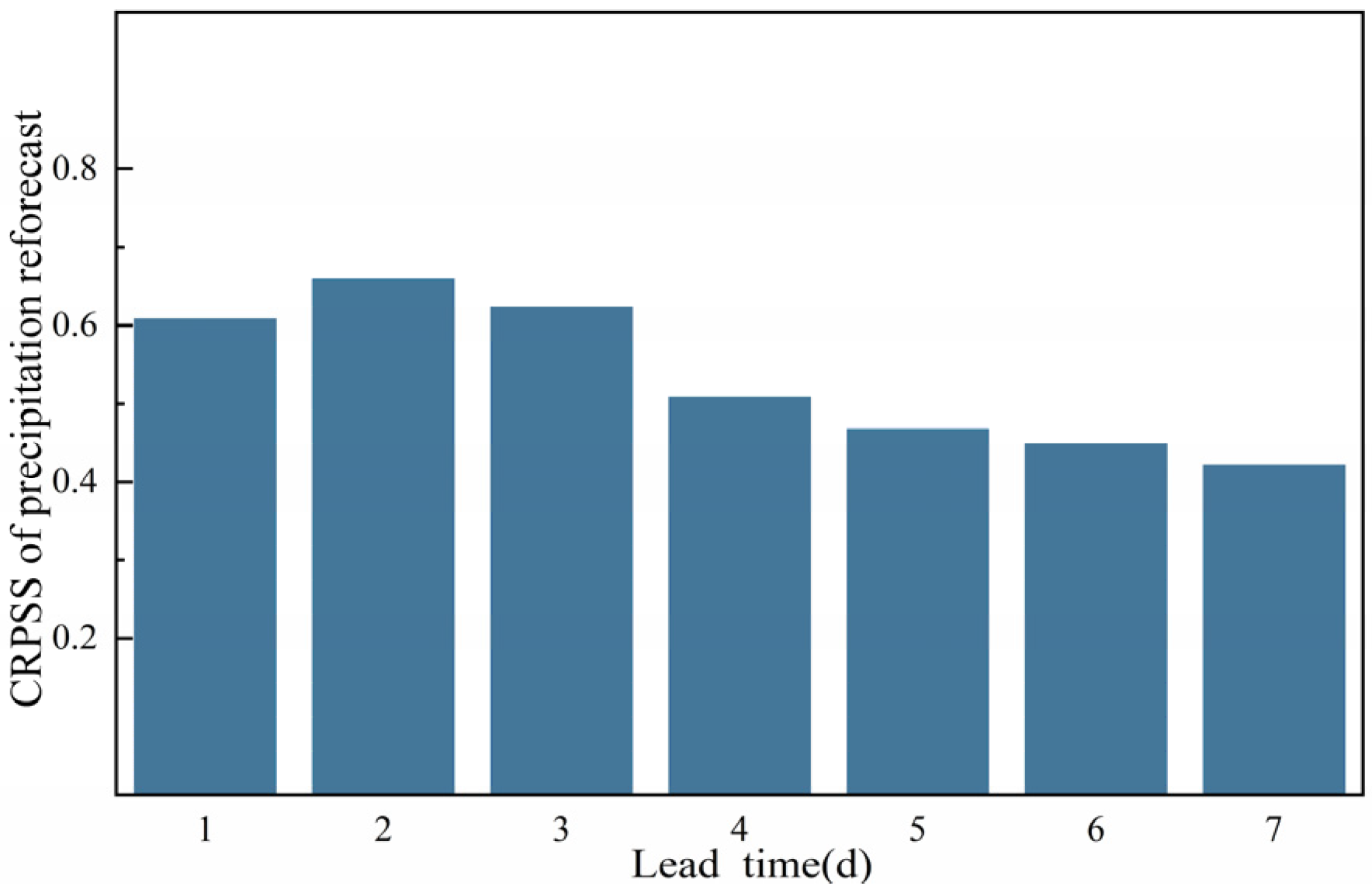
3.3. Precipitation Reforecast
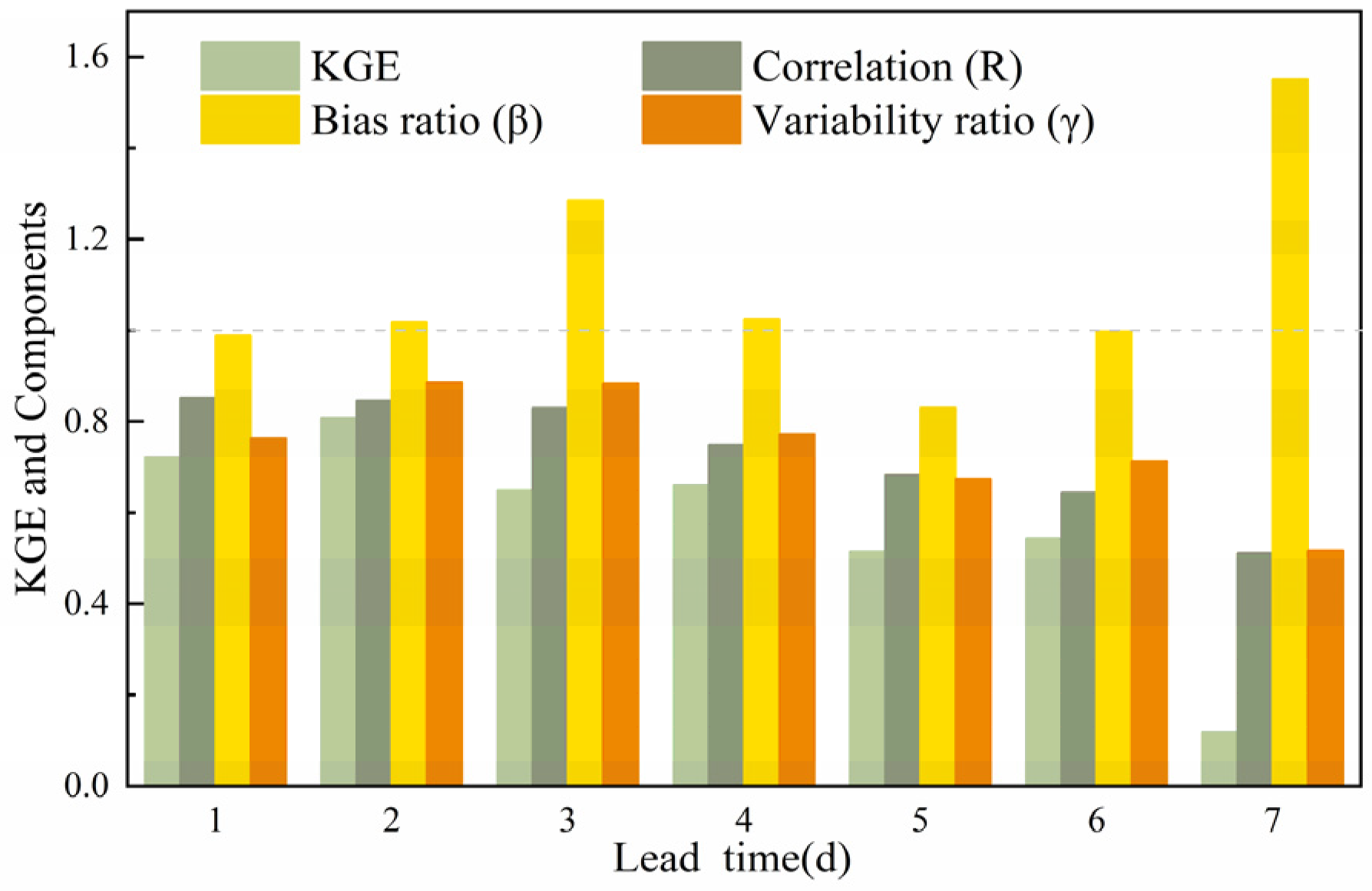
3.4. Discharge Reforecast
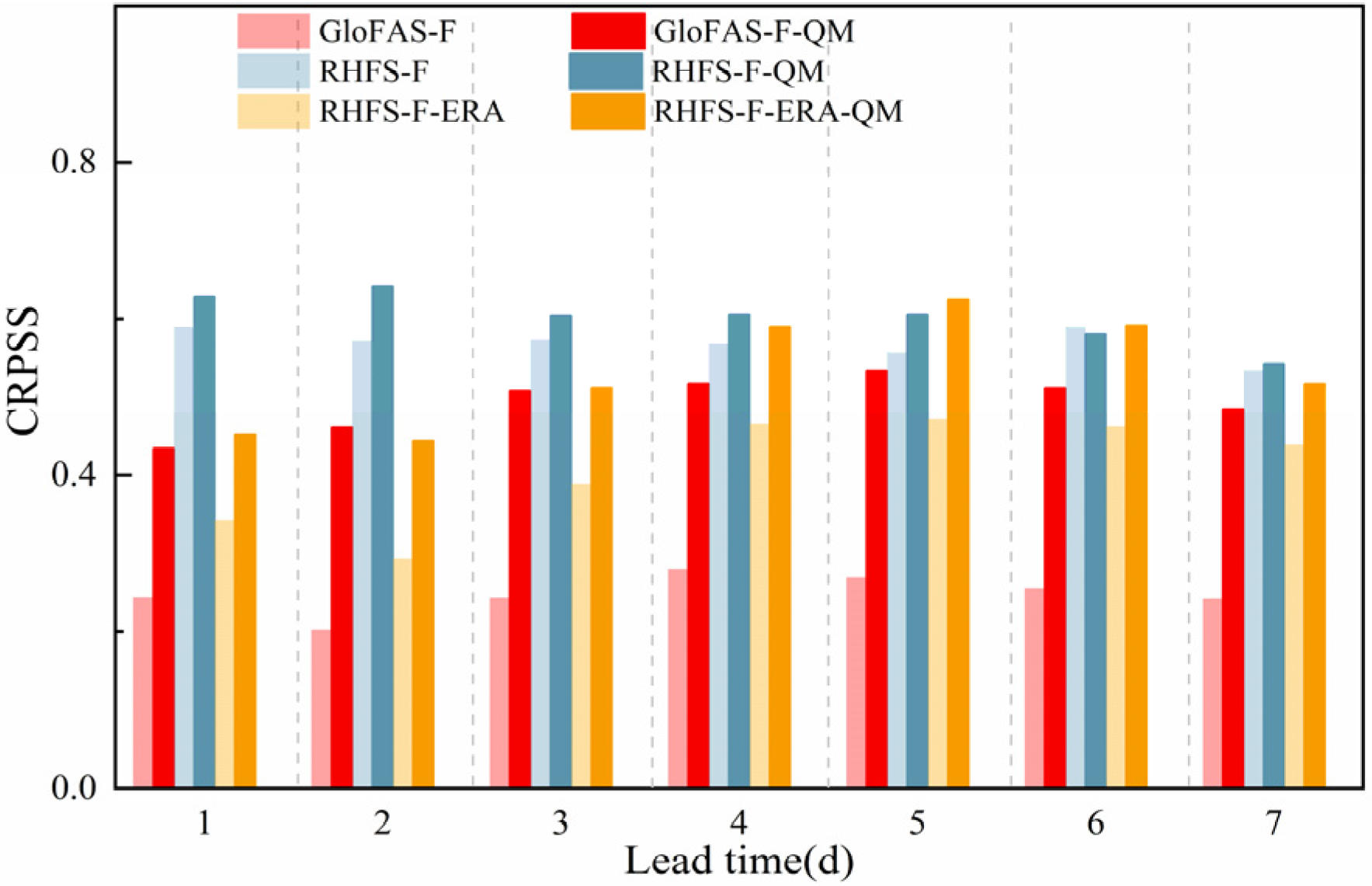
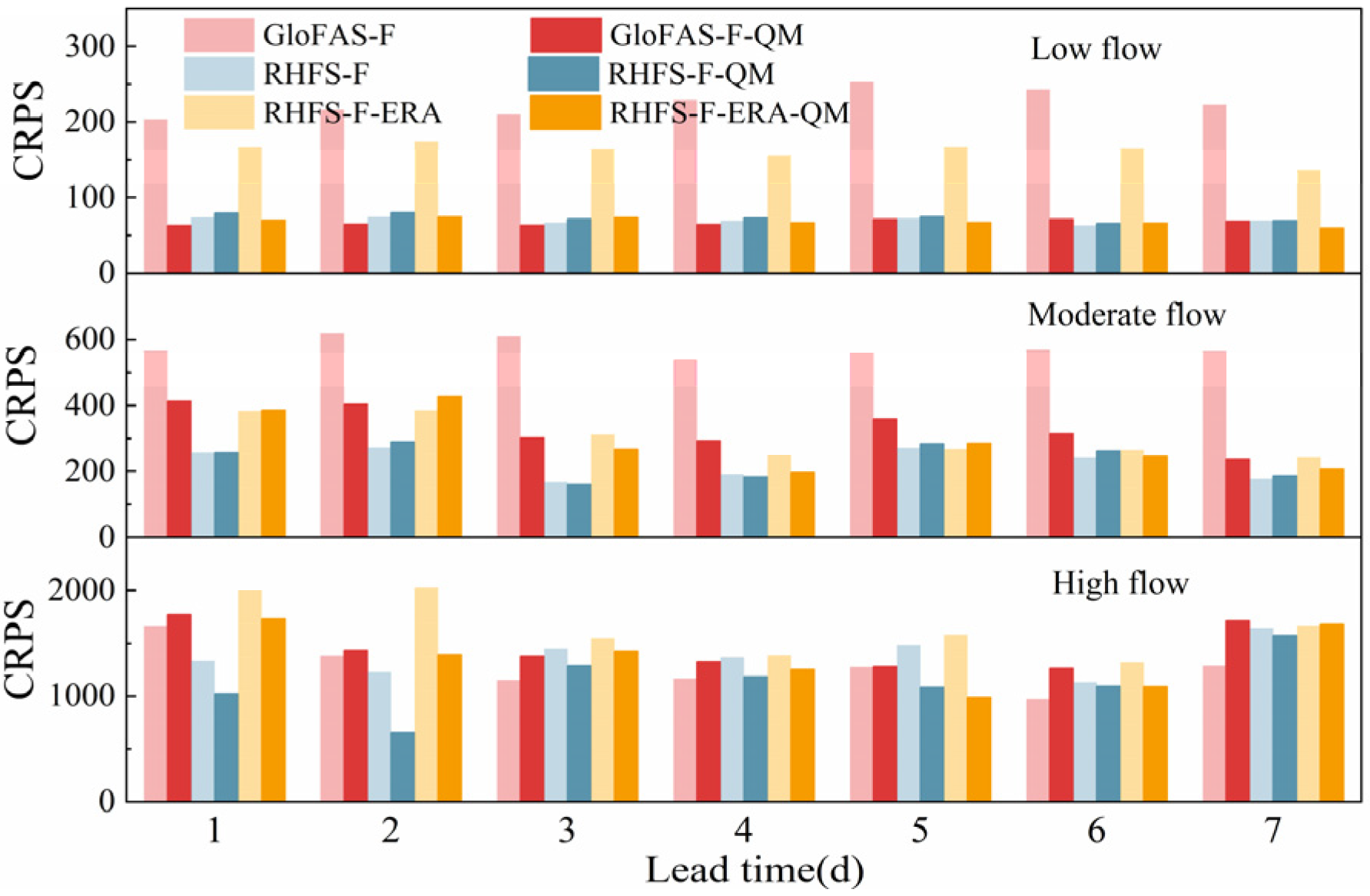
3.4.1. Discharge Ensemble Forecast
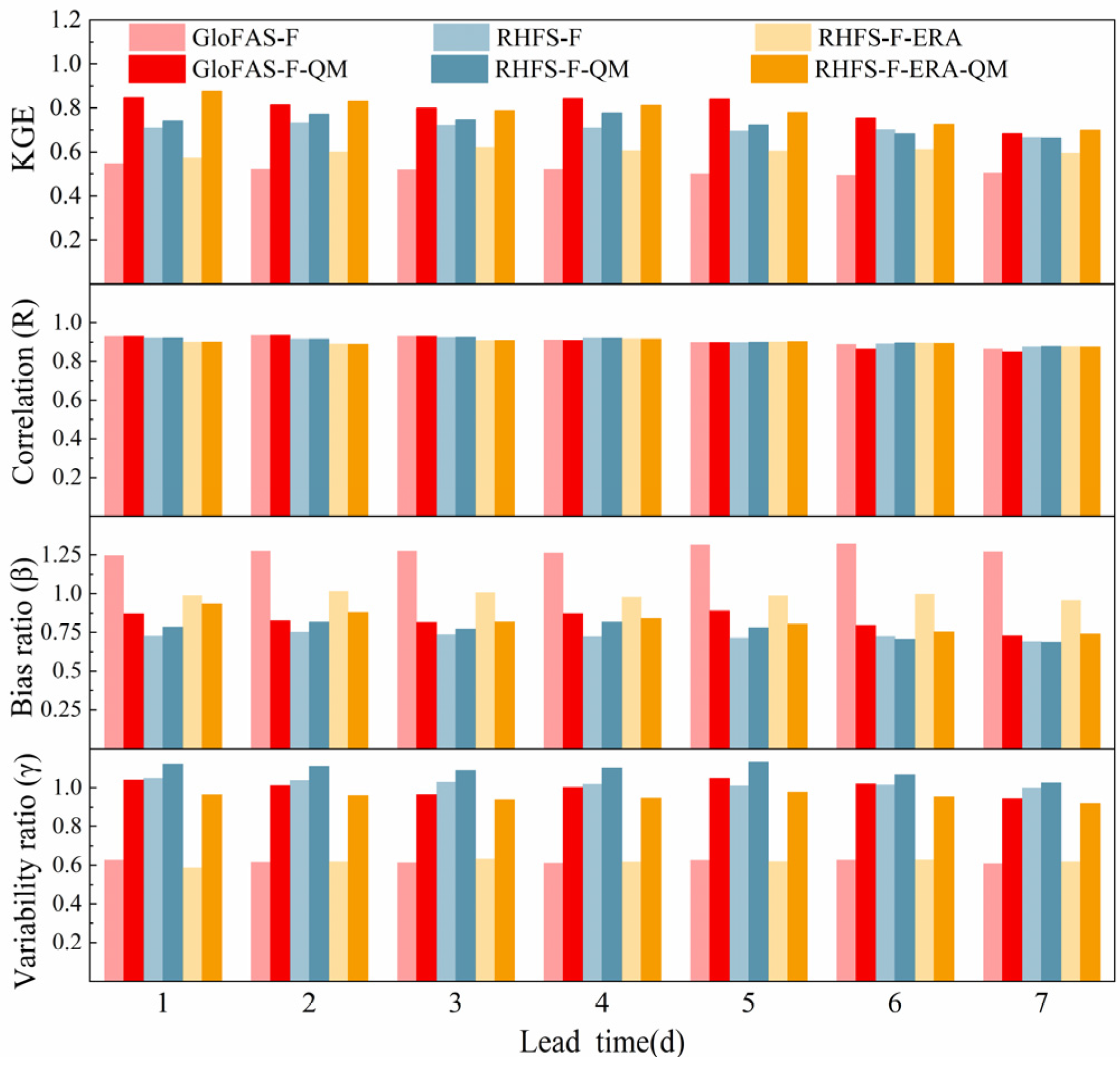
3.4.2. Discharge Ensemble Mean
4. Discussion and Conclusions
- Regarding river discharge simulations, GloFAS performed more poorly and was poorer than RHFS. This was mainly attributed to errors in the proxy-observations (ERA5) used as input to GloFAS, which did not provide good simulations of moderate and heavy daily precipitation events (above 10 mm/d), and to a model error which resulted in an overestimation of the baseflow. However, when the same ERA5 input was used, GloFAS appeared to be better than RHFS at simulating flood peaks;
- On average, GloFAS showed a worse forecast performance than RHFS. This was mainly attributed to errors in the initial conditions (based on ERA5 initial data), and to model errors. However, for high flow forecasts, GloFAS was better than RHFS for longer lead times, and GloFAS was better for all lead times when RHFS was also initialized with ERA5;
- Quantile mapping eliminated most of the initial errors, as well as part of the model and input errors, but failed to correct errors at high flow for GloFAS.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- The modified Kling–Gupta efficiency coefficient
- 2.
- Continuous ranked probability score
- 3.
- Continuous probability ranking scores skill
- 4.
- Relative flood peak error and relative flood volume error

- 5.
- Probability of detection and false alarm ratio
- 6.
- Equitable threat score
Appendix B
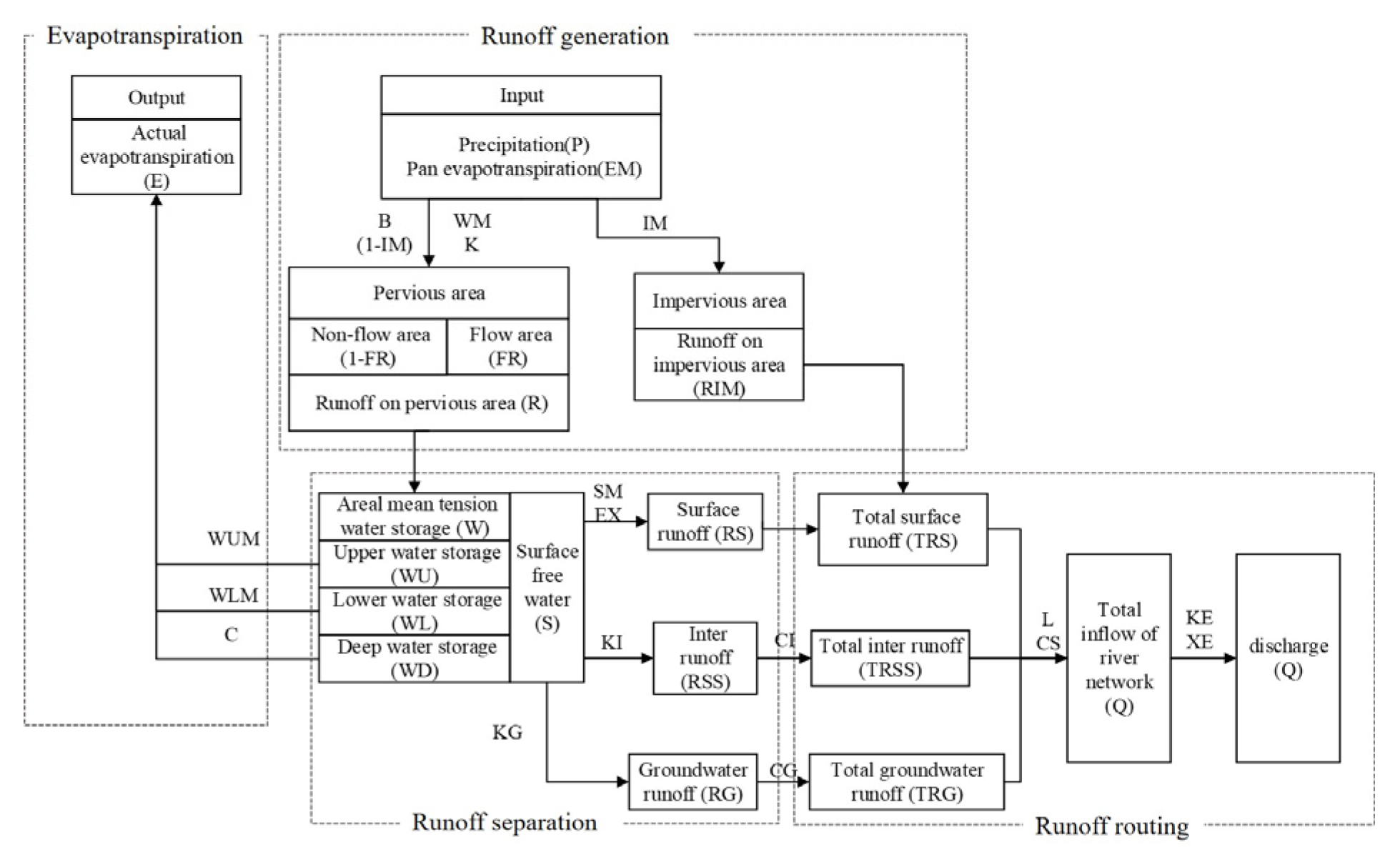
| Parameter | Meaning | Boundary | Value |
|---|---|---|---|
| K | Ratio of potential evapotranspiration to pan evaporation | 0.1–1.5 | 1 |
| WUM | Upper layer soil water storage capacity | 5–30 | 24.8 |
| WLM | Lower layer soil water storage capacity | 60–90 | 78.2 |
| C | Deep evaporation coefficient | 0.09–0.3 | 0.1 |
| WM | Maximum watershed soil water storage capacity | 70–210 | 109.1 |
| B | Exponent of soil water storage capacity curve | 0.05–0.4 | 0.33 |
| IM | Percentage of impervious area in the catchment | 0–0.5 | 0.01 |
| SM | Free water storage capacity | 1–50 | 46 |
| EX | Exponent of soil water storage capacity curve | 1–1.5 | 1.4 |
| KG | Outflow coefficient of free water storage to groundwater | 0.2–0.6 | 0.4 |
| KI | Outflow coefficient of free water storage to interflow | 0.2–0.6 | 0.4 |
| CI | Recession constant of interflow | 0.1–0.99 | 0.78 |
| CG | Recession constant of groundwater runoff | 0.7–0.999 | 0.998 |
| CS | Recession constant of surface runoff | 0.01–0.4 | 0.32 |
| L | Lag in time | - | 1 |
| KE | Routing time in channel unit (d) | 0–1 | 1 |
| XE | Weight factor of Muskingum method | 0–0.5 | 0 |
References
- Du, J.; Kong, F.; Du, S.; Li, N.; Li, Y.; Shi, P. Floods in China: Natural Disasters in China; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Duan, Q.; Pappenberger, F.; Wood, A.; Cloke, H.L.; Schaake, J.C. Handbook of Hydrometeorological Ensemble Forecasting; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Emerton, R.E.; Stephens, E.M.; Pappenberger, F.; Pagano, T.C.; Weerts, A.H.; Wood, A.W.; Salamon, P.; Brown, J.D.; Hjerdt, N.; Donnelly, C.; et al. Continental and global scale flood forecasting systems. WIREs Water 2016, 3, 391–418. [Google Scholar] [CrossRef] [Green Version]
- Gouweleeuw, B.T.; Thielen, J.; Franchello, G.; De Roo, A.P.J.; Buizza, R. Flood forecasting using medium-range probabilistic weather prediction. Hydrol. Earth Syst. Sci. 2005, 9, 365–380. [Google Scholar] [CrossRef] [Green Version]
- Pappenberger, F.; Thielen, J.; Medico, M.D. The impact of weather forecast improvements on large scale hydrology: Analysing a decade of forecasts of the European flood alert system. Hydrol. Process. 2011, 25, 1091–1113. [Google Scholar] [CrossRef]
- Saleh, F.; Ramaswamy, V.; Georgas, N.; Blumberg, A.F.; Pullen, J. A retrospective streamflow ensemble forecast for an ex-treme hydrologic event: A case study of Hurricane Irene and on the Hudson River basin. Hydrol. Earth Syst. Sci. 2016, 20, 2649–2667. [Google Scholar] [CrossRef] [Green Version]
- Roulin, E.V.S. Skill of Medium-Range Hydrological Ensemble Predictions. J. Hydrometeorol. 2005, 6, 729. [Google Scholar] [CrossRef]
- Cloke, H.L.; Pappenberger, F. Evaluating forecasts of extreme events for hydrological applications: An approach for screening unfamiliar performance measures. Meteorol. Appl. 2008, 15, 181–197. [Google Scholar] [CrossRef] [Green Version]
- Roulin, E. Skill and relative economic value of medium-range hydrological ensemble predictions. Hydrol. Earth Syst. Sci. 2007, 11, 725–737. [Google Scholar] [CrossRef] [Green Version]
- Bohn, T.J.; Sonessa, M.Y.; Lettenmaier, D.P. Seasonal hydrologic forecasting: Do multi-model ensemble averages always yield improvements in forecast skill? J. Hydrometeorol. 2010, 11, 1358–1372. [Google Scholar] [CrossRef]
- Benninga, H.J.F.; Booij, M.J.; Romanowicz, R.J.; Rientjes, T.H. Performance of ensemble streamflow forecasts under varied hydrometeorological conditions. Hydrol. Earth Syst. Sci. 2017, 21, 5273–5291. [Google Scholar] [CrossRef] [Green Version]
- Meydani, A.; Dehghanipour, A.; Schoups, G.; Tajrishy, M. Daily reservoir inflow forecasting using weather forecast downscaling and rainfall-runoff modeling: Application to Urmia Lake basin, Iran. J. Hydrol. Reg. Stud. 2022, 44, 101228. [Google Scholar] [CrossRef]
- Troin, M.; Arsenault, R.; Wood, A.W.; Brissette, F.; Martel, J.L. Generating Ensemble Streamflow Fore-casts: A Review of Methods and Approaches Over the Past 40 Years. Water Resour. Res. 2021, 57, e2020WR028392. [Google Scholar] [CrossRef]
- Sharma, S.; Siddique, R.; Reed, S.; Ahnert, P.; Mejia, A. Hydrological Model Diversity Enhances Stream-flow Forecast Skill at Short- to Medium-Range Timescales. Water Resour. Res. 2019, 55, 1510–1530. [Google Scholar] [CrossRef]
- Gomez, M.; Sharma, S.; Reed, S.; Mejia, A. Skill of ensemble flood inundation forecasts at short-to me-dium-range timescales. J. Hydrol. 2019, 568, 207–220. [Google Scholar] [CrossRef]
- Gaborit, É.; Anctil, F.; Fortin, V.; Pelletier, G. On the reliability of spatially disaggregated global ensemble rainfall forecasts. Hydrol. Process. 2013, 27, 45–56. [Google Scholar] [CrossRef]
- Siqueira, V.A.; Weerts, A.; Klein, B.; Fan, F.M.; de Paiva, R.C.D.; Collischonn, W. Postprocessing continental-scale, medium-range ensemble streamflow forecasts in South America using Ensemble Model Output Statistics and Ensem-ble Copula Coupling. J. Hydrol. 2021, 600, 126520. [Google Scholar] [CrossRef]
- He, Y.; Wetterhall, F.; Cloke, H.L.; Pappenberger, F.; Wilson, M.; Freer, J.; McGregor, G. Tracking the un-certainty in flood alerts driven by grand ensemble weather predictions. Met. Apps 2009, 16, 91–101. [Google Scholar] [CrossRef] [Green Version]
- Passerotti, G.; Massazza, G.; Pezzoli, A.; Bigi, V.; Zsótér, E.; Rosso, M. Hydrological model application in the Sirba river: Early warning system and GloFAS improvements. Water 2020, 12, 620. [Google Scholar] [CrossRef] [Green Version]
- Bischiniotis, K.; van den Hurk, B.; Zsoter, E.; Coughlan de Perez, E.; Grillakis, M.; Aerts, J.C.J.H. Evaluation of a global ensemble flood prediction system in Peru. Hydrol. Sci. J. 2019, 64, 1171–1189. [Google Scholar] [CrossRef] [Green Version]
- Coughlan de Perez, E.; Van den Hurk, B.; Van Aalst, M.K.; Amuron, I.; Bamanya, D.; Hauser, T.; Zsoter, E. Action-based flood forecasting for triggering humanitarian action. Hydrol. Earth Syst. Sci. 2016, 20, 3549–3560. [Google Scholar] [CrossRef] [Green Version]
- Harrigan, S.; Zsoter, E.; Alfieri, L.; Prudhomme, C.; Salamon, P.; Wetterhall, F.; Barnard, C.; Cloke, H.; Pappenberger, F. Glo-FAS-ERA5 operational global river discharge reanalysis 1979–present. Earth Syst. Sci. Data 2020, 12, 2043–2060. [Google Scholar] [CrossRef]
- Alfieri, L.; Burek, P.; Dutra, E. GloFAS–global ensemble streamflow forecasting and flood early warning. Hydrol. Earth Syst. Sci. 2013, 17, 1161–1175. [Google Scholar] [CrossRef] [Green Version]
- Alfieri, L.; Lorini, V.; Hirpa, F.A.; Harrigan, S.; Zsoter, E.; Prudhomme, C.; Salamon, P. A global stream-flow reanalysis for 1980–2018. J. Hydrol. X 2020, 6, 100049. [Google Scholar] [CrossRef] [PubMed]
- Senent-Aparicio, J.; Blanco-Gomez, P.; Lopez-Ballesteros, A.; JimenoSaez, P.; Perez-Sanchez, J. Evaluating the Potential of GloFAS-ERA5 River Discharge Reanalysis Data for Calibrating the SWAT Model in the Grande San Miguel River Basin (El Salvador). Remote Sens. 2021, 13, 3299. [Google Scholar] [CrossRef]
- Biondi, D.; Todini, E. Comparing Hydrological Postprocessors Including Ensemble Predictions Into Full Predictive Probability Distribution of Streamflow. Water Resour. Res. 2018, 54, 9860–9882. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q.J.R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Aminyavari, S.; Saghafian, B.; Delavar, M. Evaluation of TIGGE Ensemble Forecasts of Precipitation in Distinct Climate Regions in Iran. Adv. Atmos. Sci. 2018, 35, 457–468. [Google Scholar] [CrossRef]
- Wang, H.; Zhong, P.-A.; Zhu, F.-L.; Lu, Q.-W.; Ma, Y.-F.; Xu, S.-Y. The adaptability of typical precipitation ensemble prediction systems in the Huaihe River basin, China. Stoch. Environ. Res. Risk Assess. 2021, 35, 515–529. [Google Scholar] [CrossRef]
- Aminyavari, S.S.B. Probabilistic streamflow forecast based on spatial post-processing of TIGGE precipitation forecasts. Sto-Chastic Environ. Res. Risk Assess. 2019, 33, 1939–1950. [Google Scholar] [CrossRef]
- Dai, G.; Mu, M.; Jiang, Z. Evaluation of the forecast performance for North Atlantic Oscillation onset. Adv. Atmos. Pheric Sci. 2019, 36, 753–765. [Google Scholar] [CrossRef]
- Zhao, R.J.; Zhang, Y.L.; Fang, L.R.; Liu, X.R.; Zhang, Q.S. The Xinanjiang model. In Proceedings of the Oxford Symposium on Hydrological Forecasting IAHS Publication, Oxford, UK, 15–18 April 1980. [Google Scholar]
- Bonyadi, M.R.; Michalewicz, Z. Particle Swarm Optimization for Single Objective Continuous Space Problems: A Review. Evol. Comput. 2017, 25, 1–54. [Google Scholar] [CrossRef]
- Van der Knijff, J.M.; Younis, J.; de Roo, A.P.J. LISFLOOD: A GIS-based distributed model for river basin scale water balance and flood simulation. Int. J. Geogr. Inf. Sci. 2010, 24, 189–212. [Google Scholar] [CrossRef]
- Boe, J.; Terray, L.; Habets, F.; Martin, E. Statistical and dynamical downscaling of the Seine basin cli-mate for hydro-meteorological studies. Int. J. Climatol. 2007, 27, 1643–1655. [Google Scholar] [CrossRef]
- Jiang, Q.; Li, W.; Fan, Z.; He, X.; Sun, W.; Chen, S.; Wen, J.; Gao, J.; Wang, J. Evaluation of the ERA5 re-analysis precipitation dataset over Chinese Mainland. J. Hydrol. 2021, 595, 125660. [Google Scholar] [CrossRef]
- Zsoter, E.; Cloke, H.; Stephens, E.; de Rosnay, P.; MuñozSabater, J.; Prudhomme, C.; Pappenberger, F. How well do operational numerical weather prediction setups represent hydrology. J. Hydrometeorol. 2019, 20, 1533–1552. [Google Scholar] [CrossRef]
- Zsoter, E.; Pappenberger, F.; Smith, P.; Emerton, R.; Dutra, E.; Wetterhall, F.; Balsamo, G. Building a multi-model flood prediction system with the TIGGE archive. J. Hydrometeorol. 2016, 17, 2923–2940. [Google Scholar] [CrossRef]
- Hassler, B.; Lauer, A. Comparison of Reanalysis and Observational Precipitation Datasets Including ERA5 and WFDE5. Atmosphere 2021, 12, 1462. [Google Scholar] [CrossRef]
- Lavers, D.A.; Simmons, A.; Vamborg, F.; Rodwell, M.J. An evaluation of ERA5 precipitation for climate monitoring. Quart. Ly J. R. Meteorol. Soc. 2022, 148, 3152–3165. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decompos. of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.R.; Huang, W.W.; Huang, G.H.; Huang, K.; Li, Y.P.; Kong, X.M. Bivariate hydrologic risk analysis based on a coupled entropy-copula method for the Xiangxi River in the Three Gorges Reservoir area, China. Appl Clim. 2016, 125, 381–397. [Google Scholar] [CrossRef]
- Wan, X.; Yang, Q.; Jiang, P.; Zhong, P.A. A Hybrid Model for Real-Time Probabilistic Flood Forecasting Using Elman Neural Network with Heterogeneity of Error Distributions. Water Resour. Manag. 2019, 33, 4027–4050. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, L.; Singh, V.P.; Cao, H.; Wang, D. Determination of the distribution of flood forecasting error. Nat. Hazards 2015, 75, 1389–1402. [Google Scholar] [CrossRef]
- Ganguli, P.; Reddy, M.J. Probabilistic assessment of flood risks using trivariate copulas. Appl. Clim. 2013, 111, 341–360. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, J.; Lu, C. Integrated Hydrologic and Hydrodynamic Models to Improve Flood Simulation Capability in the Data-Scarce Three Gorges Reservoir Region. Water 2020, 12, 1462. [Google Scholar] [CrossRef]




| Mode | Name | System | Input | Initialization Data | Post-Processing |
|---|---|---|---|---|---|
| Simulations | RHFS-S (RHFS-S-QM) | RHFS | Observation | No (yes) | |
| GloFAS-S (GloFAS-S-QM) | GloFAS | ERA5 | |||
| RHFS-S-ERA5 (RHFS-S-ERA5-QM) | RHFS | ERA5 | |||
| Forecasts | RHFS-F (RHFS-F-QM) | RHFS | ECMWF reforecast | Observation | |
| GloFAS-F (GloFAS-F-QM) | GloFAS | ERA5 | |||
| RHFS-F-ERA5 (RHFS-F-ERA5-QM) | RHFS | ERA5 | |||
| Flood Code | Relative Flood Peak Error (%) | |||||
|---|---|---|---|---|---|---|
| GloFAS–S | GloFAS–S–QM | RHFS–S | RHFS–S–QM | RHFS–S–ERA | RHFS–S–ERA–QM | |
| 1(1) | −57.8 | −68.7 | −30.7 | −26.3 | −80.7 | −72.8 |
| 1(2) | −42.2 | −39.5 | −27.6 | −27.5 | −60.7 | −42.8 |
| 1(3) | −1.8 | 1.8 | −7.0 | −6.8 | −38.5 | −13.6 |
| 1(4) | −10.2 | 3.2 | −22.5 | −21.8 | −44.1 | −13.6 |
| 2 | −51.3 | −60.9 | −29.7 | −24.7 | −67.7 | −54.9 |
| 3 | −43.6 | −33.2 | −7.0 | −6.1 | −50.6 | −22.6 |
| 4 | 46.7 | 54.4 | −42.7 | −53.1 | −13.8 | 33.7 |
| Absolute mean | 36.2 | 37.4 | 23.9 | 23.8 | 50.9 | 36.3 |
| Flood Code | Relative Flood Volume Error (%) | |||||
|---|---|---|---|---|---|---|
| GloFAS−S | GloFAS−S−QM | RHFS−S | RHFS−S−QM | RHFS−S−ERA | RHFS−S−ERA−QM | |
| 1 | −44.5 | −26.0 | −15.4 | −12.2 | −59 | −40.9 |
| 2 | −81.9 | −71.2 | −32.6 | −26.9 | −67.8 | −57.6 |
| 3 | −51.2 | −38.9 | 4.4 | 1.4 | −45.4 | −22.0 |
| 4 | 110.8 | 154.1 | −51.9 | −66.5 | 63.2 | 140.8 |
| Absolute mean | 72.1 | 72.6 | 26.1 | 26.8 | 58.9 | 65.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhong, P.-a.; Zsoter, E.; Prudhomme, C.; Pappenberger, F.; Xu, B. Regional Adaptability of Global and Regional Hydrological Forecast System. Water 2023, 15, 347. https://doi.org/10.3390/w15020347
Wang H, Zhong P-a, Zsoter E, Prudhomme C, Pappenberger F, Xu B. Regional Adaptability of Global and Regional Hydrological Forecast System. Water. 2023; 15(2):347. https://doi.org/10.3390/w15020347
Chicago/Turabian StyleWang, Han, Ping-an Zhong, Ervin Zsoter, Christel Prudhomme, Florian Pappenberger, and Bin Xu. 2023. "Regional Adaptability of Global and Regional Hydrological Forecast System" Water 15, no. 2: 347. https://doi.org/10.3390/w15020347







