Simulation of Contaminant Transport through the Vadose Zone: A Continuum Mechanical Approach within the Framework of the Extended Theory of Porous Media (eTPM)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theory of Porous Media (TPM)
2.2. Extended Theory of Porous Media (eTPM)
2.3. Model Assumptions
2.4. Field Equations
2.5. Constitutive Model
2.6. Numerical Treatment
3. Results and Discussion
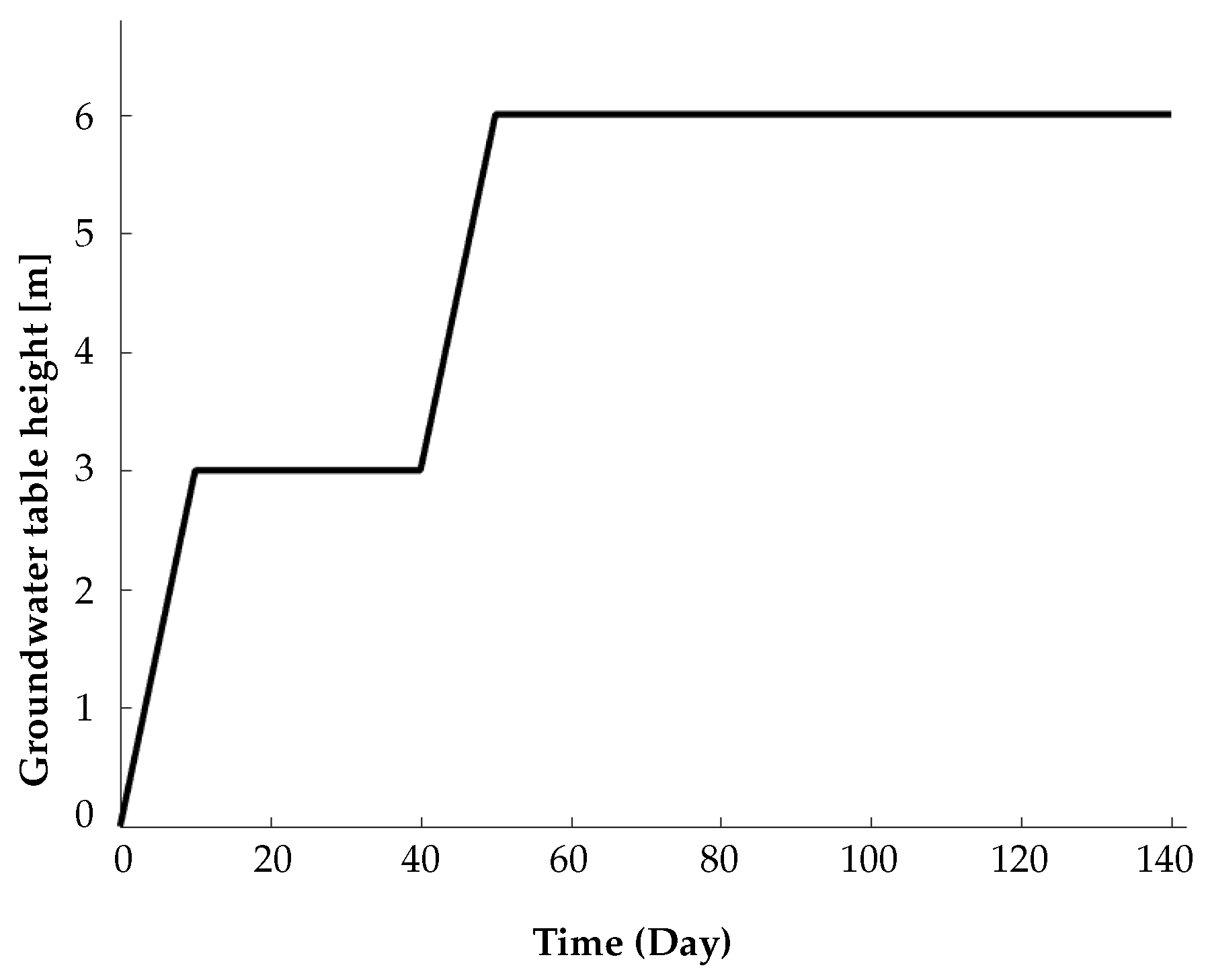
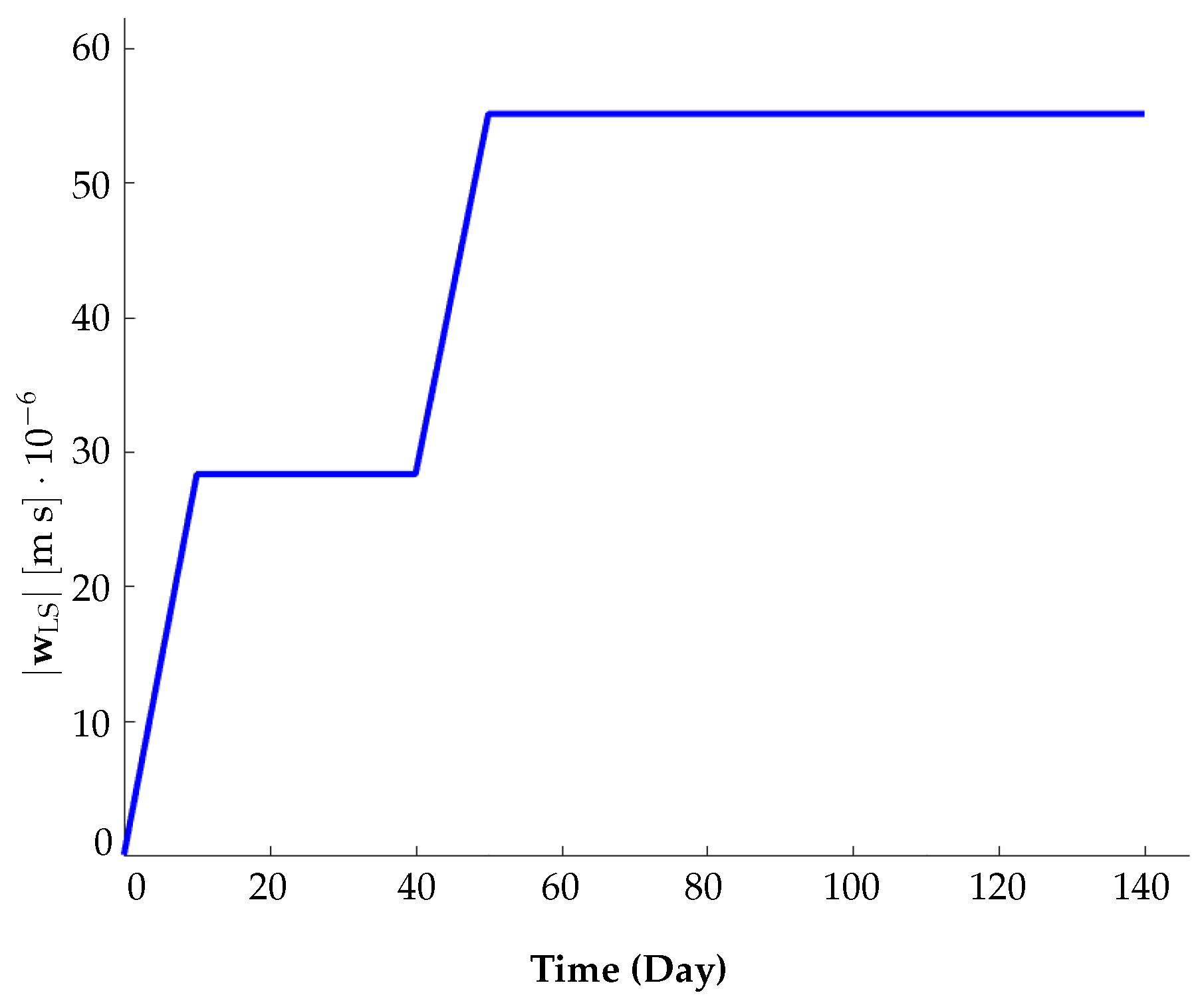
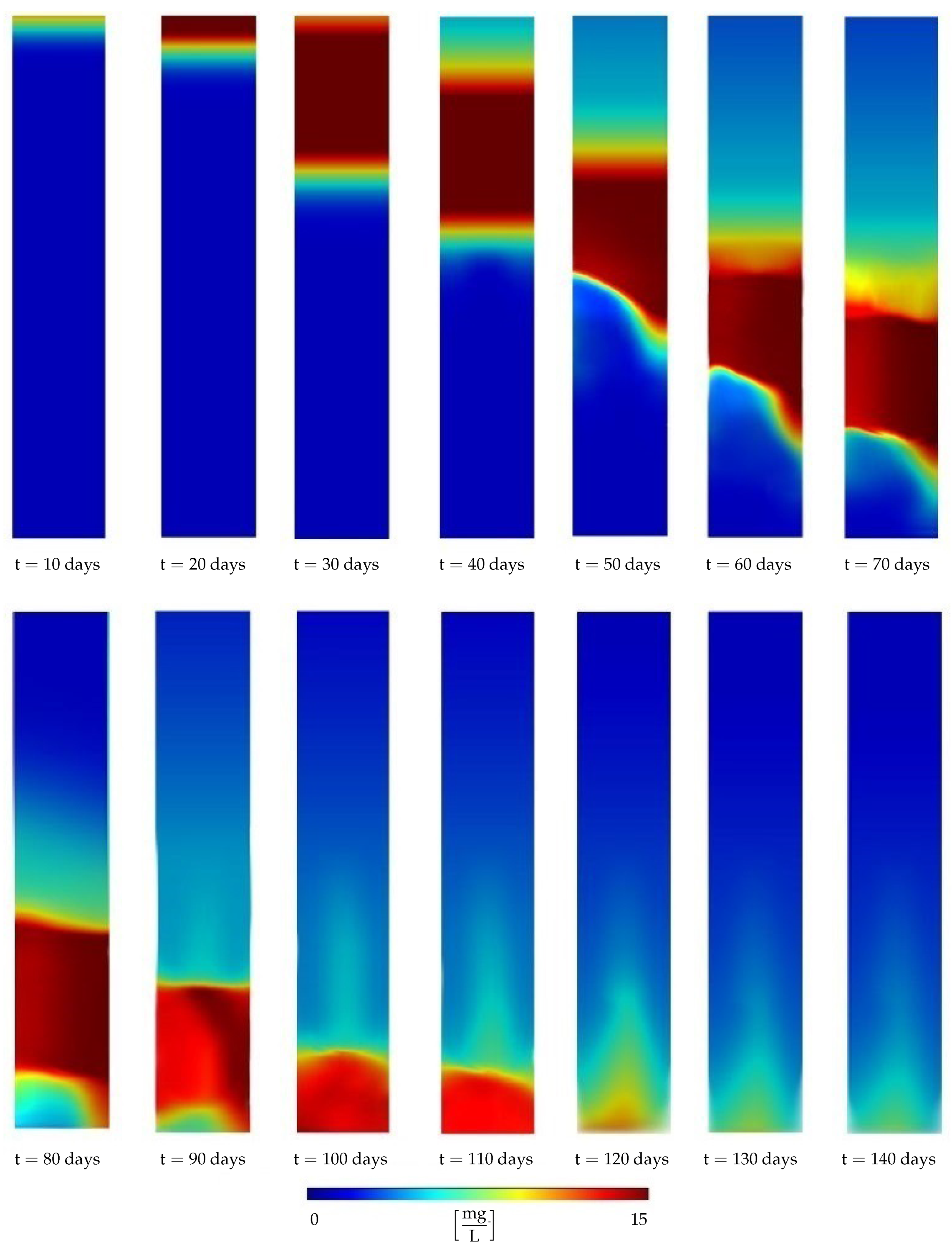
Numerical Example
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| eTPM | Extended Theory of Porous Media |
| REV | Representative Elementary Volume |
| TPM | Theory of Porous Media |
Appendix A. Kinematic
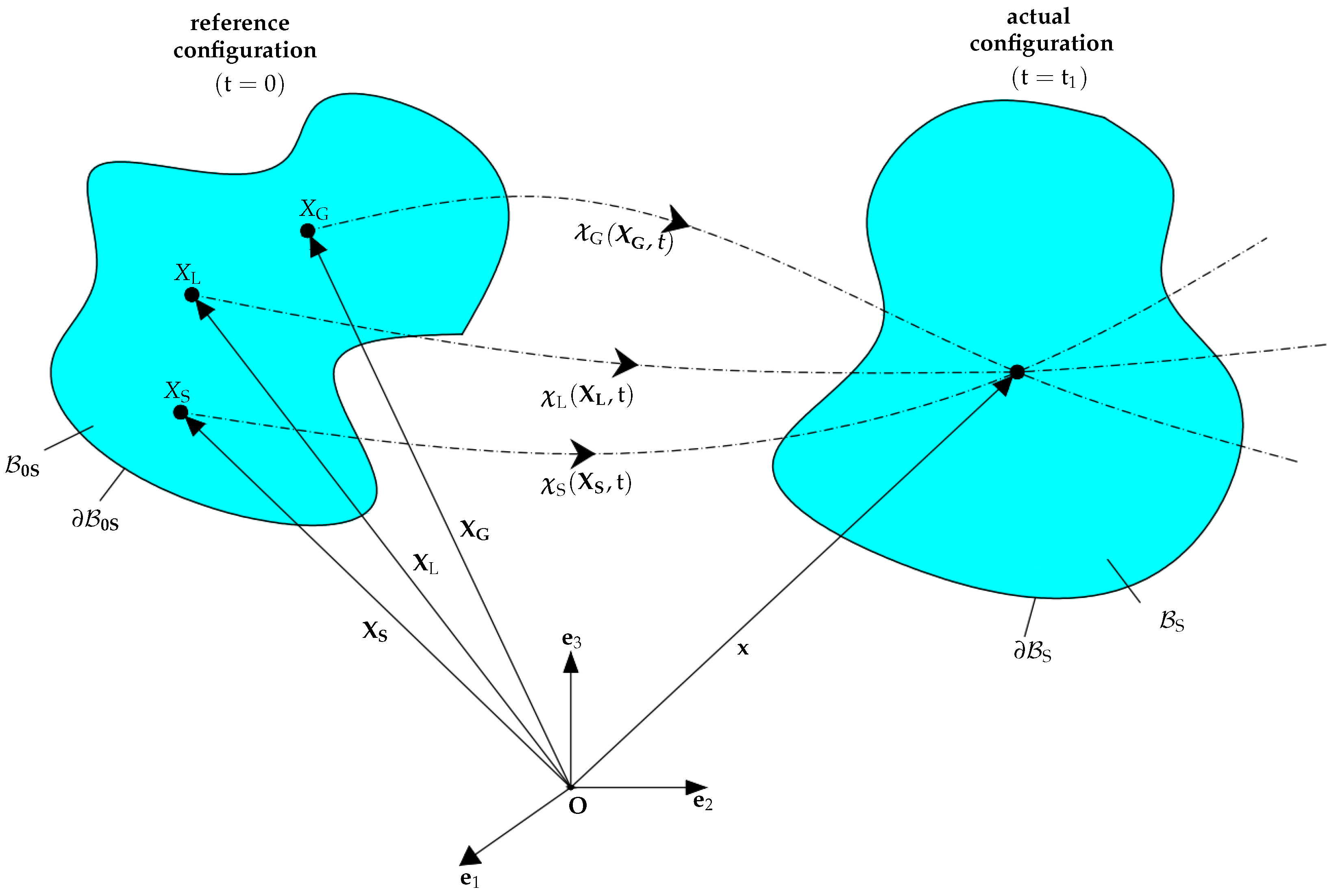
Appendix A.1. Evaluation of Entropy Inequality
Appendix A.2. Evaluation of Energy Preserving Terms
Appendix B. Evaluation of Dissipation Terms
References
- Pfletschinger, H.; Prömmel, K.; Schüth, C.; Herbst, M.; Engelhardt, I. Sensitivity of vadose zone water fluxes to climate shifts in arid settings. Vadose Zone J. 2014, 13, vzj2013.02.0043. [Google Scholar] [CrossRef] [Green Version]
- Moradi, A.; Smits, K.M.; Lu, N.; McCartney, J.S. Heat transfer in unsaturated soil with application to borehole thermal energy storage. Vadose Zone J. 2016, 15, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Javadi, A.A.; AL-Najjar, M.M.; Evans, B. Flow and contaminant transport model for unsaturated soil. In Theoretical and Numerical Unsaturated Soil Mechanics; Springer: Berlin/Heidelberg, Germany, 2007; pp. 135–141. [Google Scholar]
- Dahan, O. Real-time monitoring of the vadose zone as a key to groundwater protection from pollution hazard. WIT Trans. Ecol. Environ. 2015, 196, 351–362. [Google Scholar]
- Harter, T.; Hopmans, J.W.; Feddes, R. Role of Vadose Zone Flow Processes in Regional Scale Hydrology: Review, Opportunities and Challenges; Kluwer: Alphen aan den Rijn, The Netherlands, 2004. [Google Scholar]
- Nimmo, J.R. Unsaturated zone flow processes. Encycl. Hydrol. Sci. 2005, 4, 2299–2322. [Google Scholar]
- Leeson, J.; Edwards, A.; Smith, J.; Potter, H. Hydrological Risk Assessments for Landfills and the Derivation of Groundwater Control and Trigger Levels; Environmental Agency: Solihull, UK, 2002.
- Culver, T.B.; Shoemaker, C.A.; Lion, L.W. Impact of vapor sorption on the subsurface transport of volatile organic compounds: A numerical model and analysis. Water Resour. Res. 1991, 27, 2259–2270. [Google Scholar] [CrossRef]
- Clement, T.P.; Hooker, B.S.; Skeen, R.S. Numerical modeling of biologically reactive transport near nutrient injection well. J. Environ. Eng. 1996, 122, 833–839. [Google Scholar] [CrossRef]
- Guyonnet, D.; Perrochet, P.; Côme, B.; Seguin, J.J.; Parriaux, A. On the hydro-dispersive equivalence between multi-layered mineral barriers. J. Contam. Hydrol. 2001, 51, 215–231. [Google Scholar] [CrossRef]
- Islam, J.; Singhal, N. A one-dimensional reactive multi-component landfill leachate transport model. Environ. Model. Softw. 2002, 17, 531–543. [Google Scholar] [CrossRef]
- Kačur, J.; Malengier, B.; Remešikova, M. Solution of contaminant transport with equilibrium and non-equilibrium adsorption. Comput. Methods Appl. Mech. Eng. 2005, 194, 479–489. [Google Scholar] [CrossRef]
- Waddill, D.W.; Widdowson, M.A. Three-dimensional model for subsurface transport and biodegradation. J. Environ. Eng. 1998, 124, 336–344. [Google Scholar] [CrossRef]
- Baehr, A.L.; Stackelberg, P.E.; Baker, R.J. Evaluation of the atmosphere as a source of volatile organic compounds in shallow groundwater. Water Resour. Res. 1999, 35, 127–136. [Google Scholar] [CrossRef]
- Sun, Y.; Petersen, J.N.; Buscheck, T.A.; Nitao, J.J. Analytical solutions for reactive transport of multiple volatile contaminants in the vadose zone. Transp. Porous Media 2002, 49, 175–190. [Google Scholar] [CrossRef]
- Sander, G.; Braddock, R. Analytical solutions to the transient, unsaturated transport of water and contaminants through horizontal porous media. Adv. Water Resour. 2005, 28, 1102–1111. [Google Scholar] [CrossRef]
- Weeks, E.P.; Earp, D.E.; Thompson, G.M. Use of atmospheric fluorocarbons F-11 and F-12 to determine the diffusion parameters of the unsaturated zone in the Southern High Plains of Texas. Water Resour. Res. 1982, 18, 1365–1378. [Google Scholar] [CrossRef]
- Seyedpour, S. Simulation of Contaminant Transport in Groundwater: From Pore-Scale to Large-Scale; Shaker Verlag: Herzogenrath, Germany, 2021. [Google Scholar]
- Frost, N.K.; Patel, M.K.; Lai, C.H. CFD analysis of one-dimensional infiltration in vadose zone. J. Algorithms Comput. Technol. 2007, 1, 477–494. [Google Scholar] [CrossRef]
- Sheng, D.; Smith, D.W. Numerical modelling of competitive components transport with non-linear adsorption. Int. J. Numer. Anal. Methods Geomech. 2000, 24, 47–71. [Google Scholar] [CrossRef]
- Seyedpour, S.; Henning, C.; Kirmizakis, P.; Herbrandt, S.; Ickstadt, K.; Doherty, R.; Ricken, T. Uncertainty with Varying Subsurface Permeabilities Reduced Using Coupled Random Field and Extended Theory of Porous Media Contaminant Transport Models. Water 2023, 15, 159. [Google Scholar] [CrossRef]
- Seyedpour, S.M.; Kirmizakis, P.; Brennan, P.; Doherty, R.; Ricken, T. Optimal remediation design and simulation of groundwater flow coupled to contaminant transport using genetic algorithm and radial point collocation method (RPCM). Sci. Total Environ. 2019, 669, 389–399. [Google Scholar] [CrossRef] [Green Version]
- Rao, P.; Medina, M.A., Jr. A multiple domain algorithm for modeling two dimensional contaminant transport flows. Appl. Math. Comput. 2006, 174, 117–133. [Google Scholar] [CrossRef]
- Rao, P.; Medina, M.A., Jr. A multiple domain algorithm for modeling one-dimensional transient contaminant transport flows. Appl. Math. Comput. 2005, 167, 1–15. [Google Scholar] [CrossRef]
- Kuntz, D.; Grathwohl, P. Comparison of steady-state and transient flow conditions on reactive transport of contaminants in the vadose soil zone. J. Hydrol. 2009, 369, 225–233. [Google Scholar] [CrossRef]
- Bunsri, T.; Sivakumar, M.; Hagare, D. Simulation of water and contaminant transport through vadose zone-redistribution system. In Hydraulic Conductivity-Issues, Determination and Applications; InTech: Rang-Du-Fliers, France, 2011. [Google Scholar]
- Rajsekhar, K.; Sharma, P.K.; Shukla, S.K. Numerical modeling of virus transport through unsaturated porous media. Cogent Geosci. 2016, 2, 1220444. [Google Scholar] [CrossRef]
- Kaykhosravi, S.; Khan, U.T.; Jadidi, A. A comprehensive review of low impact development models for research, conceptual, preliminary and detailed design applications. Water 2018, 10, 1541. [Google Scholar] [CrossRef] [Green Version]
- Silva, J.A.K.; Šimůnek, J.; McCray, J.E. A modified HYDRUS model for simulating PFAS transport in the vadose zone. Water 2020, 12, 2758. [Google Scholar] [CrossRef]
- Twarakavi, N.K.C.; Šimůnek, J.; Seo, S. Evaluating interactions between groundwater and vadose zone using the HYDRUS-based flow package for MODFLOW. Vadose Zone J. 2008, 7, 757–768. [Google Scholar] [CrossRef] [Green Version]
- Ehlers, W. Poröse Medien: Ein Kontinuumsmechanisches Modell auf der Basis der Mischungstheorie; Universität-GH Essen: Essen, Germany, 1989. [Google Scholar]
- de Boer, R. Theory of Porous Media: Highlightsinthe Historical Development and Current State; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Ehlers, W. Foundations of multiphasic and porous materials. In Porous Media; Springer: Berlin/Heidelberg, Germany, 2002; pp. 3–86. [Google Scholar]
- Ehlers, W.; Bluhm, J. Porous Media: Theory, Experiments and Numerical Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Bowen, R. Toward a thermodynamics and mechanics of mixtures. Arch. Ration. Mech. Anal. 1967, 24, 370–403. [Google Scholar] [CrossRef]
- Ustohalova, V.; Ricken, T.; Widmann, R. Estimation of landfill emission lifespan using process oriented modeling. Waste Manag. 2006, 26, 442–450. [Google Scholar] [CrossRef]
- Robeck, M.; Ricken, T.; Widmann, R. A finite element simulation of biological conversion processes in landfills. Waste Manag. 2011, 31, 663–669. [Google Scholar] [CrossRef]
- Ricken, T.; Sindern, A.; Bluhm, J.; Widmann, R.; Denecke, M.; Gehrke, T.; Schmidt, T.C. Concentration driven phase transitions in multiphase porous media with application to methane oxidation in landfill cover layers. ZAMM-J. Appl. Math. Mech. Für Angew. Math. Und Mech. 2014, 94, 609–622. [Google Scholar] [CrossRef]
- Seyedpour, S.; Ricken, T. Modeling of contaminant migration in groundwater: A continuum mechanical approach using in the theory of porous media. PAMM 2016, 16, 487–488. [Google Scholar] [CrossRef]
- Schulte, M.; Jochmann, M.A.; Gehrke, T.; Thom, A.; Ricken, T.; Denecke, M.; Schmidt, T.C. Characterization of methane oxidation in a simulated landfill cover system by comparing molecular and stable isotope mass balances. Waste Manag. 2017, 69, 281–288. [Google Scholar] [CrossRef] [PubMed]
- Seyedpour, S.M.; Janmaleki, M.; Henning, C.; Sanati-Nezhad, A.; Ricken, T. Contaminant transport in soil: A comparison of the Theory of Porous Media approach with the microfluidic visualisation. Sci. Total. Environ. 2019, 686, 1272–1281. [Google Scholar] [CrossRef] [PubMed]
- Seyedpour, S.M.; Valizadeh, I.; Kirmizakis, P.; Doherty, R.; Ricken, T. Optimization of the Groundwater Remediation Process Using a Coupled Genetic Algorithm-Finite Difference Method. Waste 2021, 13, 383. [Google Scholar] [CrossRef]
- Truesdell, C.; Toupin, R. The classical field theories. In Principles of Classical Mechanics and Field Theory/Prinzipien der Klassischen Mechanik und Feldtheorie; Springer: Berlin/Heidelberg, Germany, 1960; pp. 226–858. [Google Scholar]
- Mills, N. Incompressible mixtures of Newtonian fluids. Int. J. Eng. Sci. 1966, 4, 97–112. [Google Scholar] [CrossRef]
- Bowen, R.M. Compressible porous media models by use of the theory of mixtures. Int. J. Eng. Sci. 1982, 20, 697–735. [Google Scholar] [CrossRef]
- Stefan, J. Über das Gleichgewicht und Die Bewegung, Insbesondere Die Diffusion von Gasgemengen; Universitätsbibliothek Johann Christian Senckenberg: Frankfurt, Germany, 2007. [Google Scholar]
- Truesdell, C. Rational Thermodynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Ricken, T.; Werner, D.; Holzhütter, H.G.; König, M.; Dahmen, U.; Dirsch, O. Modeling function–perfusion behavior in liver lobules including tissue, blood, glucose, lactate and glycogen by use of a coupled two-scale PDE–ODE approach. Biomech. Model. Mechanobiol. 2015, 14, 515–536. [Google Scholar] [CrossRef]
- Ehlers, W. Constitutive equations for granular materials in geomechanical context. In Continuum Mechanics in Environmental Sciences and Geophysics; Springer: Berlin/Heidelberg, Germany, 1993; pp. 313–402. [Google Scholar]
- Svendsen, B.; Hutter, K. On the thermodynamics of a mixture of isotropic materials with constraints. Int. J. Eng. Sci. 1995, 33, 2021–2054. [Google Scholar] [CrossRef]
- Helmig, R. Multiphase Flow and Transport Processes in the Subsurface: A Contribution to the Modeling of Hydrosystems; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Kong, J.; Xin, P.; Hua, G.F.; Luo, Z.Y.; Shen, C.J.; Chen, D.; Li, L. Effects of vadose zone on groundwater table fluctuations in unconfined aquifers. J. Hydrol. 2015, 528, 397–407. [Google Scholar] [CrossRef]
- Liu, I.S. Method of Lagrange multipliers for exploitation of the entropy principle. Arch. Ration. Mech. Anal. 1972, 46, 131–148. [Google Scholar] [CrossRef]
- Coleman, B.D.; Noll, W. The thermodynamics of elastic materials with heat conduction and viscosity. In The Foundations of Mechanics and Thermodynamics; Springer: Berlin/Heidelberg, Germany, 1974; pp. 145–156. [Google Scholar]
- Finsterle, S. Inverse Modellierung zur Bestimmung Hydrogeologischer Parameter eines Zweiphasensystems. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 1992. [Google Scholar]
- Fredlund, D.G.; Rahardjo, H.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]



| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| soil material properties (silty sand) | 2865 | ||
| 3076 | |||
| 4615 | |||
| initial soil volume fraction | 0.58 | ||
| universal gas constant | 8.3144 | ||
| temperature | 293.15 | ||
| hydraulic parameters of the vadose zone | |||
| 2.3 | |||
| 1.4 | |||
| residual saturation of water | 0.1 | ||
| residual saturation of air | 0.1 | ||
| dynamic viscosity of water and air | |||
| initial pressure | 101.325 | ||
| diffusion coefficient of contaminant (1,4-dioxane) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seyedpour, S.M.; Thom, A.; Ricken, T. Simulation of Contaminant Transport through the Vadose Zone: A Continuum Mechanical Approach within the Framework of the Extended Theory of Porous Media (eTPM). Water 2023, 15, 343. https://doi.org/10.3390/w15020343
Seyedpour SM, Thom A, Ricken T. Simulation of Contaminant Transport through the Vadose Zone: A Continuum Mechanical Approach within the Framework of the Extended Theory of Porous Media (eTPM). Water. 2023; 15(2):343. https://doi.org/10.3390/w15020343
Chicago/Turabian StyleSeyedpour, S. M., A. Thom, and T. Ricken. 2023. "Simulation of Contaminant Transport through the Vadose Zone: A Continuum Mechanical Approach within the Framework of the Extended Theory of Porous Media (eTPM)" Water 15, no. 2: 343. https://doi.org/10.3390/w15020343
APA StyleSeyedpour, S. M., Thom, A., & Ricken, T. (2023). Simulation of Contaminant Transport through the Vadose Zone: A Continuum Mechanical Approach within the Framework of the Extended Theory of Porous Media (eTPM). Water, 15(2), 343. https://doi.org/10.3390/w15020343





