1. Introduction
In the 21st century, a number of high arch dams have been built in southwest China. The high arch dams and river valleys show unexpected deformations during the impoundment period, mainly manifested as valley-narrowing deformations, reservoir plate deformations, and the top of the dam deforming upstream. Valley-narrowing deformation is a phenomenon in which the mountain on both sides of the river deforms to the free faces and decreases the valley width. The high arch dam, a typical kind of statically indeterminate structure, is very sensitive to valley-narrowing deformation. Hence, it is of vital importance to understand the valley-narrowing deformation.
The valley-narrowing deformation at the Xiluodu Project has reached approximately 90 mm. The monitored valley-narrowing deformation of the Xiluodu arch dam project during initial impoundment is more serious than the other projects. Some researchers have studied the influence of temperature on the valley-narrowing deformation of the Xiluodu arch dam project [
1,
2] and agree that the cooling shrinkage of the bedrock in the dam upstream can cause the valley-narrowing deformation. However, the dominant mechanism of the cooling shrinkage of the bedrock is still under debate. When the reservoir starts to impound, the lower-temperature reservoir water has a cooling effect on the rock of the submerged area, and the seepage of the cold water causes heat migration, resulting in changes in the temperature fields of the reservoir bank and bedrock. When the pore pressure and temperature gradients exist in the pore medium, the pore flow has heat exchange with the solid skeleton, which leads to the redistribution of temperature, seepage, and stress fields. This phenomenon is known as the “Dufour flow” and is widely used in shallow geothermal systems [
3], enhanced geothermal systems (EGS) [
4], and water conservancy projects [
5].
The thermo-hydromechanical (THM) coupling method is generally used for theoretical and numerical simulation analysis. Noorishad et al. [
6] proposed the THM coupling basic equation for a saturated geotechnical medium. Zimmerman [
7] established a constitutive equation based on the poroelastic theory of a continuum medium and concluded that the effect of temperature on the stress field cannot be neglected. Obeid et al. [
8] and Schrefler et al. [
9] established a coupled model of unsaturated THM in a porous medium within the framework of the finite element method. Rutqvist et al. [
10,
11] studied the THM coupling problem of fractured unsaturated and saturated rock masses. It is generally assumed that the temperatures of the fluid and the medium at the same position are the same in the medium. For projects in which fractures are not developed and the fracture network is difficult to determine, the THM coupling model based on an equivalent porous medium was used in this work.
For the Xiluodu high arch dam, the significant temperature drops and fluid pressure increases within the geothermal limestone aquifer are the primary mechanisms of the valley-narrowing deformation during reservoir impounding and seepage development [
1]. Yin et al. [
2] conducted a THM analysis on the Xiluodu arch dam and emphasized the significance of geothermal in the valley-narrowing deformation. However, as reported in the THM coupling simulation of the Xiluodu dam by Zhang et al. [
12], the reservoir water had a marginal effect on the magnitude and range of temperature decrement in the bedrock. The value of the valley-narrowing deformation was about 10 mm, which was much smaller than the measured value. This numerical result indicates that the temperature drop in the impoundment case is not the main factor for the valley-narrowing deformation. Xu et al. [
13] conducted research on the limestone groundwater of the Xiluodu dam foundation after impoundment. The results showed that the replenishment water of the mountain after impoundment mainly depended on the increase in elastic storage. However, the amount of replenishment water was quite limited. A small amount of reservoir water entering the limestone-confined water cannot change the limestone groundwater temperature, and the limestone-confined water temperature in the lower part of the dam foundation does not change significantly after impoundment.
The dominant mechanisms of the variations in the bedrock temperature field are still under debate, and the internal connections between the above two viewpoints have not been studied yet. Therefore, it is necessary to further study the temporal and spatial evolution of the bedrock temperature field after impoundment. In this study, the THM coupling model was used to analyze the evolution of the temperature field of the Xiluodu dam foundation. The generation mechanisms of the short- and long-term types of temperature drops are compared from the perspectives of impoundment time and rock mass permeability. This work is expected to provide a reference for the study of the influence of temperature on valley deformation after impoundment.
2. Thermo-Hydromechanical Coupling Method
2.1. Constitutive
In this work, two equations described the thermal movement in the rock matrix and the fluid, respectively. Fluid percolation obeys Darcy’s law. Heat conduction obeys Fourier’s law. The energy conservation equations of the solid and liquid phases are as follows [
14,
15].
Solid phase energy conservation equation:
Liquid phase energy conservation equation:
where
n is the solid porosity;
v is the fluid velocity;
t is time;
h is the heat transfer coefficient of the solid–liquid phase interface;
and
are the temperatures of the solid and fluid, respectively;
and
are the solid density and liquid density, respectively;
and
are the specific heat capacities of the solid and liquid, respectively;
and
are the solid and liquid thermal conductivities, respectively.
In rock mass, the seepage velocity is generally small. It is considered that the temperature of the solid skeleton (
) and the temperature of the fluid (
) are consistent at the same position (integration point). The total energy conservation equation is written as [
14,
15,
16]:
The mass conservation equation is given as:
where
is the pore water pressure;
is the permeability tensor;
is the dynamic viscosity coefficient of fluid;
is the effective stress;
and
are the bulk moduli of the solids and fluids, respectively;
and
are the thermal expansion coefficients of the solids and fluids, respectively.
The solid constitutive equation coupled with the combined actions of temperature and seepage fields is given as [
16]:
where
is the shear modulus of the porous medium;
is the Poisson ratio for the porous medium;
and
(
) are the components of body force and displacement, respectively;
;
is the overall thermal expansion coefficient of the medium;
is the Biot coefficient.
2.2. Verification
The engineering rock mass contains complex fracture systems, and a complete description of the fracture system is unrealistic. Generally, the fractured rock mass is equivalent to a porous medium. Thermodynamic analysis of a single rock fracture can express the basic characteristics of heat exchange between the rock matrix and the water [
14,
17]. In this section, the THM coupling model is verified by an example of a single fracture with an analytical solution, and the law of heat exchange between the rock matrix and the fracture water is analyzed.
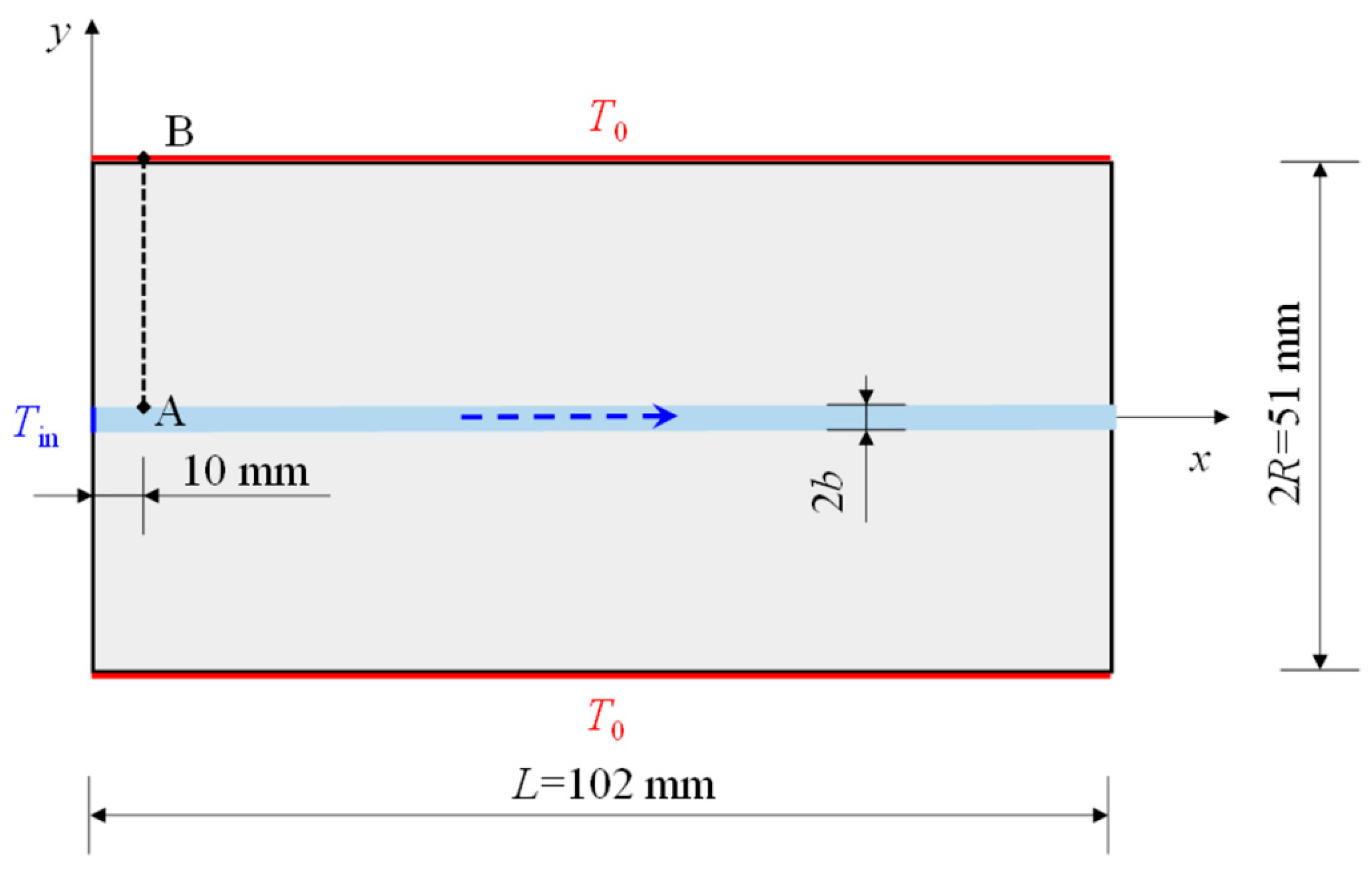
A single horizontal fracture with a constant width
was divided into homogeneous and impermeable rectangular rock equally, as shown in
Figure 1. The boundary temperature at the model,
, was
. At
and
, the boundary was adiabatic. At the inlet (
), the fluid velocity was
, and the temperature was
; at the outlet (
), the fluid velocity was free. It was assumed that: (1) heat conduction was only in the direction perpendicular to the fracture surface; (2) the thermophysical properties of water and rock were constant; and (3) the fracture was simplified as a porous medium with an infinite void ratio, i.e., the void ratio was 100. The parameters used in the numerical simulation are listed in
Table 1.
The analytical solutions of the fluid temperature in the fracture and the rock temperature under the condition of steady heat transfer are as follows [
17]:
where
is the fluid temperature at position
x in the fracture;
is the temperature of the rock matrix at the coordinates
. The parameters used in this case are listed in
Table 1.
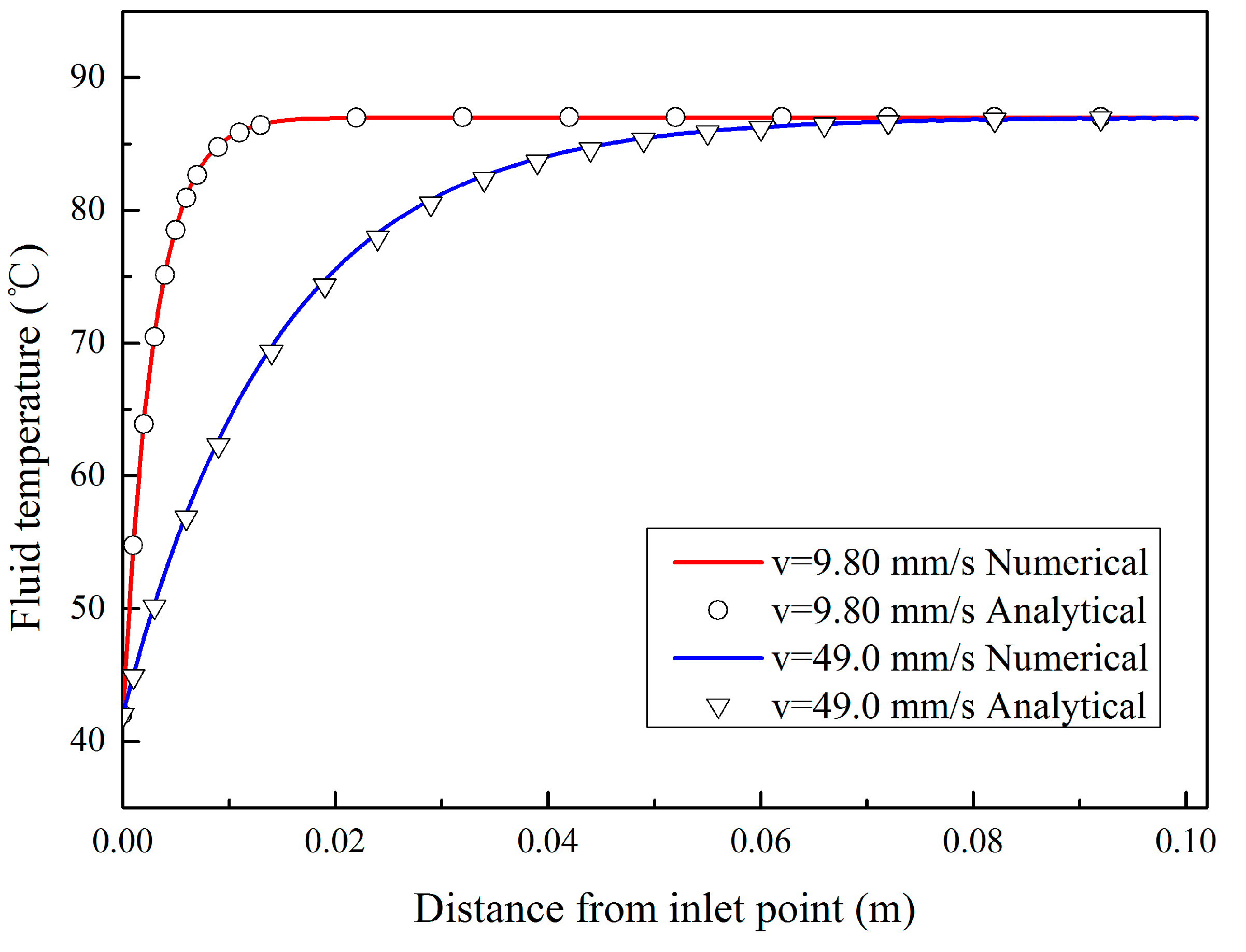
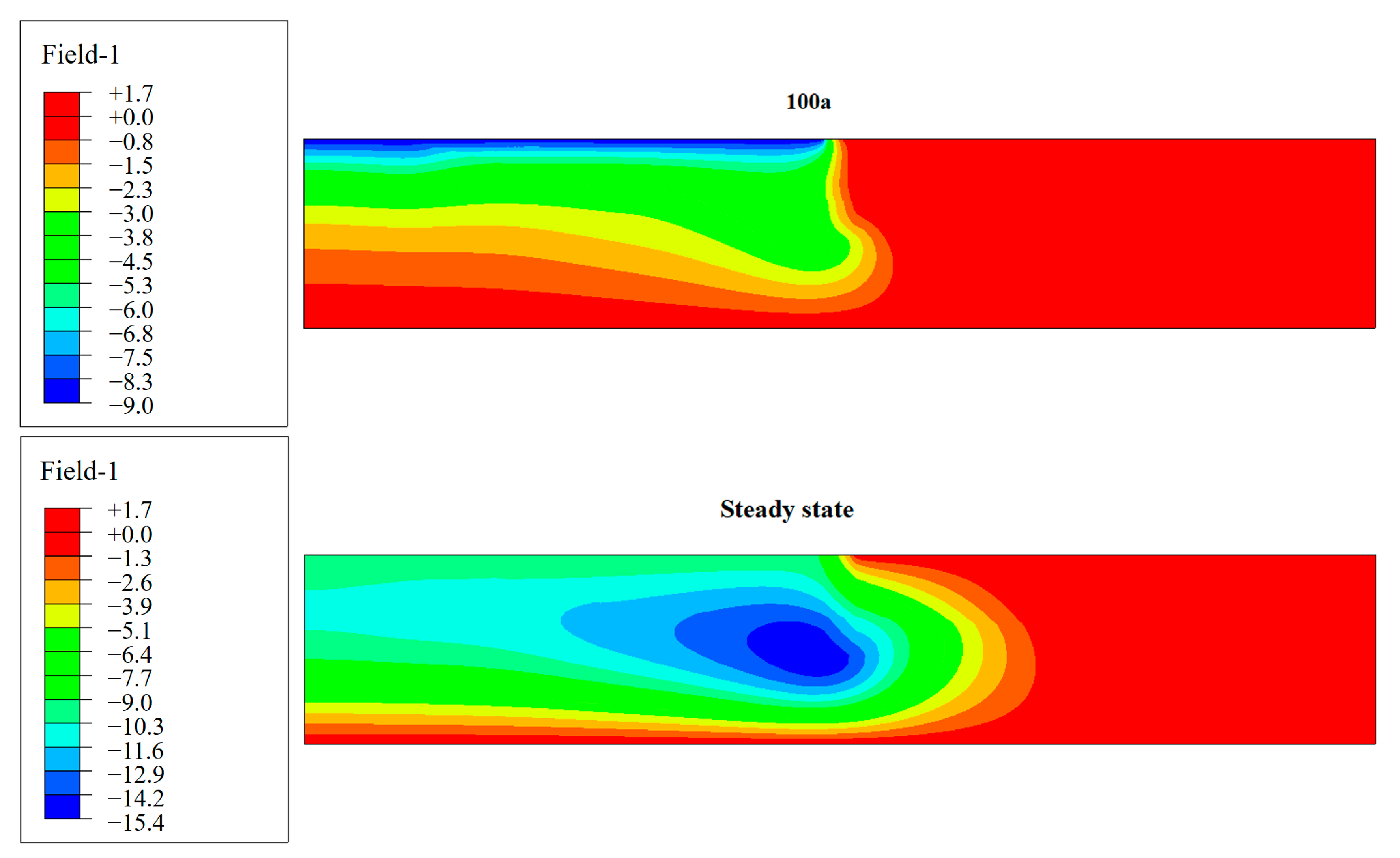
The temperatures of fluids with different flow velocities in the fracture along the flow direction and the temperature of the rock matrix along the line AB were consistent with the analytical solutions, as shown in
Figure 2 and
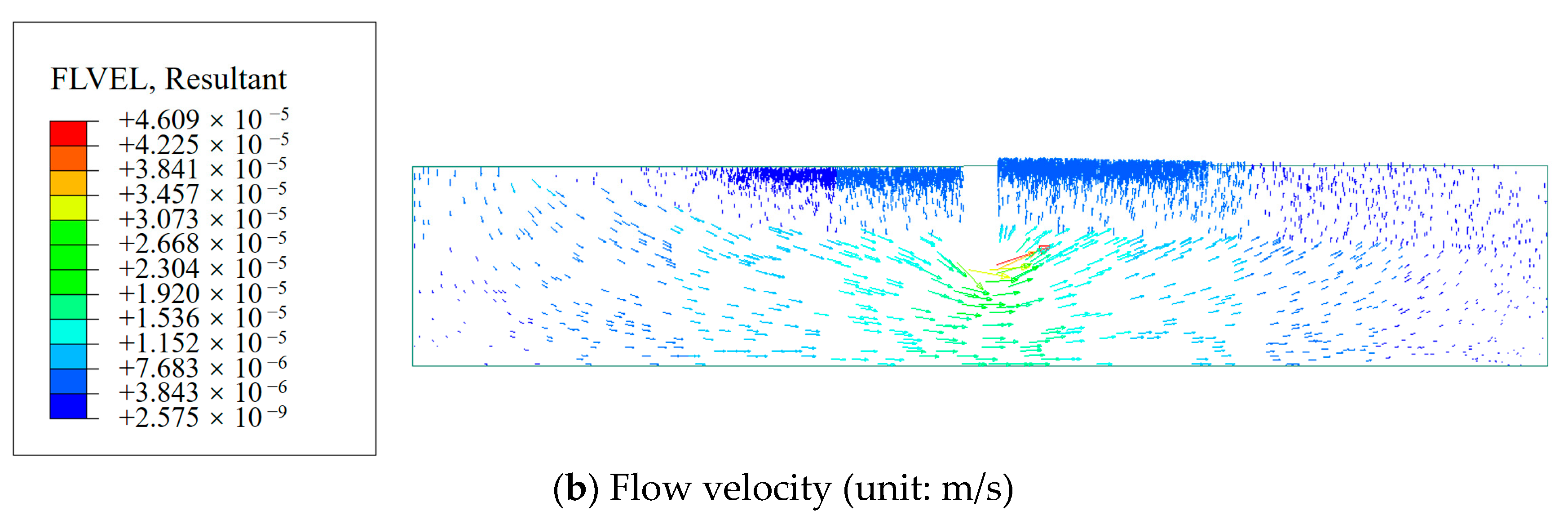
Figure 3. This shows that the numerical solution was consistent with the analytical solution.
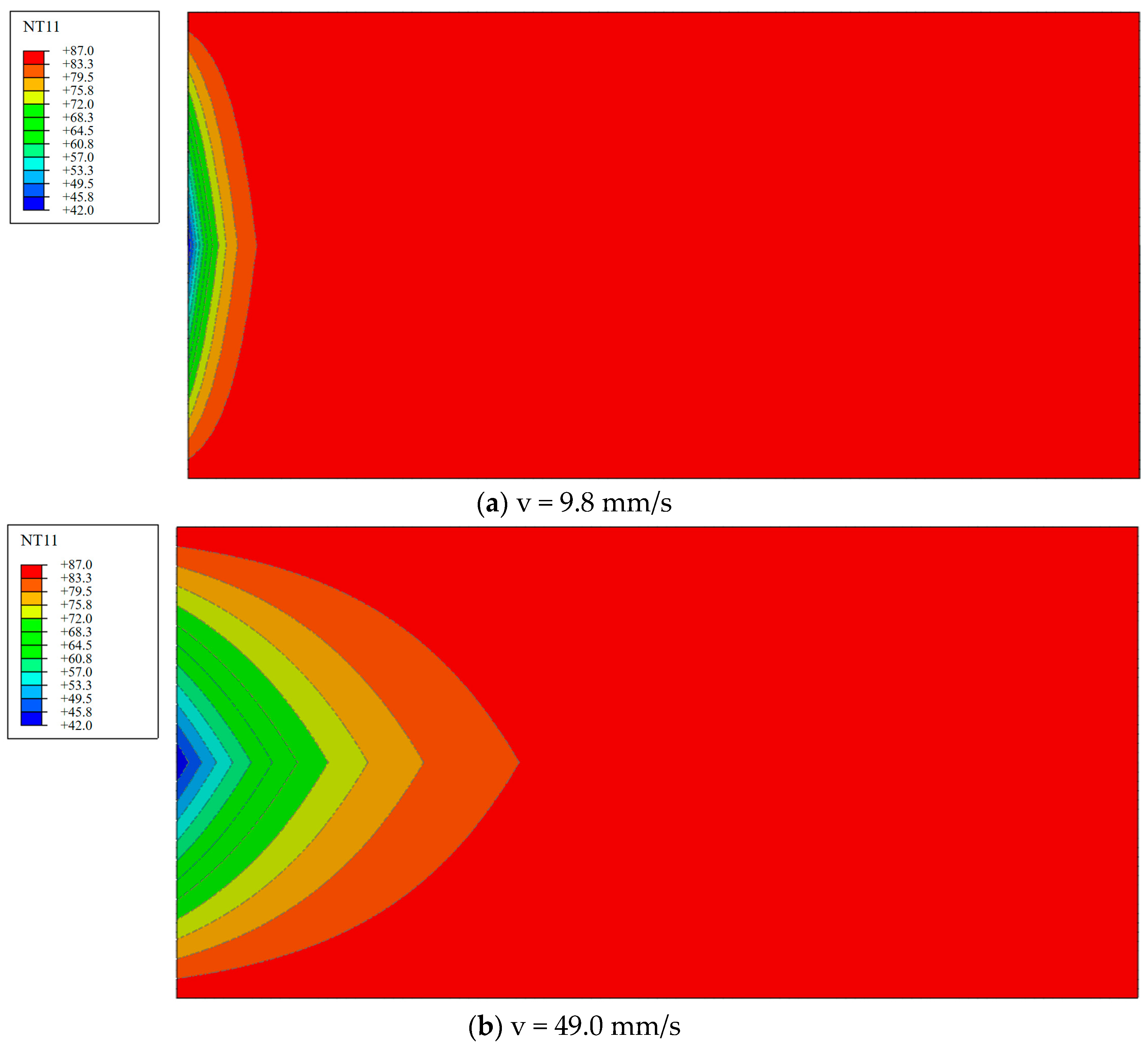
Figure 4 is a diagram of the stable temperature field formed by the two flow velocities. When the flow velocity is small, the temperature drop area is mainly near the water inlet. As the flow velocity increases, the fluid takes more heat away from the rock matrix. This phenomenon indicates that the rock matrix is sensitive to the flow velocity.
3. Evolution of the Dam Foundation Temperature Field
3.1. Finite Element Model
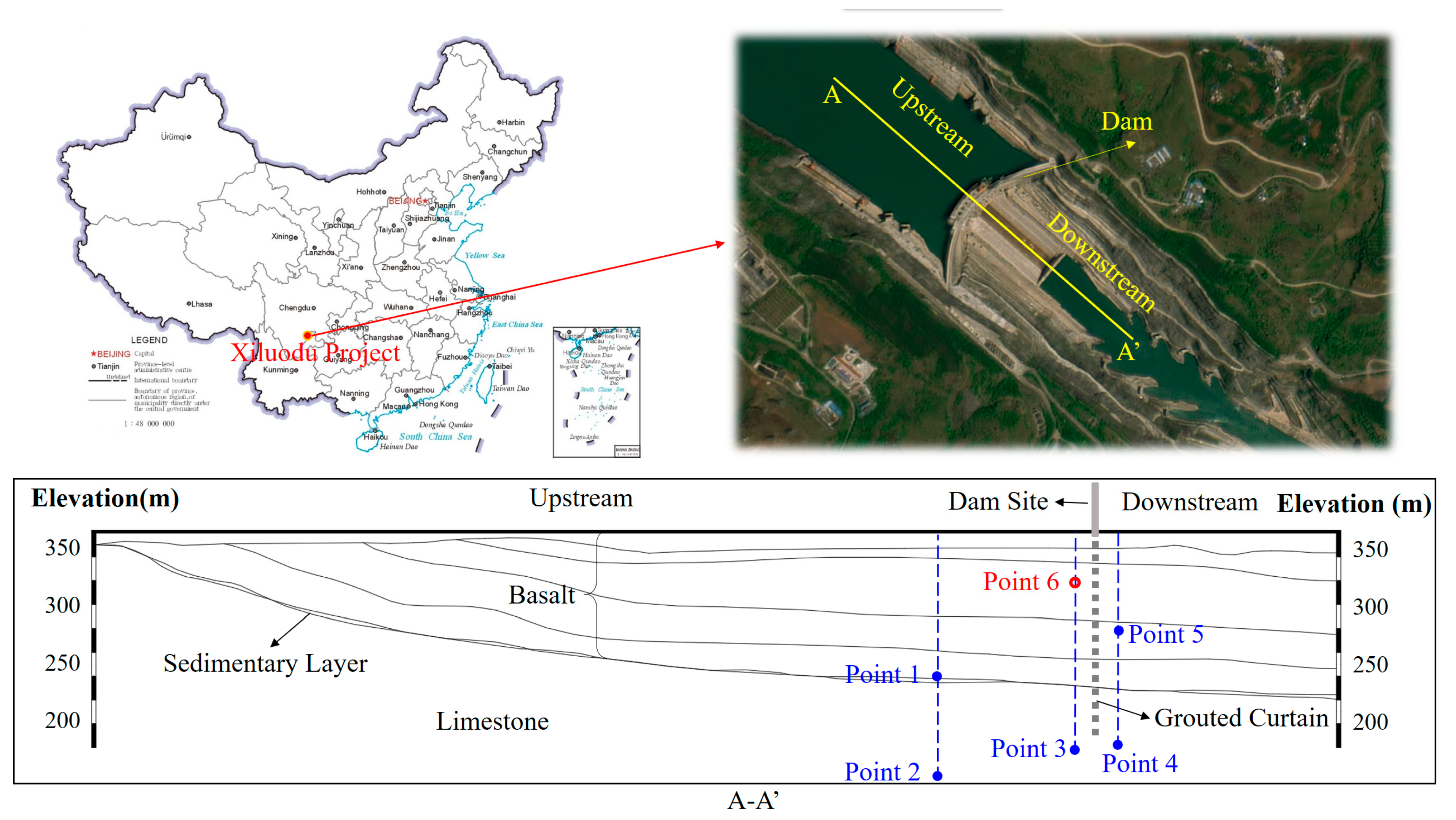
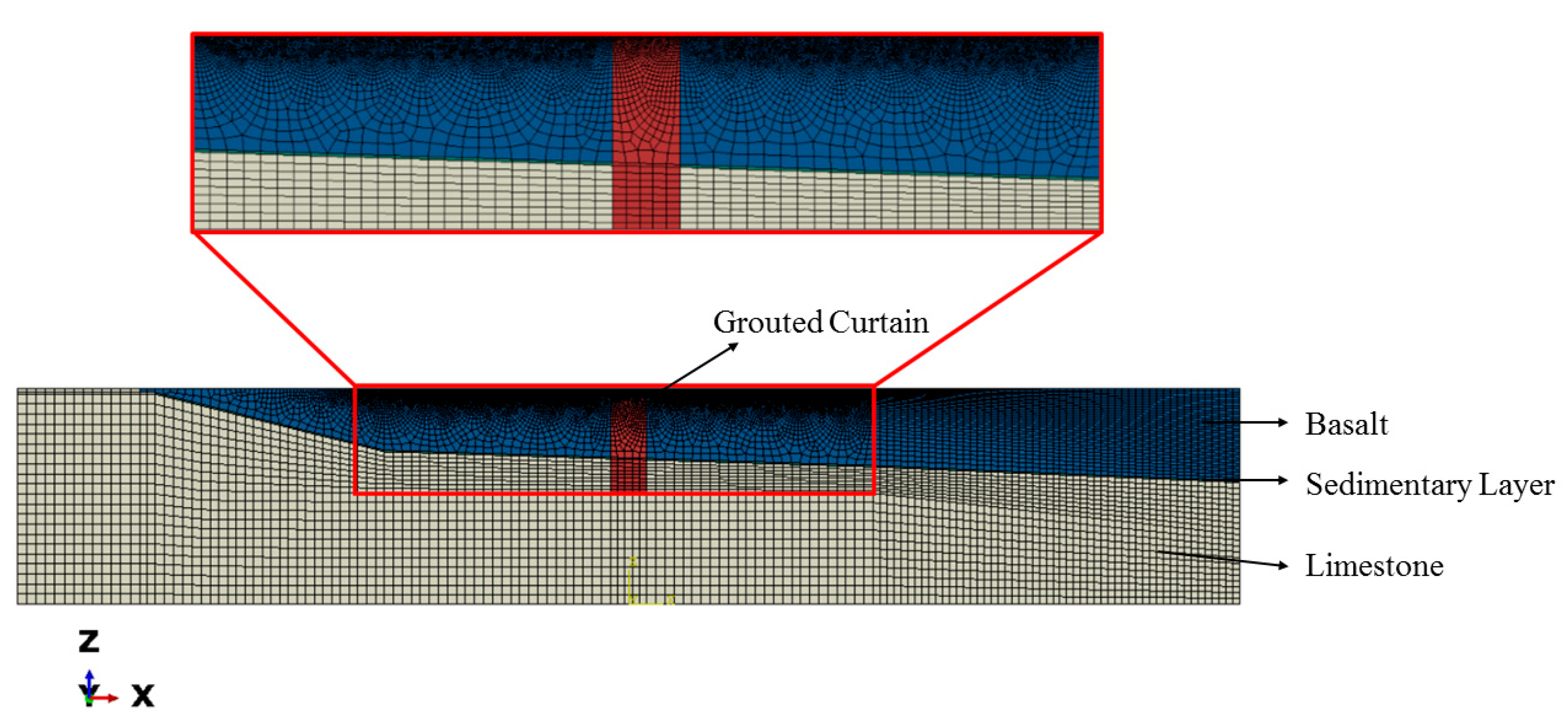
Based on the hydrogeological profiles of the Xiluodu dam site along the direction of river flow (
Figure 5), a finite element numerical analysis model of the bedrock profile was established (
Figure 6). The number of nodes was 40,770, and the number of elements was 19,809. The confined water level of Yangxin limestone is 2–3 m higher than that of the Jinsha River, and the water head of the confined layer is well synchronized with the river water level. The hydraulic gradient in the vertical river flow direction at the profile is not large [
13]; therefore, the heat transfer and water transport in the vertical river direction were not considered.
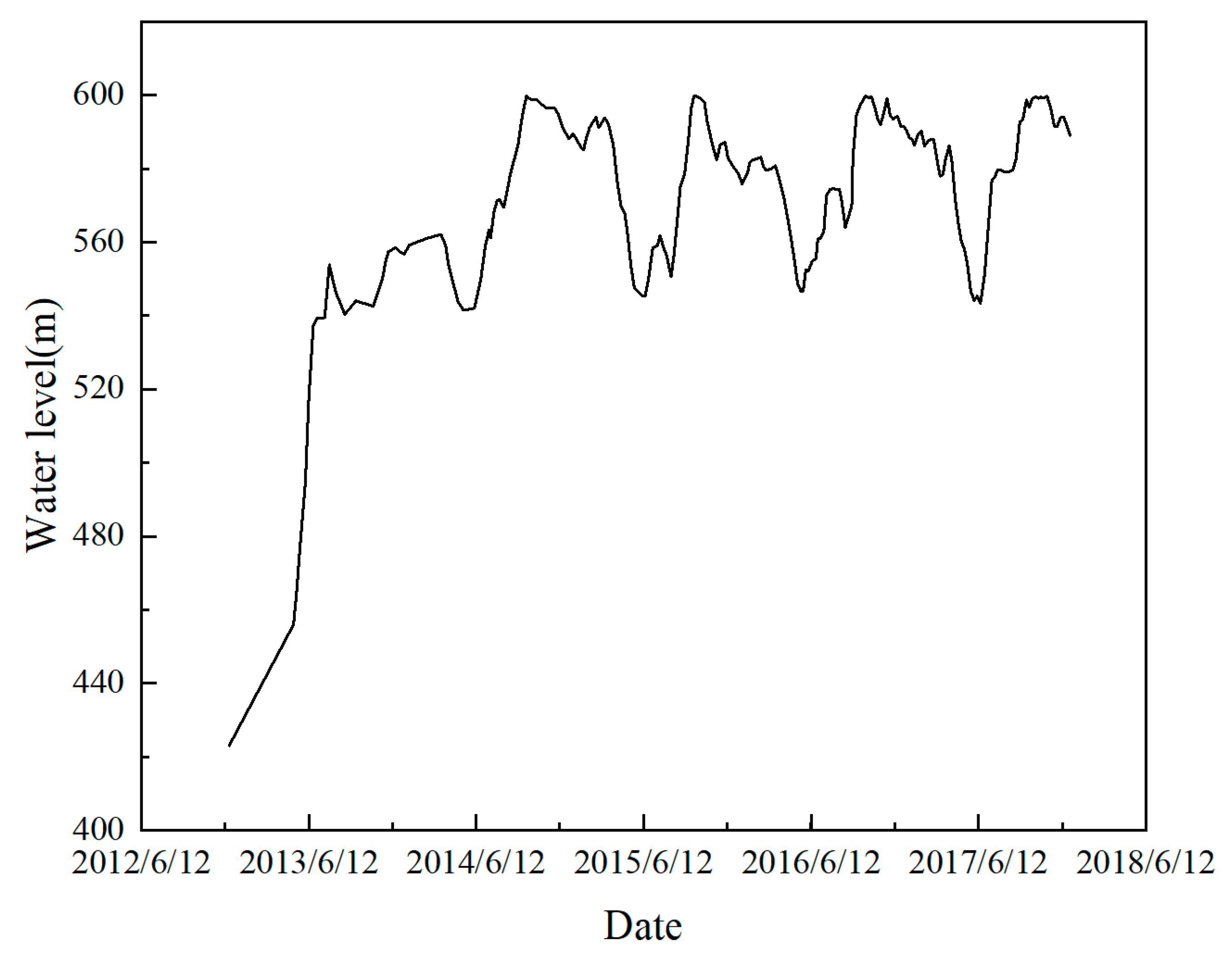
For the Xiluodu reservoir, the natural water level is 370 m, and the hydraulic gradient is 1/1000. The process of the upstream reservoir water level within 5 years after impoundment is shown in
Figure 7, and the downstream water level was kept at 370 m. According to geothermal and hydrogeological conditions [
1,
2], the bottom temperature of the bedrock was set at 41.5 °C. According to the monitoring data [
18,
19], the periodical water temperature near the depth of 20 m in the Xiluodu reservoir was 15~24 °C from November 2016 to September 2017. After impoundment, the water temperature in the deep-water layer at the bottom of the valley was constantly 15 °C. Therefore, in the simulation, the surface water temperature of the bedrock was taken as 24 °C before impoundment, and the upstream and downstream bedrock surface water temperatures were taken as 15 °C and 24 °C during impoundment. The material parameters [
5,
20] are listed in
Table 2.
3.2. Temperature Field of Bedrock before Impoundment
The temperature field of the bedrock before impoundment is shown in
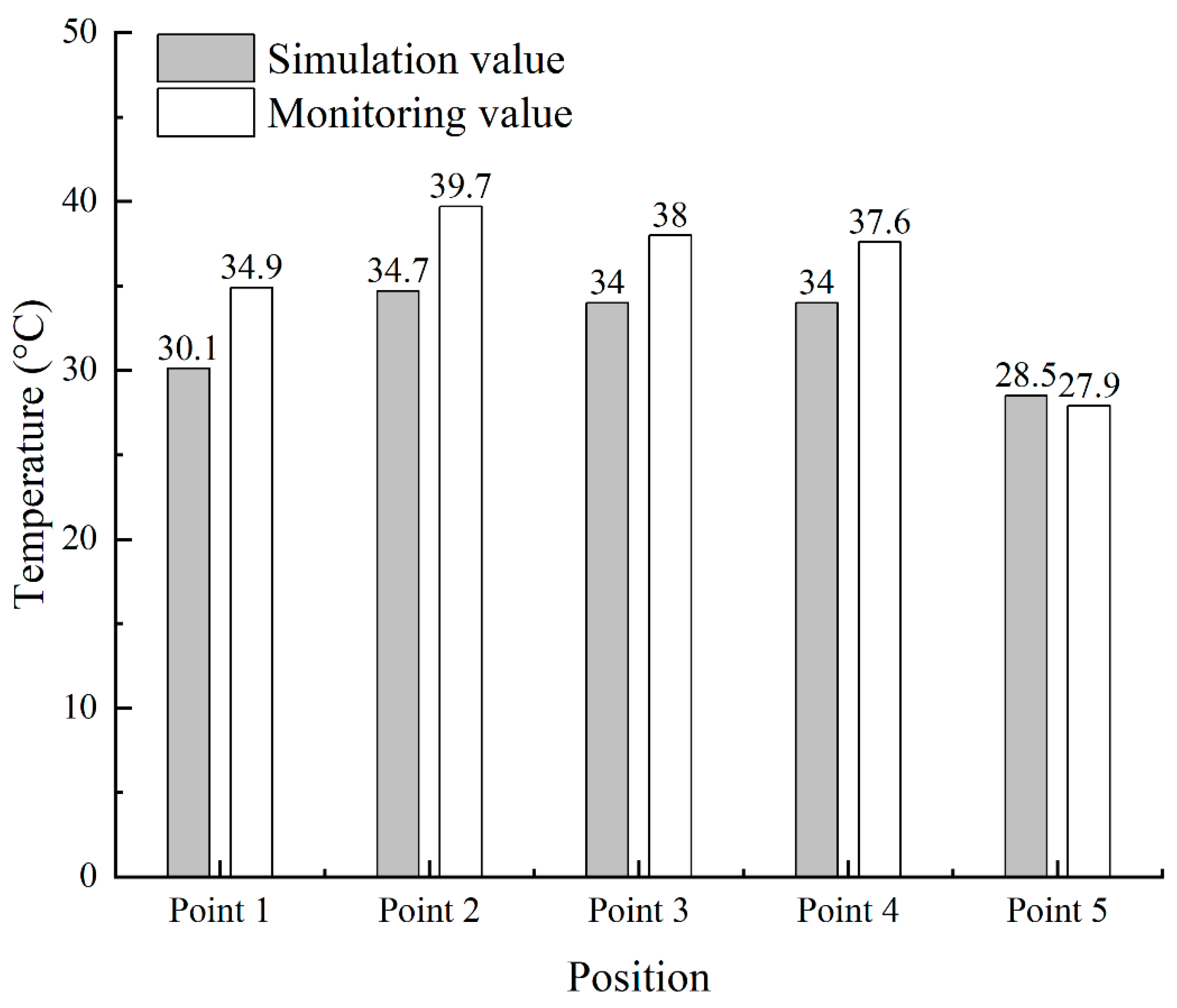
Figure 8. The calculated and monitored temperature values of the bedrock before impoundment for different monitoring points are shown in
Figure 9.
The difference between the simulated and measured initial temperature fields of bedrock measurement points 1 to 4 was about 4 °C, and measurement point 5 was about 0.6 °C. The location of the measurement points was within the vicinity of the bedrock calculation section (A-A’), and there was a temperature gradient of the bedrock temperature in the section of the river valley toward the mountains on both banks [
5], so the initial bedrock temperature field was reasonable.
3.3. Seepage State of the Bedrock after Impoundment
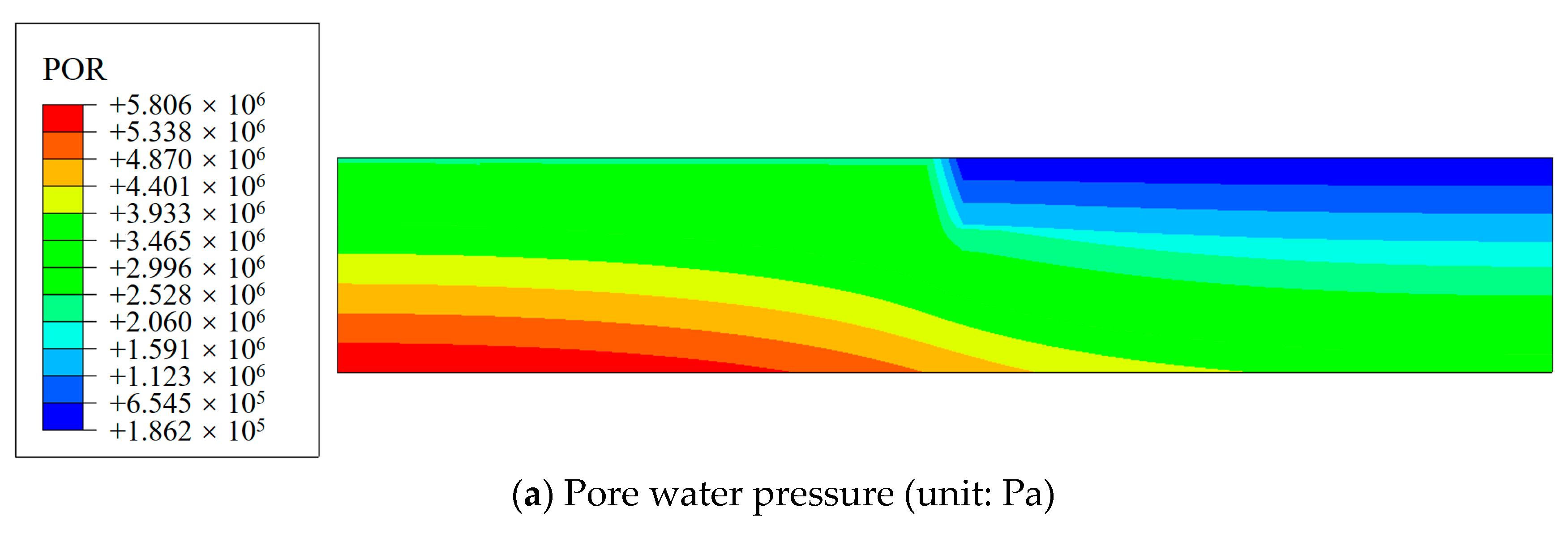
The distribution of pore water pressure and the flow velocity field at a water level of 600 m are shown in
Figure 10. Due to the existence of the grouted curtain, the reservoir water mainly flows in the limestone confined layer. Then, the reservoir water flows downstream, and the limestone-pressurized water flows upward through the sedimentary layer into the basalt layer and sinks into the river.
3.4. Analysis of the Temperature Field after Impoundment
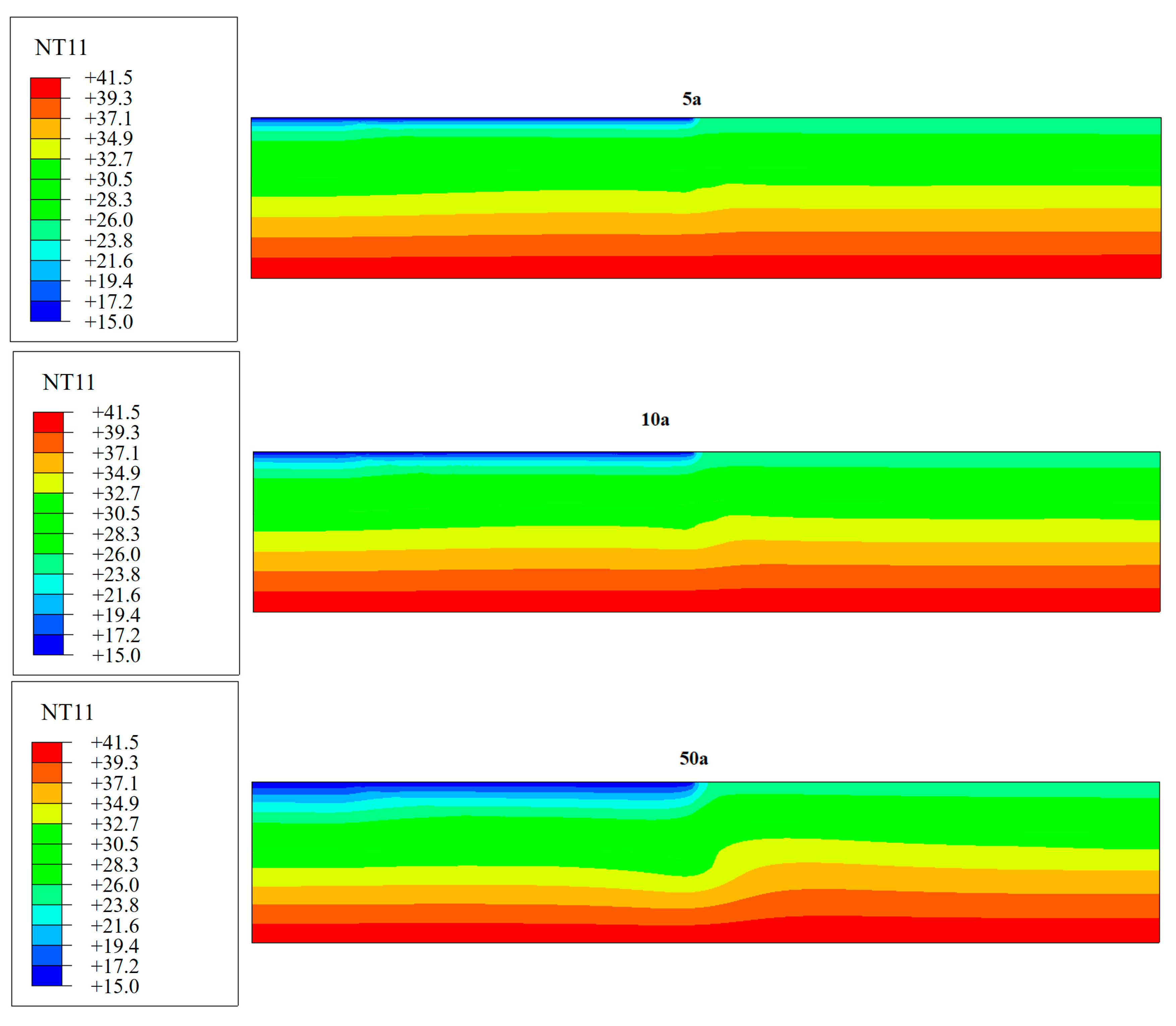
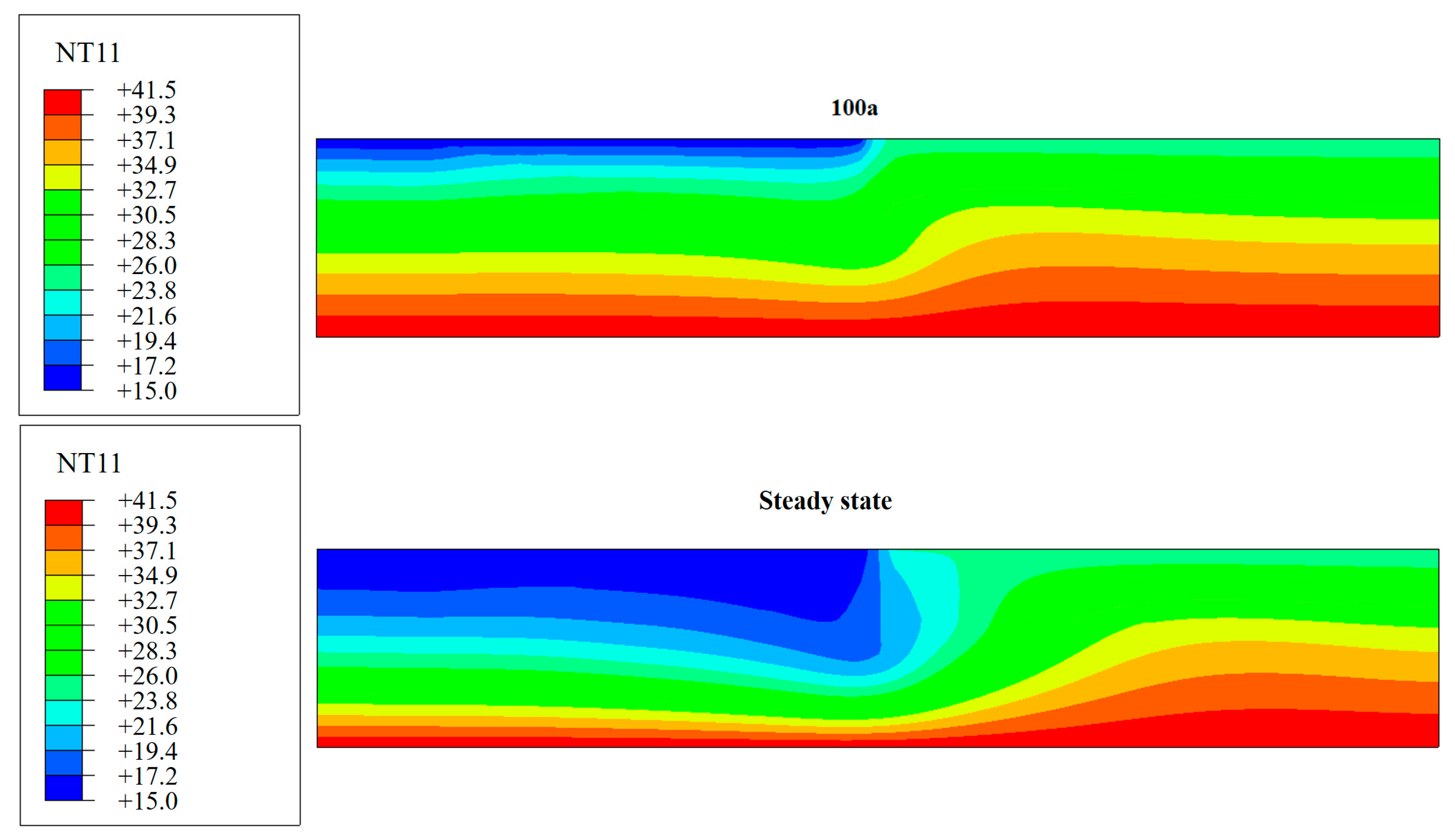
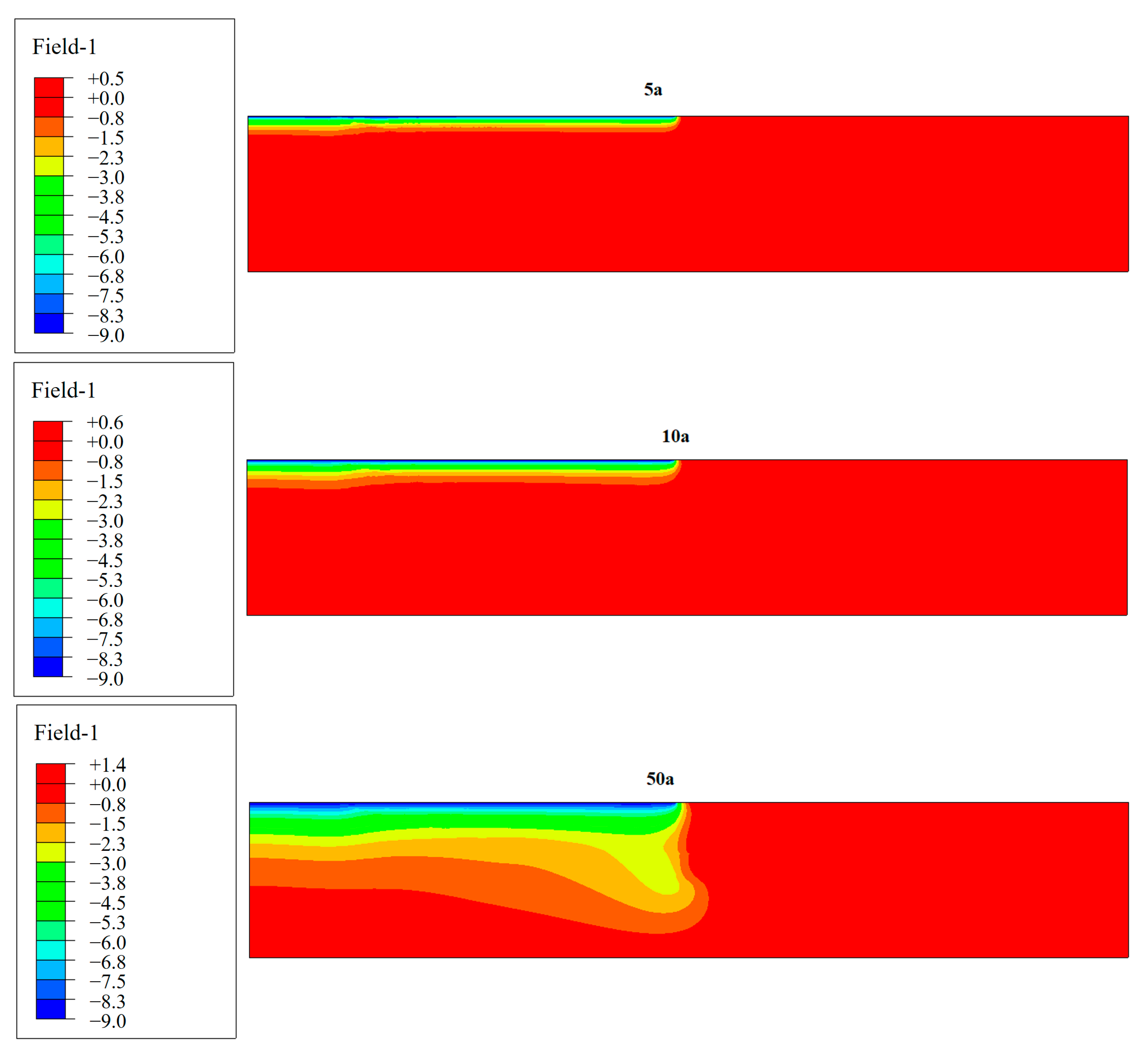
The bedrock temperature fields and bedrock temperature drop fields at the dam site after impoundment are shown in
Figure 11 and
Figure 12. The temperature distribution along the depth direction at 50 m before the grouted curtain at different times during the impoundment is shown in
Figure 13.
During the 5–10 years of the initial impoundment, the temperature drop mainly occurred on the bedrock surface. The temperature drop range was about 50 m, and it dropped by 9 °C. The bedrock temperature gradually decreased with depth, but the bedrock temperature below the 50 m depth was almost unchanged. When the water was impounded for 50 years, from the surface to a depth of 100 m, the temperature decreased by 9 to 2 °C. At a depth range of 100 m to 200 m, the temperature was reduced by 2 °C. The temperature reduction below a 200 m depth was less than 2 °C. When the water was impounded for 100 years, from the surface to the depth of 100 m, the temperature decrement ranged from 9 to 4 °C. From 100 m to 200 m in depth, the temperature reduced by 4 °C. The temperature reduction below a 200 m depth was less than 4 °C. Comparing the distribution of the temperature field, after the temperature field of the foundation was stabilized, the temperature drop amplitude was 15 °C. It appeared at a depth of about 200 m in front of the grouted curtain. Comparing the distributions of the stable temperature field, the temperature field of the bedrock after 100 years is still far from the stable state. The temperature reduction process is much longer than 100 years.
3.5. The Influence of Rock Permeability on Temperature Field
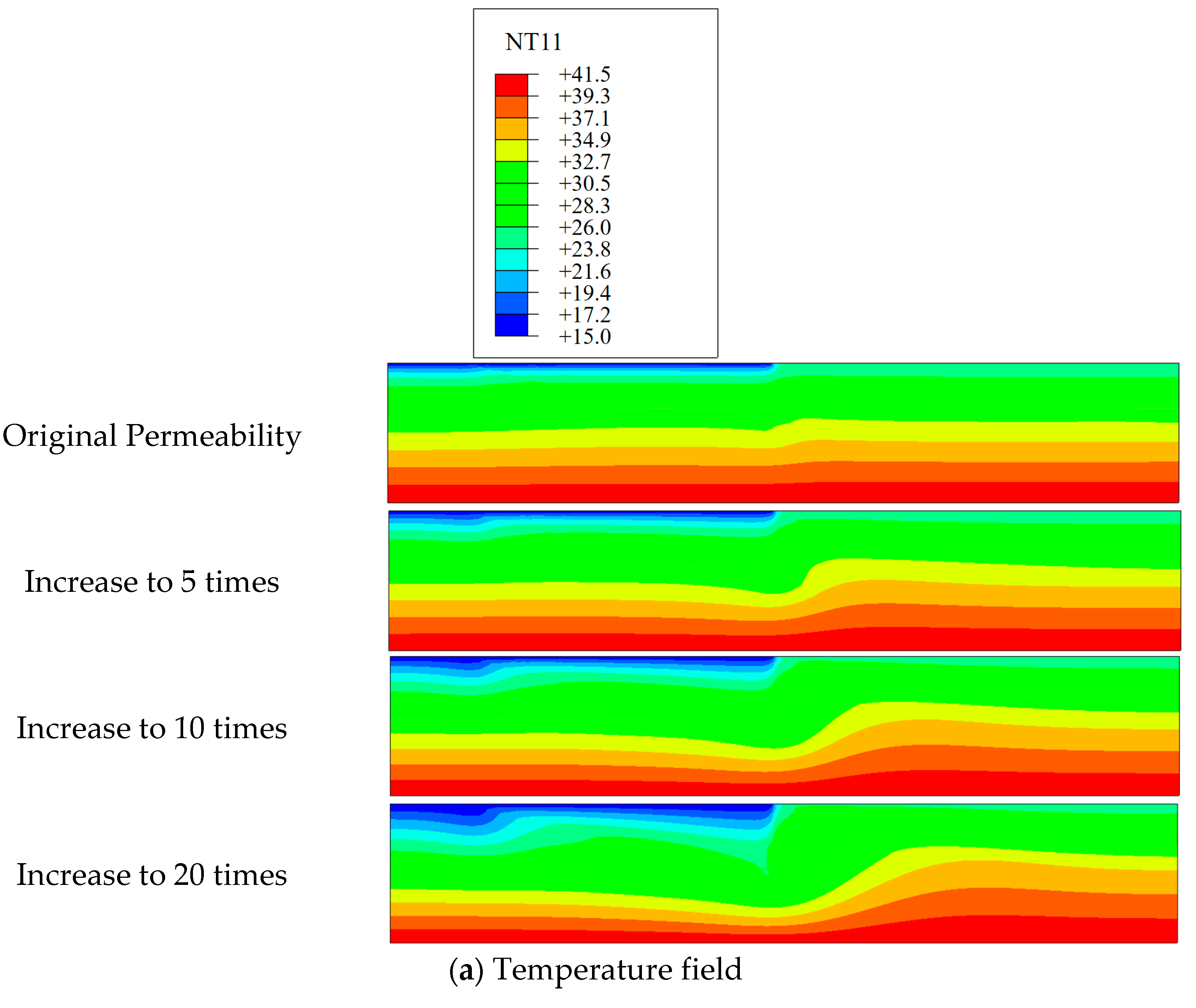
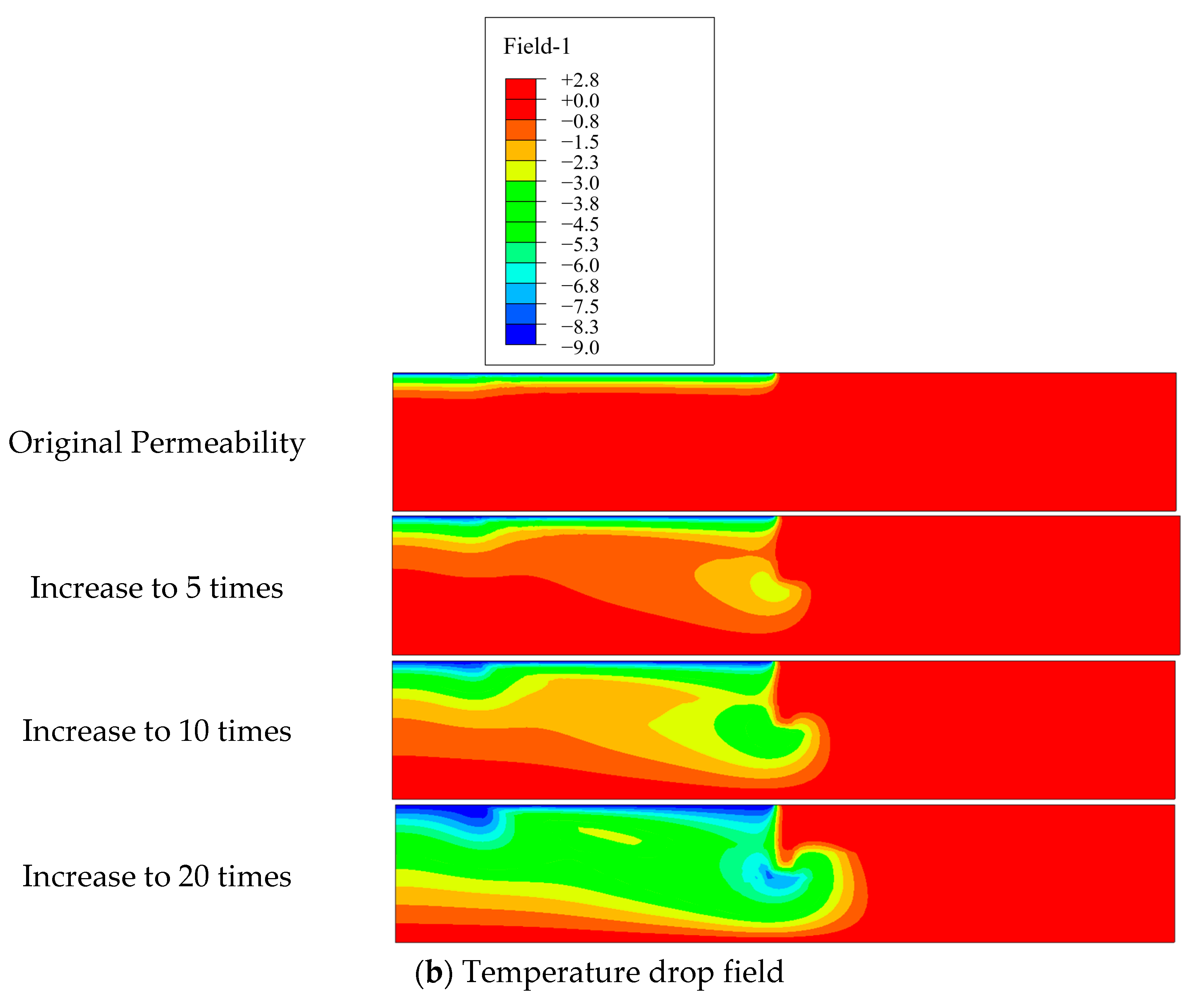
The actual rock mass contains fractures, and the permeability coefficient of the fractures is much larger than that of the complete rock. The equivalent continuum model is usually used to simulate fractured rock, and the fracture network is equivalent by adjusting the permeability coefficient. The velocity of the pore water is sensitive to the permeability of the bedrock, and the pore water flow causes heat transfer, which in turn causes the redistribution of the rock temperature field. The distribution of the temperature field and temperature drop field after 10 years of reservoir impoundment with different permeability coefficients is shown in
Figure 14. With an increase in the permeability coefficient, the temperature drop range of the bedrock surface increased, and the effect of upstream cold water infiltration bypassing the grout curtain leading to temperature drop gradually became obvious as well. Finally, it formed a large temperature drop area in front of the grouted curtain deep in the bedrock.
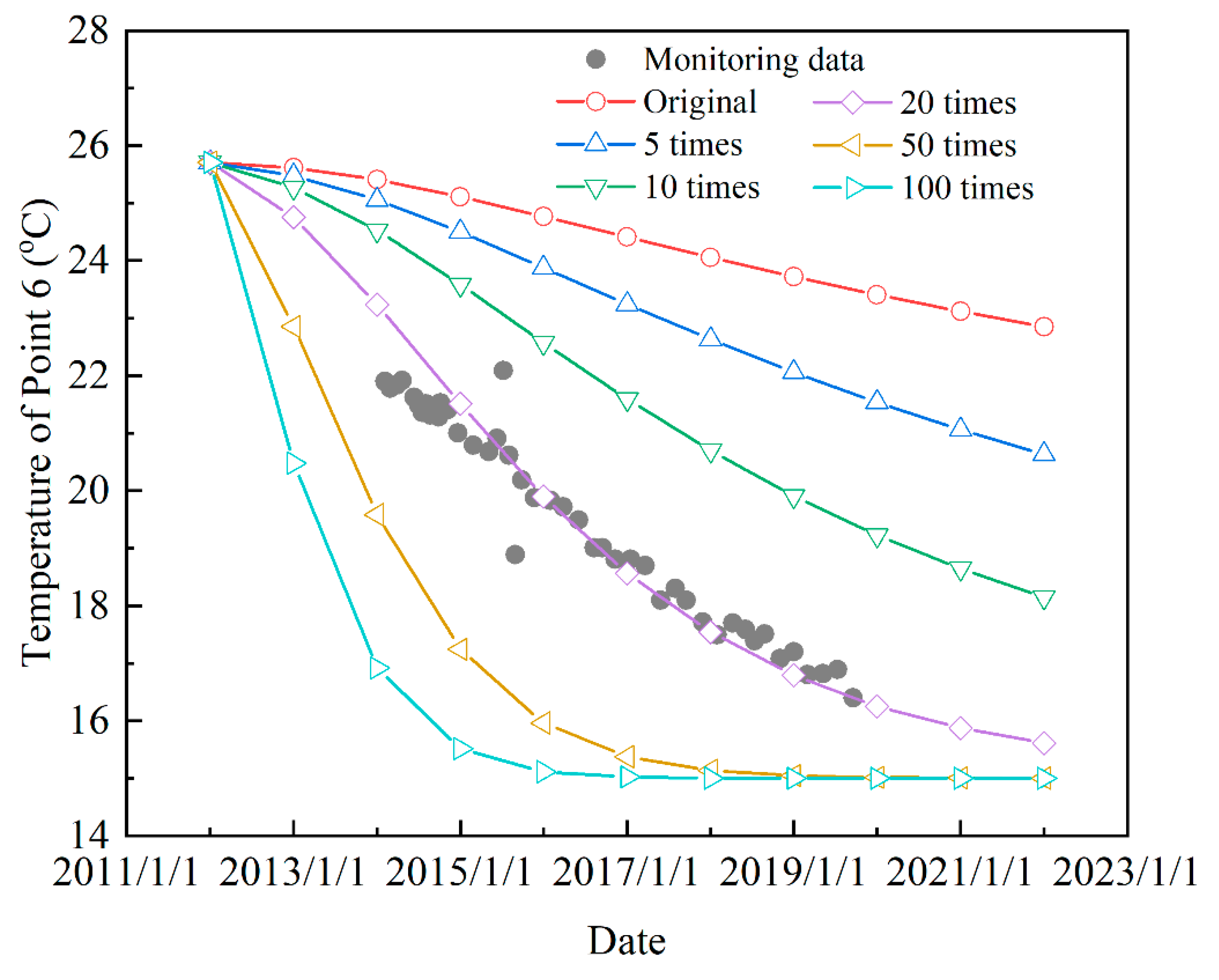
By increasing the bedrock permeability to 5 times, 10 times, 20 times, 50 times, and 100 times the initial permeability, the temperature at Point 6 (as shown in
Figure 5) in bedrock with different permeabilities varied with the water storage date, as shown in
Figure 15. When the permeability of the bedrock increased to 20 times, the calculated temperature at Point 6 agreed with the monitored value. This phenomenon indicates that the temperature distribution of the bedrock is sensitive to the permeability of the bedrock.
The bedrock temperature at different depths in front of the grouted curtain when the reservoir was impounded for 10 years is reported in
Figure 16. Without considering the fracture permeability or the Dufour flow of pore water, the temperature drop mainly occurred on the bedrock surface. The temperature drop range was about 50 m from the bedrock surface, and the maximum temperature decrement was 9 °C. With the increase in depth, the temperature decreased gradually. The temperature of the bedrock below the depth of 50 m was almost unchanged. In cases with 1 time, 5 times, 10 times, and 20 times the original permeability coefficient, the temperature decreased by 0.7 °C, 2 °C, 3.5 °C, and 6.2 °C from a depth of 100 m to 200 m, respectively. These results indicate that the increase in the permeability coefficient has a great influence on the temperature drop in the range of 50~200 m in depth during the 10 years of reservoir impoundment. It should be noted that when the permeability coefficient increased by 20 times and the depth of the bedrock increased from 100 m to 200 m, the temperature decrease range was 6.2 °C, which agrees with the real situation.
3.6. Mechanism of Temperature Drop
Based on the numerical simulations above, one can find that the mechanisms of temperature drop can be divided into short-term and long-term types. For the short-term type, the reservoir water has a cooling effect on the submerged area at the beginning of impoundment. The water and heat exchange occurs on the bedrock surface. The temperature drops significantly on the bedrock surface at the initial stage, and the temperature decrement gradually expands downward from the bedrock surface. With the development of seepage in the deep bedrock, the cooler infiltrating water bypasses the grouted curtain tip and then passes over the sedimentary rock and basalt. When the bedrock (intact basalt and limestone) has a small permeability coefficient, impoundment has a marginal effect on the deep temperature field in the initial impoundment (i.e., within 10 years of impoundment). This phenomenon corresponds to the viewpoint of surface temperature drop. For the long-term type, if the impoundment time is long enough (static state), a significant temperature drop may appear at a depth of about 200 m and a depth of 50 m in front of the grouted curtain. This phenomenon shows a temperature drop of 15 °C (
Figure 12), which corresponds to the view of a deep temperature drop after stabilization.
As mentioned above, when the permeability coefficient increased by 20 times and the depth of the bedrock increased from 100 m to 200 m, the temperature decrease range was 6.2 °C, which is far less than 15 °C (
Figure 16). Overall, the temperature field is dynamic, which is manifested as the gradual development of the temperature drop from the shallow layer of the bedrock to the deep layer after impoundment. The surface temperature drop occurs in the bedrock with limited impoundment time or low permeability. The deep temperature drop occurs when the impoundment time is long enough or the temperature field tends to be stable in bedrock with high permeability.
The consideration of a large-value temperature drop deep in the bedrock overestimates the effect of water storage on the bedrock temperature field. It should be noted that the temperature distribution of the bedrock is sensitive to the permeability of the bedrock.
4. Conclusions
The coupling interactions between the temperature and seepage fields of the bedrock in the Xiluodu arch dam were numerically studied to explain the effect of seepage development on the bedrock temperature distribution during the impoundment period. The dominant mechanism of the impoundment temperature drop was revealed. The main conclusions are as follows:
(1) The bedrock temperature field dynamically changes with the reservoir water level, which is manifested as the gradual development of the temperature drop from the shallow layer of the bedrock to the deep temperature drop. The types of bedrock temperature drops after impoundment can be divided into a short-term type and a long-term type.
(2) For the short-term type, the maximum temperature drop of 9 °C is caused by the heat exchange between the bedrock surface layer and the reservoir water during the initial impoundment. The temperature drop depth is about 50 m. The temperature of the bedrock below the depth of 50~200 m is almost unchanged.
(3) For the long-term type, the maximum temperature drop of 15 °C in front of the grouted curtain is caused by the long-term infiltration of cold water from upstream to downstream bypassing the grout curtain. When a static seepage is formed, the maximum temperature drop of 15 °C is located at a depth of 200 m in front of the grouting curtain. It takes a long time (more than 100 years) for the bedrock temperature field to reach the static state.
(4) The valley-narrowing deformation occurs mainly in the initial impoundment, which corresponds to the short-term type. The valley-narrowing deformation may be overestimated if the long-term type of bedrock temperature drop is considered. Hence, when studying the effect of bedrock temperature change caused by an impoundment on valley-narrowing deformation, the bedrock temperature field change due to impoundment should be dominated by the short-term type, and the bedrock temperature field change due to impoundment should focus on the cooling of the bedrock surface by the reservoir water.
It should be noted that the temperature distribution of the bedrock is sensitive to the permeability of the bedrock. The permeability of the bedrock is dominated by fractures. However, the distribution of real natural fractures is complex. In this paper, an equivalent porous medium assumption was used to simulate water flow in the bedrock. Further research on the model should take natural fracture into account.
Author Contributions
Conceptualization, Q.R. and L.S.; methodology, L.Z.; software, L.Z. and L.S.; validation, L.S. and L.Z.; formal analysis, M.T. and L.S.; investigation, M.T., J.G. and W.L.; resources, Q.R.; data curation, L.Z.; writing—original draft preparation, L.Z.; writing—review and editing, L.Z.; visualization, L.Z.; supervision, Q.R. and L.S; project administration, Q.R.; funding acquisition, Q.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Nature Science Foundation of China (Grant No. 51739006) and the Fundamental Research Funds for the Central Universities (Grant No. B220201030, B220204001).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are available from the corresponding author upon reasonable request.
Acknowledgments
The authors are sincerely thankful for the funding support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jiang, H.; Zhang, C.-H.; Zhou, Y.-D.; Pan, J.-W.; Wang, J.-T.; Wu, M.-X.; Fan, Q.-X. Mechanism for large-scale canyon deformations due to filling of large reservoir of hydropower project. Sci. Rep. 2020, 10, 12155. [Google Scholar] [CrossRef] [PubMed]
- Yin, T.; Li, Q.; Hu, Y.; Yu, S.; Liang, G. Coupled Thermo-Hydro-Mechanical Analysis of Valley Narrowing Deformation of High Arch Dam: A Case Study of the Xiluodu Project in China. Appl. Sci. 2020, 10, 524. [Google Scholar] [CrossRef] [Green Version]
- Tamizdoust, M.M.; Ghasemi-Fare, O. A fully coupled thermo-poro-mechanical finite element analysis to predict the thermal pressurization and thermally induced pore fluid flow in soil media. Comput. Geotech. 2020, 117, 103250. [Google Scholar] [CrossRef]
- Liu, W.; Zeng, Q.; Yao, J. Numerical simulation of elasto-plastic hydraulic fracture propagation in deep reservoir coupled with temperature field. J. Pet. Sci. Eng. 2018, 171, 115–126. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, J. Abnormal characteristics analysis of groundwater temperature field in canyon areas. Adv. Water Sci. 2003, 14, 62–66. [Google Scholar]
- Noorishad, J.; Tsang, C.; Witherspoon, P. Coupled thermal-hydraulic-mechanical phenomena in saturated fractured porous rocks: Numerical approach. J. Geophys. Res. Solid Earth 1984, 89, 10365–10373. [Google Scholar] [CrossRef] [Green Version]
- Zimmerman, R. Coupling in poroelasticity and thermoelasticity. Int. J. Rock Mech. Min. Sci. 2000, 37, 79–87. [Google Scholar] [CrossRef]
- Obeid, W.; Mounajed, G.; Alliche, A. Mathematical formulation of thermo-hygro-mechanical coupling problem in non-saturated porous media. Comput. Methods Appl. Mech. Eng. 2001, 190, 5105–5122. [Google Scholar] [CrossRef]
- Schrefler, B. Multiphase flow in deforming porous material. Int. J. Numer. Methods Eng. 2004, 60, 27–50. [Google Scholar] [CrossRef]
- Rutqvist, J.; Börgesson, L.; Chijimatsu, M.; Kobayashi, A.; Jing, L.; Nguyen, T.; Noorishad, J.; Tsang, C.-F. Thermohydromechanics of partially saturated geological media: Governing equations and formulation of four finite element models. Int. J. Rock Mech. Min. Sci. 2001, 38, 105–127. [Google Scholar] [CrossRef]
- Rutqvist, J.; Wu, Y.-S.; Tsang, C.-F.; Bodvarsson, G. A modeling approach for analysis of coupled multiphase fluid flow, heat transfer, and deformation in fractured porous rock. Int. J. Rock Mech. Min. Sci. 2002, 39, 429–442. [Google Scholar] [CrossRef]
- Zhang, G.; Cheng, H.; Zhou, Q.; Liu, Y. Analysis of mechanism of valley creep deformation of high arch dam during impoundment. China Sci. Pap. 2019, 14, 77–84. [Google Scholar]
- Xu, H.; Cui, C.; Zhang, S. Analysis on changes of limestone hydrogeological conditions before and after impoundment of Xiluodu Hydropower Station. Yangtze River 2021, 52, 65–70. [Google Scholar]
- Sun, Z.; Zhang, X.; Xu, Y.; Yao, J.; Wang, H.; Lv, S.; Sun, Z.; Huang, Y.; Cai, M.; Huang, X. Numerical simulation of the heat extraction in EGS with thermal-hydraulic-mechanical coupling method based on discrete fractures model. Energy 2017, 120, 20–33. [Google Scholar] [CrossRef]
- Guo, T.; Tang, S.; Sun, J.; Gong, F.; Liu, X.; Qu, Z.; Zhang, W. A coupled thermal-hydraulic-mechanical modeling and evaluation of geothermal extraction in the enhanced geothermal system based on analytic hierarchy process and fuzzy comprehensive evaluation. Appl. Energy 2020, 258, 113981. [Google Scholar] [CrossRef]
- Zhang, W.; Qu, Z.; Guo, T.; Wang, Z. Study of the enhanced geothermal system (EGS) heat mining from variably fractured hot dry rock under thermal stress. Renew. Energy 2019, 143, 855–871. [Google Scholar] [CrossRef]
- Zhao, Z. On the heat transfer coefficient between rock fracture walls and flowing fluid. Comput. Geotech. 2014, 59, 105–111. [Google Scholar] [CrossRef]
- Xie, Q.; Liu, Z.; Fang, X.; Chen, Y.; Li, C.; MacIntyre, S. Understanding the temperature variations and thermal structure of a subtropical deep river-run reservoir before and after impoundment. Water 2017, 9, 603. [Google Scholar] [CrossRef]
- Xie, Q.; Liu, Z.; Chen, Y.; Chen, X.; Kenneth, T. Observation and analysis of diurnal water temperature variation in Xiluodu Reservoir. Adv. Water Sci. 2018, 29, 523–536. [Google Scholar]
- Zhu, B. Thermal Stresses and Temperature Control of Mass Concrete; China Electric Power Press: Beijing, China, 1998. [Google Scholar]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).