Time-Lapse ERT, Moment Analysis, and Numerical Modeling for Estimating the Hydraulic Conductivity of Unsaturated Rock
Abstract
:1. Introduction
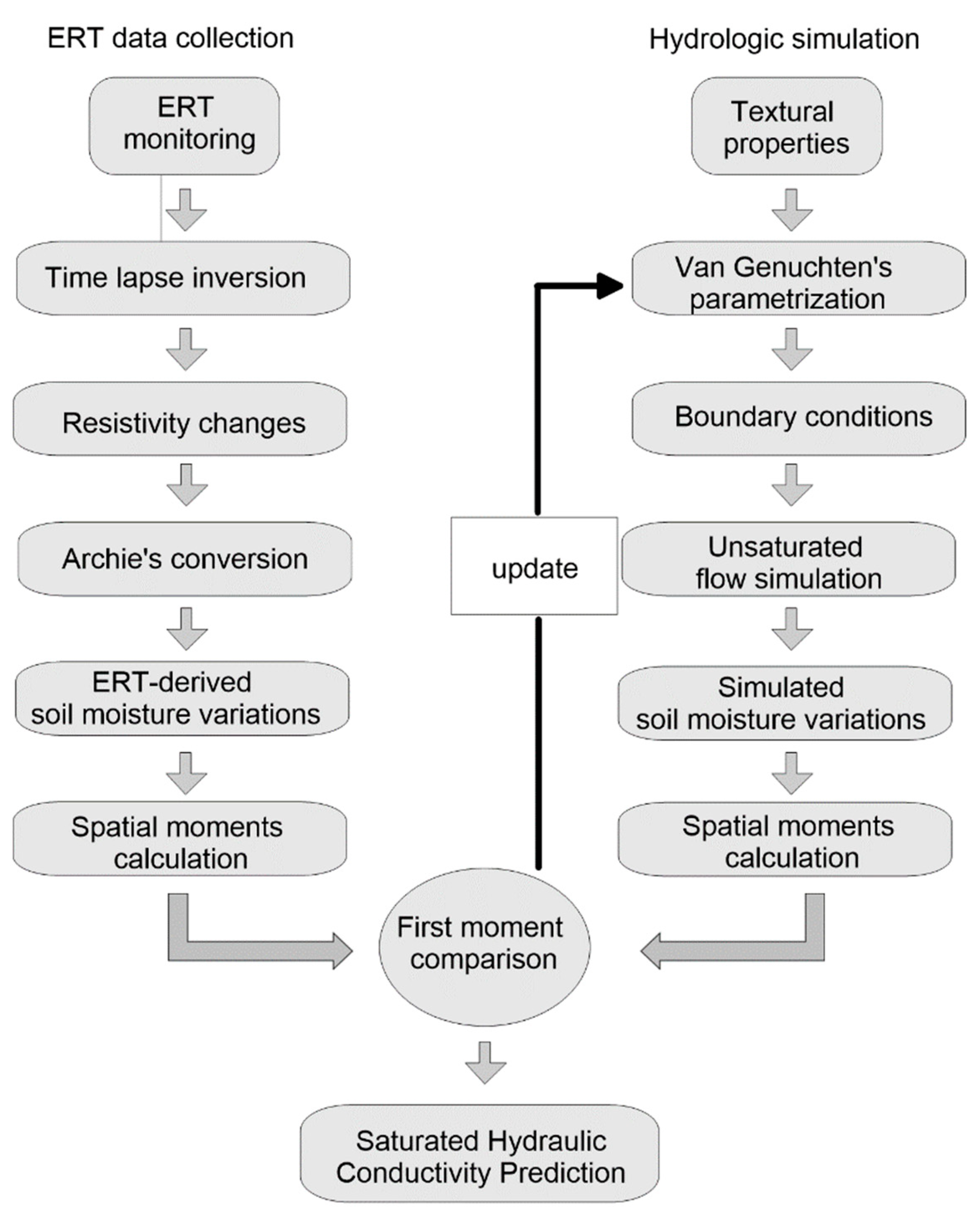
2. Materials and Methods
2.1. Properties of the Investigated Rock
2.2. The Hydrogeophysical Test
2.3. Forward Hydrological Modeling: Richards’ Equation
2.4. Moment Analysis
3. Results
3.1. ERT-Derived Water Content Outputs
3.2. Moment Analysis Derived from the ERT Dataset
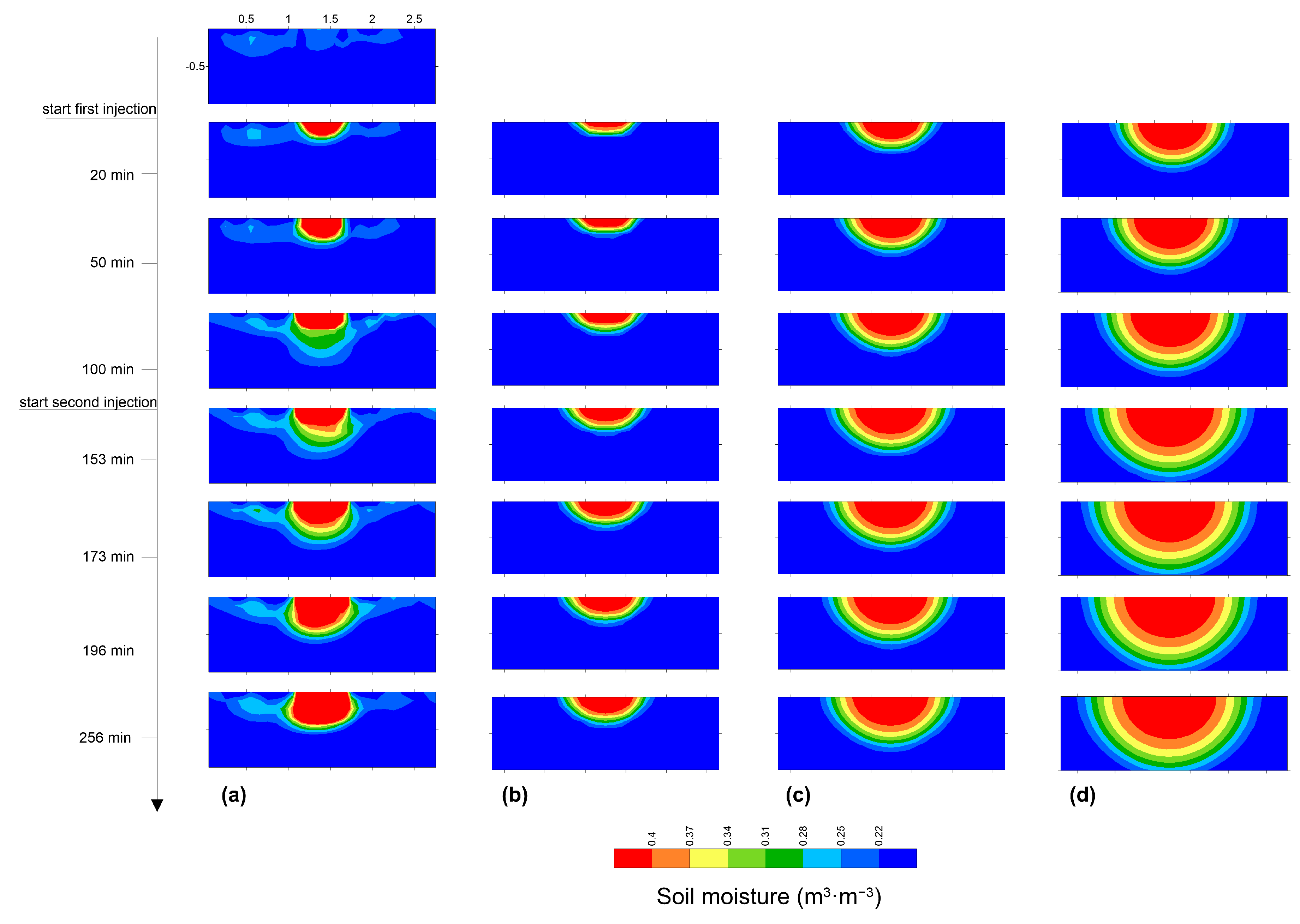
3.3. Numerical Simulations
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Richards, L.A. Capillary conduction of liquids in porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Klute, A. Laboratory measurement of hydraulic conductivity of saturated soil. In Methods of Soil Analysis: Part 1 Physical and Mineralogical Properties, Including Statistics of Measurement and Sampling; John Wiley & Sons: Hoboken, NJ, USA, 1965; Volume 9, pp. 210–221. [Google Scholar]
- Hamilton, J.M.; Daniel, D.E.; Olson, R.E. Measurement of hydraulic conductivity of partially saturated soils. In Permeability and Groundwater Contaminant Transport; Zimmie, T.F., Riggs, C.O., Eds.; American Society for Testing and Materials: Baltimore, MD, USA, 1981; pp. 182–196. [Google Scholar]
- Nimmo, J.R.; Schmidt, K.M.; Perkins, K.S.; Stock, J.D. Rapid Measurement of Field-Saturated Hydraulic Conductivity for Areal Characterization. Vadose Zone J. 2009, 8, 142–149. [Google Scholar] [CrossRef]
- Angulo-Jaramillo, R.; Vandervaere, J.P.; Roulier, S.; Thony, J.L.; Gaudet, J.P.; Vauclin, M. Field measurement of soil surface hydraulic properties by disc and ring infiltrometers: A review and recent developments. Soil Tillage Res. 2000, 55, 1–29. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Elrick, D.E.; Youngs, E.G.; Amoozegar, A.; Booltink, H.W.G.; Bouma, J. Saturated and field-saturated water flow parameters. In Methods of Soil Analysis. Part 4. Physical Methods; Dane, J.H., Topp, G.C., Eds.; Wiley SSSA: Madison, WI, USA, 2002; pp. 797–878. [Google Scholar]
- Bouwer, H. Rapid field measurement of air entry value and hydraulic conductivity of soil as significant parameters in flow system analysis. Water Resour. Res. 1966, 2, 729–738. [Google Scholar] [CrossRef]
- Youngs, E.G. Estimating hydraulic conductivity values from ring infiltrometer measurements. J. Soil Sci. 1987, 38, 623–632. [Google Scholar] [CrossRef]
- Bogena, H.R.; Huisman, J.A.; Oberdosrster, C.A.; Vereecken, H. Evaluation of a Low-Cost Soil Water Content Sensor for Wireless Network Application. J. Hydrol. 2007, 344, 32–42. [Google Scholar] [CrossRef]
- Kizito, F.; Campbell, C.G.; Cobos, D.R.; Teare, B.L.; Carter, B.; Hopmans, J.W. Frequency, Electrical Conductivity and Temperature Analysis of a Low-Cost Capacitance Soil Moisture Sensor. J. Hydrol. 2008, 352, 367–378. [Google Scholar] [CrossRef]
- Caputo, M.C.; De Carlo, L. Field measurement of hydraulic conductivity of rocks. In Hydraulic Conductivity—Issues, Determination and Applications; Elango, L., Ed.; Intech Open: London, UK, 2011; pp. 285–306. [Google Scholar] [CrossRef]
- Caputo, M.C.; De Carlo, L.; Masciopinto, C.; Nimmo, J.R. Measurement of field-saturated hydraulic conductivity on fractured rock outcrops near Altamura (Southern Italy) with an adjustable large ring infiltrometer. Environ. Earth Sci. 2010, 60, 583–590. [Google Scholar] [CrossRef]
- Masciopinto, C.; Liso, S.I.; Caputo, M.C.; De Carlo, L. An Integrated Approach Based on Numerical Modelling and Geophysical Survey to Map Groundwater Salinity in Fractured Coastal Aquifers. Water 2017, 9, 875. [Google Scholar] [CrossRef]
- Furman, A.; Ferré, T.P.A.; Warrick, A.W. Optimization of ERT Surveys for Monitoring Transient Hydrological Events Using Perturbation Sensitivity and Genetic Algorithms. Vadose Zone J. 2004, 3, 1230–1239. [Google Scholar] [CrossRef]
- Perri, M.T.; De Vita, R.; Masciale, R.; Portoghese, I.; Chirico, G.B.; Cassiani, G. Time-lapse Mise-à-la-Masse measurements and modelling for tracer test monitoring in a shallow aquifer. J. Hydrol. 2018, 561, 461–477. [Google Scholar] [CrossRef]
- Daily, W.; Ramirez, A.; LaBrecque, D.; Nitao, J. Electrical resistivity tomography of vadose water movement. Water Resour. Res. 1992, 28, 1429–1444. [Google Scholar] [CrossRef]
- Garré, S.; Hyndman, D.; Mary, B.; Werban, U. Geophysics conquering new territories: The rise of “agrogeophysics”. Vadose Zone J. 2021, 20, e20115. [Google Scholar] [CrossRef]
- De Carlo, L.; Battilani, A.; Solimando, D.; Caputo, M.C. Application of time-lapse ERT to determine the impact of using brackish wastewater for maize irrigation. J. Hydrol. 2019, 582, 124465. [Google Scholar] [CrossRef]
- Camporese, M.; Cassiani, G.; Deiana, R.; Salandin, P. Assessment of local hydraulic properties from electrical resistivity tomography monitoring of a three-dimensional synthetic tracer test experiment. Water Resour. Res. 2011, 47, W12508. [Google Scholar] [CrossRef]
- Binley, A.; Kemna, A. DC resistivity and induced polarization methods. In Hydrogeophysics; Rubin, Y., Hubbard, S.S., Eds.; Springer: Dordrecht, The Netherlands, 2005; Volume 50, pp. 129–156. [Google Scholar]
- De Carlo, L.; Berardi, M.; Vurro, M.; Caputo, M.C. Geophysical and hydrological data assimilation to monitor water content dynamics in the rocky unsaturated zone. Environ. Monit. Assess. 2018, 190, 310. [Google Scholar] [CrossRef]
- Camporese, M.; Cassiani, G.; Deiana, R.; Salandin, P.; Binley, A. Coupled and uncoupled hydrogeophysical inversions using ensemble Kalman filter assimilation of ERT-monitored tracer test data. Water Resour. Res. 2015, 51, 3277–3291. [Google Scholar] [CrossRef]
- Ferrè, T.P.A.; Bentley, L.; Binley, A.; Linde, N.; Kemna, A.; Singha, K.; Holliger, K.; Huisman, J.A.; Minsley, B. Critical steps for the continuing advancement of hydrogeophysics. Eos 2009, 90, 200. [Google Scholar] [CrossRef] [Green Version]
- Mboh, C.; Huisman, J.; Gaelen, N.; Rings, J.; Vereecken, H. Coupled hydrogeophysical inversion of electrical resistances and inflow measurements for topsoil hydraulic properties under constant head infiltration. Near Surf. Geophys. 2012, 10, 413–426. [Google Scholar] [CrossRef]
- Rossi, M.; Manoli, G.; Pasetto, D.; Deiana, R.; Ferraris, S.; Strobbia, C.; Putti, M.; Cassiani, G. Coupled inverse modeling of a controlled irrigation experiment using multiple hydro-geophysical data. Adv. Water Resour. 2015, 82, 150–165. [Google Scholar] [CrossRef]
- Camporese, M.; Paniconi, C.; Putti, M.; Salandin, P. Comparison of data assimilation techniques for a coupled model of surface and subsurface flow. Vadose Zone J. 2009, 8, 837–845. [Google Scholar] [CrossRef] [Green Version]
- Kitanidis, P.K. Prediction by the method of moments of transport in a heterogeneous formation. J. Hydrol. 1988, 102, 453–473. [Google Scholar] [CrossRef]
- Govindaraju, R.S.; Das, B.S. Moment Analysis for Subsurface Hydrologic Applications; Springer: Dordrecht, The Netherlands, 2007; p. 296. [Google Scholar] [CrossRef]
- Ye, M.; Khaleel, R.; Yeh, T.-C.J. Stochastic analysis of moisture plume dynamics of a field injection experiment. Water Resour. Res. 2005, 41, W03013. [Google Scholar] [CrossRef] [Green Version]
- Farzamian, M.; Monteiro Santos, F.A.; Khalil, M.A. Estimation of unsaturated hydraulic parameters in sandstone using electrical resistivity tomography under a water injection test. J. Appl. Geophys. 2015, 121, 71–83. [Google Scholar] [CrossRef]
- Singha, K.; Gorelick, S.M. Saline tracer visualized with three-dimensional electrical resistivity tomography: Field-scale spatial moment analysis. Water Resour. Res. 2005, 41, W05023. [Google Scholar] [CrossRef]
- Caputo, M.C.; Nimmo, J. Quasi-steady centrifuge method of unsaturated hydraulic properties. Water Resour. Res. 2005, 41, W11504. [Google Scholar] [CrossRef] [Green Version]
- Turturro, A.C.; Caputo, M.C.; Perkins, K.S.; Nimmo, J.R. Does the Darcy-Buckingham Law Apply to Flow Through Unsaturated Porous Rock? Water 2020, 12, 2668. [Google Scholar] [CrossRef]
- Turturro, A.C.; Caputo, M.C.; Gerke, H.H. Mercury Intrusion Porosimetry and Centrifuge Methods for Extended-Range Retention Curves of Soil and Porous Rock Samples. Vadose Zone J. 2021, 21, e20176. [Google Scholar] [CrossRef]
- Caputo, M.C.; De Carlo, L.; Turturro, A.C. HYPROP FIT to Model Rock Water Retention Curves Estimated by Different Methods. Water 2022, 14, 3443. [Google Scholar] [CrossRef]
- Andriani, G.F.; Pastore, N.; Giasi, C.I.; Parise, M. Hydraulic properties of unsaturated calcarenites by means of a new integrated approach. J. Hydrol. 2021, 602, 126730. [Google Scholar] [CrossRef]
- Lappala, E.G.; Healy, R.W.; Weeks, E.P. Documentation of Computer Program VS2D to Solve the Equations of Fluid Flow in Variably Saturated Porous Media; Water Resources Investigations Report 83-4099; USGS: Denver, CO, USA, 1987; p. 193.
- Hsieh, P.A.; Wingle, W.; Healy, R.W. VS2DI—A Graphical Software Package for Simulating Fluid Flow and Solute or Energy Transport in Variably Saturated Porous Media; Water-Resources Investigations Report 99-4130; USGS: Lakewood, CO, USA, 2000; p. 20.
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Rivett, M.O.; Wealthall, G.P.; Dearden, R.A.; McAlary, T.A. Review of unsaturated-zone transport and attenuation of volatile organic compound (VOC) plumes leached from shallow source zones. J. Contam. Hydrol. 2011, 123, 130–156. [Google Scholar] [CrossRef] [PubMed]
- Troldborg, M.; Binning, P.; Nielsen, S.; Kjeldsen, P.; Christensen, A. Unsaturated zone leaching models for assessing risk to groundwater of contaminated sites. J. Contam. Hydrol. 2009, 105, 28–37. [Google Scholar] [CrossRef]
- Jacques, D.; Šimůnek, J.; Mallants, D.; van Genuchten, M.T. Modelling coupled water flow, solute transport and geochemical reactions affecting heavy metal migration in a podzol soil. Geoderma 2008, 145, 449–461. [Google Scholar] [CrossRef]
- Shentu, J.; Li, X.; Han, R.; Chen, Q.; Shen, D.; Qi, S. Effect of site hydrological conditions and soil aggregate sizes on the stabilization of heavy metals (Cu, Ni, Pb, Zn) by biochar. Sci. Total Environ. 2022, 802, 149949. [Google Scholar] [CrossRef] [PubMed]
- Motz, E.C.; Cey, E.; Ryan, M.C. Vadose Zone Microbial Transport Below At-Grade Distribution of Wastewater Effluent. Water Air Soil Pollut. 2012, 223, 771–785. [Google Scholar] [CrossRef]
- Sousa, M.R.; Jones, J.P.; Frind, E.O.; Rudolph, D.L. A simple method to assess unsaturated zone time lag in the travel time from ground surface to receptor. J. Contam. Hydrol. 2013, 144, 138–151. [Google Scholar] [CrossRef]
- Jeong, J.; Park, E.; Han, W.S.; Kim, K.Y.; Oh, J.; Ha, K.; Yoon, H.; Yun, S.T. A method of estimating sequential average unsaturated zone travel times from precipitation and water table level time series data. J. Hydrol. 2017, 554, 570–581. [Google Scholar] [CrossRef]
- Dahan, O. Vadose Zone Monitoring as a Key to Groundwater Protection. Front. Water 2020, 2, 599569. [Google Scholar] [CrossRef]
- Day-Lewis, F.D.; Singha, K.; Binley, A.M. Applying petrophysical models to radar travel time and electrical resistivity tomograms: Resolution-dependent limitations. J. Geophys. Res. 2005, 110, B08206. [Google Scholar] [CrossRef] [Green Version]
- Cassiani, G.; Ursino, N.; Deiana, R.; Vignoli, G.; Boaga, J.; Rossi, M.; Perri, M.T.; Blaschek, M.; Duttmann, R.; Meyer, S.; et al. Noninvasive monitoring of soil static characteristics and dynamic states: A case study highlighting vegetation effects on agricultural land. Vadose Zone J. 2012, 11, vzj2011.0195. [Google Scholar] [CrossRef] [Green Version]
- Farzamian, M.; Autovino, D.; Basile, A.; De Mascellis, R.; Dragonetti, G.; Monteiro Santos, F.; Binley, A.M.; Coppola, A. Assessing the dynamics of soil salinity with time-lapse inversion of electromagnetic data guided by hydrological modelling. Hydrol. Earth Syst. Sci. 2021, 25, 1509–1527. [Google Scholar] [CrossRef]
- Looms, M.C.; Jensen, K.H.; Binley, A.M.; Nielsen, L. Monitoring unsaturated flow and transport using cross-borehole geophysical methods. Vadose Zone J. 2008, 8, 227–237. [Google Scholar] [CrossRef] [Green Version]
- Dragonetti, G.; Farzamian, M.; Coppola, A.; Basile, A.; Monteiro Santos, F. In-situ estimation of soil hydraulic and hydrodispersive properties by inversion of Electromagnetic Induction measurements and soil hydrological modeling. Hydrol. Earth Syst. Sci. 2022, 26, 5119–5136. [Google Scholar] [CrossRef]
- Binley, A.M.; Hubbard, S.S.; Huisman, J.A.; Revil, A.; Robinson, D.A.; Singha, K.; Slater, L.D. The emergence of hydrogeophysics for improved understanding of subsurface processes over multiple scales. Water Resour. Res. 2015, 51, 3837–3866. [Google Scholar] [CrossRef]

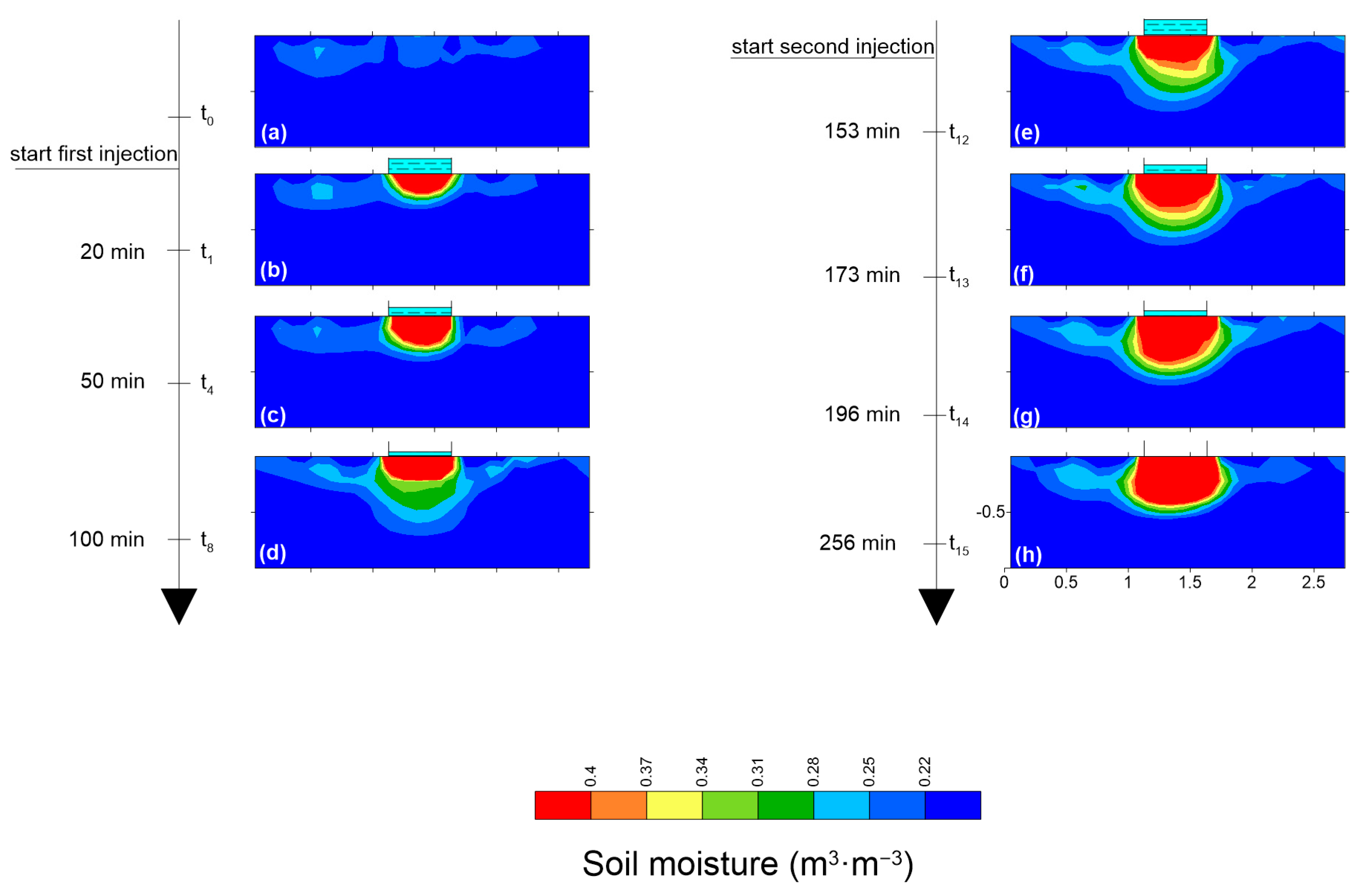
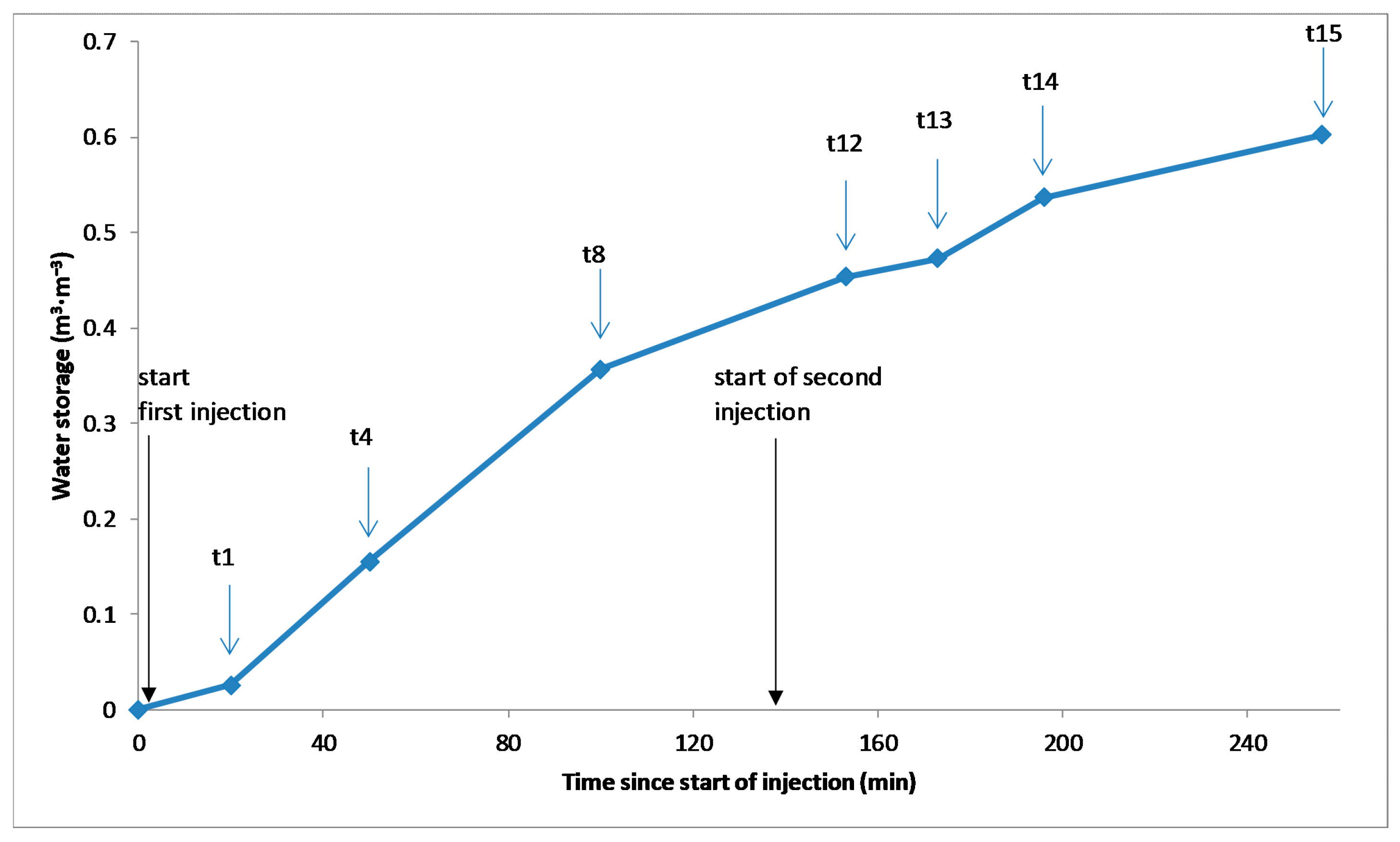

| Infiltration Test | Time Point (hh:mm) | Hydraulic Head (cm) | ERT Observation |
|---|---|---|---|
| 11:20 | t0 | ||
| Start first injection | 11:43 | 3.1 | |
| 12:03 | 2.0 | t1 | |
| 12:33 | 1.0 | t4 | |
| Stop infiltration measurements | 12:43 | 0.8 | |
| 13:23 | t8 | ||
| Start second injection | 14:01 | 3.3 | |
| 14:16 | 2.5 | t12 | |
| 14:36 | 2.1 | t13 | |
| 14:59 | 1.6 | t14 | |
| Stop infiltration measurements | 15:09 | 1.3 | |
| 15:59 | 0.2 | t15 |
| Parameter | Scenario A | Scenario B | Scenario C | Scenario D | Scenario E |
|---|---|---|---|---|---|
| Saturated Khh (cm·min−1) | 0.1 | 0.25 | 0.35 | 0.75 | 1 |
| Khh/Kzz | 1 | ||||
| Specific storage, Ss (m−1) | 1.6 × 10−4 | ||||
| Effective porosity, φ | 0.45 | ||||
| θ, initial moisture content (m3·m−3) | 0.22 | ||||
| θr, residual moisture content (m3·m−3) | 0.02547 | ||||
| α (cm−1) | 0.07721 | ||||
| n | 1.7541 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Carlo, L.; Farzamian, M.; Turturro, A.C.; Caputo, M.C. Time-Lapse ERT, Moment Analysis, and Numerical Modeling for Estimating the Hydraulic Conductivity of Unsaturated Rock. Water 2023, 15, 332. https://doi.org/10.3390/w15020332
De Carlo L, Farzamian M, Turturro AC, Caputo MC. Time-Lapse ERT, Moment Analysis, and Numerical Modeling for Estimating the Hydraulic Conductivity of Unsaturated Rock. Water. 2023; 15(2):332. https://doi.org/10.3390/w15020332
Chicago/Turabian StyleDe Carlo, Lorenzo, Mohammad Farzamian, Antonietta Celeste Turturro, and Maria Clementina Caputo. 2023. "Time-Lapse ERT, Moment Analysis, and Numerical Modeling for Estimating the Hydraulic Conductivity of Unsaturated Rock" Water 15, no. 2: 332. https://doi.org/10.3390/w15020332
APA StyleDe Carlo, L., Farzamian, M., Turturro, A. C., & Caputo, M. C. (2023). Time-Lapse ERT, Moment Analysis, and Numerical Modeling for Estimating the Hydraulic Conductivity of Unsaturated Rock. Water, 15(2), 332. https://doi.org/10.3390/w15020332









