An Investigation on the Effect of Leakages on the Water Quality Parameters in Distribution Networks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Leakage Mathematical Modeling
2.2. Simulation Process
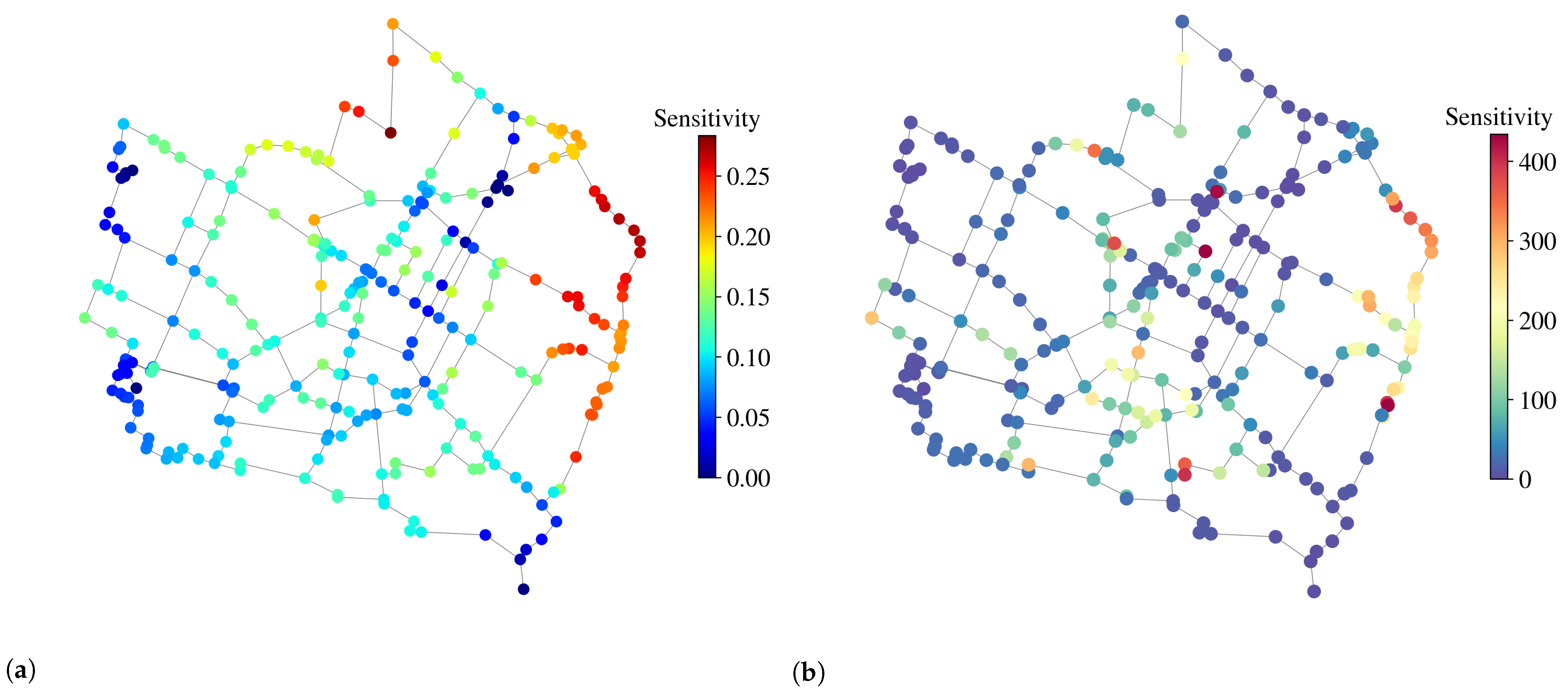
2.3. Nodes’ Sensitivity to Leakage
2.4. Graph Theory and Shortest Path
2.5. Evaluation Method
3. Case Study
4. Results
4.1. Sensitivity Analysis
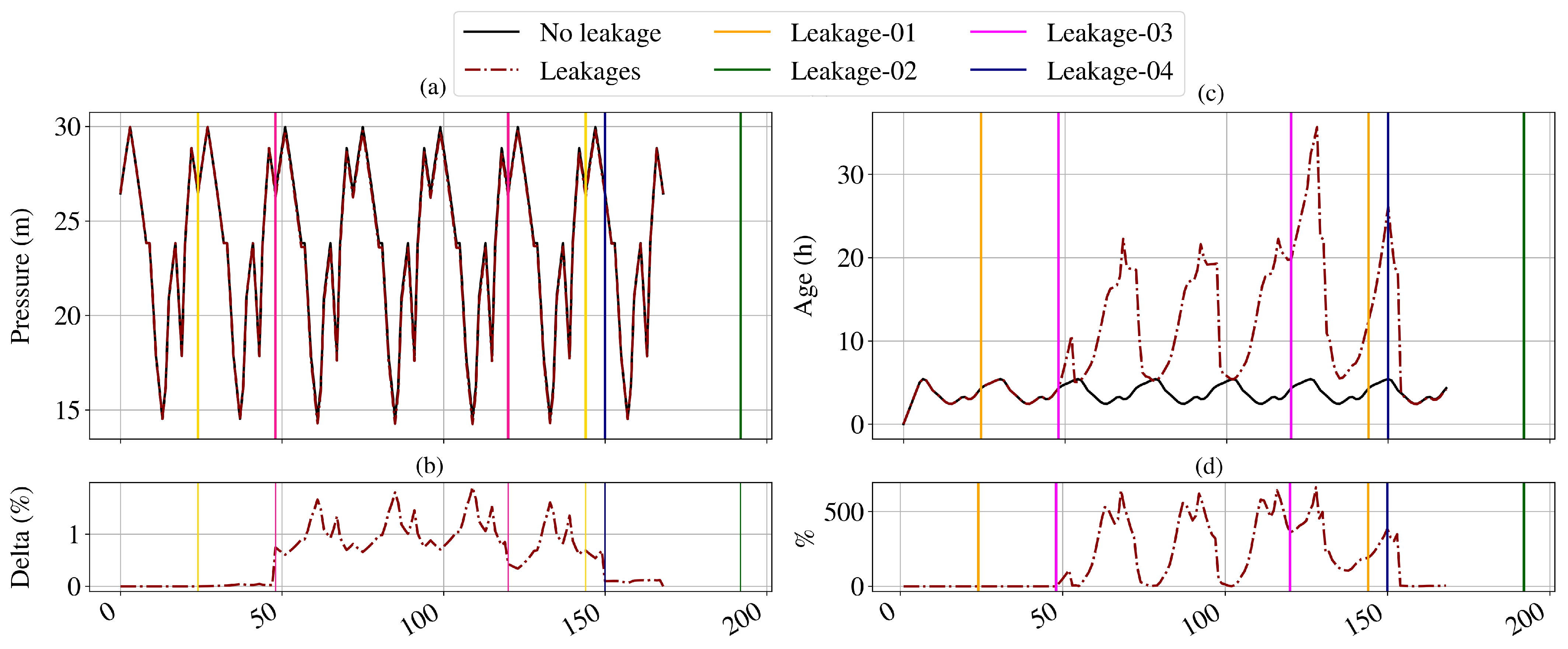
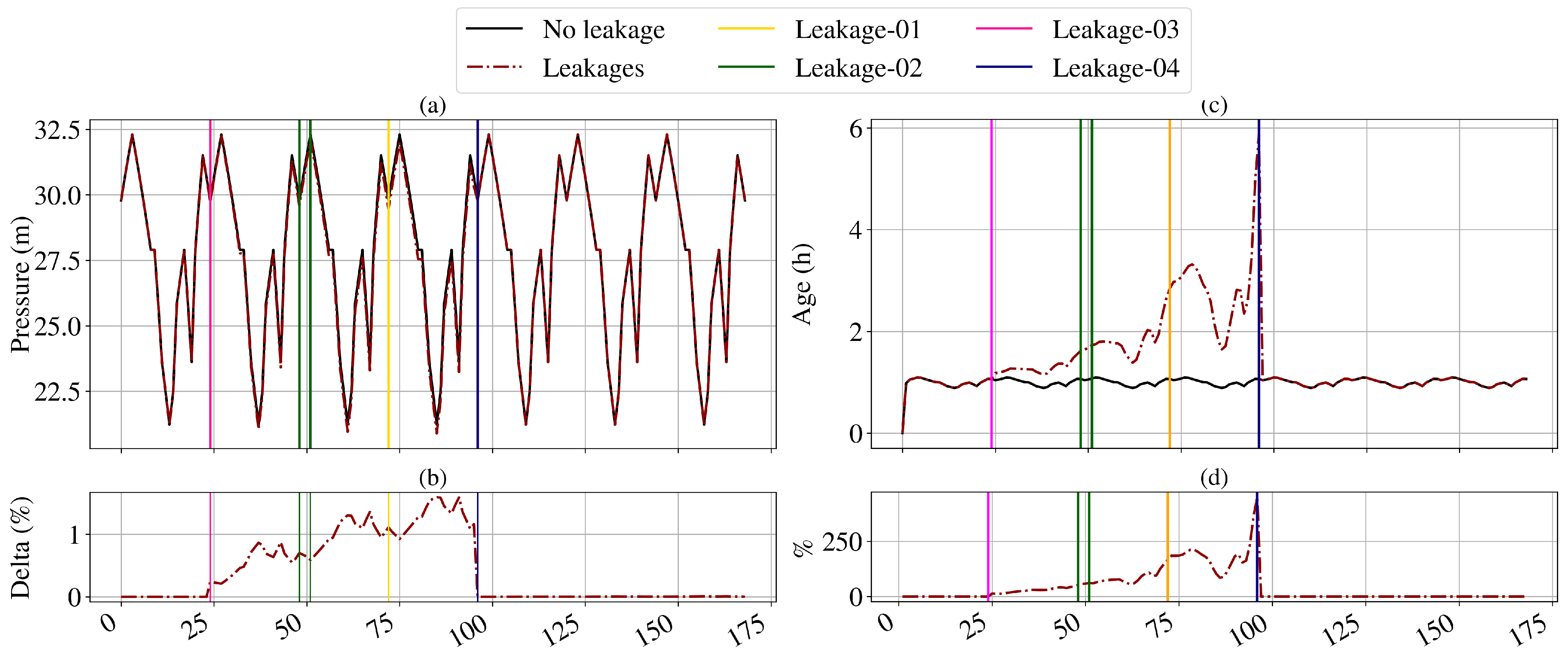
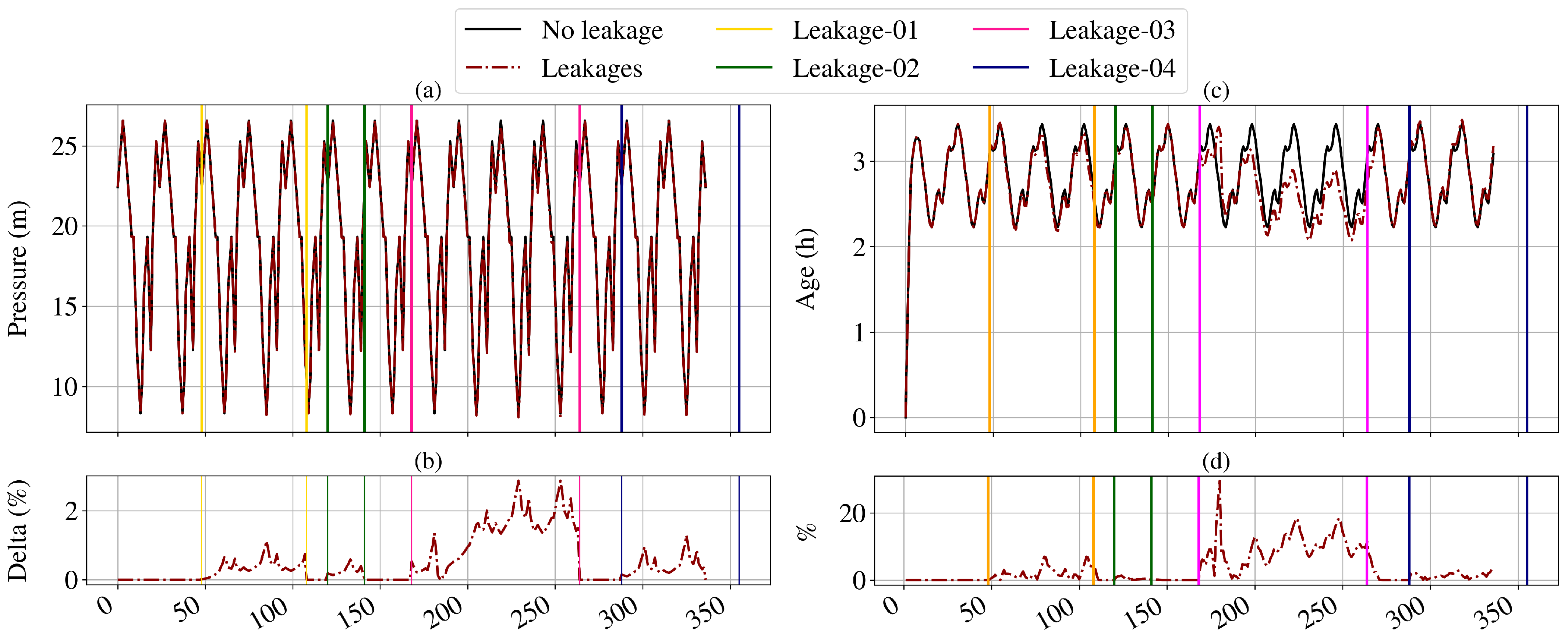
4.2. Pressure and Quality
4.2.1. Chlorine Simulations
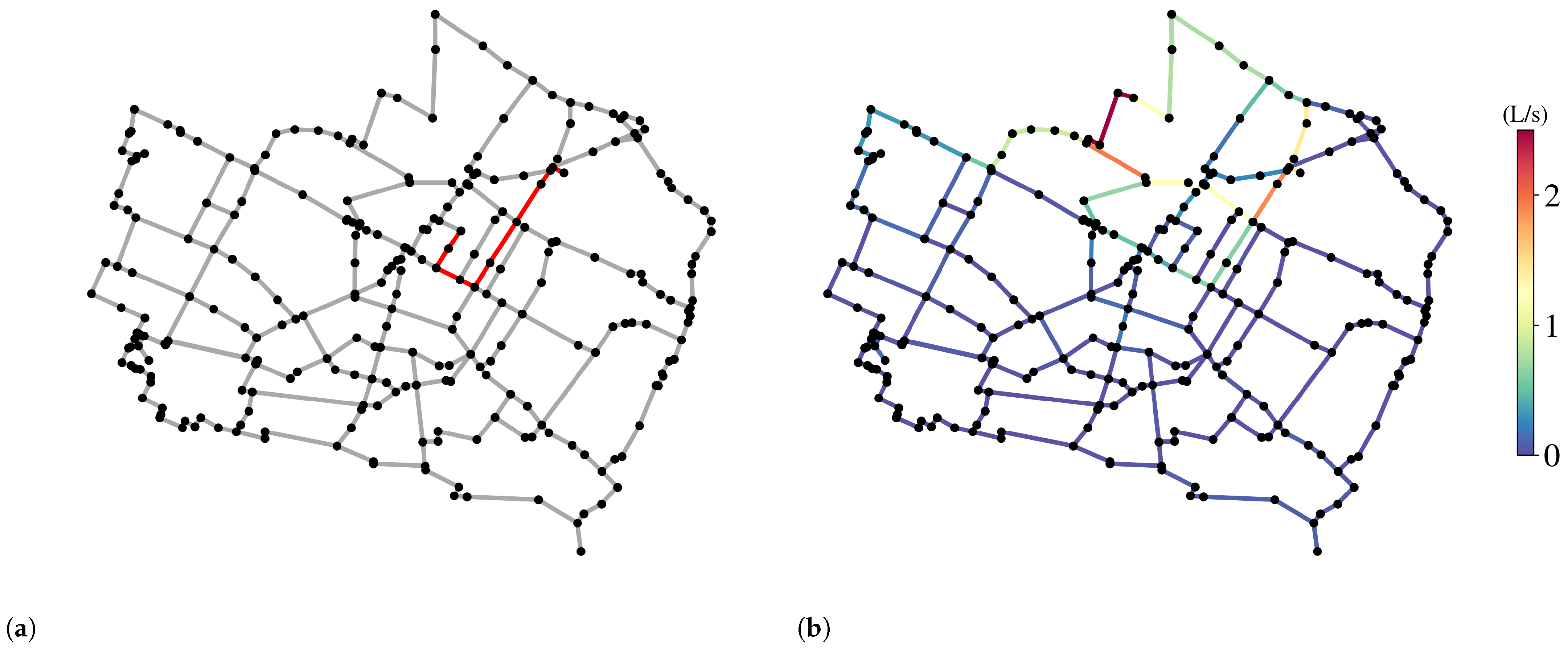
4.2.2. Shortest Path and Flow Changes
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marinho, C.d.S.R.; Flor, T.B.M.; Pinheiro, J.M.F.; Ferreira, M.Â.F. Objetivos de Desenvolvimento do Milênio: Impacto de ações assistenciais e mudanças socioeconômicas e sanitárias na mortalidade de crianças. Cad. Saúde Pública 2020, 36. [Google Scholar] [CrossRef] [PubMed]
- Hunter, P.R.; MacDonald, A.M.; Carter, R.C. Water supply and health. PloS Med. 2010, 7, e1000361. [Google Scholar] [CrossRef] [Green Version]
- Howard, G.; Bartram, J.; Water, S.; World Health Organization. Domestic Water Quantity, Service Level and Health; World Health Organization: Geneva, Swtitzerland, 2003. [Google Scholar]
- Brasil, G. O Brasil e os ODM—ODM Brasil. 2013. Available online: http://www.odmbrasil.gov.br/o-brasil-e-os-odm (accessed on 26 October 2022).
- WHO. Joint Monitoring Programme for Water Supply and Sanitation: Report on Intercountry Workshop, Jakarta, Indonesia, 27–29 April 2009; Technical Report; WHO Regional Office for South-East Asia: New Delhi, India, 2010. [Google Scholar]
- Rebouças, A.C. Água no Brasil: Abundância, desperdício e escassez. Bahia Análise Dados 2003, 13, 341–345. [Google Scholar]
- BRASIL, T. Desafios para Disponibilidade Hídrica e Avanço da Eficiência do Saneamento Básico, 2019. Acesso Em 2020, 22, 341–345. [Google Scholar]
- Goulet, J.A.; Coutu, S.; Smith, I.F. Model falsification diagnosis and sensor placement for leak detection in pressurized pipe networks. Adv. Eng. Inform. 2013, 27, 261–269. [Google Scholar] [CrossRef] [Green Version]
- Aslam, H.; Kaur, M.; Sasi, S.; Mortula, M.M.; Yehia, S.; Ali, T. Detection of leaks in water distribution system using non-destructive techniques. In Proceedings of the IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2018; Volume 150, p. 012004. [Google Scholar]
- Khan, M.; Nobahar, M.; Stanley, P.; Ivoke, J. Investigation of Underground Water Leakage Using Ground Penetration Radar 447 (GPR). In International Foundations Congress and Equipment Expo, Dallas; American Society of Civil Engineers: Reston, VA, USA, 2021; pp. 10–20. [Google Scholar]
- Khulief, Y.; Khalifa, A.; Mansour, R.B.; Habib, M. Acoustic detection of leaks in water pipelines using measurements inside pipe. J. Pipeline Syst. Eng. Pract. 2012, 3, 47–54. [Google Scholar] [CrossRef]
- Abdulshaheed, A.; Mustapha, F.; Ghavamian, A. A pressure-based method for monitoring leaks in a pipe distribution system: A Review. Renew. Sustain. Energy Rev. 2017, 69, 902–911. [Google Scholar] [CrossRef]
- Sadeghioon, A.M.; Metje, N.; Chapman, D.; Anthony, C. Water pipeline failure detection using distributed relative pressure and temperature measurements and anomaly detection algorithms. Urban Water J. 2018, 15, 287–295. [Google Scholar] [CrossRef] [Green Version]
- Capponi, C.; Ferrante, M.; Zecchin, A.C.; Gong, J. Leak detection in a branched system by inverse transient analysis with the admittance matrix method. Water Resour. Manag. 2017, 31, 4075–4089. [Google Scholar] [CrossRef] [Green Version]
- Diao, X.; Shen, G.; Jiang, J.; Chen, Q.; Wang, Z.; Ni, L.; Mebarki, A.; Dou, Z. Leak detection and location in liquid pipelines by analyzing the first transient pressure wave with unsteady friction. J. Loss Prev. Process. Ind. 2019, 60, 303–310. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S. A review of data-driven approaches for burst detection in water distribution systems. Urban Water J. 2017, 14, 972–983. [Google Scholar] [CrossRef]
- Zanfei, A.; Menapace, A.; Brentan, B.M.; Righetti, M.; Herrera, M. Novel approach for burst detection in water distribution systems based on graph neural networks. Sustain. Cities Soc. 2022, 86, 104090. [Google Scholar] [CrossRef]
- Jung, D.; Lansey, K. Water distribution system burst detection using a nonlinear Kalman filter. J. Water Resour. Plan. Manag. 2015, 141, 04014070. [Google Scholar] [CrossRef]
- Xu, T.; Zeng, Z.; Huang, X.; Li, J.; Feng, H. Pipeline leak detection based on variational mode decomposition and support vector machine using an interior spherical detector. Process. Saf. Environ. Prot. 2021, 153, 167–177. [Google Scholar] [CrossRef]
- Romano, M.; Kapelan, Z.; Savić, D.A. Automated detection of pipe bursts and other events in water distribution systems. J. Water Resour. Plan. Manag. 2014, 140, 457–467. [Google Scholar] [CrossRef] [Green Version]
- Pereira, T.; Barros, D.; Meirelles, G.; Brentan, B. Real-time leak detection from signal filtering via independent component analysis. Xxiv SimpóSio Bras. Recur. Hídrico 2021, 1. [Google Scholar]
- Smith, A.H.; Lingas, E.O.; Rahman, M. Contamination of drinking-water by arsenic in Bangladesh: A public health emergency. Bull. World Health Organ. 2000, 78, 1093–1103. [Google Scholar]
- Fox, S.; Shepherd, W.; Collins, R.; Boxall, J. Experimental quantification of contaminant ingress into a buried leaking pipe during transient events. J. Hydraul. Eng. 2016, 142, 04015036. [Google Scholar] [CrossRef]
- Collins, R.; Boxall, J. Influence of ground conditions on intrusion flows through apertures in distribution pipes. J. Hydraul. Eng. 2013, 139, 1052–1061. [Google Scholar] [CrossRef]
- Arad, J.; Housh, M.; Perelman, L.; Ostfeld, A. A dynamic thresholds scheme for contaminant event detection in water distribution systems. Water Res. 2013, 47, 1899–1908. [Google Scholar] [CrossRef]
- Perelman, L.; Arad, J.; Housh, M.; Ostfeld, A. Event detection in water distribution systems from multivariate water quality time series. Environ. Sci. Technol. 2012, 46, 8212–8219. [Google Scholar] [CrossRef]
- Kumar, J.; Sreepathi, S.; Brill, E.D.; Ranjithan, R.; Mahinthakumar, G. Detection of leaks in water distribution system using routine water quality measurements. In Proceedings of the World Environmental and Water Resources Congress 2010: Challenges of Change, Providence, RI, USA, 16–20 May 2010; pp. 4185–4192. [Google Scholar]
- Klise, K.A.; Murray, R.; Haxton, T. An Overview of the Water Network Tool for Resilience (WNTR). In Proceedings of the 1st International WDSA / CCWI 2018 Joint Conference, Kingston, ON, Canada, 23–25 July 2018. [Google Scholar]
- Rossman, L.A. EPANET 2: Users Manual; Nations Risk Management Research Laboratory Office of Research and Development: Cincinnati, OH, USA, 2000; Volume 486, pp. 1–200.
- Klise, K.A.; Hart, D.; Moriarty, D.M.; Bynum, M.L.; Murray, R.; Burkhardt, J.; Haxton, T. Water Network Tool for Resilience (WNTR) User Manual; Technical Report; Sandia National Lab.(SNL-NM): Albuquerque, NM, USA, 2017. [Google Scholar]
- Seyoum, A.G.; Tanyimboh, T.T. Integration of hydraulic and water quality modelling in distribution networks: EPANET-PMX. Water Resour. Manag. 2017, 31, 4485–4503. [Google Scholar] [CrossRef] [Green Version]
- Zanfei, A.; Brentan, B.M.; Menapace, A.; Righetti, M.; Herrera, M. Graph convolutional recurrent neural networks for water demand forecasting. Water Resour. Res. 2022, 58, e2022WR032299. [Google Scholar] [CrossRef]
- Bezerra, D.; Souza, R.; Meirelles, G.; Brentan, B. Leak detection in water distribution networks based on graph signal processing of pressure data. Int. Jt. Conf. Water Distrib. Syst. Anal. 2022, 86, 14073. [Google Scholar]
- Hagberg, A.; Swart, P.; S Chult, D. Exploring Network Structure, Dynamics, and Function Using NetworkX; Technical Report; Los Alamos National Lab.(LANL): Los Alamos, NM, USA, 2008. [Google Scholar]
- Mao, G.; Zhang, N. Analysis of average shortest-path length of scale-free network. J. Appl. Math. 2013, 2013, 865643. [Google Scholar] [CrossRef]
- Bragalli, C.; D’Ambrosio, C.; Lee, J.; Lodi, A.; Toth, P. On the optimal design of water distribution networks: A practical MINLP approach. Optim. Eng. 2012, 13, 219–246. [Google Scholar] [CrossRef]
- Bezerra, D.; Giaducianni, C.; Herrera, M.; Di Nardo, A.; Brentan, B. Pressure Sensors Placement for Leakage Detection Using Graph Signal Processing and Sampling Theory. In Proceedings of the 39th IAHR World Congress, Granada, Spain, 19–24 June 2022. [Google Scholar]
- Lenzi, C.; Bragalli, C.; Bolognesi, A.; Artina, S. From energy balance to energy efficiency indicators including water losses. Water Sci. Technol. Water Supply 2013, 13, 889–895. [Google Scholar] [CrossRef]
- Quiñones-Grueiro, M.; Milián, M.A.; Rivero, M.S.; Neto, A.J.S.; Llanes-Santiago, O. Robust leak localization in water distribution networks using computational intelligence. Neurocomputing 2021, 438, 195–208. [Google Scholar] [CrossRef]
- Gobet, J.; Rychen, P.; Madore, C.; Skinner, N.; Van Buel, H.; Jaggi, F. Development of an on-line chlorine sensor for water quality monitoring in public distribution networks. Water Sci. Technol. Water Supply 2001, 1, 211–216. [Google Scholar] [CrossRef]
- Cheng, W.p.; Liu, E.h.; Liu, J.q. A novel statistical model for water age estimation in water distribution networks. Math. Probl. Eng. 2015, 2015. [Google Scholar] [CrossRef] [Green Version]
- Cardoso, S.M.; Barros, D.B.; Oliveira, E.; Brentan, B.; Ribeiro, L. Optimal sensor placement for contamination detection: A multi-objective and probabilistic approach. Environ. Model. Softw. 2021, 135, 104896. [Google Scholar] [CrossRef]
- Fisher, I.; Kastl, G.; Sathasivan, A. New model of chlorine-wall reaction for simulating chlorine concentration in drinking water distribution systems. Water Res. 2017, 125, 427–437. [Google Scholar] [CrossRef]
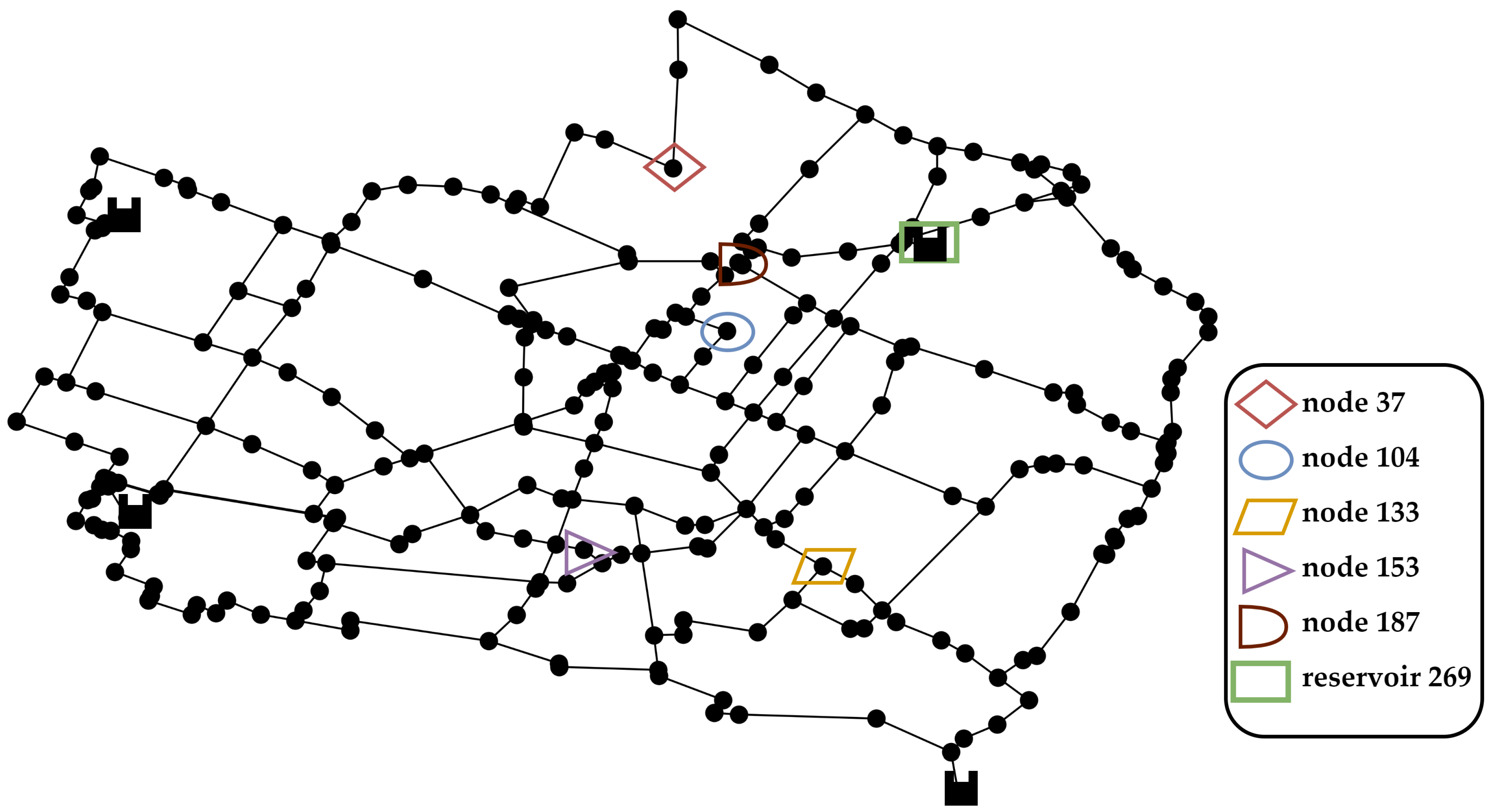




| Scenario A | Junction 01 | Junction 02 | Junction 03 | Junction 04 |
| Nodes | 188 | 122 | 50 | 45 |
| 110 | 263 | 241 | 49 | |
| Start leakage (days) | 1 | 2 | 2 | 5 |
| Duration leakage (hour) | 120 | 144 | 72 | 30 |
| Start form | Three days of raise | Five days of raise | Abrupt | Two days of raise |
| Scenario B | Junction 01 | Junction 02 | Junction 03 | Junction 04 |
| Nodes | 255 | 137 | 29 | 136 |
| Start leakage (days) | 3 | 2 | 1 | 4 |
| Duration leakage (hour) | 24 | 3 | 72 | No end |
| Start form | One day of raise | Abrupt | Two days of raise | Seven days of raise |
| Scenario C | Junction 01 | Junction 02 | Junction 03 | Junction 04 |
| Nodes | 213 | 45 | 150 | 156 |
| Start leakage (days) | 2 | 5 | 7 | 12 |
| Duration leakage (hour) | 60 | 21 | 96 | 67.2 |
| Start form | Two days of raise | Abrupt | Three days of raise | One days of raise |
| Scenario A | ||||
| Nodes | 188 | 122 | 50 | 35 |
| Flows (LPS) | 2.55 | 1.45 | 4.34 | 1.31 |
| Nodes | 110 | 263 | 241 | 49 |
| Flows (LPS) | 2.36 | 1.38 | 4.47 | 0.98 |
| Scenario B | ||||
| Nodes | 255 | 137 | 29 | 136 |
| Flows (LPS) | 2.00 | 1.59 | 4.78 | 0.83 |
| Scenario C | ||||
| Nodes | 213 | 45 | 150 | 156 |
| Flows (LPS) | 2.23 | 1.52 | 3.39 | 1.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barros, D.; Almeida, I.; Zanfei, A.; Meirelles, G.; Luvizotto, E., Jr.; Brentan, B. An Investigation on the Effect of Leakages on the Water Quality Parameters in Distribution Networks. Water 2023, 15, 324. https://doi.org/10.3390/w15020324
Barros D, Almeida I, Zanfei A, Meirelles G, Luvizotto E Jr., Brentan B. An Investigation on the Effect of Leakages on the Water Quality Parameters in Distribution Networks. Water. 2023; 15(2):324. https://doi.org/10.3390/w15020324
Chicago/Turabian StyleBarros, Daniel, Isabela Almeida, Ariele Zanfei, Gustavo Meirelles, Edevar Luvizotto, Jr., and Bruno Brentan. 2023. "An Investigation on the Effect of Leakages on the Water Quality Parameters in Distribution Networks" Water 15, no. 2: 324. https://doi.org/10.3390/w15020324
APA StyleBarros, D., Almeida, I., Zanfei, A., Meirelles, G., Luvizotto, E., Jr., & Brentan, B. (2023). An Investigation on the Effect of Leakages on the Water Quality Parameters in Distribution Networks. Water, 15(2), 324. https://doi.org/10.3390/w15020324














