Impacts of Spatiotemporal Gaps in Satellite Soil Moisture Data on Hydrological Data Assimilation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Hydrological Modeling
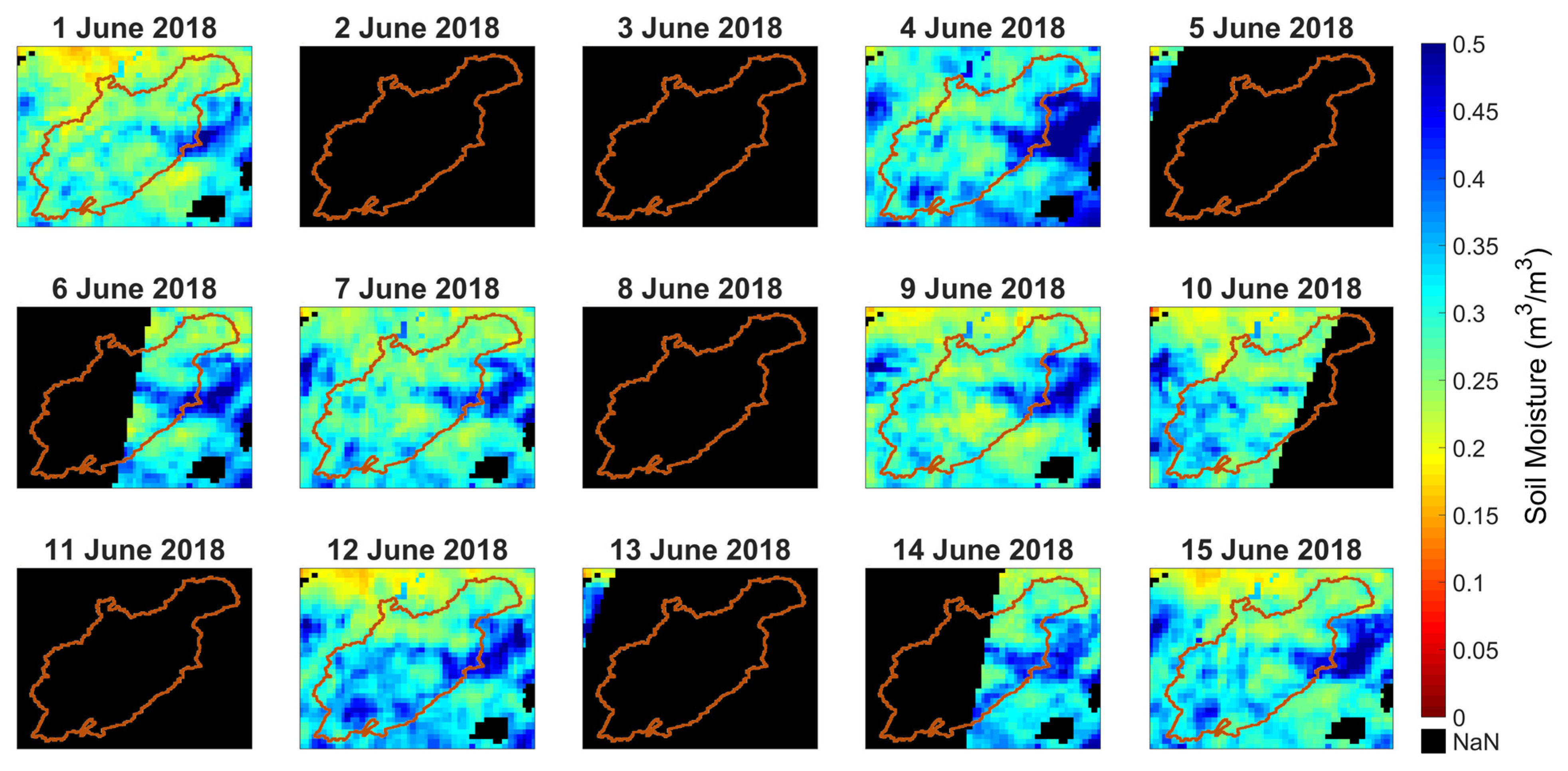
2.3. Remotely Sensed Soil Moisture
2.4. Data Assimilation
2.4.1. Ensemble Kalman Filter (EnKF)
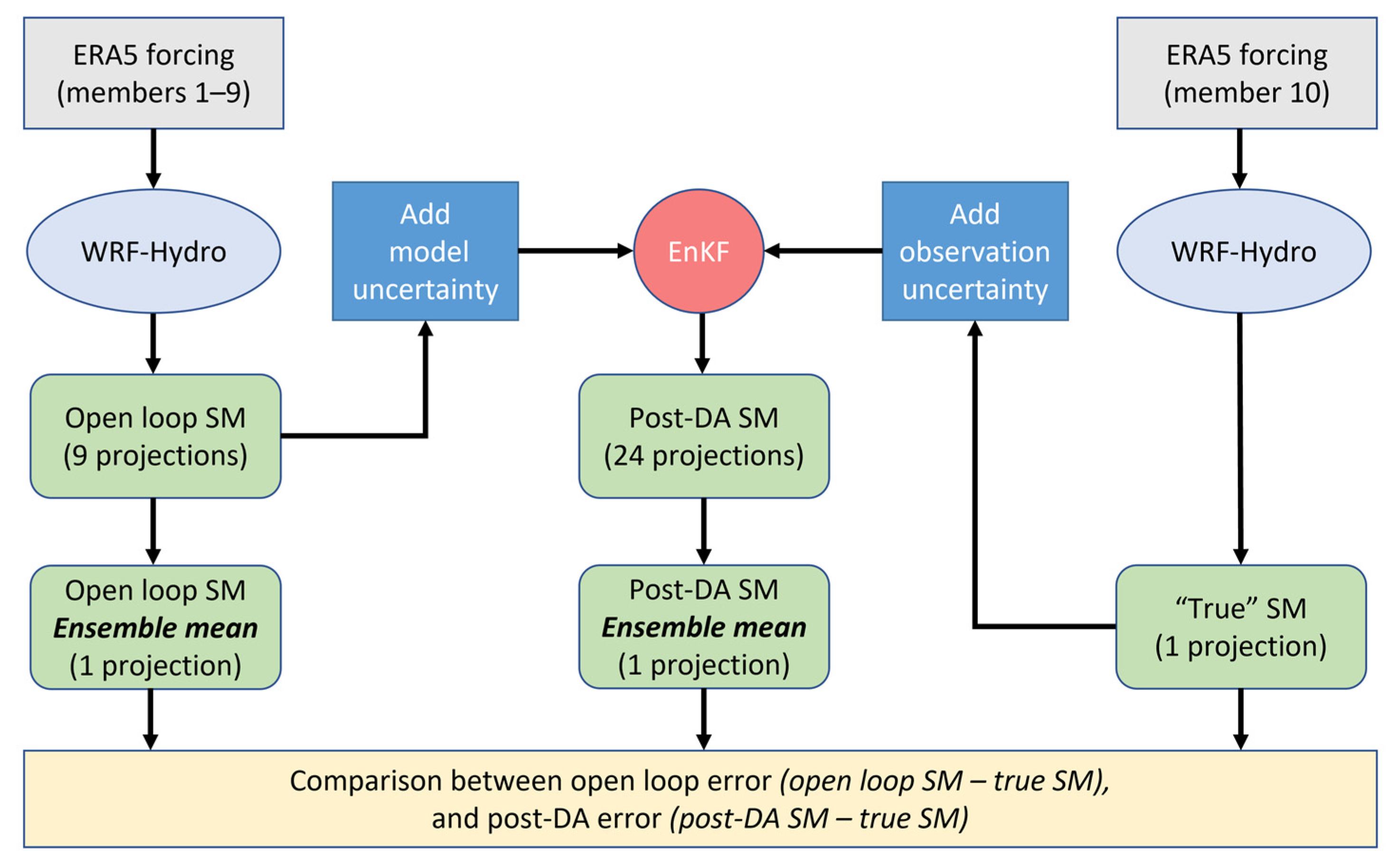
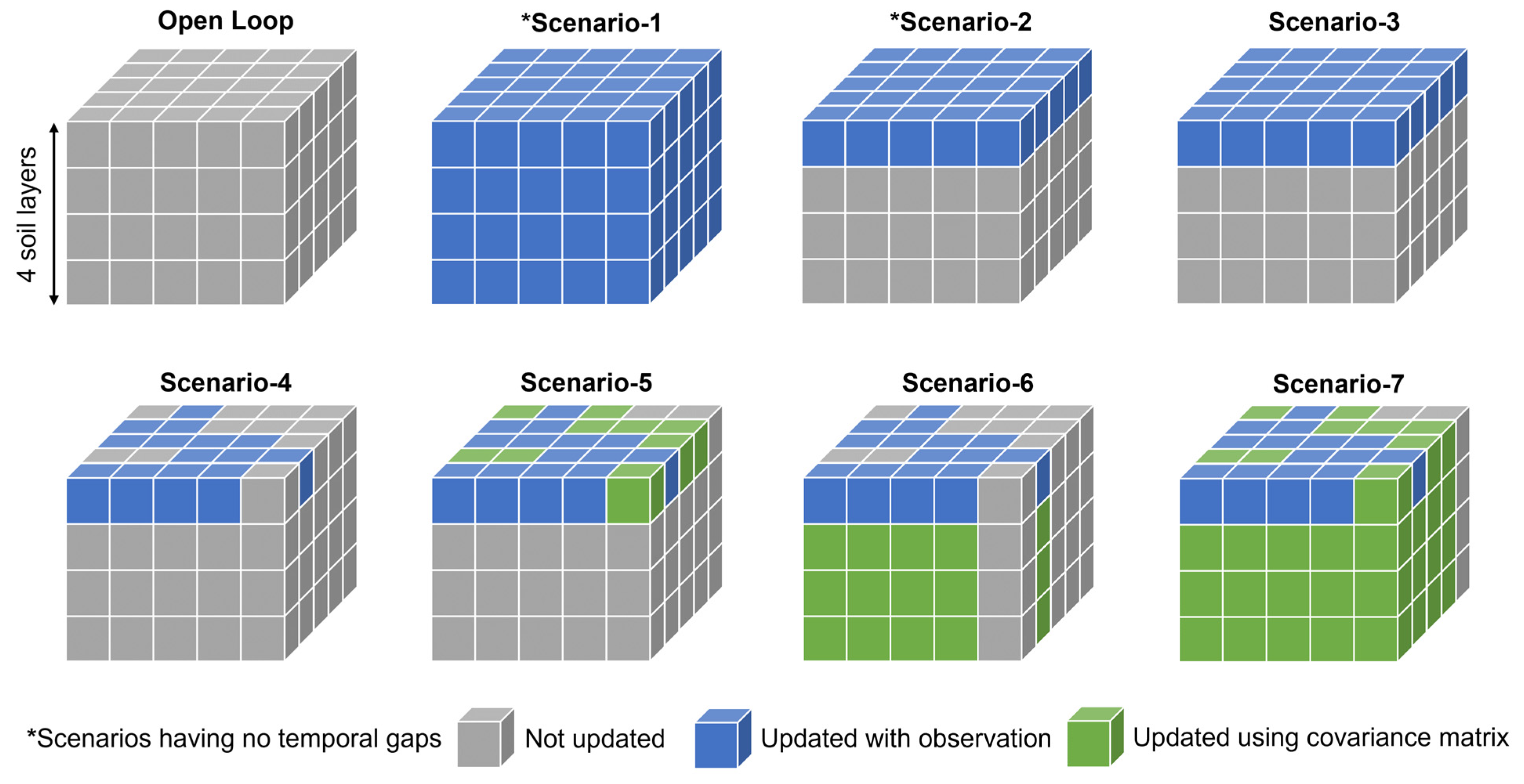
2.4.2. Synthetic Experiments
2.4.3. Real-Data Experiments
3. Results and Discussion
3.1. Model Calibration and Validation
3.2. Synthetic Experiments
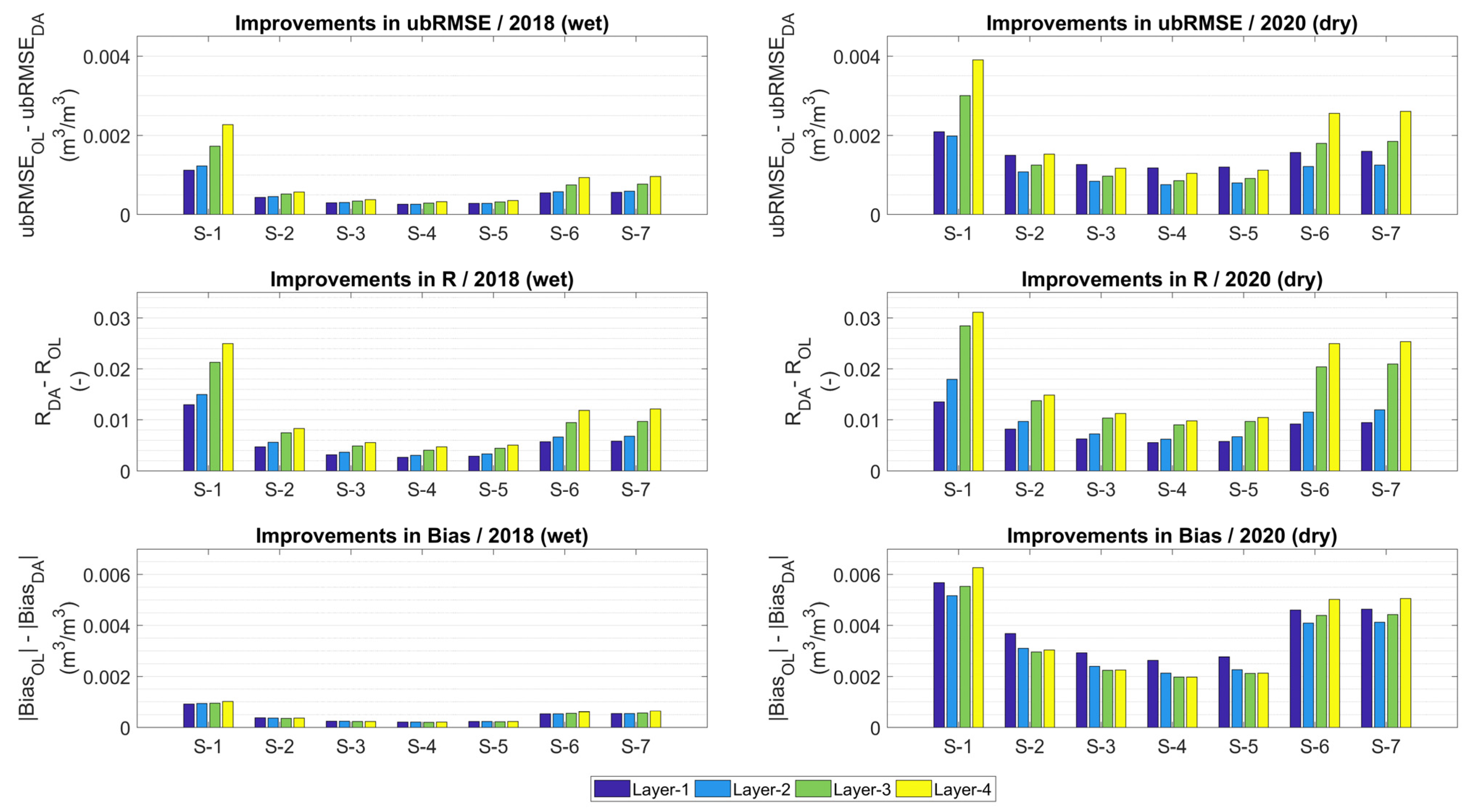
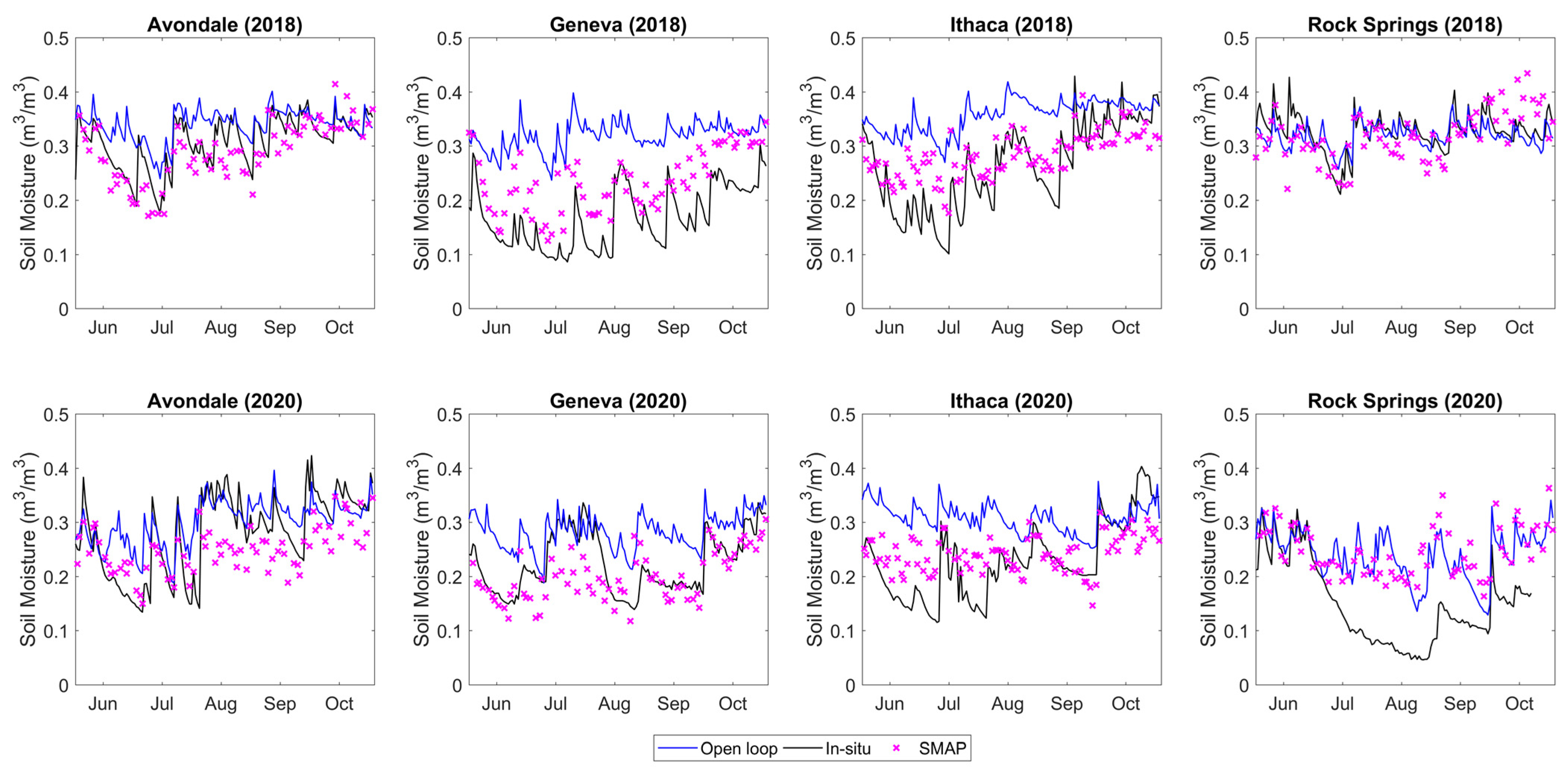
3.3. Real-Data Experiments
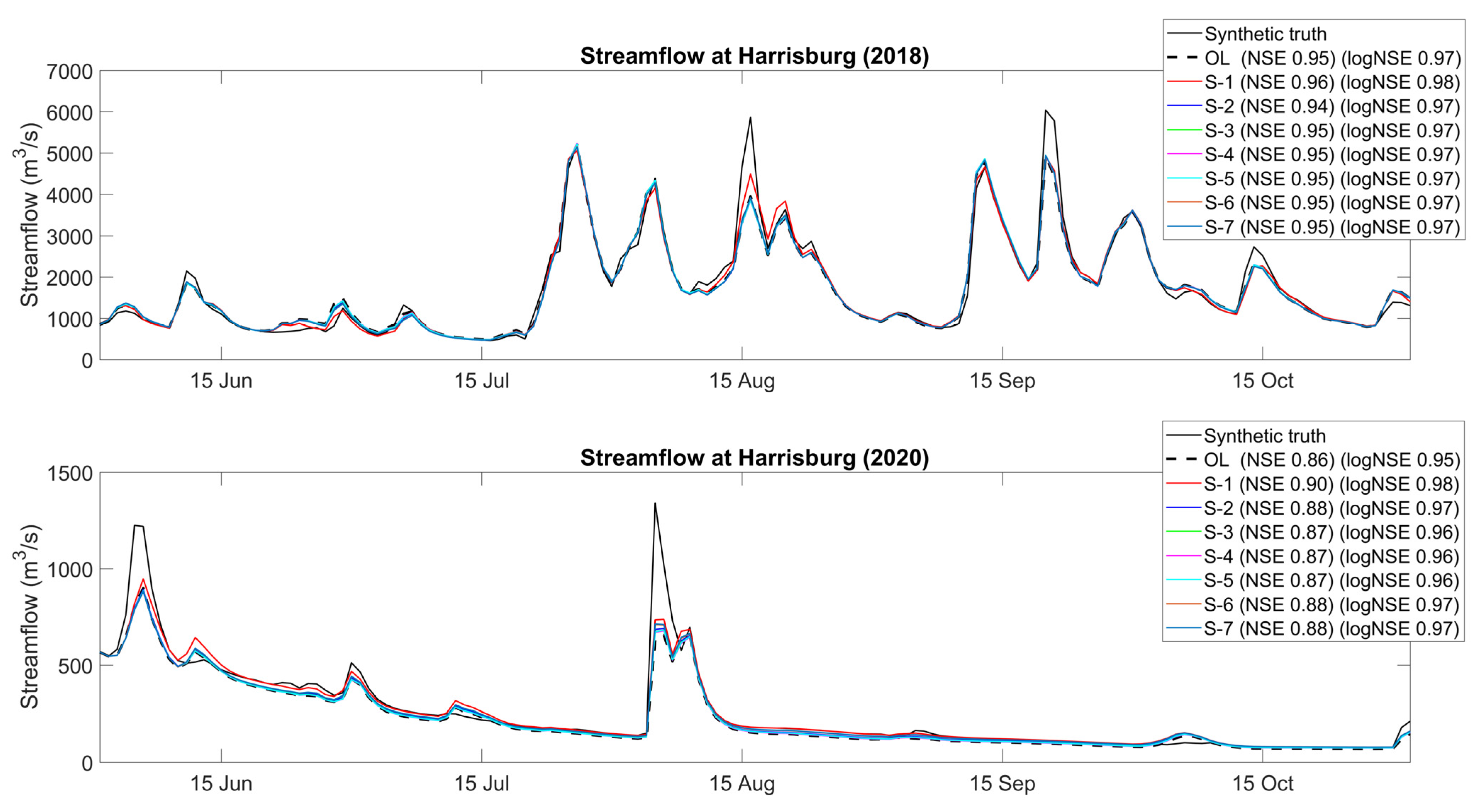
3.4. Streamflow Modeling Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peng, J.; Albergel, C.; Balenzano, A.; Brocca, L.; Cartus, O.; Cosh, M.H.; Crow, W.T.; Dabrowska-Zielinska, K.; Dadson, S.; Davidson, M.W.; et al. A roadmap for high-resolution satellite soil moisture applications–confronting product characteristics with user requirements. Remote Sens. Environ. 2021, 252, 112162. [Google Scholar] [CrossRef]
- Gruber, A.; De Lannoy, G.; Crow, W. A Monte Carlo based adaptive Kalman filtering framework for soil moisture data assimilation. Remote Sens. Environ. 2019, 228, 105–114. [Google Scholar] [CrossRef]
- Dorigo, W.; Himmelbauer, I.; Aberer, D.; Schremmer, L.; Petrakovic, I.; Zappa, L.; Preimesberger, W.; Xaver, A.; Annor, F.; Ardö, J.; et al. The International Soil Moisture Network: Serving Earth system science for over a decade. Hydrol. Earth Syst. Sci. 2021, 25, 5749–5804. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements of the global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef] [Green Version]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Babaeian, E.; Sadeghi, M.; Jones, S.B.; Montzka, C.; Vereecken, H.; Tuller, M. Ground, proximal, and satellite remote sensing of soil moisture. Rev. Geophys. 2019, 57, 530–616. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; Bindlish, R.; Bringer, A.; Horton, D.; Johnson, J.T. Soil moisture retrieval using a time-series ratio algorithm for the NISAR mission. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Brussels, Belgium, 11–16 July 2021. [Google Scholar] [CrossRef]
- Massari, C.; Brocca, L.; Tarpanelli, A.; Moramarco, T. Data assimilation of satellite soil moisture into rainfall-runoff modelling: A complex recipe? Remote Sens. 2015, 7, 11403–11433. [Google Scholar] [CrossRef] [Green Version]
- Kolassa, J.; Reichle, R.H.; Draper, C.S. Merging active and passive microwave observations in soil moisture data assimilation. Remote Sens. Environ. 2017, 191, 117–130. [Google Scholar] [CrossRef]
- Lievens, H.; Reichle, R.H.; Liu, Q.; De Lannoy, G.J.M.; Dunbar, R.S.; Kim, S.B.; Das, N.N.; Cosh, M.; Walker, J.P.; Wagner, W. Joint Sentinel-1 and SMAP data assimilation to improve soil moisture estimates. Geophys. Res. Lett. 2017, 44, 6145–6153. [Google Scholar] [CrossRef] [PubMed]
- Dumedah, G.; Walker, J.P.; Merlin, O. Root-zone soil moisture estimation from assimilation of downscaled Soil Moisture and Ocean Salinity data. Adv. Water Resour. 2015, 84, 14–22. [Google Scholar] [CrossRef]
- Draper, C.S.; Reichle, R.H.; De Lannoy, G.J.M.; Liu, Q. Assimilation of passive and active microwave soil moisture retrievals. Geophys. Res. Lett. 2012, 39, L04401. [Google Scholar] [CrossRef] [Green Version]
- Blyverket, J.; Hamer, P.D.; Bertino, L.; Albergel, C.; Fairbairn, D.; Lahoz, W.A. An Evaluation of the EnKF vs. EnOI and the Assimilation of SMAP, SMOS and ESA CCI Soil Moisture Data over the Contiguous US. Remote Sens. 2019, 11, 478. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.V.; Reichle, R.H.; Harrison, K.W.; Peters-Lidard, C.D.; Yatheendradas, S.; Santanello, J.A. A comparison of methods for a priori bias correction in soil moisture data assimilation. Water Resour. Res. 2012, 48, W03515. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Pan, M.; Wanders, N.; Kumar, D.N.; Wood, E.F. Four decades of microwave satellite soil moisture observations: Part 1. A review of retrieval algorithms. Adv. Water Resour. 2017, 109, 106–120. [Google Scholar] [CrossRef]
- Han, X.; Li, X.; Hendricks Franssen, H.J.; Vereecken, H.; Montzka, C. Spatial horizontal correlation characteristics in the land data assimilation of soil moisture. Hydrol. Earth Syst. Sci. 2012, 16, 1349–1363. [Google Scholar] [CrossRef] [Green Version]
- Yan, H.; Moradkhani, H. Combined assimilation of streamflow and satellite soil moisture with the particle filter and geostatistical modelling. Adv. Water Resour. 2016, 94, 364–378. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, A.K.; De Lannoy, G.J.; Reichle, R.H.; Houser, P.R. Assimilation and downscaling of satellite observed soil moisture over the Little River Experimental Watershed in Georgia, USA. Adv. Water Resour. 2013, 52, 19–33. [Google Scholar] [CrossRef]
- Evensen, G. The ensemble Kalman filter: Theoretical formulation and practical implementation. Ocean Dyn. 2016, 53, 343–367. [Google Scholar] [CrossRef]
- Rouf, T.; Girotto, M.; Houser, P.; Maggioni, V. Assimilating satellite-based soil moisture observations in a land surface model: The effect of spatial resolution. J. Hydrol. X 2021, 13, 100105. [Google Scholar] [CrossRef]
- Baguis, P.; Roulin, E. Soil moisture data assimilation in a hydrological model: A case study in Belgium using large-scale satellite data. Remote Sens. 2017, 9, 820. [Google Scholar] [CrossRef] [Green Version]
- López López, P.; Wanders, N.; Schellekens, J.; Renzullo, L.J.; Sutanudjaja, E.H.; Bierkens, M.F. Improved large-scale hydrological modelling through the assimilation of streamflow and downscaled satellite soil moisture observations. Hydrol. Earth Syst. Sci. 2016, 20, 3059–3076. [Google Scholar] [CrossRef] [Green Version]
- De Santis, D.; Biondi, D.; Crow, W.T.; Camici, S.; Modanesi, S.; Brocca, L.; Massari, C. Assimilation of satellite soil moisture products for river flow prediction: An extensive experiment in over 700 catchments throughout Europe. Water Resour. Res. 2021, 57, e2021WR029643. [Google Scholar] [CrossRef]
- Massari, C.; Camici, S.; Ciabatta, L.; Brocca, L. Exploiting satellite-based surface soil moisture for flood forecasting in the Mediterranean area: State update versus rainfall correction. Remote Sens. 2018, 10, 292. [Google Scholar] [CrossRef] [Green Version]
- Leroux, D.J.; Pellarin, T.; Vischel, T.; Cohard, J.-M.; Gascon, T.; Gibon, F.; Mialon, A.; Galle, S.; Peugeot, C.; Seguis, L. Assimilation of SMOS soil moisture into a distributed hydrological model and impacts on the water cycle variables over the Ouémé catchment in Benin. Hydrol. Earth Syst. Sci. 2016, 20, 2827–2840. [Google Scholar] [CrossRef] [Green Version]
- Patil, A.; Ramsankaran, R.A.A.J. Improved streamflow simulations by coupling soil moisture analytical relationship in EnKF based hydrological data assimilation framework. Adv. Water Resour. 2018, 121, 173–188. [Google Scholar] [CrossRef]
- Cenci, L.; Pulvirenti, L.; Boni, G.; Chini, M.; Matgen, P.; Gabellani, S.; Squicciarino, G.; Pierdicca, N. An evaluation of the potential of Sentinel 1 for improving flash flood predictions via soil moisture–data assimilation. Adv. Geosci. 2017, 44, 89–100. [Google Scholar] [CrossRef] [Green Version]
- Ciupak, M.; Ozga-Zielinski, B.; Adamowski, J.; Deo, R.C.; Kochanek, K. Correcting satellite precipitation data and assimilating satellite-derived soil moisture data to generate ensemble hydrological forecasts within the HBV rainfall-runoff model. Water 2019, 11, 2138. [Google Scholar] [CrossRef] [Green Version]
- Patil, A.; Ramsankaran, R.A.A.J. Improving streamflow simulations and forecasting performance of SWAT model by assimilating remotely sensed soil moisture observations. J. Hydrol. 2017, 555, 683–696. [Google Scholar] [CrossRef]
- Meng, S.; Xie, X.; Liang, S. Assimilation of soil moisture and streamflow observations to improve flood forecasting with considering runoff routing lags. J. Hydrol. 2017, 550, 568–579. [Google Scholar] [CrossRef]
- Tian, S.; Renzullo, L.J.; Pipunic, R.C.; Lerat, J.; Sharples, W.; Donnelly, C. Satellite soil moisture data assimilation for improved operational continental water balance prediction. Hydrol. Earth Syst. Sci. 2021, 25, 4567–4584. [Google Scholar] [CrossRef]
- Mao, Y.; Crow, W.T.; Nijssen, B. A framework for diagnosing factors degrading the streamflow performance of a soil moisture data assimilation system. J. Hydrometeorol. 2018, 20, 79–97. [Google Scholar] [CrossRef]
- Fairbairn, D.; Barbu, A.L.; Napoly, A.; Albergel, C.; Mahfouf, J.F.; Calvet, J.C. The effect of satellite-derived surface soil moisture and leaf area index land data assimilation on streamflow simulations over France. Hydrol. Earth Syst. Sci. 2017, 21, 2015–2033. [Google Scholar] [CrossRef] [Green Version]
- De Lannoy, G.J.; Reichle, R.H. Assimilation of SMOS brightness temperatures or soil moisture retrievals into a land surface model. Hydrol. Earth Syst. Sci. 2016, 20, 4895–4911. [Google Scholar] [CrossRef] [Green Version]
- Ridler, M.E.; Madsen, H.; Stisen, S.; Bircher, S.; Fensholt, R. Assimilation of SMOS-derived soil moisture in a fully integrated hydrological and soil-vegetation-atmosphere transfer model in Western Denmark. Water Resour. Res. 2014, 50, 8962–8981. [Google Scholar] [CrossRef]
- Jackson, J.K.; Huryn, A.D.; Strayer, D.L.; Courtemanch, D.L.; Sweeney, B.W. Atlantic Coast Rivers of the Southeastern United States. In Rivers of North America, 1st ed.; Benke, A.C., Cushing, C.E., Eds.; Elsevier Academic Press: Cambridge, MA, USA, 2005; pp. 20–71. [Google Scholar]
- Ray, R.L.; Beighley, R.E.; Yoon, Y. Integrating runoff generation and flow routing in Susquehanna River Basin to characterize key hydrologic processes contributing to maximum annual flood events. J. Hydrol. Eng. 2016, 21, 04016026. [Google Scholar] [CrossRef]
- DePhilip, M.; Moberg, T. Ecosystem Flow Recommendations for the Susquehanna River Basin; The Nature Conservancy: Harrisburg, PA, USA, 2010. [Google Scholar]
- Schaefer, G.L.; Cosh, M.H.; Jackson, T.J. The USDA natural resources conservation service soil climate analysis network (SCAN). J. Atmos. Oceanic Technol. 2007, 24, 2073–2077. [Google Scholar] [CrossRef]
- Bell, J.E.; Palecki, M.A.; Baker, C.B.; Collins, W.G.; Lawrimore, J.H.; Leeper, R.; Hall, M.E.; Kochendorfer, J.; Meyers, T.P.; Wilson, T.; et al. US Climate Reference Network soil moisture and temperature observations. J. Hydrometeorol. 2013, 14, 977–988. [Google Scholar] [CrossRef]
- Gochis, D.J.; Barlage, M.; Cabell, R.; Casali, M.; Dugger, A.; FitzGerald, K.; McAllister, J.; McCreight, A.; RafieeiNasab, L.; Read, K.; et al. The WRF-Hydro Modeling System Technical Description, Version (5.1.1); NCAR Technical Note; UCAR: Boulder, CO, USA, 2020. [Google Scholar]
- Niu, G.-Y.; Yang, Z.-L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116, D12109. [Google Scholar] [CrossRef] [Green Version]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M.; et al. A Description of the Advanced Research WRF Version 4; NCAR Technical Note; UCAR: Boulder, CO, USA, 2019. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorolog. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Asadzadeh, M.; Tolson, B. Pareto archived dynamically dimensioned search with hypervolume-based selection for multi-objective optimization. Eng. Optim. 2013, 45, 1489–1509. [Google Scholar] [CrossRef]
- Tolson, B.A.; Shoemaker, C.A. Dynamically dimensioned search algorithm for computationally efficient watershed model calibration. Water Resour. Res. 2007, 43, W01413. [Google Scholar] [CrossRef] [Green Version]
- Loizu, J.; Massari, C.; Alvarez-Mozos, J.; Tarpanelli, A.; Brocca, L.; Casali, J. On the assimilation set-up of ASCAT soil moisture data for improving streamflow catchment simulation. Adv. Water Resour. 2018, 111, 86–104. [Google Scholar] [CrossRef]
- Sun, L.; Seidou, O.; Nistor, I.; Liu, K. Review of the Kalman-type hydrological data assimilation. Hydrol. Sci. J. 2015, 61, 2348–2366. [Google Scholar] [CrossRef] [Green Version]
- Montzka, C.; Pauwels, V.R.N.; Franssen, H.H.; Han, X.; Vereecken, H. Multivariate and multiscale data assimilation in terrestrial systems: A review. Sensors 2012, 12, 16291–16333. [Google Scholar] [CrossRef] [Green Version]
- Wanders, N.; Karssenberg, D.; De Roo, A.; De Jong, S.M.; Bierkens, M.F.P. The suitability of remotely sensed soil moisture for improving operational flood forecasting. Hydrol. Earth Syst. Sci. 2014, 18, 2343–2357. [Google Scholar] [CrossRef] [Green Version]
- Reichle, R.H.; Koster, R.D. Assessing the impact of horizontal error correlations in background fields on soil moisture estimation. J. Hydrometeorol. 2003, 4, 1229–1242. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D. Bias reduction in short records of satellite soil moisture. Geophys. Res. Lett. 2004, 31, L19501. [Google Scholar] [CrossRef] [Green Version]
- Renzullo, L.J.; Van Dijk, A.I.J.M.; Perraud, J.M.; Collins, D.; Henderson, B.; Jin, H.; Smith, A.; McJannet, D.L. Continental satellite soil moisture data assimilation improves root-zone moisture analysis for water resources assessment. J. Hydrol. 2014, 519, 2747–2762. [Google Scholar] [CrossRef]
- Kumar, S.V.; Reichle, R.H.; Koster, R.D.; Crow, W.T.; Peters-Lidard, C.D. Role of subsurface physics in the assimilation of surface soil moisture observations. J. Hydrometeorol. 2009, 10, 1534–1547. [Google Scholar] [CrossRef]
- Yilmaz, M.T.; Crow, W.T. The optimality of potential rescaling approaches in land data assimilation. J. Hydrometeorol. 2013, 14, 650–660. [Google Scholar] [CrossRef]
- Lievens, H.; Tomer, S.; Al Bitar, A.; De Lannoy, G.; Drusch, M.; Dumedah, G.; Franssen, H.-J.H.; Kerr, Y.; Martens, B.; Pan, M.; et al. SMOS soil moisture assimilation for improved hydrologic simulation in the Murray Darling Basin, Australia. Remote Sens. Environ. 2015, 168, 146–162. [Google Scholar] [CrossRef]
- Samuel, J.; Coulibaly, P.; Dumedah, G.; Moradkhani, H. Assessing model state and forecasts variation in hydrologic data assimilation. J. Hydrol. 2014, 513, 127–141. [Google Scholar] [CrossRef]
- Trudel, M.; Leconte, R.; Paniconi, C. Analysis of the hydrological response of a distributed physically-based model using post-assimilation (EnKF) diagnostics of streamflow and in situ soil moisture observations. J. Hydrol. 2014, 514, 192–201. [Google Scholar] [CrossRef]

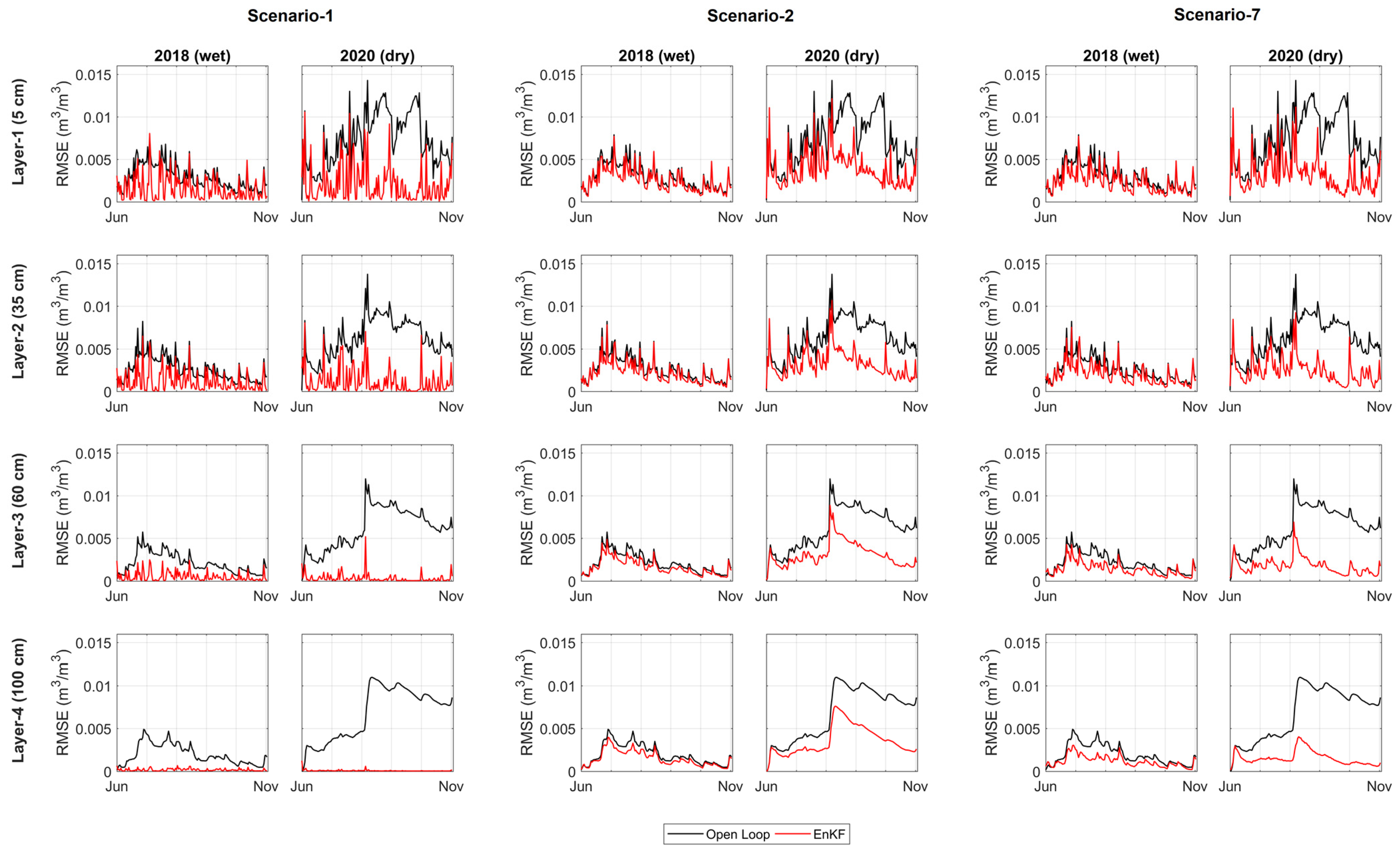
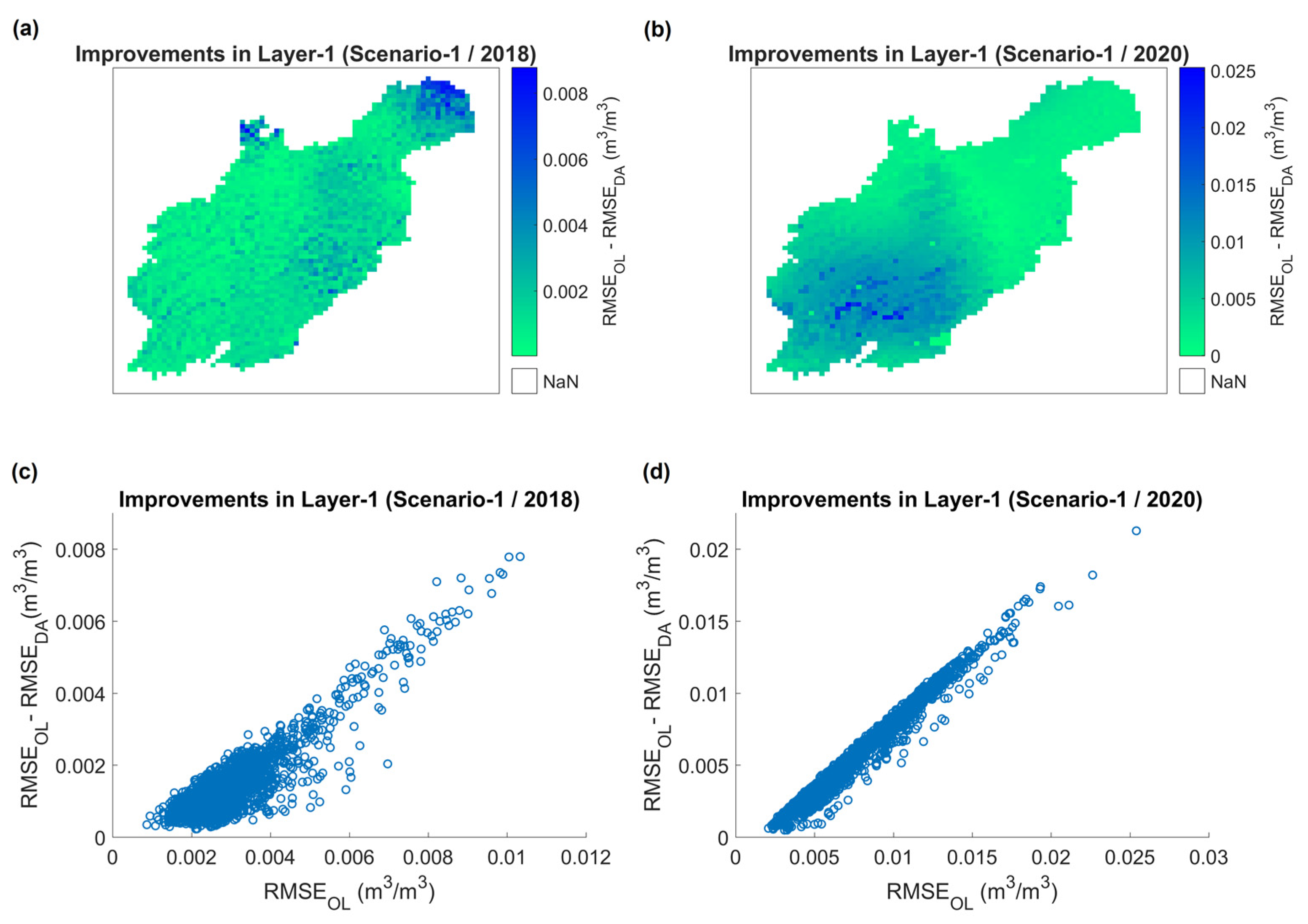

| Soil Layer | Calibration (2011/Wet Year) | Validation (2018/Wet Year) | Validation (2020/Dry Year) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Soil Moisture | Flow | Soil Moisture | Flow | Soil Moisture | Flow | |||||||
| R | ubRMSE (m3/m3) | Bias (m3/m3) | NSE | R | ubRMSE (m3/m3) | Bias (m3/m3) | NSE | R | ubRMSE (m3/m3) | Bias (m3/m3) | NSE | |
| Layer 1 | 0.81 | 0.056 | 0.092 | 0.78 | 0.68 | 0.041 | 0.071 | 0.77 | 0.57 | 0.053 | 0.062 | 0.71 |
| Layer 2 | 0.84 | 0.048 | 0.103 | 0.68 | 0.037 | 0.064 | 0.75 | 0.042 | 0.079 | |||
| Layer 3 | 0.75 | 0.026 | 0.062 | 0.63 | 0.027 | 0.054 | 0.64 | 0.021 | 0.044 | |||
| Performance Metrics | Layer 1 | Layer 2 | Layer 3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2018 (Wet) | 2020 (Dry) | 2018 (Wet) | 2020 (Dry) | 2018 (Wet) | 2020 (Dry) | |||||||||
| OL | RS | DA | OL | RS | DA | OL | DA | OL | DA | OL | DA | OL | DA | |
| ubRMSE (m3/m3) | 0.041 | 0.040 | 0.040 | 0.053 | 0.052 | 0.051 | 0.037 | 0.036 | 0.042 | 0.041 | 0.027 | 0.028 | 0.021 | 0.022 |
| R | 0.68 | 0.73 | 0.72 | 0.57 | 0.61 | 0.66 | 0.68 | 0.71 | 0.75 | 0.78 | 0.63 | 0.64 | 0.64 | 0.60 |
| Bias (m3/m3) | 0.071 | 0.026 | 0.071 | 0.062 | 0.039 | 0.062 | 0.064 | 0.064 | 0.079 | 0.079 | 0.054 | 0.054 | 0.044 | 0.044 |
| Measurement Location | Layer 1 | Layer 2 | Layer 3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2018 (Wet) | 2020 (Dry) | 2018 (Wet) | 2020 (Dry) | 2018 (Wet) | 2020 (Dry) | |||||||||
| OL | RS | DA | OL | RS | DA | OL | DA | OL | DA | OL | DA | OL | DA | |
| Avondale | 0.77 | 0.82 | 0.81 | 0.76 | 0.70 | 0.75 | 0.73 | 0.76 | 0.76 | 0.71 | 0.33 | 0.24 | 0.84 | 0.86 |
| Geneva | 0.50 | 0.78 | 0.54 | 0.67 | 0.61 | 0.70 | 0.47 | 0.52 | 0.71 | 0.74 | 0.47 | 0.57 | 0.16 | 0.27 |
| Ithaca | 0.79 | 0.80 | 0.84 | 0.25 | 0.57 | 0.54 | 0.85 | 0.88 | 0.73 | 0.86 | 0.85 | 0.88 | 0.69 | 0.69 |
| Rock Springs | 0.68 | 0.53 | 0.68 | 0.62 | 0.56 | 0.66 | 0.68 | 0.70 | 0.80 | 0.82 | 0.87 | 0.85 | 0.85 | 0.58 |
| Scenario | 2018 (Wet) | 2020 (Dry) | ||
|---|---|---|---|---|
| NSE | log-NSE | NSE | log-NSE | |
| Open Loop | 0.77 | 0.82 | 0.71 | 0.61 |
| Scenario 7 | 0.77 | 0.84 | 0.70 | 0.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, K.; Leconte, R.; Trudel, M. Impacts of Spatiotemporal Gaps in Satellite Soil Moisture Data on Hydrological Data Assimilation. Water 2023, 15, 321. https://doi.org/10.3390/w15020321
Mohammed K, Leconte R, Trudel M. Impacts of Spatiotemporal Gaps in Satellite Soil Moisture Data on Hydrological Data Assimilation. Water. 2023; 15(2):321. https://doi.org/10.3390/w15020321
Chicago/Turabian StyleMohammed, Khaled, Robert Leconte, and Mélanie Trudel. 2023. "Impacts of Spatiotemporal Gaps in Satellite Soil Moisture Data on Hydrological Data Assimilation" Water 15, no. 2: 321. https://doi.org/10.3390/w15020321






