Research on the Uplift Pressure Prediction of Concrete Dams Based on the CNN-GRU Model
Abstract
:1. Introduction
2. Methodology
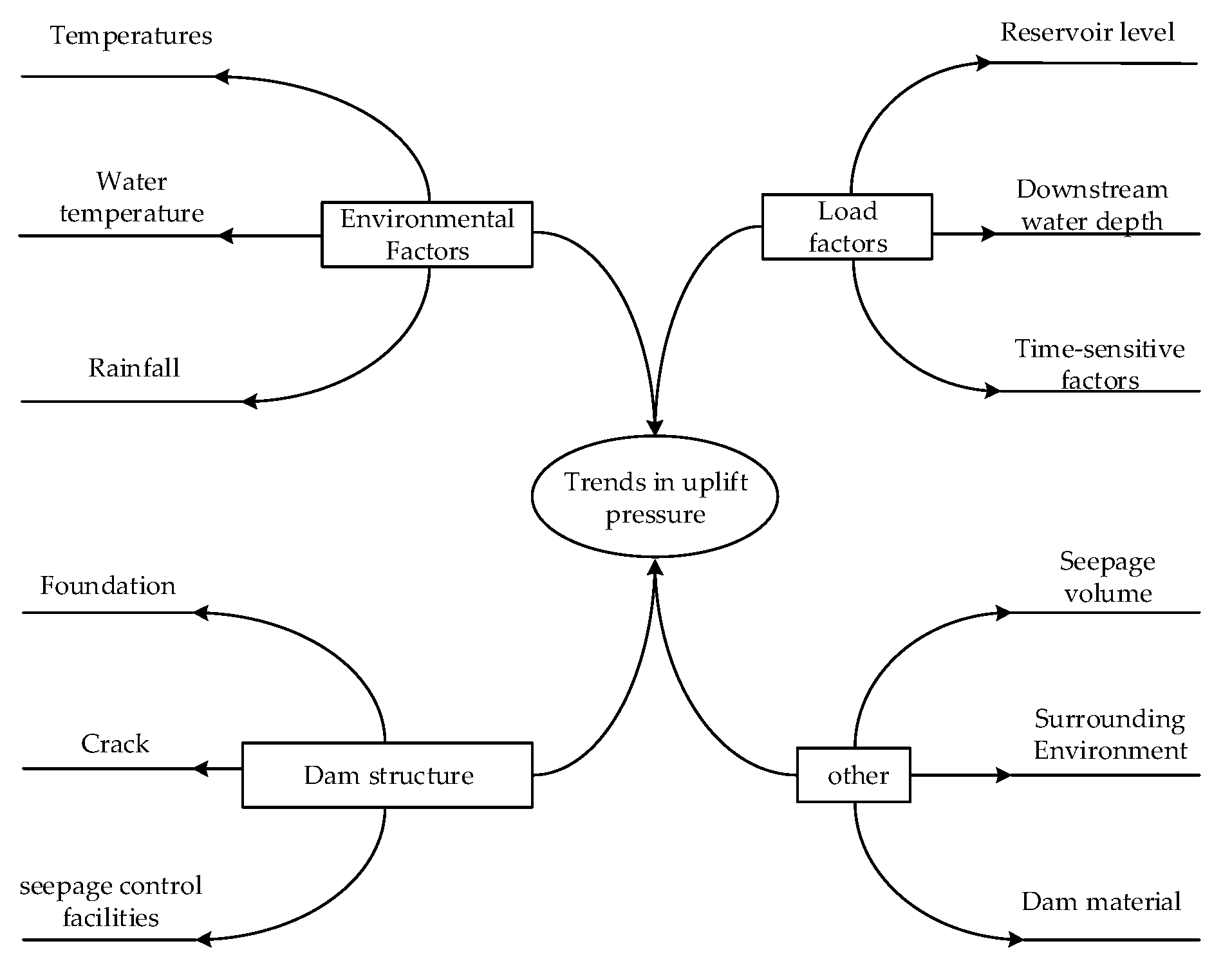
2.1. Problem Description
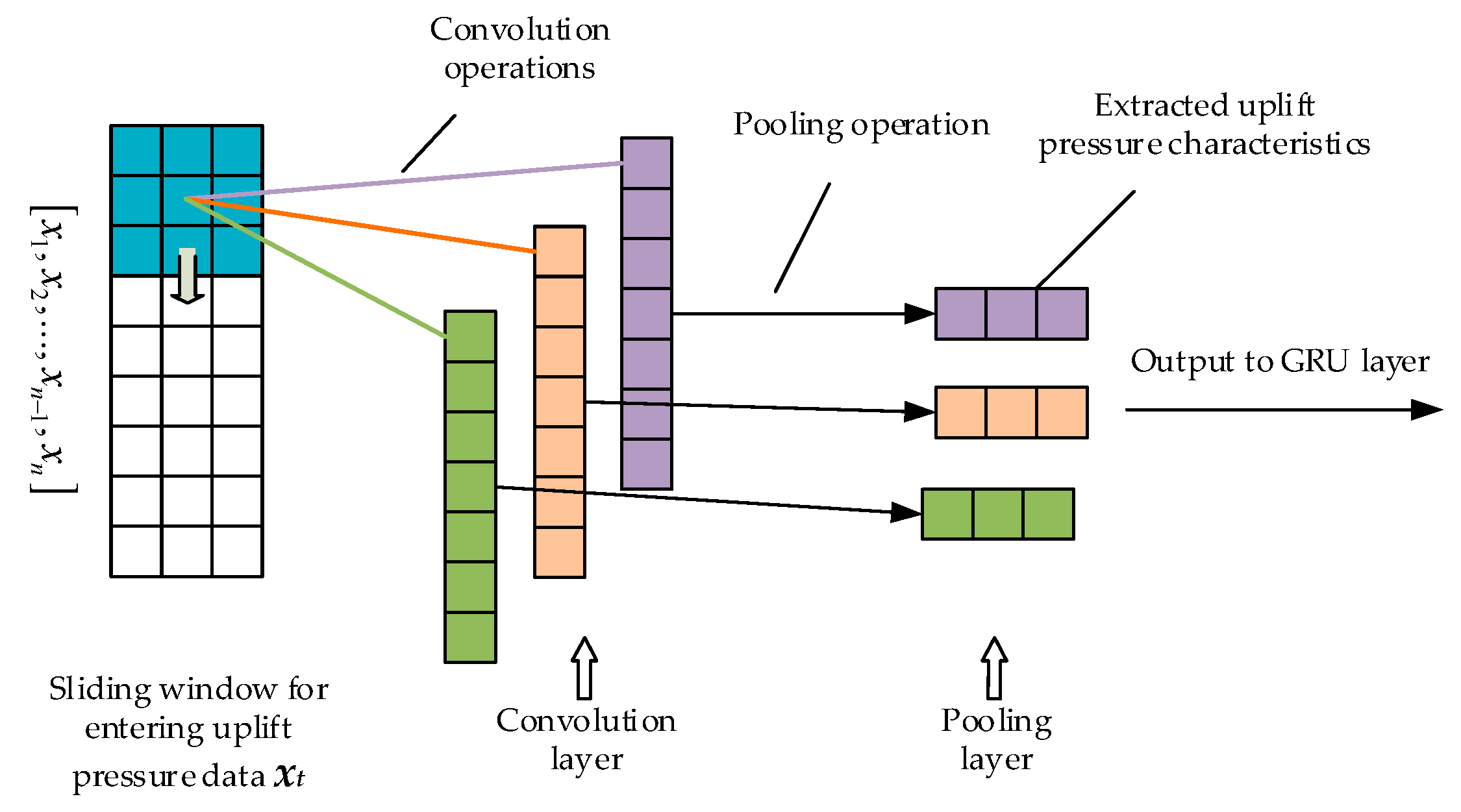
2.2. Extraction of Uplift Pressure Features Based on the CNN Network
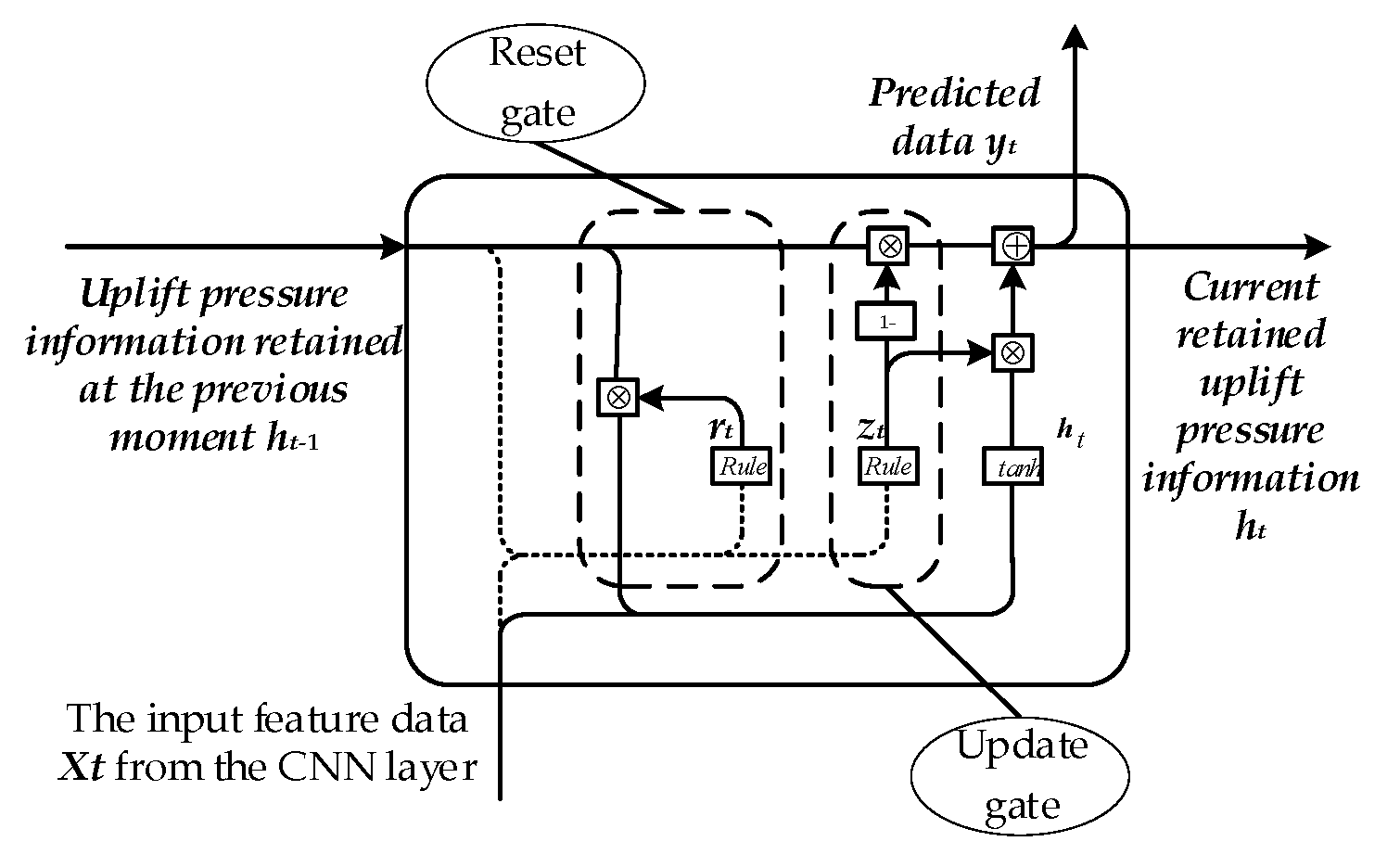
2.3. Prediction Model for Uplift Pressure Based on the GRU Network
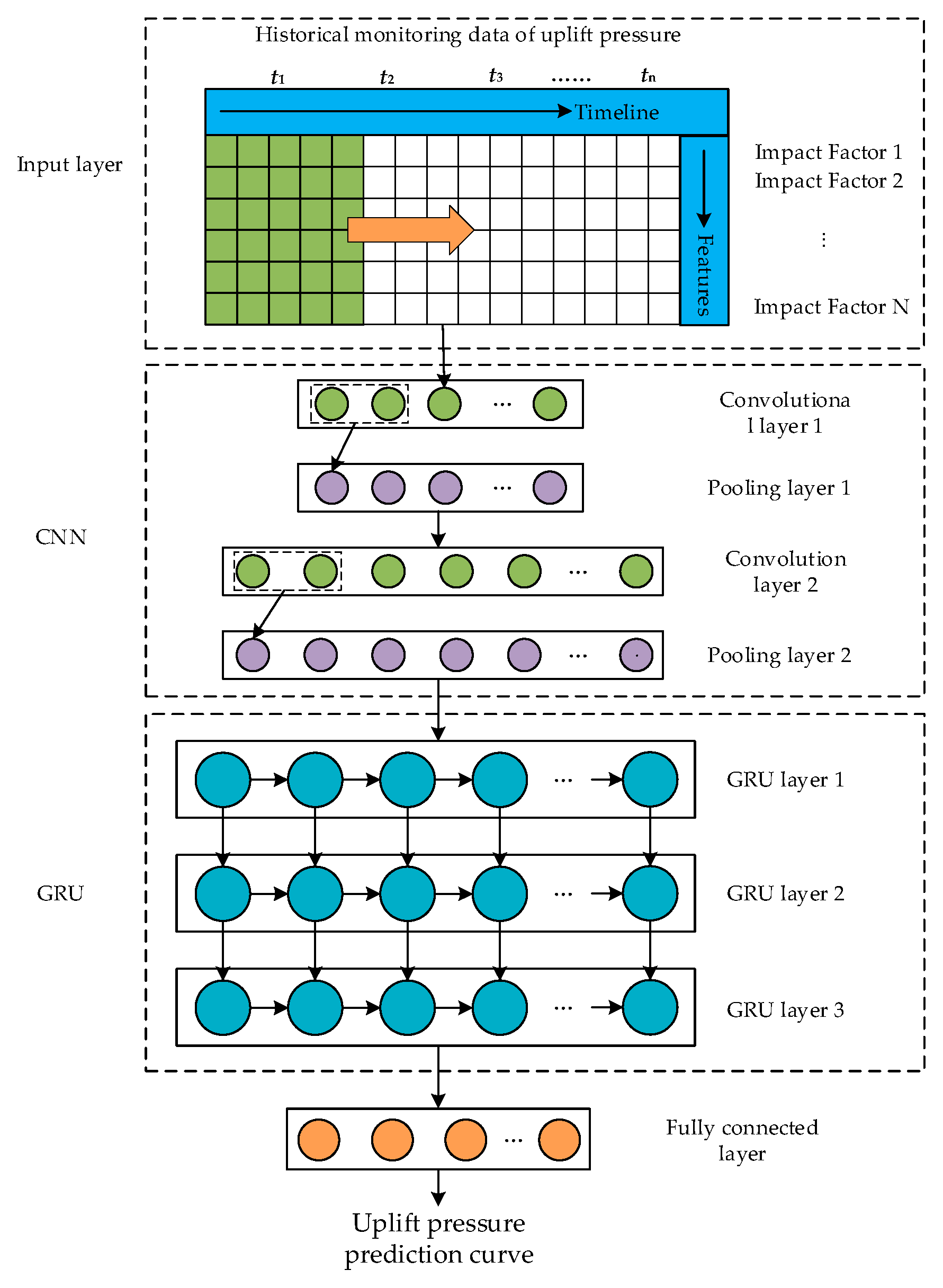
2.4. Construction of the CNN-GRU Model for Uplift Pressure Prediction
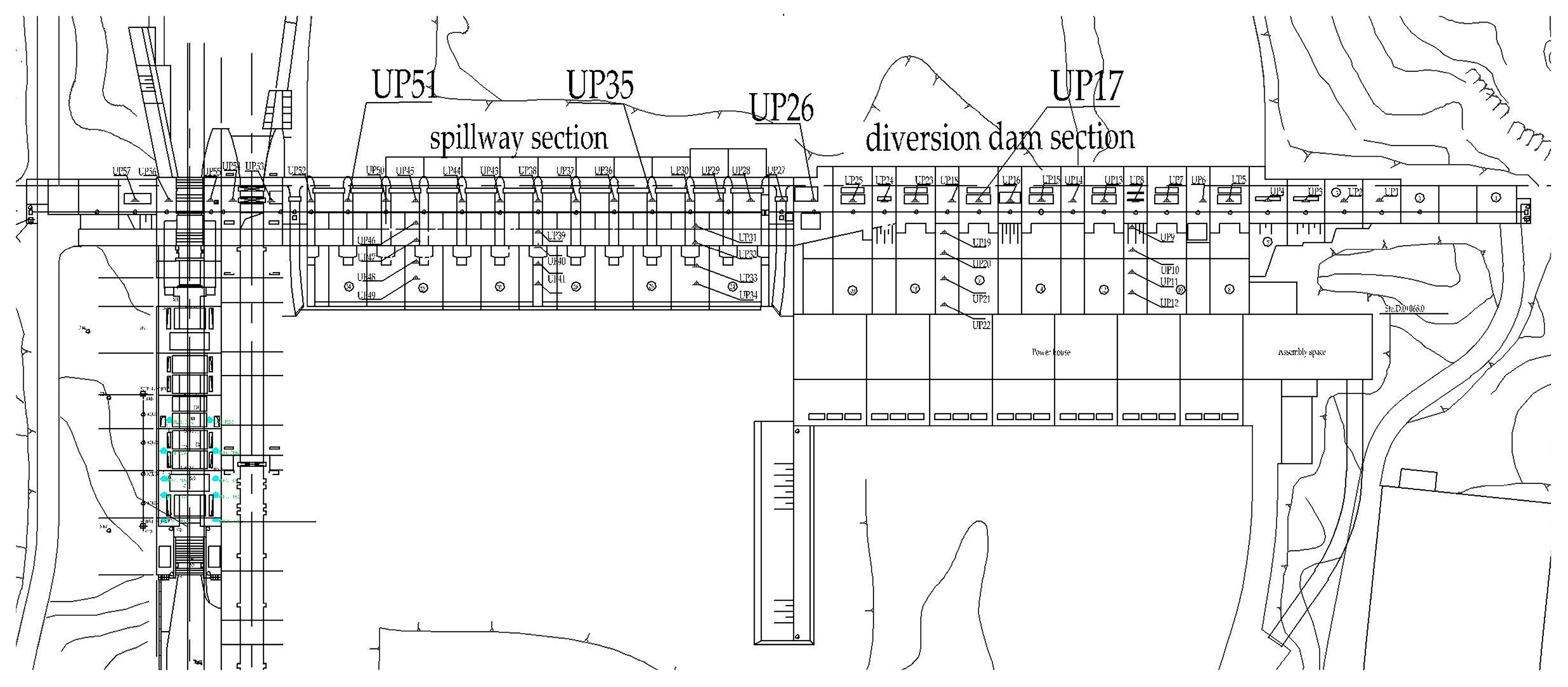
2.5. Background of a Dam Project
3. Results
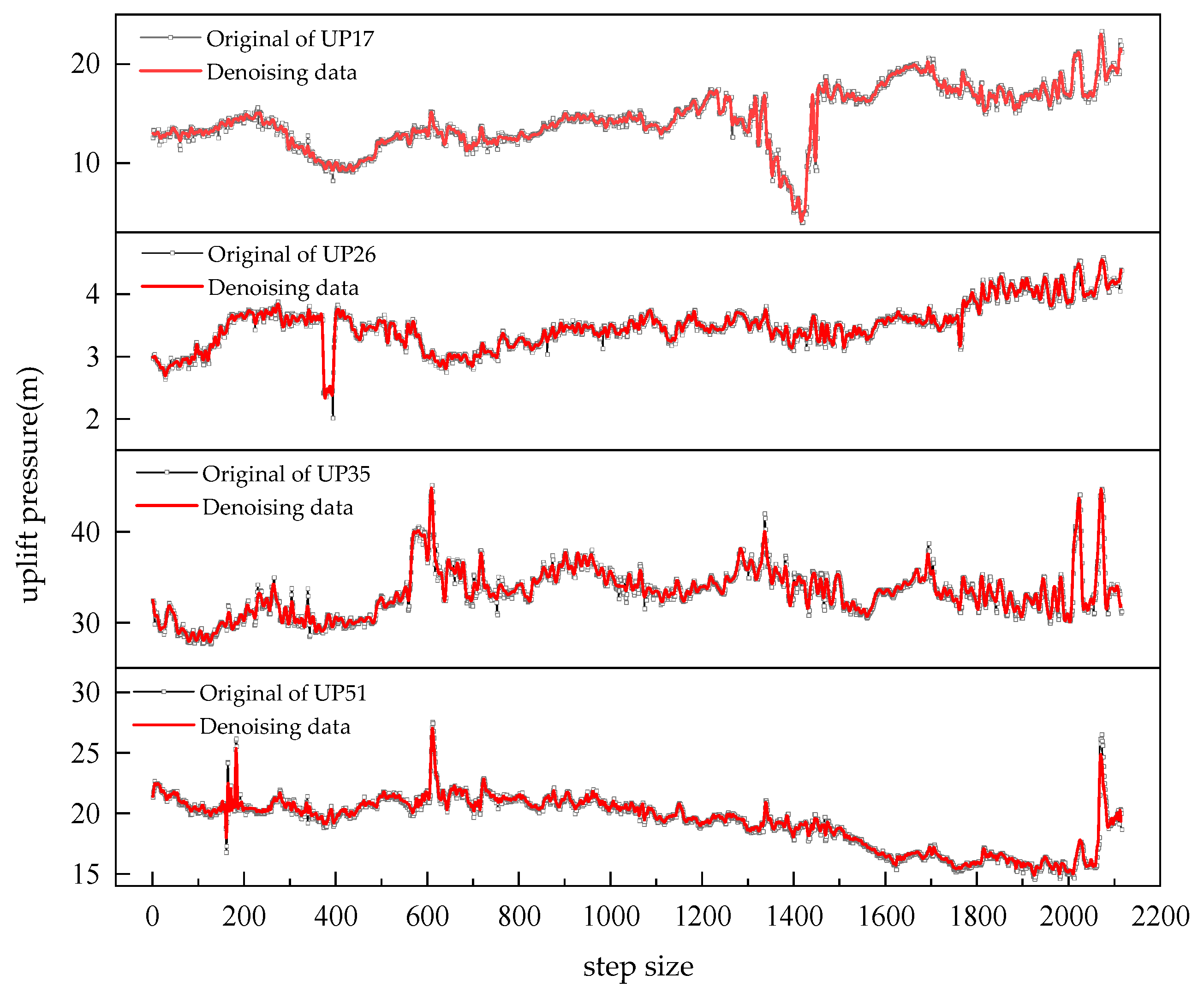
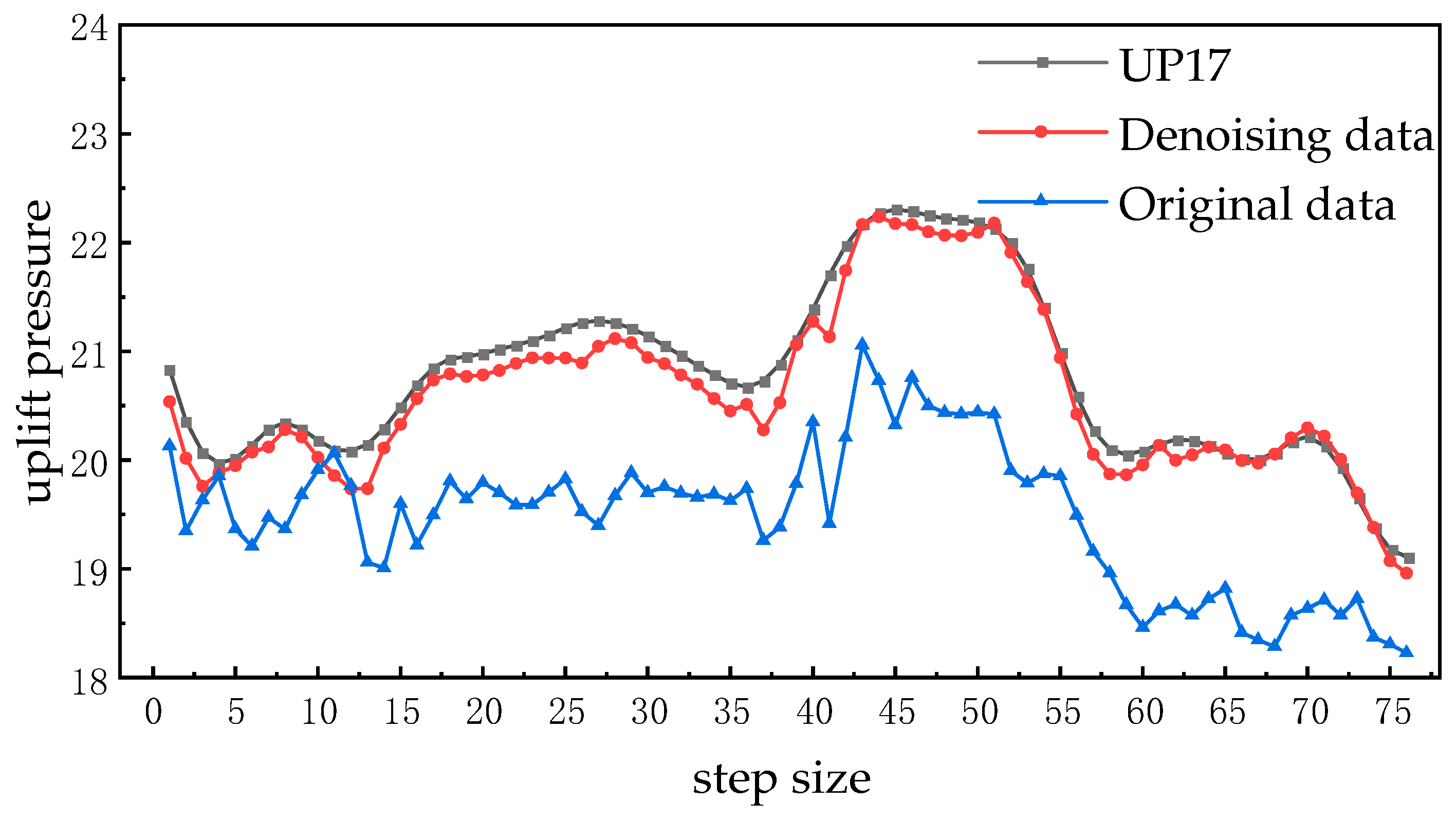
3.1. Denoising of Uplift Pressure-Monitoring Data
3.2. Impact Factor and Input Data Set Analysis
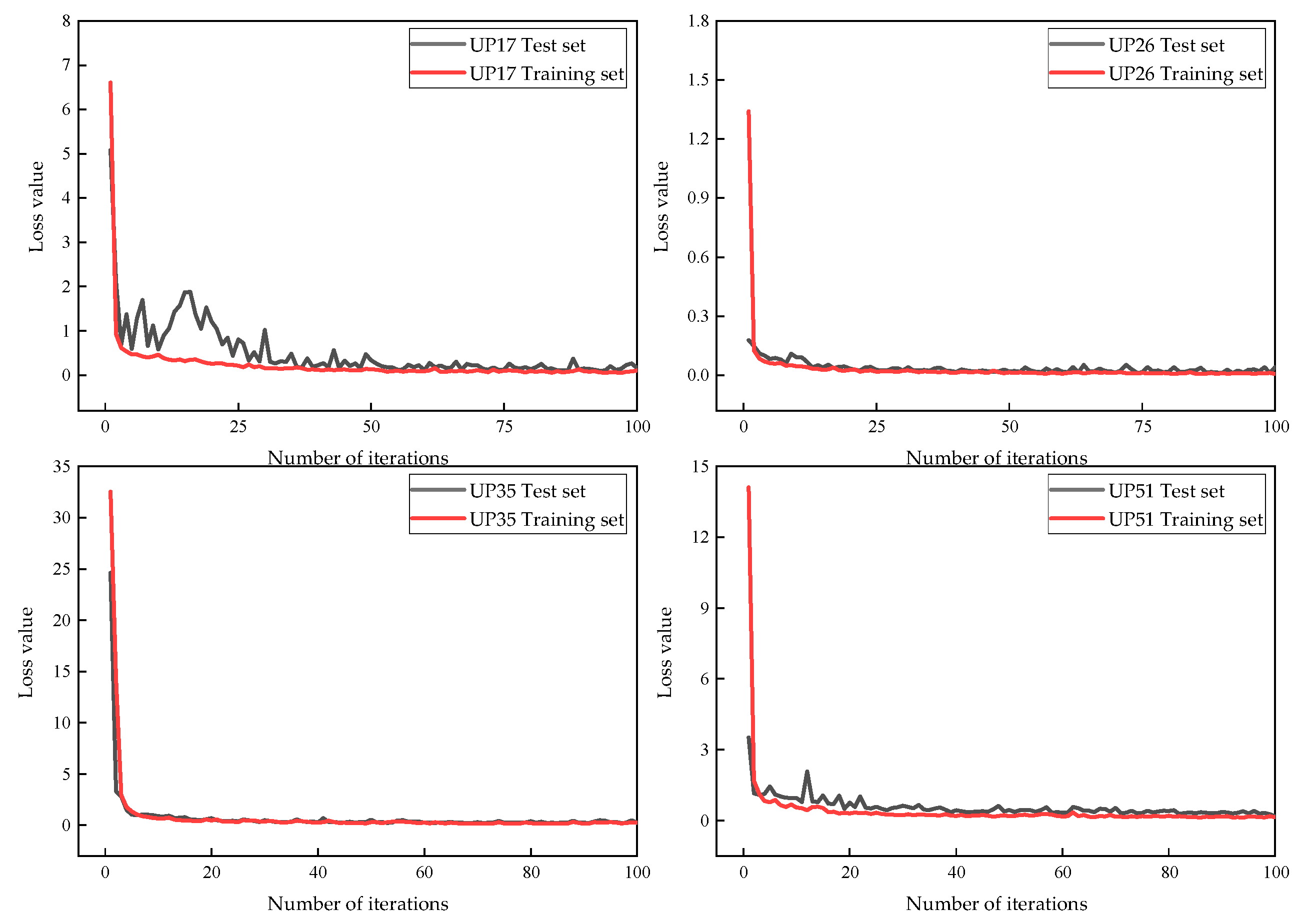
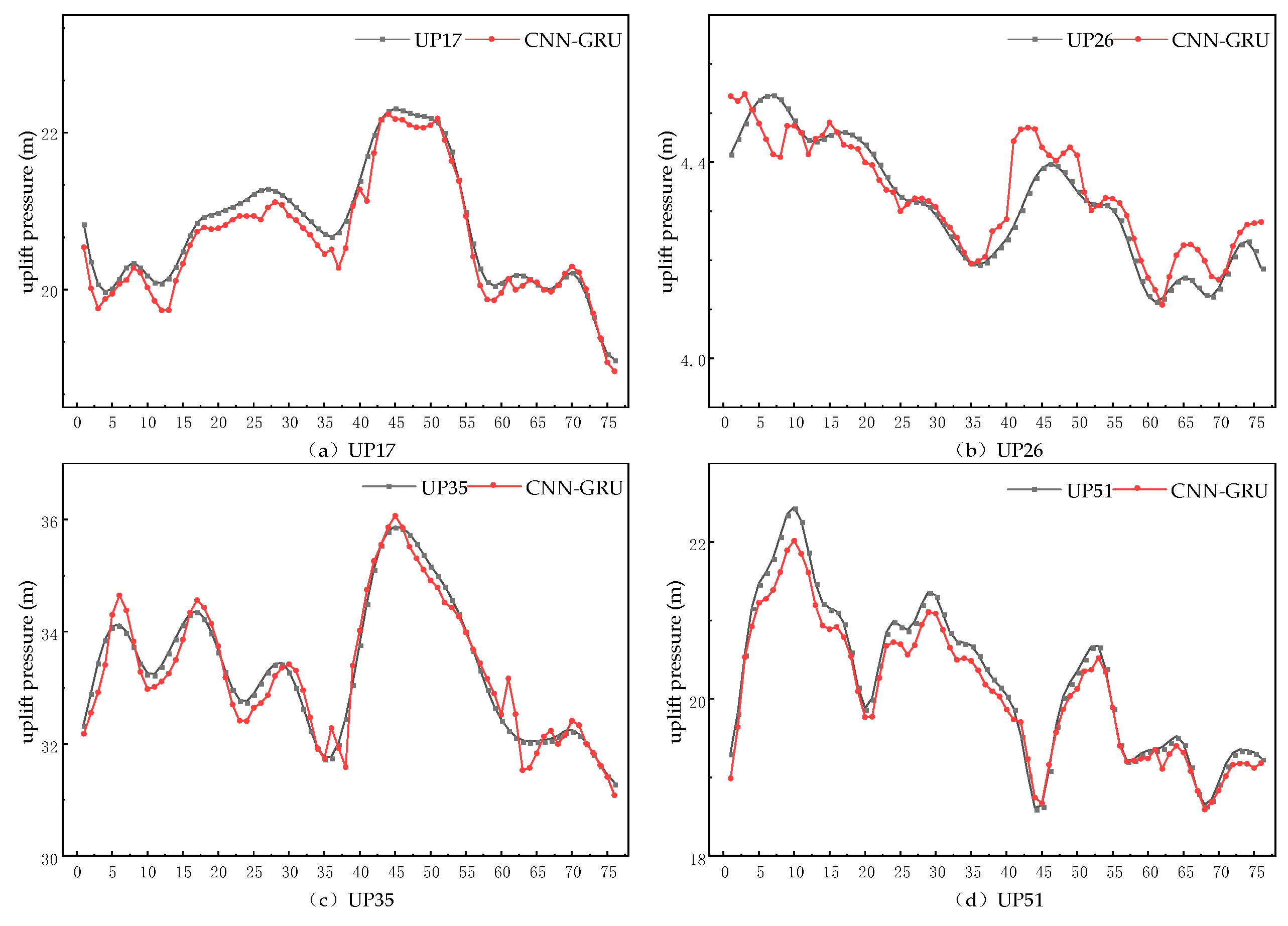
3.3. Model Prediction
4. Discussion
4.1. Analysis of the Denoising Effect of Uplift Pressure-Monitoring Data
4.2. Analysis of the Uplift Pressure Prediction Results
- (1)
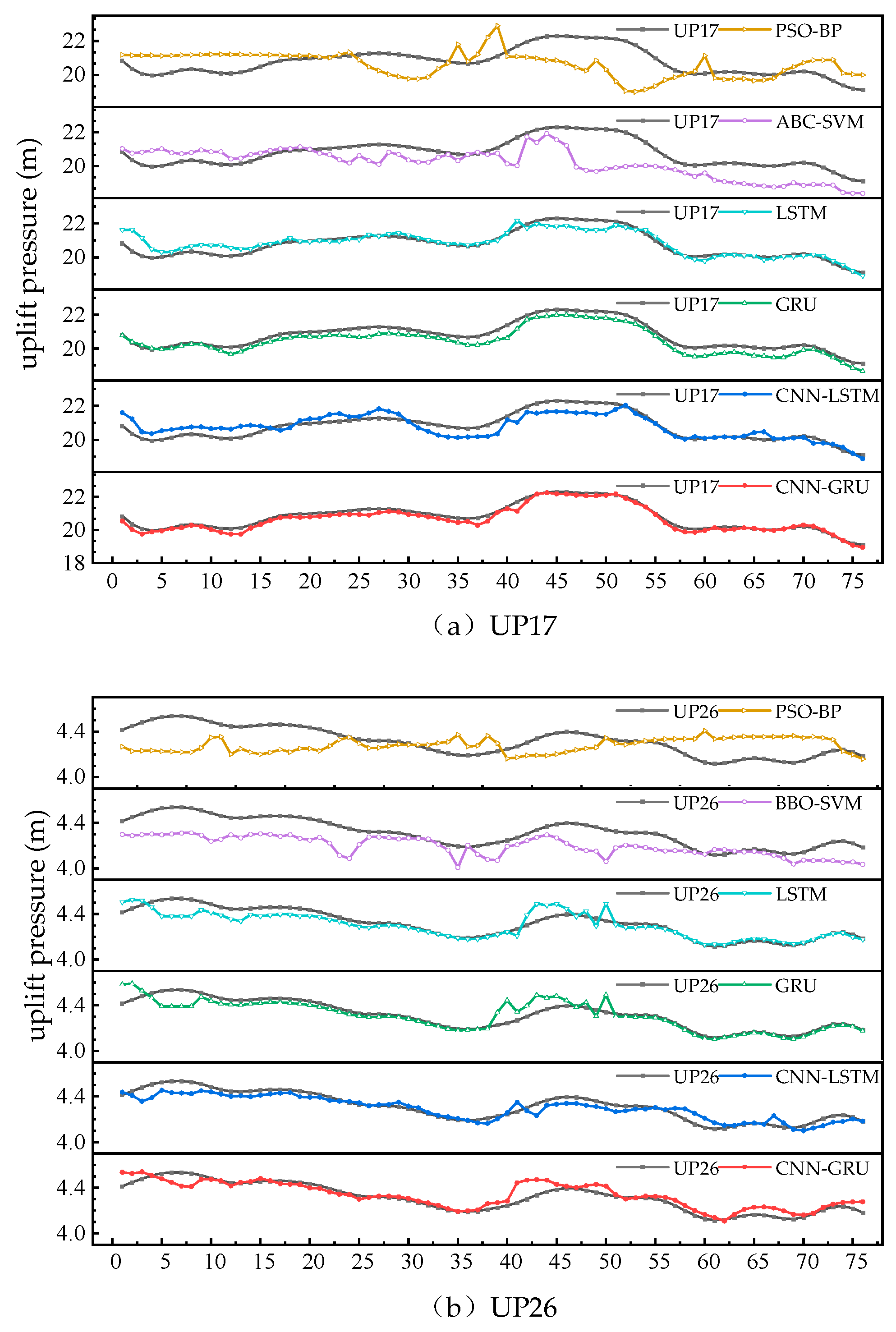
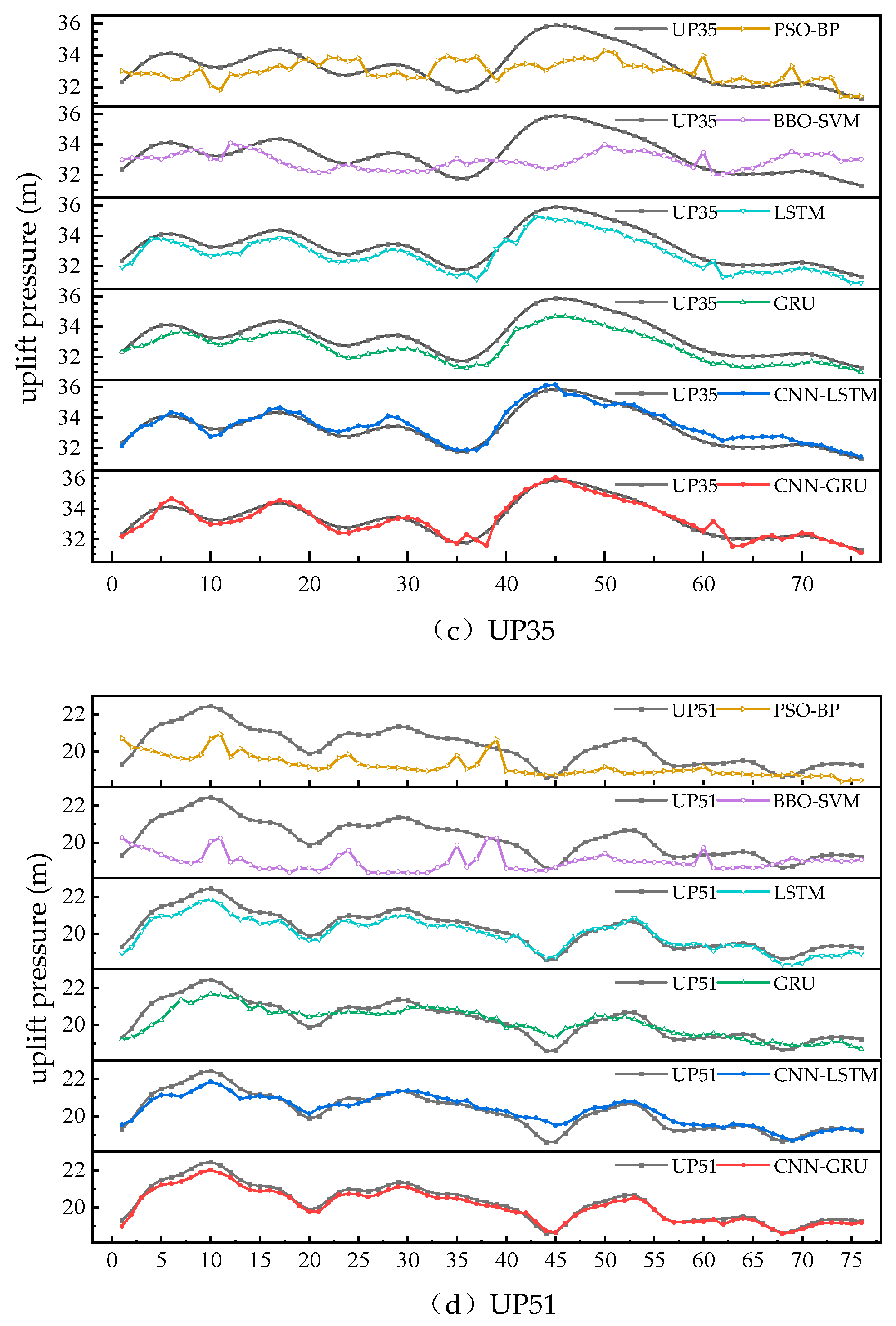
- The BP and SVM causal models were considerably weaker than the deep learning models in terms of prediction performance, both in terms of overall trends and local inflection points.
- (2)
- The overall trend of the prediction curves of LSTM and GRU was basically the same as the monitoring value of the uplift pressure, but the trend of the prediction curve in the local inflection point area deviated from the monitoring curve, and the local inflection point could not be accurately predicted.
- (3)
- The fitting effect of the CNN-GRU model on the overall trend and local fluctuations was substantially better than that of the GRU model and the LSTM model, and it could more accurately describe the overall and local inflection points of the uplift pressure, and its prediction curve was closer to the monitoring curve of the uplift pressure.
- (4)
- The CNN-GRU model fits similarly to the CNN-LSTM model on the overall trend and local fluctuations at the UP26, UP35, and UP51 measurement points. However, the CNN-GRU model performs considerably better than the CNN-LSTM model at the UP17 measurement point.
- (1)
- Although causal models, such as BP and SVM, have reasonable prediction results for small sample data, they are unable to learn from data with time series characteristics, resulting in unsatisfactory prediction results for large sample data. In addition, the running time of the model in Table 6 shows that the running time of the SVM model increases exponentially when dealing with large sample data. This is because SVM usually uses the kernel matrix of the dataset to describe the similarity between samples, and when dealing with large sample data, the number of matrix elements increases squarely, resulting in unsatisfactory computational power and operational efficiency.
- (2)
- The LSTM model, GRU model, and CNN-GRU model, which consider the time series characteristics of historical uplift pressure-monitoring data, have obvious advantages over the PSO-BP model and ABC-SVM model. The performance of the LSTM model and GRU model is similar, but because the GRU model integrates the forget gate and input gate of the LSTM model into an update gate, which reduces the parameters required for training the GRU model [29], the training iteration of the GRU model is faster than that of the LSTM model with lower computational cost and higher operational efficiency.
- (3)
- The LSTM model and GRU model do not perform accurately enough on some of the measurement points with more fluctuations due to the inability to mine the potentially hidden information on the local fluctuation features of some of the measurement points. In contrast, CNN is able to extract the continuous and discontinuous features of sequence data and mine the variation characteristics of local fluctuation of uplift pressure, so the CNN-GRU model has better results compared with the LSTM model and GRU model.
- (4)
- The CNN-LSTM model predicts similarly to the CNN-GRU model, but because the model requires too many parameters to be trained and the amount of data is small, overfitting occurs at some prediction points, which makes the prediction results less than ideal.
- (1)
- The model proposed in this study has only been validated for uplift pressure prediction, and its suitability in different scenarios cannot be determined.
- (2)
- There are many hyperparameters involved in the model, and hyperparameters are adjustment knobs that control the structure, function, efficiency, and other functions of the model. These parameters basically have different settings in various scenarios, and currently, there are no uniform selection criteria, so they can only be determined by repeated trials in actual situations. Finding the optimal configuration of hyperparameters in these deep learning models in the high-dimensional data space involved in the field of dam safety monitoring is a major challenge and a difficulty to overcome in the future.
- (3)
- The model established in this study mainly focuses on individual measurement points for prediction while considering the time dimension of monitoring data, but each monitoring point of the dam will also be affected by the spatial dimension, i.e., the changing pattern of each monitoring point will be different under different spatial distribution locations. Therefore, determining the correlation links of each monitoring point of the dam in the spatial dimension, studying the variation law of each point under various spatial distributions, and establishing a dam safety prediction model with coupled spatio-temporal correlation characteristics are directions for future development.
5. Conclusions
- (1)
- In this study, the CNN-GRU model is proposed, in which the CNN network is used to extract potential connections and hidden information among the influencing factors of uplift pressure, and the GRU network is used to learn time series correlation features in the monitoring data for uplift pressure.
- (2)
- The CNN-GRU model was used to predict the uplift pressure data: MAE was 0.1554, 0.0398, 0.2306, and 0.1827. RMSE errors were 0.1903, 0.0548, 0.2916, and 0.2127.
- (3)
- In comparison with the CNN-LSTM, LSTM, GRU, PSO-BP, and ABC-SVM models, the CNN-GRU model constructed in this study has a better prediction effect on the overall trend and local fluctuation of the uplift pressure. Based on the accuracy assessment index, the model is more accurate than the other models, and the prediction curves are close to the surveillance data. The model can improve the utilization of dam safety monitoring results and has engineering practicality for safe dam operation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kalinina, A.; Spada, M.; Burgherr, P. Application of a Bayesian hierarchical modeling for risk assessment of accidents at hydropower dams. Saf. Sci. 2018, 110, 164–177. [Google Scholar] [CrossRef]
- Wen, Z.; Zhou, R.; Su, H. MR and stacked GRUs neural network combined model and its application for deformation prediction of concrete dam. Expert Syst. Appl. 2022, 201, 117272. [Google Scholar] [CrossRef]
- Ma, C.; Zhao, T.; Li, G.; Zhang, A.; Cheng, L. Intelligent Anomaly Identification of Uplift Pressure Monitoring Data and Structural Diagnosis of Concrete Dam. Appl. Sci. 2022, 12, 612. [Google Scholar] [CrossRef]
- Pereira, R.; Batista, A.L.; Neves, L.C.; Casaca, J.M. A priori uplift pressure model for concrete dam foundations based on piezometric monitoring data. Struct. Infrastruct. Eng. 2021, 17, 1523–1534. [Google Scholar] [CrossRef]
- Belmokre, A.; Mihoubi, M.K.; Santillan, D. Seepage and dam deformation analyses with statistical models: Support vector regression machine and random forest. In Proceedings of the 3rd International Conference on Structural Integrity, ICSI 2019, Funchal, Portugal, 2–5 September 2019; Volume 17, pp. 698–703. [Google Scholar] [CrossRef]
- Ishfaque, M.; Dai, Q.; Haq, N.u.; Jadoon, K.; Shahzad, S.M.; Janjuhah, H.T. Use of Recurrent Neural Network with Long Short-Term Memory for Seepage Prediction at Tarbela Dam, KP, Pakistan. Energies 2022, 15, 3123. [Google Scholar] [CrossRef]
- Salazar, F.; Toledo, M.A.; Oñate, E.; Morán, R. An empirical comparison of machine learning techniques for dam behaviour modelling. Struct. Saf. 2015, 56, 9–17. [Google Scholar] [CrossRef] [Green Version]
- Ranković, V.; Grujović, N.; Divac, D.; Milivojević, N. Development of support vector regression identification model for prediction of dam structural behaviour. Struct. Saf. 2014, 48, 33–39. [Google Scholar] [CrossRef]
- Su, H.; Li, X.; Yang, B.; Wen, Z. Wavelet support vector machine-based prediction model of dam deformation. Mech. Syst. Signal Proc. 2018, 110, 412–427. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, H.; Tannant, D.D.; Lin, C.; Xia, D.; Liu, X.; Zhang, Y.; Ma, J. Combined forecasting model with CEEMD-LCSS reconstruction and the ABC-SVR method for landslide displacement prediction. J. Clean. Prod. 2021, 293, 126205. [Google Scholar] [CrossRef]
- Liu, H.-F.; Ren, C.; Zheng, Z.-T.; Liang, Y.-J.; Lu, X.-J. Study of a Gray Genetic BP Neural Network Model in Fault Monitoring and a Diagnosis System for Dam Safety. ISPRS Int. J. Geo-Inf. 2018, 7, 4. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Feng, X. Prediction of dam horizontal displacement based on CNN-LSTM and attention mechanism. Acad. J. Archit. Geotech. Eng. 2021, 3, 6. [Google Scholar] [CrossRef]
- Zhu, Y.; Gao, Y.; Wang, Z.; Cao, G.; Wang, R.; Lu, S.; Li, W.; Nie, W.; Zhang, Z. A Tailings Dam Long-Term Deformation Prediction Method Based on Empirical Mode Decomposition and LSTM Model Combined with Attention Mechanism. Water 2022, 14, 1229. [Google Scholar] [CrossRef]
- Cho, M.; Kim, C.; Jung, K.; Jung, H. Water Level Prediction Model Applying a Long Short-Term Memory (LSTM)–Gated Recurrent Unit (GRU) Method for Flood Prediction. Water 2022, 14, 2221. [Google Scholar] [CrossRef]
- Jia, P.; Zhang, H.; Liu, X.; Gong, X. Short-term photovoltaic power forecasting based on VMD and ISSA-GRU. IEEE Access 2021, 9, 105939–105950. [Google Scholar] [CrossRef]
- Yang, B.; Xiao, T.; Wang, L.; Huang, W. Using Complementary Ensemble Empirical Mode Decomposition and Gated Recurrent Unit to Predict Landslide Displacements in Dam Reservoir. Sensors 2022, 22, 1320. [Google Scholar] [CrossRef]
- Dai, Y.; Wang, Y.; Leng, M.; Yang, X.; Zhou, Q. LOWESS smoothing and Random Forest based GRU model: A short-term photovoltaic power generation forecasting method. Energy 2022, 256, 124661. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, P.; Peng, X.; Wu, Z.; Yuan, H. Fault location of transmission line based on CNN-LSTM double-ended combined model. Energy Rep. 2022, 8, 781–791. [Google Scholar] [CrossRef]
- Li, W.; Logenthiran, T.; Woo, W.L. Multi-GRU prediction system for electricity generation’s planning and operation. IET Gener. Transm. Distrib. 2019, 13, 1630–1637. [Google Scholar] [CrossRef]
- Yi, D.; Ahn, J.; Ji, S. An Effective Optimization Method for Machine Learning Based on ADAM. Appl. Sci. 2020, 10, 1073. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Lian, J.; Liu, Z.; Wang, H.; Dong, X. Adaptive variational mode decomposition method for signal processing based on mode characteristic. Mech. Syst. Signal Proc. 2018, 107, 53–77. [Google Scholar] [CrossRef]
- Li, F.; Ma, G.; Chen, S.; Huang, W. An ensemble modeling approach to forecast daily reservoir inflow using bidirectional long-and short-term memory (Bi-LSTM), variational mode decomposition (VMD), and energy entropy method. Water Resour. Manag. 2021, 35, 2941–2963. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, G.; Li, M.; Yin, H. Variational mode decomposition denoising combined the detrended fluctuation analysis. Signal Process. 2016, 125, 349–364. [Google Scholar] [CrossRef]
- Wu, Q.; Lin, H. Daily urban air quality index forecasting based on variational mode decomposition, sample entropy and LSTM neural network. Sustain. Cities Soc. 2019, 50, 101657. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, D.N.; Yang, J.M.; Liu, Z.H. Short-term PV Power Prediction based on VMD-SE-TCAN Model. J. Comput. 2022, 33, 25–36. [Google Scholar] [CrossRef]
- Li, X.; Su, H.; Hu, J. The Prediction Model of Dam Uplift Pressure Based on Random Forest. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Phuket, Thailand, 2–5 August 2017; Volume 229, p. 012025. [Google Scholar] [CrossRef] [Green Version]
- Lin, G.; Lin, A.; Gu, D. Using support vector regression and K-nearest neighbors for short-term traffic flow prediction based on maximal information coefficient. Inf. Sci. 2022, 608, 517–531. [Google Scholar] [CrossRef]
- Gao, S.; Huang, Y.; Zhang, S.; Han, J.; Wang, G.; Zhang, M.; Lin, Q. Short-term runoff prediction with GRU and LSTM networks without requiring time step optimization during sample generation. J. Hydrol. 2020, 589, 125188. [Google Scholar] [CrossRef]
| Network Structure | Experimental Parameters | Parameter Value |
|---|---|---|
| Overall Structure | optimization algorithm | Adam |
| batch size | 128 | |
| epochs | 100 | |
| CNN structure (2 layers) | convolution kernels | 16, 32 |
| kernel size | 2 | |
| strides | 2 | |
| activation | ||
| pool size | 2 | |
| strides | 2 | |
| GRU structure (3 layers) | hidden neurons | 64, 64, 64 |
| dropout | 0.2 | |
| activation | ||
| Fully connected layer (1 layer) | units | 1 |
| activation | None |
| Dam Section | Left Bank Water Blocking Section | Diversion Section | Discharge Section | Spillway Section | Bottom Outlet Section | Ship Lock | Right -Shore Water Blocking Section |
|---|---|---|---|---|---|---|---|
| Number | 1#~7# | 8#~21# | 22# | 23#~35# | 36# | 37#~38# | 39#~42# |
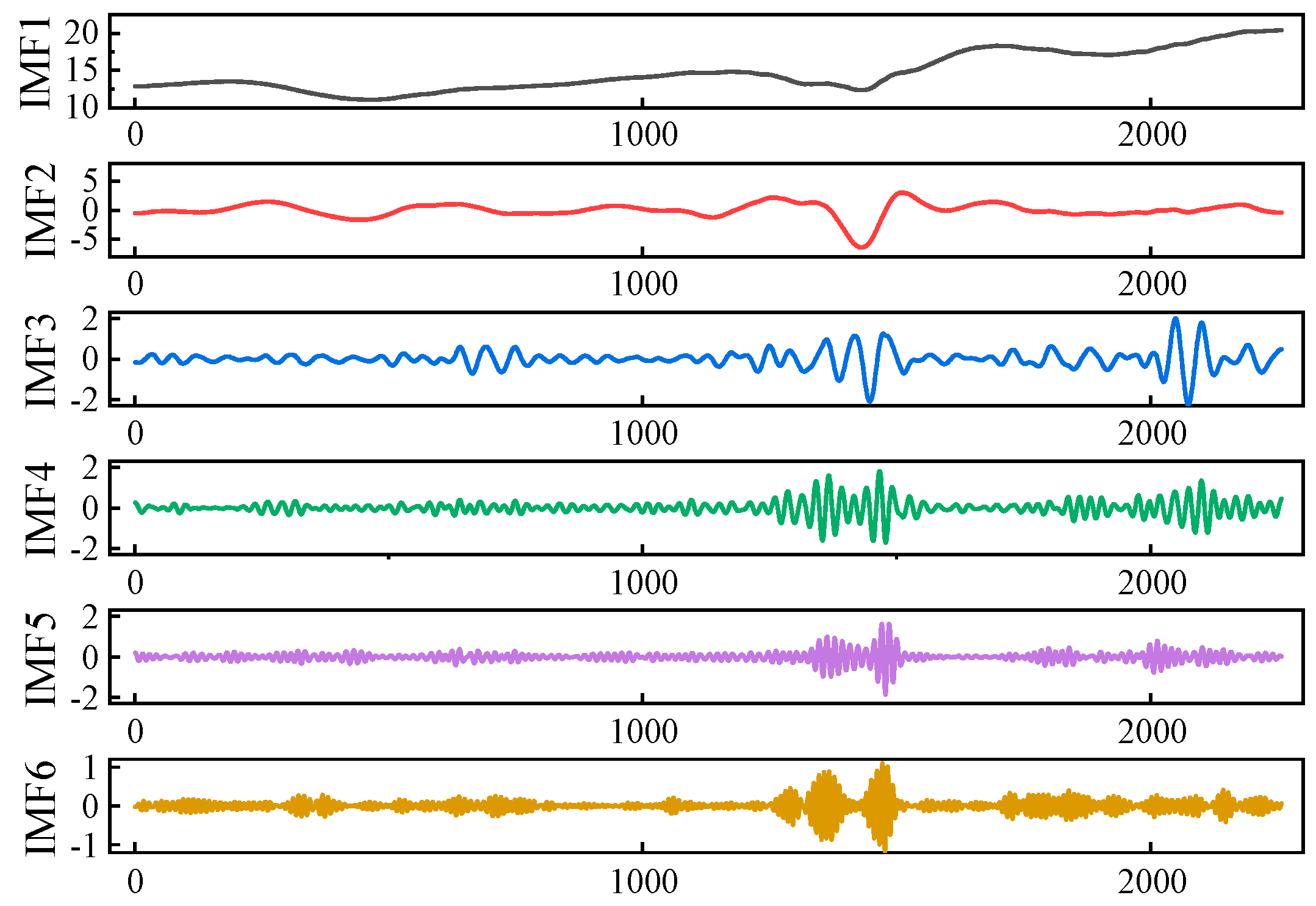
| Subsequences | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 |
|---|---|---|---|---|---|---|
| SE | 0.0111 | 0.0438 | 0.2094 | 0.4050 | 0.5324 | 0.4856 |
| Component Name | Factors | Whether to Be Selected | |
|---|---|---|---|
| Time effects | θ | 0.8995 | Y |
| lnθ | 0.8995 | Y | |
| Water pressure component | HU | 0.1945 | N |
| (HU)2 | 0.1945 | N | |
| HU(2–3) | 0.2078 | N | |
| HU(4–7) | 0.2175 | N | |
| H(U8–15) | 0.2487 | Y | |
| HU(16–30) | 0.2675 | Y | |
| HU(31–60) | 0.2537 | Y | |
| HD | 0.2451 | Y | |
| Temperature component | T0–1 | 0.4725 | N |
| T2–7 | 0.5147 | N | |
| T8–15 | 0.5253 | N | |
| T16–30 | 0.6071 | Y | |
| T31–60 | 0.6064 | Y | |
| T61–120 | 0.7076 | Y | |
| Rainfall component | R0–1 | 0.1908 | N |
| R2–3 | 0.1562 | N | |
| R4–7 | 0.1723 | N | |
| R8–15 | 0.1804 | N | |
| R16–30 | 0.1912 | N | |
| R31–60 | 0.1984 | N |
| UP17 | RMSE | MAE |
|---|---|---|
| Original data | 1.3614 | 1.2890 |
| denoised data | 0.1903 | 0.1554 |
| Points | UP17 | UP26 | ||||
| Models | RMSE/(m) | MAE/(m) | Time/s | RMSE/(m) | MAE/(m) | Time/s |
| LSTM | 0.3312 | 0.2309 | 325.12 | 0.0605 | 0.0429 | 353.95 |
| GRU | 0.3638 | 0.3321 | 199.23 | 0.0629 | 0.0426 | 277.76 |
| CNN-GRU | 0.1903 | 0.1554 | 276.38 | 0.0548 | 0.0398 | 291.83 |
| PSO-BP | 1.0973 | 0.8919 | 215.43 | 0.1674 | 0.1416 | 212.69 |
| ABC-SVM | 1.0165 | 0.8303 | 464.51 | 0.1438 | 0.1225 | 582.21 |
| Points | UP35 | UP51 | ||||
| Models | RMSE/(m) | MAE/(m) | Time/s | RMSE/(m) | MAE/(m) | Time/s |
| LSTM | 0.5650 | 0.5305 | 382.02 | 0.3549 | 0.3059 | 321.54 |
| GRU | 0.7577 | 0.6967 | 300.28 | 0.4484 | 0.3602 | 183.03 |
| CNN-GRU | 0.2916 | 0.2306 | 310.53 | 0.2127 | 0.1827 | 222.77 |
| PSO-BP | 1.1081 | 0.8951 | 154.85 | 1.2607 | 1.0787 | 186 |
| ABC-SVM | 1.2673 | 0.9972 | 569.27 | 1.6306 | 1.3256 | 523.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, G.; Wang, S.; Xiao, M.; Hu, S. Research on the Uplift Pressure Prediction of Concrete Dams Based on the CNN-GRU Model. Water 2023, 15, 319. https://doi.org/10.3390/w15020319
Hua G, Wang S, Xiao M, Hu S. Research on the Uplift Pressure Prediction of Concrete Dams Based on the CNN-GRU Model. Water. 2023; 15(2):319. https://doi.org/10.3390/w15020319
Chicago/Turabian StyleHua, Guowei, Shijie Wang, Meng Xiao, and Shaohua Hu. 2023. "Research on the Uplift Pressure Prediction of Concrete Dams Based on the CNN-GRU Model" Water 15, no. 2: 319. https://doi.org/10.3390/w15020319
APA StyleHua, G., Wang, S., Xiao, M., & Hu, S. (2023). Research on the Uplift Pressure Prediction of Concrete Dams Based on the CNN-GRU Model. Water, 15(2), 319. https://doi.org/10.3390/w15020319





