Experimental Study of Geometric Shape and Size of Sill Effects on the Hydraulic Performance of Sluice Gates
Abstract
:1. Introduction
2. Materials and Methods
Experimental Set-Up
3. Results
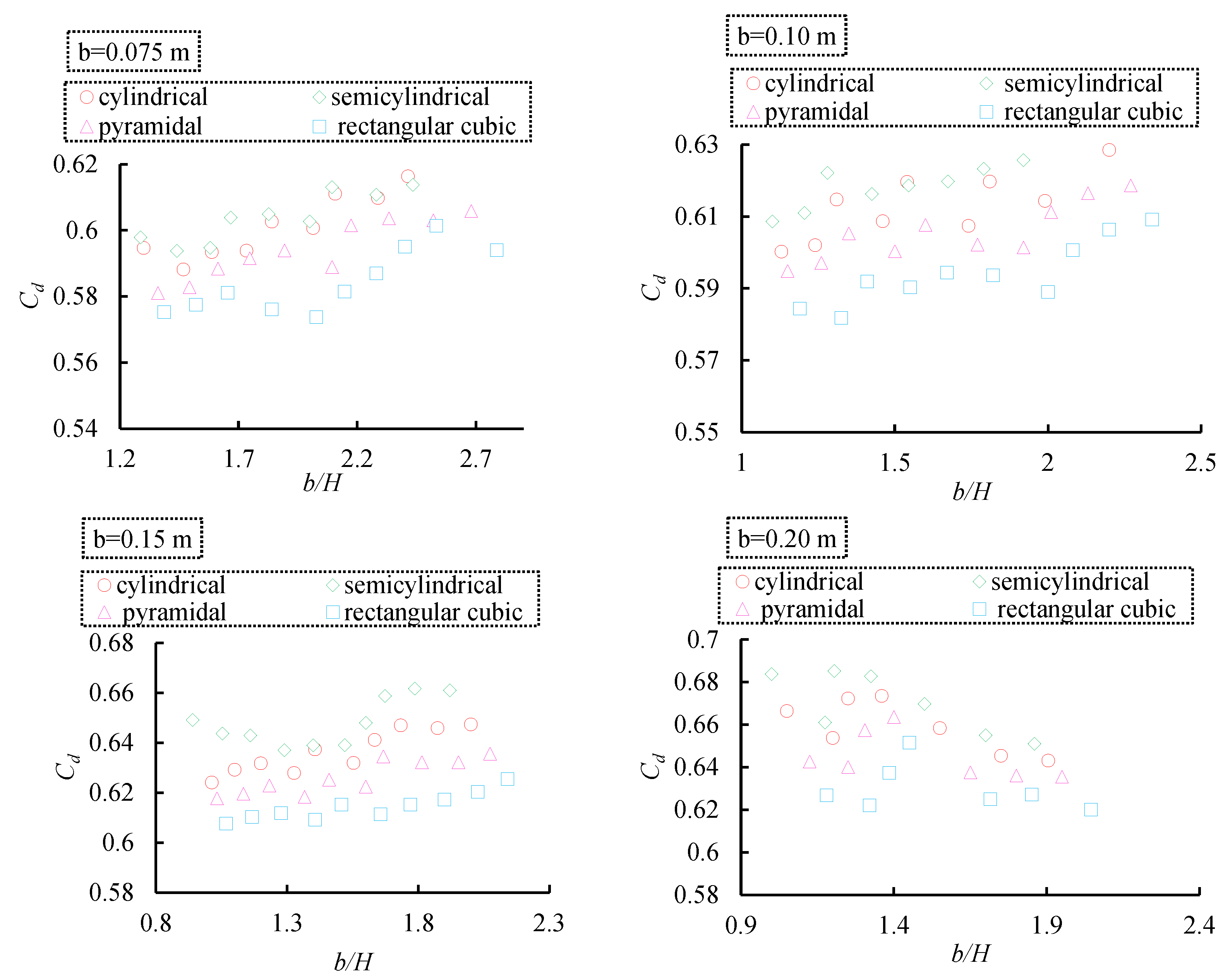
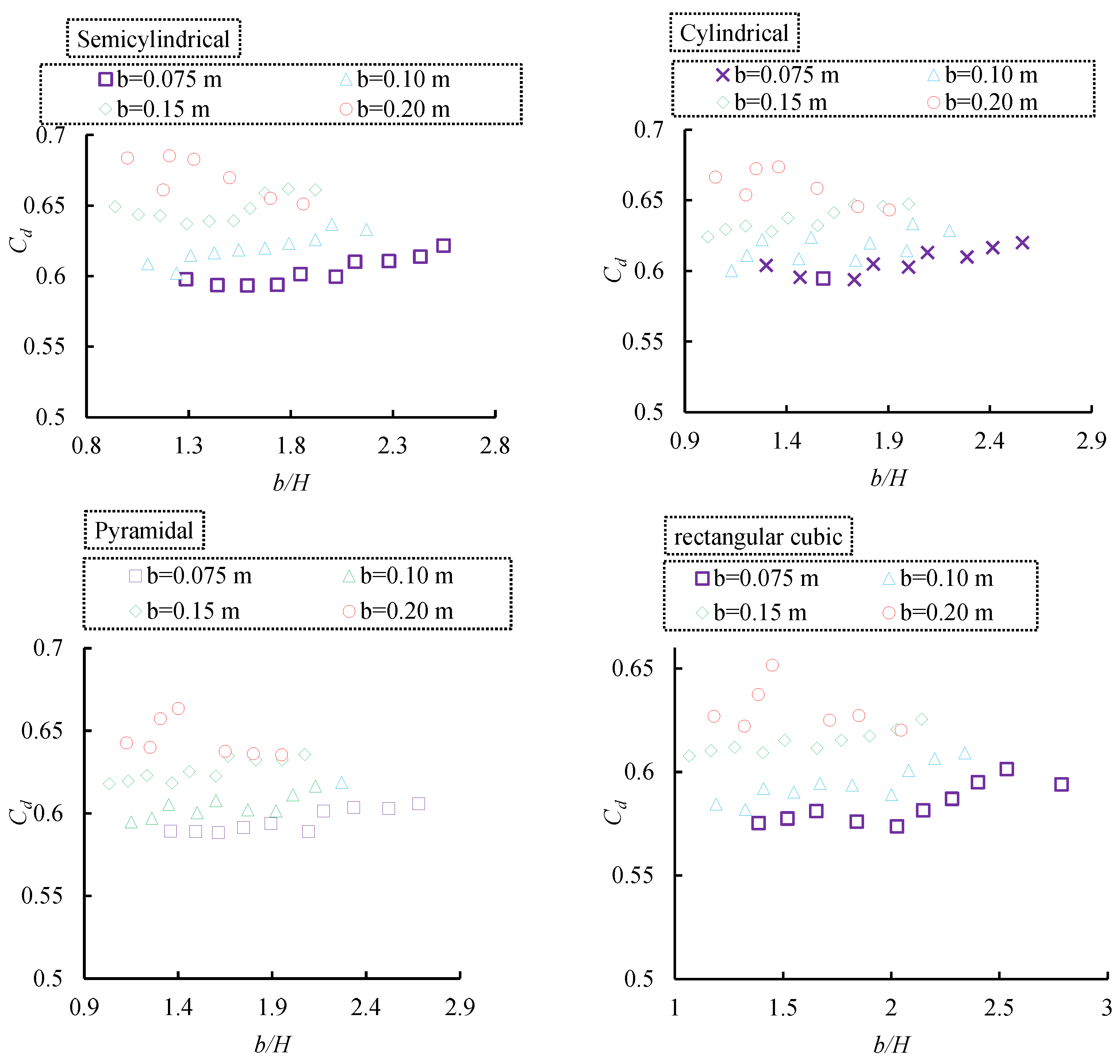
3.1. Effect of Sill Geometry and Width on Discharge Coefficient
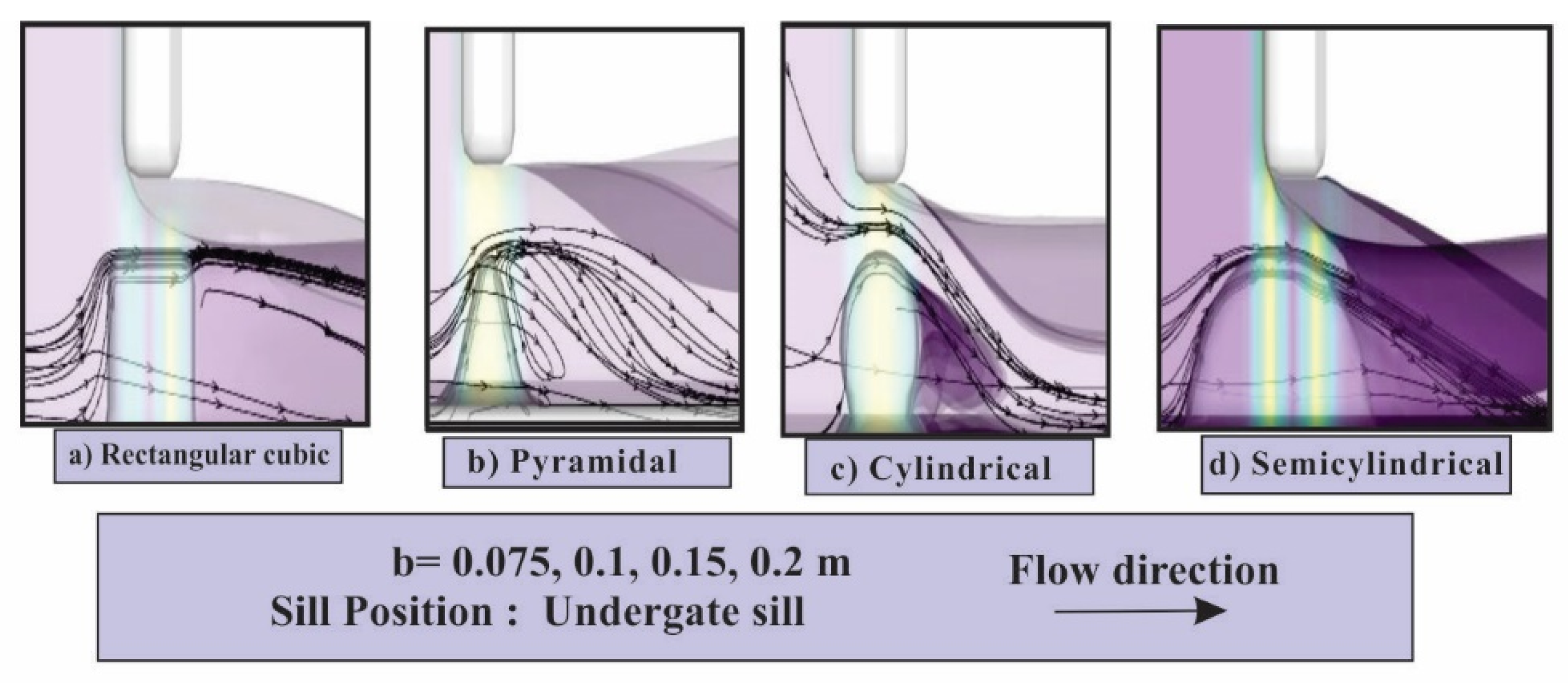
3.1.1. Hydraulic Jump Characteristic with Sill
3.1.2. Non-Sill Mode
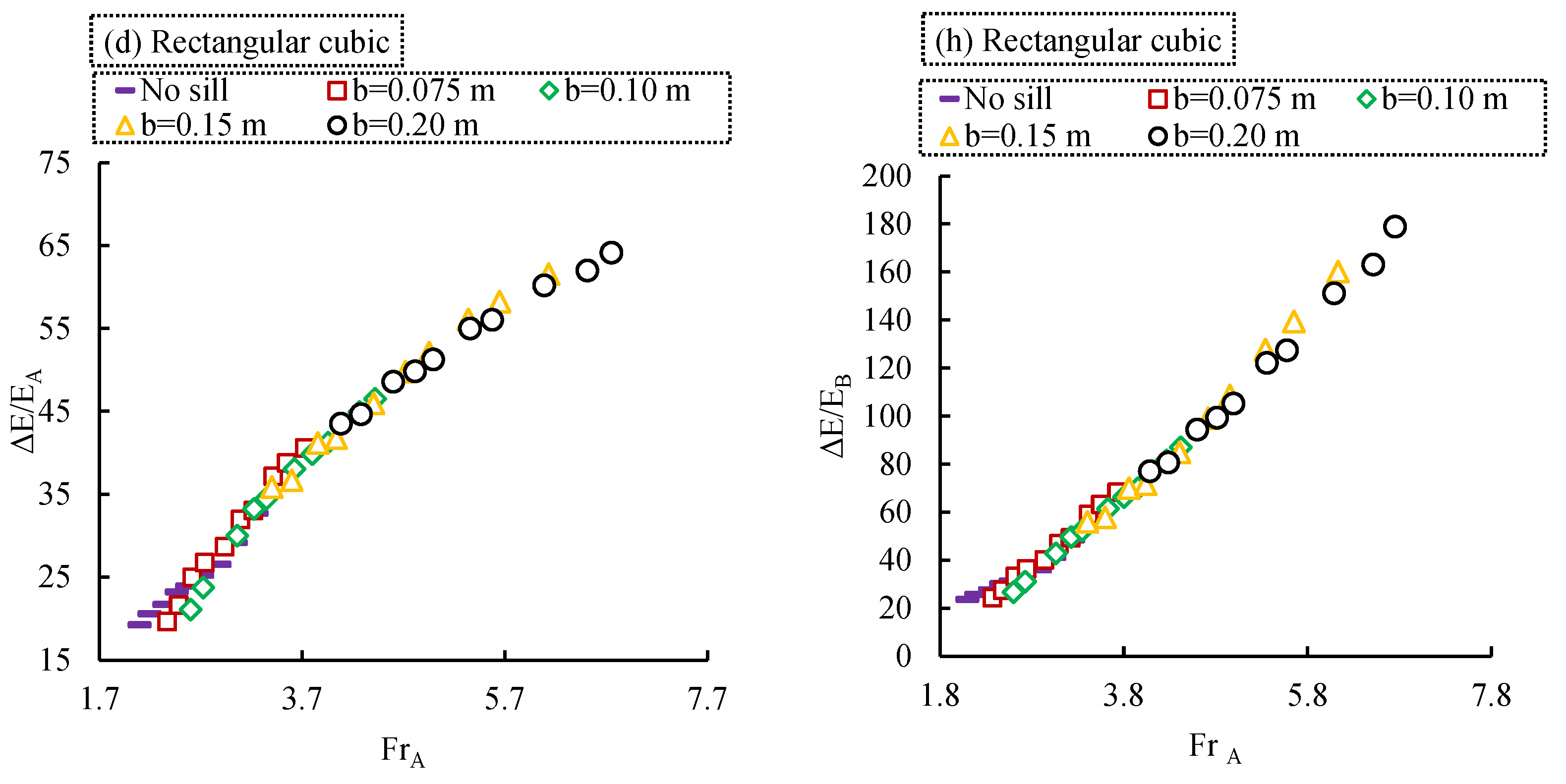
3.1.3. The Effect of Sill Width on Hydraulic Jump Performance
3.1.4. The Effect of Sill Width on the Performance of Hydraulic Jump Relative Depths
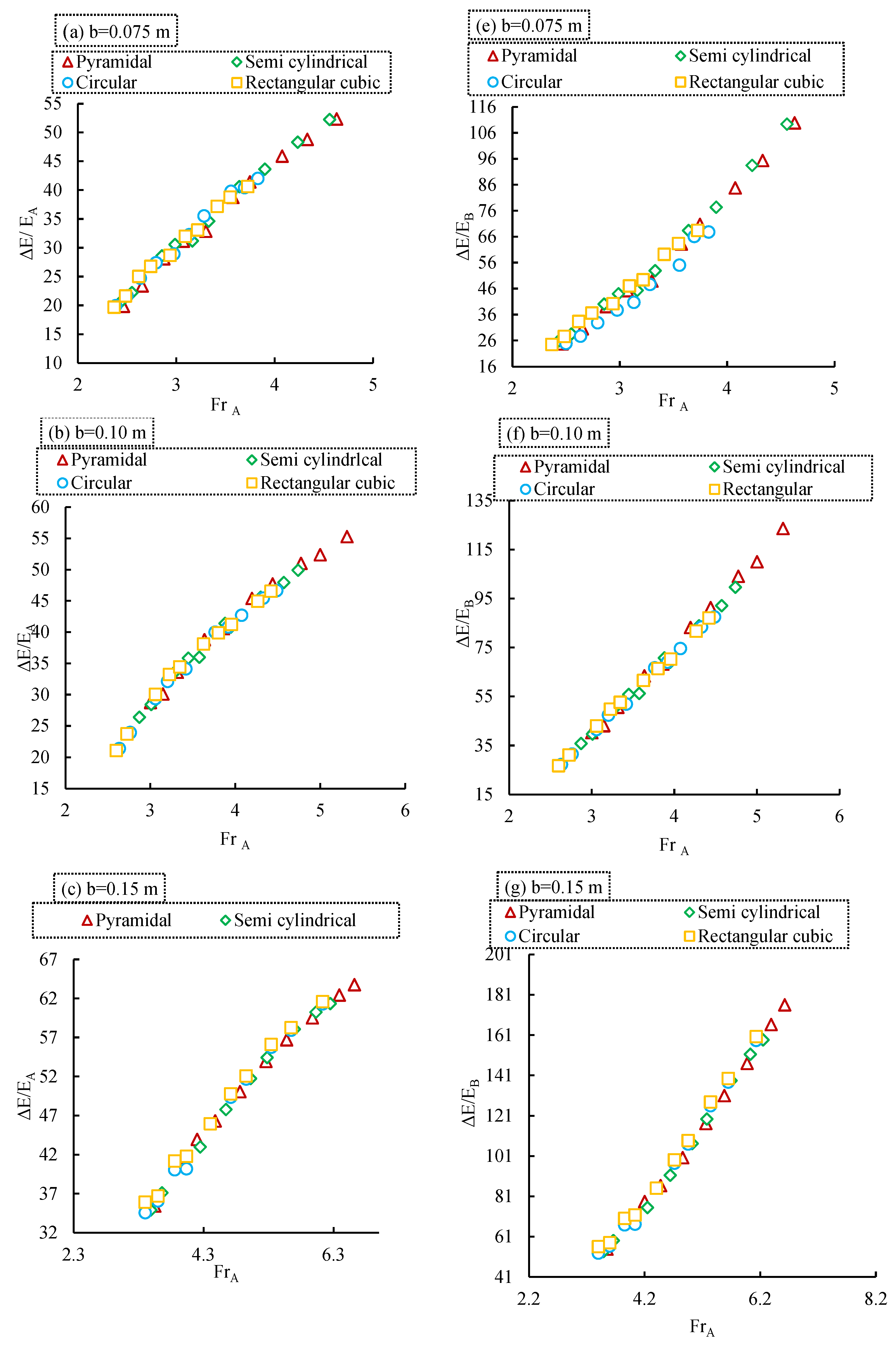
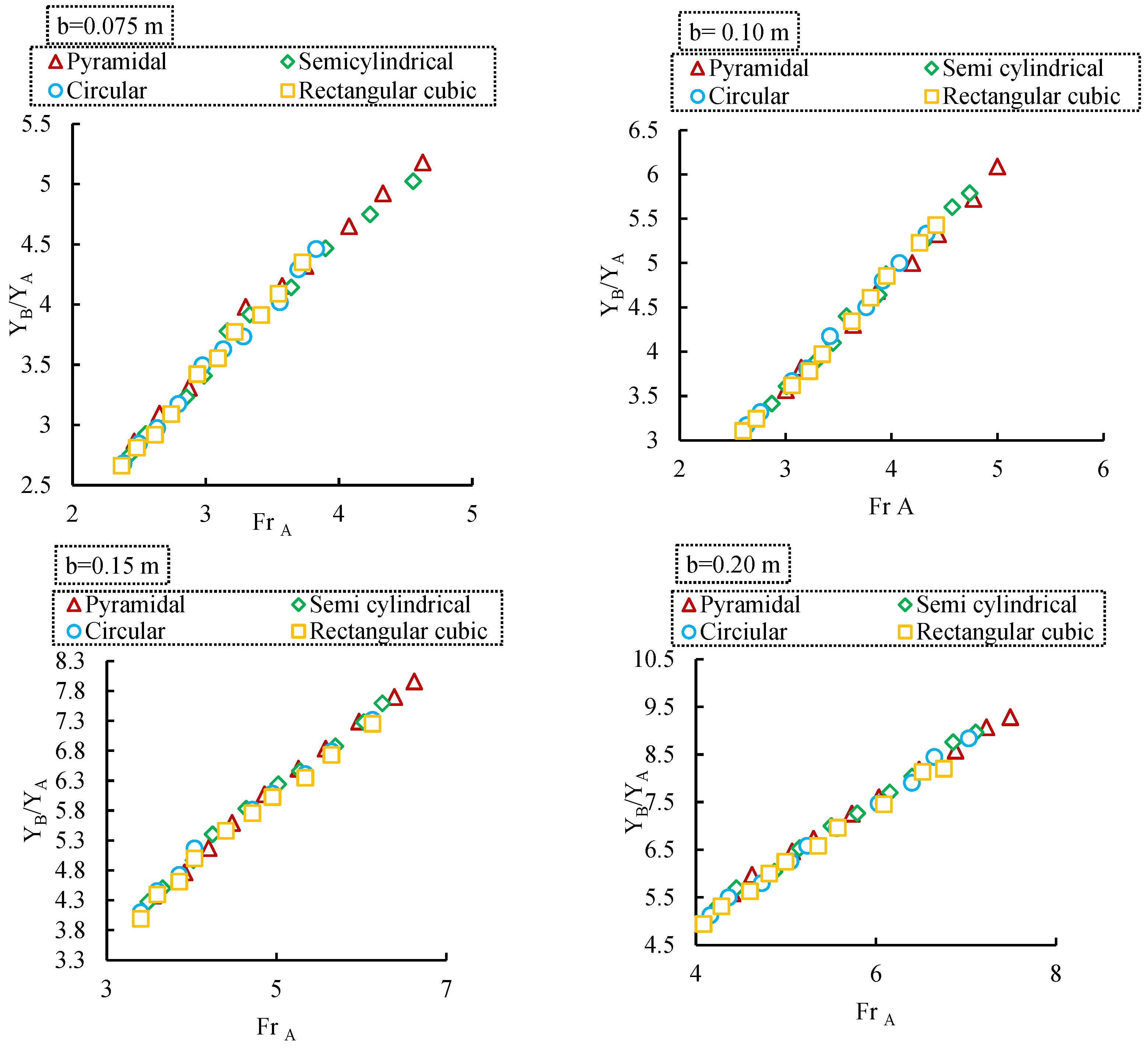
3.1.5. Effect of Sill Geometry on Hydraulic Jump Performance
3.1.6. The Effect of Sill Geometry on the Performance of Hydraulic Jump Relative Depths
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Seyed Hoshiyar, S.M.; Pirmoradian, N.; Ashrafzadeh, A.; Parvaresh Rizi, A. Performance Assessment of a Water Deliery Canal to Improve Agricultural Water Distribution. Water Resour. Manag. 2021, 35, 2487–2501. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Norouzi, R.; Abbaszadeh, H.; Kuriqi, A.; Di Francesco, S. Influence of Sill on the Hydraulic Regime in Sluice Gates: An Experimental and Numerical Analysis. Fluids 2022, 7, 244. [Google Scholar] [CrossRef]
- Henry, H. Discussion of Diffusion of Submerged Jets, by Albertson, ML, Dai, YB. Trans. Am. Soc. Civ. Eng. 1950, 115, 687–694. [Google Scholar]
- Rajaratnam, N.; Subramanya, K. Flow Equation for the Sluice Gate. J. Irrig. Drain. Div. 1967, 93, 167–186. [Google Scholar] [CrossRef]
- Swamee, P.K. Sluice-gate discharge equations. J. Irrig. Drain. Eng. 1992, 118, 56–60. [Google Scholar] [CrossRef]
- Ferro, V. Simultaneous Flow over and under a gate. Irrig. Drain. Eng. 2000, 126, 190–193. [Google Scholar]
- Reda, A.E.R. Modeling of flow characteristics beneath vertical and inclined sluice gates using artificial neural networks. Ain Shams Eng. J. 2016, 7, 917–924. [Google Scholar]
- Salmasi, F.; Abraham, J. Prediction of discharge coefficients for sluice gates equipped with different geometric sills under the gate using multiple non-linear regression (MNLR). J. Hydrol. 2020, 597, 125728. [Google Scholar] [CrossRef]
- Pástor, M.; Bocko, J.; Lengvarský, P.; Sivák, P.; Šarga, P. Experimental and Numerical Analysis of 60-Year-Old Sluice Gate Affected by Long-Term Operation. Materials 2020, 13, 5201. [Google Scholar] [CrossRef]
- Shivapur, A.V.; Prakash, M.N.S. Inclined sluice gate for flow measurement. ISH J. Hydraul. Eng. 2005, 11, 46–56. [Google Scholar] [CrossRef]
- Rajaratnam, N. Hydraulic jumps. In Advances in Hydroscience; Elsevier: Amsterdam, The Netherlands, 1967; Volume 4, pp. 197–280. [Google Scholar]
- Rajaratnam, N. Hydraulic jump on rough bed. Trans. Eng. Inst. Can. 1968, 11, 1–8. [Google Scholar]
- Ali, H.S.M. Effect of Roughened-Bed Stilling Basin on Length of Rectangular Hydraulic Jump. J. Hydraul. Eng. 1991, 117, 83–93. [Google Scholar] [CrossRef]
- Alhamid, A.A. Effective roughness on horizontal rectangular stilling basins. Trans. Ecol. Environ. 1994, 8, 8. [Google Scholar]
- Ead, S.A.; Rajaratnam, N. Hydraulic jumps on corrugated beds. J. Hydraul. Eng. 2002, 128, 656–663. [Google Scholar] [CrossRef]
- Tokyay, N.D. Effect of Channel Bed Corrugations on Hydraulic Jumps. In Impacts of Global Climate Change; ASCE: Reston, VA, USA, 2005; pp. 1–9. [Google Scholar] [CrossRef]
- Izadjoo, F.; Shafai-Bejestan, M. Corrugated bed hydraulic jump stilling basin. J. Appl. Sci. 2007, 7, 1164–1169. [Google Scholar] [CrossRef] [Green Version]
- Abbaspour, A.; Dalir, A.H.; Farsadizadeh, D.; Sadraddini, A.A. Effect of sinusoidal corrugated bed on hydraulic jump characteristics. J. Hydro-Environ. Res. 2009, 3, 109–117. [Google Scholar] [CrossRef]
- Ellayn, A.F.; Sun, Z.-L. Hydraulic jump basins with wedge-shaped baffles. J. Zhejiang Univ. A 2012, 13, 519–525. [Google Scholar] [CrossRef]
- Samadi-Boroujeni, H.; Ghazali, M.; Gorbani, B.; Nafchi, R.F. Effect of triangular corrugated beds on the hydraulic jump characteristics. Can. J. Civ. Eng. 2013, 40, 841–847. [Google Scholar] [CrossRef]
- Parsamehr, P.; Farsadizadeh, D.; Dalir, A.H.; Abbaspour, A.; Esfahani, M.J.N. Characteristics of hydraulic jump on rough bed with adverse slope. ISH J. Hydraul. Eng. 2017, 23, 301–307. [Google Scholar] [CrossRef]
- Nasr Esfahani, M.J.; Shafai Bejestan, M. Design of stilling sasins using artificial roughness. J. Civ. Eng. 2012, 2, 159–163. [Google Scholar]
- Parsamehr, P.; Hosseinzadeh Dalir, A.; Farsadi, D.; Abbaspour, A. Hydraulic jump on the bed with semi-cylindrical roughness. J. Water Soil 2012, 26, 775–785. [Google Scholar] [CrossRef]
- Neisi, K.; Shafai, B.M. Characteristics of S-jump on Roughened Bed Stilling Basin. J. Water Sci. Res. 2013, 5, 25–34. [Google Scholar]
- Jalil, S.A.; Sarhan, S.A.; Yaseen, M.S. Hydraulic Jump Properties Downstream a Sluice Gate with Prismatic Sill. Res. J. Appl. Sci. Eng. Technol. 2015, 11, 447–453. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Norouzi, R.; Ebadzadeh, P. Experimental and numerical study of sluice gate flow pattern with non- suppressed sill and its effect on discharge coefficient in free-flow conditions. J. Hydr. Struct. 2022, 8, 1–20. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Hasannia, V.; Norouzi, R.; Sihag, P.; Sadeghfam, S. Investigating the Effect of Horizontal Screen on Hydraulic Parameters of Vertical Drop. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 45, 1909–1917. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Noruzi, R.; Ebadzadeh, P. Experimental Investigation of non-suppressed sill effect with different geometry on flow pattern and discharge coefficient of sluice. J. Hydr. 2022, 17, 47–63. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Norouzi, R.; Ebadzadeh, P. Evaluation Effect of changing the sill geometries and positions on discharge coefficient of vertical sluice gate. J. Civ. Environ. Eng. 2022, 10, 46–68. [Google Scholar] [CrossRef]
- Lauria, A.; Calomino, F.; Alfonsi, G.; D’Ippolito, A. Discharge coefficients for sluice gates set in weirs at different upstream wall inclinations. Water 2020, 12, 245. [Google Scholar] [CrossRef] [Green Version]
- Madadi, M.R.; Hosseinzadeh, D.A.; Farsadizadeh, D. Investigation of flow characteristics above trapezoidal broad-crested weirs. Flow Meas. Instrument. 2014, 38, 139–148. [Google Scholar] [CrossRef]
- Nasrabadi, M.; Mehri, Y.; Ghassemi, A.; Omid, M.H. Predicting submerged hydraulic jump characteristics using machine learning methods. Water Supply 2021, 21, 4180–4194. [Google Scholar] [CrossRef]
- Raju, R. Scale effects in analysis of discharge characteristics of weir and sluice gates. In Scale Effects in Modeling Hydraulic Structures; Kobus, H., Ed.; Springer: Esslingen am Neckar, Germany, 1984. [Google Scholar]
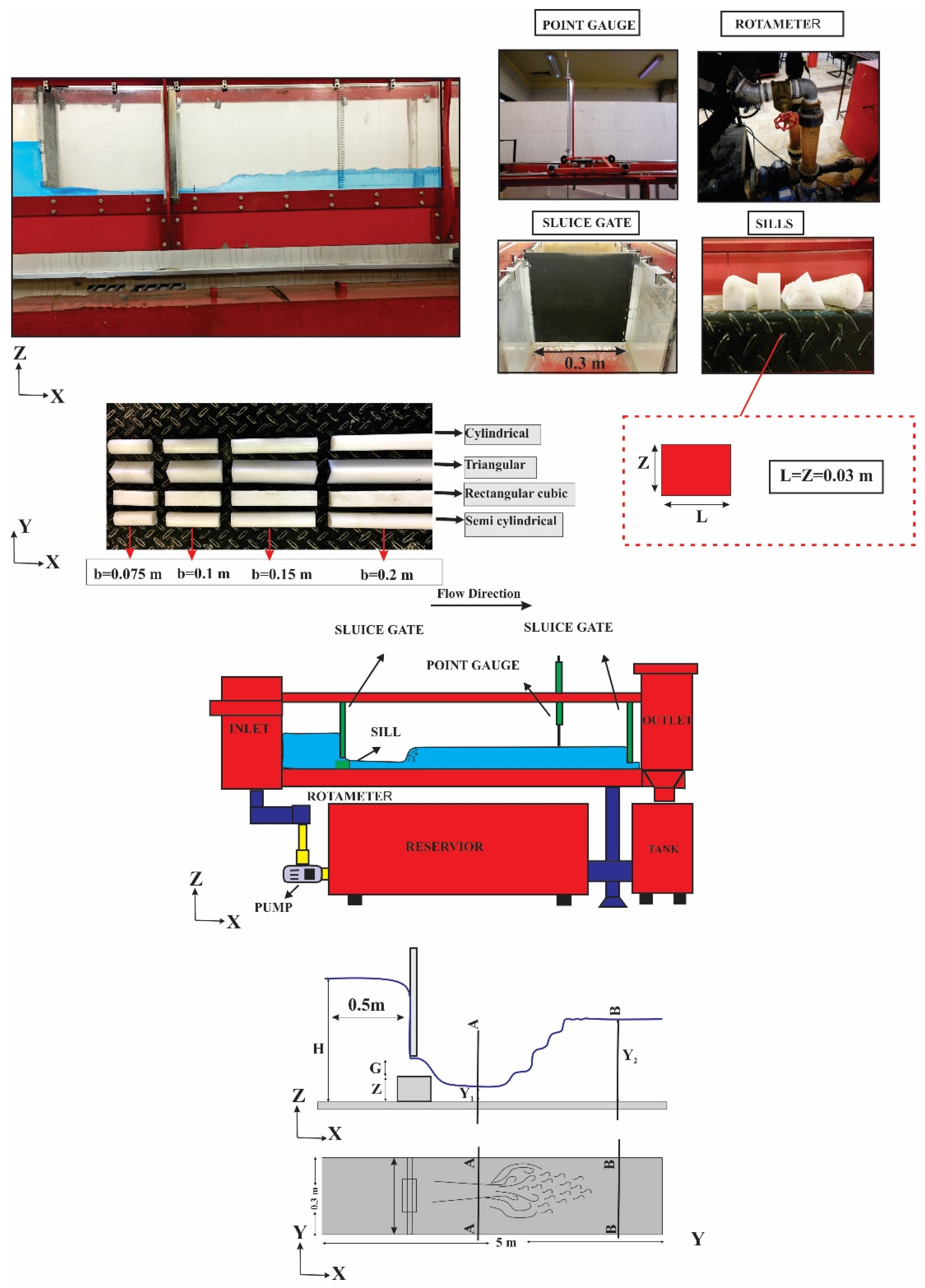



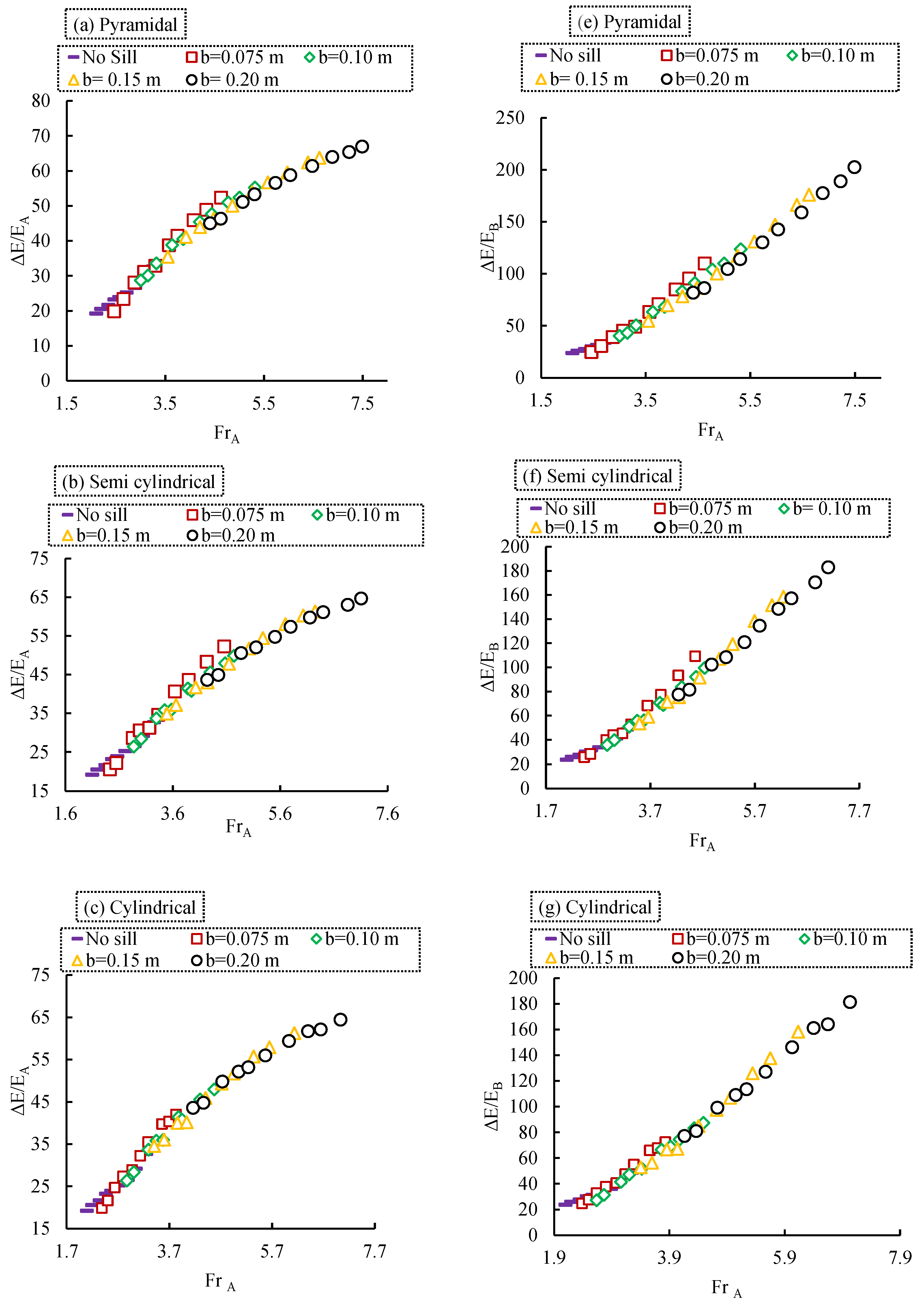
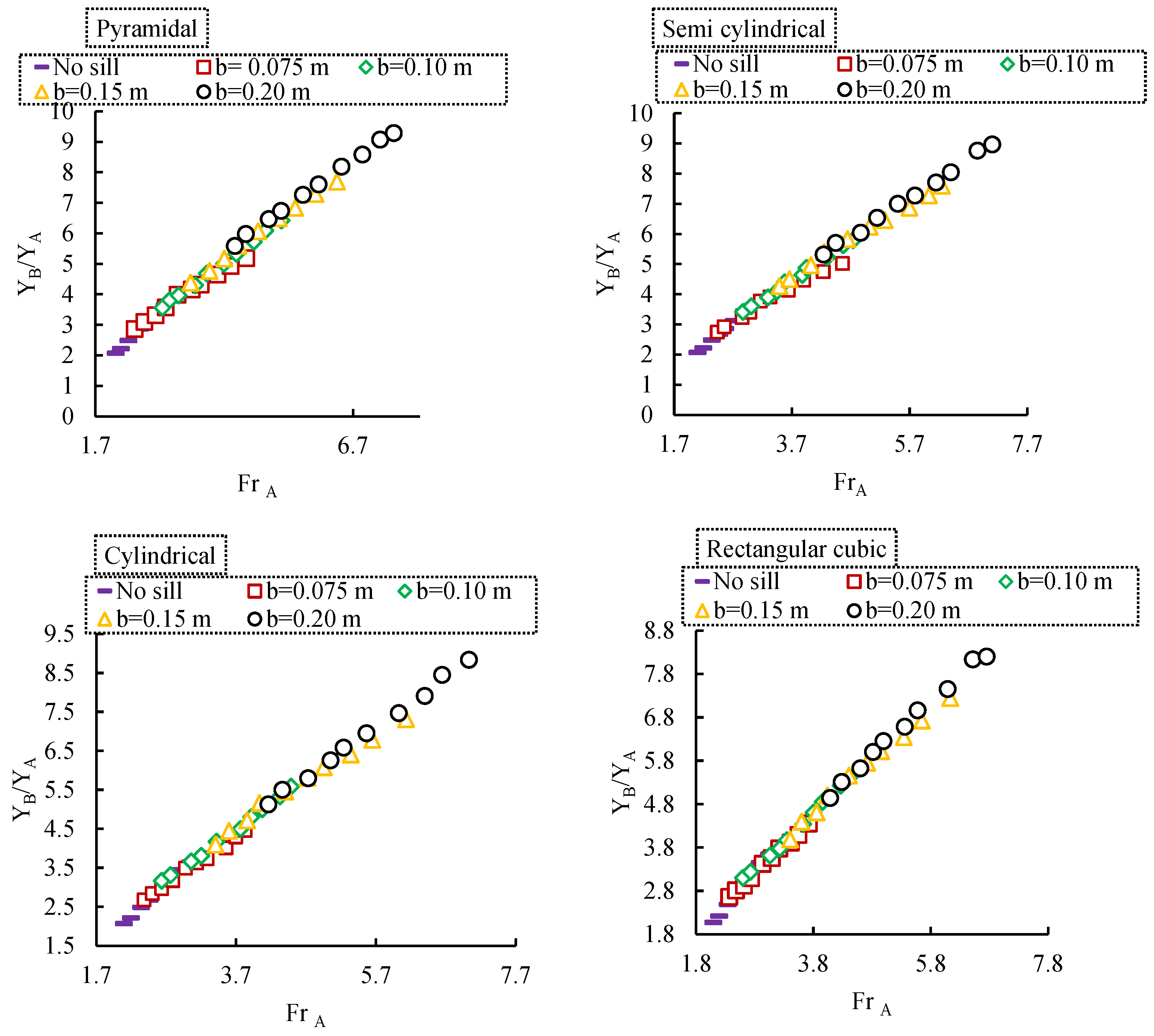

| Sill Geometry | Height (m) | Length (m) | Width (m) |
|---|---|---|---|
| Rectangular cubic | 0.03 | 0.03 | 0.075–0.20 |
| Pyramidal | 0.03 | 0.03 | 0.075–0.20 |
| Cylindrical | Cylindrical diameter = 0.03 | ||
| Semi-cylindrical | Semi-cylindrical diameter = 0.03 | ||
| Rectangular Cubic | Pyramidal | Cylindrical | Semi-Cylindrical | Sill Width (m) |
|---|---|---|---|---|
| 3.9 | 5.7 | 7.4 | 7.4 | b = 0.075 |
| 12.1 | 14.7 | 17.2 | 19.1 | b = 0.20 |
| Rectangular Cubic | Cylindrical | Semi-Cylindrical | Pyramidal | Sill Width (m) | ||||
|---|---|---|---|---|---|---|---|---|
| ΔE/EB | ΔE/EA | ΔE/EB | ΔE/EA | ΔE/EB | ΔE/EA | ΔE/EB | ΔE/EA | Sill withs |
| 33 | 21.2 | 35.4 | 22.3 | 59 | 34.9 | 68 | 39.4 | b = 0.075 m |
| 260 | 115.3 | 260.2 | 116 | 268 | 118.9 | 295.9 | 125.4 | b = 0.20 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daneshfaraz, R.; Norouzi, R.; Ebadzadeh, P.; Di Francesco, S.; Abraham, J.P. Experimental Study of Geometric Shape and Size of Sill Effects on the Hydraulic Performance of Sluice Gates. Water 2023, 15, 314. https://doi.org/10.3390/w15020314
Daneshfaraz R, Norouzi R, Ebadzadeh P, Di Francesco S, Abraham JP. Experimental Study of Geometric Shape and Size of Sill Effects on the Hydraulic Performance of Sluice Gates. Water. 2023; 15(2):314. https://doi.org/10.3390/w15020314
Chicago/Turabian StyleDaneshfaraz, Rasoul, Reza Norouzi, Parisa Ebadzadeh, Silvia Di Francesco, and John Patrick Abraham. 2023. "Experimental Study of Geometric Shape and Size of Sill Effects on the Hydraulic Performance of Sluice Gates" Water 15, no. 2: 314. https://doi.org/10.3390/w15020314
APA StyleDaneshfaraz, R., Norouzi, R., Ebadzadeh, P., Di Francesco, S., & Abraham, J. P. (2023). Experimental Study of Geometric Shape and Size of Sill Effects on the Hydraulic Performance of Sluice Gates. Water, 15(2), 314. https://doi.org/10.3390/w15020314










