Application of a Regionalization Method for Estimating Flash Floods: Cuautepec Basin, Mexico
Abstract
:1. Introduction
2. Methodology
2.1. Rainfall Regionalization Method Based on Variation Coefficient
2.2. Estimation of the Design Storm from Regional Factors
- The historical average maximum annual rainfall of the basin is estimated from an isohyet map and the approximate location of the basin centroid.
- The regional factor for the study site corresponding to the analyzed return period is selected.
- The historical average maximum annual rainfall is multiplied by the regional factor, thus obtaining the total annual maximum accumulated rainfall of 24 h.
- Rainfall previously obtained is affected by a reduction factor per area obtained with the basin area and the equation that corresponds to the study area.
- One-hour total rainfall is estimated from twenty-four-hour total rainfall data, calculated in step 4 with the help of the convective factor corresponding to the analysis site.
- Chen and Bell tables [16] are used to estimate precipitation values for durations between 1 and 24 h or for durations less than one hour or greater than 24 h.
- The design mass curve for the selected Δt is presented. The bars of the design hyetograph, not yet sorted, are defined for the duration of the selected storm.
- To shape the design storm, a block ordering process is carried out (alternating blocks are traditionally used in statistical storms, but in the case of flash floods, a skewness in the hyetograph must be considered).
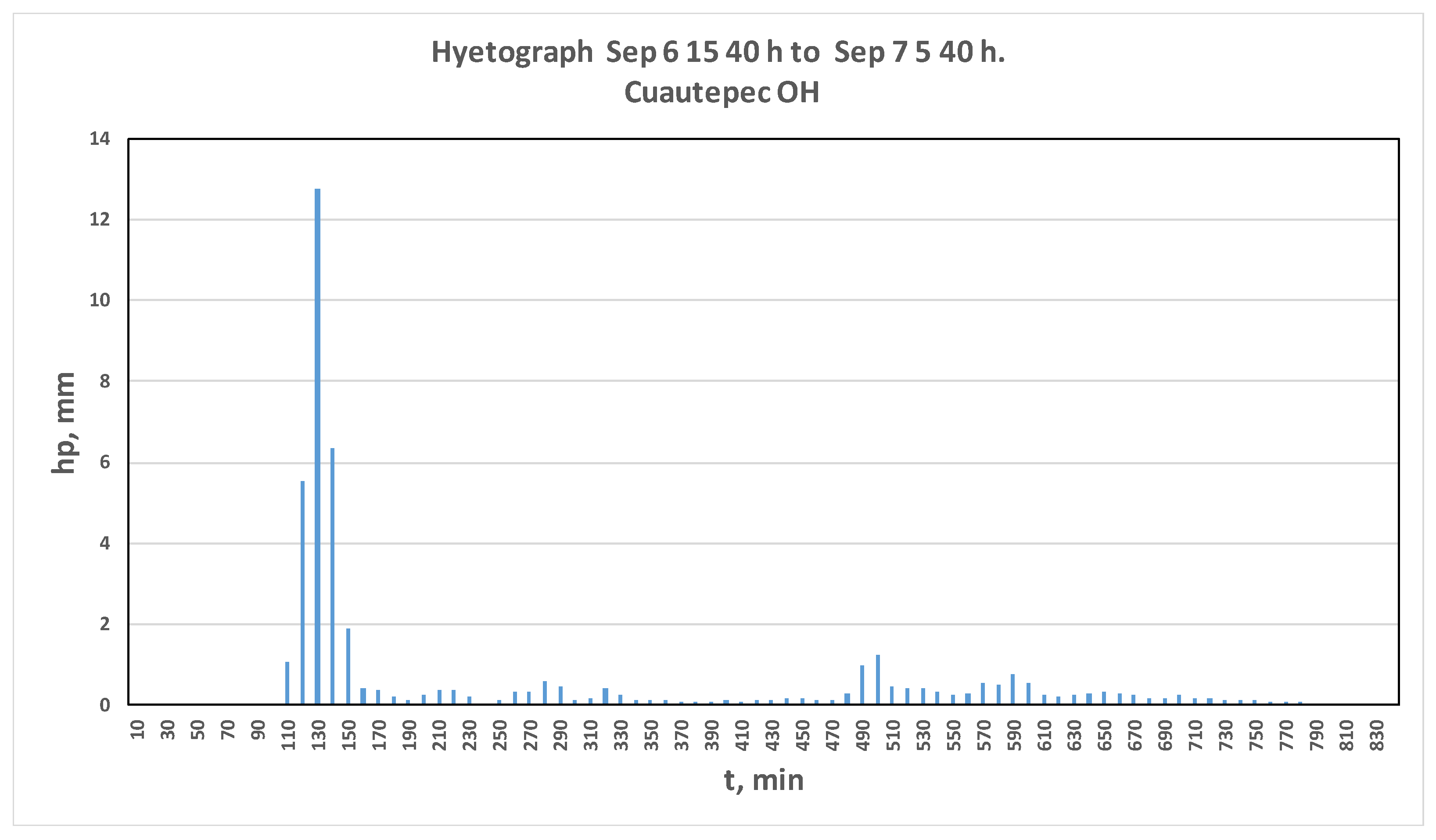
2.3. Construction of the Design Hyetograph Using Flash Flood Shape
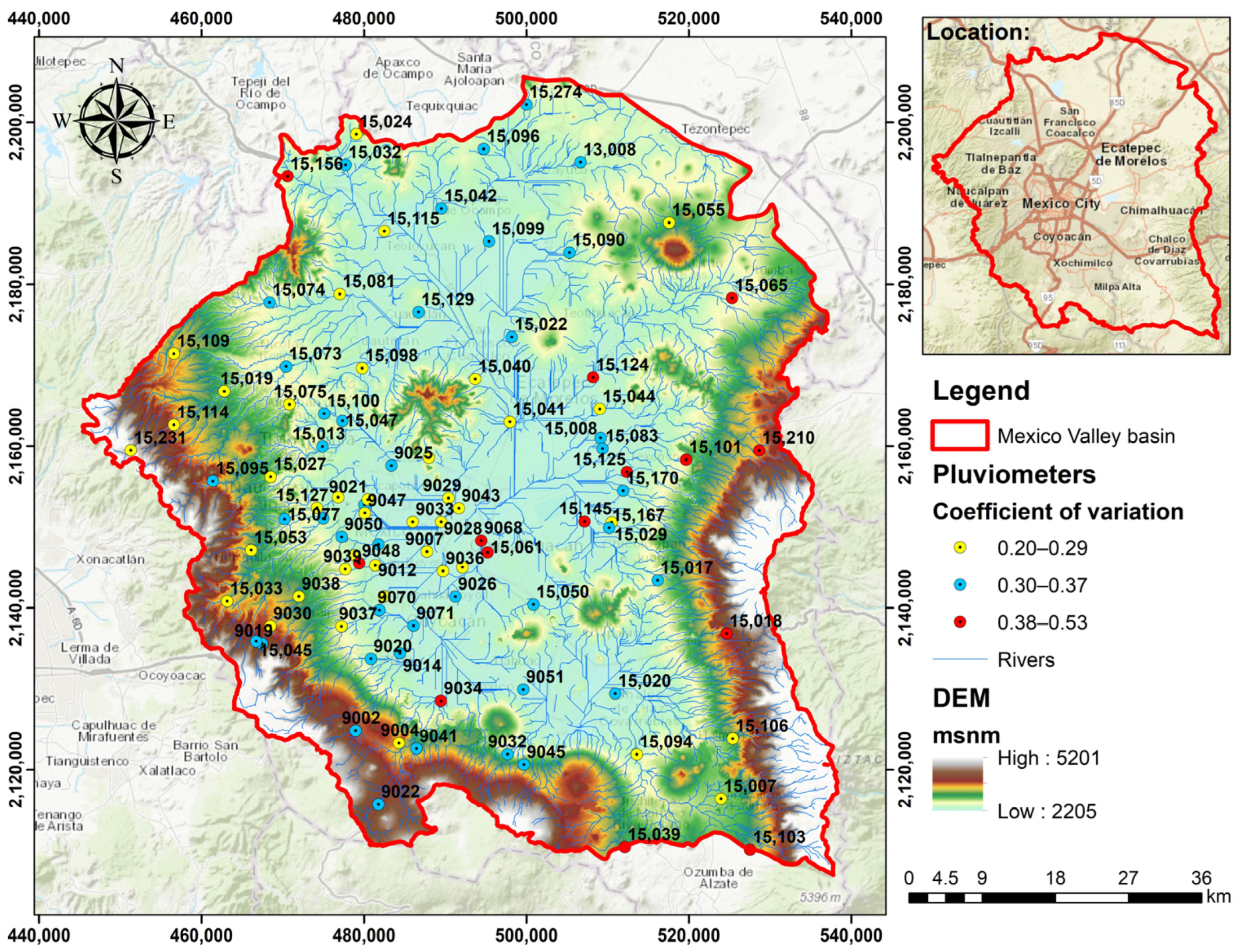
2.4. Study Site and Data Set
2.5. Hydrological Region for Mexico Valley River Basin
2.6. Area Reduction Factor Equation
2.7. Convective Factor
2.8. K-Factors to Move to Durations Other than One Hour
2.8.1. Hec-HMS Software
2.8.2. Iber
2.8.3. Hec-Ras 2d
3. Results and Discussion
3.1. Flash Flood Hyetographs Obtained for Different Return Periods
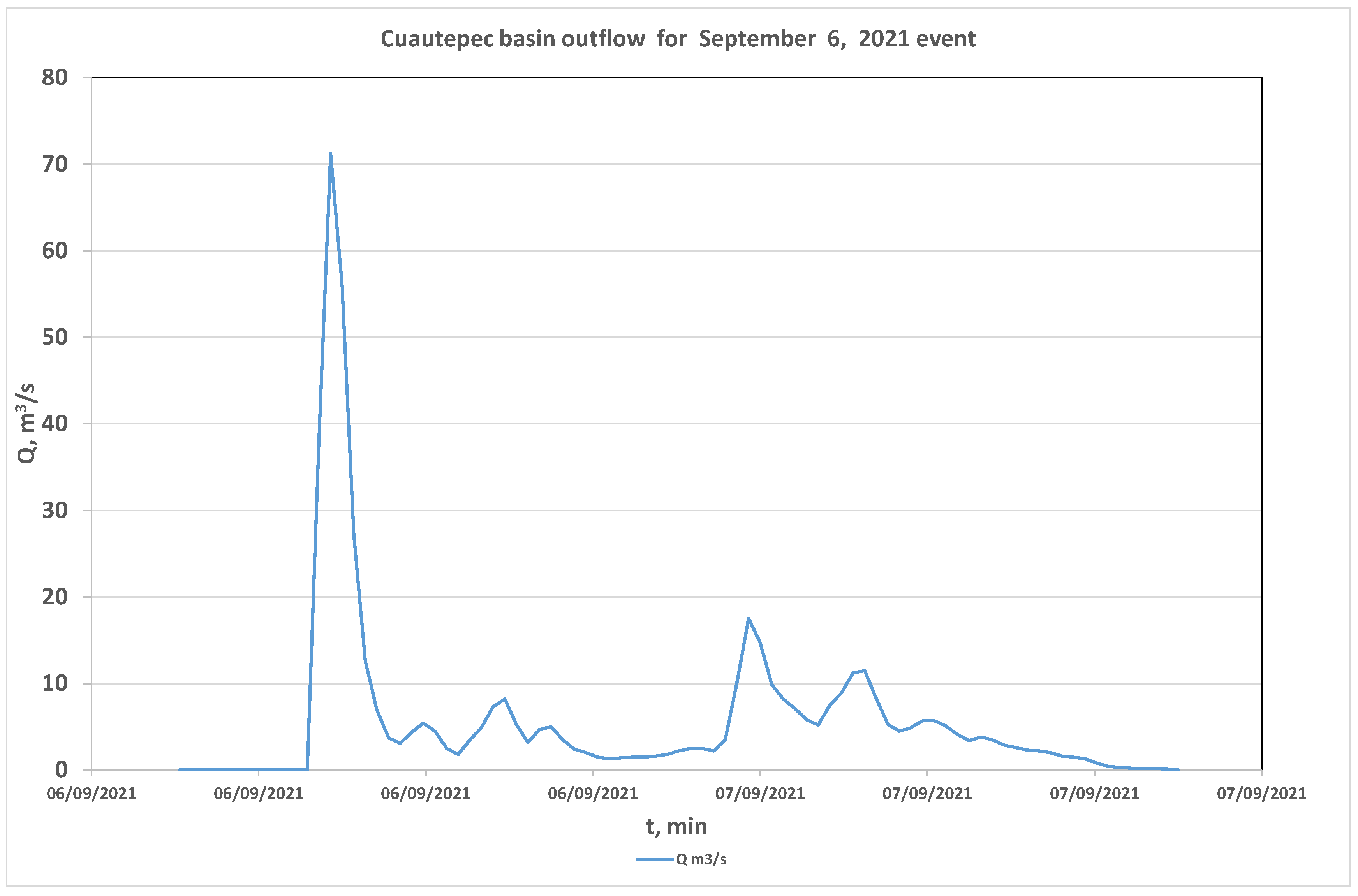
3.2. Simulation of the Historic Flood Using Hec-HMS
3.3. Hydrographs Produced by Hyetographs for Different Tr Calculated with Hec-Hms
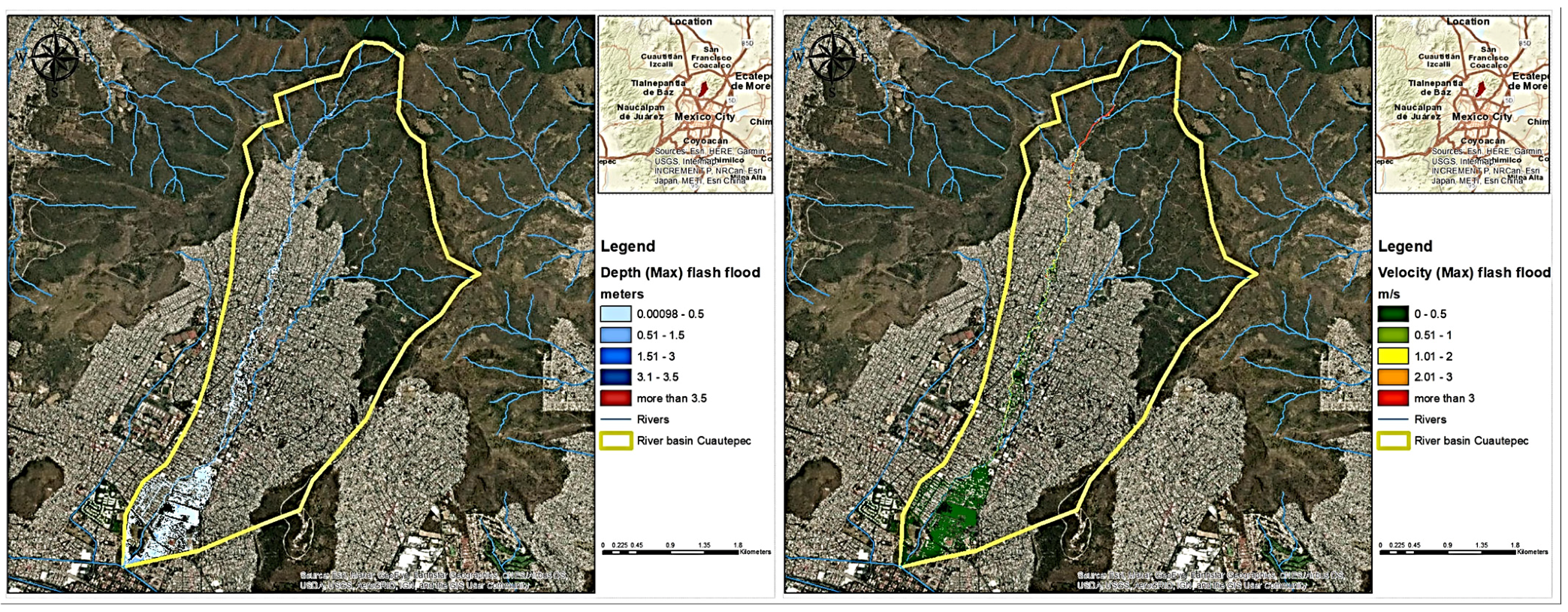
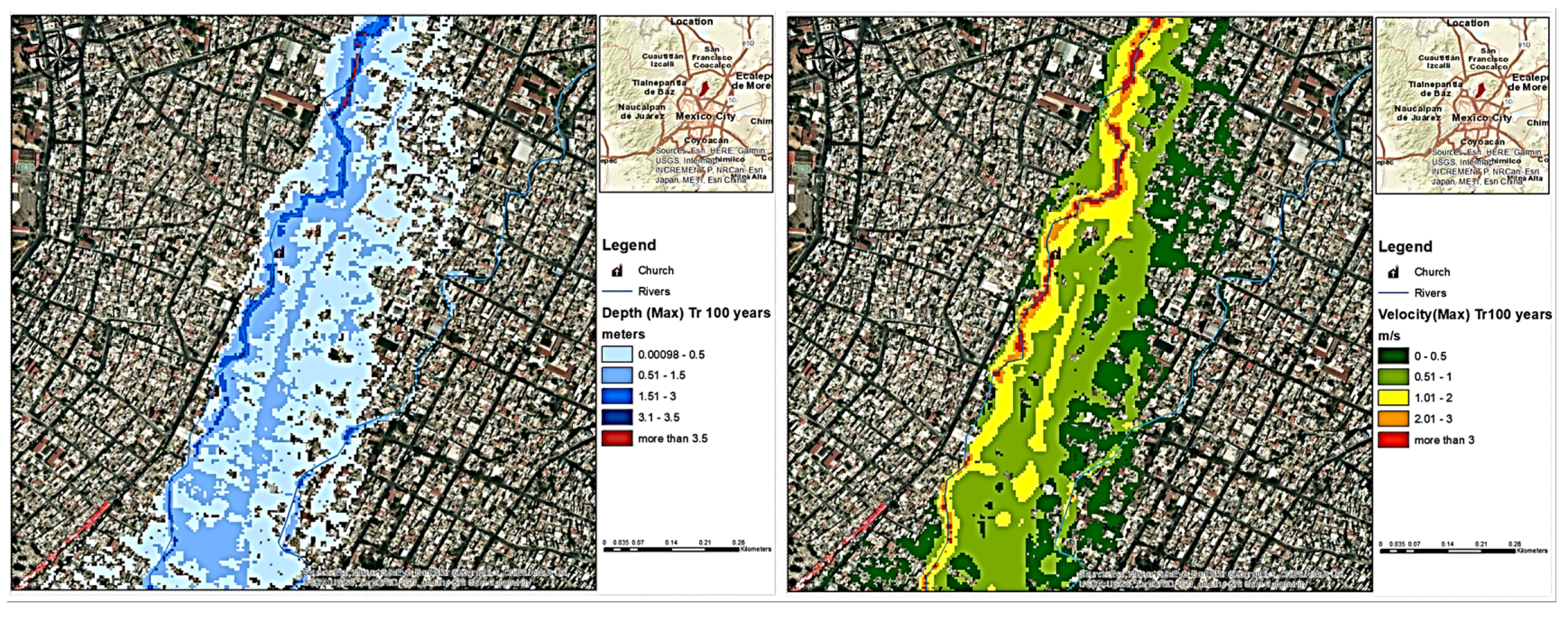
3.4. Depth and Velocity Maps of Historic Flash Flood
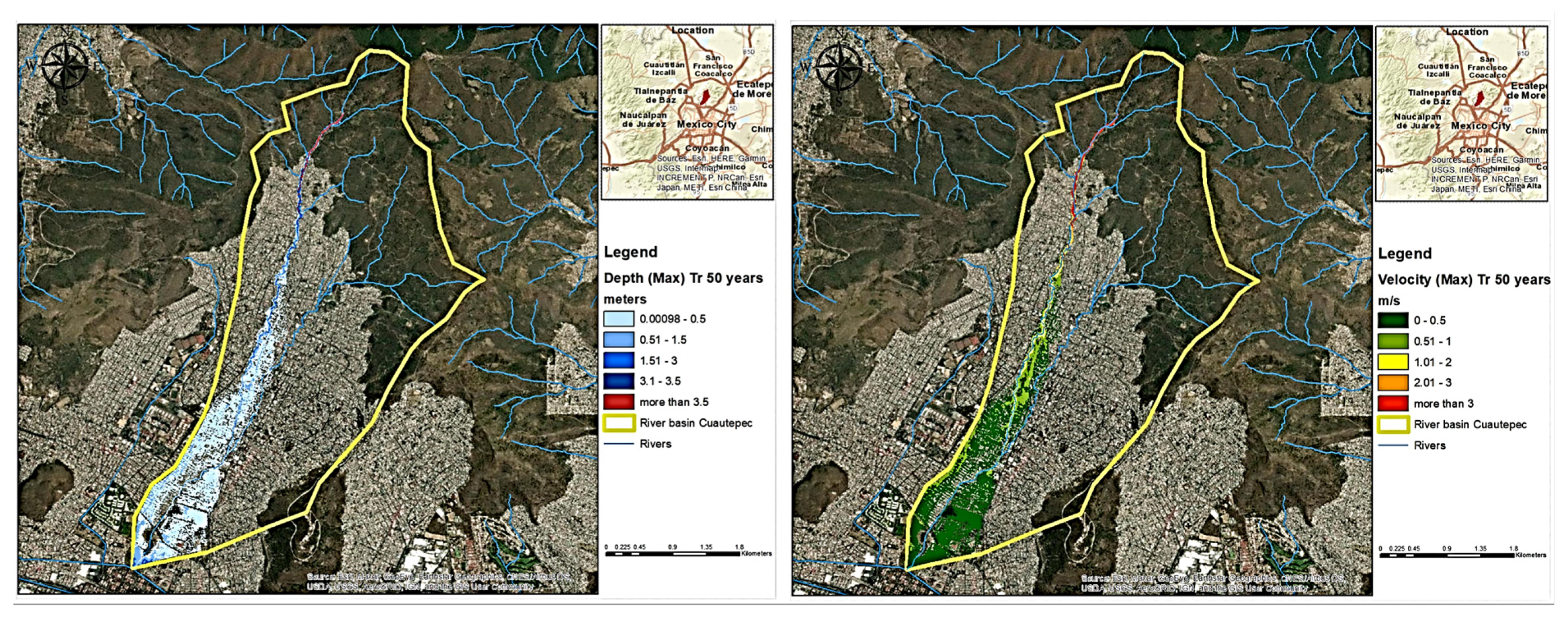
3.5. Flash Flood for Tr = 50 Years
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- National Weather Service. 2022. Available online: https://www.weather.gov/phi/FlashFloodingDefinition (accessed on 5 November 2022).
- Akstinas, V.; Meilutytė-Lukauskienė, D.; Kriaučiūnienė, J.; Šarauskienė, D. Features and causes of catastrophic floods in the Nemunas River basin. Hydrol. Res. 2020, 51, 308–321. [Google Scholar] [CrossRef]
- Garzón, H.M.G.; Ortega, B.J.; Garrote, R.J. Las avenidas torrenciales en cauces efímeros: Ramblas y abanicos aluviales. Torrential floods in ephemeral streams: Wadies and alluvial fans. Enseñanza Cienc. Tierra 2009, 17, 264–276. [Google Scholar]
- Aroca, J.E. Importancia de las Abstracciones Iniciales para la Génesis de Avenidas en Cuencas de Montaña. Master’s Thesis, Universidad de Cantabria, Cantabria, Spain, 2014; 50p. [Google Scholar]
- Green, W.H.; Ampt, G.A. Studies on soil physics: Part, I. The flow of air and water through soils. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar]
- Liu, J.; Zhang, J.; Feng, J. Green–Ampt model for layered soils with nonuniform initial water content under unsteady infiltration. Soil Sci. Soc. Am. J. 2008, 72, 1041–1047. [Google Scholar] [CrossRef]
- Vannasy, M.; Nakagoshi, N. Estimating Direct Runoff from Storm Rainfall Using NRCS Runoff Method and GIS Mapping in Vientiane City, Laos. Int. J. Grid Distrib. Comput. 2016, 9, 253–266. [Google Scholar] [CrossRef]
- Karbasi, M.; Shokoohi, A.; Saghafian, B. Loss of Life Estimation Due to Flash Floods in Residential Areas using a Regional Model. Water Resour. Manag. 2018, 32, 4575–4589. [Google Scholar] [CrossRef]
- Aristizábal, E.; Arango, C.M.I.; García, L.I.K. Definición y clasificación de las avenidas torrenciales y su impacto en los Andes colombianos. Cuad. Geogr. Rev. Colomb. Geogr. 2020, 1, 242–258. [Google Scholar] [CrossRef] [Green Version]
- Bilasco, S.; Hognogi, G.G.; Ros, C.S.; Pop, A.M.; Iuliu, V.; Fodorean, I.; Marian-Potra, A.C.; Sestras, P. Flash Flood Risk Assessment and Mitigation in Digital-Era Governance Using Unmanned Aerial Vehicle and GIS Spatial Analyses Case Study: Small River Basins. Remote Sens. 2022, 14, 2481. [Google Scholar] [CrossRef]
- Shuvo, S.D.; Rashid, T.; Panda, S.K.; Das, S.; Abdul, Q.D. Forecasting of pre-monsoon flash flood events in the northeastern Bangladesh using coupled hydrometeorological NWP modelling system. Meteorol. Atmos Phys. 2021, 133, 1603–1625. [Google Scholar] [CrossRef]
- Kim, E.; Choi, H. Assessment of Vulnerability to Extreme Flash Floods in Design Storms. Int. J. Environ. Res. Public Health 2011, 8, 2907–2922. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kong, F.; Huang, W.; Wang, Z.; Song, X. Effectof Unit Hydrographs and Rainfall Hyetographs on Critical Rainfall Estimates of Flash Flood. Adv. Meteorol. 2020, 2020, 2801963. [Google Scholar] [CrossRef]
- Domínguez, R.R.; Carrizosa, E.E.; Fuentes-Mariles, G.E.; Arganis-Juárez, M.L.; Osnaya, J.O.; Galván, T.A. G Análisis regional para la estimación de precipitaciones de diseño en la República Mexicana Regional Analysis in approaching design rainfall in Mexican Republic. Tecnol. Cienc. Agua. 2018, 9, 5–29. [Google Scholar] [CrossRef]
- Hec-HMS. 2022. Available online: https://www.hec.usace.army.mil/software/hec-hms/ (accessed on 3 November 2022).
- Chen, C.L. Rainfall Intensity-Duration-Frequency Formulas. J. Hydraul. Eng. 1982, 109, 1603–1621. [Google Scholar] [CrossRef]
- La Jornada. 2022. Available online: https://www.jornada.com.mx/2009/11/04/capital/032n1cap (accessed on 1 November 2022).
- Milenio. 2021. Available online: https://www.milenio.com/politica/comunidad/declaran-desastre-natural-27-municipios-afectaciones-grace (accessed on 1 November 2022).
- La Silla Rota. 2021. Available online: https://lasillarota.com/hidalgo/estado/2021/9/8/por-inundaciones-en-tula-el-mezquital-mil-casas-danadas-15-decesos-295643.html (accessed on 2 November 2022).
- El País. 2021. Available online: https://elpais.com/mexico/2021-09-07/al-menos-dos-muertos-tras-una-fuerte-tormenta-en-ecatepec.html (accessed on 2 November 2022).
- Domínguez, R.; Carrizosa, E.; Arganis, M.; Santana, A.; De Luna, F.; Mendoza, R.; Hernández, D.; González, S.; Vázquez, R.; Hernández, A. Proyectos y Estudios para Mejorar la Infraestructura de Drenaje, Actualización del Manual de obras Hidráulicas de la Ciudad de México; Technical Report; Informe Técnico para SACMEX: Mexico City, Mexico, 2022. [Google Scholar]
- González. Contribución al Análisis de Frecuencias de Valores Extremos de los Gastos Máximos en un Río; Serie Azul; Instituto de Ingeniería, UNAM: Mexico City, Mexico, 1970. [Google Scholar]
- Bedient, P.B.; Huber, W.C. Hydrology and Floodplain Analysis; Addison-Wesley: Boston, MA, USA, 1992. [Google Scholar]
- Mockus, V. National Engineering Handbook, Section 4: Hydrology; United States Department of Agriculture (USDA), Soil Conservation Service (SCS): Washington, DC, USA, 1969. [Google Scholar]
- Bladé, E.; Cea, L.; Corestein, G.; Escolano, E.; Puertas, J.; Vázquez-Cendón, E.; Dolz, J.; Coll, A. Iber: Herramienta de simulación numérica del flujo en ríos. Rev. Int. Métodos Numéricos Cálculo Diseño Ing. 2014, 30, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Available online: https://www.hec.usace.army.mil/software/hec-ras/ (accessed on 10 November 2022).
- Costabile, P.; Costanzo, C.; Ferraro, D.; Macchione, F.; Petaccia, G. Performances of the New HEC-RAS Version 5 for 2-D Hydrodynamic-Based Rainfall-Runoff Simulations at Basin Scale: Comparison with a State-of-the Art Model. Water 2020, 12, 2326. [Google Scholar] [CrossRef]
- NSW. Floodplain Development Manual, the Management of Flood Liable Land; News South Wales Government, Department of Infrastructure, Planning and Natural Resources: Sidney, NSW, Australia, 2005. [Google Scholar]
- CONAGUA. Lineamiento para la Elaboración de Mapas de Peligro por Inundación; GASIR: Mexico City, México, 2014. [Google Scholar]
- Velez, M.L.; Fuentes, M.; Rubio, G.H.; De Luna, C.F. Flood hazard maps as a tool for assessing the risk of damage to homes. In Proceedings of the XXIII National Hydraulic Congress, Puerto Vallarta, Jalisco, Mexico, 14 October 2014. [Google Scholar]
- Musolino, G.; Ahmadian, R.; Xia, J.; Falconer, R.A. Mapping the danger to life in flash flood events adopting a mechanics based methodology and planning evacuation routes. J. Flood Risk Manag. 2019, 1, e12627. [Google Scholar] [CrossRef]
- Nanía, L.S.; León, A.S.; García, M.H. Hydrologic-Hydraulic Model for Simulating Dual Drainage and Flooding in Urban Areas: Application to a Catchment in the Metropolitan Area of Chicago. J. Hydrol. Eng. 2015, 20, 04014071. [Google Scholar] [CrossRef]









| Tr, Years | CVM (D-GUMBEL) |
|---|---|
| 2 | 0.94 |
| 5 | 1.2 |
| 10 | 1.39 |
| 20 | 1.59 |
| 50 | 1.88 |
| 100 | 2.09 |
| 200 | 2.29 |
| 500 | 2.56 |
| 1000 | 2.76 |
| 2000 | 2.97 |
| 5000 | 3.23 |
| 10,000 | 3.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arganis, M.; Preciado, M.; Luna, F.D.; Cruz, L.; Domínguez, R.; Santana, O. Application of a Regionalization Method for Estimating Flash Floods: Cuautepec Basin, Mexico. Water 2023, 15, 303. https://doi.org/10.3390/w15020303
Arganis M, Preciado M, Luna FD, Cruz L, Domínguez R, Santana O. Application of a Regionalization Method for Estimating Flash Floods: Cuautepec Basin, Mexico. Water. 2023; 15(2):303. https://doi.org/10.3390/w15020303
Chicago/Turabian StyleArganis, Maritza, Margarita Preciado, Faustino De Luna, Liliana Cruz, Ramón Domínguez, and Olaf Santana. 2023. "Application of a Regionalization Method for Estimating Flash Floods: Cuautepec Basin, Mexico" Water 15, no. 2: 303. https://doi.org/10.3390/w15020303








