Evaporation Dynamics of Sessile and Suspended Almost-Spherical Droplets from a Biphilic Surface
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of Materials
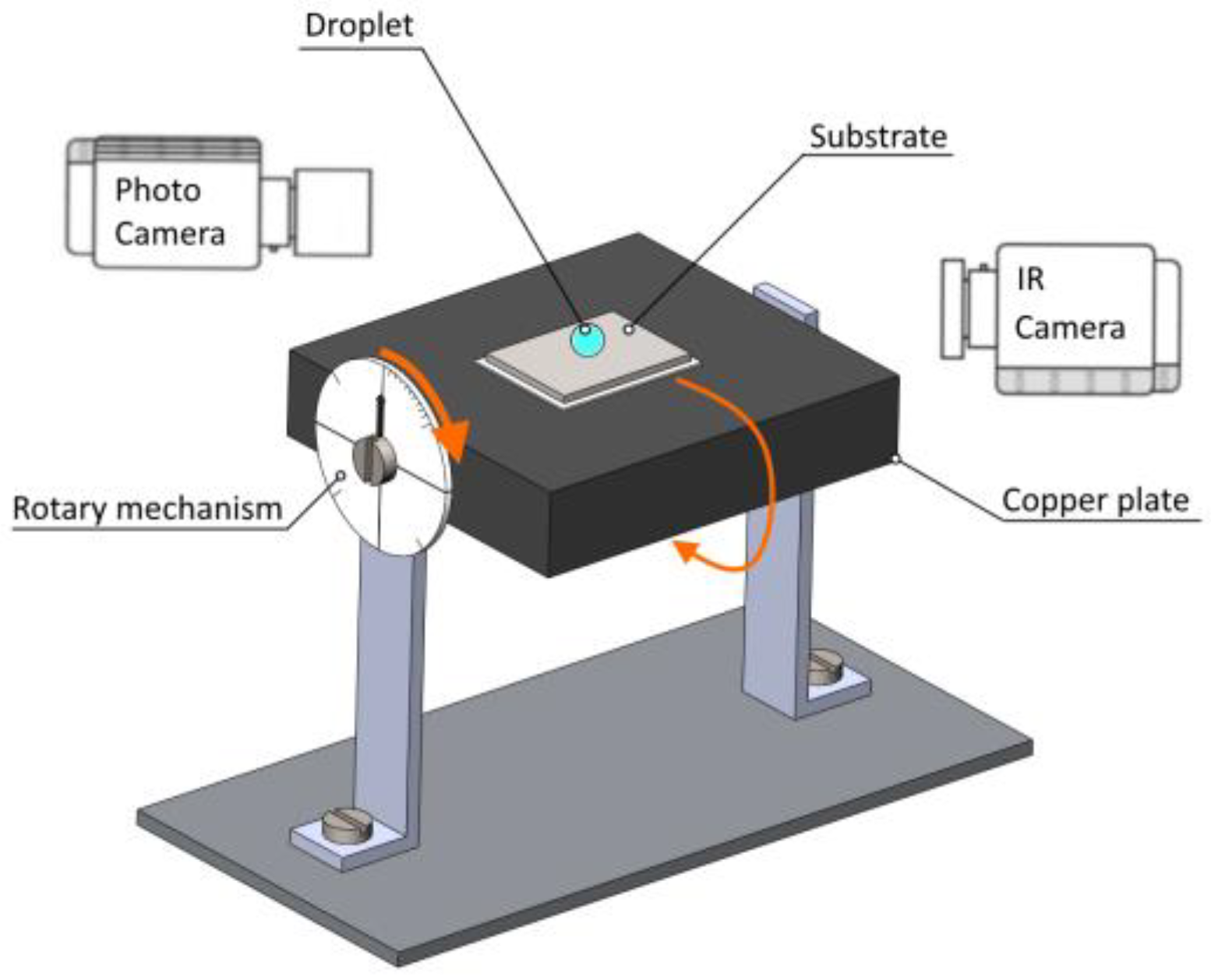
2.2. Experimental Setup
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lim, T.; Han, S.; Chung, J.; Chung, J.T.; Ko, S.; Grigoropoulos, C.P. Experimental Study on Spreading and Evaporation of Inkjet Printed Pico-Liter Droplet on a Heated Substrate. Int. J. Heat Mass Transf. 2009, 52, 431–441. [Google Scholar] [CrossRef]
- Pan, Z.; Dash, S.; Weibel, J.A.; Garimella, S.V. Assessment of Water Droplet Evaporation Mechanisms on Hydrophobic and Superhydrophobic Substrates. Langmuir 2013, 29, 15831–15841. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Zhu, H.; Frantz, J.M.; Reding, M.E.; Chan, K.C.; Ozkan, H.E. Evaporation and Coverage Area of Pesticide Droplets on Hairy and Waxy Leaves. Biosyst. Eng. 2009, 104, 324–334. [Google Scholar] [CrossRef]
- Li, W.; Ji, W.; Sun, H.; Lan, D.; Wang, Y. Pattern Formation in Drying Sessile and Pendant Droplet: Interactions of Gravity Settling, Interface Shrinkage, and Capillary Flow. Langmuir 2019, 35, 113–119. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, J.; Mukhopadhyay, A.; Rao, G.V.; Sanyal, D. Analysis of Evaporation of Dense Cluster of Bicomponent Fuel Droplets in a Spray Using a Spherical Cell Model. Int. J. Therm. Sci. 2008, 47, 584–590. [Google Scholar] [CrossRef]
- Eslamian, M. Spray-on Thin Film PV Solar Cells: Advances, Potentials and Challenges. Coatings 2014, 4, 60–84. [Google Scholar] [CrossRef] [Green Version]
- Hsu, C.C.; Su, T.W.; Wu, C.H.; Kuo, L.S.; Chen, P.H. Influence of Surface Temperature and Wettability on Droplet Evaporation. Appl. Phys. Lett. 2015, 106, 141602. [Google Scholar] [CrossRef]
- Shin, D.H.; Lee, S.H.; Jung, J.Y.; Yoo, J.Y. Evaporating Characteristics of Sessile Droplet on Hydrophobic and Hydrophilic Surfaces. Microelectron. Eng. 2009, 86, 1350–1353. [Google Scholar] [CrossRef]
- Gao, M.; Kong, P.; Zhang, L.X.; Liu, J.N. An Experimental Investigation of Sessile Droplets Evaporation on Hydrophilic and Hydrophobic Heating Surface with Constant Heat Flux. Int. Commun. Heat Mass Transf. 2017, 88, 262–268. [Google Scholar] [CrossRef]
- Hampton, M.A.; Nguyen, T.A.H.; Nguyen, A.V.; Xu, Z.P.; Huang, L.; Rudolph, V. Influence of Surface Orientation on the Organization of Nanoparticles in Drying Nanofluid Droplets. J. Colloid Interface Sci. 2012, 377, 456–462. [Google Scholar] [CrossRef]
- Putnam, S.A.; Briones, A.M.; Ervin, J.S.; Hanchak, M.S.; Byrd, L.W.; Jones, J.G. Interfacial Heat Transfer during Microdroplet Evaporation on a Laser Heated Surface. Int. J. Heat Mass Transf. 2012, 55, 6307–6320. [Google Scholar] [CrossRef]
- Deng, W.; Gomez, A. Electrospray Cooling for Microelectronics. Int. J. Heat Mass Transf. 2011, 54, 2270–2275. [Google Scholar] [CrossRef]
- Dugas, V.; Broutin, J.; Souteyrand, E. Droplet Evaporation Study Applied to DNA Chip Manufacturing. Langmuir 2005, 21, 9130–9136. [Google Scholar] [CrossRef]
- Li, G.; Flores, S.M.; Vavilala, C.; Schmittel, M.; Graf, K. Evaporation Dynamics of Microdroplets on Self-Assembled Monolayers of Dialkyl Disulfides. Langmuir 2009, 25, 13438–13447. [Google Scholar] [CrossRef]
- Kim, J. Spray Cooling Heat Transfer: The State of the Art. Int. J. Heat Fluid Flow 2007, 28, 753–767. [Google Scholar] [CrossRef]
- Putnam, S.A.; Briones, A.M.; Byrd, L.W.; Ervin, J.S.; Hanchak, M.S.; White, A.; Jones, J.G. Microdroplet Evaporation on Superheated Surfaces. Int. J. Heat Mass Transf. 2012, 55, 5793–5807. [Google Scholar] [CrossRef]
- Chen, R.H.; Phuoc, T.X.; Martello, D. Effects of Nanoparticles on Nanofluid Droplet Evaporation. Int. J. Heat Mass Transf. 2010, 53, 3677–3682. [Google Scholar] [CrossRef]
- Park, J.; Moon, J. Control of Colloidal Particle Deposit Patterns within Picoliter Droplets Ejected by Ink-Jet Printing. Langmuir 2006, 22, 3506–3513. [Google Scholar] [CrossRef]
- Kumari, N.; Garimella, S.V. Characterization of the Heat Transfer Accompanying Electrowetting or Gravity-Induced Droplet Motion. Int. J. Heat Mass Transf. 2011, 54, 4037–4050. [Google Scholar] [CrossRef]
- Cheng, W.L.; Han, F.Y.; Liu, Q.N.; Zhao, R.; Fan, H.-l. Experimental and Theoretical Investigation of Surface Temperature Non-Uniformity of Spray Cooling. Energy 2011, 36, 249–257. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, P.X.; Hu, Y.T.; Li, J. Experimental Investigation of Continual-and Intermittent-Spray Cooling. Exp. Heat Transf. 2013, 26, 453–469. [Google Scholar] [CrossRef]
- Chen, P.; Harmand, S.; Szunerits, S.; Boukherroub, R. Evaporation Behavior of PEGylated Graphene Oxide Nanofluid Droplets on Heated Substrate. Int. J. Therm. Sci. 2019, 135, 445–458. [Google Scholar] [CrossRef]
- Kelly-Zion, P.L.; Pursell, C.J.; Vaidya, S.; Batra, J. Evaporation of Sessile Drops under Combined Diffusion and Natural Convection. Colloids Surf. A Physicochem. Eng. Asp. 2011, 381, 31–36. [Google Scholar] [CrossRef] [Green Version]
- Lopes, M.C.; Bonaccurso, E.; Gambaryan-Roisman, T.; Stephan, P. Influence of the Substrate Thermal Properties on Sessile Droplet Evaporation: Effect of Transient Heat Transport. Colloids Surf. A Physicochem. Eng. Asp. 2013, 432, 64–70. [Google Scholar] [CrossRef]
- Crafton, E.F.; Black, W.Z. Heat Transfer and Evaporation Rates of Small Liquid Droplets on Heated Horizontal Surfaces. Int. J. Heat Mass Transf. 2004, 47, 1187–1200. [Google Scholar] [CrossRef]
- Tran, T.; Staat, H.J.J.; Prosperetti, A.; Sun, C.; Lohse, D. Drop Impact on Superheated Surfaces. Phys. Rev. Lett. 2012, 108, 036101. [Google Scholar] [CrossRef] [Green Version]
- Picknett, R.G.; Bexon, R. The Evaporation of Sessile or Pendant Drops in Still Air. J. Colloid Interface Sci. 1977, 61, 336–350. [Google Scholar] [CrossRef]
- Yu, H.-Z.; Soolaman, D.M.; Rowe, A.W.; Banks, J.T. Evaporation of Water Microdroplets on Self-Assembled Monolayers: From Pinning to Shrinking. ChemPhysChem 2004, 5, 1035–1038. [Google Scholar] [CrossRef]
- Fang, X.; Pimentel, M.; Sokolov, J.; Rafailovich, M. Dewetting of the Three-Phase Contact Line on Solids. Langmuir 2010, 26, 7682–7685. [Google Scholar] [CrossRef]
- Uno, K.; Hayashi, K.; Hayashi, T.; Ito, K.; Kitano, H. Particle Adsorption in Evaporating Droplets of Polymer Latex Dispersions on Hydrophilic and Hydrophobic Surfaces. Colloid Polym. Sci. 1998, 276, 810–815. [Google Scholar] [CrossRef]
- Nguyen, T.A.H.; Nguyen, A.V.; Hampton, M.A.; Xu, Z.P.; Huang, L.; Rudolph, V. Theoretical and Experimental Analysis of Droplet Evaporation on Solid Surfaces. Chem. Eng. Sci. 2012, 69, 522–529. [Google Scholar] [CrossRef]
- Hu, H.; Larson, R.G. Evaporation of a Sessile Droplet on a Substrate. J. Phys. Chem. B 2002, 106, 1334–1344. [Google Scholar] [CrossRef]
- Lee, K.S.; Cheah, C.Y.; Copleston, R.J.; Starov, V.M.; Sefiane, K. Spreading and Evaporation of Sessile Droplets: Universal Behaviour in the Case of Complete Wetting. Colloids Surf. A Physicochem. Eng. Asp. 2008, 323, 63–72. [Google Scholar] [CrossRef]
- Furuta, T.; Isobe, T.; Sakai, M.; Matsushita, S.; Nakajima, A. Wetting Mode Transition of Nanoliter Scale Water Droplets during Evaporation on Superhydrophobic Surfaces with Random Roughness Structure. Appl. Surf. Sci. 2012, 258, 2378–2383. [Google Scholar] [CrossRef]
- Deegan, R.D.; Bakajin, O.; Dupont, T.F.; Huber, G.; Nagel, S.R.; Witten, T.A. Capillary Flow as the Cause of Ring Stains from Dried Liquid Drops. Nature 1997, 389, 827–829. [Google Scholar] [CrossRef]
- Gao, L.; McCarthy, T.J. Wetting 101°. Langmuir 2009, 24, 14105–14115. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Zhou, L.; Du, X.; Yang, Y. Numerical Investigation on Conjugate Heat Transfer of Evaporating Thin Film in a Sessile Droplet. Int. J. Heat Mass Transf. 2016, 101, 10–19. [Google Scholar] [CrossRef]
- Gibbons, M.J.; Di Marco, P.; Robinson, A.J. Local Heat Transfer to an Evaporating Superhydrophobic Droplet. Int. J. Heat Mass Transf. 2018, 121, 641–652. [Google Scholar] [CrossRef]
- Rahimzadeh, A.; Eslamian, M. Experimental Study on the Evaporation of Sessile Droplets Excited by Vertical and Horizontal Ultrasonic Vibration. Int. J. Heat Mass Transf. 2017, 114, 786–795. [Google Scholar] [CrossRef]
- Yu, Y.S.; Wang, Z.; Zhao, Y.P. Experimental and Theoretical Investigations of Evaporation of Sessile Water Droplet on Hydrophobic Surfaces. J. Colloid Interface Sci. 2012, 365, 254–259. [Google Scholar] [CrossRef]
- Deegan, R.D.; Bakajin, O.; Dupont, T.F.; Huber, G.; Nagel, S.R.; Witten, T.A. Contact Line Deposits in an Evaporating Drop. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2000, 62, 756–765. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Birdi, K.S.; Vu, D.T. Wettability and the Evaporation Rates of Fluids from Solid Surfaces. J. Adhes. Sci. Technol. 1993, 7, 485–493. [Google Scholar] [CrossRef]
- Qi, W.; Li, J.; Weisensee, P.B. Evaporation of Sessile Water Droplets on Horizontal and Vertical Biphobic Patterned Surfaces. Langmuir 2019, 35, 17185–17192. [Google Scholar] [CrossRef] [Green Version]
- Raj, R.; Enright, R.; Zhu, Y.; Adera, S.; Wang, E.N. Unified Model for Contact Angle Hysteresis on Heterogeneous and Superhydrophobic Surfaces. Langmuir 2012, 28, 15777–15788. [Google Scholar] [CrossRef] [PubMed]
- Serdyukov, V.; Starinskiy, S.; Malakhov, I.; Safonov, A.; Surtaev, A. Laser Texturing of Silicon Surface to Enhance Nucleate Pool Boiling Heat Transfer. Appl. Therm. Eng. 2021, 194, 117102. [Google Scholar] [CrossRef]
- Khanikar, V.; Mudawar, I.; Fisher, T. Effects of Carbon Nanotube Coating on Flow Boiling in a Micro-Channel. Int. J. Heat Mass Transf. 2009, 52, 3805–3817. [Google Scholar] [CrossRef]
- Sathyamurthi, V.; Ahn, H.S.; Banerjee, D.; Lau, S.C. Subcooled Pool Boiling Experiments on Horizontal Heaters Coated with Carbon Nanotubes. J. Heat Transf. 2009, 131, 071501. [Google Scholar] [CrossRef] [Green Version]
- Motezakker, A.R.; Sadaghiani, A.K.; Çelik, S.; Larsen, T.; Villanueva, L.G.; Koşar, A. Optimum Ratio of Hydrophobic to Hydrophilic Areas of Biphilic Surfaces in Thermal Fluid Systems Involving Boiling. Int. J. Heat Mass Transf. 2019, 135, 164–174. [Google Scholar] [CrossRef]
- Pradhan, T.K.; Panigrahi, P.K. Evaporation Induced Natural Convection inside a Droplet of Aqueous Solution Placed on a Superhydrophobic Surface. Colloids Surf. A Physicochem. Eng. Asp. 2017, 530, 1–12. [Google Scholar] [CrossRef]
- Starinskiy, S.V.; Rodionov, A.A.; Shukhov, Y.G.; Safonov, A.I.; Maximovskiy, E.A.; Sulyaeva, V.S.; Bulgakov, A. V Formation of Periodic Superhydrophilic Microstructures by Infrared Nanosecond Laser Processing of Single-Crystal Silicon. Appl. Surf. Sci. 2020, 512, 145753. [Google Scholar] [CrossRef]
- Starinskiy, S.V.; Bulgakov, A.V.; Gatapova, E.Y.; Shukhov, Y.G.; Sulyaeva, V.S.; Timoshenko, N.I.; Safonov, A.I. Transition from Superhydrophilic to Superhydrophobic of Silicon Wafer by a Combination of Laser Treatment and Fluoropolymer Deposition. J. Phys. D Appl. Phys. 2018, 51, 255307. [Google Scholar] [CrossRef]
- Tsai, P.; Lammertink, R.G.H.; Wessling, M.; Lohse, D. Evaporation-Triggered Wetting Transition for Water Droplets upon Hydrophobic Microstructures. Phys. Rev. Lett. 2010, 104, 2–3. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Borodulin, V.Y.; Letushko, V.N.; Nizovtsev, M.I.; Sterlyagov, A.N. The Experimental Study of Evaporation of Water–Alcohol Solution Droplets. Colloid J. 2019, 81, 219–225. [Google Scholar] [CrossRef]
- Kim, J.Y.; Hwang, I.G.; Weon, B.M. Evaporation of inclined water droplets. Sci. Rep. 2017, 7, 42848. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Starinskaya, E.; Miskiv, N.; Terekhov, V.; Safonov, A.; Li, Y.; Lei, M.-K.; Starinskiy, S. Evaporation Dynamics of Sessile and Suspended Almost-Spherical Droplets from a Biphilic Surface. Water 2023, 15, 273. https://doi.org/10.3390/w15020273
Starinskaya E, Miskiv N, Terekhov V, Safonov A, Li Y, Lei M-K, Starinskiy S. Evaporation Dynamics of Sessile and Suspended Almost-Spherical Droplets from a Biphilic Surface. Water. 2023; 15(2):273. https://doi.org/10.3390/w15020273
Chicago/Turabian StyleStarinskaya, Elena, Nikolay Miskiv, Vladimir Terekhov, Alexey Safonov, Yupeng Li, Ming-Kai Lei, and Sergey Starinskiy. 2023. "Evaporation Dynamics of Sessile and Suspended Almost-Spherical Droplets from a Biphilic Surface" Water 15, no. 2: 273. https://doi.org/10.3390/w15020273




