Performance of Semi-Active Flapping Hydrofoil with Arc Trajectory
Abstract
:1. Introduction
2. Description and Definition of Flapping Foil Propulsion
2.1. Geometric Structure and Motion
2.2. Nondimensional Propulsive Indicators
3. Computational Method and Validation
3.1. Governing Equations
3.2. Mesh and Method
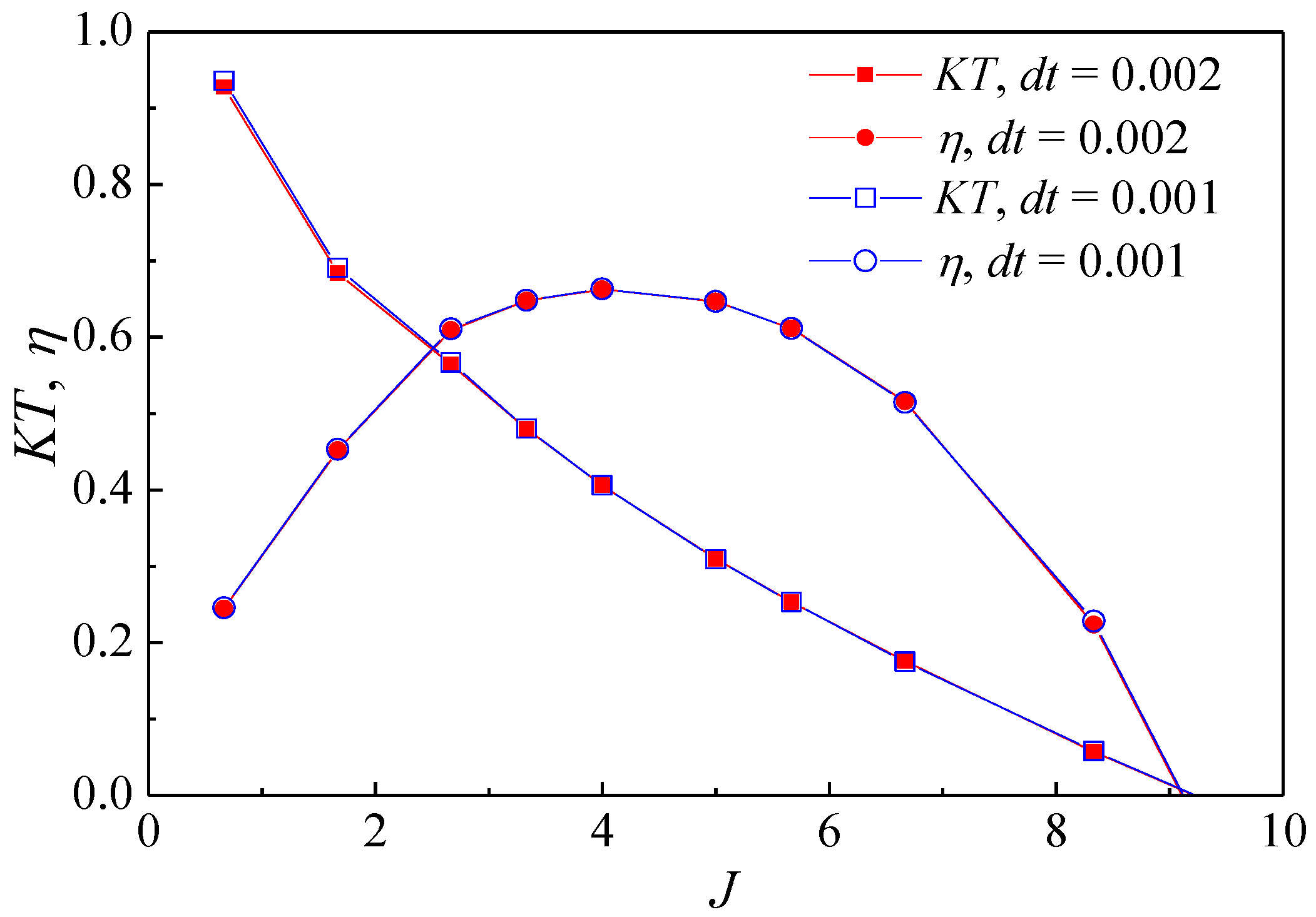
3.3. Validation
4. Results and Analysis
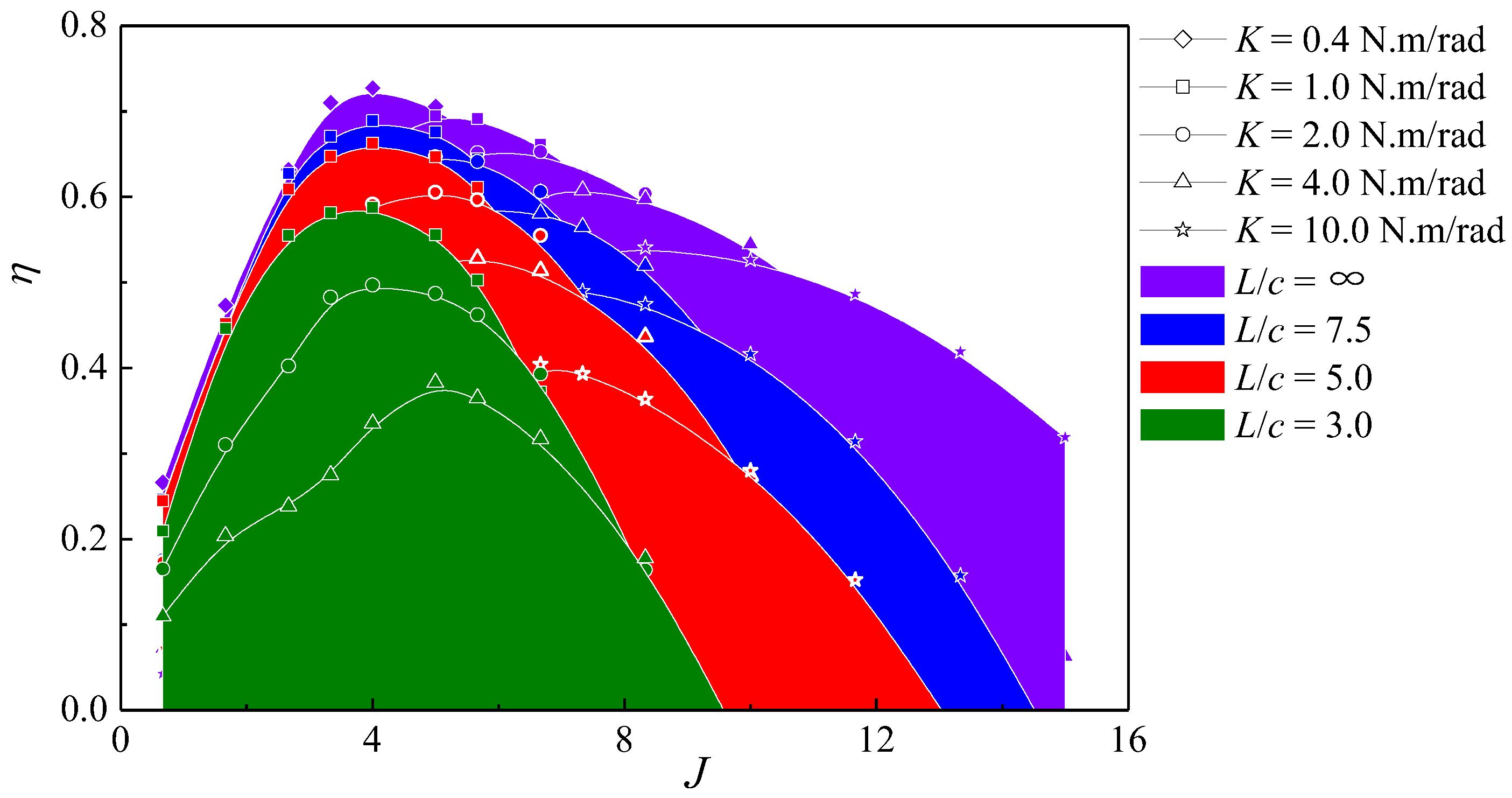
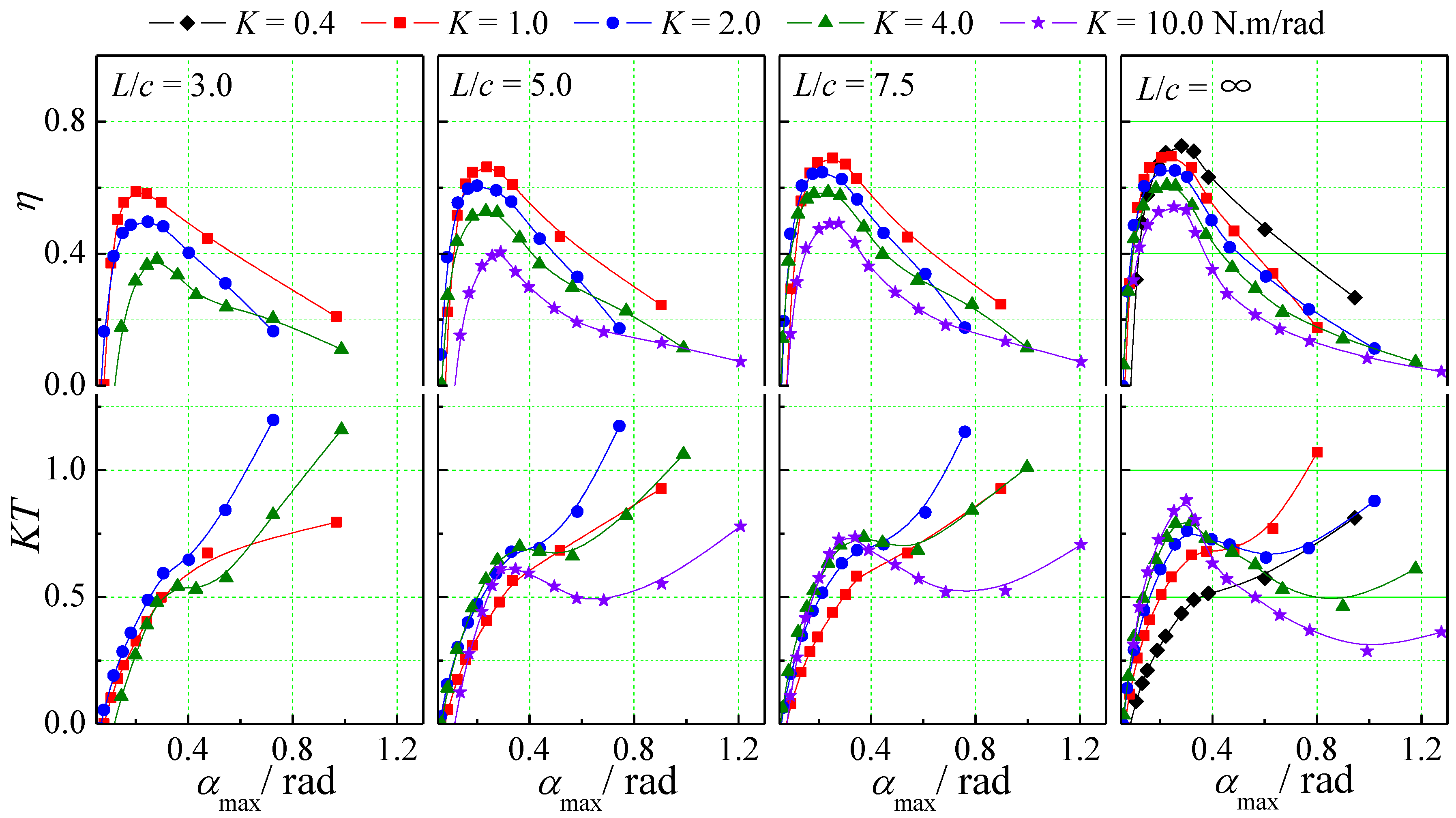
4.1. Propulsive Efficiency and the Thrust Coefficient
4.2. Angle of Attack Analysis
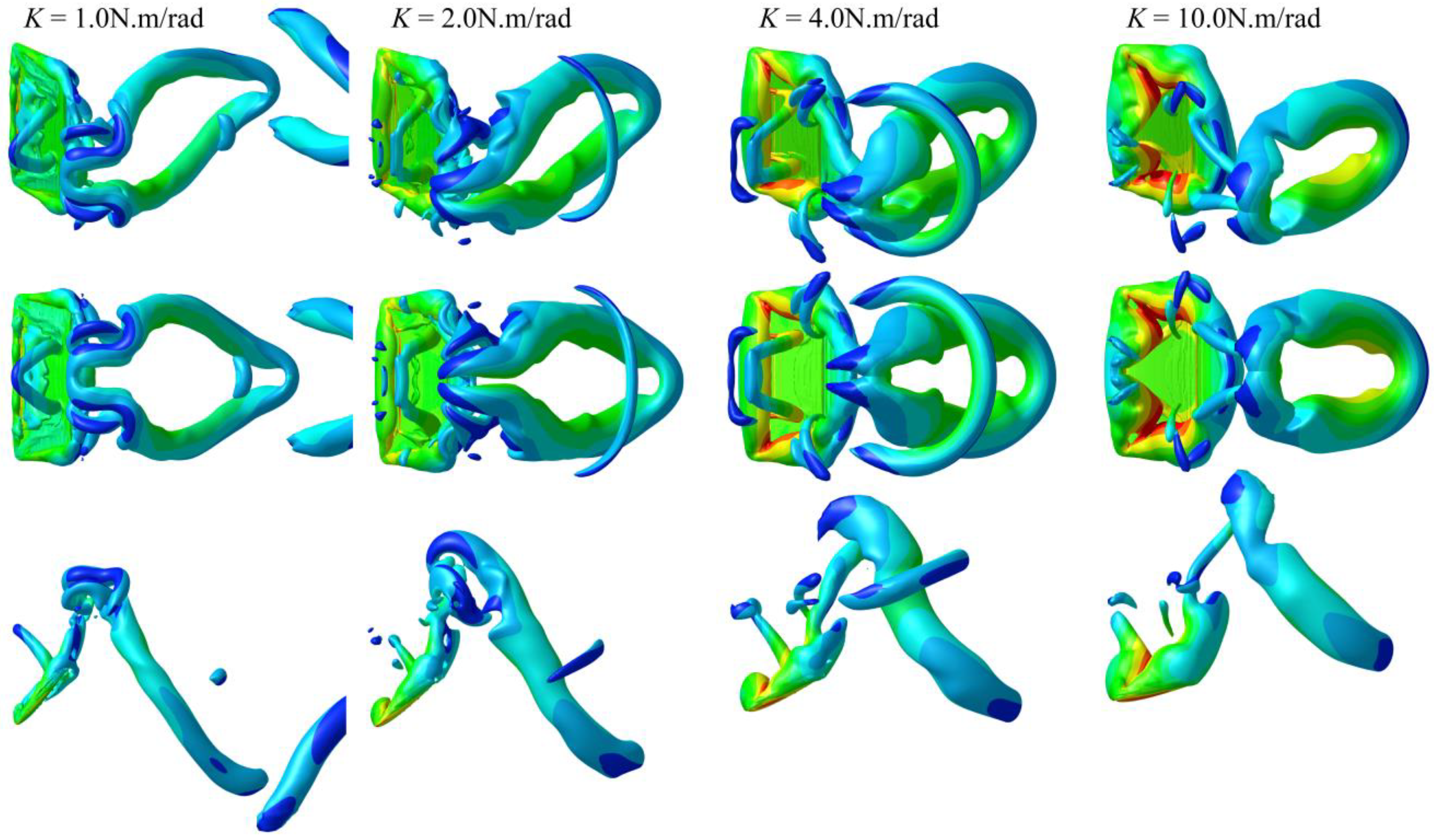
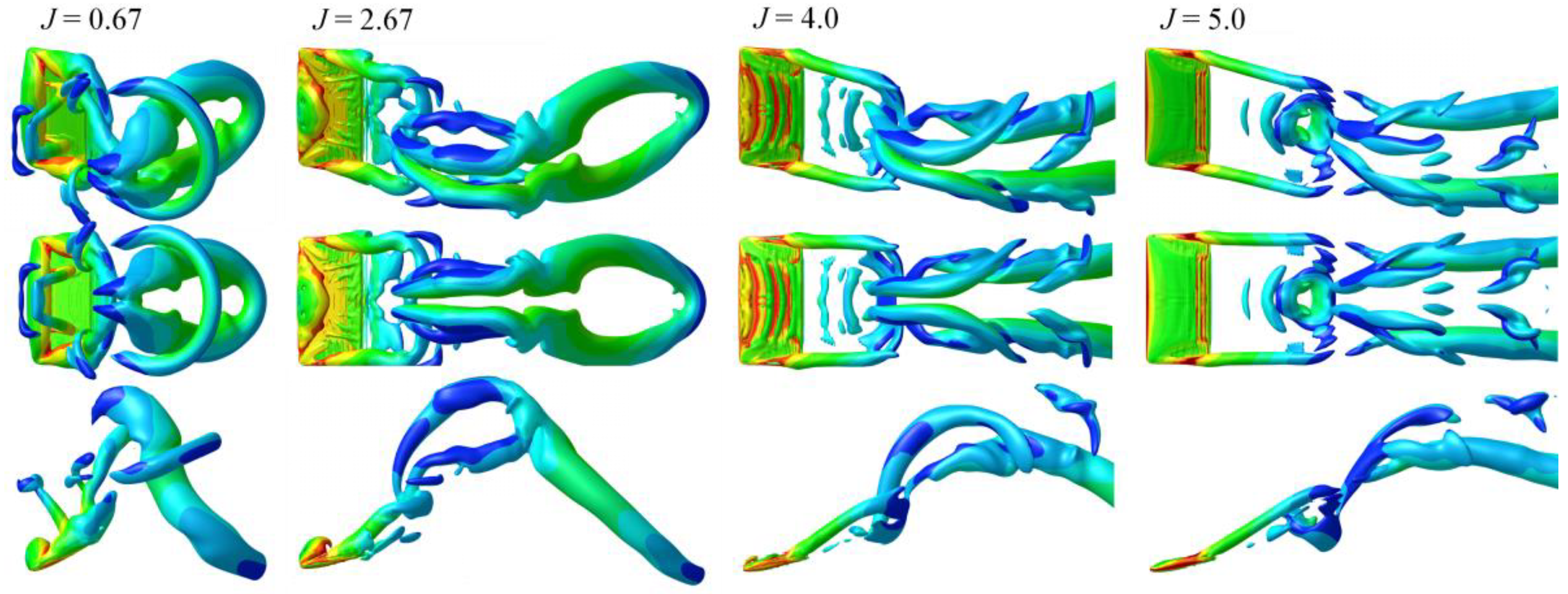
4.3. Analysis of Vortex Structure
5. Conclusions
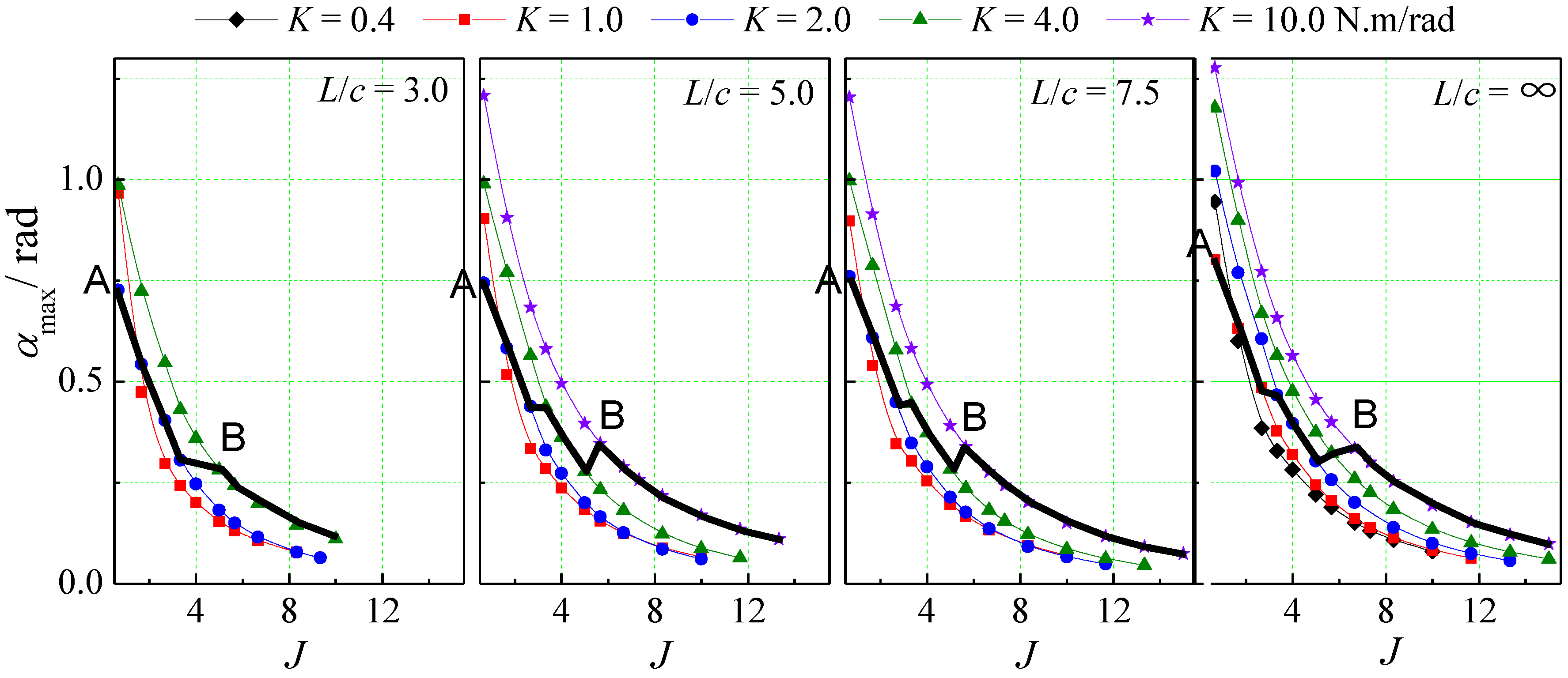
- The influence of arm length and spring stiffness on the performance of the semi-active flapping foil is very clear. Increasing the length of the swing arm is beneficial to improving the peak efficiency of this semi-active flapping foil with circular-arc trajectory. At the same swing arm length, reducing the spring stiffness is also conducive to improving the peak efficiency of the flapping foil. The analysis of the maximum angle of attack shows that there is a definite corresponding relationship between the maximum angle of attack and the peak efficiency. For the flapping foil with the small aspect ratio NACA0012 airfoil structure, its peak efficiency is usually concentrated near , and it can maintain high efficiency within a certain range of .
- The influencing factors of the thrust coefficient of the semi-active flapping foil propulsion are complex. The length of the swinging arm, the spring stiffness, and the advance coefficient can all have a significant impact on the thrust coefficient of the flapping foil. On the whole, compared with the conventional semi-active foil, the elliptical trajectory system also has a large thrust coefficient at low advance coefficient. The curve of the thrust coefficient decreases monotonically with the increase in advance coefficient when the spring stiffness is small. Under the condition of high spring stiffness, there is a peak value and a valley value of the thrust coefficient. According to the analysis of the flow field, the reason for the thrust valley may be the combined effect of the swing angle and the angle of attack. At the valley point of the thrust coefficient, the angle of attack of the flapping foil is large, so the vortex separation of foil is significant and the lift value is low. At the same time, the swing angle is small, so the contribution of lift to the thrust is low, which leads to the appearance of the thrust valley. In addition, by comparing the thrust coefficient and the maximum angle of attack , it is found that too large or too small is unfavorable to the thrust under the working condition of the intermediate advance stage, and the peak thrust tends to appear in the range .
- The flow-field analysis of the low aspect ratio airfoil shows that the vortex rings are interlocked in the wake field of the flapping foil at a low advance speed. With the increase in advance coefficient, the vortex rings are gradually lengthened first, and then separated from each other. When the advance coefficient is further increased, the vortex ring is split into a tip vortex and separated vortex on the airfoil surface. From the reverse analysis, the vortex ring is the result of the tip vortex and the separated vortex on the airfoil surface sticking together, while the vortex ring interlocking is formed by the compression of the vortex ring in space.
Author Contributions
Funding
Conflicts of Interest
References
- Triantafyllou, M.S.; Triantafyllou, G.S. An efficient swimming machine. Scientific 1995, 272, 64–70. [Google Scholar] [CrossRef]
- Liu, H.X.; Su, Y.M.; Pang, Y.G. Numerical study on swing gliding swimming of tuna like underwater robot. Ship Mech. 2020, 24, 145–153. (In Chinese) [Google Scholar]
- Luo, Y.; Xia, Q.; Shi, G.; Pan, G.; Chen, D. The effect of variable stiffness of tuna-like fish body and fin on swimming performance. Bioinspiration Biomim. 2020, 16, 016003. [Google Scholar] [CrossRef] [PubMed]
- Esposito, C.J.; Tangorra, J.L.; Flammang, B.E.; Lauder, G.V. A robotic fish caudal fin: Effects of stiffness and motor program on locomotor performance. J. Exp. Biol. 2012, 215, 56–67. [Google Scholar] [CrossRef] [Green Version]
- Desvignes, T.; Robbins, A.E.; Carey, A.; Bailon-Zambrano, R.; Nichols, J.; Postlethwait, J.; Stankunas, K. Coordinated patterning of zebrafish caudal fin symmetry by a central and two peripheral organizers. Dev. Dyn. 2022, 251, 1306–1321. [Google Scholar] [CrossRef]
- Borazjani, I.; Sotiropoulos, F. Numerical investigation of the hydrodynamics of carangiform swimming in the transitional and inertial flow regimes. J. Exp. Biol. 2009, 211, 1541–1558. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.Y.; Zhu, B.W.; Wang, Z.H.; Yu, Y.L. Study on propagation characteristics of deformed curvature waves of fish swimming in eel mode. Acta Mech. Sin. 2019, 51, 1022–1030. (In Chinese) [Google Scholar]
- Huang, Z.; Ma, S.; Bagheri, H.; Ren, C.; Marvi, H. The Impact of Dorsal Fin Design on the Swimming Performance of a Snake-Like Robot. IEEE Robot. Autom. Lett. 2022, 7, 4939–4944. [Google Scholar] [CrossRef]
- Cheng, X.; Guang, P.; Qiaogao, H. Performance Analysis of Airfoil Flow Field of a Mannequin-like Flexible Submersible. Digit. Ocean. Underw. Warf. 2020, 3, 265–270. (In Chinese) [Google Scholar]
- Wei, Z.; Hu, Y.; Long, W.; Jia, Y. Development of a flipper propelled turtle-like underwater robot and its CPG-based control algorithm. In Proceedings of the IEEE Conference on Decision & Control, Cancun, Mexico, 9–11 December 2008. [Google Scholar]
- Mannam, N.P.B.; Krishnankutty, P.; Vijayakumaran, H.; Sunny, R.C. Experimental and Numerical Study of Penguin Mode Flapping Foil Propulsion System for Ships. J. Bionic Eng. 2017, 14, 770–780. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, X.; Tian, X.; Li, X.; Lu, W. A review on fluid dynamics of flapping foils. Ocean. Eng. 2020, 195, 106712. [Google Scholar] [CrossRef]
- Von Ellenrieder, K.D.; Parker, K.; Soria, J. Flow structures behind a heaving and pitching finite-span wing. J. Fluid Mech. 2003, 490, 129–138. [Google Scholar] [CrossRef]
- Anderson, J.M.; Streitlien, K.; Barrett, D.S.; Triantafyllou, M.S. Oscillating Foils of High Propulsive Efficiency. J. Fluid Mech. 1998, 360, 41–72. [Google Scholar] [CrossRef]
- Li, M.Y. Flow Mechanism Analysis and Experimental Study of Swing Wing Propulsion. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2019. [Google Scholar]
- Mei, L.; Zhou, J.; Yu, D.; Shi, W.; Pan, X.; Li, M. Parametric Analysis for Underwater Flapping Foil Propulsor. Water 2021, 13, 2103. [Google Scholar] [CrossRef]
- Thaweewat, N.; Phoemsapthawee, S.; Juntasaro, V. Semi-active flapping foil for marine propulsion. Ocean. Eng. 2018, 147, 556–564. [Google Scholar] [CrossRef]
- Schnipper, T.; Andersen, A.; Bohr, T. Vortex wakes of a flapping foil. J. Fluids Mech. 2009, 633, 411. [Google Scholar] [CrossRef] [Green Version]
- Andersen, A.; Bohr, T.; Schnipper, T.; Walther, J.H. Wake structure and thrust generation of a flapping foil in two-dimensional flow. J. Fluids Mech. 2017, 812, R4. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.; Strom, B.; Mandre, S.; Breuer, K. Energy Harvesting Performance and Flow Structure of an Oscillating Hydrofoil with Finite Span. J. Fluids Struct. 2017, 70, 314–326. [Google Scholar] [CrossRef]
- Bøckmann, E.; Steen, S. Experiments with actively pitch-controlled and spring-loaded oscillating foils. Appl. Ocean. Res. 2014, 48, 227–235. [Google Scholar] [CrossRef]
- Yang, F.; Shi, W.; Wang, D. Systematic Study on Propulsive Performance of Tandem Hydrofoils for a Wave Glider. Ocean. Eng. 2019, 179, 361–370. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Yan, W.; Yu, D.; Pan, X.; Zhao, X. An adaptive angle of attack flapping foil propeller and its design method Invention. Patents 2021. (In Chinese) [Google Scholar]
- Xiao, Q.; Hu, J.; Liu, H. Effect of Torsional Stiffness and Inertia on the Dynamics of Low Aspect Ratio Flapping Wings. Bioinspiration Biomim. 2014, 9, 16008. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Phoemsapthawee, S.; Thaweewat, N.; Juntasaro, V. Influence of Resonance on the Performance of Semi-Active Flapping Propulsor. Ship Technol. Res. 2020, 67, 51–60. [Google Scholar] [CrossRef]
- Esfahani, J.A.; Barati, E.; Karbasian, H.R. Fluid structures of flapping airfoil with elliptical motion trajectory. Comput. Fluids 2015, 108, 142–155. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, F.; Wang, D.; Jiang, X. Numerical investigation of a new three-degree-of-freedom motion trajectory on propulsion performance of flapping foils for UUVs. Ocean. Eng. 2021, 224, 108763. [Google Scholar] [CrossRef]
- Mei, L.; Yan, W.; Zhou, J.; Yu, D.; Wu, P. Working characteristics of self-pitching flapping foil propulsor. MARINE 2021, 412. [Google Scholar] [CrossRef]
- Floc’h, F.; Phoemsapthawee, S.; Laurens, J.M.; Leroux, J.B. Porpoising foil as a propulsion system. Ocean. Eng. 2012, 39, 53–61. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Shenghao, Z.; Lei, M.; Junwei, Z. Numerical prediction of hydrodynamic performance of propeller with different shape swinging wings. Chin. J. Ship Res. 2021, 16, 50. (In Chinese) [Google Scholar]
- Read, D.A.; Hover, F.S.; Triantafyllou, M.S. Forces on oscillating foils for propulsion and maneuvering. J. Fluids Struct. 2003, 17, 163–183. [Google Scholar] [CrossRef]
- Schouveiler, L.; Hover, F.S.; Triantafyllou, M.S. Performance of flapping foil propulsion. J. Fluids Struct. 2005, 20, 949–959. [Google Scholar] [CrossRef]
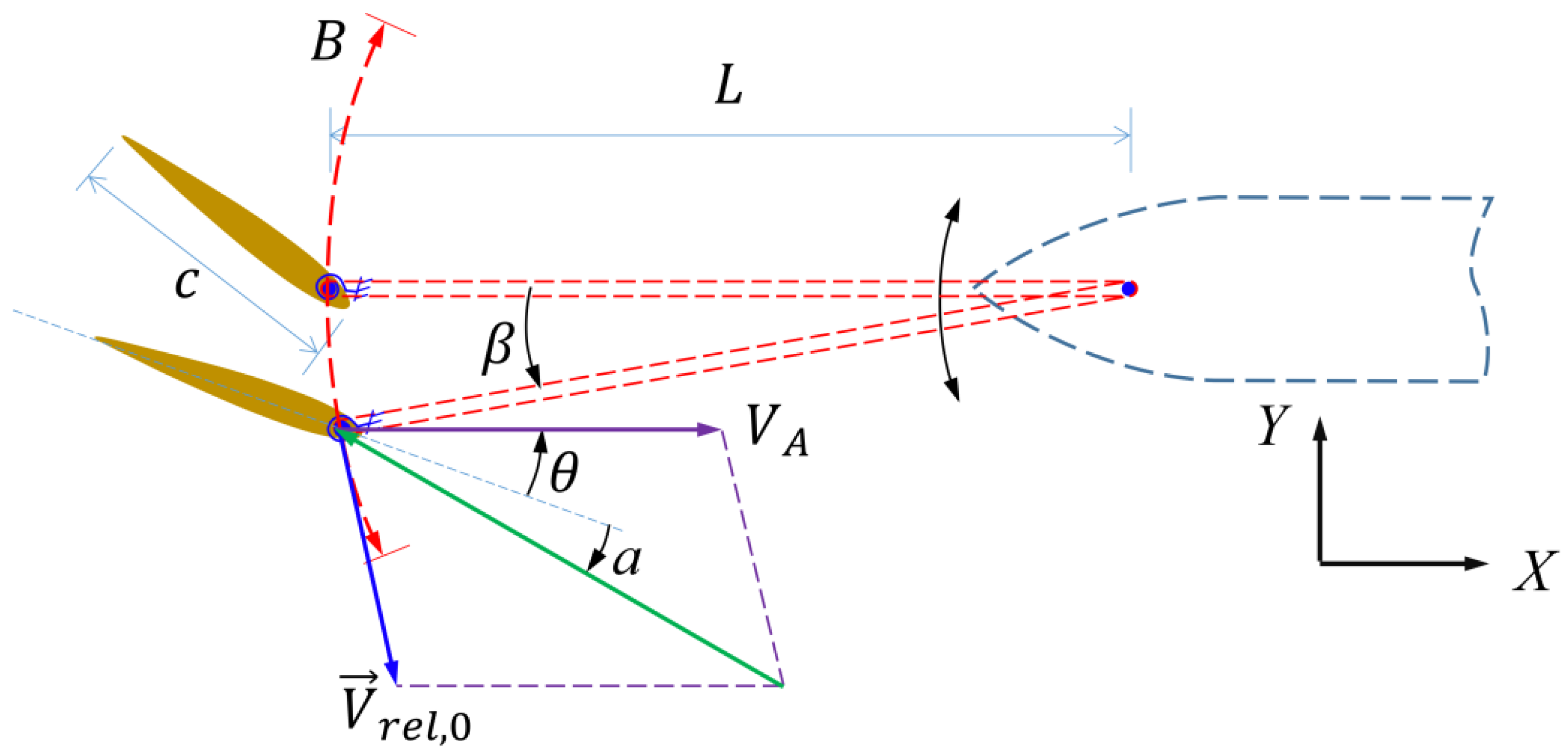
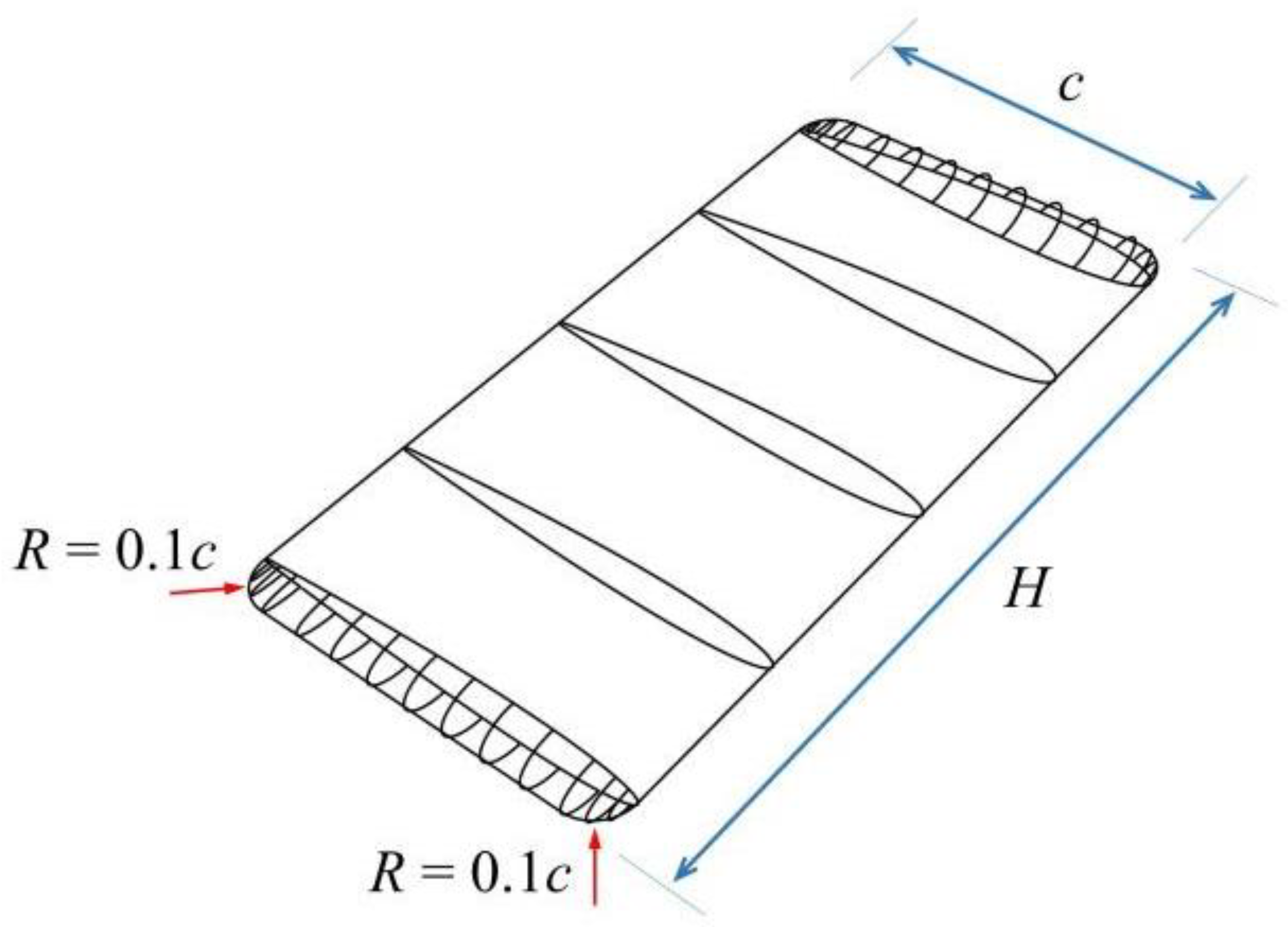





| Symbol | Units | Definition |
|---|---|---|
| VA | m/s | speed of the hull |
| T | s | period of the flapping hydrofoil |
| L/c | m | arm length |
| c | m | chord length of the flapping hydrofoil |
| H | m | spanwise of the flapping hydrofoil |
| R | m | radius of round corners designed at both ends of the span direction of the flapping hydrofoil |
| β | radian | swing angle of the swing arm |
| f | Hz | swing frequency of the swing arm |
| θ | radian | pitching angle of the flapping hydrofoil |
| Vrel,0 | m/s | pitching center speed of the foil relative to the hull |
| Vx0,Vy0 | m/s | velocity components of Vrel,0 |
| Fx0,Fy0 | m | X-direction force, Y-direction force exerted by the swing arm on the pitching center of flapping foil, respectively |
| Mz0 | N m | torque exerted by the swing arm on the pitching center of flapping foil |
| Mz | N m | fluid moment imposed on foil |
| K | Nm/rad | torsion spring stiffness |
| I | Kg m2 | rotational inertia about the axis of the flapping hydrofoil considering the attached water |
| N | average thrust in the forward direction | |
| α (AoA) | radian | angle of attack of flapping hydrofoil |
| St | St number of flapping hydrofoil | |
| J | advance coefficient | |
| KT | thrust coefficient | |
| η | propulsive efficiency of flapping hydrofoil |
| Direction | Hydrofoil Surface Region | Refinement Area |
|---|---|---|
| spanwise/Z | ||
| chordwise/X | ||
| normal direction/Y |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Yan, W.; Mei, L.; Shi, W. Performance of Semi-Active Flapping Hydrofoil with Arc Trajectory. Water 2023, 15, 269. https://doi.org/10.3390/w15020269
Zhou J, Yan W, Mei L, Shi W. Performance of Semi-Active Flapping Hydrofoil with Arc Trajectory. Water. 2023; 15(2):269. https://doi.org/10.3390/w15020269
Chicago/Turabian StyleZhou, Junwei, Wenhui Yan, Lei Mei, and Weichao Shi. 2023. "Performance of Semi-Active Flapping Hydrofoil with Arc Trajectory" Water 15, no. 2: 269. https://doi.org/10.3390/w15020269
APA StyleZhou, J., Yan, W., Mei, L., & Shi, W. (2023). Performance of Semi-Active Flapping Hydrofoil with Arc Trajectory. Water, 15(2), 269. https://doi.org/10.3390/w15020269







