Analysis of the Influence of Water Level Change on the Seepage Field and Stability of a Slope Based on a Numerical Simulation Method
Abstract
:1. Introduction
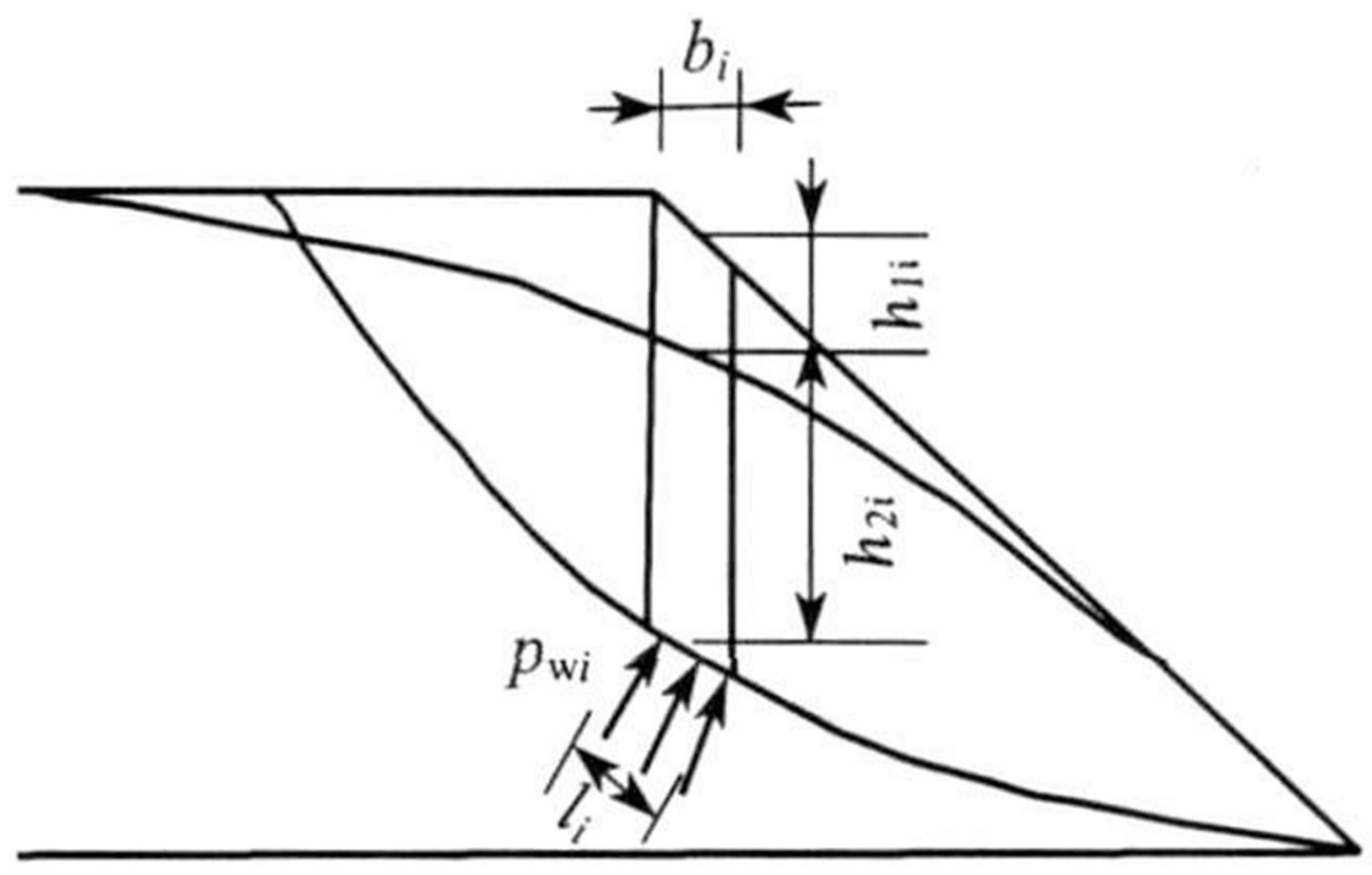
2. Unsaturated–Unstable Seepage and Slope Stability Analysis Theory
- When k/μv < 1/10, the wetting surface in the dam still remains about 90% of the total initial water head after the reservoir water level drops.
- When k/μv > 60, the wetting surface in the dam remains below 10% of the total water head, and the wetting line in the slope is approximately a straight line, which is more consistent with the shape of the wetting line in slow-down mode, and the water level drop is regarded as a slow drop.
- When the ratio is in the range of 1/10 < k/μv < 60, the mode is the intermediate slow drop–sudden drop category.
3. Design and Verification of Model Tests and Numerical Simulations
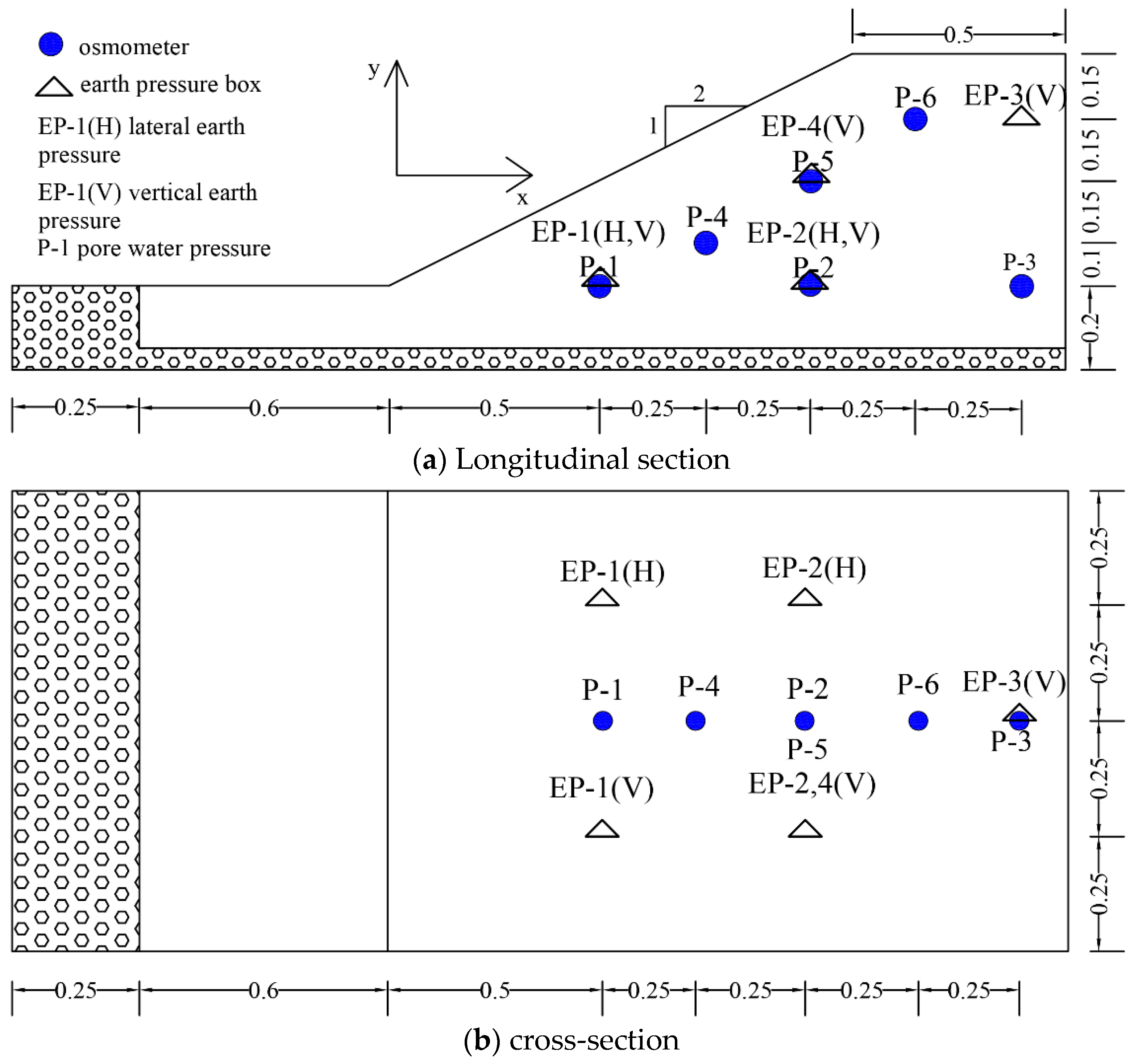
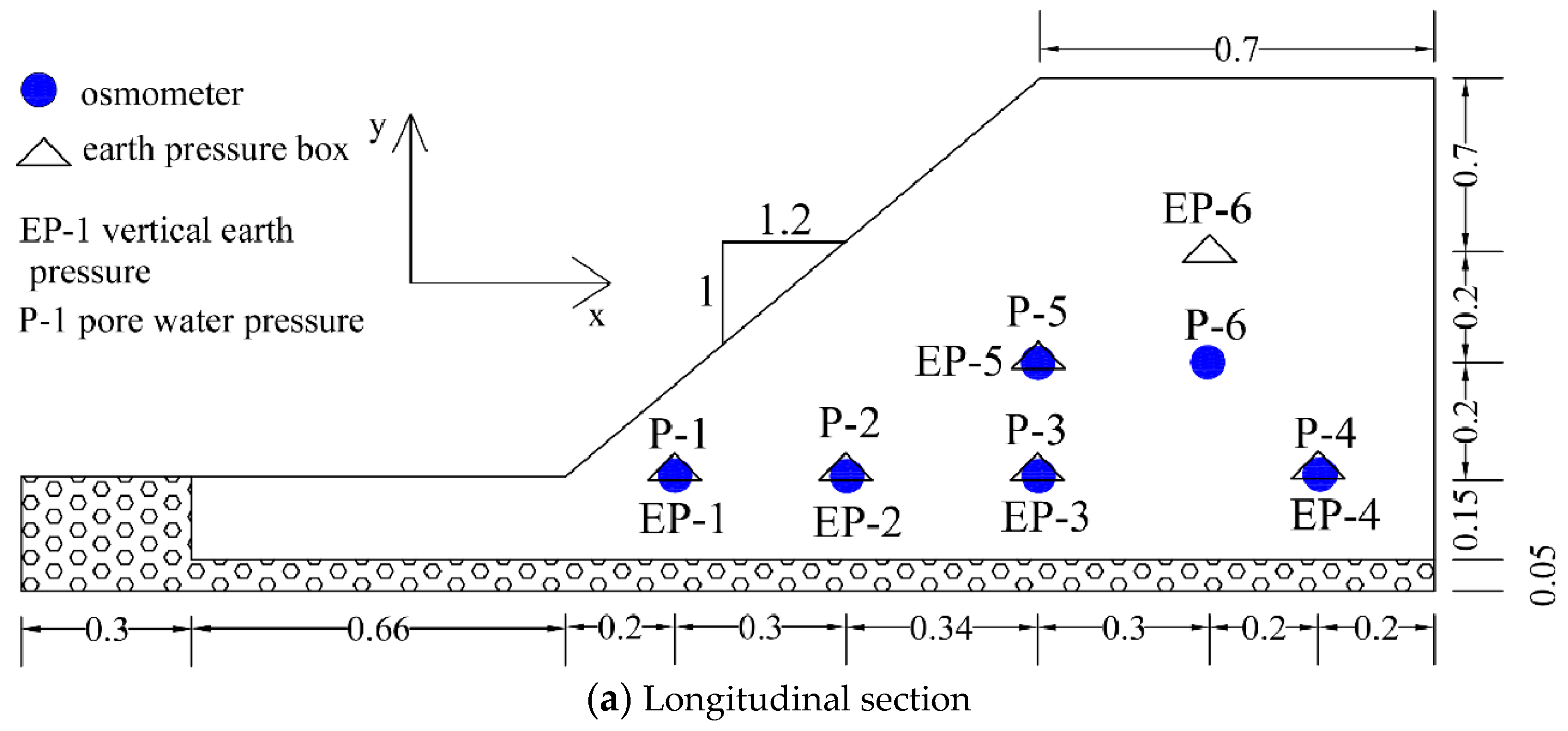
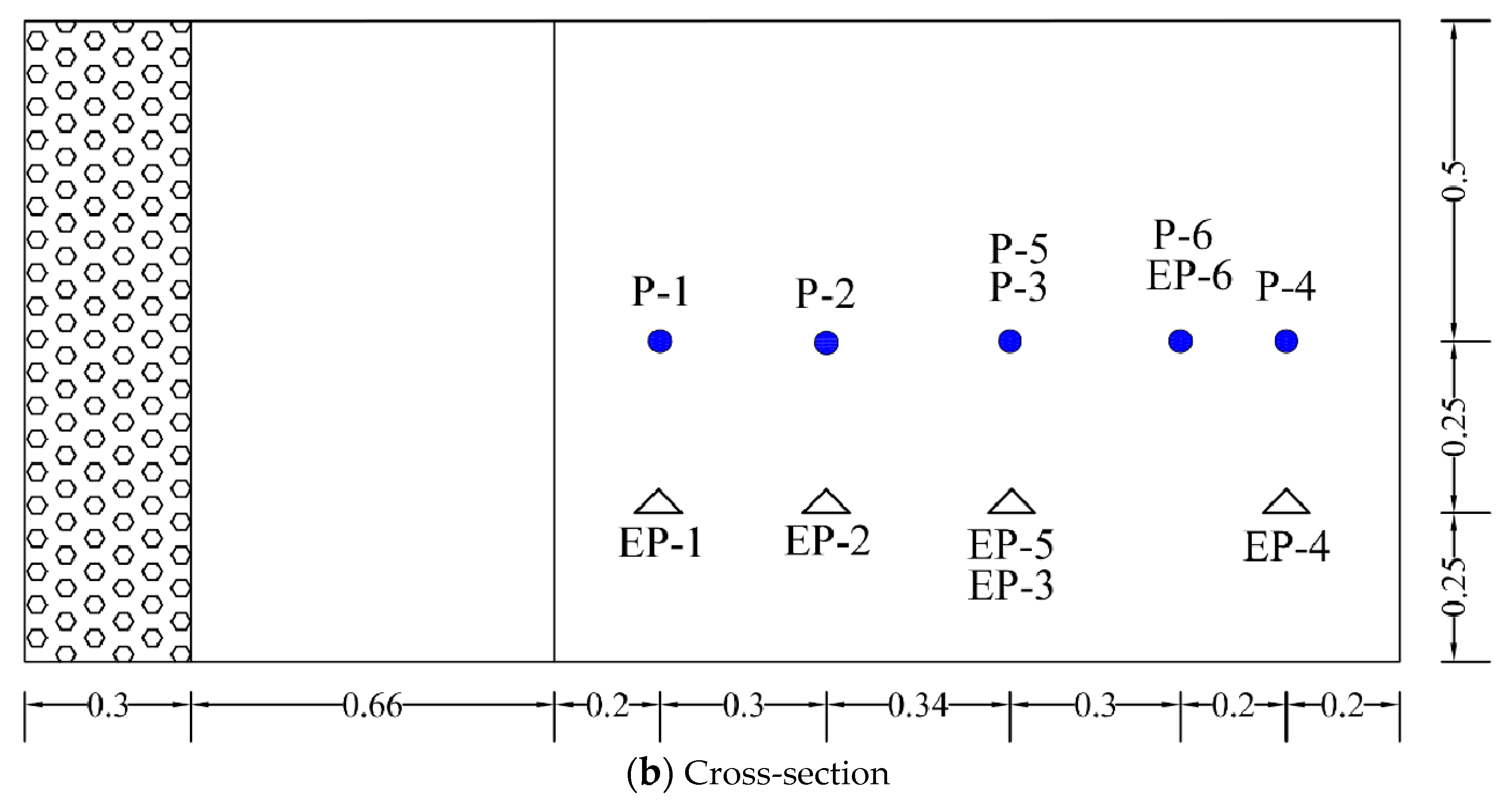
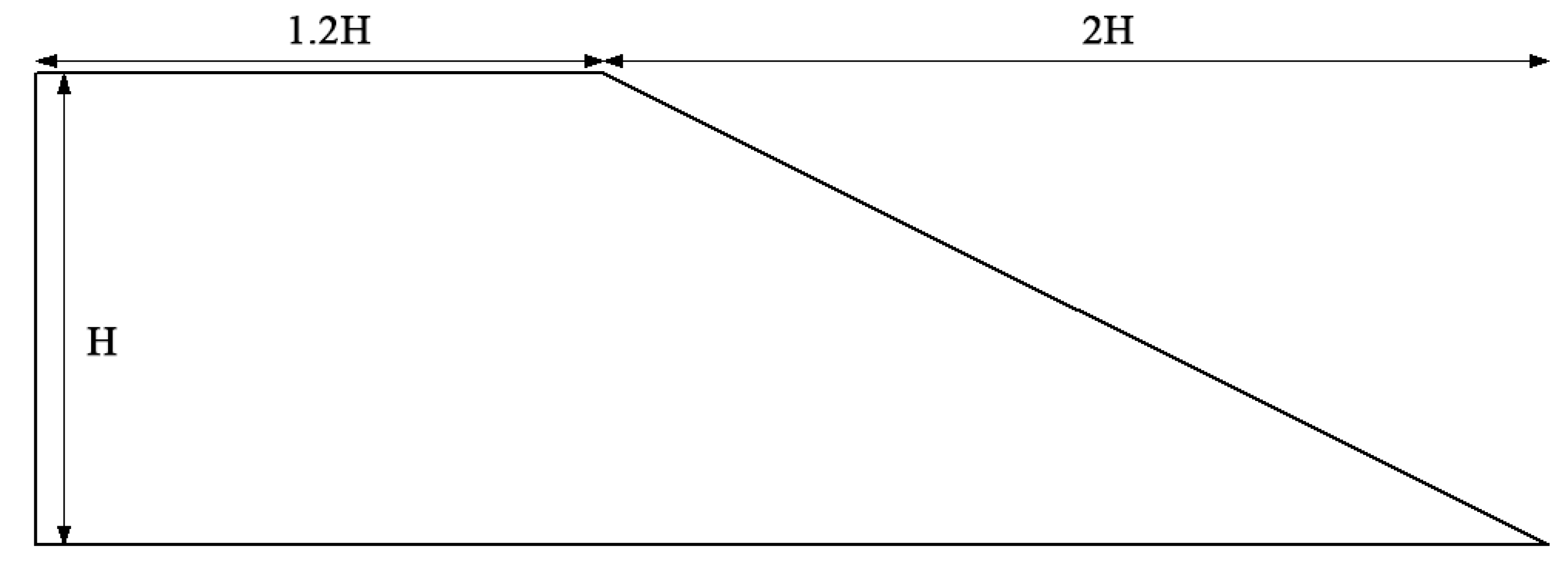
3.1. Slope Model Test
3.2. GeoStudio Numerical Simulation
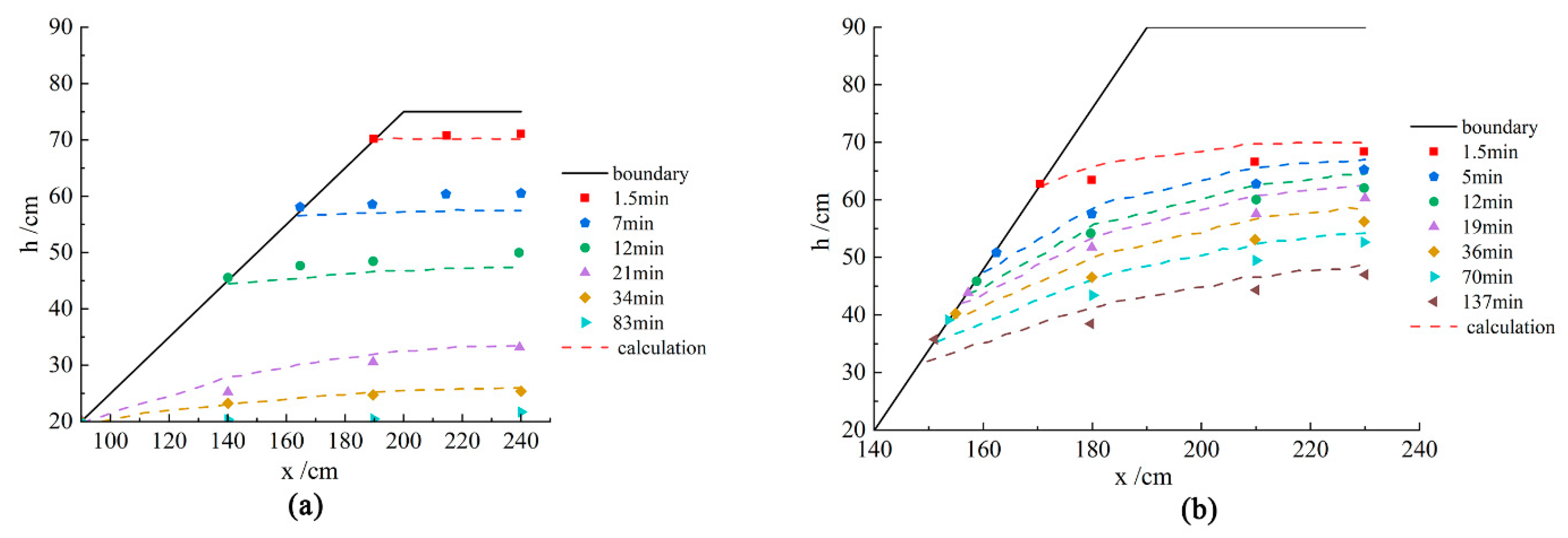
3.3. Comparison and Verification of Model Test and Numerical Simulation Results
4. Analysis of Influence of Water Level Fall on Slope Stability
4.1. Analysis of Influence of Water Level Falling Speed on Slope Stability
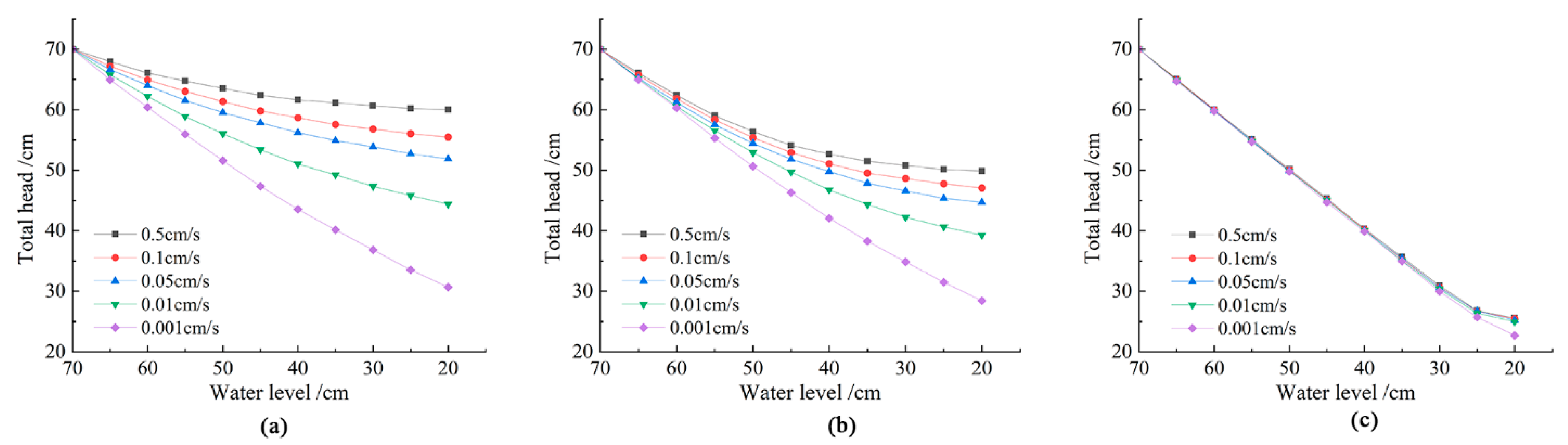
4.1.1. Influence of Falling Speed on Seepage Field
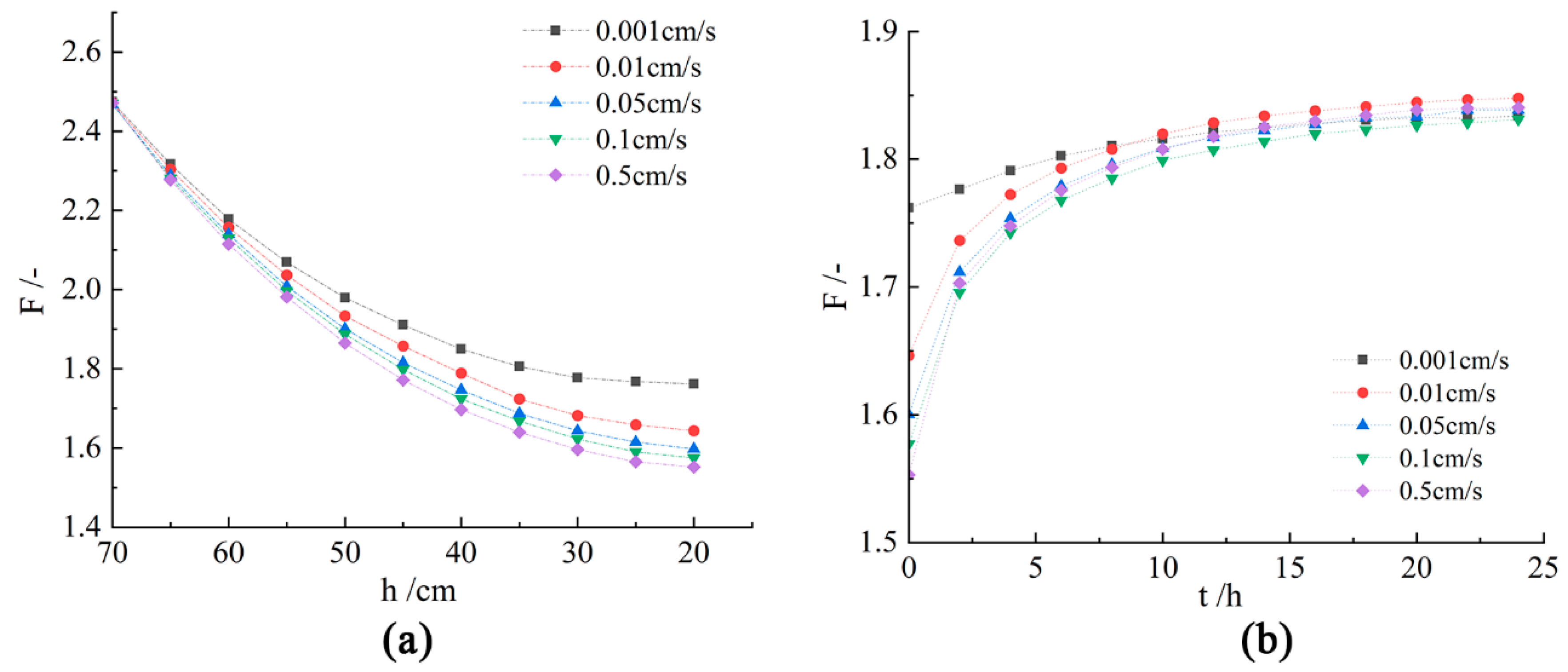
4.1.2. Influence of Water Level Falling Speed on Slope Safety Factor
4.2. Influence of Drop Ratio on Slope Stability
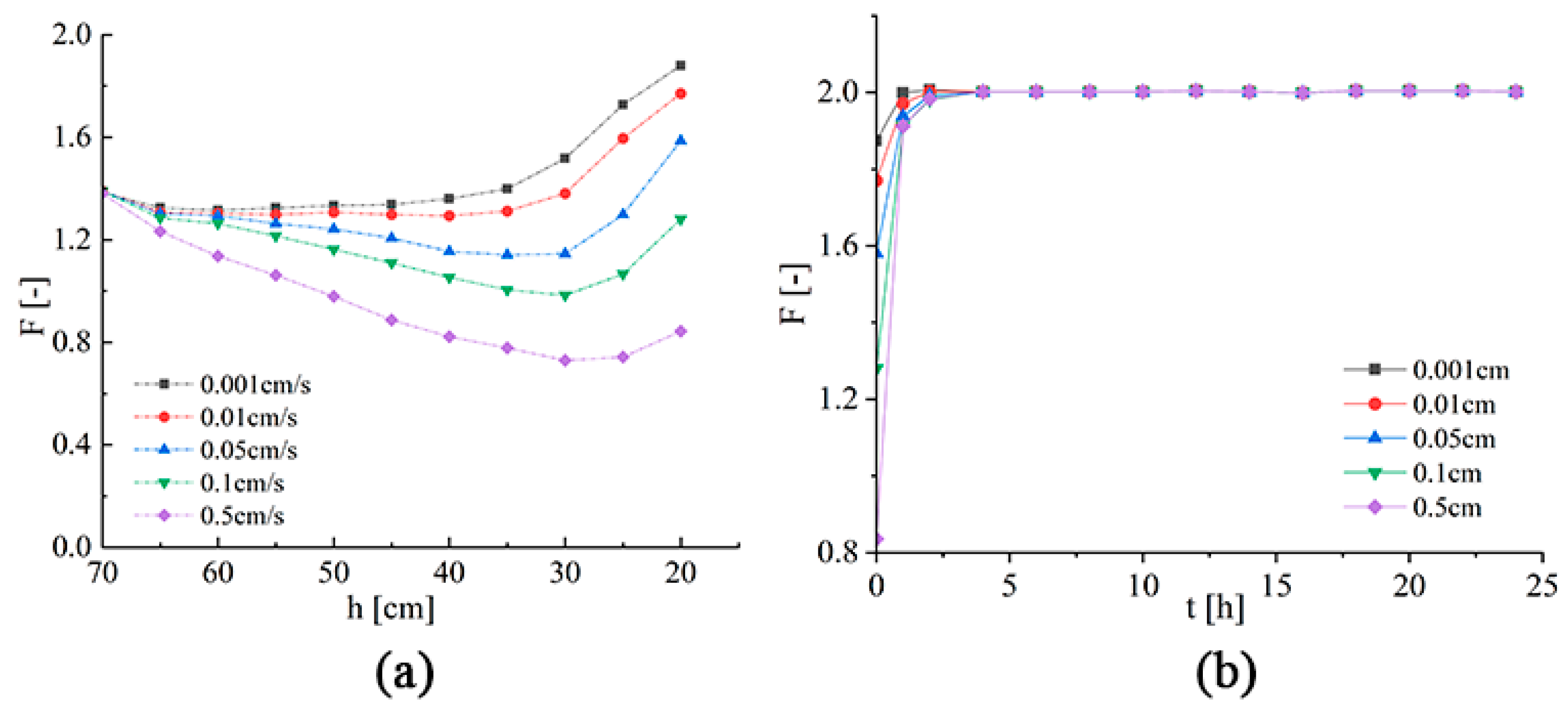
4.2.1. Influence of Drop Ratio on Seepage Field of Slope
4.2.2. Influence of Drop Ratio on Safety Factor of Slope
4.3. Influence of Filling Materials on Slope Stability
4.3.1. Influence of Permeability Coefficient on Seepage Field of Slope
4.3.2. Influence of Permeability Coefficient on the Slope Safety Factor
5. Practical Application of Modeling Methods
6. Conclusions
- When the water level in front of the slope falls at different speeds, the greater this speed, the greater the downward seepage force formed by the seepage field of the slope to the slope body. When the water level in front of the slope falls at a constant speed, the penetration force is greater at the position closer to the slope.
- When the speed at which the water level before the slope falls increases, the safety factor of the slope decreases. When the water level in front of the slope falls at different speeds, the change curve of the safety factor is steeper when the speed is more, and the safety factor value of the same water level before the slope is smaller. The safety factor of the slope when the water level falls at a speed of 0.5 cm/s (as studied in this paper) has a maximum falling range of 37% during the water level change process.
- With an increase in the drop ratio, the safety factor of the slope decreases. When the drop ratio is constant, the loss of stability is worse if the initial water level is lower. Due to the difference in soil mechanical properties, under the condition of the drawdown of water levels in front of the slope, the noncohesive medium sand slope is more prone to instability failure than the cohesive silt slope.
- When this modeling method is applied to matrix suction, it is found that the effect of matrix suction increases the safety factor of the slope. When the speed of the fall of the water level in front of the slope decreases, after the water level in the front of the slope is stable, the unsaturated area formed in the slope is larger, and the influence of the matrix suction on the stability of the slope also increases.
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.C.; Li, Y.R.; Liu, Y.S.; Huang, Y.X.; Wang, Y.S.; Lu, Z. Characteristics and prevention mechanisms of artificial slope instability in the Chinese Loess Plateau. CATENA 2021, 207, 105621. [Google Scholar] [CrossRef]
- Filho, O.A.; Fernandes, M.A. Landslide analysis of unsaturated soil slopes based on rainfall and matric suction data. Bull. Eng. Geol. Environ. 2019, 78, 4167–4185. [Google Scholar] [CrossRef]
- Cong, S.Y.; Tang, L.; Ling, X.Z.; Xing, W.Q.; Geng, L.; Li, X.Y.; Li, G.Y.; Li, H. Three-Dimensional Numerical Investigation on the Seepage Field and Stability of Soil Slope Subjected to Snowmelt Infiltration. Water 2021, 13, 2729. [Google Scholar] [CrossRef]
- Schorg, A.J.; Romano, S.P. Shallow and deep water aquatic vegetation potential for a midlatitude pool of the Upper Mississippi River System with drawdown. River Res. Appl. 2018, 34, 310–316. [Google Scholar] [CrossRef]
- Gan, B.R.; Yang, X.G.; Liao, H.M.; Zhou, J.W. Flood Routing Process and High Dam Interception of Natural Discharge from the 2018 Baige Landslide-Dammed Lake. Water 2020, 12, 605. [Google Scholar] [CrossRef] [Green Version]
- Luo, F.Y.; Zhang, G.; Ma, C.H. On the Soil Slope Failure Mechanism Considering the Mutual Effect of Bedrock and Drawdown. Int. J. Geomech. 2021, 21, 04020247. [Google Scholar] [CrossRef]
- Sun, D.M.; Zang, Y.G.; Semprich, S. Effects of Airflow Induced by Rainfall Infiltration on Unsaturated Soil Slope Stability. Transp. Porous Media 2015, 107, 821–841. [Google Scholar] [CrossRef]
- Wang, Y.X.; Chai, J.R.; Cao, J.; Qin, Y.; Xu, Z.G.; Zhang, X.W. Effects of seepage on a three-layered slope and its stability analysis under rainfall conditions. Nat. Hazards 2020, 102, 1269–1278. [Google Scholar] [CrossRef]
- Zhu, C.Q.; Cheng, H.L.; Chen, Z.Y.; Huang, Y. Simulation-based hazard management of a constructed landfill for flow slide scenario. Nat. Hazards 2021, 106, 1867–1878. [Google Scholar] [CrossRef]
- Zhu, C.Q.; Huang, Y.; Zhan, L.T. SPH-based simulation of flow process of a landslide at Hongao landfill in China. Nat. Hazards 2018, 93, 1113–1126. [Google Scholar] [CrossRef]
- Mekrishu, W.N.; Singh, S.K.; Ningthoujam, P.S.; Piuthaimei, G.Z. A study on the causative and triggering factors of multiple landslides in Lalmati, Nagaland and development of a sinking zone. Himal. Geol. 2022, 43, 73–84. [Google Scholar]
- Hou, X.P.; Chen, S.H.; Shahrour, I. Judgement of rapid drawdown conditions in slope stability analysis. Bull. Eng. Geol. Environ. 2021, 80, 4379–4387. [Google Scholar] [CrossRef]
- Liu, S.J.; Luo, F.Y.; Zhang, G. Centrifuge model tests on pile-reinforced slopes subjected to drawdown. J. Rock Mech. Geotech. Eng. 2020, 12, 1290–1300. [Google Scholar] [CrossRef]
- Sui, W.H.; Zheng, G.S. An experimental investigation on slope stability under drawdown conditions using transparent soils. Bull. Eng. Geol. Environ. 2018, 77, 977–985. [Google Scholar] [CrossRef]
- Wang, L.; Sun, D.A.; Li, L. 3D stability of partially saturated soil slopes after rapid drawdown by a new layer-wise summation method. Landslides 2019, 16, 295–313. [Google Scholar] [CrossRef]
- Zhou, J.F.; Qin, C.B. Stability analysis of unsaturated soil slopes under reservoir drawdown and rainfall conditions: Steady and transient state analysis. Comput. Geotech. 2022, 142, 104541. [Google Scholar] [CrossRef]
- Xue-wu, W.; Shang-jie, X.; Fa-ning, D. Analysis of stability of dam slope during rapid drawdown of reservoir water level. Rock Soil Mech. 2010, 31, 2760–2764. [Google Scholar]
- Zhou, J.-W.; Xu, F.-G.; Yang, X.-G.; Yang, Y.-C.; Lu, P.-Y. Comprehensive analyses of the initiation and landslide-generated wave processes of the 24 June 2015 Hongyanzi landslide at the Three Gorges Reservoir, China. Landslides 2016, 13, 589–601. [Google Scholar] [CrossRef]
- Moharrami, A.; Hassanzadeh, Y.; Salmasi, F.; Moradi, G.; Moharrami, G. Performance of the horizontal drains in upstream shell of earth dams on the upstream slope stability during rapid drawdown conditions. Arab. J. Geosci. 2014, 7, 1957–1964. [Google Scholar] [CrossRef]
- Özer, A.T.; Bromwell, L.G. Stability assessment of an earth dam on silt/clay tailings foundation: A case study. Eng. Geol. 2012, 151, 89–99. [Google Scholar] [CrossRef]
- Siacara, A.; Beck, A.T.; Futai, M.M. Reliability analysis of rapid drawdown of an earth dam using direct coupling. Comput. Geotech. 2020, 118, 103336. [Google Scholar] [CrossRef]
- Babanouri, N.; Dehghani, H. Investigating a potential reservoir landslide and suggesting its treatment using limit-equilibrium and numerical methods. J. Mt. Sci. 2017, 14, 432–441. [Google Scholar] [CrossRef]
- Bhaskar, P.; Puppala, A.J.; Boluk, B. Influence of Unsaturated Hydraulic Properties on Transient Seepage and Stability Analysis of an Earthen Dam. Int. J. Geomech. 2022, 22, 04022105. [Google Scholar] [CrossRef]
- Biniyaz, A.; Azmoon, B.; Liu, Z. Coupled transient saturated-unsaturated seepage and limit equilibrium analysis for slopes: Influence of rapid water level changes. Acta Geotech. 2022, 17, 2139–2156. [Google Scholar] [CrossRef]
- Xu, J.S.; Yang, X.L. Three-dimensional stability analysis of slope in unsaturated soils considering strength nonlinearity under water drawdown. Eng. Geol. 2018, 237, 102–115. [Google Scholar] [CrossRef]
- Cen, W.J.; Li, D.J.; Wang, H. Impact of transient seepage on slope stability of earth-rock dams with geomembrane barrier defects. Environ. Geotech. 2020, 7, 581–590. [Google Scholar] [CrossRef]
- Gao, X.C.; Liu, H.L.; Zhang, W.G.; Wang, W.; Wang, Z.Y. Influences of reservoir water level drawdown on slope stability and reliability analysis. Georisk-Assess. Manag. Risk Eng. Syst. Geohazards 2019, 13, 145–153. [Google Scholar] [CrossRef]
- Zhou, X.P.; Wei, X.; Liu, C.; Cheng, H. Three-Dimensional Stability Analysis of Bank Slopes with Reservoir Drawdown Based on Rigorous Limit Equilibrium Method. Int. J. Geomech. 2020, 20, 04020229. [Google Scholar] [CrossRef]
- Jinlong, L.; Jili, W.; Changwang, L. EFM Simulation on the influence of water level fluctuation on slope stability. Water Power 2007, 33, 41–44. [Google Scholar]
- Chen, Y.; Tian, R.; Li, H. Phosphorus transportation in runoff as influenced by cationic non-classic polarization: A simulation study. J. Soils Sediments 2020, 20, 308–319. [Google Scholar] [CrossRef]
- Liang, J.X.; Sui, W.H. Sensitivity Analysis of Anchored Slopes under Water Level Fluctuations: A Case Study of Cangjiang Bridge-Yingpan Slope in China. Appl. Sci. 2021, 11, 7137. [Google Scholar] [CrossRef]
- Tang, M.G.; Xu, Q.; Yang, H.; Li, S.L.; Iqbal, J.; Fu, X.L.; Huang, X.B.; Cheng, W.M. Activity law and hydraulics mechanism of landslides with different sliding surface and permeability in the Three Gorges Reservoir Area, China. Eng. Geol. 2019, 260, 105212. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Huang, X.Y.; Liu, W.; Wang, L. Study on the Hydraulic Parameters of Woshaxi Landslide Soils during Water Level Drawdown of Three Gorges Reservoir. Geofluids 2020, 2020, 6283791. [Google Scholar] [CrossRef]
- Song, K.; Yan, E.; Zhang, G.; Lu, S.; Yi, Q. Effect of hydraulic properties of soil and fluctuation velocity of reservoir water on landslide stability. Environ. Earth Sci. 2015, 74, 5319–5329. [Google Scholar] [CrossRef]
- Huang, M.S.; Jia, C.Q. Strength reduction FEM in stability analysis of soil slopes subjected to transient unsaturated seepage. Comput. Geotech. 2009, 36, 93–101. [Google Scholar] [CrossRef]
- Pakmanesh, M.; Jahromi, S.H.M.; Khosrojerdi, A.; Darvishi, H.H.; Babazadeh, H. Experimental and numerical study of upstream slope stability in an earth dam reservoir under rapid drawdown conditions. Prog. Comput. Fluid Dyn. 2021, 21, 248–260. [Google Scholar] [CrossRef]
- Cao, J.T. Numerical simulation study on the slope stability of earth-rock dam considering dynamic action based on complex geological environment. Fresenius Environ. Bull. 2020, 29, 10924–10932. [Google Scholar]
- Oh, W.T.; Vanapalli, S.K. Modeling the stress versus settlement behavior of shallow foundations in unsaturated cohesive soils extending the modified total stress approach. Soils Found. 2018, 58, 382–397. [Google Scholar] [CrossRef]
- Zeng, L.; Liu, J.; Zhang, J.H.; Bian, H.B.; Lu, W.H. Effect of Colluvial Soil Slope Fracture’s Anisotropy Characteristics on Rainwater Infiltration Process. Adv. Civ. Eng. 2018, 2018, 7351628. [Google Scholar] [CrossRef] [Green Version]
- Alateya, H.; Asr, A.A. Numerical investigation into the stability of earth dam slopes considering the effects of cavities. Eng. Comput. 2020, 37, 1397–1421. [Google Scholar] [CrossRef]
- Jadid, R.; Montoya, B.M.; Bennett, V.; Gabr, M.A. Effect of repeated rise and fall of water level on seepage-induced deformation and related stability analysis of Princeville levee. Eng. Geol. 2020, 266, 105458. [Google Scholar] [CrossRef]
- Jiang, P.; Huang, Y.; Tao, Z.P.; Zhu, J.H.; Wang, N.; Qiao, J.W. Deformation Characteristics and Safety Evaluation of the Throw Filling Soft Clay Cofferdam under Super-Historical Flood Conditions. Adv. Civ. Eng. 2022, 2022, 9578477. [Google Scholar] [CrossRef]
- Nagy-Gode, F.K.; Torok, A. Rainfall-Induced or Lake-Water-Level-Controlled Landslide? An Example from the Steep Slopes of Lake Balaton, Hungary. Water 2022, 14, 1169. [Google Scholar] [CrossRef]
- Rotaru, A.; Bejan, F.; Almohamad, D. Sustainable Slope Stability Analysis: A Critical Study on Methods. Sustainability 2022, 14, 8847. [Google Scholar] [CrossRef]
- Rabie, M. Comparison study between traditional and finite element methods for slopes under heavy rainfall. HBRC J. 2014, 10, 160–168. [Google Scholar] [CrossRef] [Green Version]
- Kaczmarek, L.D.; Popielski, P. Selected components of geological structures and numerical modelling of slope stability. Open Geosci. 2019, 11, 208–218. [Google Scholar] [CrossRef]
- Mao, C. Seepage Computation Analysis & Control; China Water Resources and Hydropower Press: Beijing, China, 2003. [Google Scholar]
- Jia, C.; Huang, M.; Wang, G. Analysis of Stability of Soil Slope During Rapid Drawdown of Water Table. J.-Tongji Univ. 2008, 36, 304. [Google Scholar]
- Zucca, M.; Crespi, P.G.; Longarini, N. Seismic vulnerability assessment of an Italian historical masonry dry dock. Case Stud. Struct. Eng. 2017, 7, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Lane, P.; Griffiths, D. Assessment or stability of slopes under drawdown conditions. J. Geotech. Geoenviron. Eng. 2000, 126, 443–450. [Google Scholar] [CrossRef]
- Nian, T.K.; Wan, S.S.; Jiang, J.C.; Luan, M.T. Finite element analysis of slope stability under drawdown conditions by strength reduction technique. Rock Soil Mech. 2010, 31, 2264–2269. [Google Scholar]
- Zheng, Y.-R.; Shi, W.; Kong, W.-X. Calculation of seepage forces and phreatic surface under drawdown conditions. Chin. J. Rock Mech. Eng. 2004, 23, 3203–3210. [Google Scholar]
- Zhang, W.-J.; Zhan, L.; Ling, D. Influence of reservoir water level fluctuations on stability of unsaturated soil banks. J.-Zhejiang Univ. Eng. Sci. 2006, 40, 1365. [Google Scholar]
- Duncan, J.M. State of the art: Limit equilibrium and finite-element analysis of slopes—Closure. J. Geotech. Geoenviron. Eng. 1997, 123, 894. [Google Scholar] [CrossRef]



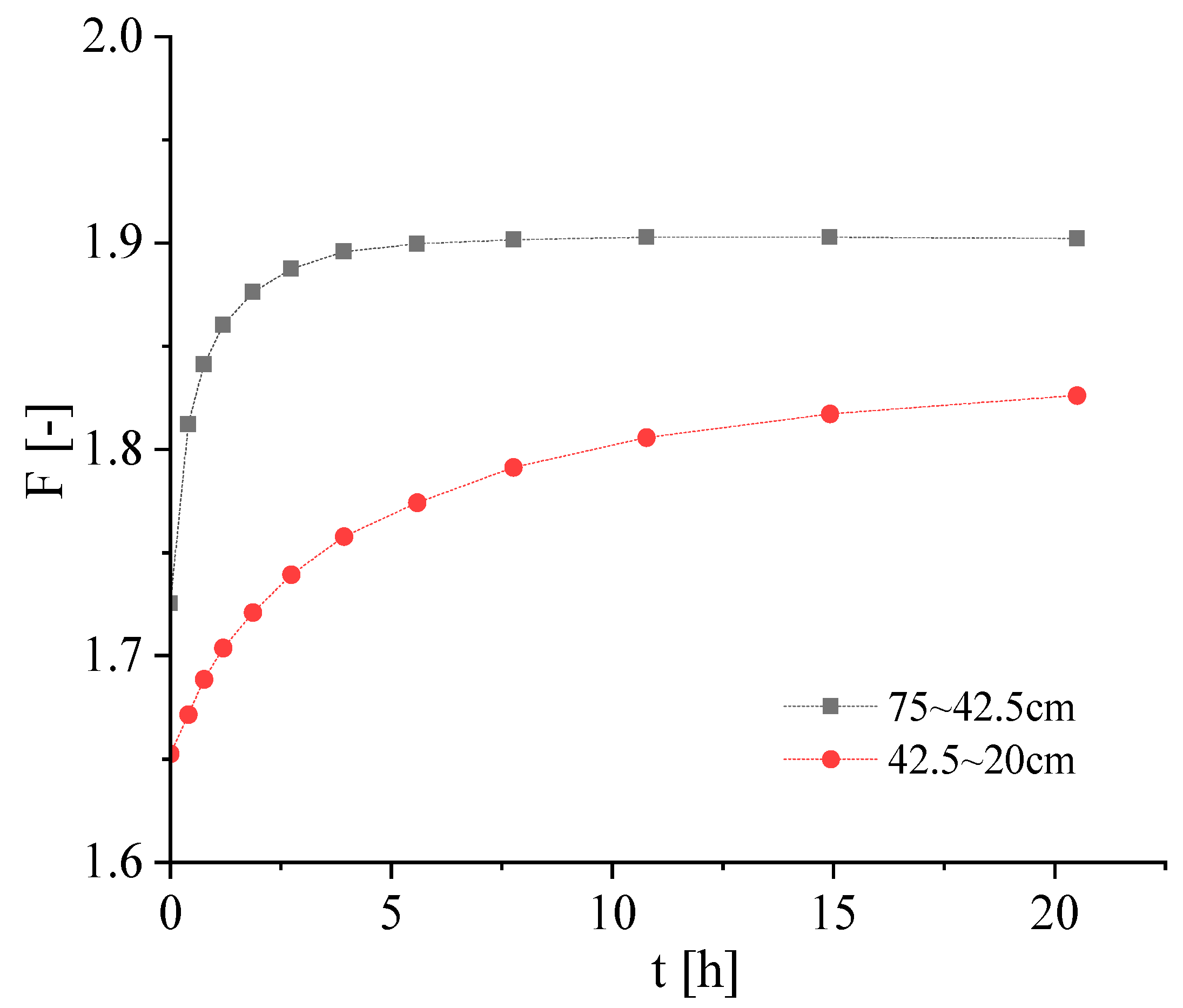

| Soil | Natural Weight γ (kN/m3) | Permeability Coefficient k (cm/s) | Cohesion c (kPa) | Friction Angle φ (°) |
|---|---|---|---|---|
| Medium sand | 19.4 | 2.4 × 10−2 | 0 | 32 |
| Silt | 23.0 | 1.9 × 10−4 | 1.92 | 23 |
| Filling Material | Slope Ratio (Height: Width) | Slope Height (cm) | Landing Velocity (cm/s) | Drop (cm) |
|---|---|---|---|---|
| Medium sand | 1:2 | 75 | 0.043 | 54 |
| Silt | 1:0.7 | 90 | 0.15 | 46 |
| V (cm/s) | Bishop | Janbu | Ordinay | Morgenstern–Price | ||||
|---|---|---|---|---|---|---|---|---|
| Yes | No | Yes | No | Yes | No | Yes | No | |
| 0.5 | 1.555 | 1.553 | 1.432 | 1.428 | 1.449 | 1.446 | 1.553 | 1.550 |
| 0.05 | 1.606 | 1.594 | 1.485 | 1.458 | 1.493 | 1.469 | 1.604 | 1.592 |
| 0.001 | 1.762 | 1.713 | 1.654 | 1.559 | 1.660 | 1.597 | 1.761 | 1.711 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Li, Z.; Yang, K.; Wang, G.; Hu, R. Analysis of the Influence of Water Level Change on the Seepage Field and Stability of a Slope Based on a Numerical Simulation Method. Water 2023, 15, 216. https://doi.org/10.3390/w15020216
Sun Y, Li Z, Yang K, Wang G, Hu R. Analysis of the Influence of Water Level Change on the Seepage Field and Stability of a Slope Based on a Numerical Simulation Method. Water. 2023; 15(2):216. https://doi.org/10.3390/w15020216
Chicago/Turabian StyleSun, Yongshuai, Zhihui Li, Ke Yang, Guihe Wang, and Ruilin Hu. 2023. "Analysis of the Influence of Water Level Change on the Seepage Field and Stability of a Slope Based on a Numerical Simulation Method" Water 15, no. 2: 216. https://doi.org/10.3390/w15020216






