Permeability Tests and Numerical Simulation of Argillaceous Dolomite in the Jurong Pumped-Storage Power Station, China
Abstract
:1. Introduction
2. Case Study
2.1. Project Overview
2.2. Stratal and Distribution Characteristics of Argillaceous Dolomite
3. Methods
3.1. Water Pressure Test
3.2. Seepage Failure Test
3.3. Variable Head Permeability Test
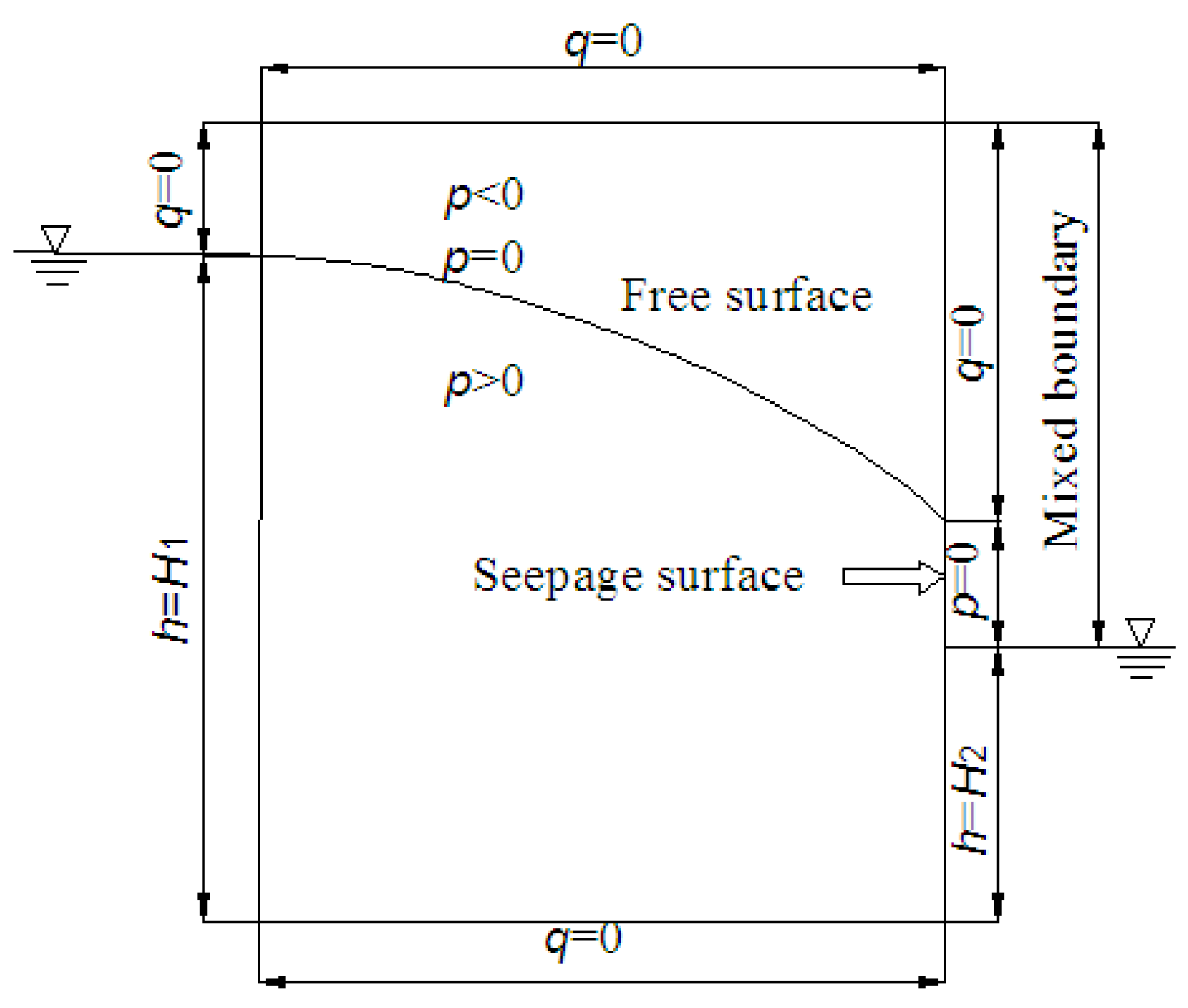
3.4. Numerical Simulation Method
4. Analysis of Results and Discussion
4.1. Permeability Tests
4.2. Seepage Failure Tests
4.3. Numerical Simulation
4.3.1. Model Area Discretization
4.3.2. Parameter Inversion Results
4.3.3. Simulation and Prediction Results of Groundwater
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ning, W.; Tang, H. Dynamic Response Law and Failure Mechanism of Slope with Weak Interlayer under Combined Action of Reservoir Water and Seismic Force. Water 2023, 15, 1956. [Google Scholar] [CrossRef]
- Yu, L.; Zheng, X.; Liu, Z.; Zhou, C.; Zhang, L. Multiscale Modelling of the Seepage-Induced Failure of a Soft Rock Slope. Acta Geotech. 2022, 17, 4717–4738. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, T. Failure Modes of Weak Interlayers with Different Dip Angles in Red Mudstone Strata, Northwest China. Bull. Eng. Geol. Environ. 2023, 82, 156. [Google Scholar] [CrossRef]
- Wei, E.; Hu, B.; Tian, K.; Cen, P.; Zhang, Z.; Wang, Z.; Chang, S. Study on the Nonlinear Damage Creep Model of the Weak Interlayer. Adv. Civ. Eng. 2022, 2022, 3566521. [Google Scholar] [CrossRef]
- Wang, Y.; Zhong, F.; Chu, H.; Wang, L. Study on Mechanism of Slope Instability with Weak Interlayer. Appl. Mech. Mater. 2011, 71–78, 3615–3618. [Google Scholar] [CrossRef]
- Cao, P.; Youdao, W.; Yixian, W.; Haiping, Y.; Bingxiang, Y. Study on Nonlinear Damage Creep Constitutive Model for High-Stress Soft Rock. Environ. Earth Sci. 2016, 75, 900. [Google Scholar] [CrossRef]
- Chen, F.; Su, R.; Yang, L.; Yang, X.; Jiao, H.; Zhu, C. Study on Surrounding Rock Deformation Laws of an Argillaceous Soft Rock Roadway Based on the Creep Damage Model. Front. Earth Sci. 2022, 10, 914170. [Google Scholar] [CrossRef]
- Luo, Z.; Zhang, Y.; Du, S.; Huang, M.; Lyu, Y. Experimental Study on Shear Performance of Saw-Tooth Rock Joint with Weak Interlayer under Different Moisture Contents and Filling Degrees. Front. Earth Sci. 2023, 10, 982937. [Google Scholar] [CrossRef]
- Zhao, N.; Zhang, Y.; Miao, H.; Meng, L. Study on the Creep and Fracture Evolution Mechanism of Rock Mass with Weak Interlayers. Adv. Mater. Sci. Eng. 2022, 2022, 5004306. [Google Scholar] [CrossRef]
- Hu, Q.; Cai, Q.; He, L.; Yang, X.; Ye, T.; Shi, R. Determination of the Peak and Residual Shear Strengths of the Sandwich Material in Slopes. Adv. Mater. Sci. Eng. 2017, 2017, 9641258. [Google Scholar] [CrossRef]
- Zhang, S.; Yun, X.; Song, Y.; Liu, W.; Yang, L. Fluid-Structure Coupling Creep Characteristics of Red-Bed Soft Rock in South China. Water 2022, 14, 4088. [Google Scholar] [CrossRef]
- Tomanovic, Z. Rheological Model of Soft Rock Creep Based on the Tests on Marl. Mech. Time Depend. Mater. 2006, 10, 135–154. [Google Scholar] [CrossRef]
- Luo, X.; Cao, P.; Liu, T.; Zhao, Q.; Meng, G.; Fan, Z.; Xie, W. Mechanical Behaviour of Anchored Rock Containing Weak Interlayer under Uniaxial Compression: Laboratory Test and Coupled DEM–FEM Simulation. Minerals 2022, 12, 492. [Google Scholar] [CrossRef]
- Li, L.-q.; Ju, N.-p. Effect of the Inclined Weak Interlayers on the Rainfall Response of a Bedded Rock Slope. J. Mt. Sci. 2016, 13, 1663–1674. [Google Scholar] [CrossRef]
- Huang, F.; Zhu, H.; Xu, Q.; Cai, Y.; Zhuang, X. The Effect of Weak Interlayer on the Failure Pattern of Rock Mass around Tunnel—Scaled Model Tests and Numerical Analysis. Tunn. Undergr. Space Technol. 2013, 35, 207–218. [Google Scholar] [CrossRef]
- He, Z.; Wang, B. Instability Process Model Test for Bedding Rock Slope with Weak Interlayer under Different Rainfall Conditions. Adv. Civ. Eng. 2018, 2018, 8201031. [Google Scholar] [CrossRef]
- Rong, P.; Zuo, Y.; Lin, J.; Chen, Q.; Zheng, L.; Jin, K. Study of Mechanical Properties and Failure Characteristics of Combined Rock Mass with Weak Interlayer. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 89. [Google Scholar] [CrossRef]
- Jeon, S.; Kim, J.; Seo, Y.; Hong, C. Effect of a Fault and Weak Plane on the Stability of a Tunnel in Rock—A Scaled Model Test and Numerical Analysis. Int. J. Rock Mech. Min. Sci. 2004, 41, 658–663. [Google Scholar] [CrossRef]
- Liu, X.; Han, Y.; Li, D.; Tu, Y.; Deng, Z.; Yu, C.; Wu, X. Anti-Pull Mechanisms and Weak Interlayer Parameter Sensitivity Analysis of Tunnel-Type Anchorages in Soft Rock with Underlying Weak Interlayers. Eng. Geol. 2019, 253, 123–136. [Google Scholar] [CrossRef]
- Li, J.; Zhang, B.; Sui, B. Stability Analysis of Rock Slope with Multilayer Weak Interlayer. Adv. Civ. Eng. 2021, 2021, 1409240. [Google Scholar] [CrossRef]
- Lin, S.S.; Lo, C.M.; Lin, Y.C. Investigating the Deformation and Failure Characteristics of Argillite Consequent Slope Using Discrete Element Method and Burgers Model. Environ. Earth Sci. 2017, 76, 81. [Google Scholar] [CrossRef]
- Liu, X.; Du, X.; Zhou, J.; Sun, J. Finite Element Analysis of Deformation Characteristic for Weak Interlayer Foundation. Adv. Mater. Res. 2012, 594–597, 552–556. [Google Scholar] [CrossRef]
- Huang, M.; Wang, H.; Sheng, D.; Liu, Y. Rotational-Translational Mechanism for the Upper Bound Stability Analysis of Slopes with Weak Interlayer. Comput. Geotech. 2013, 53, 133–141. [Google Scholar] [CrossRef]
- Huang, M.; Fan, X.; Wang, H. Three-Dimensional Upper Bound Stability Analysis of Slopes with Weak Interlayer Based on Rotational-Translational Mechanisms. Eng. Geol. 2017, 223, 82–91. [Google Scholar] [CrossRef]
- Miao, K.; Bai, Z.; Huang, Y.; Huang, Y.; Su, Y. Research on Seepage Control of Jurong Pumped Storage Hydroelectric Power Station. Water 2022, 14, 141. [Google Scholar] [CrossRef]
- Chen, L.; Dong, X.; Miao, K.; Yang, W.; Huang, Y. Characteristics and Connectivity Analysis of Hidden Karst in Jurong Pumped Storage Power Station Area, China. Water 2023, 15, 2562. [Google Scholar] [CrossRef]
- SL 31-2003; Water Conservancy and Hydropower Engineering Borehole Pressure Test Specification. Ministry of Water Resources of the People’s Republic of China: Beijing, China, 2003.
- YS/T 5225-2016; Geotechnical Test Protocol. Ministry of Industry and Information Technology of the People’s Republic of China: Beijing, China, 2016.
- Phoon, K.-K.; Tan, T.S.; Chong, P.C. Numerical simulation of Richards equation in partially saturated porous media under relaxation and mass balance. Geotech. Geol. Eng. 2007, 25, 525–541. [Google Scholar] [CrossRef]









| Number | Distribution Location | Occurrence | Width (mm) | Geological Description | Exposure Length (m) |
|---|---|---|---|---|---|
| UR1 | Northwest side of the upper reservoir | N75° E SW∠45° | 15–40 | It is yellow-brown and contains mud and rock debris. It is weakly weathered with siliceous material. There is a small leakage at the contact surface of dolomite. | |
| UP1 | Right side of underground powerhouse | N75° W SW∠45° | 15–20 | It is grey-yellow, mixes with mud, and is weakly to slightly weathered during excavation. It exhibits complete to strong weathering after exposure to the air. | |
| UP2 | N75° W SW∠45° | 15–20 | It is white and greyish-yellow and exhibits weak weathering. | ||
| UP3 | N75° E SE∠60° | 15–20 | It is grey-white and yellowish-brown, contains mud, and exhibits slight weathering. |
| Number of Tests | Hydraulic Conductivity (cm/s) | |||
|---|---|---|---|---|
| UR1 | UP1 | UP2 | UP3 | |
| 1 | 2.657 × 10−5 | 1.078 × 10−4 | 0.987 × 10−4 | 5.769 × 10−4 |
| 2 | 3.128 × 10−5 | 1.188 × 10−4 | 1.130 × 10−4 | 4.903 × 10−4 |
| 3 | 2.662 × 10−5 | 1.182 × 10−4 | 1.203 × 10−4 | 3.255 × 10−4 |
| 4 | 2.084 × 10−5 | 1.226 × 10−4 | 1.428 × 10−4 | 3.831 × 10−4 |
| 5 | 3.983 × 10−5 | 1.287 × 10−4 | 1.457 × 10−4 | 4.066 × 10−4 |
| Number of Boreholes | Measured Groundwater Level (m) | Calculated Groundwater Level (m) | Absolute Error (m) | Relative Error (%) |
|---|---|---|---|---|
| Z2 | 80.30 | 79.6 | 0.70 | 0.19 |
| Z4 | 158.90 | 159.65 | 0.75 | 0.47 |
| Z5 | 151.33 | 151.16 | 0.17 | 0.11 |
| Z9 | 130.20 | 130.28 | 0.08 | 0.06 |
| Z10 | 120.70 | 121.53 | 0.83 | 0.53 |
| Z13 | 131.52 | 131.8 | 0.28 | 0.21 |
| Z15 | 127.92 | 128.74 | 0.82 | 0.64 |
| Z16 | 151.96 | 150.47 | 1.49 | 0.98 |
| Z17 | 150.12 | 149.13 | 0.99 | 0.66 |
| Z21 | 177.17 | 177.58 | 0.41 | 0.23 |
| Number of Schemes | The Upper/Lower Reservoir Water Level (m) | Anti-Seepage and Drainage Measures | Calculated Hydraulic Head (m) | Critical Head for Seepage Failure for UP1 (m) | Critical Head for Seepage Failure for UP2 (m) | Seepage Failure |
|---|---|---|---|---|---|---|
| 1 | 267/81 | Fully enclosed anti-seepage and drainage | 80 | 160 | 150 | No |
| 2 | 267/81 | Anti-seepage and drainage around the underground powerhouse | 82 | 160 | 150 | No |
| 3 | 267/81 | No anti-seepage measures | 160 | 160 | 150 | Yes |
| 4 | 267/81 | Anti-seepage and drainage around the underground powerhouse | 98 | 160 | 150 | No |
| 5 | 246/81 | Fully enclosed anti-seepage and drainage | 59 | 160 | 150 | No |
| 6 | 246/81 | Anti-seepage and drainage around the underground powerhouse | 61 | 160 | 150 | No |
| 7 | 246/81 | No anti-seepage measures | 140 | 160 | 150 | No |
| 8 | 246/81 | Anti-seepage and drainage around the underground powerhouse | 77 | 160 | 150 | No |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Yang, W.; Zhang, J.; Huang, Y.; Zou, L. Permeability Tests and Numerical Simulation of Argillaceous Dolomite in the Jurong Pumped-Storage Power Station, China. Water 2023, 15, 3320. https://doi.org/10.3390/w15183320
Zhu X, Yang W, Zhang J, Huang Y, Zou L. Permeability Tests and Numerical Simulation of Argillaceous Dolomite in the Jurong Pumped-Storage Power Station, China. Water. 2023; 15(18):3320. https://doi.org/10.3390/w15183320
Chicago/Turabian StyleZhu, Xufen, Wenjie Yang, Jie Zhang, Yong Huang, and Lifang Zou. 2023. "Permeability Tests and Numerical Simulation of Argillaceous Dolomite in the Jurong Pumped-Storage Power Station, China" Water 15, no. 18: 3320. https://doi.org/10.3390/w15183320




