A General Method to Improve Runoff Prediction in Ungauged Basins Based on Remotely Sensed Actual Evapotranspiration Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site and Materials
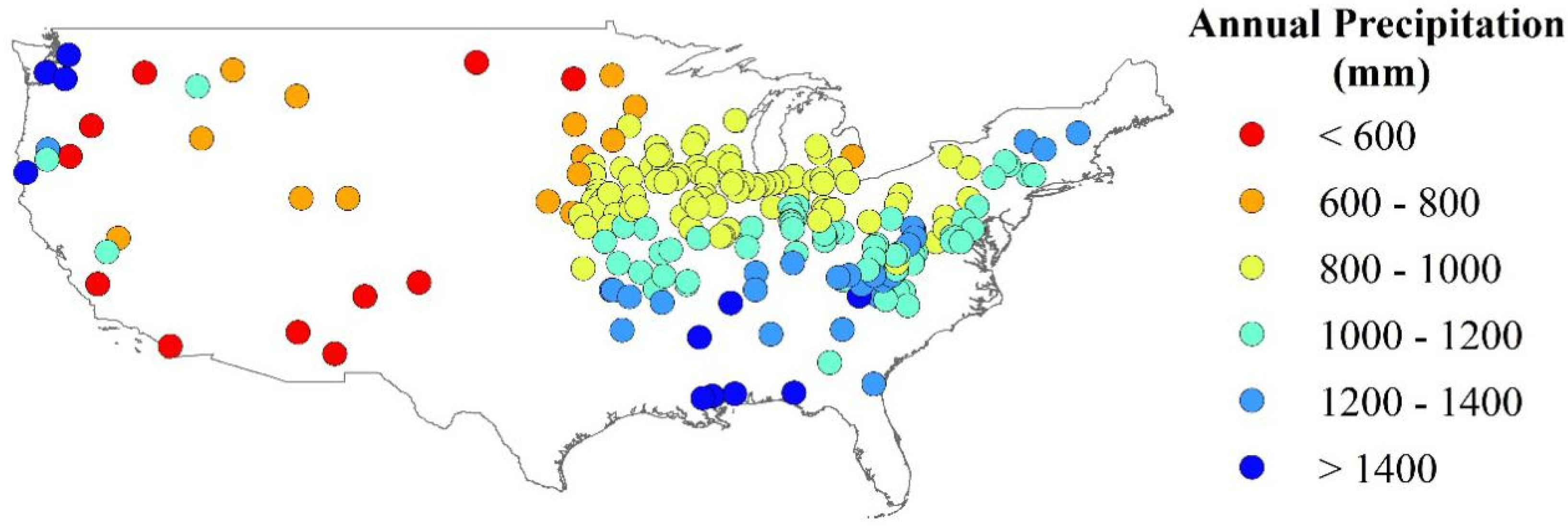
2.1.1. Study Site and Data Sources
2.1.2. Data Implementation
2.2. Methodology
2.2.1. RR Models
- (1)
- Xinanjiang model
- (2)
- SIMHYD
- (3)
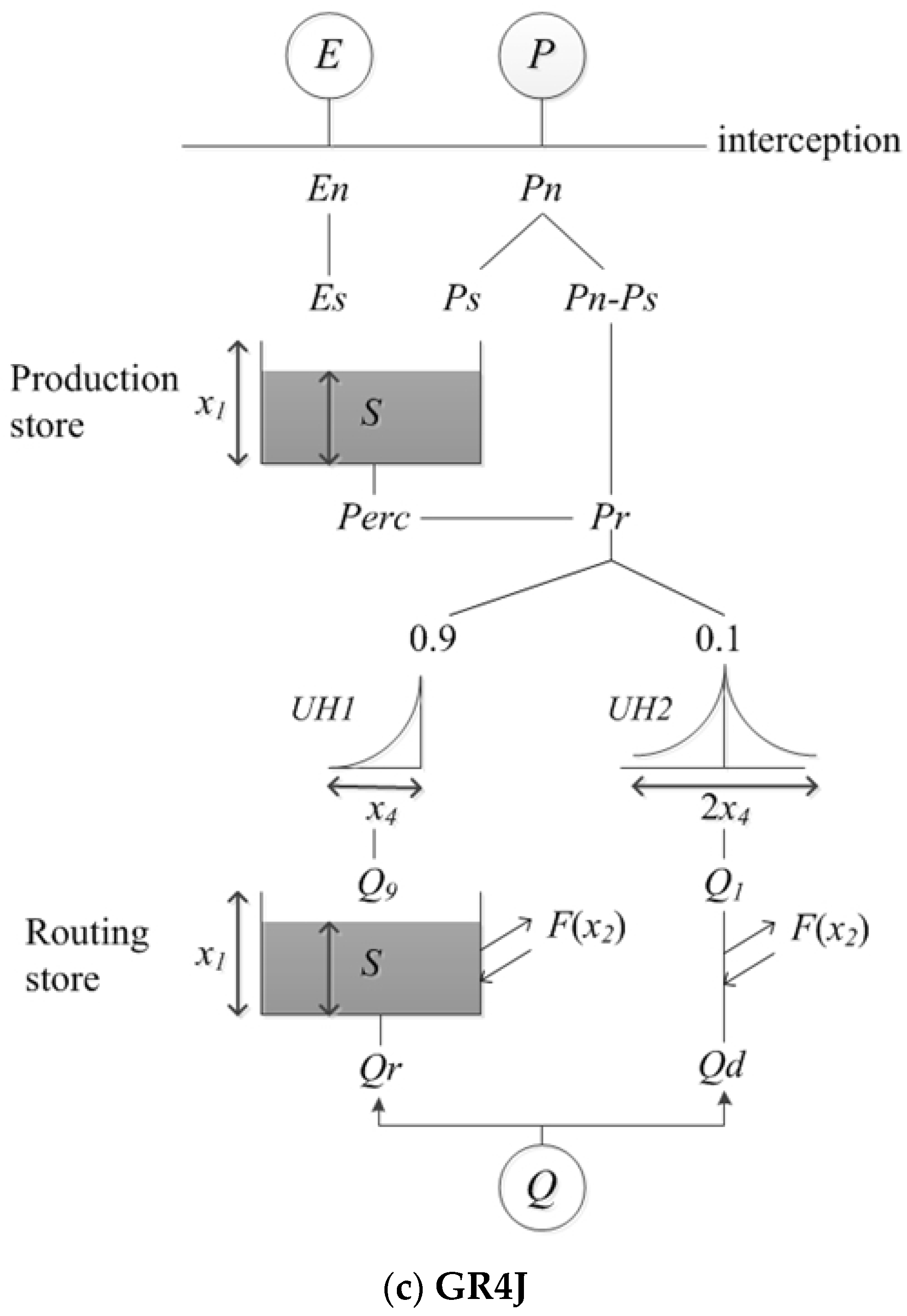
- GR4J
2.2.2. Model Calibration, Regionalization, and Evaluation
- (1)
- Model calibration
- (2)
- Parameter regionalization
- (3)
- Model evaluation
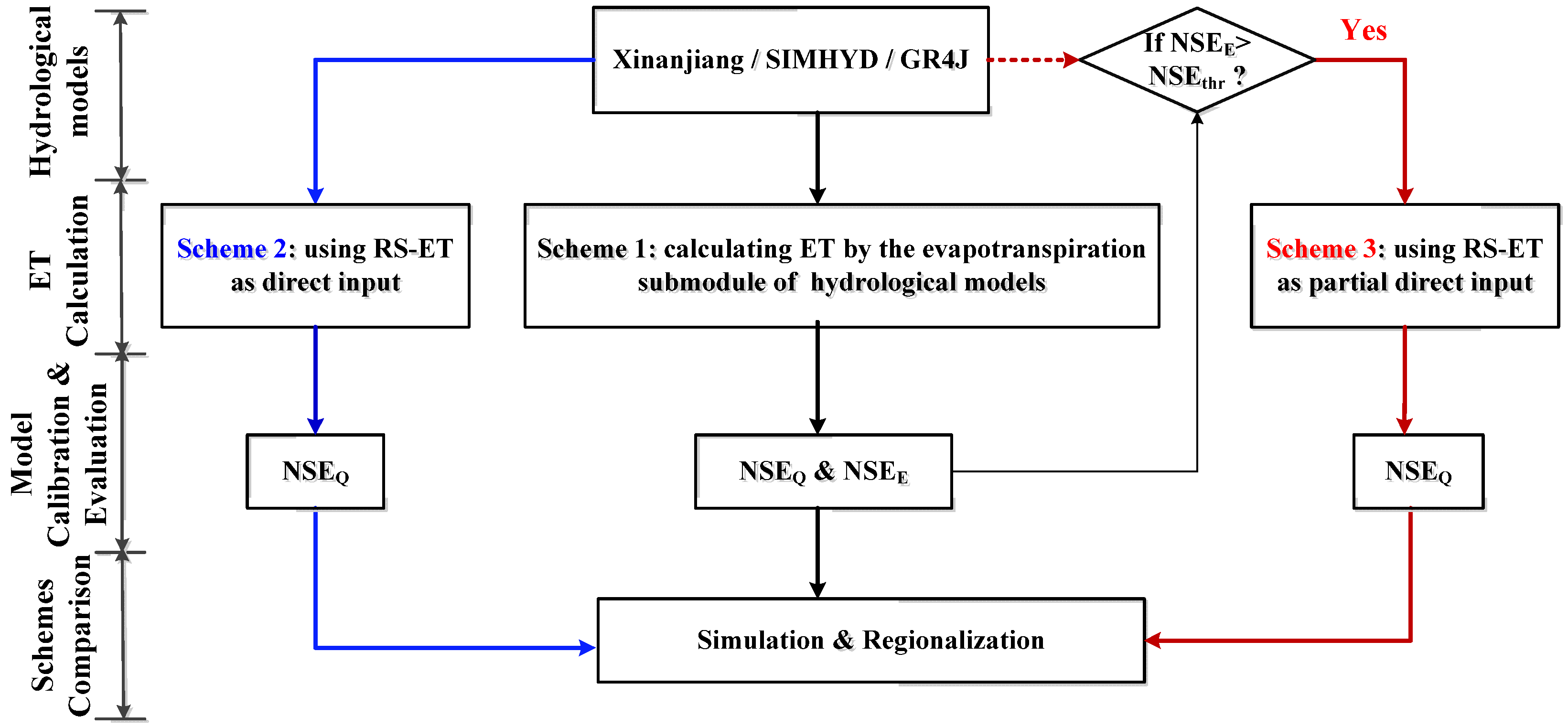
2.2.3. Modeling Scheme
- (1)
- Scheme 1
- (2)
- Scheme 2
- (3)
- Scheme 3
3. Results and Discussion
3.1. Conventional Streamflow Prediction
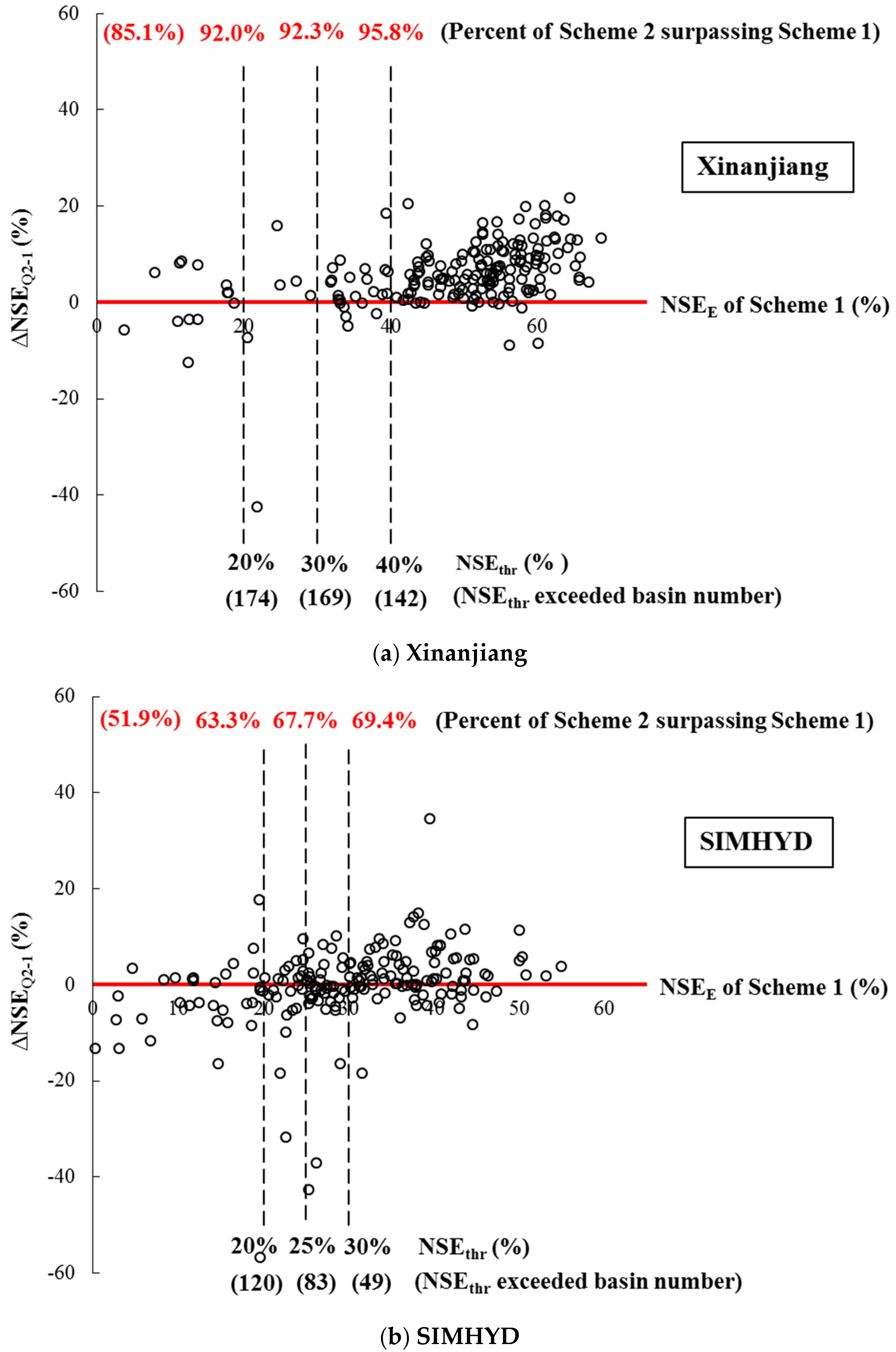
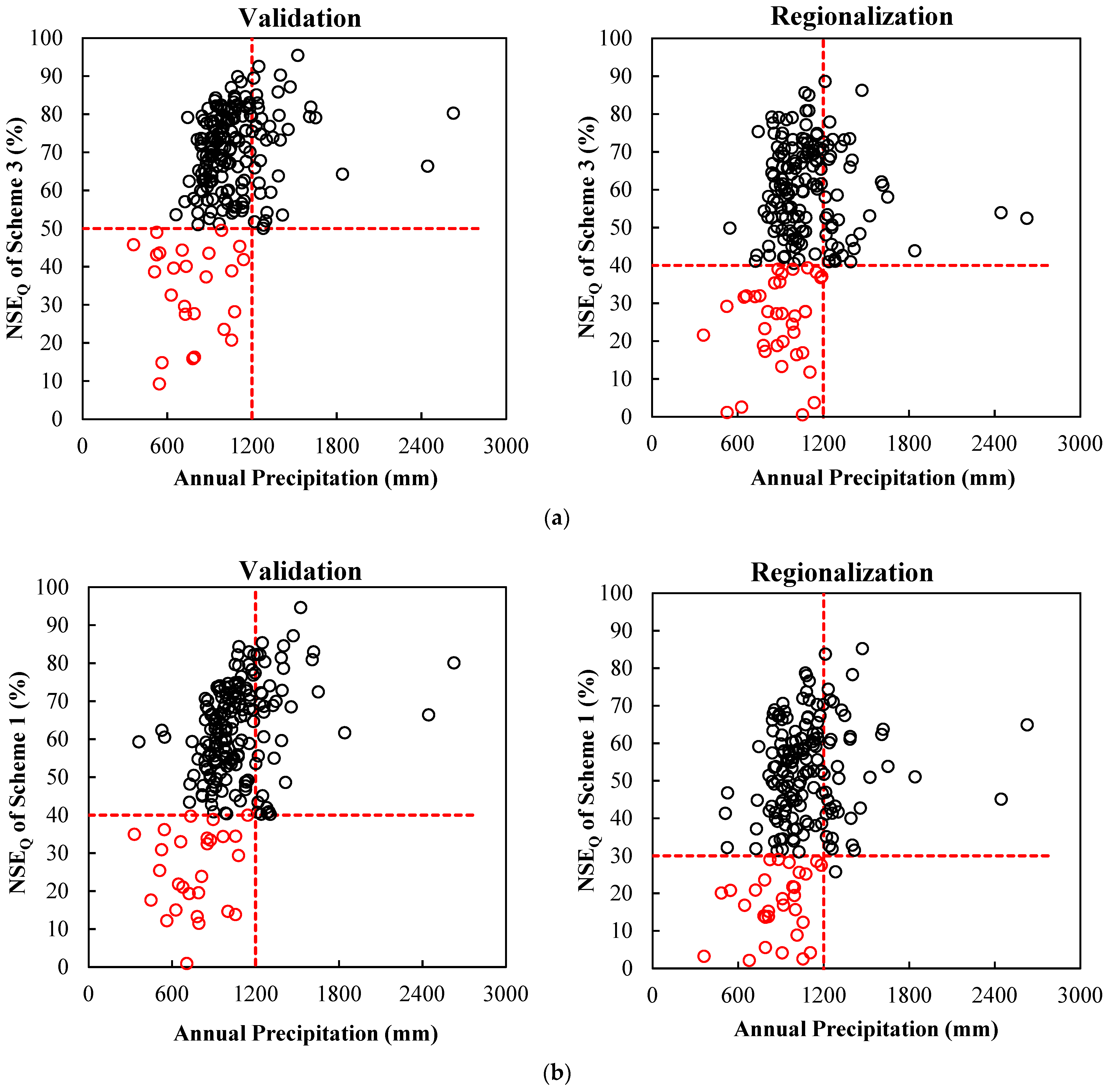
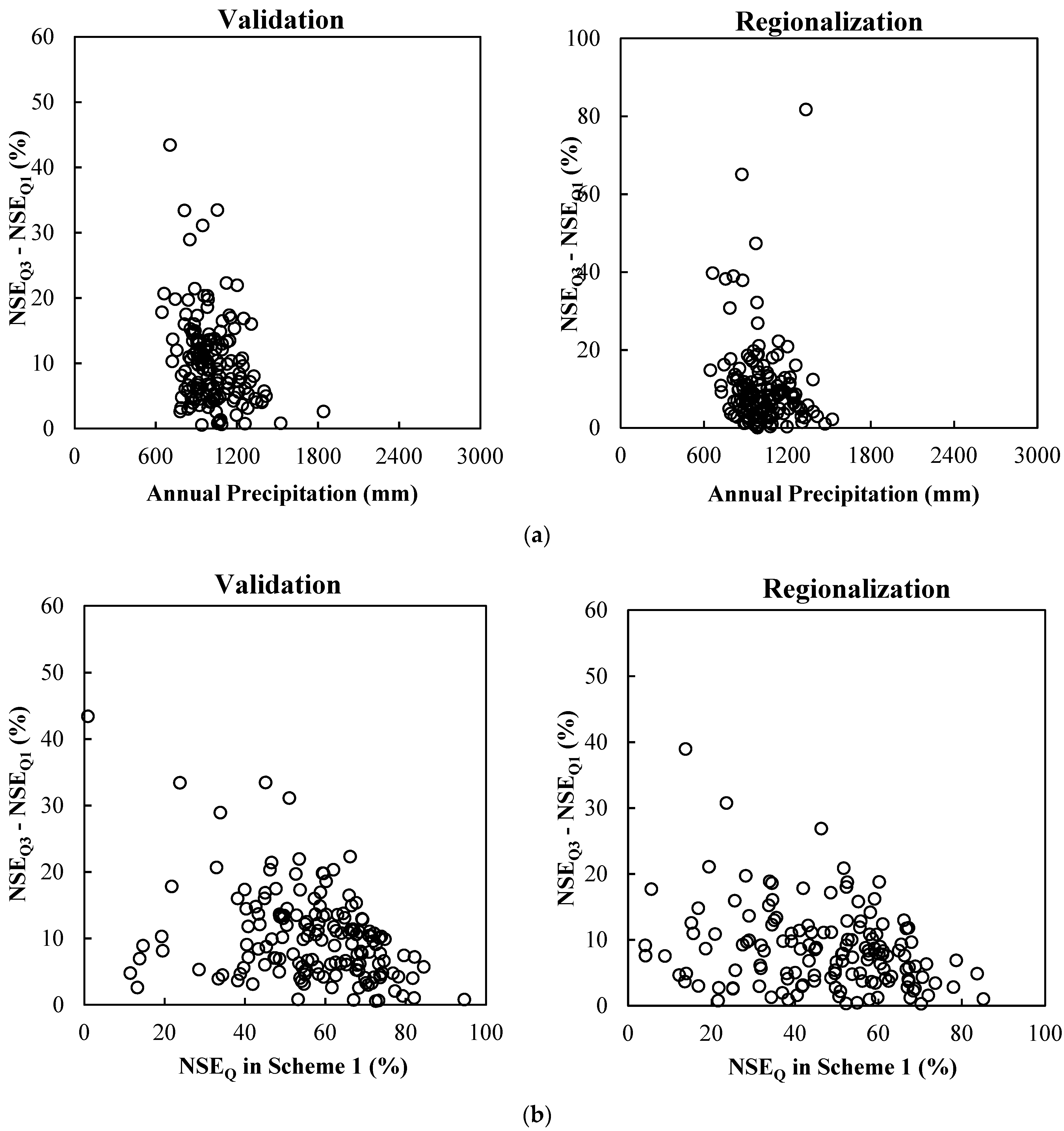
3.2. Selection of RS-ET Utilization Threshold
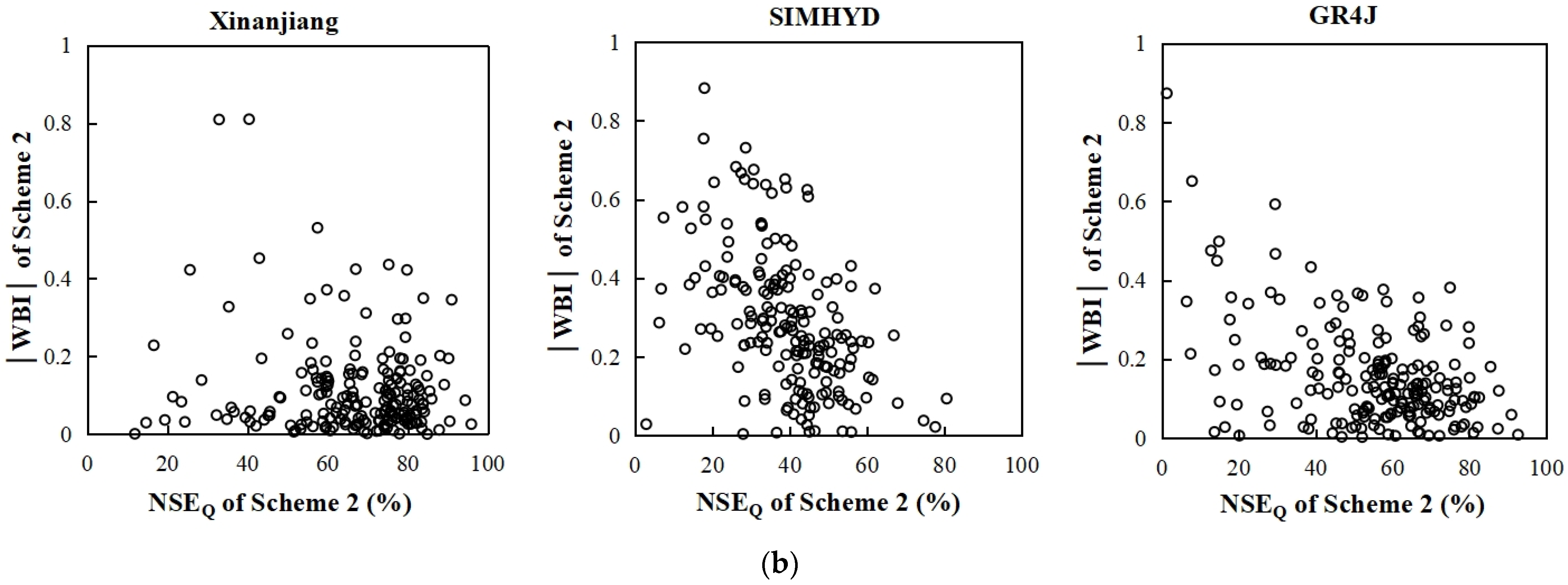
3.3. Streamflow Prediction Using RS-ET
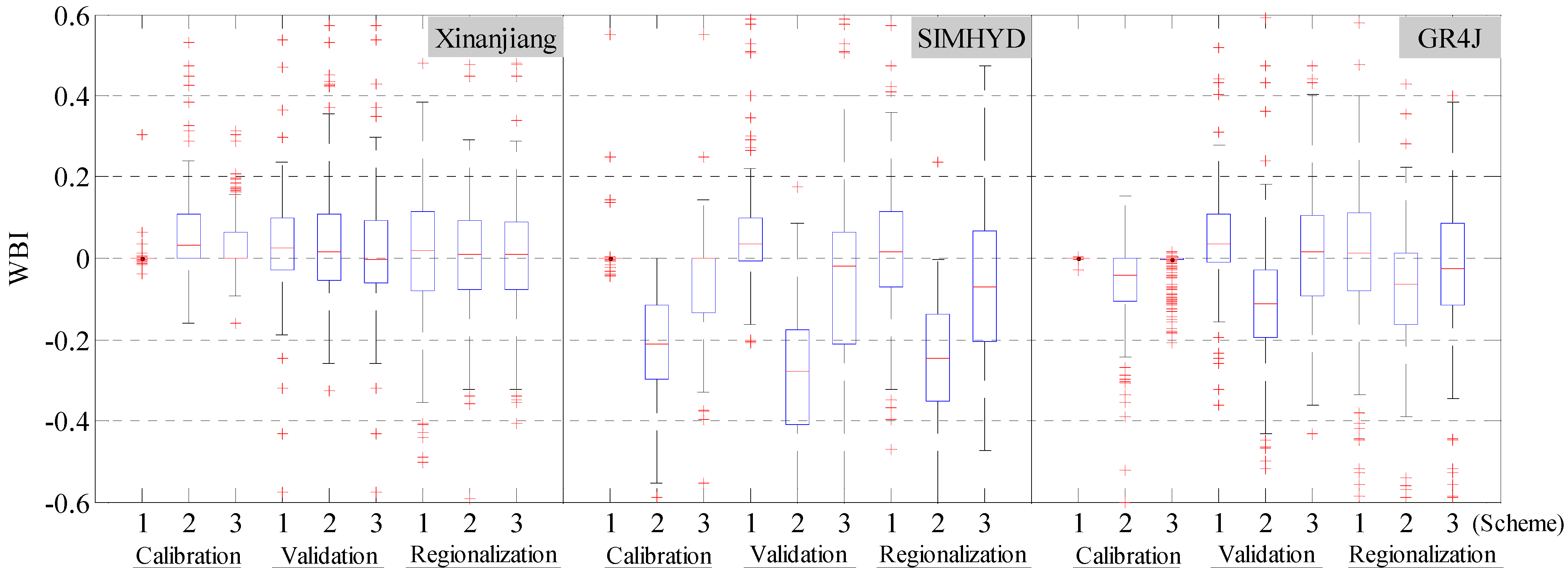
3.4. Water Balance Condition
3.5. Regional Spatial Patterns
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sivapalan, M.; Takeuchi, K.; Franks, S.W.; Zehe, E. IAHS Decade on Predictions in Ungauged Basins (PUB), 2003–2012: Shaping an exciting future for the hydrological sciences. Hydrol. Sci. J. 2003, 48, 857–880. [Google Scholar] [CrossRef]
- Zhang, Y.; Chiew, F.H.S. Relative merits of different methods for runoff predictions in ungauged catchments. Water Resour. Res. 2009, 45, W07412. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, Y.; Zhang, L.; Wang, Z. Regionalization of hydrological modeling for predicting streamflow in ungauged catchments: A comprehensive review. Wiley Interdiscip. Rev. Water 2020, 8, e1487. [Google Scholar] [CrossRef]
- Yang, X.; Li, F.; Qi, W.; Zhang, M.; Xu, C.Y. Regionalization methods for PUB: A comprehensive review of progress after the PUB decade. Hydrol. Res. 2023, 54, 885–900. [Google Scholar] [CrossRef]
- Lakshmi, V. The role of satellite remote sensing in the Prediction of Ungauged Basins. Hydrol. Process. 2004, 18, 1029–1034. [Google Scholar] [CrossRef]
- Yoon, H.N.; Marshall, L.; Sharma, A.; Kim, S. Bayesian Model Calibration Using Surrogate Streamflow in Ungauged Catchments. Water Resour. Res. 2022, 58, e2021WR031287. [Google Scholar] [CrossRef]
- Hrachowitz, M.; Savenije, H.H.G.; Blschl, G.; Mcdonnell, J.J.; Cudennec, C. A decade of Predictions in Ungauged Basins (PUB)—A review. Hydrol. Sci. J. 2013, 58, 1198–1255. [Google Scholar] [CrossRef]
- Dembélé, M.; Ceperley, N.; Zwart, S.J.; Salvadore, E.; Mariethoz, G.; Schaefli, B. Potential of satellite and reanalysis evaporation datasets for hydrological modelling under various model calibration strategies. Adv. Water. Res. 2020, 143, 103667. [Google Scholar] [CrossRef]
- Guo, D.; Westra, S.; Maier, H.R. Impact of evapotranspiration process representation on runoff projections from conceptual rainfall-runoff models. Water Resour. Res. 2017, 53, 435–454. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, Z.; Shao, Q.; He, H.; Guo, X. A two-step calibration framework for hydrological parameter regionalization based on streamflow and remote sensing evapotranspiration. J. Hydrol. 2022, 613, 128320. [Google Scholar] [CrossRef]
- Zhang, Y.; Chiew, F.H.S.; Zhang, L.; Li, H. Use of Remotely Sensed Actual Evapotranspiration to Improve Rainfall–Runoff Modeling in Southeast Australia. J. Hydrometeorol. 2009, 10, 969–980. [Google Scholar] [CrossRef]
- Vervoort, R.W.; Miechels, S.F.; Ogtrop, F.F.V.; Guillaume, J.H.A. Remotely sensed evapotranspiration to calibrate a lumped conceptual model: Pitfalls and opportunities. J. Hydrol. 2014, 519, 3223–3236. [Google Scholar] [CrossRef]
- Kunnath-Poovakka, A.; Ryu, D.; Renzullo, L.J.; George, B. The efficacy of calibrating hydrologic model using remotely sensed evapotranspiration and soil moisture for streamflow prediction. J. Hydrol. 2016, 535, 509–524. [Google Scholar] [CrossRef]
- Gui, Z.; Liu, P.; Cheng, L.; Guo, S.; Wang, H.; Zhang, L. Improving runoffff prediction using remotely sensed actual evapotranspiration during rainless periods. J. Hydrol. Eng. 2019, 24, 04019050.1–04019050.12. [Google Scholar] [CrossRef]
- Herman, M.R.; Nejadhashemi, A.P.; Abouali, M.; Hernandez-Suarez, J.S.; Daneshvar, F.; Zhang, Z.; Anderson, M.C.; Sadeghi, A.M.; Hain, C.R.; Sharifi, A. Evaluating the role of evapotranspiration remote sensing data in improving hydrological modeling predictability. J. Hydrol. 2018, 556, 39–49. [Google Scholar] [CrossRef]
- Yang, Y.; Guan, K.; Peng, B.; Pan, M.; Franz, T.E. High-resolution spatially explicit land surface model calibration using field-scale satellite-based daily evapotranspiration product. J. Hydrol. 2020, 596, 125730. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, Y.; Ma, Q.; Wang, P.; Ge, Y.; Yu, W. A parallel computing-based and spatially stepwise strategy for constraining a semi-distributed hydrological model with streamflow observations and satellite-based evapotranspiration. J. Hydrol. 2021, 599, 126359. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y.; Chiew, F.H.S.; Xu, S. Predicting runoff in ungauged catchments by using Xinanjiang model with MODIS leaf area index. J. Hydrol. 2009, 370, 155–162. [Google Scholar] [CrossRef]
- Taconet, O.; Bernard, R.; Vidal-Madjar, D. Evapotranspiration over an Agricultural Region Using a Surface Flux/Temperature Model Based on NOAA-AVHRR Data. J. Clim. Appl. Meteorol. 1986, 25, 284–307. [Google Scholar] [CrossRef]
- Nemani, R.R.; Running, S.W. Estimation of regional surface resistance to evapotranspiration from NDVI and Thermal-IR AVHRR data. J. Appl. Meteorol. 1989, 28, 276–284. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Nemani, R.R.; Running, S.W. A continuous satellite-derived global record of land surface evapotranspiration from 1983 to 2006. Water Resour. Res. 2010, 46, 109–118. [Google Scholar] [CrossRef]
- Cleugh, H.A.; Leuning, R.; Mu, Q.; Running, S.W. Regional evaporation estimates from flux tower and MODIS satellite data. Remote Sens. Environ. 2007, 106, 285–304. [Google Scholar] [CrossRef]
- Leuning, R.; Zhang, Y.Q.; Rajaud, A.; Cleugh, H.; Tu, K. A simple surface conductance model to estimate regional evaporation using MODIS leaf area index and the Penman-Monteith equation. Water Resour. Res. 2008, 44, 652–655. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Chiew, F.H.S.; Zhang, L.; Leuning, R.; Cleugh, H.A. Estimating catchment evaporation and runoff using MODIS leaf area index and the Penman-Monteith equation. Water Resour. Res. 2008, 44, 2183–2188. [Google Scholar] [CrossRef]
- Guerschman, J.P.; Van Dijk, A.I.J.M.; Mattersdorf, G.; Beringer, J.; Hutley, L.B.; Leuning, R.; Pipunic, R.C.; Sherman, B.S. Scaling of potential evapotranspiration with MODIS data reproduces flux observations and catchment water balance observations across Australia. J. Hydrol. 2009, 369, 107–119. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Y.; Vaze, J.; Lane, P.; Xu, S. Improving runoff estimates using remote sensing vegetation data for bushfire impacted catchments. Agr. Forest. Meteorol. 2013, 182–183, 332–341. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Vaze, J.; Chiew, F.H.S.; Liu, Y. Incorporating vegetation time series to improve rainfall-runoff model predictions in gauged and ungauged catchments. In Proceedings of the 19th International Congress on Modelling and Simulation, Perth, Australia, 12–16 December 2011. [Google Scholar]
- Szilagyi, J. Application of MODIS-Based Monthly Evapotranspiration Rates in Runoff Modeling: A Case Study in Nebraska, USA. Open J. Mod. Hydrol. 2013, 3, 172–178. [Google Scholar] [CrossRef]
- Roy, T.; Gupta, H.V.; Serrat-Capdevila, A.; Valdes, J.B. Using satellite-based evapotranspiration estimates to improve the structure of a simple conceptual rainfall and -runoff model. Hydrol. Earth Syst. Sci. 2017, 21, 879–896. [Google Scholar] [CrossRef]
- Duan, Q.; Schaake, J.; Andréassian, V.; Franks, S.; Goteti, G.; Gupta, H.V.; Gusev, Y.M.; Habets, F.; Hall, A.; Hay, L. Model parameter estimation experiment (MOPEX): An overview of science strategy and major results from the second and third workshops. J. Hydrol. 2006, 320, 3–17. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; de Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2010, 7, 453–469. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. Comment on “Characteristics and trends in various forms of the Palmer Drought Severity Index (PDSI) during 1900–2008” by Aiguo Dai. J. Geophys. Res. 2011, 116, D19112. [Google Scholar] [CrossRef]
- Mátyás, C.; Sun, G. Forests in a water limited world under climate change. Environ. Res. Lett. 2014, 9, 085001. [Google Scholar] [CrossRef]
- Wang, D.; Alimohammadi, N. Responses of annual runoff, evaporation, and storage change to climate variability at the watershed scale. Water Resour. Res. 2012, 48, W05546. [Google Scholar] [CrossRef]
- Chen, X.; Alimohammadi, N.; Wang, D. Modeling interannual variability of seasonal evaporation and storage change based on the extended Budyko framework. Water Resour. Res. 2013, 49, 6067–6078. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. Regionalisation of catchment model parameters. J. Hydrol. 2004, 287, 95–123. [Google Scholar] [CrossRef]
- Oudin, L.; Andréassian, V.; Perrin, C.; Michel, C.; Le Moine, N. Spatial proximity, physical similarity, regression and ungaged catchments: A comparison of regionalization approaches based on 913 French catchments. Water Resour. Res. 2008, 44, W03413. [Google Scholar] [CrossRef]
- Zhao, R.J.; Liu, X.R.; Singh, V.P. The Xinanjiang model. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Littleton, CO, USA, 1995; pp. 371–381. [Google Scholar]
- Chiew, F.H.S.; Peel, M.C.; Western, A.W.; Singh, V.; Frevert, D. Application and testing of the simple rainfall-runoff model SIMHYD. In Mathematical Models of Small Watershed Hydrology and Applications; Water Resources Publication: Littleton, CO, USA, 2002; pp. 335–367. [Google Scholar]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Zhao, R.J. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar] [CrossRef]
- Edijatno; Nascimento, N.D.O.; Yang, X.; Makhlouf, Z.; Michel, C. GR3J: A daily watershed model with three free parameters. Hydrol. Sci. J. 1999, 44, 263–277. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Rosenbrock, H.H. An Automatic Method for Finding the Greatest or Least Value of a Function. Comput. J. 1960, 3, 175–184. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Li, Z.; Liu, P.; Deng, C.; Guo, S.; He, P.; Wang, C. Evaluation of Estimation of Distribution Algorithm to Calibrate Computationally Intensive Hydrologic Model. J. Hydrol. Eng. 2016, 21, 04016012. [Google Scholar] [CrossRef]
- Kittel, C.M.M.; Arildsen, A.L.; Dybkjr, S.; Hansen, E.R.; Bauer-Gottwein, P. Informing hydrological models of poorly gauged river catchments—A parameter regionalization and calibration approach. J. Hydrol. 2020, 587, 124999. [Google Scholar] [CrossRef]
- Yang, X.; Magnusson, J.; Huang, S.; Beldring, S.; Xu, C.Y. Dependence of regionalization methods on the complexity of hydrological models in multiple climatic regions. J. Hydrol. 2019, 582, 124357. [Google Scholar] [CrossRef]
- Yang, X.; Magnusson, J.; Xu, C.Y. Transferability of regionalization methods under changing climate. J. Hydrol. 2018, 568, 67–81. [Google Scholar] [CrossRef]
- Arsenault, R.; Breton-Dufour, M.; Poulin, A.; Dallaire, G.; Romero-Lopez, R. Streamflow prediction in ungauged basins: Analysis of regionalization methods in a hydrologically heterogeneous region of Mexico. Hydrol. Sci. J. J. Des Sci. Hydrol. 2019, 64, 1297–1311. [Google Scholar] [CrossRef]
- Beck, H.E.; Pan, M.; Lin, P.; Seibert, J.; Dijk, A.I.J.M.V.; Wood, E.F. Global Fully Distributed Parameter Regionalization Based on Observed Streamflow From 4229 Headwater Catchments. J. Geophys. Res. Atmos. 2020, 125, e2019JD031485. [Google Scholar] [CrossRef]
- Young, A.R. Stream flow simulation within UK ungauged catchments using a daily rainfall-runoff model. J. Hydrol. 2006, 320, 155–172. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” Measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y.; Zhou, X. Predicting Surface Runoff from Catchment to Large Region. Adv. Meteorol. 2015, 2015, 720967. [Google Scholar] [CrossRef]
- Rientjes, T.H.M.; Muthuwatta, L.P.; Bos, M.G.; Booij, M.J.; Bhatti, H.A. Multi-variable calibration of a semi-distributed hydrological model using streamflow data and satellite-based evapotranspiration. J. Hydrol. 2013, 505, 276–290. [Google Scholar] [CrossRef]
- Budyko, M.I. Climate and Life; Academic Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Madadgar, S.; Moradkhani, H. Improved Bayesian multimodeling: Integration of copulas and Bayesian model averaging. Water Resour. Res. 2014, 50, 9586–9603. [Google Scholar] [CrossRef]
- Budyko, M.I. The Heat Balance of the Earth’s Surface. Eurasian Geogr. Econ. 1961, 2, 3–13. [Google Scholar] [CrossRef]
- Liu, W.; Wang, L.; Zhou, J.; Li, Y.; Sun, F.; Fu, G.; Li, X.; Sang, Y.F. A worldwide evaluation of basin-scale evapotranspiration estimates against the water balance method. J. Hydrol. 2016, 538, 82–95. [Google Scholar] [CrossRef]


| Study | RS-ET or Vegetation Data/RR Model Used | Location/Climate/Number of Catchments/Size Range of Catchment/Length of Time Series/Time Step | RR Modeling Using RS-ET As Direct Input/Regionalization Method | Key Results |
|---|---|---|---|---|
| 1. Zhang et al. [24] | ET estimated from MODIS LAI with the Penman–Monteith (PM) equation/SIMHYD | The Murray-Darling Basin in Australia/N/A/120/50–2000 km2/5 years/annual | Deriving discharge from water balance estimates (RRS = P − ERS)/the spatial proximity method | (1) The simulated RRS in gauged/ungauged basins had an accuracy similar to that of SIMHYD in the gauged catchments. (2) N/A (3) RS-ET was successfully used to estimate long-term runoff in semi-humid and humid regions. |
| 2. Li et al. [18] | ET estimated from MODIS LAI with the PM equation/Xinanjiang model | Southeast Australia/semi-arid and semi-humid/ 210/50–2000 km2/7 years/ daily | Modification of the Xinanjiang model to use MODIS LAI directly/the spatial proximity method and the physical similarity method | (1) Incorporation of MODIS LAI into Xinanjiang model improved both the model calibration and prediction of runoff in ungauged catchments. (2) N/A (3) N/A |
| 3. Zhang et al. [11] | ET estimated from MODIS LAI with the PM equation/SIMHYD | Southeast Australia/N/A/120/50–2000 km2/5 years/daily | Modification of SIMHYD to use MODIS-LAI directly/the spatial proximity method | (1) The runoff simulation results were reduced, while the regionalization results were improved significantly. (2) N/A (3) N/A |
| 4. Zhang and Chiew [2] | ET estimated from MODIS LAI with the PM equation/Xinanjiang and SIMHYD | Southeast Australia /relatively unimpacted/210/50–2000 km2/13 years/daily | The two models are revised to incorporate RS-LAI/the spatial proximity method, the physical similarity method, and the integrated similarity method | (1) The revised models generally perform better than the original RR models, but the improvements are marginal. (2) N/A (3) The revised models give significantly better results in the poorer modeled ungauged catchments. |
| 5. Zhang et al. [27] | LAI from AVHRR/SIMHYD | Australia/N/A/470/50–5000 km2/26 years/daily | Modification of SIMHYD to incorporate RS-LAI directly (SIMHYD-ET)/the spatial proximity method | (1) For both model calibration and regionalization, the runoff modeled by the SIMHYD-ET model are similar to (or only very marginally better than) those simulated by the original SIMHYD model. (2) N/A (3) The SIMHYD-ET outperformed SIMHYD especially for poorly simulated catchments with low NSE of daily runoff and high water balance errors. |
| 6. Szilagyi [28] | RS-ET estimated with CREMAP method/a lumped conceptual model of Jakeman and Hornberger (JH model) | The Little Nemaha River in Nebraska, USA/continental/1/2051 km2/6 years/daily | Modification of the JH model to incorporate CREAMP-ET directly/N/A | (1) The accuracy of runoff simulation remained practically unchanged. (2) N/A (3) N/A |
| 7. Zhou et al. [26] | ET estimated from MODIS LAI with the PM equation/Xinanjiang | Southeast Australian/bushfire impacted/4/360–900 km2/28 years/daily | Modification of Xinanjiang model to incorporate RS-LAI directly (Xinanjiang-ET model)/N/A | (1) Inclusion of RS-LAI resulted in a slight improvement of runoff simulation and noticeable decrease in water balance errors. (2) N/A (3) Use of RS-LAI can improve runoff simulation in three wetter catchments, not in a dry catchment. |
| 8. Willem Vervoort et al. [12] | MODIS-ET from Montana University/IHACRES | New South Wales, Australia/semi-arid/4/146–2184 km2/12 years/daily | To replace the ET sub-module directly with RS-ET data/the spatial proximity method | (1) Using RS-ET reduced runoff simulation performance. (2) N/A (3) N/A |
| 9. Roy et al. [29] | ET from GLEAM/HYMOD | The Nyangores River basin in Kenya and Tanzania/N/A/1/697 km2/7.5 years/daily | Modification of HYMOD to simulate ET as by GLEAM/N/A | (1) The modified model can provide improved simulations of streamflow. (2) N/A (3) N/A |
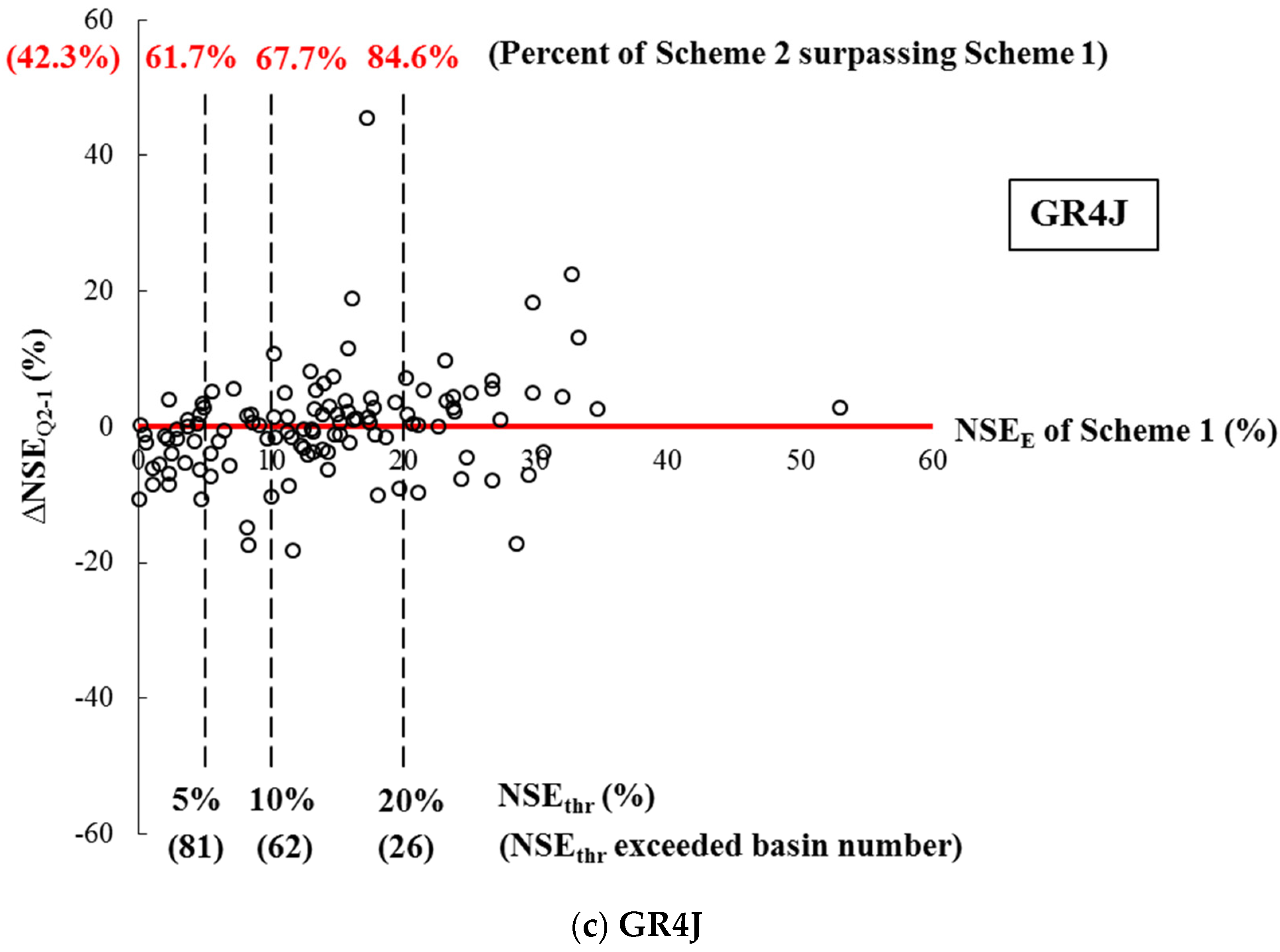
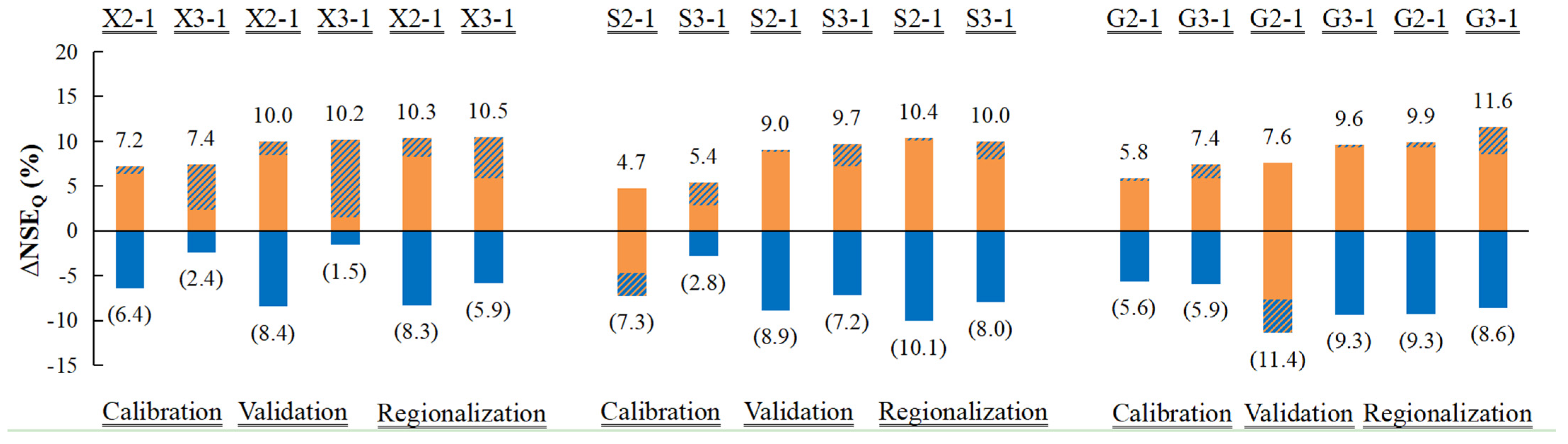
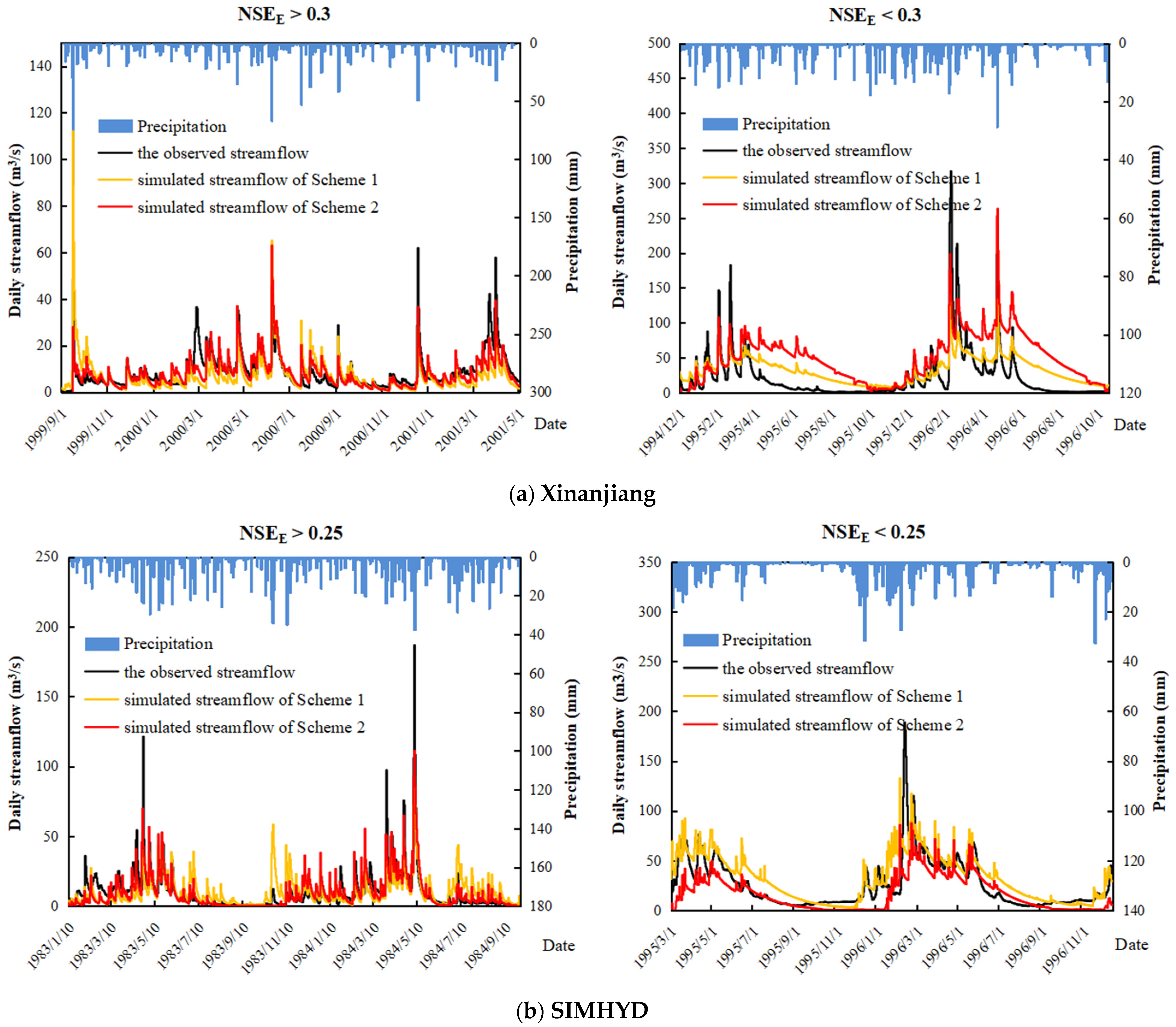
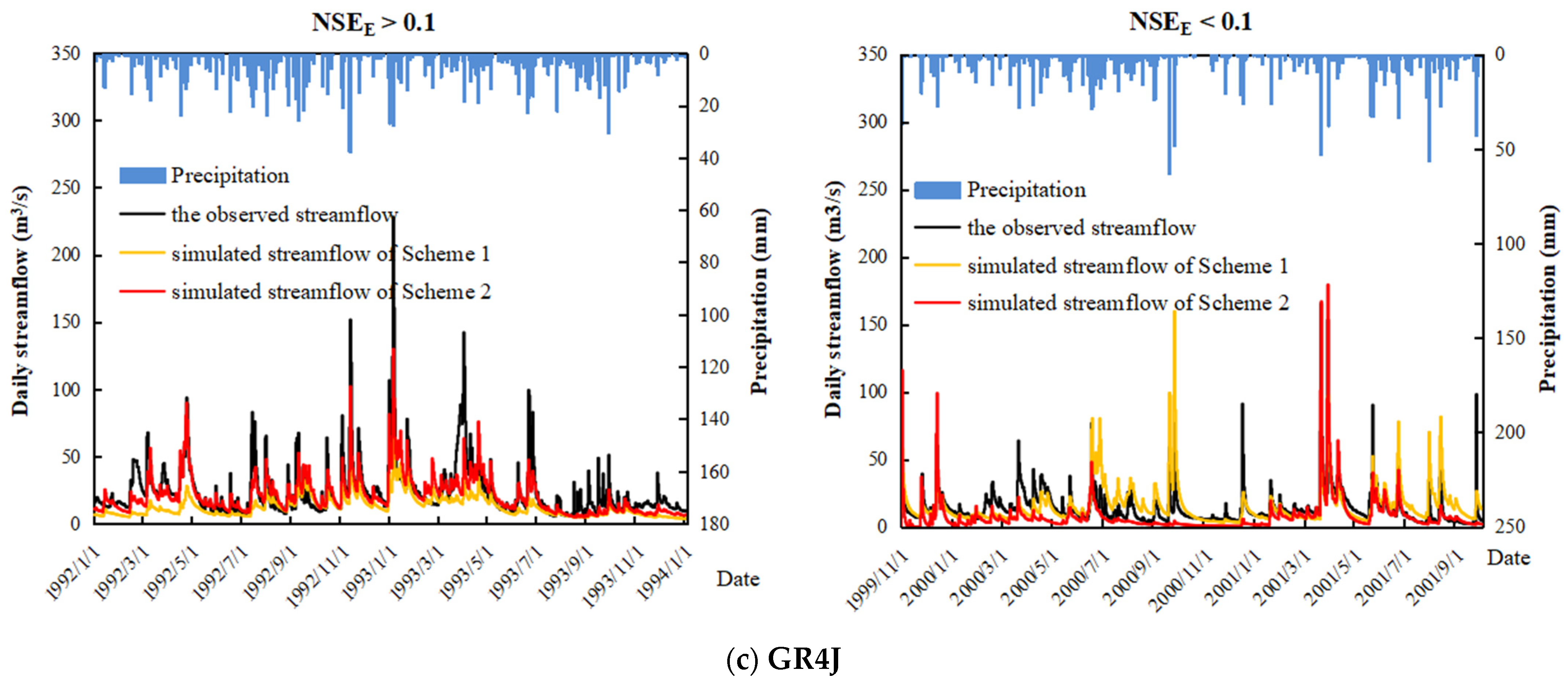
| 10. This study | ET estimated from AVHRR NDVI/Xinanjiang, GR4J and SIMHYD | The MOPEX basins in the continental United States/highly diverse/401/67–10,329 km2/21 years/daily | (i) Scheme 2: Using RS-ET as direct input; (ii) Scheme 3: Using RS-ET as partial direct input/the spatial proximity method | (1) Using RS-ET as direct input improved model performances for the Xinanjiang model, but worsened runoff prediction for SIMHYD and GR4J in most cases; using RS-ET as partial direct input improved runoff prediction in 91.1%, 59.0%, and 53.2% basins for Xinanjiang, SIMHYD, and GR4J, respectively. (2) If the simulated ET from a particular hydrological model matches the RS-ET data well, then the RS-ET data may be used as direct input in this model. (3) The efficacy of using RS-ET is superior for relatively arid and originally poorly simulated basins. |
| Model | Model Performance (%) | Calibration | Validation | Regionalization | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 25 | 50 | 75 | 25 | 50 | 75 | 25 | 50 | 75 | ||
| Xinanjiang | NSEQ | 52.22 | 64.67 | 74.05 | 46.85 | 59.39 | 70.15 | 29.01 | 45.84 | 59.27 |
| NSEE | 36.59 | 50.86 | 56.92 | 39.87 | 51.30 | 57.69 | 33.19 | 48.21 | 56.38 | |
| SIMHYD | NSEQ | 32.70 | 42.01 | 49.64 | 28.55 | 39.93 | 47.81 | 18.27 | 32.96 | 41.90 |
| NSEE | 20.18 | 28.30 | 37.43 | 16.12 | 23.40 | 30.92 | 15.51 | 26.25 | 33.27 | |
| GR4J | NSEQ | 57.22 | 65.79 | 72.68 | 50.73 | 63.44 | 73.22 | 25.91 | 46.53 | 62.06 |
| NSEE | −10.61 | 2.69 | 14.65 | −12.47 | 4.88 | 16.67 | −9.50 | 3.12 | 14.13 | |
| Model | Periods | Percent (Basin Numbers) | |
|---|---|---|---|
| Scheme 2 > Scheme 1 | Scheme 3 > Scheme 1 | ||
| Xinanjiang model | Calibration | 85.1% (177/208) | 92.3% (156/169) |
| Validation | 86.1% (179/208) | 93.5% (158/169) | |
| Regionalization | 85.1% (177/208) | 91.1% (154/169) | |
| SIMHYD | Calibration | 51.9% (108/208) | 67.5% (56/83) |
| Validation | 40.4% (84/208) | 56.6% (47/83) | |
| Regionalization | 50.5% (105/208) | 59.0% (49/83) | |
| GR4J | Calibration | 42.3% (88/208) | 67.7% (42/62) |
| Validation | 32.2% (67/208) | 45.2% (28/62) | |
| Regionalization | 38.0% (79/208) | 53.2% (33/62) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gui, Z.; Zhang, F.; Chang, D.; Xie, A.; Yue, K.; Wang, H. A General Method to Improve Runoff Prediction in Ungauged Basins Based on Remotely Sensed Actual Evapotranspiration Data. Water 2023, 15, 3307. https://doi.org/10.3390/w15183307
Gui Z, Zhang F, Chang D, Xie A, Yue K, Wang H. A General Method to Improve Runoff Prediction in Ungauged Basins Based on Remotely Sensed Actual Evapotranspiration Data. Water. 2023; 15(18):3307. https://doi.org/10.3390/w15183307
Chicago/Turabian StyleGui, Ziling, Feng Zhang, Da Chang, Aili Xie, Kedong Yue, and Hao Wang. 2023. "A General Method to Improve Runoff Prediction in Ungauged Basins Based on Remotely Sensed Actual Evapotranspiration Data" Water 15, no. 18: 3307. https://doi.org/10.3390/w15183307