Tracking Multiphase Flows through Steep Reservoirs with External Constraint
Abstract
:1. Introduction
2. Mathematical Modeling
2.1. Governing Equations for Fluid Phase
2.2. Governing Equations for the Particle Phase
3. Solution to the Problem
4. Approximate Analytical Technique
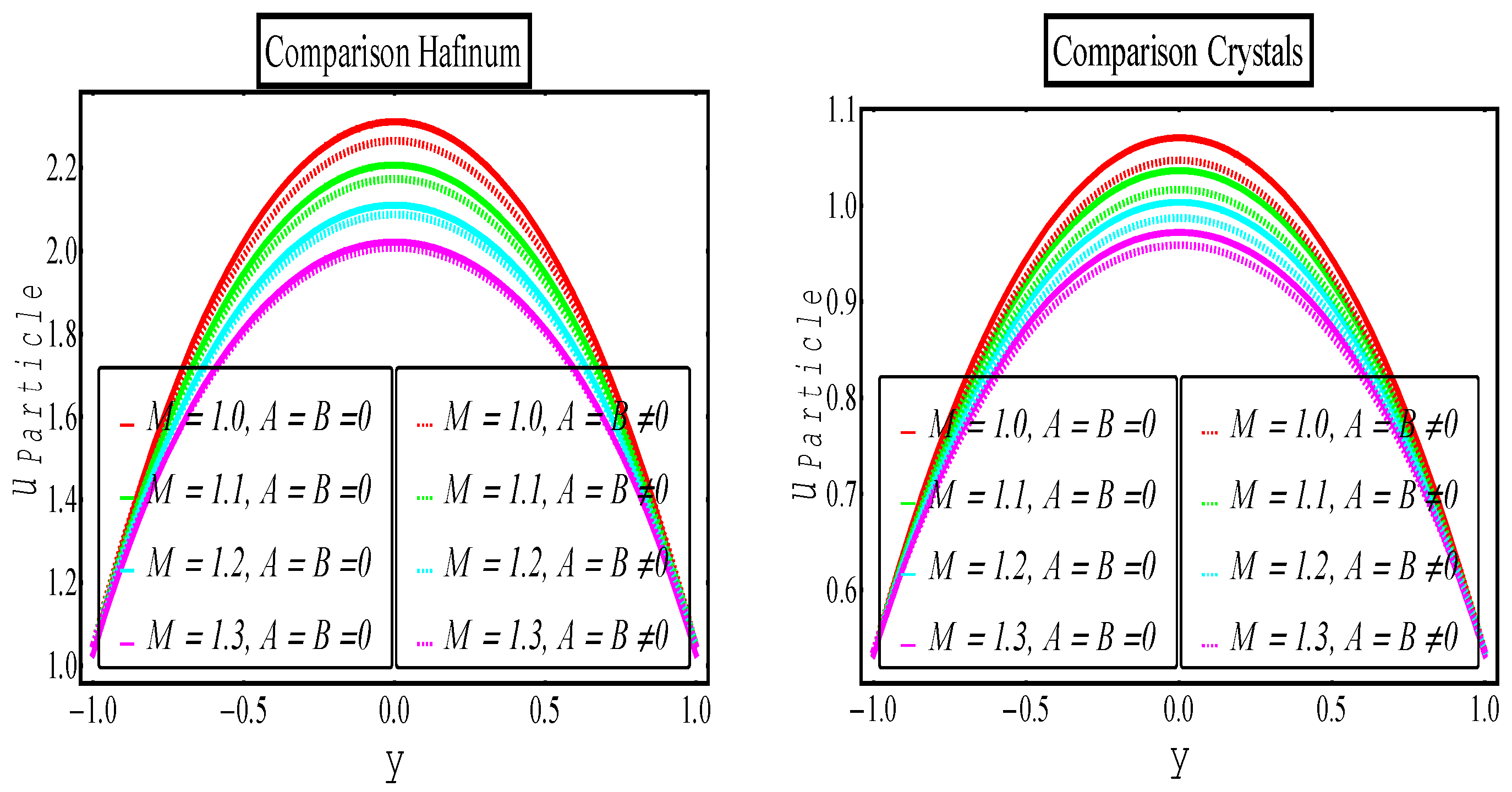
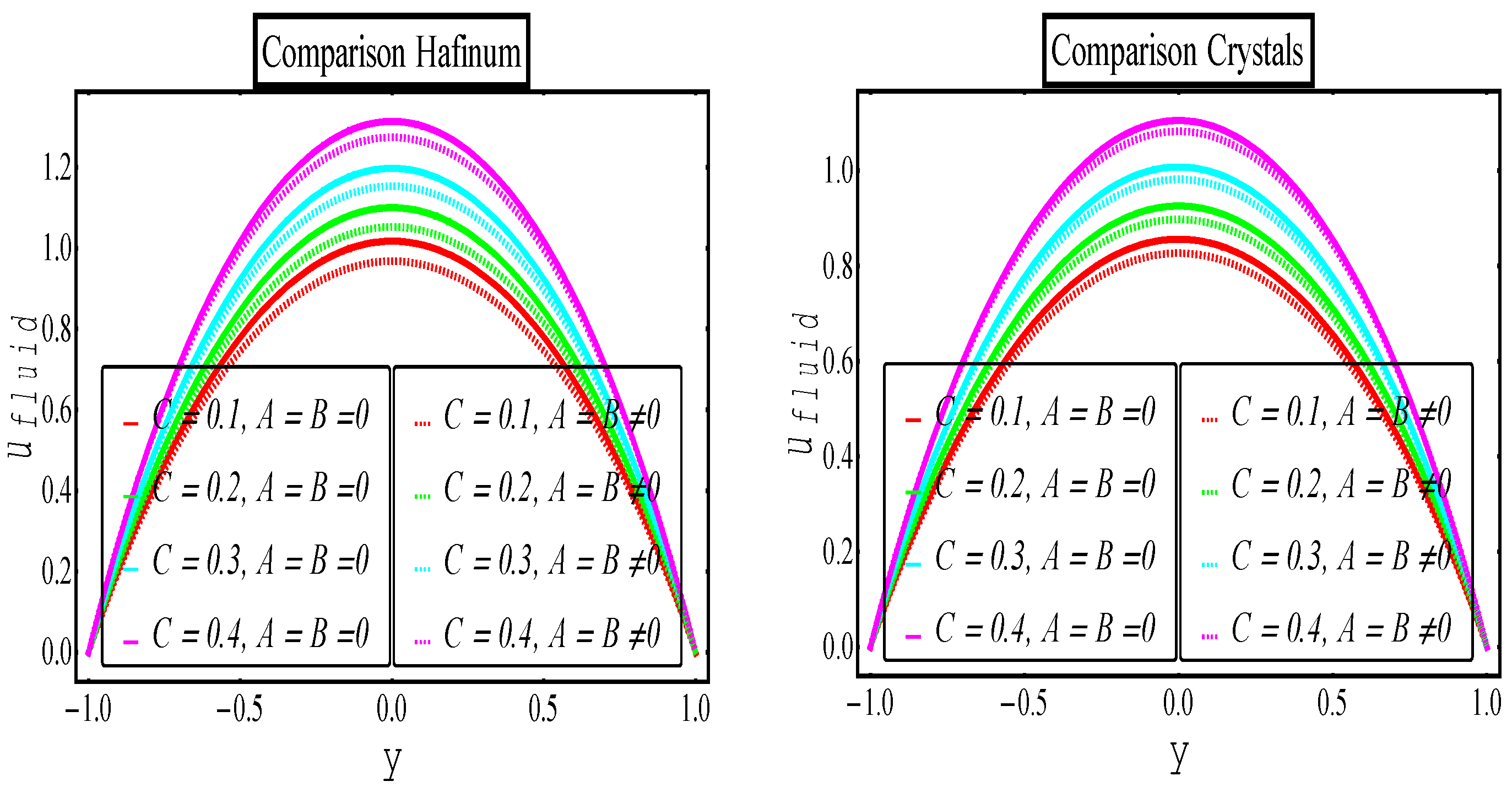
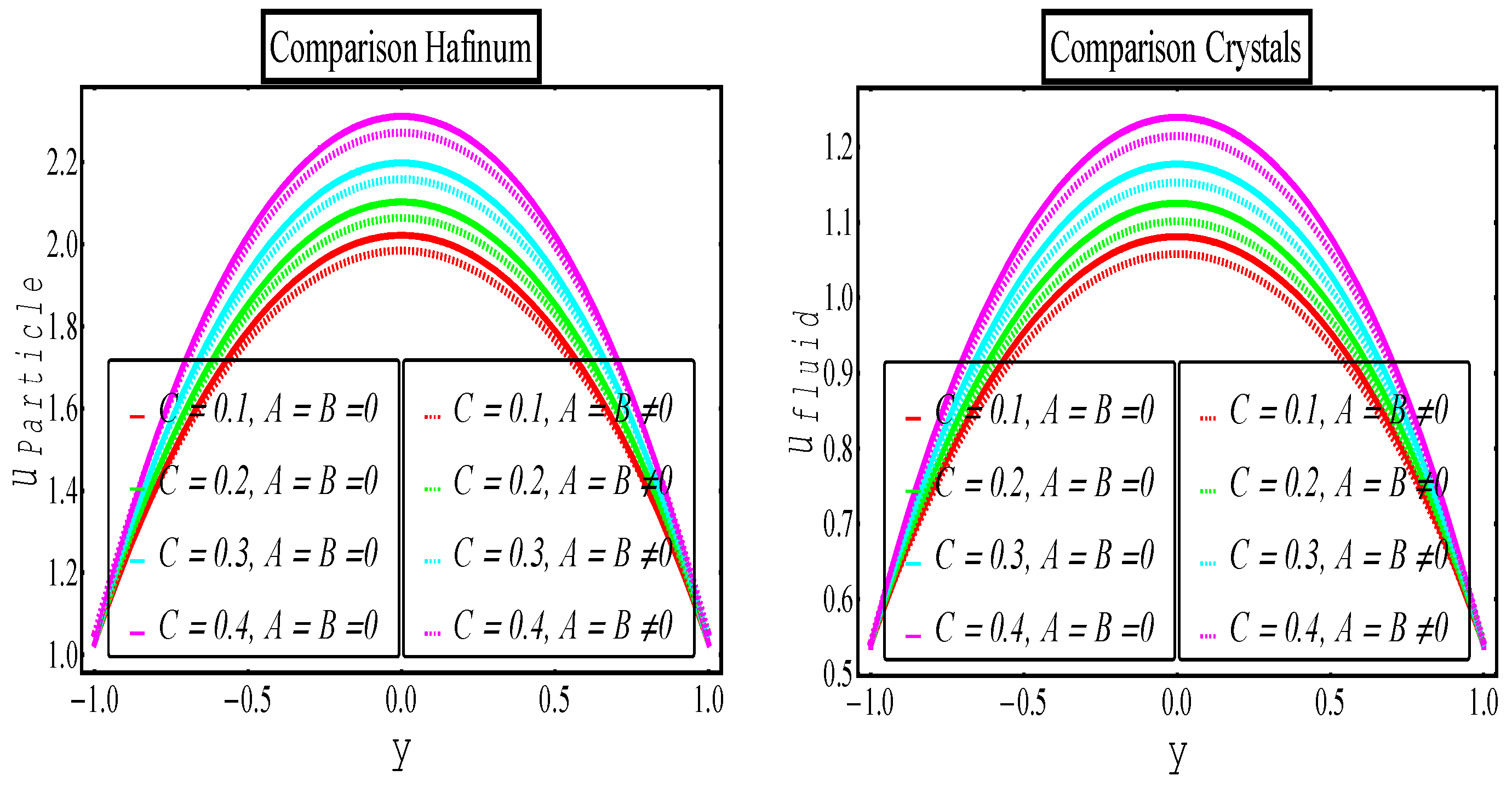
5. Results and Discussion
6. Comparative Analysis
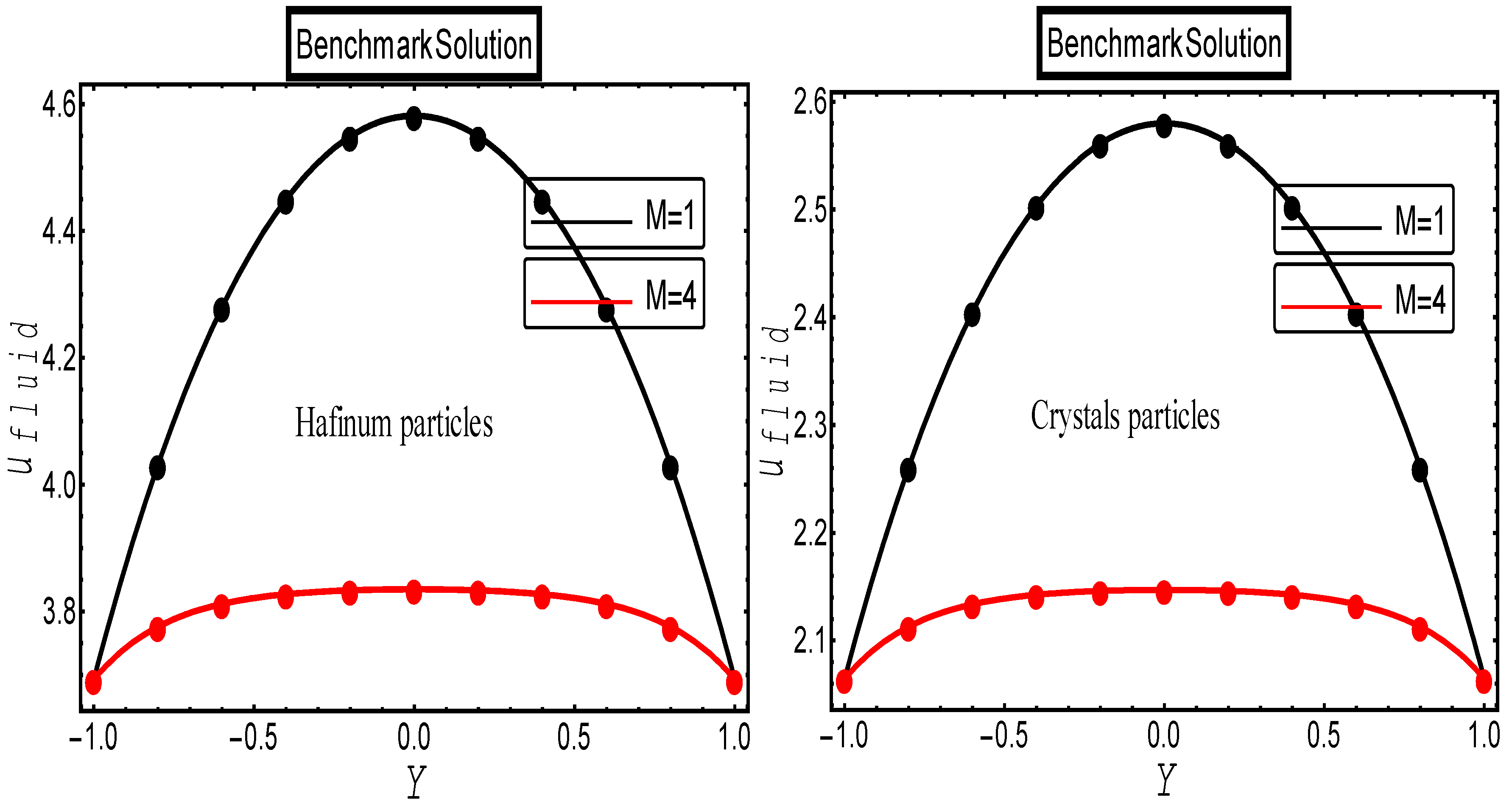
6.1. Current Study vs. a Previous Study
6.2. Eyring–Powell Multiphase vs. Newtonian Multiphase
6.3. Computational Validation
7. Concluding Remarks
- ➢
- The flow dynamics of multiphase suspensions are influenced by strong magnetic fields.
- ➢
- Promising results for the momentum of each flow can be achieved by adding extra particles.
- ➢
- Metallic suspensions produce better outcomes than those with crystals.
- ➢
- Theoretical and numerical findings were compared to an existing study for the limiting case and were found to be in good coherence.
- ➢
- The momentum of Eyring–Powell multiphase suspensions reduces due to their strong internal viscous forces.
- ➢
- The results of this study enhance our understanding of underground flows, specifically in the petroleum industry, with a particular focus on multiphase flows.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Stress tensor | Material time derivative | ||
| Velocity vector of fluid phase (m/s) | Velocity vector of particle phase (m/s) | ||
| Material constant of first order | Length (m) | ||
| Material constant of second order | The pressure | ||
| Current vector | Magnetic force | ||
| Drag force | Perturbation parameter | ||
| Hartmann number | 𝐹𝑟 | Froude number | |
| Angle of inclination | Density number | ||
| Rivlin–Ericksen tensor | Electrical conductivity | ||
| Density of the fluid (kg/m3) | The density of particle (kg/m3) | ||
| Time (s) | Gravitational force (N) | ||
| Material constants of Eyring–Powell fluid | Material constants of Eyring–Powell fluid | ||
| Viscosity | |||
| Subscripts | |||
| 𝑝 | Particle | 𝑓 | Fluid |
Appendix A
References
- Powell, R.E.; Eyring, H. Mechanisms for the relaxation theory of viscosity. Nature 1944, 154, 427–428. [Google Scholar] [CrossRef]
- Ali, N.; Nazeer, M.; Nazeer, F. Flow and Heat Transfer Analysis of an Eyring–Powell Fluid in a Pipe. Z. Naturforschung A 2018, 73, 265–274. [Google Scholar] [CrossRef]
- Nazeer, M.; Ahmad, F.; Saleem, A.; Saeed, M.; Naveed, S.; Shaheen, M.; Al Aidarous, E. Effects of Constant and Space-Dependent Viscosity on Eyring–Powell Fluid in a Pipe: Comparison of the Perturbation and Explicit Finite Difference Methods. Z. Naturforschung A 2019, 74, 961–969. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Kumar, R.; Bahadur, S.; Seth, G.S. Modeling and interpretation of peristaltic transport of Eyring–Powell fluid through uniform/non-uniform channel with Joule heating and wall flexibility. Chin. J. Phys. 2022, 80, 167–182. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Ishak, A.; Sherifm, E.S.M.; Sarris, I.E.; Eldin, S.M.; Pop, I. Analysis of assisting and opposing flows of the eyring-powell fluid on the wall jet nanoparticles with significant impacts of irregular heat source/sink. Case Stud. Therm. Eng. 2023, 49, 103209. [Google Scholar] [CrossRef]
- Khan, Z.; Rasheed, H.U.; Abbas, T.; Khan, W.; Khan, I.; Baleanu, D.; Nisar, K.N. Analysis of Eyring–Powell fluid flow used as a coating material for wire with variable viscosity effect along with thermal radiation and joule heating. Crystals 2020, 10, 168. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Study of shiny film coating on multi-fluid flows of a rotating disk suspended with nano-sized silver and gold particles: A comparative analysis. Coatings 2018, 8, 422. [Google Scholar] [CrossRef]
- Hussain, F.; Ellahi, R.; Zeeshan, A. Mathematical models of electro-magnetohydrodynamic multiphase flows synthesis with nano-sized Hafnium particles. Appl. Sci. 2018, 8, 275. [Google Scholar] [CrossRef]
- Zhang, C.; Su, H.; Zhang, J. On the computation of compressible multiphase flows with heat and mass transfer in elastic pipelines. J. Comput. Phys. 2023, 490, 112257. [Google Scholar] [CrossRef]
- Jiang, J.; Tomin, P.; Tchelepi, H. Accelerated Nonlinear Domain Decomposition Solver for Multi-phase Flow and Transport in Porous Media. J. Comput. Phys. 2023, 490, 112328. [Google Scholar] [CrossRef]
- Al Kubaisy, J.; Salinas, P.; Jackson, M.D. A hybrid pressure approximation in the control volume finite element method for multiphase flow and transport in heterogeneous porous media. J. Comput. Phys. 2023, 475, 111839. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Zeeshan, A.; Ijaz, N. Slip effects and endoscopy analysis on blood flow of particle-fluid suspension induced by peristaltic wave. J. Mol. Liq. 2016, 218, 240–245. [Google Scholar] [CrossRef]
- Abdelsalam, S.I.; Zaher, A.Z. Leveraging elasticity to uncover the role of rabinowitsch suspension through a wavelike conduit: Consolidated blood suspension application. Mathematics 2021, 9, 2008. [Google Scholar] [CrossRef]
- He, W.; Ruhani, B.; Toghraie, D.; Izadpanahi, N.; Esfahani, N.N.; Karimipour, A.; Afrand, M. Using of artificial neural networks (ANNs) to predict the thermal conductivity of zinc oxide–silver (50%–50%)/water hybrid Newtonian nanofluid. Int. Commun. Heat Mass Transf. 2020, 116, 104645. [Google Scholar] [CrossRef]
- Yan, S.R.; Toghraie, D.; Abdulkareem, L.A.; Alizadeh, A.A.; Barnoon, P.; Afrand, M. The rheological behavior of MWCNTs–ZnO/Water–Ethylene glycol hybrid non-Newtonian nanofluid by using of an experimental investigation. J. Mater. Res. Technol. 2020, 9, 8401–8406. [Google Scholar] [CrossRef]
- Unyong, B.; Vadivel, R.; Govindaraju, M.; Anbuvithya, R.; Gunasekaran, N. Entropy analysis for ethylene glycol hybrid nanofluid flow with elastic deformation, radiation, non-uniform heat generation/absorption, and inclined Lorentz force effects. Case Stud. Therm. Eng. 2022, 30, 101639. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Ellahi, R.; Doranehgard, M.H. Numerical study on the hybrid nanofluid (Co3O4-Go/H2O) flow over a circular elastic surface with non-Darcy medium: Application in solar energy. J. Mol. Liq. 2022, 361, 119655. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Bég, O.A.; Ellahi, R.; Doranehgard, M.H.; Rabiei, F. Electro-magnetohydrodynamics hybrid nanofluid flow with gold and magnesium oxide nanoparticles through vertical parallel plates. J. Magn. Magn. Mater. 2022, 564, 170136. [Google Scholar] [CrossRef]
- Riaz, A.; Zeeshan, A.; Bhatti, M.M.; Ellahi, R. Peristaltic propulsion of Jeffrey nano-liquid and heat transfer through a symmetrical duct with moving walls in a porous medium. Phys. A Stat. Mech. Appl. 2020, 545, 123788. [Google Scholar] [CrossRef]
- Awan, A.U.; Ali, B.; Shah, S.A.A.; Oreijah, M.; Guedri, K.; Eldin, S.M. Numerical analysis of heat transfer in Ellis hybrid nanofluid flow subject to a stretching cylinder. Case Stud. Therm. Eng. 2023, 49, 103222. [Google Scholar] [CrossRef]
- Saleem, S.; Hussain, F.; Irfan, M.; Siddique, I.; Nazeer, M.; Eldin, S.M. Theoretical investigation of heat transfer analysis in Ellis nanofluid flow through the divergent channel. Case Stud. Therm. Eng. 2023, 48, 103140. [Google Scholar] [CrossRef]
- Vidya Shree, R.; Patil Mallikarjun, B.; Kumbinarasaiah, S. Entropy generation on an MHD Casson fluid flow in an inclined channel with a permeable walls through Hermite wavelet method. Results Control Optim. 2023, 12, 100261. [Google Scholar]
- Noreen, S.; Kausar, T.; Tripathi, D.; Ain, Q.U.; Lu, D.C. Heat transfer analysis on creeping flow Carreau fluid driven by peristaltic pumping in an inclined asymmetric channel. Therm. Sci. Eng. Prog. 2020, 17, 100486. [Google Scholar] [CrossRef]
- Li, J.; Lv, J.Q.; Sivakumar, V.; Chen, Y.; Huang, X.; Lv, Y.; Chouw, N. Shear strength of stiffened steel shear walls with considering the gravity load effect through a three-segment distribution. Structures 2021, 29, 265–272. [Google Scholar] [CrossRef]
- Song, X.; Li, D.; Sun, X.; Mou, X.; Cheng, Y.F.; Yang, Y. Numerical modeling of the critical pipeline inclination for the elimination of the water accumulation on the pipe floor in oil-water fluid flow. Petroleum 2020, 7, 209–221. [Google Scholar] [CrossRef]
- Nazeer, M.; Hussain, F.; Shahzad, Q.; Khan, M.I.; Kadry, S.; Chu, Y.M. Perturbation solution of the multiphase flows of third grade dispersions suspended with Hafnium and crystal particles. Surf. Interfaces 2020, 22, 100803. [Google Scholar] [CrossRef]
- Hartmann, J. Theory of the laminar flow of an electrically conductive liquid in a homogeneous magnetic field. Mat.-Fys. Medd. 1937, 6, 15. [Google Scholar]
- Maheswari, C.; Ramana, R.M.; Shaw, S.M.; Dharmaiah, G.; Noeiaghdam, S. Numerical investigation on MHD forchheimer flow of Fe3O4-H2O, Cu-H2O and Ag-H2O nanofluids over permeable stretching sheet with radiation. Results Eng. 2023, 18, 101194. [Google Scholar] [CrossRef]
- Turabi, Y.U.; Amin, A.; Munir, S.; Farooq, U. Investigating flow features and heat/mass transfer in two-layer vertical channel with Gr-TiO2 hybrid nanofluid under MHD and radiation effects. J. Magn. Magn. Mater. 2023, 578, 170800. [Google Scholar] [CrossRef]
- Nazeer, M.; Nazir, M.W.; Ali, N.; Javed, T.; Abdelmohsen, S.A.; Khan, M.I. Momentum and thermal transport analysis in MHD nanofluid through the thermally heated square conduit: Finite element method. J. Magn. Magn. Mater. 2023, 580, 170954. [Google Scholar] [CrossRef]
- Saha, T.; Islam, T.; Yeasmin, S.; Parveen, N. Thermal influence of heated fin on MHD natural convection flow of nanofluids inside a wavy square cavity. Int. J. Thermofluids 2023, 18, 100338. [Google Scholar] [CrossRef]
- Mekheimer, K.S.; El Shehawey, E.F.; Elaw, A.M. Peristaltic motion of a particle-fluid suspension in a planar channel. Int. J. Theor. Phys. 1998, 37, 2895–2920. [Google Scholar] [CrossRef]
- Srivastava, V.P. Particle-fluid suspension model of blood flow through stenotic vessels with applications. Int. J. Bio-Med. Comput. 1995, 38, 141–154. [Google Scholar] [CrossRef] [PubMed]
- Hussain, F.; Subia, G.S.; Nazeer, M.; Ghafar, M.M.; Ali, Z.; Hussain, A. Simultaneous effects of Brownian motion and thermophoretic force on Eyring–Powell fluid through porous geometry. Z. Naturforschung A 2021, 76, 569–580. [Google Scholar] [CrossRef]
- Nazeer, M.; Ramesh, K.; Farooq, H.; Shahzad, Q. Impact of gold and silver nanoparticles in highly viscous flows with different body forces. Int. J. Model. Simul. 2023, 43, 376–392. [Google Scholar] [CrossRef]
- Daprà, I.; Scarpi, G. Perturbation Solution for Pulsatile Flow of a Non-Newtonian Fluid in a Rock Fracture: A Logarithmic Model. Water 2020, 12, 1341. [Google Scholar] [CrossRef]
- Zeeshan, A.; Hussain, F.; Ellahi, R.; Vafai, K. A study of gravitational and magnetic effects on coupled stress bi-phase liquid suspended with crystal and Hafnium particles down in steep channel. J. Mol. Liq. 2019, 286, 110898. [Google Scholar] [CrossRef]

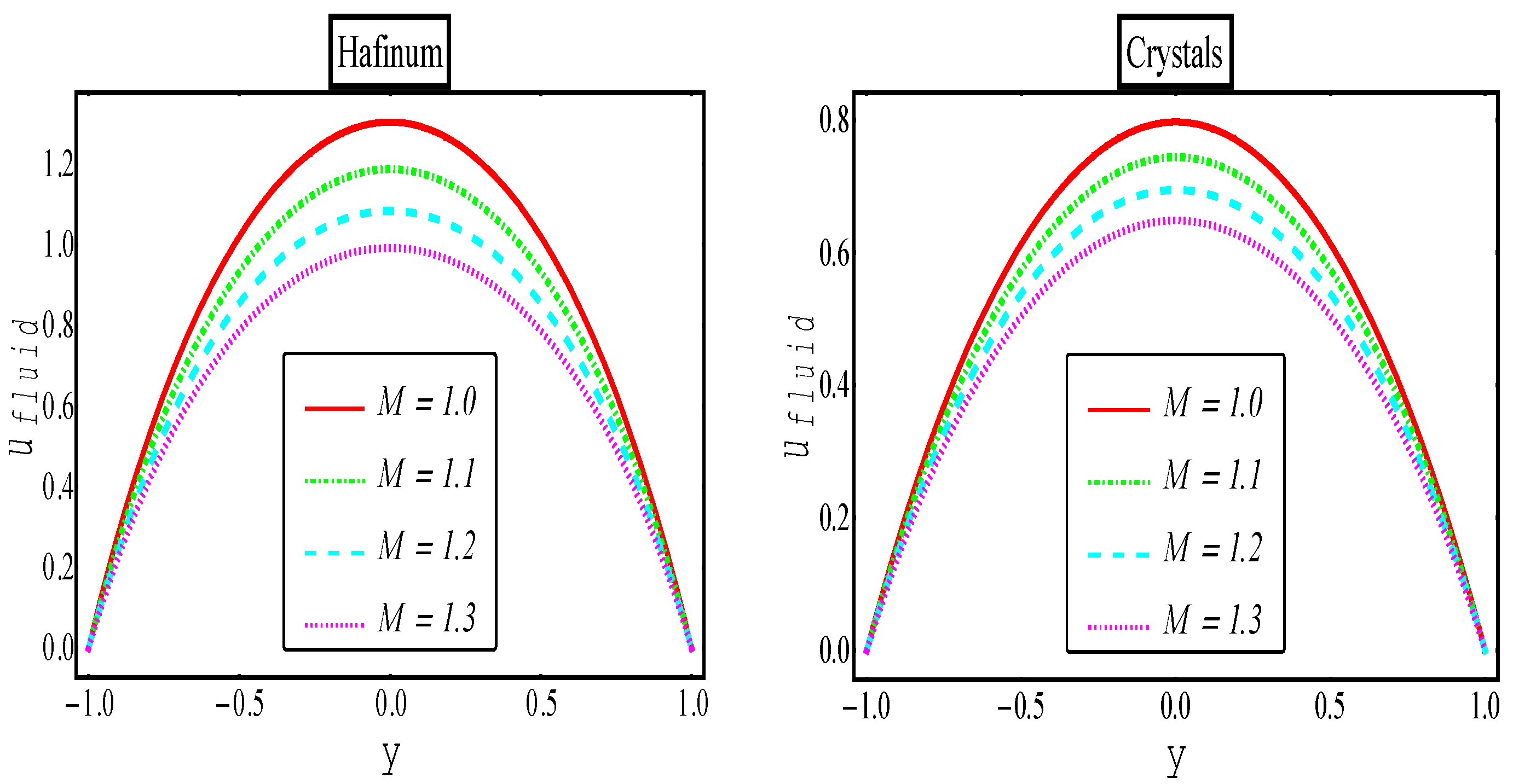


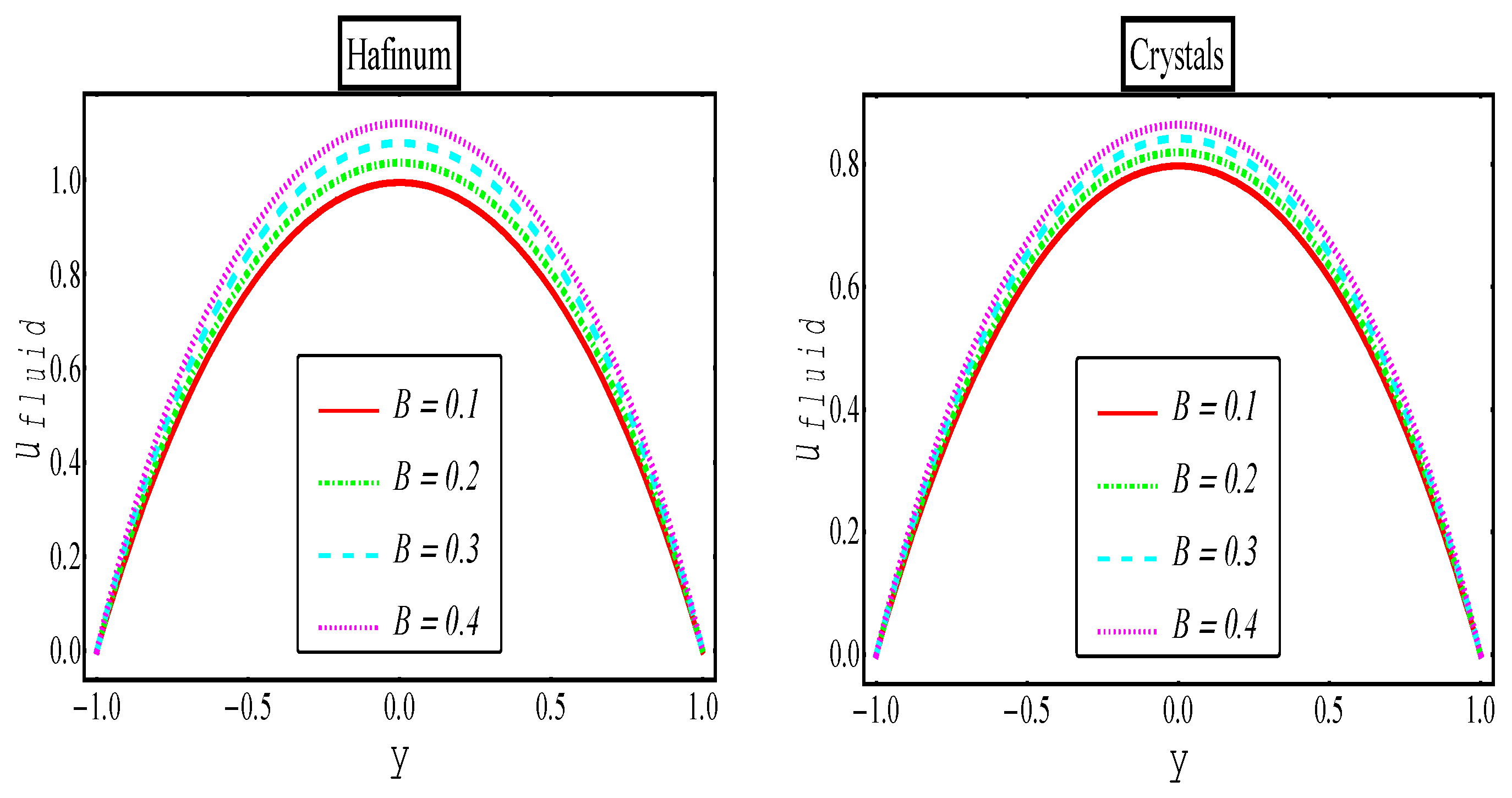
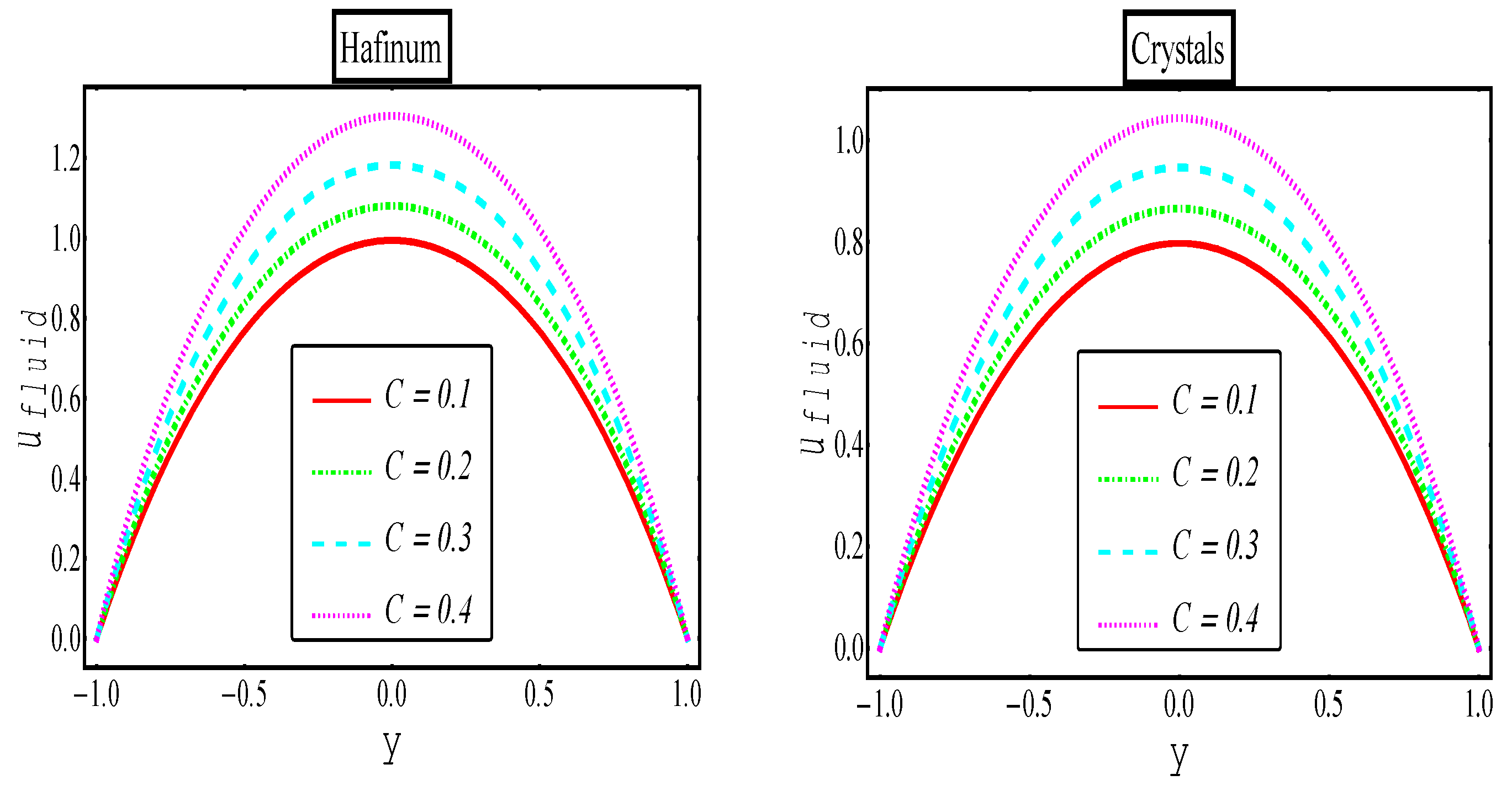
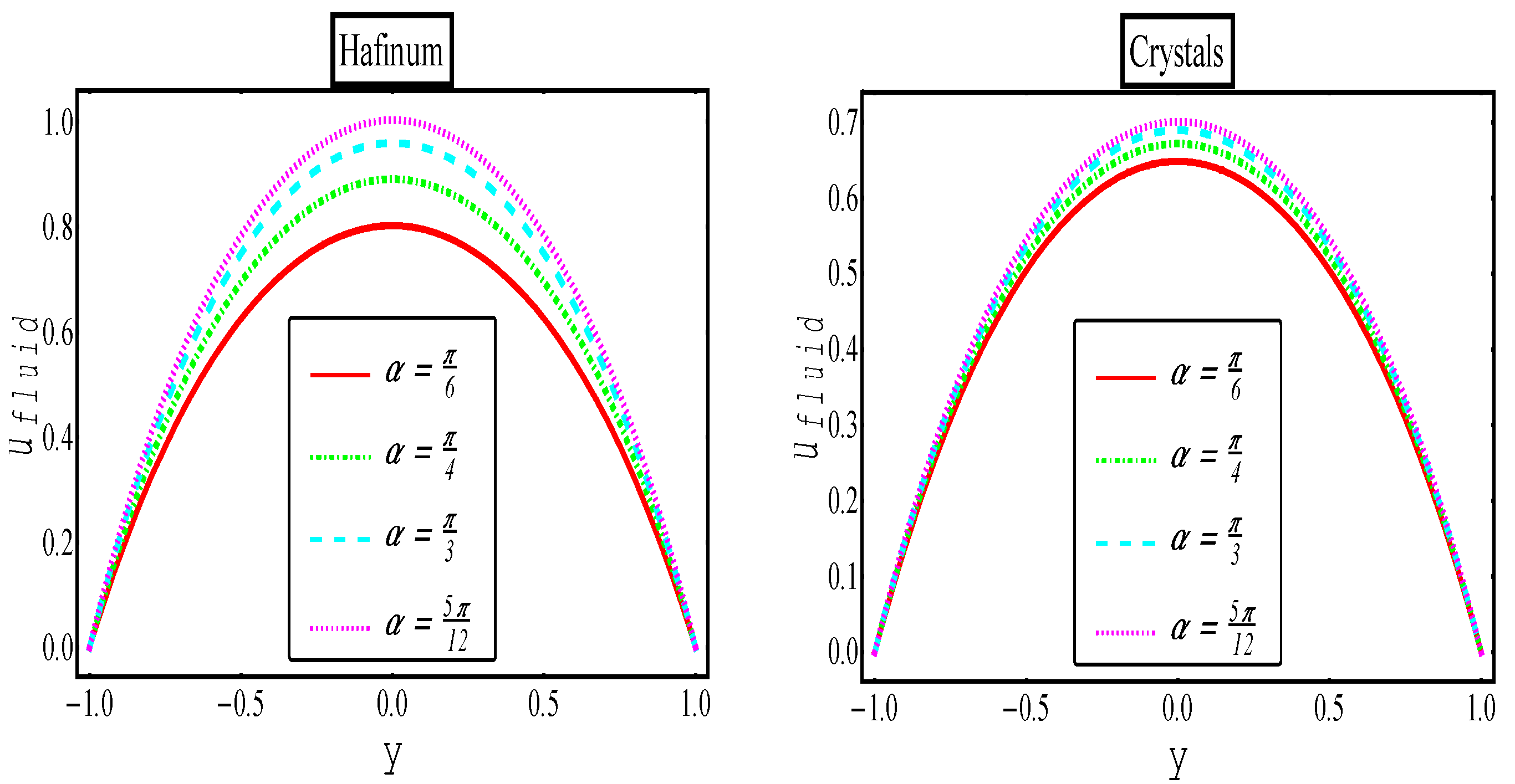

Hafnium Particles | |||
|---|---|---|---|
| M | C | Newtonian | Eyring–Powell |
| 1.3 | 0.4 | 1.01527 | 0.824234 |
| 1.2 | 0.4 | 0.93194 | 0.971763 |
| 1.1 | 0.4 | 0.900418 | 1.05023 |
| 1.0 | 0.4 | 0.980922 | 1.2324 |
| 1.0 | 0.3 | 1.06759 | 1.1058 |
| 1.0 | 0.2 | 0.973297 | 1.00306 |
| 1.0 | 0.1 | 0.894159 | 0.91756 |
| Parameters | Crystal Particles | ||
|---|---|---|---|
| M | C | Newtonian | Eyring–Powell |
| 1.3 | 0.4 | 0.855782 | 0.801604 |
| 1.2 | 0.4 | 0.931944 | 0.905695 |
| 1.1 | 0.4 | 1.01527 | 0.98921 |
| 1.0 | 0.4 | 1.10496 | 1.08234 |
| 1.0 | 0.3 | 1.00737 | 0.981451 |
| 1.0 | 0.2 | 0.925465 | 0.897408 |
| 1.0 | 0.1 | 0.855782 | 0.826402 |
| Parameters | Hafnium Particles | ||
|---|---|---|---|
| Newtonian | Eyring–Powell | ||
| 5.2 | 0.798299 | 0.883064 | |
| 4.8 | 0.805479 | 0.910807 | |
| 4.4 | 0.814704 | 0.946691 | |
| 4.0 | 0.826833 | 0.802453 | |
| 4.0 | 0.855782 | 0.891055 | |
| 4.0 | 0.877995 | 0.959776 | |
| 4.0 | 0.891959 | 1.00333 | |
| Parameters | Crystal Particles | ||
|---|---|---|---|
| Newtonian | Eyring–Powell | ||
| 5.2 | 0.798299 | 0.767867 | |
| 4.8 | 0.805479 | 0.775143 | |
| 4.4 | 0.814704 | 0.784506 | |
| 4.0 | 0.826833 | 0.796842 | |
| 4.0 | 0.855782 | 0.826402 | |
| 4.0 | 0.877995 | 0.849201 | |
| 4.0 | 0.891959 | 0.863585 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nazeer, M.; Ali, W.; Hussain, F. Tracking Multiphase Flows through Steep Reservoirs with External Constraint. Water 2023, 15, 3300. https://doi.org/10.3390/w15183300
Nazeer M, Ali W, Hussain F. Tracking Multiphase Flows through Steep Reservoirs with External Constraint. Water. 2023; 15(18):3300. https://doi.org/10.3390/w15183300
Chicago/Turabian StyleNazeer, Mubbashar, Waqas Ali, and Farooq Hussain. 2023. "Tracking Multiphase Flows through Steep Reservoirs with External Constraint" Water 15, no. 18: 3300. https://doi.org/10.3390/w15183300





