A Dynamic Estuarine Classification of the Vertical Structure Based on the Water Column Density Slope and the Potential Energy Anomaly
Abstract
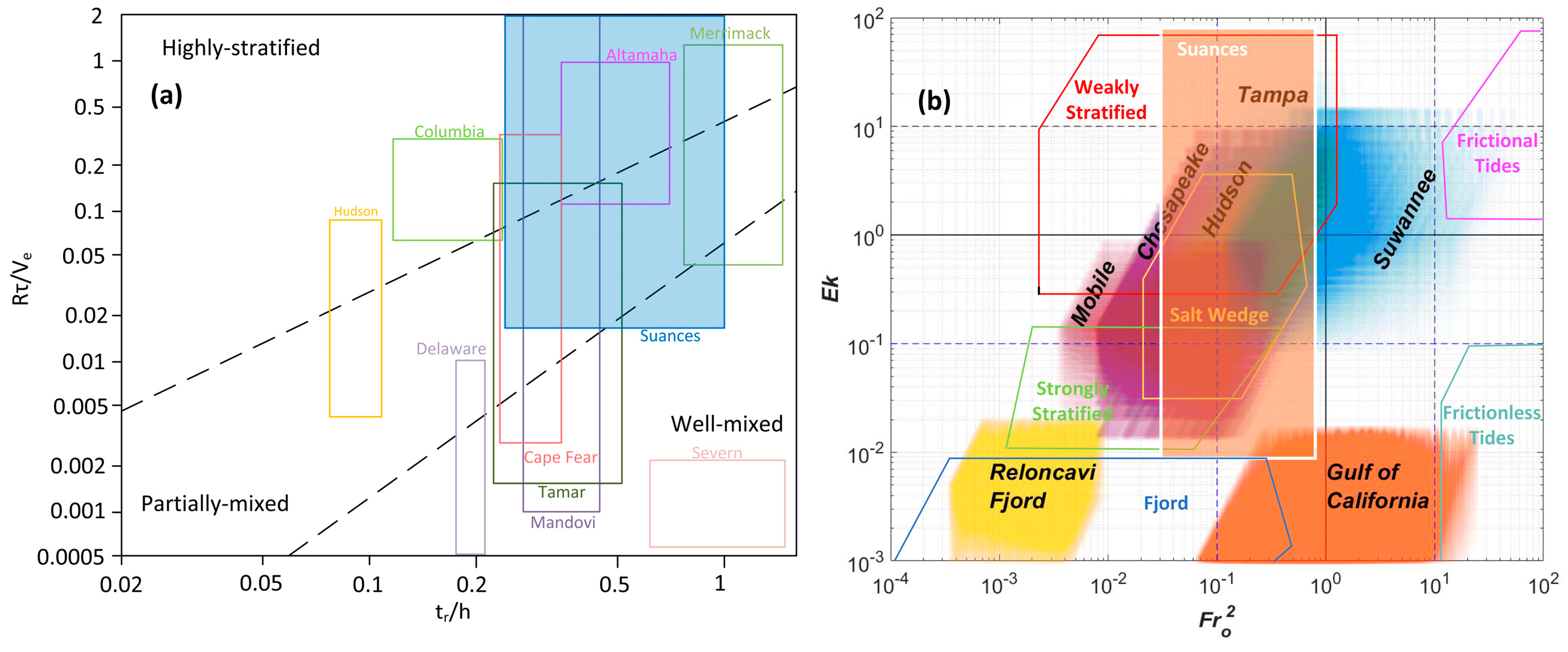
:1. Introduction
2. Materials and Methods
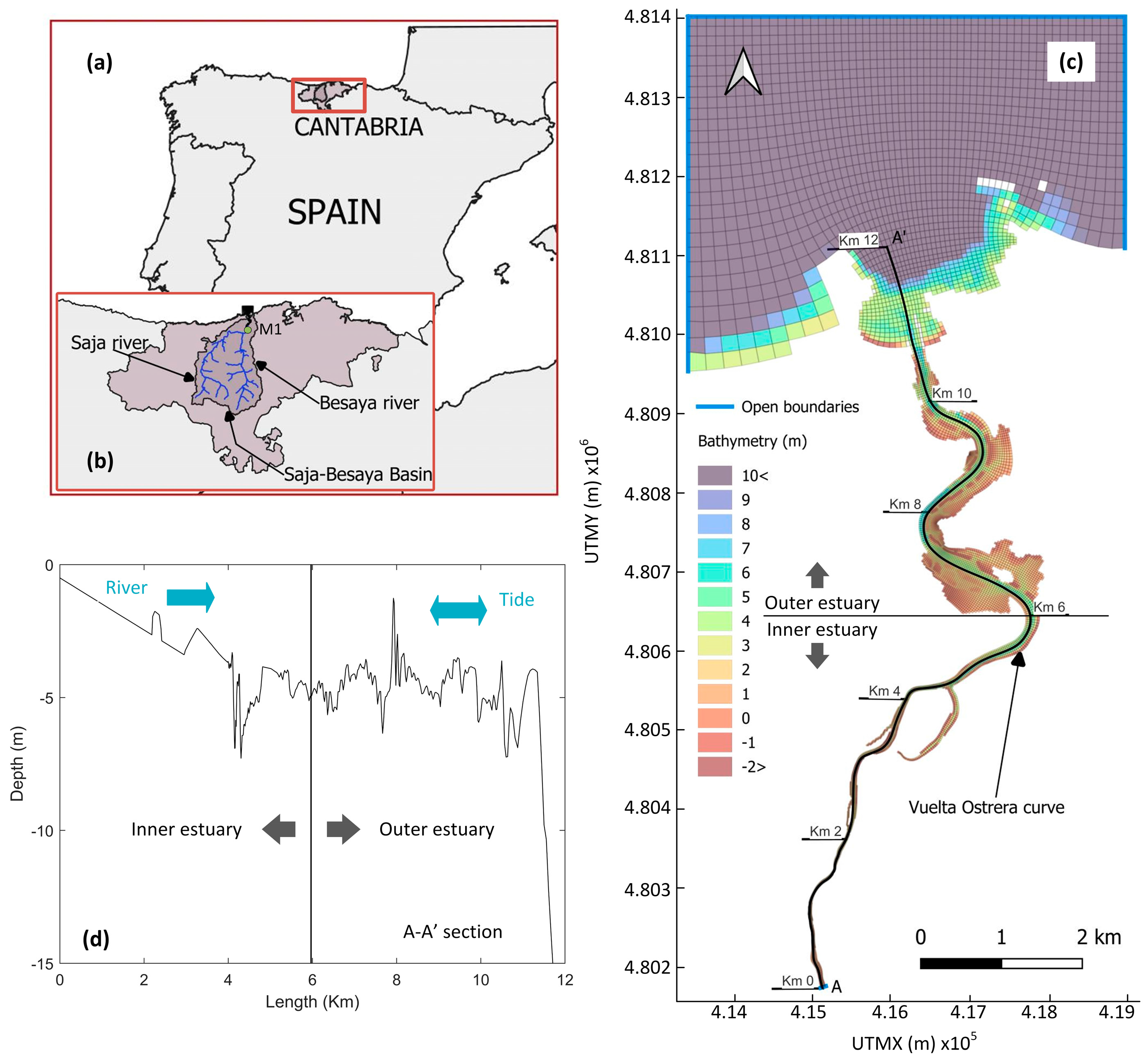
2.1. Study Area and Setup of the 3D Hydrodynamic Model
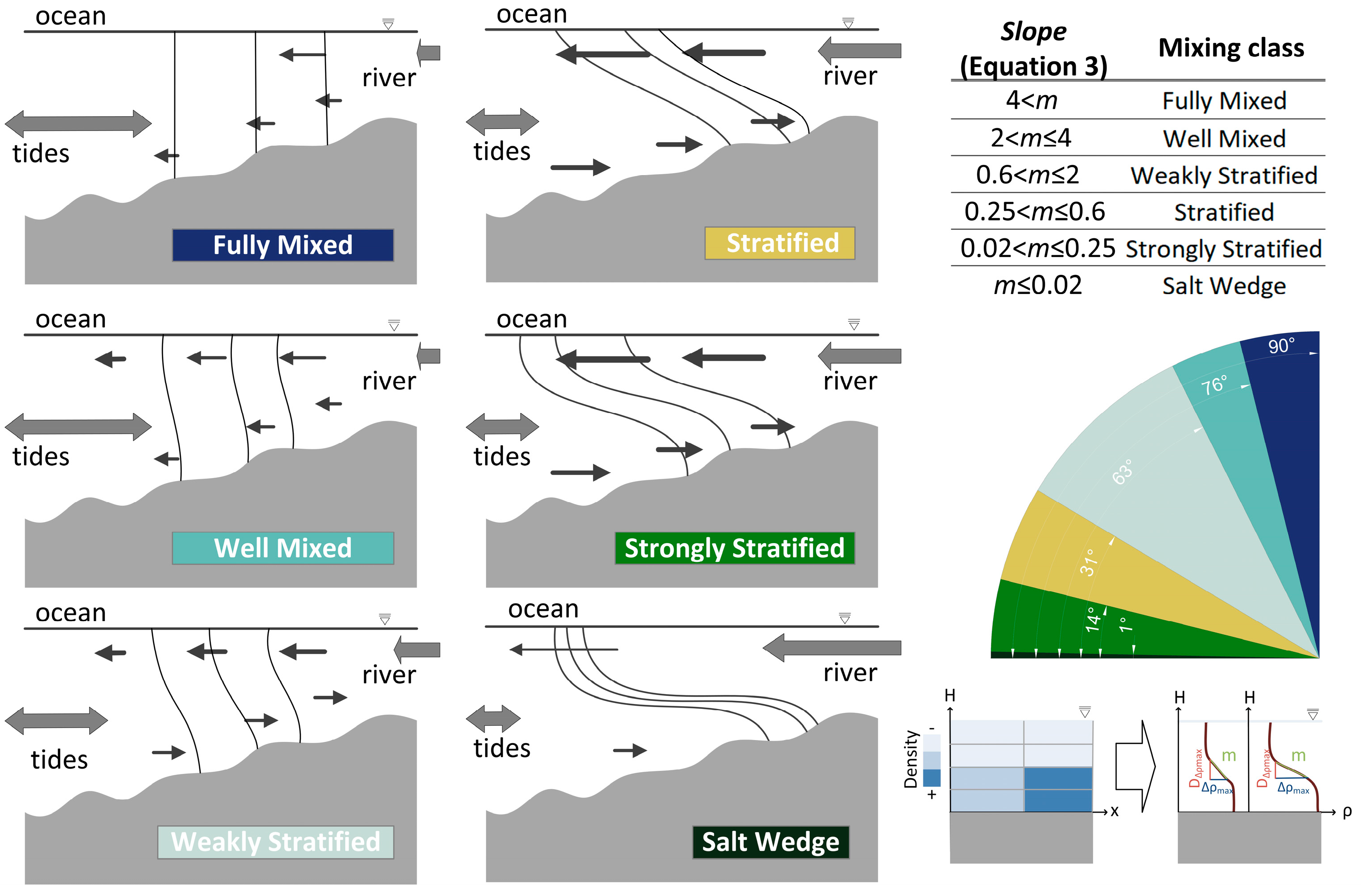
2.2. Classification of the Estuarine Vertical Structure According to the Density Profile Slope ()
2.3. Relationship between the Density Profile Slope and the Potential Energy Anomaly
2.4. Methodology to Classify Mixing Classes According to the Vertical Structure at a Local Scale
3. Results
3.1. Relationship between the Density Profile Slope and the Potential Energy Anomaly in the Suances Estuary
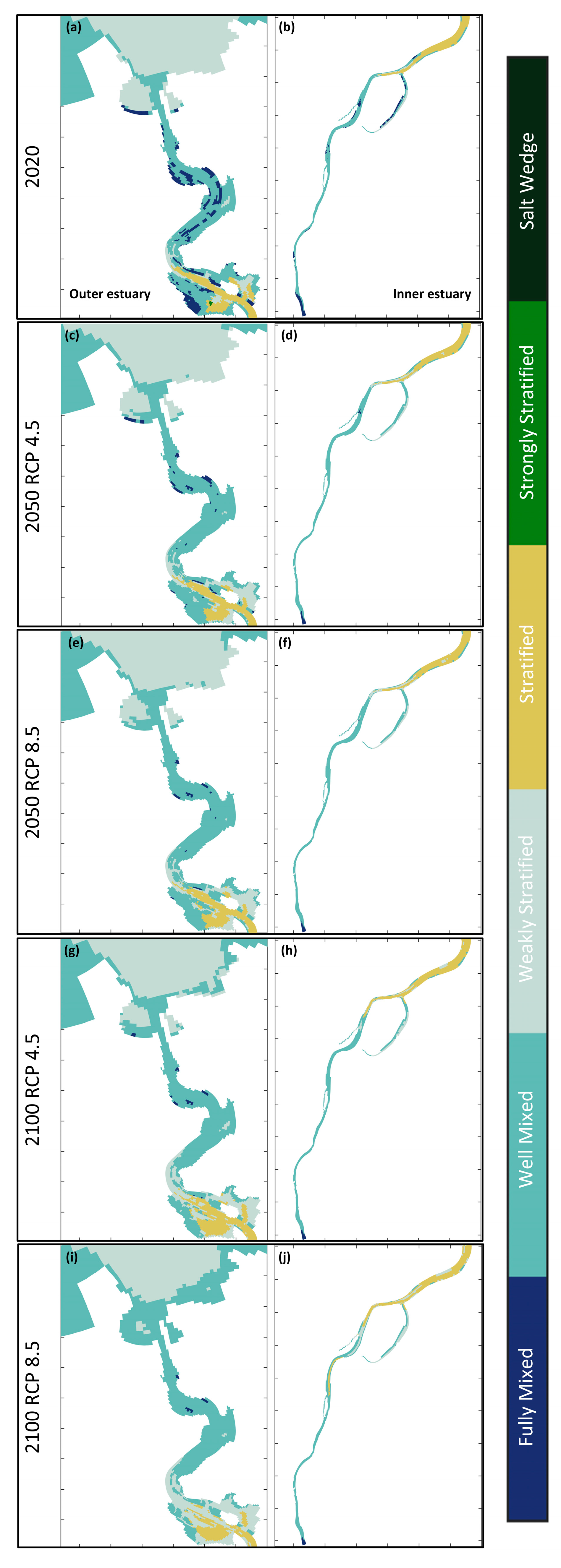
3.2. Spatiotemporal Evolution of Vertical Mixing Classes in the Suances Estuary
4. Discussion
4.1. Relationship between Vertical Structure and Density Slopes to Establish Vertical Mixing Classes
4.2. Classification of the Suances Estuary Using Other Methodologies
4.3. Dynamic Classification of Estuarine Vertical Structure and Projected Modifications under Climate Change
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Simpson, J.H.; Hughes, D.G.; Morris, N.C.G. The relation of seasonal stratification to tidal mixing on the continental shelf. Deep-Sea Res. 1977, 24, 327–340. [Google Scholar]
- Geyer, W.; Scully, M.; Ralston, D. Quantifying vertical mixing in estuaries. Environ. Fluid Mech. 2008, 8, 495–509. [Google Scholar] [CrossRef]
- Bárcena, J.F.; Camus, P.; García, A.; Álvarez, C. Selecting model scenarios of real hydrodynamic forcings on mesotidal and macrotidal estuaries influenced by river discharges using K-means clustering. Environ. Model. Softw. 2015, 68, 70–82. [Google Scholar] [CrossRef]
- Zhang, R.; Hong, B.; Zhu, L.; Gong, W.; Zhang, H. Responses of estuarine circulation to the morphological evolution in a 1 convergent, microtidal estuary. Ocean Sci. 2022, 18, 213–231. [Google Scholar] [CrossRef]
- Couceiro, M.A.; Schettini, C.A.; Siegle, E. Modeling an arrested salt-wedge estuary subjected to variable river flow. Reg. Stud. Mar. Sci. 2021, 47, 101993. [Google Scholar] [CrossRef]
- Khadami, F.; Kawanisi, K.; Al Sawaf, M.B.; Gusti, G.N.N.; Xiao, C. Spatiotemporal Response of Currents and Mixing to the Interaction of Tides and River Runoff in a Mesotidal Estuary. Ocean Sci. J. 2022, 57, 37–51. [Google Scholar] [CrossRef]
- Ralston, D.K.; Geyer, W.R.; Lerczak, J.A. Structure, variability, and salt flux in a strongly forced salt wedge estuary. J. Geophys. Res. Atmos. 2010, 115, C06005. [Google Scholar] [CrossRef]
- Rijnsburger, S.; Flores, R.P.; Pietrzak, J.D.; Horner-Devine, A.R.; Souza, A.J. The Influence of Tide and Wind on the Propagation of Fronts in a Shallow River Plume. J. Geophys. Res. Oceans 2018, 123, 5426–5442. [Google Scholar] [CrossRef]
- Ross, L.; Valle-Levinson, A.; Sottolichio, A.; Huybrechts, N. Lateral variability of subtidal flow at the mid-reaches of a macrotidal estuary. J. Geophys. Res. Oceans 2017, 122, 7651–7673. [Google Scholar] [CrossRef]
- Bárcena, J.F.; García, A.; García, J.; Álvarez, C.; Revilla, J. Surface analysis of free surface and velocity to changes in river flow and tidal amplitude on a shallow mesotidal estuary: An application in Suances Estuary (Nothern Spain). J. Hidrology 2012, 420, 301–308. [Google Scholar] [CrossRef]
- García, A.; Juanes, J.A.; Álvarez, C.; Revilla, J.A.; Medina, R. Assesment of the response of a shallow macrotidal estuary to changes in hydrological and wastewater inputs through numerical modelling. Ecol. Model. 2010, 221, 1194–1208. [Google Scholar] [CrossRef]
- Vijith, V.; Sundar, D.; Shetye, S. Time-dependence of salinity in monsoonal estuaries. Estuar. Coast. Shelf Sci. 2009, 85, 601–608. [Google Scholar] [CrossRef]
- Buschman, F.A.; Hoitink, A.J.F.; van der Vegt, M.; Hoekstra, P. Subtidal water level variation controlled by river flow and tides. Water Resour. Res. 2009, 45, 601–608. [Google Scholar] [CrossRef]
- Warner, J.C.; Geyer, W.R.; Lerczak, J.A. Numerical modeling of an estuary: A comprehensive skill assessment. J. Geophys. Res. Atmos. 2005, 110, C5. [Google Scholar] [CrossRef]
- Decastro, M.; Gomez-Gesteira, M.; Prego, R.; Alvarez, I. Ria–ocean exchange driven by tides in the Ria of Ferrol (NW Spain). Estuar. Coast. Shelf Sci. 2004, 61, 15–24. [Google Scholar] [CrossRef]
- Geyer, W.R.; Ralston, D.K.; Chen, J. Mechanisms of Exchange Flow in an Estuary with a Narrow, Deep Channel and Wide, Shallow Shoals. J. Geophys. Res. Oceans 2020, 125, e2020JC016092. [Google Scholar] [CrossRef]
- Becker, M.L.; Luettich, R.A., Jr.; Mallin, M.A. Hydrodynamic behavior of the Cape Fear River and estuarine system: A synthesis and observational investigation of discharge–salinity intrusion relationships. Estuar. Coast. Shelf Sci. 2010, 88, 407–418. [Google Scholar] [CrossRef]
- Uncles, R.; Stephens, J.; Law, D. Turbidity maximum in the macrotidal, highly turbid Humber Estuary, UK: Flocs, fluid mud, stationary suspensions and tidal bores. Estuar. Coast. Shelf Sci. 2006, 67, 30–52. [Google Scholar] [CrossRef]
- Du, J.; Park, K.; Shen, J.; Dzwonkowski, B.; Yu, X.; Yoon, B.I. Role of Baroclinic Processes on Flushing Characteristics in a Highly Stratified Estuarine System, Mobile Bay, Alabama. J. Geophys. Res. Oceans 2018, 123, 4518–4537. [Google Scholar] [CrossRef]
- Pritchard, D. Estuarine hydrography. Adv. Geophys. 1952, 1, 243–280. [Google Scholar] [CrossRef]
- Hansen, D.V.; Rattray, M. New dimensions in estuary classification. Limnol. Oceanogr. 1966, 11, 319–326. [Google Scholar] [CrossRef]
- Geyer, W.R.; MacCready, P. The Estuarine Circulation. Annu. Rev. Fluid Mech. 2014, 46, 175–197. [Google Scholar] [CrossRef]
- Guha, A.; Lawrence, G.A. Estuary Classification Revisited. J. Phys. Oceanogr. 2013, 43, 1566–1571. [Google Scholar] [CrossRef]
- Vijith, V.; Shetye, S. A stratification prediction diagram from characteristics of geometry, tides and runoff for estuaries with a prominent channel. Estuar. Coast. Shelf Sci. 2012, 98, 101–107. [Google Scholar] [CrossRef]
- Valle-Levinson, A. Dynamics-based classification of semienclosed basins. Reg. Stud. Mar. Sci. 2021, 46, 101866. [Google Scholar] [CrossRef]
- Lupiola, J.; Bárcena, J.F.; García-Alba, J.; García, A. A numerical study of the mixing and stratification alterations in estuaries due to climate change using the potential energy anomaly. Front. Mar. Sci. 2023, 10, 1206006. [Google Scholar] [CrossRef]
- Yang, F.; Ji, X.; Zhang, W.; Zou, H.; Jiang, W.; Xu, Y. Characteristics and Driving Mechanisms of Salinity Stratification during the Wet Season in the Pearl River Estuary, China. J. Mar. Sci. Eng. 2022, 10, 1927. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, L.; Wang, Y.; Jiang, C. The Impact of Tidal Straining and Advection on the Stratification in a Partially Mixed Estuary. Water 2023, 15, 339. [Google Scholar] [CrossRef]
- Yamaguchi, R.; Suga, T.; Richards, K.J.; Qiu, B. Diagnosing the development of seasonal stratification using the potential energy anomaly in the North Pacific. Clim. Dyn. 2019, 53, 4667–4681. [Google Scholar] [CrossRef]
- Lenoch, L.K.; Survey, U.G.; Stumpner, P.R.; Burau, J.R.; Loken, L.; Sadro, S. Dispersion and Stratification Dynamics in the Upper Sacramento River Deep Water Ship Channel. San Fr. Estuary Watershed Sci. 2021, 19, 1–29. [Google Scholar] [CrossRef]
- Hamada, T.; Kim, S. Stratification potential-energy anomaly index standardized by external tide level. Estuar. Coast. Shelf Sci. 2021, 250, 107138. [Google Scholar] [CrossRef]
- Simpson, J.H.; Crisp, D.J.; Hearn, C. The shelf-sea fronts: Implications of their existence and behaviour. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1981, 302, 531–546. [Google Scholar] [CrossRef]
- González, M.; Medina, R.; Gonzalez-Ondina, J.; Osorio, A.; Méndez, F.J.; García, E. An integrated coastal modeling system for analyzing beach processes and beach restoration projects, SMC. Comput. Geosci. 2007, 33, 916–931. [Google Scholar] [CrossRef]
- Bárcena, J.F.; García, A.; Gómez, A.G.; Álvarez, C.; Juanes, J.A.; Revilla, J.A. Spatial and temporal flushing time approach in estuaries influenced by river and tide. An application in Suances Estuary (Northern Spain). Estuar. Coast. Shelf Sci. 2012, 112, 40–51. [Google Scholar] [CrossRef]
- Bárcena, J.F.; García-Alba, J.; García, A.; Álvarez, C. Analysis of stratification patterns in river-influenced mesotidal and macrotidal estuaries using 3D hydrodynamic modelling and K-means clustering. Estuar. Coast. Shelf Sci. 2016, 181, 1–13. [Google Scholar] [CrossRef]
- Bárcena, J.F.; Gómez, A.G.; García, A.; Álvarez, C.; Juanes, J.A. Quantifying and mapping the vulnerability of estuaries to point-source pollution using a multi-metric assessment: The Estuarine Vulnerability Index (EVI). Ecol. Indic. 2017, 76, 159–169. [Google Scholar] [CrossRef]
- Nicholson, J.; Broker, I.; Roelvink, J.A.; Price, D.; Tanguy, J.M.; Moreno, L. Intercomparison of coastal area morphodynamic models. Coast. Eng. 1997, 31, 97–123. [Google Scholar] [CrossRef]
- Lesser, G.R.; Roelvink, J.A.; van Kester, J.A.; Stelling, G.S. Development and validation of a three-dimensional morphological model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- Chung, T. Computational Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2002; 1012p. [Google Scholar]
- Stelling, G. On the Construction of Computational Methods for Shallow Water Flow Problems. Ph.D. Thesis, TUDelft, Delft, The Netherlands, 1983. Available online: http://resolver.tudelft.nl/uuid:d3b818cb-9f91-4369-a03e-d90c8c175a96 (accessed on 6 July 2021).
- Stelling, G.; Leendertse, I. Approximation of Convective Processes by Cyclic ADI Methods. In Proceedings of the 11th International Conference on Estuarine and Coastal Modeling, American Society of Civil Engineers, Reston, VA, USA; 1991; pp. 771–782. [Google Scholar]
- UNESCO. Background papers and supporting data on the international equation of state. Tech. Rep. UNESCO 1981, 31, 174. [Google Scholar]
- Rodi, W. Examples of calculation methods for flow and mixing in stratified fluids. J. Geophys. Res. Atmos. 1987, 92, 5305–5328. [Google Scholar] [CrossRef]
- García-Alba, J.; Gómez, A.; Sámano, M.; García, A.; Juanes, J. A 3-d model to analyze environmental effects of dredging operations–application to the port of Marin, Spain. Adv. Geosci. 2014, 39, 95–99. Available online: http://hdl.handle.net/10902/4596 (accessed on 10 December 2022). [CrossRef]
- Jiménez, M.; Castanedo, S.; Zhou, Z.; Coco, G.; Medina, R.; Rodriguez-Iturbe, I. Scaling properties of tidal networks. Water Resour. Res. 2014, 50, 4585–4602. [Google Scholar] [CrossRef]
- Sotillo, M.G.; Cailleau, S.; Lorente, P.; Levier, B.R.; Aznar, R.; Reffray, G.; Amo-Baladrón, A.; Chanut, J.; Benkiran, M.; Alvarez-Fanjul, E. The MyOcean IBI Ocean Forecast and Reanalysis Systems: Operational products and roadmap to the future Copernicus Service. J. Oper. Oceanogr. 2015, 8, 63–79. [Google Scholar] [CrossRef]
- Álvarez, C.; Garcia, E.; Prieto, C.; Rojo, J.; Tejerina, B. Aplicación de un modelo logístico triparamétrico a la estimación de caudales diarios en la cuenca del río Nam Ngum (Laos). In Proceedings of the IV Jornadas de Ingeniería del Agua: “La Precipitación y los Procesos Erosivos”, Córdoba, Spain, 21–22 October 2015; Volume B.8, pp. 255–268. [Google Scholar]
- OECC. Fundación Biodiversidad Visor de escenarios de cambio climático de AdapteCCa. Available online: http://escenarios.adaptecca.es (accessed on 10 December 2022).
- IPCC. Summary for Policymakers. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; Po, H.-O., Roberts, D.C., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegría, A., Nicolai, M., Okem, A., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2019; pp. 3–35. [Google Scholar] [CrossRef]
- Skliris, N.; Marsh, R.; Mecking, J.V.; Zika, J.D. Changing water cycle and freshwater transports in the Atlantic Ocean in observations and CMIP5 models. Clim. Dyn. 2020, 54, 4971–4989. [Google Scholar] [CrossRef]
- Kang, K.R.; Di Iorio, D. Depth- and current-induced effects on wave propagation into the Altamaha River Estuary, Georgia. Estuar. Coast. Shelf Sci. 2007, 66, 395–408. [Google Scholar] [CrossRef]
- Jay, D.A.; Smith, J.D. Residual circulation in shallow estuaries: Highly stratified estuaries, narrow estuaries. J. Geophys. Res. Atmos. 1990, 95, 711–731. [Google Scholar] [CrossRef]
- Cook, T.L.; Sommerfield, C.K.; Wong, K.-C. Observations of tidal and springtime sediment transport in the upper Delaware Estuary. Estuar. Coast. Shelf Sci. 2007, 72, 235–246. [Google Scholar] [CrossRef]
- Geyer, W.R.; Trowbridge, J.H.; Bowen, M.M. The Dynamics of a Partially Mixed Estuary. J. Phys. Oceanogr. 2000, 30, 2035–2048. [Google Scholar] [CrossRef]
- Uncles, R.J. Physical properties and processes in the Bristol Channel and Severn Estuary. Mar. Pollut. Bull. 2010, 61, 5–20. [Google Scholar] [CrossRef]
- Harcourt-Baldwin, J.-L.; Diedericks, G. Numerical modelling and analysis of temperature controlled density currents in Tomales Bay, California. Estuar. Coast. Shelf Sci. 2006, 66, 417–428. [Google Scholar] [CrossRef]
- Noernberg, M.A.; Rodrigo, P.A.; Luersen, D.M. Seasonal and fortnightly variability of the hydrodynamic regime at Babitonga Bay, Southern of Brazil. Reg. Stud. Mar. Sci. 2020, 40, 101518. [Google Scholar] [CrossRef]
- Xing, Y.; Ai, C.; Jin, S. A three-dimensional hydrodynamic and salinity transport model of estuarine circulation with an application to a macrotidal estuary. Appl. Ocean Res. 2013, 39, 53–71. [Google Scholar] [CrossRef]
- Zachopoulos, K.; Kokkos, N.; Sylaios, G. Salt wedge intrusion modeling along the lower reaches of a Mediterranean river. Reg. Stud. Mar. Sci. 2020, 39, 101467. [Google Scholar] [CrossRef]
- Grabemann, I.; Uncles, R.J.; Krause, G.; Stephens, J.A. Behaviour of Turbidity Maxima in the Tamar (U.K.) and Weser (F.R.G.) Estuaries. Estuar. Coast. Shelf Sci. 1997, 45, 235–246. [Google Scholar] [CrossRef]
- The MathWorks Inc. MATLAB. (2022); Version 9.12.0 (R2022a); The MathWorks Inc.: Natick, MA, USA, 2022; Available online: https://www.mathworks.com (accessed on 10 December 2022).
- García-Alba, J.; Bárcena, J.F.; Ugarteburu, C.; García, A. Artificial neural networks as emulators of process-based models to analyse bathing water quality in estuaries. Water Res. 2019, 150, 283–295. [Google Scholar] [CrossRef]
- García-Alba, J.; Bárcena, J.F.; Pedraz, L.; Fernández, F.; García, A.; Mecías, M.; Costas-Veigas, J.; Samano, M.L.; Szpilman, D. SOSeas Web App: An assessment web-based decision support tool to predict. J. Oper. Oceanogr. 2021, 16, 155–174. [Google Scholar] [CrossRef]
- MacCready, P.; Geyer, W.R.; Burchard, H. Estuarine Exchange Flow Is Related to Mixing through the Salinity Variance Budget. J. Phys. Oceanogr. 2018, 48, 1375–1384. [Google Scholar] [CrossRef]
- Otero, L.J.; Hernandez, H.I.; Higgins, A.E.; Restrepo, J.C.; Álvarez, O.A. Interannual and seasonal variability of stratification and mixing in a high-discharge micro-tidal delta: Magdalena River. J. Mar. Syst. 2021, 224, 103621. [Google Scholar] [CrossRef]
- Pereira, H.; Sousa, M.C.; Vieira, L.R.; Morgado, F.; Dias, J.M. Modelling Salt Intrusion and Estuarine Plumes under Climate Change Scenarios in Two Transitional Ecosystems from the NW Atlantic Coast. J. Mar. Sci. Eng. 2022, 10, 262. [Google Scholar] [CrossRef]
- Menten, G.; Melo, W.; Pinho, J.; Iglesias, I.; Carmo, J.A.D. Simulation of Saltwater Intrusion in the Minho River Estuary under Sea Level Rise Scenarios. Water 2023, 15, 2313. [Google Scholar] [CrossRef]
- Robins, P.E.; Skov, M.W.; Lewis, M.J.; Giménez, L.; Davies, A.G.; Malham, S.K.; Neill, S.P.; McDonald, J.E.; Whitton, T.A.; Jackson, S.E.; et al. Impact of climate change on UK estuaries: A review of past trends and potential projections. Estuar. Coast. Shelf Sci. 2016, 169, 119–135. [Google Scholar] [CrossRef]
- Ma, M.; Zhang, W.; Chen, W.; Deng, J.; Schrum, C. Impacts of morphological change and sea-level rise on stratification in the Pearl River Estuary. Front. Mar. Sci. 2023, 10, 1072080. [Google Scholar] [CrossRef]

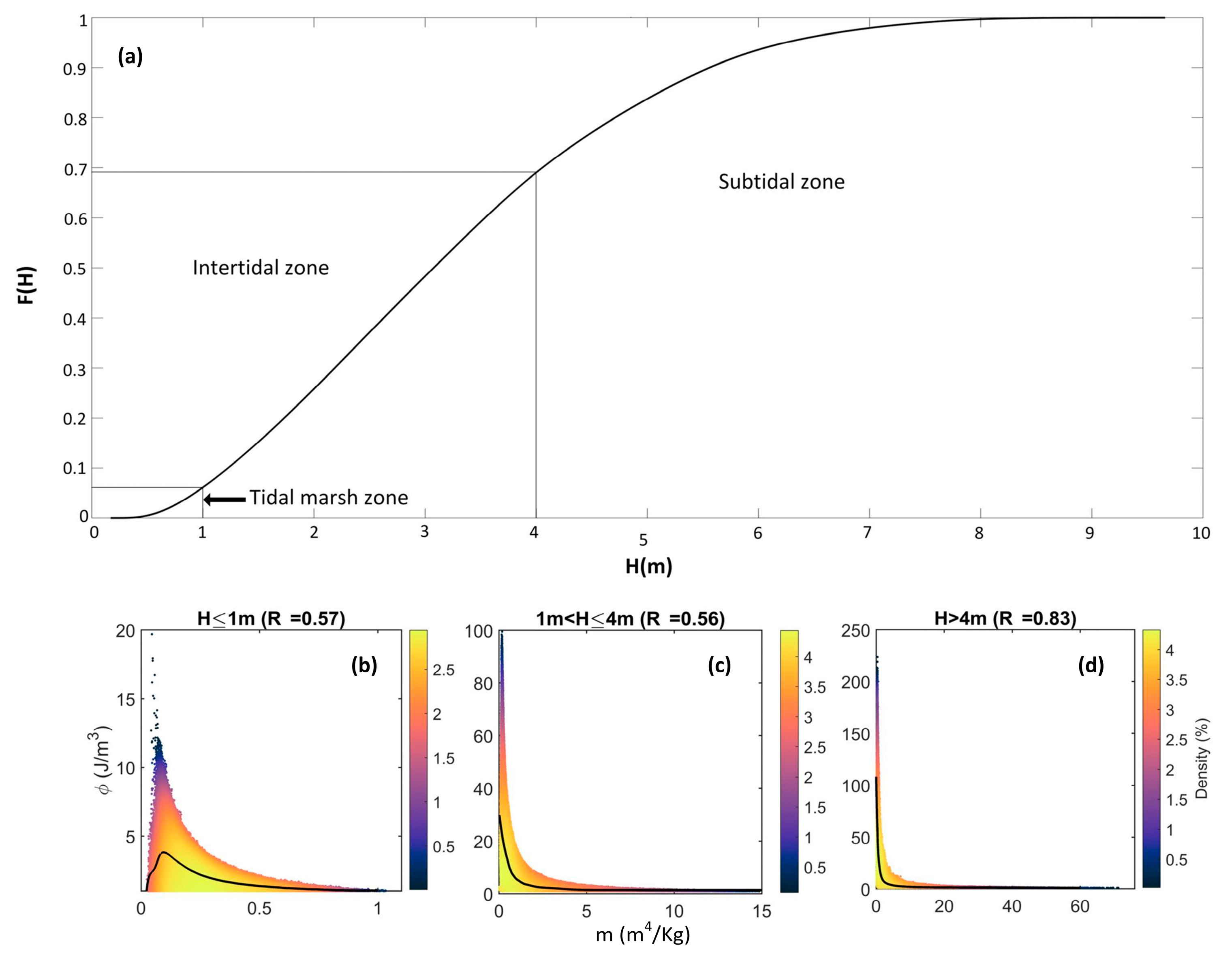


| Adjustment Method | R (H ≤ 1 m) | R (1 m < H ≤ 4 m) | R (H > 4 m) |
|---|---|---|---|
| Polynomial | 0.31 | 0.23 | 0.29 |
| Exponential | 0.31 | 0.29 | 0.69 |
| Linear | 0.27 | 0.15 | 0.19 |
| Logarithmic | 0.30 | 0.26 | 0.55 |
| Power | 0.28 | 0.25 | 0.68 |
| ANN | 0.57 | 0.56 | 0.83 |
| Vertical Mixing Classes | ϕ (H ≤ 1 m) | ϕ (1 m < H ≤ 4 m) | ϕ (H > 4 m) |
|---|---|---|---|
| Fully Mixed | ϕ = 0 | ϕ = 0 | ϕ = 0 |
| Well Mixed | 0 < ϕ ≤ 1.0 | 0 < ϕ ≤ 2.7 | 0 < ϕ ≤ 8.3 |
| Weakly Stratified | 1.0 < ϕ ≤ 1.2 | 2.7 < ϕ ≤ 9.8 | 8.3 < ϕ ≤ 34.1 |
| Stratified | 1.2 < ϕ ≤ 2.1 | 9.8 < ϕ≤ 19.4 | 34.1 < ϕ ≤ 70.1 |
| Strongly Stratified | 2.1 < ϕ | 19.4 < ϕ ≤ 29.9 | 70.1 < ϕ ≤ 104.7 |
| Salt Wedge | - | 29.9 < ϕ | 104.7 < ϕ |
| Estuary | Reference | Slope | Literature Classification | Proposed Classification |
|---|---|---|---|---|
| Altamaha | [51] | 3.6 | Mixed | Well Mixed |
| 0.63 | Weakly Stratified | Weakly Stratified | ||
| 0.05 | Strongly Stratified | Strongly Stratified | ||
| 0.15 | Highly Stratified | Strongly Stratified | ||
| Babitonga bay | [57] | 0.95 | Weakly Stratified | Weakly Stratified |
| 0.92 | Weakly Stratified | Weakly Stratified | ||
| 0.33 | Stratified | Stratified | ||
| 0.34 | Stratified | Stratified | ||
| Cape Fear | [17] | 0.39 | Partially Mixed | Stratified |
| 0.48 | Partially Mixed | Stratified | ||
| 0.56 | Partially Mixed | Stratified | ||
| 0.47 | Partially Mixed | Stratified | ||
| Columbia | [52] | 3 | Weakly Stratified | Well Mixed |
| 3 | Weakly Stratified | Well Mixed | ||
| 4.25 | Weakly Stratified | Fully Mixed | ||
| 0.35 | Substantial Stratification | Stratified | ||
| 0.66 | Substantial Stratification | Weakly Stratified | ||
| 0.53 | Substantial Stratification | Stratified | ||
| Delaware | [53] | 8.5 | Mixed | Fully Mixed |
| 2.48 | Weakly Stratified | Well Mixed | ||
| 28 | Mixed | Fully Mixed | ||
| 4 | Weakly Stratified | Weakly Stratified | ||
| 0.22 | Weakly Stratified | Strongly Stratified | ||
| Hudson | [54] | 0.24 | Stratified | Strongly Stratified |
| [14] | 0.22 | Strongly Stratified | Strongly Stratified | |
| 1.02 | Weakly Stratified | Weakly Stratified | ||
| Humber | [18] | 2.1 | Well Mixed | Well Mixed |
| 9.75 | Well Mixed | Fully Mixed | ||
| Mandovi | [12] | 21 | Well Mixed | Fully Mixed |
| 13.83 | Well Mixed | Fully Mixed | ||
| 0.09 | Salt Wedge | Strongly Stratified | ||
| 0.19 | Salt Wedge | Strongly Stratified | ||
| 1.82 | Partially Mixed | Weakly Stratified | ||
| 6.66 | Well Mixed | Fully Mixed | ||
| Merrimack | [7] | 0.15 | Strongly Stratified | Strongly Stratified |
| 0.19 | Strongly Stratified | Strongly Stratified | ||
| 0.18 | Strongly Stratified | Strongly Stratified | ||
| 0.24 | Stratified | Strongly Stratified | ||
| 0.63 | Stratified | Stratified | ||
| 0.35 | Stratified | Stratified | ||
| [2] | 0.18 | Highly Stratified | Strongly Stratified | |
| Oujiang | [58] | 7.6 | Well Mixed | Fully Mixed |
| 7.95 | Well Mixed | Fully Mixed | ||
| 6.6 | Well Mixed | Fully Mixed | ||
| 1.88 | Well Mixed | Weakly Stratified | ||
| 0.34 | Partial Mixed | Stratified | ||
| 0.45 | Partial Mixed | Stratified | ||
| Ria Ferrol | [15] | 6.6 | Well Mixed | Fully Mixed |
| Severn | [55] | 18.6 | Well Mixed | Fully Mixed |
| Strymon | [59] | 0.02 | Salt Wedge | Salt Wedge |
| 0.027 | Salt Wedge | Strongly Stratified | ||
| 0.015 | Salt Wedge | Salt Wedge | ||
| 0.016 | Salt Wedge | Salt Wedge | ||
| Tamar | [60] | 0.1 | Stratified | Strongly Stratified |
| Tomales Bay | [56] | 0.29 | Stratified | Stratified |
| Vertical Mixing Classes | RCP 4.5 | RCP 8.5 | ||||
|---|---|---|---|---|---|---|
| a | b | R | a | b | R | |
| Fully mixed | −0.05 | 104.81 | 0.85 | −0.0509 | 106.4 | 0.81 |
| Well mixed | 0.0601 | −66.834 | 0.92 | 0.1443 | −237.42 | 1.00 |
| Weakly stratified | −0.0227 | 83.277 | 0.89 | −0.0939 | 227.6 | 0.96 |
| Stratified | 0.013 | −22.055 | 0.91 | 0.0009 | 2.6145 | 0.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lupiola, J.; Bárcena, J.F.; García-Alba, J.; García, A. A Dynamic Estuarine Classification of the Vertical Structure Based on the Water Column Density Slope and the Potential Energy Anomaly. Water 2023, 15, 3294. https://doi.org/10.3390/w15183294
Lupiola J, Bárcena JF, García-Alba J, García A. A Dynamic Estuarine Classification of the Vertical Structure Based on the Water Column Density Slope and the Potential Energy Anomaly. Water. 2023; 15(18):3294. https://doi.org/10.3390/w15183294
Chicago/Turabian StyleLupiola, Jagoba, Javier F. Bárcena, Javier García-Alba, and Andrés García. 2023. "A Dynamic Estuarine Classification of the Vertical Structure Based on the Water Column Density Slope and the Potential Energy Anomaly" Water 15, no. 18: 3294. https://doi.org/10.3390/w15183294





